Preparation and Quasi-Isentropic Loading Characteristics of Ti-Pt Periodically Modulated Gradient Material
-
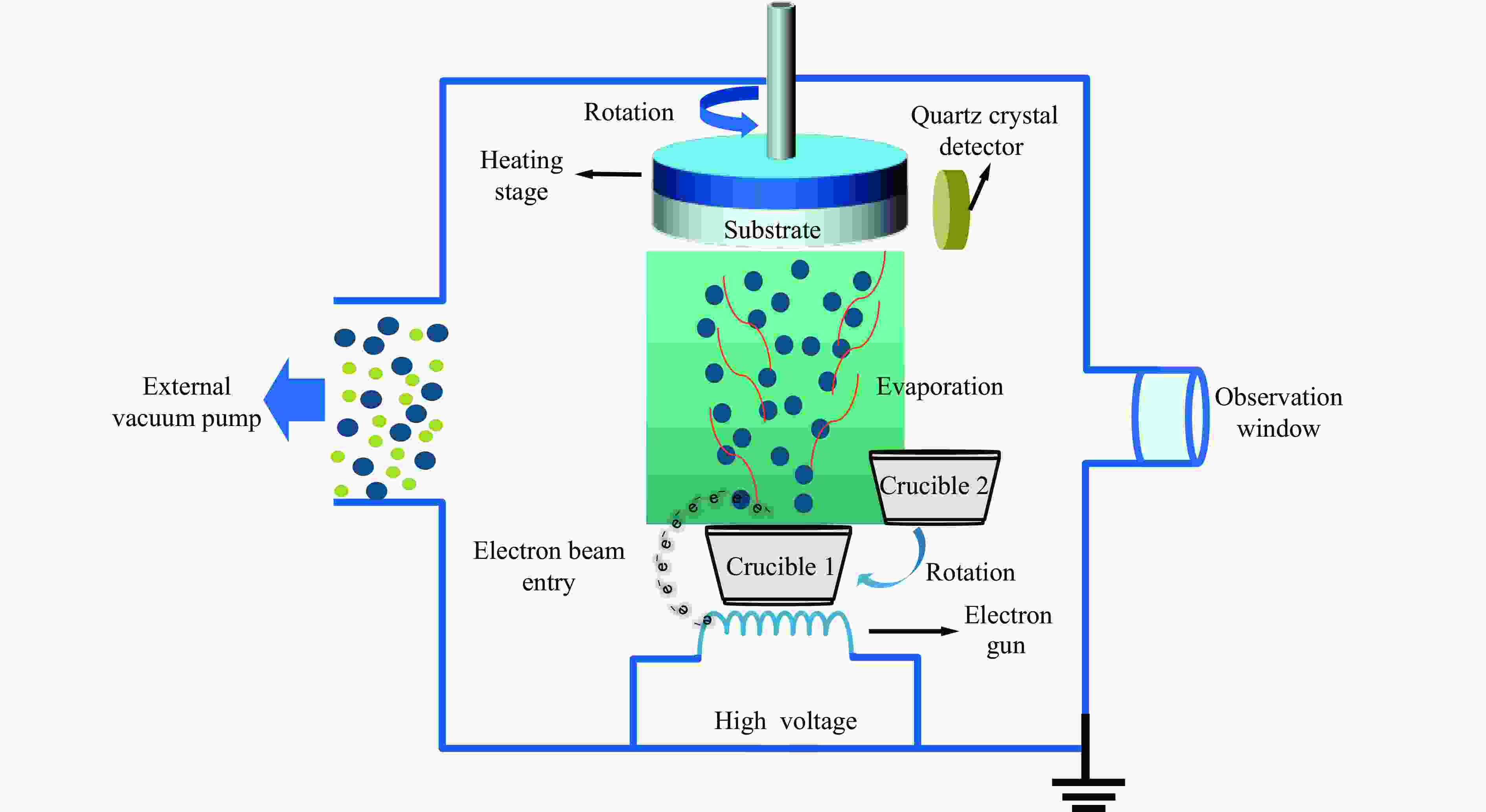
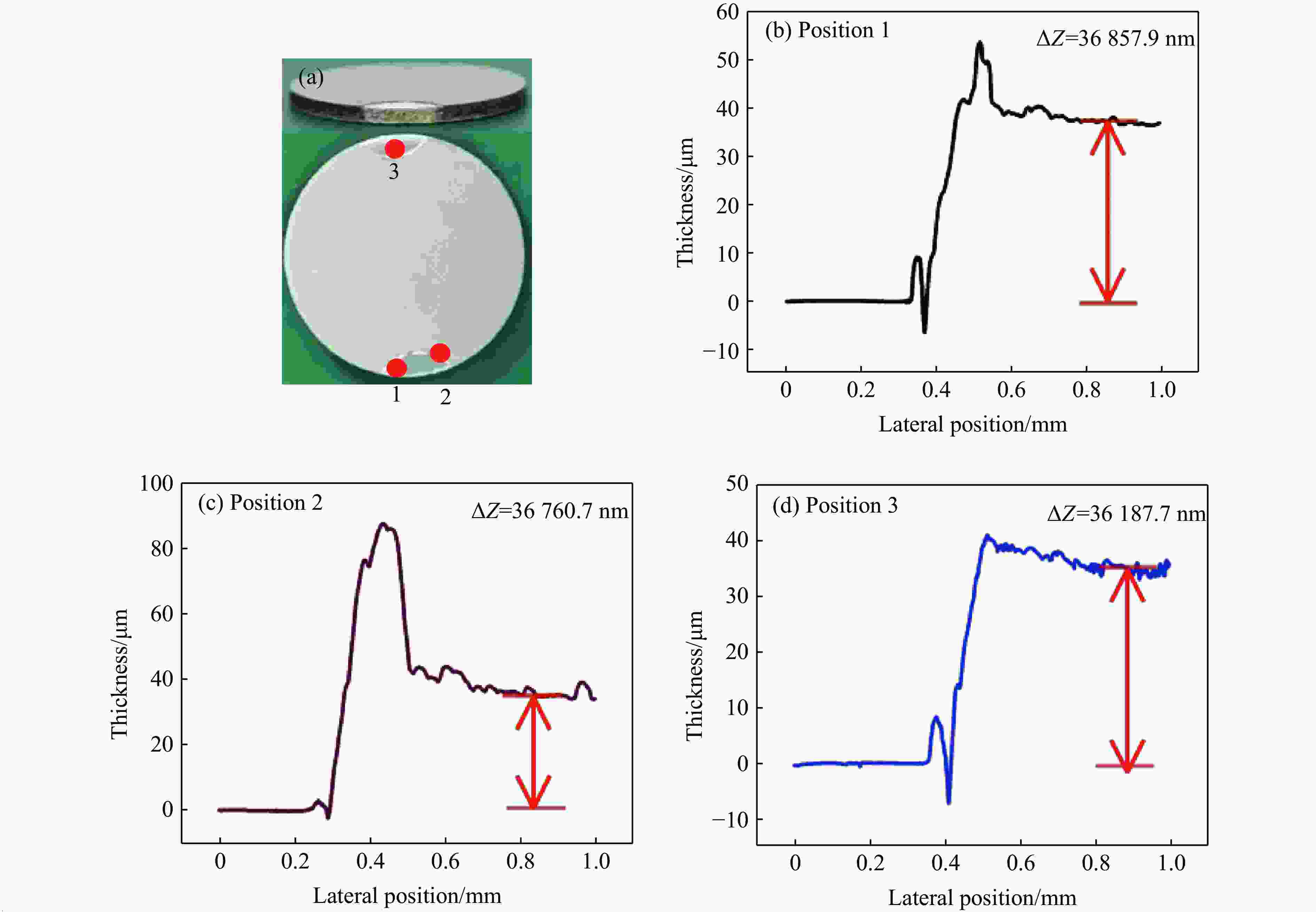
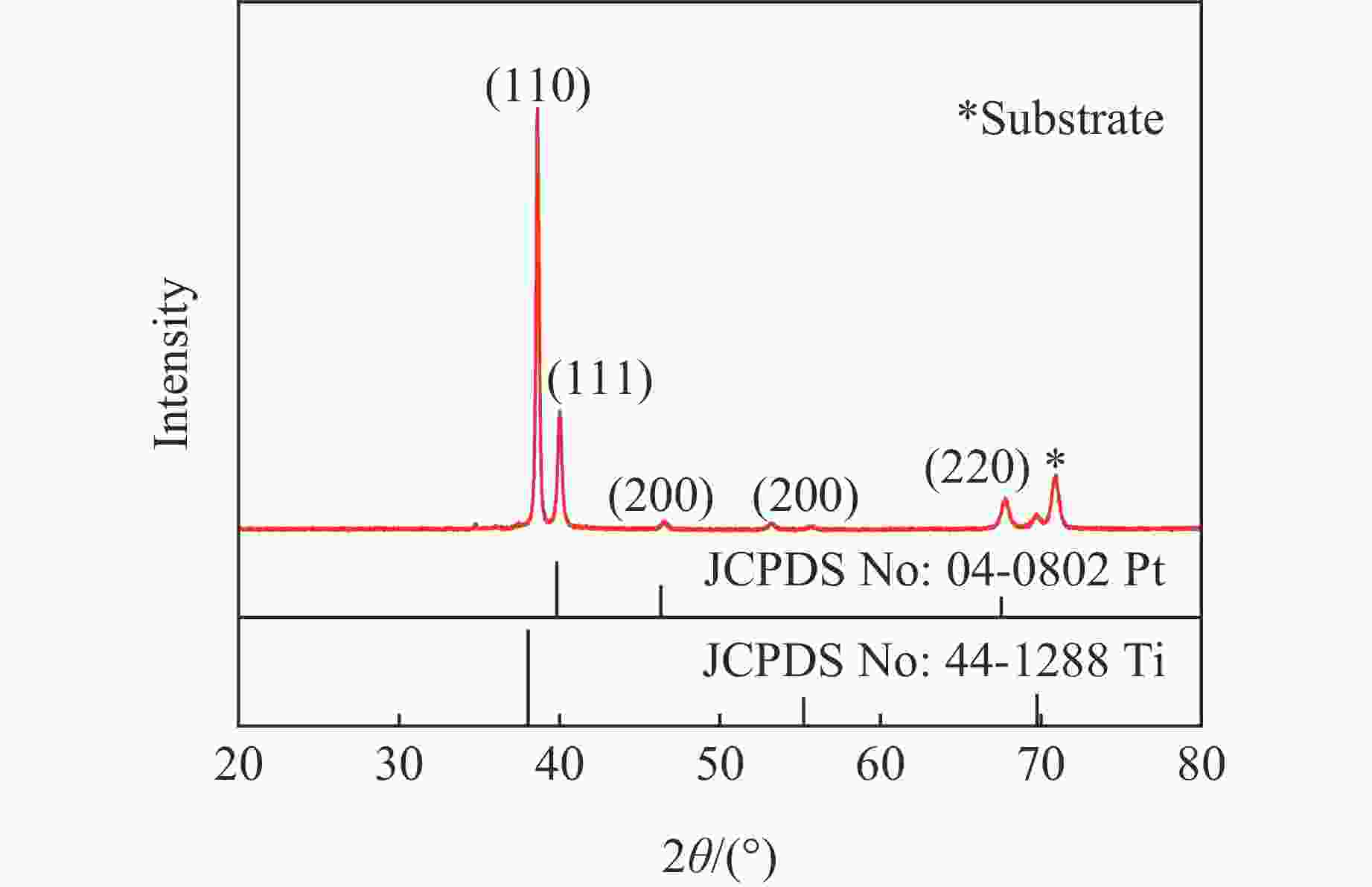
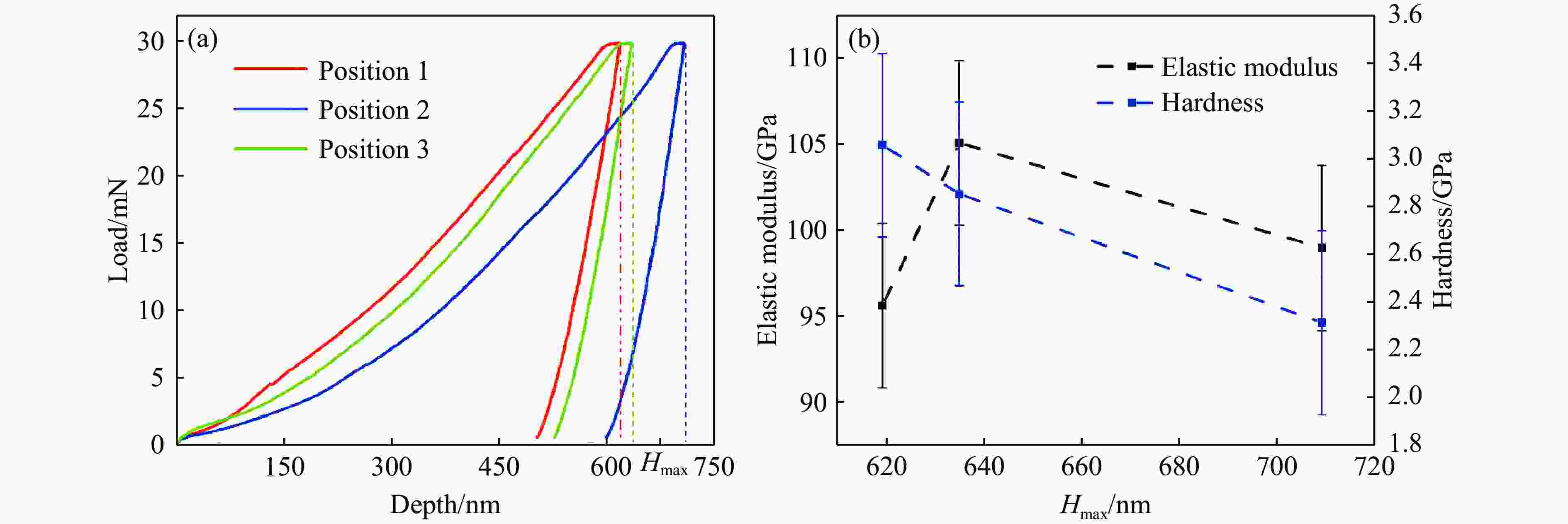
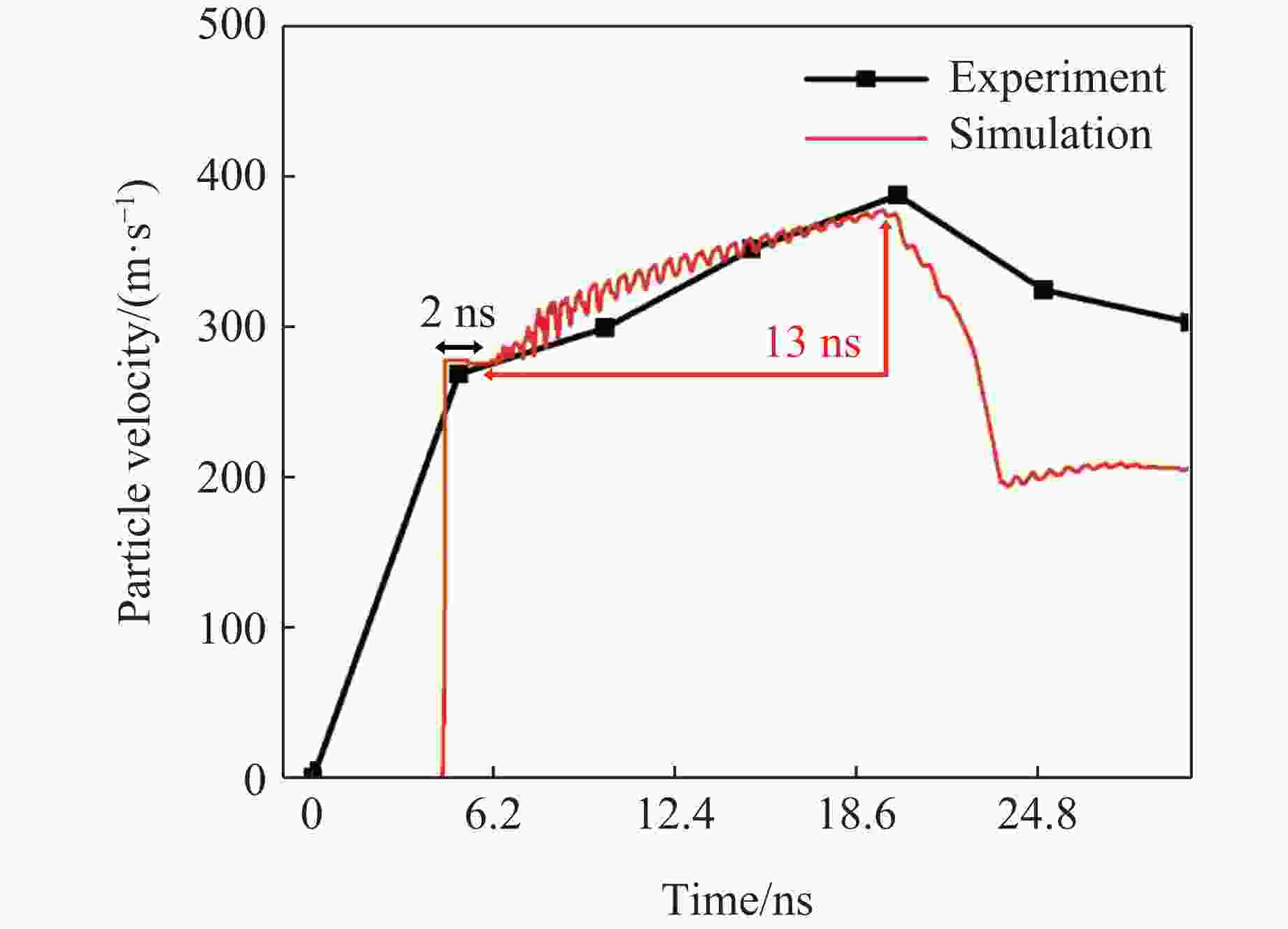
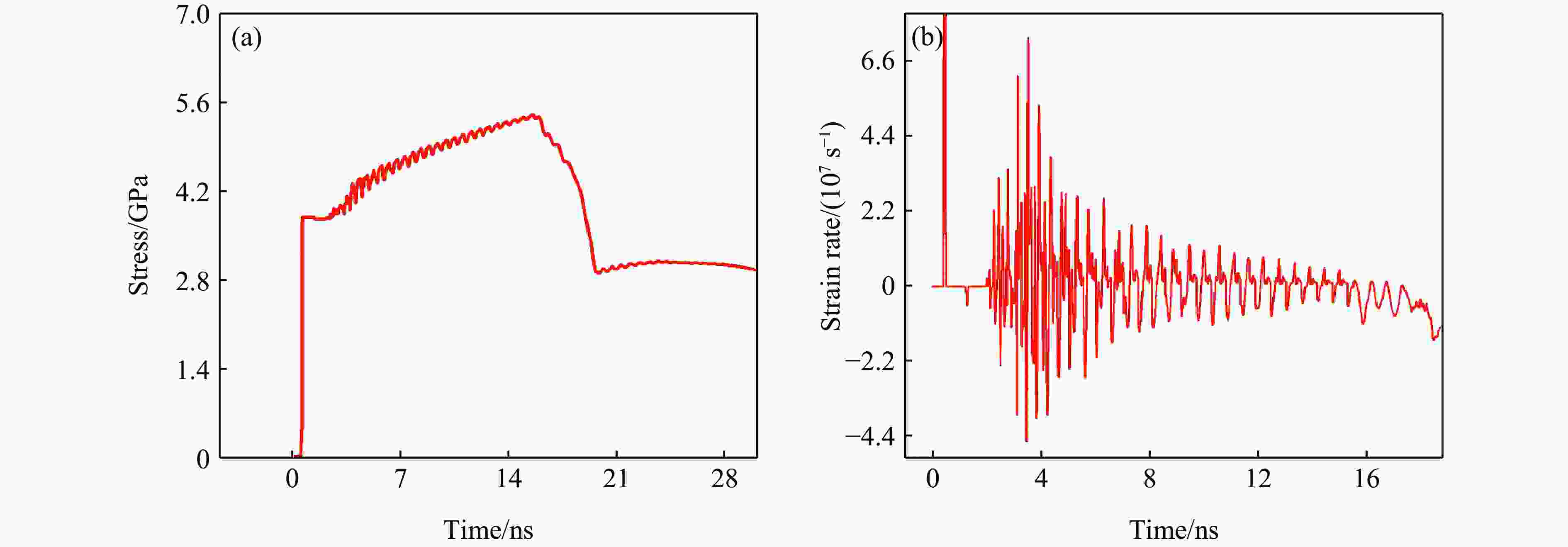
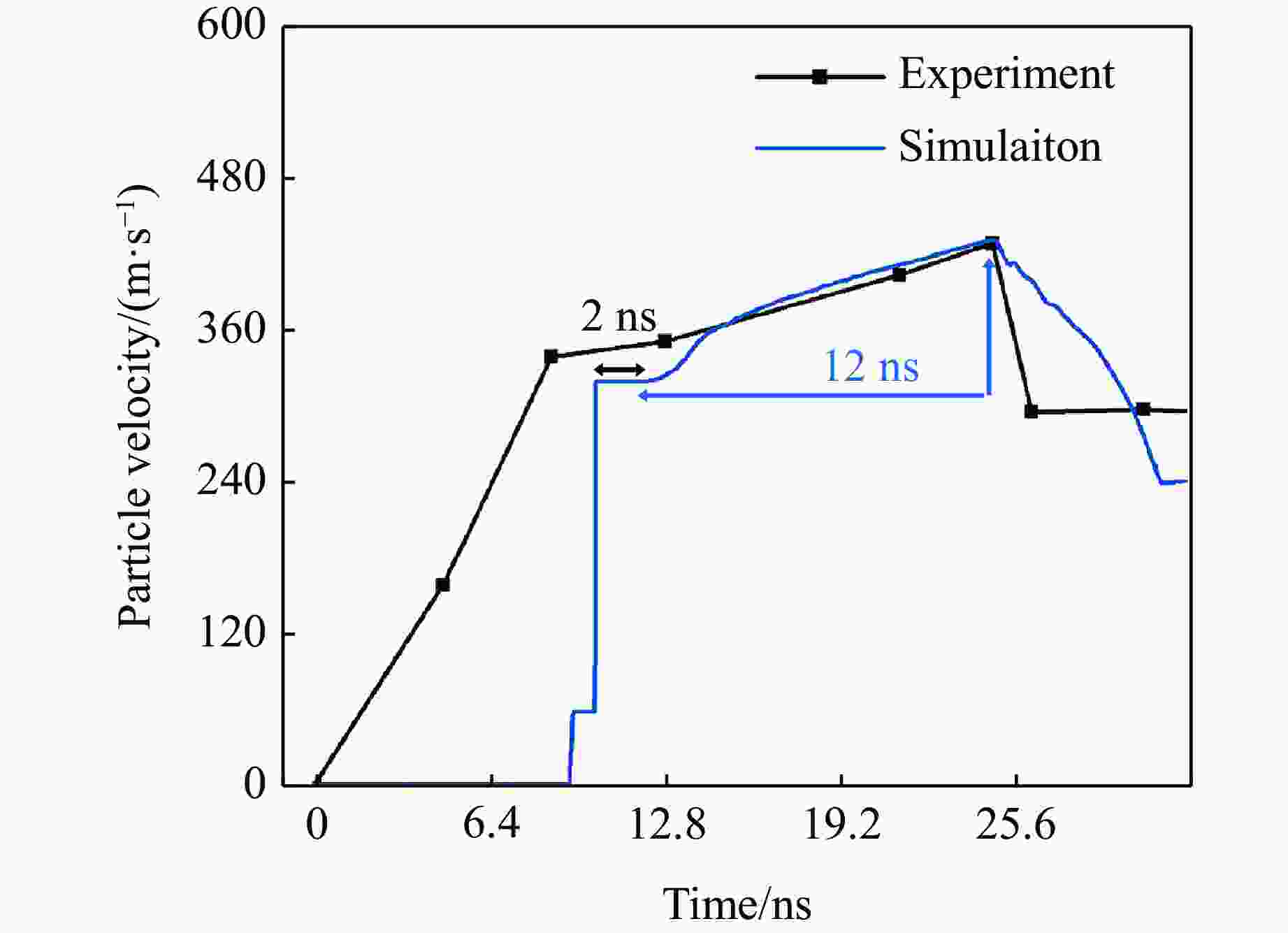
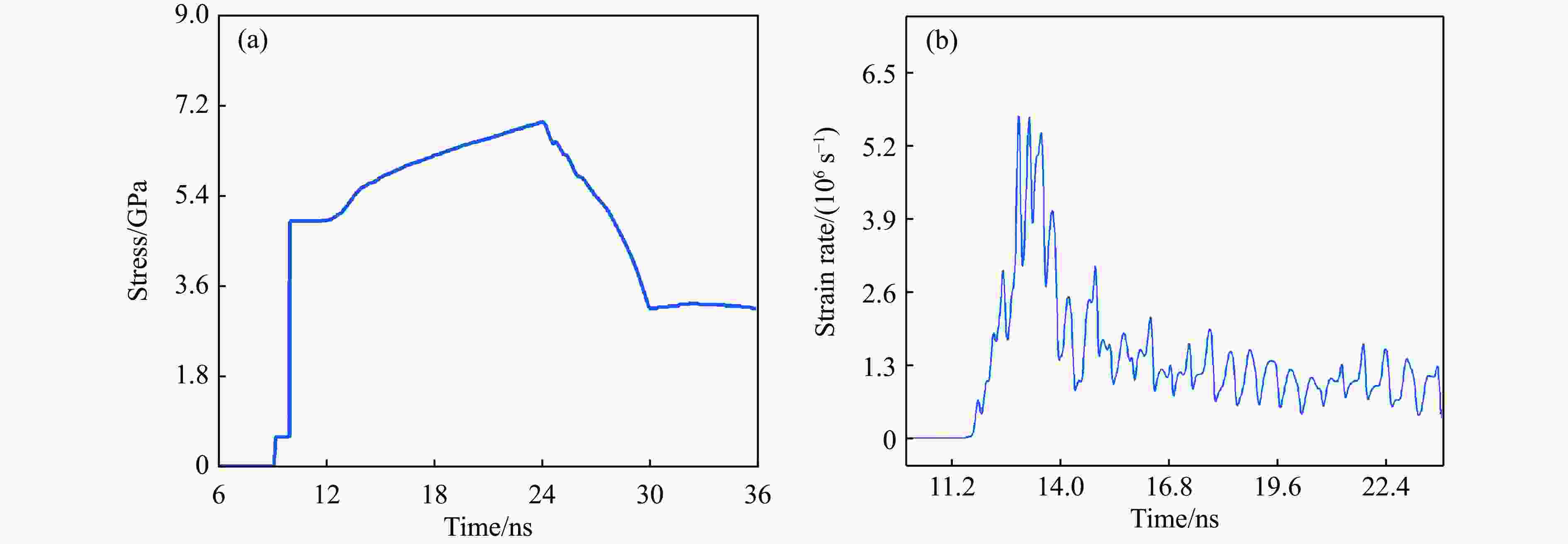
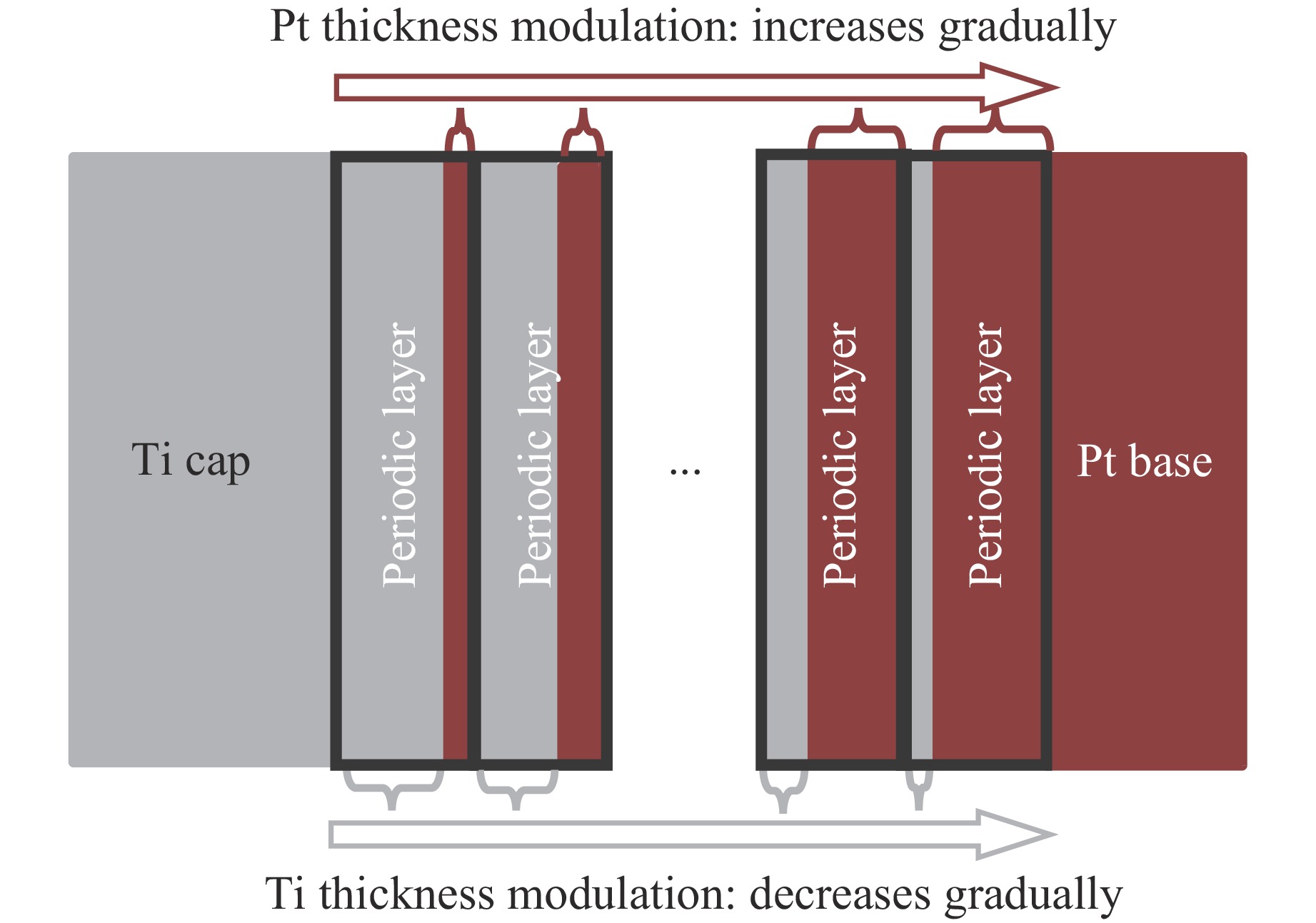
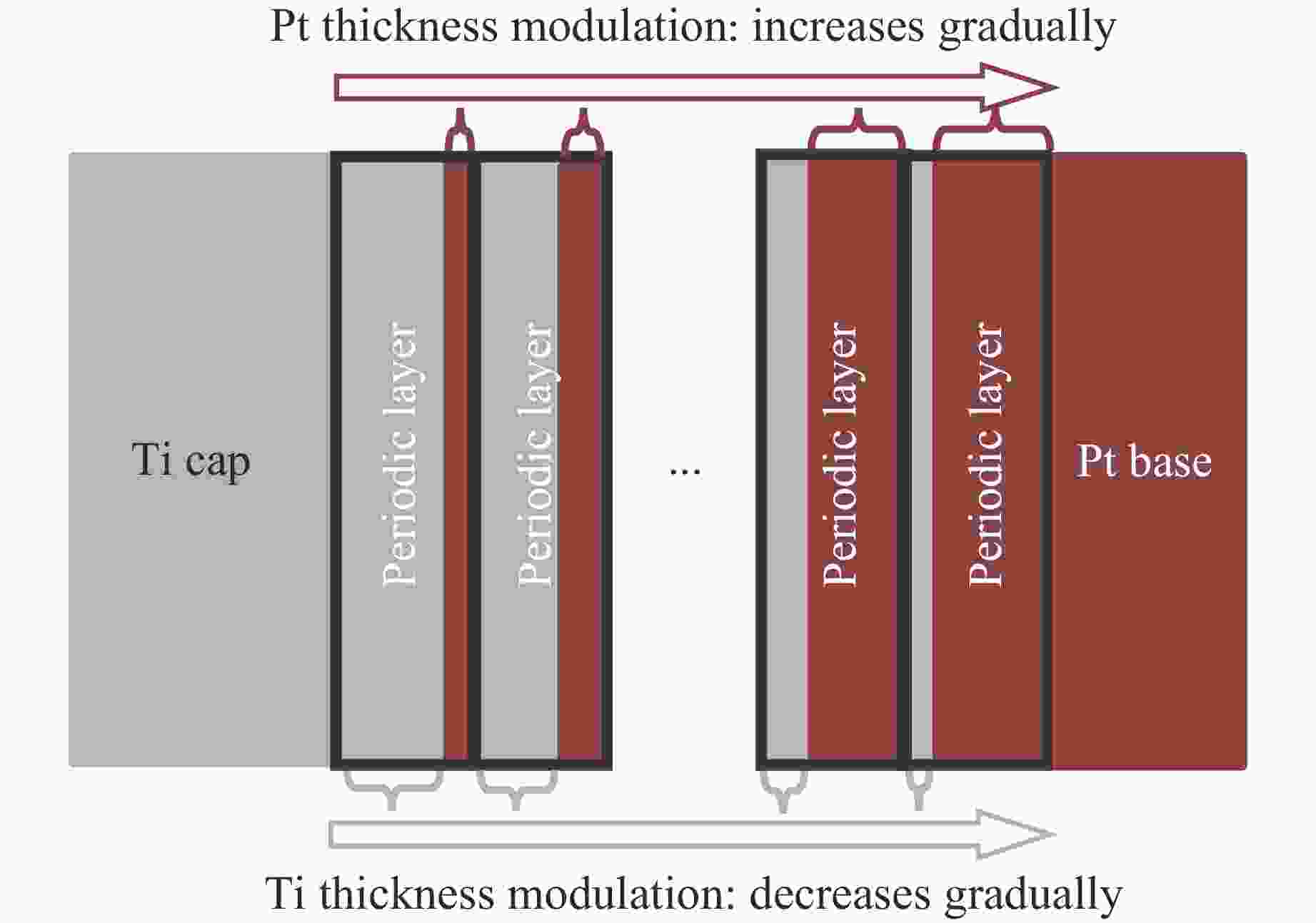
摘要: 基于波阻抗梯度材料的准等熵加载技术是掌握材料动态响应特性的重要技术手段，对于提升材料服役性能至关重要。采用电子束蒸发镀膜技术成功制备出Ti-Pt周期调制梯度材料，通过对周期层内双组分（Ti和Pt单层）厚度的调控，实现了波阻抗的宏观梯度变化。梯度材料实测总厚度与理论设计总厚度的误差仅为1.67%，并且实测平均硬度及弹性模量分别为2.8和99.8 GPa。材料内部层界面清晰，物相分析未发现金属合金相。利用一级轻气炮驱动Ti-Pt周期调制梯度材料加载5 μm厚Al靶，在Al靶内产生冲击-准等熵加载波形。数值模拟结果与实验曲线在上升趋势上吻合良好，5 μm厚Al靶处的粒子速度、应力和应变率曲线的准等熵段存在较大起伏，应变率曲线在正负值间持续振荡，并且振幅较大。应力云图显示周期调制梯度材料在加载过程中会形成多个波系的追赶、叠加、整合。数值模拟结果显示，当靶材厚度为60 μm时，波系完成整合，转变为连续的压缩波。结合数值模拟结果开展了60 μm厚Al靶的轻气炮加载实验，粒子速度曲线和应力曲线的准等熵段转变为平滑的加载波形，应变率曲线准等熵段振幅显著减小，实现了良好的准等熵加载效果。研究结果表明，周期调制梯度材料与靶材厚度需进行匹配设计，研究结果可为新型周期调制梯度结构的应用提供指导。
-
关键词:
- Ti-Pt周期调制梯度材料 /
- 电子束蒸发镀膜 /
- 准等熵加载 /
- 波系分析
Abstract: The quasi-isentropic loading technique based on wave impedance gradient materials is a crucial method for understanding the dynamic response characteristics of materials, which is essential for enhancing material service performance. In this study, Ti-Pt periodically modulated gradient materials were successfully prepared using electron beam evaporation deposition technology. By adjusting the thickness of the two components (Ti and Pt single layers) within the periodic layers, a macroscopic gradient in wave impedance was achieved. The total thickness error between the measured gradient material and the theoretical design was only 1.67%, with an average hardness and elastic modulus of 2.8 and 99.8 GPa, respectively. The interfaces between the internal layers of the material were clear, and no metal alloy phases were detected in the phase analysis. The Ti-Pt periodically modulated gradient material was loaded onto a 5 μm-thickness Al target by a one-stage light gas gun, generating a shock-quasi-isentropic loading waveform within the Al target. Numerical simulation results showed good agreement in the rising trend with the experimental curve. For the 5 μm-thickness Al target, the particle velocity, stress, and strain rate curves exhibit significant fluctuations in the quasi-isentropic stage, with the strain rate curve oscillating continuously between positive and negative values with large amplitudes. Stress contour maps indicate that the loading process of the periodically modulated gradient material involved the chasing, superposition, and integration of multiple wave systems. Simulation shows that when the target thickness is 60 μm, the wave systems complete integration and change into continuous compression wave loading. Based on the simulation result, light gas gun loading experiment for the Al target with a thickness of 60 μm were conducted. The particle velocity and stress curves in the quasi-isentropic stage change into smooth loading waveforms, and the strain rate curve remains overall positive, achieving a good quasi-isentropic loading. This indicates that the periodically modulated gradient material and target thickness need to be designed to match each other. The results of this study provide a guidance for the application of novel periodically modulated gradient structures. -
图 1 Ti-Pt周期调制梯度材料结构示意图
Figure 1. Schematic diagram of Ti-Pt periodically modulated gradient material
图 2 Ti-Pt周期调制梯度材料的(a)波阻抗随位置的分布曲线和(b)周期层内Ti和Pt的质量分数随位置的变化曲线
Figure 2. (a) Wave impedance and (b) the mass fraction of Ti and Pt with position for Ti-Pt periodically modulated gradient material
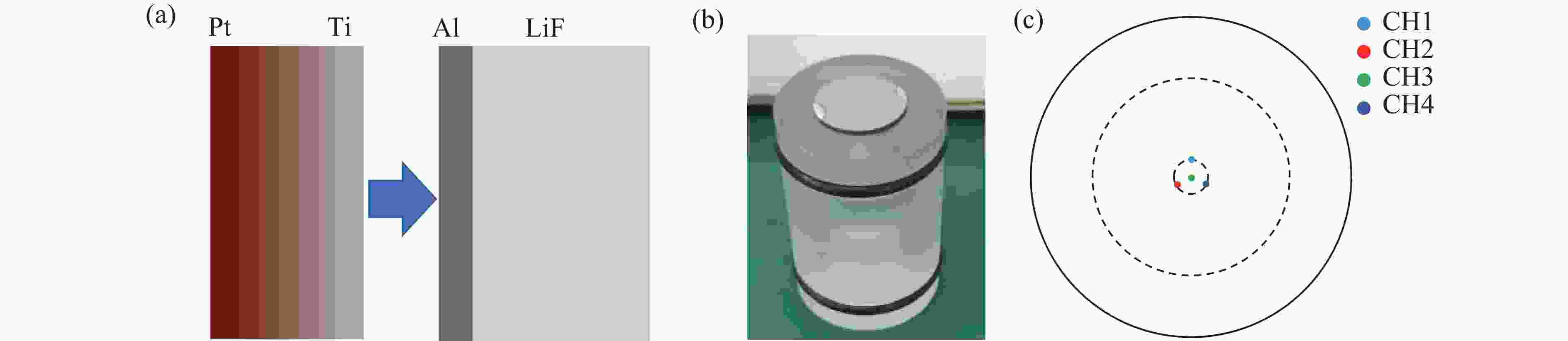
图 4 Ti-Pt周期调制梯度材料的准等熵加载实验设计：(a) Ti-Pt周期调制梯度材料撞击Al靶示意图，(b) 粘结Ti-Pt周期调制梯度材料的弹托，(c) LiF窗口背面分布的光纤测速点
Figure 4. Experimental design of Ti-Pt periodically modulated gradient material: (a) schematic diagram of Ti-Pt periodically modulated gradient material impacting Al target; (b) a projectile bonded with Ti-Pt periodically modulated gradient material; (c) the distribution of velocity measurement fiber on the back of LiF window
图 5 Ti-Pt周期调制梯度材料的厚度测试结果：(a) 样品厚度测试点，(b)～(d) 不同位置处测得的样品厚度
Figure 5. Thickness test results of Ti-Pt periodically modulated gradient material sample: (a) thickness test points of sample at different locations; (b)–(d) thickness of the sample measured at different locations
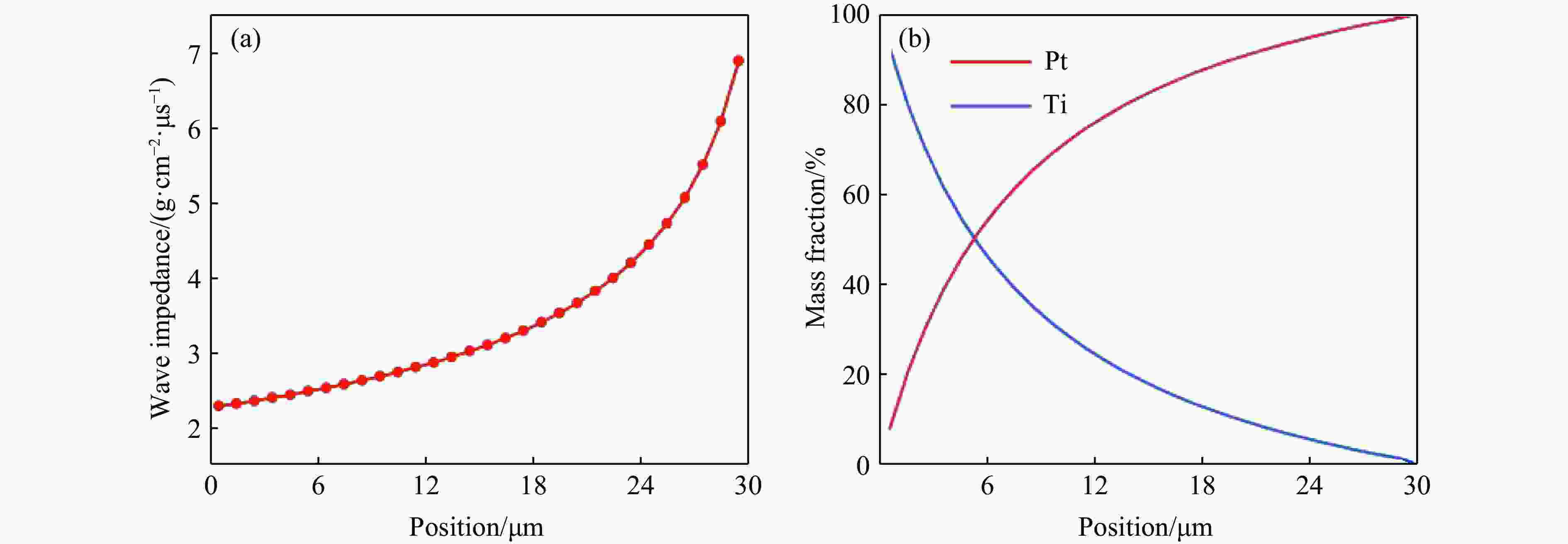
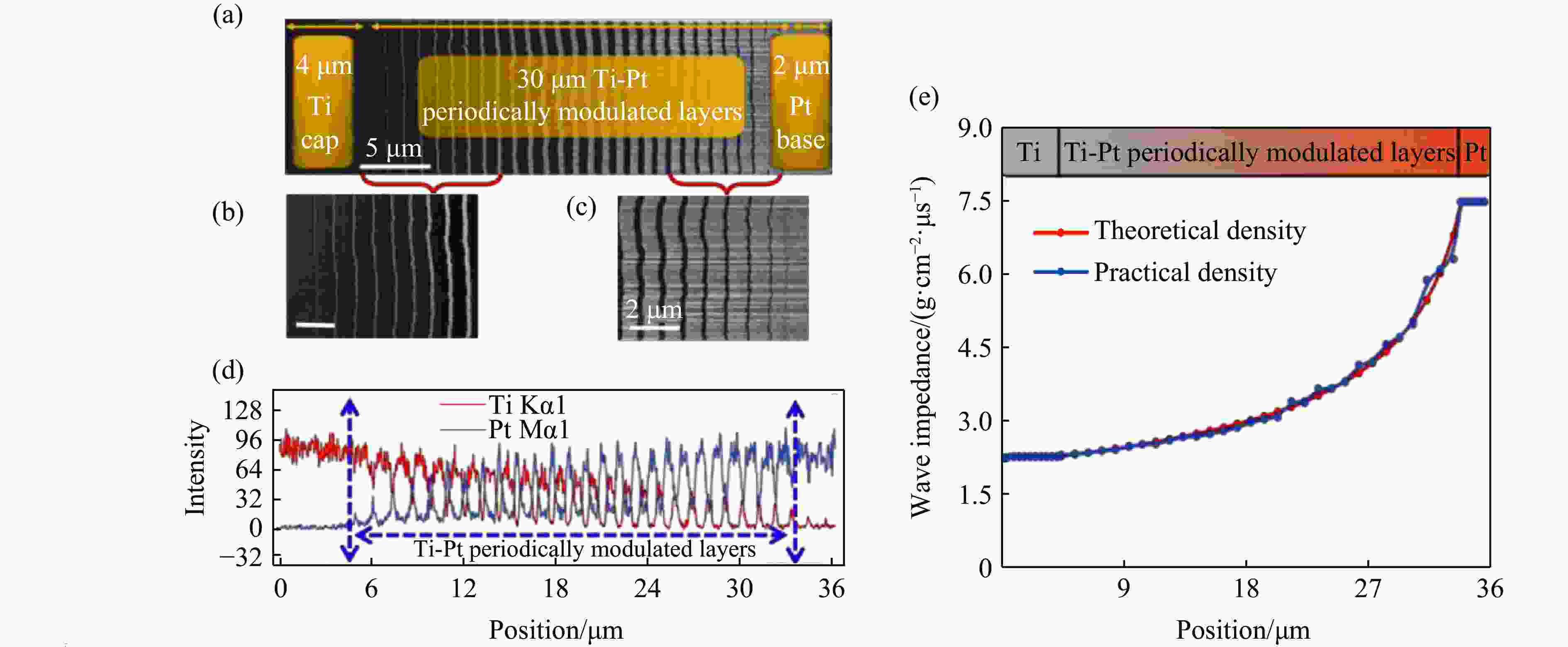
图 6 Ti-Pt周期调制梯度材料的截面形貌(a)，富Ti区的形貌(b)，富Pt区的截面形貌(c)， 能谱分析图(d)，理论与实际波阻抗随位置的分布曲线(e)
Figure 6. Overall view (a); Ti-rich region view (b); Pt-rich region view (c); energy spectrum analysis diagram (d); theoretical and practical wave impedance distribution curve with position (e) for the Ti-Pt periodically modulated gradient material
图 7 Ti-Pt周期调制梯度材料的XRD谱
Figure 7. XRD patterns of Ti-Pt periodically modulated gradient material
图 8 Ti-Pt周期调制梯度材料3个不同位置处的纳米压痕测试结果：(a) 加-卸载曲线，(b) 硬度及弹性模量
Figure 8. Nanoindentation test results of Ti-Pt periodically modulated gradient material at three different positions: (a) load-unload curve; (b) hardness and elastic modulus
图 9 Ti-Pt周期调制梯度材料撞击5 μm厚Al靶过程中实验和数值模拟获得的粒子速度-时间曲线
Figure 9. Experimental and simulated particle velocity-time curves of Ti-Pt periodically modulated gradient material impacting 5 μm-thickness Al target
图 10 Ti-Pt周期调制梯度材料撞击5 μm厚Al靶的数值模拟结果：(a)应力-时间曲线和(b)应变率-时间曲线
Figure 10. Simulation curves of Ti-Pt periodically modulated gradient material impacting 5 μm Al target: (a) stress-time curve; (b) strain rate-time curve
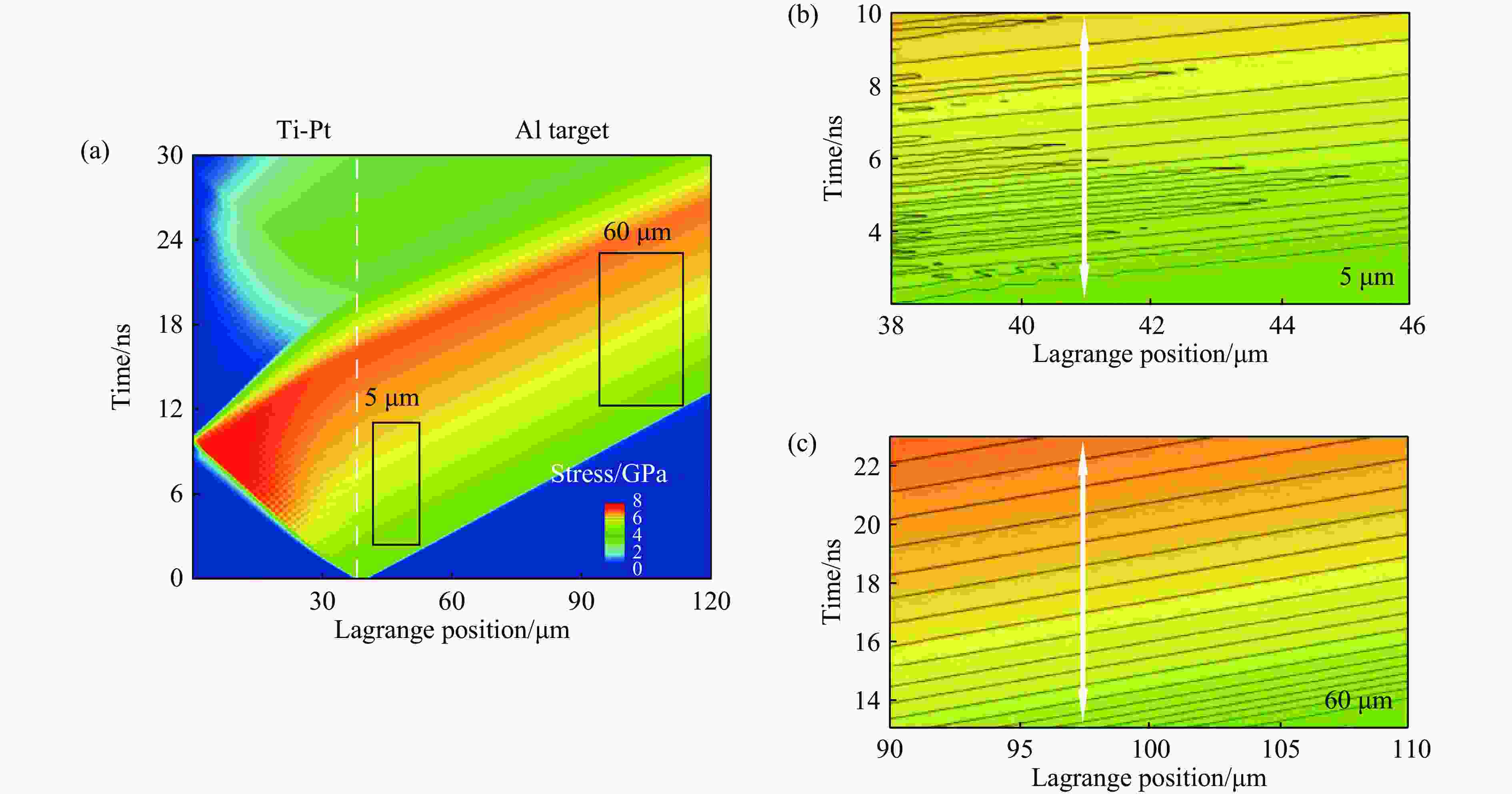
图 11 Ti-Pt周期调制梯度材料撞击Al靶时的应力云图：(a) 0～120 μm区间内的应力云图，(b) 38～47 μm区间内的应力细节云图，(c) 90～110 μm区间内的应力云图
Figure 11. Stress contour map during Ti-Pt periodically modulated gradient material impacting Al target: (a) stress contour map from 0 to 120 μm; (b) detailed stress contour map from 38 μm to 47 μm; (c) detailed stress contour map from 90 μm to 110 μm
图 12 Ti-Pt周期调制梯度材料在撞击60 μm厚Al靶过程中实验与数值模拟获得的粒子速度-时间曲线
Figure 12. Experimental and simulated particle velocity-time curves of Ti-Pt periodically modulated gradient material impacting 60 μm-thickness Al target
图 13 Ti-Pt 周期调制梯度材料撞击60 μm厚Al靶过程中数值模拟获得的曲线：(a)应力-时间曲线，(b)应变率-时间关系曲线
Figure 13. Simulation curves of Ti-Pt periodically modulated gradient material impacting 60 μm Al target: (a) stress-time curve; (b) strain rate-time curve
-
[1] HUANG H J, FEI Y W, CAI L C, et al. Evidence for an oxygen-depleted liquid outer core of the Earth [J]. Nature, 2011, 479(7374): 513–516. doi: 10.1038/nature10621 [2] NAKAJIMA Y, IMADA S, HIROSE K, et al. Carbon-depleted outer core revealed by sound velocity measurements of liquid iron-carbon alloy [J]. Nature Communications, 2015, 6(1): 8942. doi: 10.1038/ncomms9942 [3] SMITH R F, EGGERT J H, SWIFT D C, et al. Time-dependence of the alpha to epsilon phase transformation in iron [J]. Journal of Applied Physics, 2013, 114(22): 223507. doi: 10.1063/1.4839655 [4] VOGLER T J. On measuring the strength of metals at ultrahigh strain rates [J]. Journal of Applied Physics, 2009, 106(5): 053530. doi: 10.1063/1.3204777 [5] MILLOT M, COPPARI F, RYGG J R, et al. Nanosecond X-ray diffraction of shock-compressed superionic water ice [J]. Nature, 2019, 569(7755): 251–255. doi: 10.1038/s41586-019-1114-6 [6] SINGH A, SHIVLING V D, KHOSLA P K, et al. Strain hardening and shock mitigation response of polyurethane under high strain rates [J]. AIP Advances, 2021, 11(11): 115306. doi: 10.1063/5.0068403 [7] 谭华, 俞宇颖. 超高应变率准等熵加载和冲击加载下金属材料的强度 [J]. 高能量密度物理, 2010(3/4): 97–120. [8] NGUYEN J H, ORLIKOWSKI D, STREITZ F H, et al. High-pressure tailored compression: controlled thermodynamic paths [J]. Journal of Applied Physics, 2006, 100(2): 023508. doi: 10.1063/1.2214209 [9] BROWN N P, SPECHT P E, BROWN J L. Quasi-isentropic compression of an additively manufactured aluminum alloy to 14.8 GPa [J]. Journal of Applied Physics, 2022, 132(22): 225106. doi: 10.1063/5.0127989 [10] SHU H, LI J T, TU Y C, et al. Measurement of the sound velocity of shock compressed water [J]. Scientific Reports, 2021, 11(1): 6116. doi: 10.1038/s41598-021-84978-0 [11] MARTIN L P, PATTERSON J R, ORLIKOWSKI D, et al. Application of tape-cast graded impedance impactors for light-gas gun experiments [J]. Journal of Applied Physics, 2007, 102(2): 023507. doi: 10.1063/1.2756058 [12] TAN Y, LI X M, YU Y Y, et al. Research on phase transition and strength under ramp compression with graded density impactor [J]. EPJ Web of Conferences, 2018, 183: 02058. doi: 10.1051/epjconf/201818302058 [13] BASTEA M, REISMAN D B. Ramp compression experiments―a sensitivity study [J]. AIP Conference Proceedings, 2007, 955(1): 1169–1172. doi: 10.1063/1.2832927 [14] KELLY J P, NGUYEN J H, LIND J, et al. Application of Al-Cu-W-Ta graded density impactors in dynamic ramp compression experiments [J]. Journal of Applied Physics, 2019, 125(14): 145902. doi: 10.1063/1.5055398 [15] BROWN J L, ADAMS D P, ALEXANDER C S, et al. Estimates of Ta strength at ultrahigh pressures and strain rates using thin-film graded-density impactors [J]. Physical Review B, 2019, 99(21): 214105. doi: 10.1103/PhysRevB.99.214105 [16] RAY A, SINGLA A. Development of semiempirical equation of state of binary functionally graded materials and its influence on generation of ramp compression: comparison with bilayer graded density impactors [J]. Physical Review B, 2021, 103(5): 054301. doi: 10.1103/PhysRevB.103.054301 [17] 沈强, 张联盟, 王传彬, 等. 梯度飞片材料的波阻抗分布设计与优化 [J]. 物理学报, 2003, 52(7): 1663–1667. doi: 10.7498/aps.52.1663SHEN Q, ZHANG L M, WANG C B, et al. Design and optimization of wave impedance distribution for flyer materials [J]. Acta Physica Sinica, 2003, 52(7): 1663–1667. doi: 10.7498/aps.52.1663 [18] 刘石豪, 张振海, 牛兰杰, 等. 高能量冲击加载试验装置研究进展 [J]. 探测与控制学报, 2023, 45(4): 14–28.LIU S H, ZHANG Z H, NIU L J, et al. A Review on high-energy impact loading test device research [J]. Journal of Detection & Control, 2023, 45(4): 14–28. [19] ROGERS J A, BASS N T, WIEST M L, et al. The pursuit of hypervelocities: a review of two-stage light gas gun aeroballistic ranges [J]. International Journal of Impact Engineering, 2024, 185: 104861. doi: 10.1016/j.ijimpeng.2023.104861 [20] ZHOU Y H, TAN Y, ZHANG R Z, et al. Dynamics of stress waves in graded density impactors during the internal ballistic process [J]. Journal of Applied Physics, 2023, 134(22): 225901. doi: 10.1063/5.0177300 [21] DEWAELE A, STUTZMANN V, BOUCHET J, et al. High pressure-temperature phase diagram and equation of state of titanium [J]. Physical Review B, 2015, 91(13): 134108. doi: 10.1103/PhysRevB.91.134108 [22] ZHA C S, MIBE K, BASSETT W A, et al. P-V-T equation of state of platinum to 80 GPa and 1 900 K from internal resistive heating/X-ray diffraction measurements [J]. Journal of Applied Physics, 2008, 103(5): 054908. doi: 10.1063/1.2844358 [23] MARSH S P. LASL shock Hugoniot data [M]. Berkeley: University of California Press, 1980. [24] 徐锡申, 张万箱. 实用物态方程理论导引 [M]. 北京: 科学出版社, 1986. [25] MEYERS M A. Dynamic behavior of materials [M]. New York: John Wiley & Sons Inc., 1994. -
下载:
点击查看大图
计量
- 文章访问数: 53
- HTML全文浏览量: 4
- PDF下载量: 7
