Progress on Equation of State of Hydrogen and Deuterium
-
摘要: 针对近二十多年的氢氘物态方程理论研究工作进行了综述分析,结合本课题组改进的自由能模型、直接量子蒙特卡洛和量子分子动力学方法的模拟结果,对多个研究小组采用不同方法获得的氢氘宽区物态方程数据进行了定量评估分析。结果表明:在当前理论框架下,仅基于第一原理数值模拟得到的氢氘物态方程能够描述的热力学相空间有限;多模型集成的H-REOS.3数据库在105 K以下温度与数值模拟结果的相对差别较大,且数据稀少,二者均不能满足工程应用需求。建议采用基于半经验模型的宽区域物态方程研究方法,即结合高精度的实验研究、数值模拟和解析模型,构建满足工程应用需求的氢氘宽区实用物态方程。Abstract: This paper reviews the research on the equation of state (EOS) for hydrogen and deuterium in the last twenty years.A quantitative analysis of the wide-range EOS for hydrogen and deuterium is given by combining the modified chemical free energy model and the modern computational techniques such as Quantum Molecular Dynamic (QMD) and Quantum Monte Carlo (QMC).It is demonstrated that the wide-range EOS obtained from ab initio calculations only covers a limited region of density-temperature space, and the H-REOS.3 database, which is obtained by integrating different models, exhibits disagreement with the modern computational results below the temperature of 105 K and its data points distribution is not dense enough.EOS of deuterium is not transformed from the H-REOS.3.Therefore, both the ab initio calculation and the H-REOS.3 are not sufficient for the engineering application, and it is necessary to construct a wide range EOS database for hydrogen and its isotopes, which combines the high-precision experiments, the modern computational techniques, and the analytical or semi-analytical models.
-
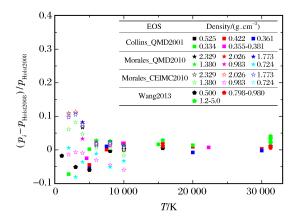
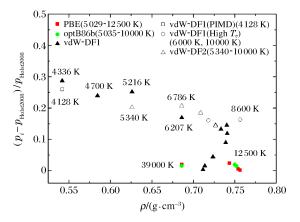
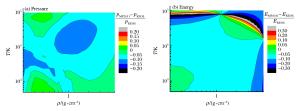
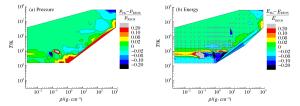
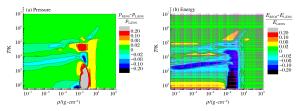
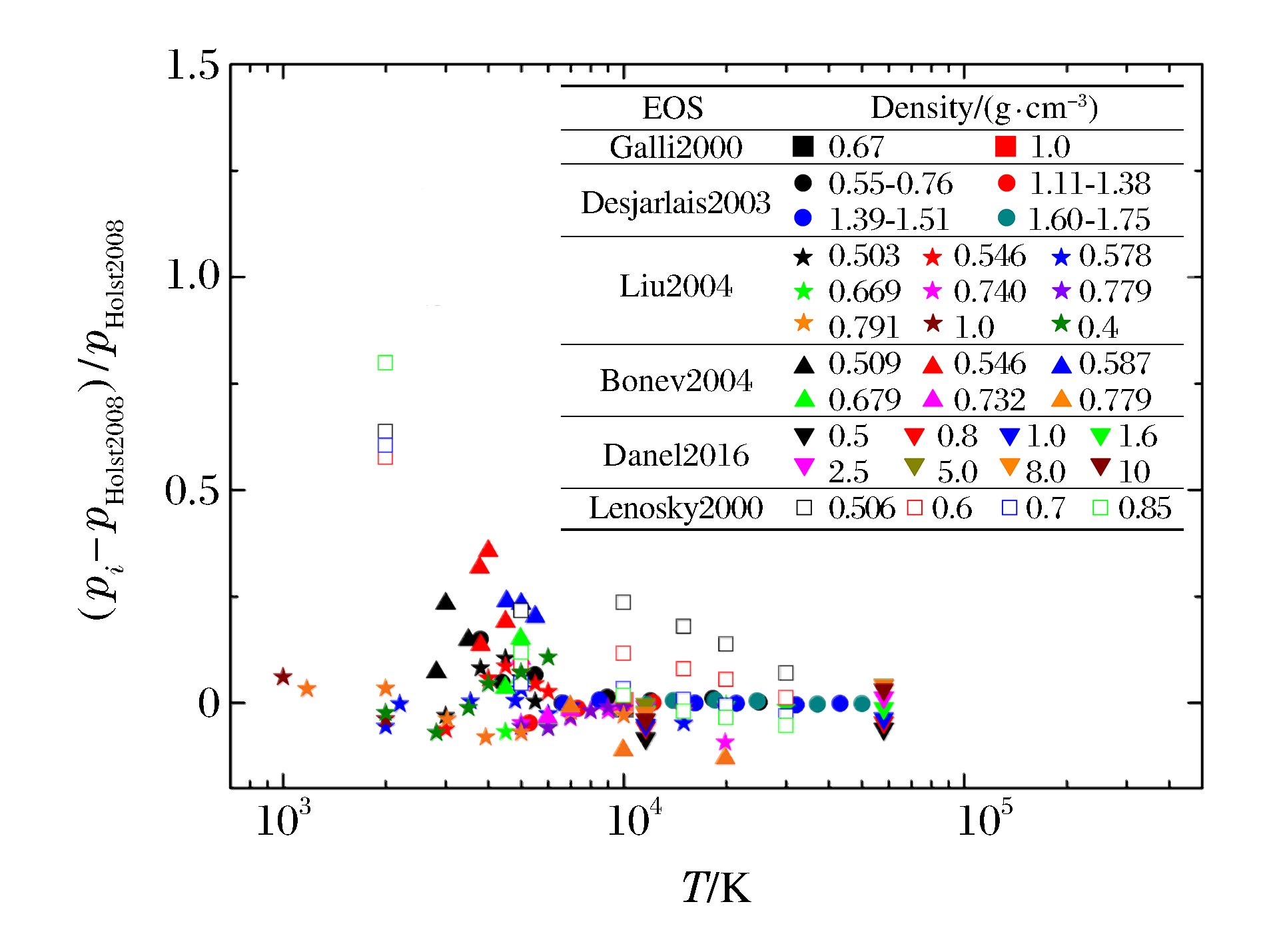
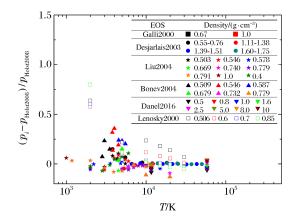
图 1 QMD模拟氘物态方程的压强相对偏差
(下标i分别指代Gali2000、Desjarlais2003、Liu2004、Bonev2004、Danel2016、Lenosky2000, 以下类似)
Figure 1. Relative differences of pressure from QMD simulation for deuterium
(The subscript i represents Gali2000, Desjarlais2003, Liu2004, Bonev2004, Danel2016, Lenosky2000, respectively.Similarly hereinafter.)
表 1 氢氘物态方程的QMD模拟工作
Table 1. Works of QMD simulation for equation of state of hydrogen and deuterium
Isotope Time Firstauthor Ref. Method Code Organization Temperature/K Density/(g·cm-3) D 1997 T. J. Lenosky [135] TBMD LANL 3 000-31 250 0.58-1.47 D 2000 G. Galli [136] CPMD GP code LLNL 10 000 0.67,1.0 D 2000 S. Bagnier [137] BOMD VASP CEA The effect of the local-spin-density-approximation functional D 2000 T. J. Lenosky [138] BOMD VASP LLNL,LANL 2 000-31 500 0.506-0.851 D 2002 F. Gygi [139] CPMD GP code LLNL The compressibility is determined by shock-induced electronic excitations D 2003 M. P. Desjarlais [140] BOMD VASP SNL 3 800-50 105 0.553-1.756 D 2004 S. A. Bonev [141] CPMD GP code LLNL 20-19 860 0.171-0.779 D 2004 H. F.Liu [149] BOMD VASP IAPCM 1 000-10 000 0.506-1.0 D 2016 J. F. Danel [142] QMD,OFWMD ABINIT,VAAQP CEA 11 604-116 045 0.2-20 D 2016 V. V. Karasiev [143] QMD,OFMD PROFESS@Q-ESPRESSO,ABINIT Universityof Florida 2 000-250 000 0.2-10, No data list D 2017 M. D. Knudson [12] QMD VASP,Diff Exc SNL, WashingtonState University H 2001 L. A. Collins [146] BOMD VASP LANL,LLNL 5 000-30 000 0.334-0.525 H 2008 B. Holst [147] BOMD VASP Institut für Physik,SNL 500-20 000 0.5-5.0 H 2010 M. A. Morales [126] BOMD,QMC QBOX,CEIMC University of Illinois,University of L'Aquila 2 000-10 000 0.724-2.329 H 2011 L. Caillabet [148] QMD,CEIMC PIMC, QMD, CEIMC CEA -116 045 0.2-5 H 2013 C. Wang [151] QMD,OFMD ABINIT IAPCM 1.564×104-5.004441×107 9.82×10-3-1.347×103 表 2 氢氘物态方程的QMC数值模拟
Table 2. Works of QMC simulation for equation of state of hydrogen and deuterium
Isotope Time Firstauthor Ref. Method Organization Temperature/K Density/(g·cm-3) D 2000 B. Militzer [114] PIMC(VDM) University of Illinois at Urbana-Champaign 105-106 0.674,0.838 D 2004 V. Bezkrovniy [155] DPIMC Universität Greifswald, Domstrasse, Germany;Russian Academy of Science 15 625-1 000 000 0.674,0.838,1.097 D 2011 S. X. Hu [46] RPIMC University of Rochester,University of California 15 665-63 822 000 0.002-1 596 H 20012003 V. S. Filinov [117]
[116]DPIMC Russian Academy of Sciences 31 250-106 0.419 H 2001 B. Militzer [114] RPIMC LLNL,University of Illinois at Urbana-Champaign 5 000-250 000 9.833×10-4-0.153 H 2004 C. Pierleoni [121] CEIMC Universita' of L'Aquila, Via Vetoio, University of Illinois at Urbana-Champaign, Université Pierre et Marie Curie 300-10 000 5.267,2.697,1.561 H 2010 M. A. Morales [126] CEIMC University of Illinois at Urbana-Champaign, University of L'Aquila, Italy 2 000-10 000 0.724-2.329 H 2011 L. Caillabet [148] QMD,CEIMC CEA 116 045 0.2-5 H 2015 Q. L. Zhang [150] DPIMC IAPCM 116 045 0.98×10-3-1 346.1 -
[1] HUBBARB W B.Interiors of the giant planets[J].Science, 1981, 214(4517):145-149. doi: 10.1126/science.214.4517.145 [2] STEVENSON D J.Interiors of the giant planets[J].Annual Review of Earth and Planetary Sciences, 1982, 10(1):257-295. doi: 10.1146/annurev.ea.10.050182.001353 [3] MCCRORY R L, MEYERHOFER D D, BETTI R, et al.Progress in direct-drive inertial confinement fusion[J].Physics of Plasmas, 2008, 15(5):055503. doi: 10.1063/1.2837048 [4] MEYERHOFER D D, MCCRORY R L, BETTI R, et al.High-performance inertial confinement fusion target implosions on OMEGA[J].Nuclear Fusion, 2011, 51(5):053010. doi: 10.1088/0029-5515/51/5/053010 [5] LINDL J D.Development of the indirect-drive approach to inertial confinement fusion and the target physics basis for ignition and gain[J].Physics of Plasmas, 1995, 2(11):3933-4024. doi: 10.1063/1.871025 [6] HU S X, GONCHAROV V N, BOEHLY T R, et al.Impact of first-principles properties of deuterium-tritium on inertial confinement fusion target designs[J].Physics of Plasmas, 2015, 22(5):056304. doi: 10.1063/1.4917477 [7] NOH J, FULGUERAS A M, SEBASTIAN L J, et al.Estimation of thermodynamic properties of hydrogen isotopes and modeling of hydrogen isotope systems using Aspen Plus simulator[J].Journal of Industrial and Engineering Chemistry, 2017, 46:1-8. doi: 10.1016/j.jiec.2016.07.053 [8] LEACHMAN J W, JACOBSEN R T, PENONCELLO S G, et al.Fundamental equations of state for parahydrogen, normal hydrogen, and orthohydrogen[J].Journal of Physical and Chemical Reference Data, 2009, 38(3):721-748. doi: 10.1063/1.3160306 [9] RICHARDSON A, LEACHMAN J W, LEMMON E W.Fundamental equation of state for deuterium[J].Journal of Physical and Chemical Reference Data, 2014, 43(1):013103. doi: 10.1063/1.4864752 [10] AZADI S, FOULKES W M C.Fate of density functional theory in the study of high-pressure solid hydrogen[J].Physical Review B, 2013, 88(1):014115. doi: 10.1103/PhysRevB.88.014115 [11] MCMAHON J M, MORALES M A, PIERLEONI C, et al.The properties of hydrogen and helium under extreme conditions[J].Reviews of Modern Physics, 2012, 84(4):1607-1653. http://d.old.wanfangdata.com.cn/Periodical/zgcljz201805001 [12] KNUDSON M D, DESJARLAIS M P.High-precision shock wave measurements of deuterium:evaluation of exchange correlation functionals at the molecular-to-atomic transition[J].Physical Review Letters, 2017, 118(3):035501. doi: 10.1103/PhysRevLett.118.035501 [13] NATOLI V V, MARTIN R M, CEPERLEY D M.Crystal structure of atomic hydrogen[J].Physical Review Letters, 1993, 70(13):1952-1955. doi: 10.1103/PhysRevLett.70.1952 [14] SILVERA F.The solid molecular hydrogens in the condensed phase:fundamentals and static properties[J].Reviews of Modern Physics, 1980, 52(2):393-452. doi: 10.1103/RevModPhys.52.393 [15] MAO H K, HEMLEY R J.Ultrahigh-pressure transitions in solid hydrogen[J].Reviews of Modern Physics, 1994, 66(2):671-692. doi: 10.1103/RevModPhys.66.671 [16] MAKSIMOV E G, SHILOV Y I.Hydrogen at high pressure[J].Physics Uspekhi, 1999, 42(11):1121-1138. doi: 10.1070/PU1999v042n11ABEH000666 [17] REDMER R, RÖPKE G.Progress in the theory of dense strongly coupled plasmas[J].Contributions to Plasma Physics, 2010, 50(10):970-985. doi: 10.1002/ctpp.201000079 [18] GRYAZNOV V K, IOSILEVSKIY I L.Thermodynamic properties of hydrogen plasma to megabars[J].Contributions to Plasma Physics, 2016, 56(3/4):352-360. doi: 10.1002/ctpp.201500115 [19] MAO H K, CHEN B, CHEN J H, et al.Recent advances in high-pressure science and technology[J].Matter and Radiation at Extremes, 2016, 1(1):59-75. doi: 10.1016/j.mre.2016.01.005 [20] GARBEROGLIO G, JANKOWSKI P, SZALEWICZ K, et al.Second virial coefficients of H2 and its isotopologues from a six-dimensional potential[J].The Journal of Chemical Physics, 2012, 137(15):154308. doi: 10.1063/1.4757565 [21] SOUERS P C.Hydrogen properties for fusion energy[M].Los Angeles:University of California Press, 1986. [22] SAKODA N, SHINDO K, SHINZATO K, et al.Review of the thermodynamic properties of hydrogen based on existing equations of state[J].International Journal of Thermophysics, 2010, 31(2):276-296. doi: 10.1007/s10765-009-0699-7 [23] LOUBEYRE P, LETOULLEC R, HÄUSERMANN D, et al.X-ray diffraction and equation of state of hydrogen at megabar pressures[J].Nature, 1996, 383(6602):702-704. doi: 10.1038/383702a0 [24] HEMLEY R J, MAO H K, GONCHAROV A F, et al.Synchrotron infrared spectroscopy to 0.15 eV of H2 and D2 at megabar pressures[J].Physical Review Letters, 1996, 76:1667. doi: 10.1103/PhysRevLett.76.1667 [25] GONCHAROV A F, GREGORYANZ E, HEMLEY R J, et al.Spectroscopic studies of the vibrational and electronic properties of solid hydrogen to 285 GPa[J].Proceedings of the National Academy of Sciences of the United States of America, 2001, 98(25):14234-14237. doi: 10.1073/pnas.201528198 [26] DATCHI F, LOUBEYRE P, LETOULLEC R.Extended and accurate determination of the melting curves of argon, helium, ice(H2O), and hydrogen(H2)[J].Physical Review B, 2000, 61(10):6535-6546. doi: 10.1103/PhysRevB.61.6535 [27] GREGORYANZ E, GONCHAROV A F, MATSUISHI K, et al.Raman spectroscopy of hot dense hydrogen[J].Physical Review Letters, 2003, 90(17):175701. doi: 10.1103/PhysRevLett.90.175701 [28] NELLIS W J, MITCHELL A C, VAN THIEL M, et al.Equation-of-state data for molecular hydrogen and deuterium at shock pressures in the range 2-76 GPa(20-760 kbar)[J].The Journal of Chemical Physics, 1983, 79(3):1480-1486. doi: 10.1063/1.445938 [29] WEIR S T, MITCHELL A C, NELLIS W J.Metallization of fluid molecular hydrogen at 140 GPa(1.4 Mbar)[J].Physical Review Letters, 1996, 76(11):1860-1863. doi: 10.1103/PhysRevLett.76.1860 [30] KNUDSON M D, HANSON D L, BAILEY J E, et al.Principal Hugoniot, reverberating wave, and mechanical reshock measurements of liquid deuterium to 400 GPa using plate impact techniques[J].Physical Review B, 2004, 69(14):144209. doi: 10.1103/PhysRevB.69.144209 [31] TRUNIN R F, URLIN V D, MEDVEDEV A B.Dynamic compression of hydrogen isotopes at megabar pressures[J].Physics-Uspekhi, 2010, 53(6):577-593. doi: 10.3367/UFNe.0180.201006d.0605 [32] BELOV S I, BORISKOV G V, BYKOV A I, et al.Shock compression of solid deuterium[J].Journal of Experimental and Theoretical Physics Letters, 2002, 76(7):433-435. doi: 10.1134/1.1528696 [33] BORISKOV G V, BYKOV A I, IL'KAEV R I, et al.Shock-wave compression of solid deuterium at a pressure of 120 GPa[J].Doklady Physics, 2003, 48(10):553-555. doi: 10.1134/1.1623535 [34] BORISKOV G V, BYKOV A I, IL'KAEV R I.Shock compression of liquid deuterium up to 109 GPa[J].Physical Review B, 2005, 71:092104. doi: 10.1103/PhysRevB.71.092104 [35] GRISHECHKIN S K, GRUZDEV S K, GRYAZNOV V K, et al.Experimental measurements of the compressibility, temperature, and light absorption in dense shock-compressed gaseous deuterium[J].Journal of Experimental and Theoretical Physics Letters, 2004, 80(6):398-404. doi: 10.1134/1.1830656 [36] DA SILVA L B, CELLIERS P, COLLINS G W, et al.Absolute equation of state measurements on shocked liquid deuterium up to 200 GPa(2 Mbar)[J].Physical Review Letters, 1997, 78(3):483-486. doi: 10.1103/PhysRevLett.78.483 [37] HICKS D G, BOEGLY T R, CELLIERS P M, et al.Laser-driven single shock compression of fluid deuterium from 45 to 220 GPa[J].Physical Review B, 2009, 79(1):014112. doi: 10.1103/PhysRevB.79.014112 [38] SANO T, OZAKI N, SAKAIYA T, et al.Laser-shock compression and Hugoniot measurements of liquid hydrogen to 55 GPa[J].Physical Review B, 2011, 83(5):054117. doi: 10.1103/PhysRevB.83.054117 [39] KERLEY G I.Equation of state for hydrogen and deuterium:SAND2003-3613.Sandia National Laboratories, 2003. [40] LOUBEYRE P, BRYGOO S, EGGERT J, et al.Extended data set for the equation of state of warm dense hydrogen isotopes[J].Physical Review B, 2012, 86(14):144115. doi: 10.1103/PhysRevB.86.144115 [41] BORISKOV G V, BYKOV A I.Isentropic compression of substances using ultra-high magnetic field:zero isotherms of protium and deuterium the pressure range up to~5 Mbar[J].Contributions to Plasma Physics, 2011, 51(4):339-348. doi: 10.1002/ctpp.v51.4 [42] EGOROV N I, BORISKOV G V, BYKOV A I, et al.Use of pulsed radiography for investigation of equations of state of substances at megabar pressures[J].Contributions to Plasma Physics, 2011, 51(4):333-338. doi: 10.1002/ctpp.v51.4 [43] MOCHALOVA M A, IL'KAEVA R I, FORTOV V E, et al.Quasi isentropic compressibility of deuterium and helium at pressures of 1 500-5 000 GPa[J].Journal of Experimental and Theoretical Physics, 2014, 119(1):146-161. doi: 10.1134/S106377611406017X [44] FORTOV V E, ILKAEV R I, ARININ V A, et al.Phase transition in a strongly nonideal deuterium plasma generated by quasi-isentropical compression at megabar pressures[J].Physical Review Letters, 2007, 99(18):185001. doi: 10.1103/PhysRevLett.99.185001 [45] GU Y J, CHEN Q F, ZHENG J, et al.The equation of state, shock-induced molecule dissociation, and transparency loss for multi-compressed dense gaseous H2+D2 mixtures[J].Journal of Applied Physics, 2012, 111(1):013513. doi: 10.1063/1.3675281 [46] HU S X, MILITZER B, GONCHAROV V N, et al.First-principles equation-of-state table of deuterium for inertial confinement fusion applications[J].Physical Review B, 2011, 84(22):224109. doi: 10.1103/PhysRevB.84.224109 [47] LIU H F, SONG H F, ZHANG Q L, et al.Validation for equation of state in wide regime:copper as prototype[J].Matter and Radiation at Extremes, 2016, 1(2):123-131. doi: 10.1016/j.mre.2016.03.002 [48] BECKER A, LORENZEN W, FORTNEY J J, et al.Ab-initio equations of state for hydrogen(H-REOS.3)and helium(He-REOS.3)and their implications for the interior of brown dwarfs[J].The Astrophysical Journal Supplement Series, 2014, 215(2):1-21. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=JJ0233882109 [49] SAUMON D, CHABRIER G.Fluid hydrogen at high density:pressure dissociation[J].Physical Review A, 1991, 44:5122-5141. doi: 10.1103/PhysRevA.44.5122 [50] SAUMON D, CHABRIER G.Fluid hydrogen at high density:pressure ionization[J].Physical Review A, 1992, 46:2084-2100. doi: 10.1103/PhysRevA.46.2084 [51] LI Q, LIU H F, ZHANG G M.The thermodynamical instability induced by pressure ionization in fluid Helium[J].Physics of Plasmas, 2016, 23(11):112709. doi: 10.1063/1.4968828 [52] MARX D, HUTTER J.Ab-initio molecular dynamics:basic theory and advanced methods[M].Cambridge, England:Cambridge University Press, 2009. [53] FOULKES W M C, MITAS L, NEEDS R J, et al.Quantum Monte Carlo simulations of solids[J].Reviews of Modern Physics, 2001, 73(1):33-83. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_1201.6214 [54] SILVERA I F, GOLDMAN V V.The isotropic intermolecular potential for H2 and D2 in the solid and gas phases[J].The Journal of Chemical Physics, 1978, 69(9):4209-4213. doi: 10.1063/1.437103 [55] ROSS M, REE F H, YOUNG D A.The equation of state of molecular hydrogen at very high density[J].The Journal of Chemical Physics, 1983, 79(3):1487-1494. doi: 10.1063/1.445939 [56] JURANEK H, REDMER R.Self-consistent fluid variational theory for pressure dissociation in dense hydrogen[J].The Journal of Chemical Physics, 2000, 112(8):3780-3786. doi: 10.1063/1.480939 [57] JURANEK H, SCHWARZ V, REDMER R.Equation-of-state for hydrogen and helium in the chemical picture[J].Journal of Physics A:Mathematical and General, 2003, 36(22):6181-6185. doi: 10.1088/0305-4470/36/22/346 [58] LIU H F, LIU W S, ZHANG W X, et al.Equations of state of H2 and D2[J].Journal of Physics Condensed Matter, 2002, 14(44):11401-11404. doi: 10.1088/0953-8984/14/44/489 [59] ROSS M.Linear-mixing model for shock-compressed liquid deuterium[J].Physical Review B, 1998, 58(2):669-677. http://adsabs.harvard.edu/abs/1998PhRvB..58..669R [60] CHEN Q F, CAI L C, CHEN D Q, et al.Pressure dissociation of dense hydrogen[J].Chinese Physics, 2005, 14(10):2077-2082. doi: 10.1088/1009-1963/14/10/025 [61] LI Q, LIU H F, ZHANG G M, et al.Response to "Comment on 'The thermodynamical instability induced by pressure ionization in fluid helium'"[J].Physics of Plasmas, 2017, 24(6):064702. doi: 10.1063/1.4984999 [62] 李琼, 刘海风, 张弓木, 等.模拟退火算法在化学自由能模型中的应用[J].计算物理, 2018.Doi: 10.19596/jswl.cnki.1001-246x.2018-7853. [63] STOLZMANN W, BLÖCKER T.Thermodynamical properties of stellar matter Ⅰ.equation of state for stellar interiors[J].Astronomy and Astrophysics, 1996, 314:1024-1040. http://adsabs.harvard.edu/abs/1996A&A...314.1024S [64] BORN M, OPPENHEIMER J R.Zur Quantenthoried der Molekeln[J].Annalen der Physik, 1927, 84(20):457-484. [65] HARTREE D R.The wave mechanics of an atom with a non-coulomb central field.Part Ⅱ.some results and discussion[J].Mathematical Proceedings of the Cambridge Philosophical Society, 1928, 24(1):111-132. doi: 10.1017/S0305004100011920 [66] FOCK V.Näaherungs methode zur Lösung des quanten mechanischen Mehrkörperproblems[J].Zeitschrift für Physik, 1930, 61(1/2):126-148. doi: 10.1007/BF01340294 [67] Martin R M.Electronic structure:basic theory and practical methods[M].Cambridge, England:Cambridge University Press, 2004. [68] 谢希德, 陆栋.固体能带理论[M].上海:复旦大学出版社, 1998. [69] KOHN W, SHAM L J.Self-consistent equations including exchange and correlation effects[J].Physical Review, 1965, 140(4A):A1133. doi: 10.1103/PhysRev.140.A1133 [70] KOHN W.Nobel lecture electronic structure of matter-wave functions ans density functionals[J].Reviews of Modern Physics, 1998, 71(5):1253-1266. https://www.nobelprize.org/prizes/chemistry/1998/kohn/lecture/ [71] HERMA F, VAN DYKE J P, ORTENBURGER I B.Improved statistical exchange approxi-mation for inhomogeneous many-electron systems[J].Physical Review Letters, 1969, 22(16):807-811. doi: 10.1103/PhysRevLett.22.807 [72] LABANOWSKI J L, ANDZELM J W.Density functional methods in chemistry[M].New York:Springer Verlag, 1991. [73] JUAN Y M, KAXIRAS E.Application of gradient corrections to density functional theory for atoms and solids[J].Physical Review B, 1993, 48(20):14944. doi: 10.1103/PhysRevB.48.14944 [74] LANGRETH D C, PERDEW J P.Theory of nonuniform electronic systems.Ⅰ.analysis of the gradient approximation and a generalization that works[J].Physical Review B, 1980, 21(12):5469-5493. http://adsabs.harvard.edu/abs/1980PhRvB..21.5469L [75] PERDEW J P, BURKE K, ERNZERHOF M.Generalized gradient approximation made simple[J].Physical Review Letters, 1996, 77(18):3865-3868. doi: 10.1103/PhysRevLett.77.3865 [76] PERDEW J P, WANG Y.Accurate and simple analytic representation of the electron gas correlation energy[J].Physical Review B, 1992, 45(23):13244. doi: 10.1103/PhysRevB.45.13244 [77] PERDEW J P, CHEVARY J A, VOSKO S H, et al.Atoms, moleules, solids, and surfaces:applications of the generalized gradient approximation for exchange and correlation[J].Physical Review B, 1992, 46(11):6671-6687. doi: 10.1103/PhysRevB.46.6671 [78] DION M, RYDBERG H, SCHRÖDER E, et al.Van der Waals density functional for general geometries[J].Physical Review Letters, 2004, 92(24):246401. doi: 10.1103/PhysRevLett.92.246401 [79] LEE K, MURRAY E D, KONG L, et al.Higher-accuracy van der Waals density functional[J].Physical Review B, 2010, 82(8):081101. doi: 10.1103/PhysRevB.82.081101 [80] IHM J, ZUNGER A, COHEN M L.Momentum-space formalism for the total energy of solids[J].Journal of Physics C:Solid State Physics, 1979, 12(21):4409-4422. doi: 10.1088/0022-3719/12/21/009 [81] PAYNE M C, TETER M P, AHAN D C, et al.Iterative minimization techniques for ab initio total-energy calculations:molecular dynamics and conjugate gradients[J].Reviews of Modern Physics, 1992, 64(4):1045-1097. doi: 10.1103/RevModPhys.64.1045 [82] SLATER J C, KOSTER G F.Simplified LCAO method for the periodic potential problem[J].Physical Review, 1954, 94(6):1498-1524. doi: 10.1103/PhysRev.94.1498 [83] HERRING C, HILL A G.The theoretical constitution of metallic beryllium[J].Physical Review, 1940, 58(2):132-162. doi: 10.1103/PhysRev.58.132 [84] HERMAN F, KILLMAN S.Atomic structure calculation[M].Englewood Cliffs, New Jersey:Prentice-Hall Inc., 1963. [85] ANDERSON O K.Linear methods in band theory[J].Physical Review B, 1975, 12(8):3060-3083. doi: 10.1103/PhysRevB.12.3060 [86] SKIVER H L.The LMTO method[M].Heidelberg:Springer-Verlag, 1984. [87] HAMANN D R, SCHLUTER M, Chiang C.Norm-conserving pseudopotentials[J].Physical Review Letters, 1979, 43(20):1494-1497. doi: 10.1103/PhysRevLett.43.1494 [88] BAICHELET G B, HAMANN D R, SCHLUTER M.Pseudopotentials that work:from H to Pu[J].Physical Review B, 1982, 26(8):4199-4228. doi: 10.1103/PhysRevB.26.4199 [89] BLOCHL P E.Projector augmented wave method[J].Physical Review B, 1994, 50(24):17953-19979. doi: 10.1103/PhysRevB.50.17953 [90] HOLZWARTH N A W, TACKETT A R, MATTHEWS G E.A projector augmented wave (PAW) code for electronic structure calculations.Part Ⅰ:atompaw for generating atom-centered functions.computer physics communications[J].Computer Physics Communications, 2001, 135(3):329-347. doi: 10.1016/S0010-4655(00)00244-7 [91] VANDERBILT D.Soft self-consistent pseudopotentials in a generalized eigenvalue formalism[J].Physical Review B, 1990, 41(11):7892-7895. doi: 10.1103/PhysRevB.41.7892 [92] LAASONEN K, CAR R, LEE C, et al.Implementation of ultrasoft pseudopotentials in ab initio molecular dynamics[J].Physical Review B, 1991, 43(8):6796-6799. doi: 10.1103/PhysRevB.43.6796 [93] KRESSE G, HAFNER J.Norm-conserving and ultrasoft pseudopotentials for first-row and transition elements[J].Journal of Physics Condensed Matter, 1994, 6(40):8245-8257. doi: 10.1088/0953-8984/6/40/015 [94] HELLMANN H.Einfuhrung in die Quantumchemie[M].Leipzig:Franz Duetsche, 1937. [95] FEYNMAN R P.Forces in molecules[J].Physical Review, 1939, 56(4):340-343. doi: 10.1103/PhysRev.56.340 [96] MARTIN R M.Electronic structure basic theory and practical methods[J].Cambridge University Press, 2004. [97] CAR R, PARRINELLO M.Unified approach for molecular dynamics and density-functional theory[J].Physical Review Letters, 1985, 55(22):2471-2474. doi: 10.1103/PhysRevLett.55.2471 [98] MARX D, HUTTE J.Modern methods and algorithms of quantum chemistry[J].NIC Series, 2000, 1:301-449. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_physics%2f0008239 [99] MERMIN N D.Thermal properties of the inhomogeneous electron gas[J].Physical Review, 1965, 137(5A):A1441-A1443. doi: 10.1103/PhysRev.137.A1441 [100] KRESSE G, HAFNER J.Ab-initio molecular dynamics for liquid metals[J].Physical Review B, 1993, 48(17):13115-13118. doi: 10.1103/PhysRevB.48.13115 [101] GONZE X, BEUKEN J M, CARACAS R, et al.First-principles computation of material properties:the ABINIT software project[J].Computational Materials Science, 2002, 25(3):478-492. doi: 10.1016/S0927-0256(02)00325-7 [102] GONZE X, RIGNANESE G M, VERSTRAETE M, et al.A brief introduction to the ABINIT software package[J].Zeitschrift für Kristallographie-Crystalline Materials, 2005, 220(5/6):558-562. doi: 10.1524/zkri.220.5.558.65066 [103] GONZE X, AMADON B, ANGLADE P M, et al.ABINIT:first-principles approach to material and nanosystem properties[J].Computer Physics Communications, 2009, 180(12):2582-2615. doi: 10.1016/j.cpc.2009.07.007 [104] ABINIT. (2018-06-10). http://www.abinit.org. [105] GYGI F. The first-principles MD code JEEP1. 6. 6. Lawrence Livermore National Laboratory, 1999-2001. [106] QBOX. (2018-07-16). http://qboxcode.org. [107] LAMBERT F, CLÉROUIN J, MAZEVET S.Structural and dynamical properties of hot dense matter by a thomas-fermi-dirac molecular-dynamics[J].Europhysics Letters, 2006, 75(5):681-687. doi: 10.1209/epl/i2006-10184-7 [108] MAZEVET S, LAMBERT F, BOTTIN F, et al.Ab-initio molecular-dynamics simulations of dense boron plasmas up to the semiclassical Thomas-Fermi regime[J].Physical Review E, 2007, 2007, 75:056404. doi: 10.1103/PhysRevE.75.056404 [109] LAMBERT F, CLEROUIN J, DANEL J F, et al.Direct verification of mixing rules in the hot and dense regime[J].Physical Review E, 2008, 77:026402. doi: 10.1103/PhysRevE.77.026402 [110] CEPERLEY D M.Path-integral calculations of normal liquid 3He[J].Physical Review Letters, 1992, 69(2):331-334. doi: 10.1103/PhysRevLett.69.331 [111] TROTTER H.On the product of semi-groups of operators[J].Proceedings of the American Mathematical Society, 1959, 10(4):545-551. doi: 10.1090/S0002-9939-1959-0108732-6 [112] MAGRO W R, CEPERLEY D M, PIERLEONI C, et al.Molecular dissociation in hot, dense hydrogen[J].Physical Review Letters, 1996, 76(8):1240-1243. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_cond-mat%2f9601118 [113] MILITZER B, CEPERLEY D M.Path integral monte carlo calculation of the deuterium hugoniot[J].Physical Review Letters, 2000, 85(9):1890-1893. doi: 10.1103/PhysRevLett.85.1890 [114] MILITZER B, CEPERLEY D M.Path integral Monte Carlo simulation of the low-density hydrogen plasma[J].Physical Review, 2001, 63(2):066404. doi: 10.1103-PhysRevE.63.066404/ [115] MILITZER B, CEPERLEY D M, KRESS J D, et al.Calculation of a deuterium double shock hugoniot from ab initio simulations[J].Physical Review Letters, 2001, 87(27):275502. doi: 10.1103/PhysRevLett.87.275502 [116] FILINOV V S, BONITZ M, LEVASHOV P R, et al.Plasma phase transition in hydrogen and electron-hole plasmas[J].Contributions to Plasma Physics, 2003, 43(5/6):290-294. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=JJ027372431 [117] FILINOV V S, BONITZ M, EBELING W, et al.Thermodynamics of hot dense H-plasmas:path integral Monte Carlo simulations and analytical approximations[J].Plasma Physics & Controlled Fusion, 2001, 43(6):743-759. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_physics%2f0103002 [118] FILINOV V S, LEVASHOV P R, BONITZ M, et al.Calculation of the shock Hugoniot of deuterium at pressures above 1 Mbar by the path-integral Monte Carlo method[J].Plasma Physics Reports, 2005, 31(8):700-704. doi: 10.1134/1.2031631 [119] 张其黎, 刘海风, 李琼, 等.氢状态方程的路径积分蒙特卡洛研究[J].计算物理, 2018.Doi: 10.19596/jswl.cnki.1001-246x.2018-7855. [120] PIERLEONI C, CEPERLEY D M.The coupled electron-ion Monte Carlo method[J].Lecture Notes in Physics, 2006, 703(1):641-683. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_physics%2f0510254 [121] PIERLEONI C, CEPERLEY D M, HOLZMANN M.Coupled electron-ion Monte Carlo calculations of dense metallic hydrogen[J].Physical Review Letters, 2004, 93(14):146402. doi: 10.1103/PhysRevLett.93.146402 [122] CAO J, BERNE B J.A Born-Oppenheimer approximation for path integrals with an application to electron solvation in polarizable fluids[J].The Journal of Chemical Physics, 1993, 99(4):2902-2916. doi: 10.1063/1.465198 [123] MCMILLAN W L.Ground state of liquid He4[J].Physical Review, 1965, 138(2A):442-451. doi: 10.1103/PhysRev.138.A442 [124] CEPERLEY D M, CHESTER G V, KALOS M H.Monte Carlo simulation of a many-fermion study[J].Physical Review B, 1977, 16(16):3081-3099. http://adsabs.harvard.edu/abs/1977PhRvB..16.3081C [125] FOULKES W M C, MITAS L, NEEDS R J, et al.Quantum Monte Carlo simulations of solids[J].Reviews of Modern Physics, 2001, 73(1):33-83. doi: 10.1103/RevModPhys.73.33 [126] MORALES M A, PIERLEONI C, CEPERLEY D M.Equation of state of metallic hydrogen from coupled electron-ion Monte Carlo simulations[J].Physical Review E, 2010, 81(1):021202. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_0906.1594 [127] TUBMAN N M, LIBERATORE E, PIERLEONI C, et al.Molecular-atomic transition along the deutrium Hugoniot curve with coupled electron-ion Monte Carlo simulations[J].Physical Review Letters, 2015, 115(4):45301. doi: 10.1103/PhysRevLett.115.045301 [128] 李名锐, 周刚, 李志康, 等.液氘单次冲击压缩的QMC模拟研究[J].高压物理学报, 2015, 29(1):1-8. http://www.gywlxb.cn/CN/abstract/abstract1774.shtmlLI M R, ZHOU G, LI Z K, et al.Single shock compression of fluid deuterium by QMC simulation[J].Chinese Journal of High Pressure Physics, 2015, 29(1):1-8. http://www.gywlxb.cn/CN/abstract/abstract1774.shtml [129] 耿华运, 孙毅.氢的高压奇异结构与金属化[J].高压物理学报, 2018, 32(2):020101. http://www.gywlxb.cn/CN/abstract/abstract2045.shtmlGENG H Y, SUN Y.On the novel structure and metallization of hydrogen under high pressure[J].Chinese Journal of High Pressure Physics, 2018, 32(2):020101. http://www.gywlxb.cn/CN/abstract/abstract2045.shtml [130] KERLEY G I.A theoretical equation of state for deuterium:No.LA-4776.Los Alamos, New Mexico:Los Alamos Scientific Laboratory, 1972. [131] SAUMON D, CHABRIER G, VAN HORN H M.An equation of state for low-mass stars and giant planets[J].The Astrophysical Journal Supplement Series, 1995, 99:713-741. doi: 10.1086/192204 [132] EBELING W.Coulomb interaction and ionization equilibrium in partially ionized plasmas[J].Physica, 1969, 43(2):293-306. doi: 10.1016/0031-8914(69)90009-3 [133] DA SILVA L B, CELLIERS P, COLLINS G W, et al.Absolute equation of state measurements on shocked liquid deuterium up to 200 GPa(2 Mbar)[J].Physical Review Letters, 1997, 78(78):483-486. http://adsabs.harvard.edu/abs/1997PhRvL..78..483D [134] YOUNG D A, COREY E M.A new global equation of state model for hot dense matter[J].Journal of Applied Physics, 1995, 78(6):3748-3755. doi: 10.1063/1.359955 [135] LENOSKY T J, KRESS J D, COLLINS L A.Molecular-dynamics modeling of the Hugoniot of shocked liquid deuterium[J].Physical Review B, 1997, 56(9):5164-5169. doi: 10.1103/PhysRevB.56.5164 [136] GALLI G, HOOD R Q, HAZI A U, et al.Ab-initio simulations of compressed liquid deuterium[J].Physical Review B, 2000, 61(2):909-912. doi: 10.1103/PhysRevB.61.909 [137] BAGNIER S, BLOTTIAU P, CLÉROUIN J.Local-spin-density-approximation molecular-dynamics simulations of dense deuterium[J].Physical Review E, 2001, 63(1):015301. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=JJ023284075 [138] LENOSKY T J, BICKHAM S R, KRESS J D, et al.Density-functional calculations of the Hugoniot of shocked liquid deuterium[J].Physical Review B, 2000, 61(1):1-4. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=JJ029469188 [139] GYGI F, GALLI G.Electronic excitations and the compressibility of deuterium[J].Physical Review B, 2002, 65(22):392-397. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=JJ024322106 [140] DESJARLAIS M P.Density-functional calculations of the liquid deuterium Hugoniot, reshock, and reverberation timing[J].Physical Review B, 2003, 68(6):575-580. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=JJ027613173 [141] BONEV S A, MILITZER B, GALLI G.Ab initio simulations of dense liquid deuterium:comparison with gas-gun shock-wave experiments[J].Physical Review B, 2004, 69(1):1985-1988. http://adsabs.harvard.edu/abs/2004PhRvB..69a4101B [142] DANEL J F, KAZANDJIAN L, PIRON R.Equation of state of warm dense deuterium and its isotopesfrom density-functional theory molecular dynamics[J].Physical Review E, 2016, 93(4):043210. doi: 10.1103/PhysRevE.93.043210 [143] KARASIEV V V, CALDERÃIN L, TRICKEY S B.Importance of finite-temperature exchange correlation for warm dense matter calculations[J].Physical Review E, 2016, 93(6):063207. doi: 10.1103/PhysRevE.93.063207 [144] KARASIEV V V, CHAKRABORTY D, SHUKRUTO O A, et al.Nonempirical generalized gradient approximation free-energy functional for orbital-free simulations[J].Physical Review B, 2013, 88(16):161108. doi: 10.1103/PhysRevB.88.161108 [145] KNUDSON M D, DESJARLAIS M P, BECKER A, et al.Direct observation of an abrupt insulator-to-metal transition in dense liquid deuterium[J].Science, 2015, 348(6242):1455. doi: 10.1126/science.aaa7471 [146] COLLINS L A, BICKHAM S R, KRESS J D.Dynamical and optical properties of warm dense hydrogen[J].Physical Review B, 2001, 63(18):184110. doi: 10.1103/PhysRevB.63.184110 [147] HOLST B, REDMER R, DESJARLAIS M.Thermophysical properties of warm dense hydrogen using quantum molecular dynamics simulations[J].Physical Review B, 2008, 77(18):184201. doi: 10.1103/PhysRevB.77.184201 [148] CAILLABET L, MAZEVET S, LOUBEYRE P.Multiphase equation of state of hydrogen from ab initio calculations in the range 0.2 to 5 g/cc up to 10 eV[J].Physical Review B, 2011, 83:094101. doi: 10.1103/PhysRevB.83.094101 [149] 刘海风, 张弓木. 液氘第一原理分子动力学模拟与实用物态方程(内部报告). 2004. [150] 张其黎, 张弓木, 赵艳红, 等.氘、氦及其混合物状态方程第一原理研究[J].物理学报, 2015, 64(9):094702. http://d.old.wanfangdata.com.cn/Periodical/wlxb201509030ZHANG Q L, ZHANG G M, ZHAO Y H, et al.Study of the equation of states for deuterium, helium, and their mixture[J].Acta Physica Sinica, 2015, 64(9):094702. http://d.old.wanfangdata.com.cn/Periodical/wlxb201509030 [151] WANG C, ZHANG P.Wide range equation of state for fluid hydrogen from density function theory[J].Physics of Plasmas, 2013, 20(9):092703. doi: 10.1063/1.4821839 [152] PIERLEONI C, CEPERLEY D M, BERNU B, et al.Equation of state of the hydrogen plasma by path intergral monte carlo simulation[J].Physical Review Letters, 1994, 73(16):2145-2149. doi: 10.1103/PhysRevLett.73.2145 [153] FILINOV V S, FORTOV V E, BONITZ M, et al.Pair distribution functions of dense partially ionized hydrogen[J].Physics Letters A, 2000, 274(5):228-235. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=JJ026129171 [154] FILINOV V S, FORTOV V E, BONITZ M, et al.Fermionic path integral Monte Carlo results for the uniform electron gas at finite temperature[J].Physical Review E, 2015, 91(3):033108. doi: 10.1103/PhysRevE.91.033108 [155] BEZKROVNIY V, FILINOV V S, KREMP D, et al.Monte Carlo results for the hydrogen Hugoniot[J].Physical Review E, 2004, 70:057401. doi: 10.1103/PhysRevE.70.057401 [156] RILLO G, MORALES M A, CEPERLEY D M, et al.Coupled electron-ion Monte Carlo simulation of hydrogen molecular crystals[J].Journal of Chemical Physics, 2018, 148(10):102314. doi: 10.1063/1.5001387 -






 下载:
下载: