Force-Thermal Coupling Response of Sapphire under Impact Loading Based on Molecular Dynamics Simulation
-
摘要: 蓝宝石因其出色的强度、硬度和光学透明度，常被选为冲击波实验中的观测窗口。深入了解蓝宝石在冲击载荷下的力学和热力学响应机制以及内部损伤原因，对准确评估其性能和稳定性至关重要。利用分子动力学模拟，从原子层面探讨蓝宝石单晶在沿(0001)晶面（C面）冲击作用下的力热响应行为。模拟结果表明，蓝宝石C面冲击作用下激活的滑移系为基于R面{$ 0 \overline 1 12$}的菱形面滑移。冲击速度为1～3 km/s时未出现滑移现象，冲击速度为4 km/s时出现菱形面滑移，冲击速度为5～6 km/s时试样出现以不规则条带为主的非均匀形变。研究表明，蓝宝石滑移系的激活不仅依赖其晶格结构，还需分剪切应力达到临界值。温度场的分析结果表明，局域温升与滑移之间存在对应关系，剪切应变集中区域的温度较高。Abstract: Sapphire is often chosen as the observation window in shock wave experiments due to its excellent strength, hardness and optical transparency. A deep understanding of the mechanical and thermodynamic response mechanisms of sapphire under impact loading and the causes of internal damage is crucial for accurately evaluating its performance and stability. In this work, molecular dynamics simulations were performed to explore the mechanical and thermal response of a sapphire single crystal under shock loading along the C-plane. The results indicate that the activated slip system after the impact loading is the rhombic plane slip based on the R-plane {$0 \overline 1 12 $}. When the impact velocity is in the range of 1−3 km/s, no slip occurs; when the impact velocity reaches 4 km/s, slip occurs. When the impact velocity reaches to the range of 5−6 km/s, the sample shows inhomogeneous deformation, mainly composed of irregular stripes. Such results suggest that the activation of the slip system in sapphire depends not only on its lattice structure, but also on the partial shear stress (which needs to reach a critical value). The analysis of the temperature field indicates that there is an intrinsic relation between the local slip and temperature increase, i.e., the formation of intense shear localization is accompanied by the higher temperature.
-
Key words:
- molecular dynamics /
- sapphire /
- impact response /
- damage type
-
图 1 蓝宝石单晶扩胞示意图（为显示方便，a、b、c轴上的长度均在单胞长度的基础上扩大了1倍）
Figure 1. Schematic diagrams of an enlarged model of sapphire single crystal (For visualization reason,the unit cell is replicated once in the a, b, and c axes.)
图 3 冲击速度为1 km/s时试样中心位置处沿z轴的正应力和剪切应力随时间的变化
Figure 3. Temporal variations of the normal and shear stresses at the central position of the sample along z axis at the shock velocity of 1 km/s
图 4 (a) t =5.0 ps时不同加载速度下的压强剖面，(b) 对应的氧原子结构示意图
Figure 4. (a) Pressure profiles at t=5.0 ps under different loading velocities; (b) the corresponding schematic diagrams of the oxygen atom structure
图 5 t=20.0 ps时不同冲击速度下试样内剪切应变等高图
Figure 5. Contour maps of shear strain inside samples under different impact velocities at t=20.0 ps
图 7 冲击速度为4 km/s时试样内部滑移面的形成和演化过程
Figure 7. Initiation and development of the shear plane inside the sample under an impact velocity of 4 km/s
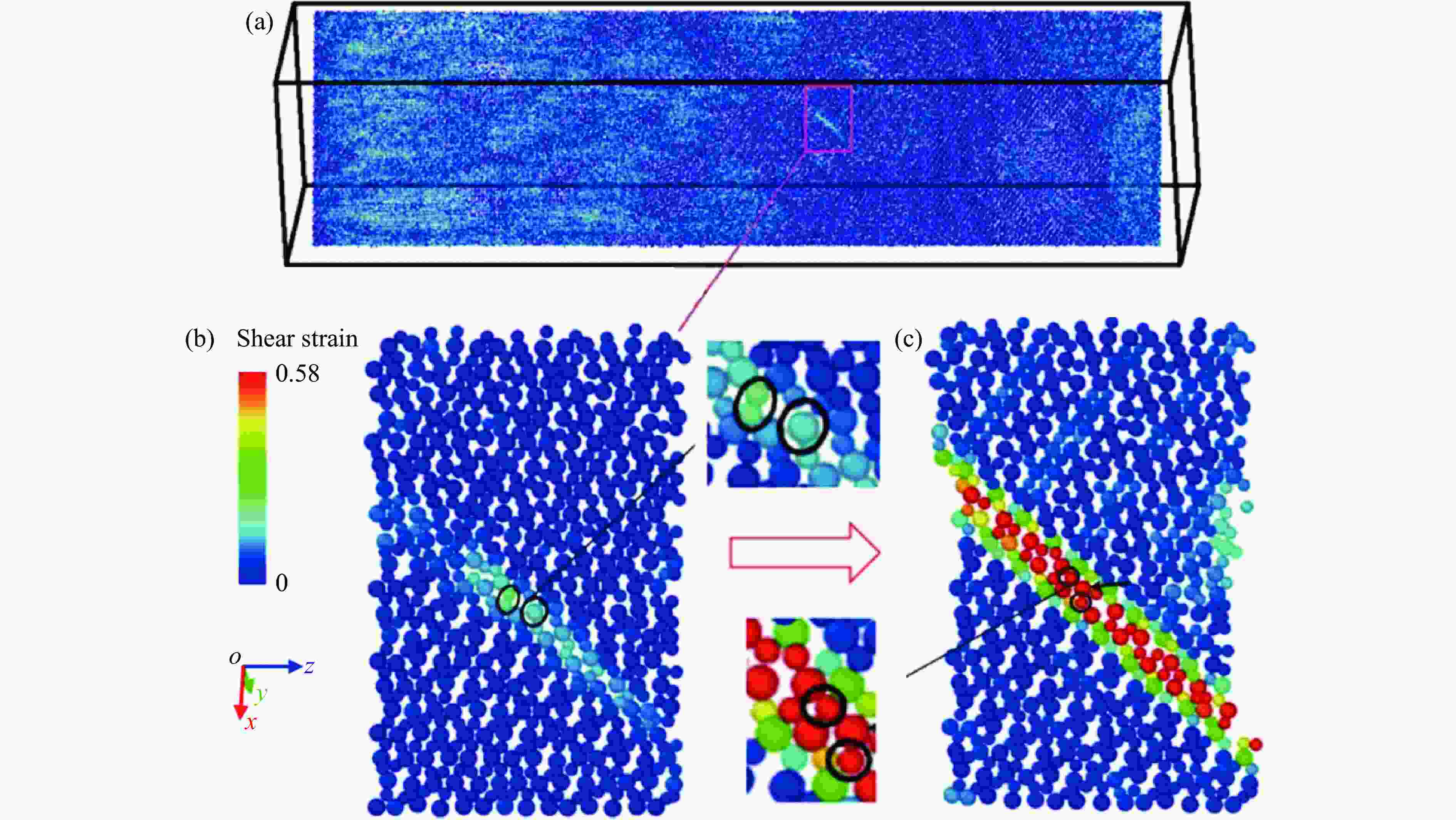
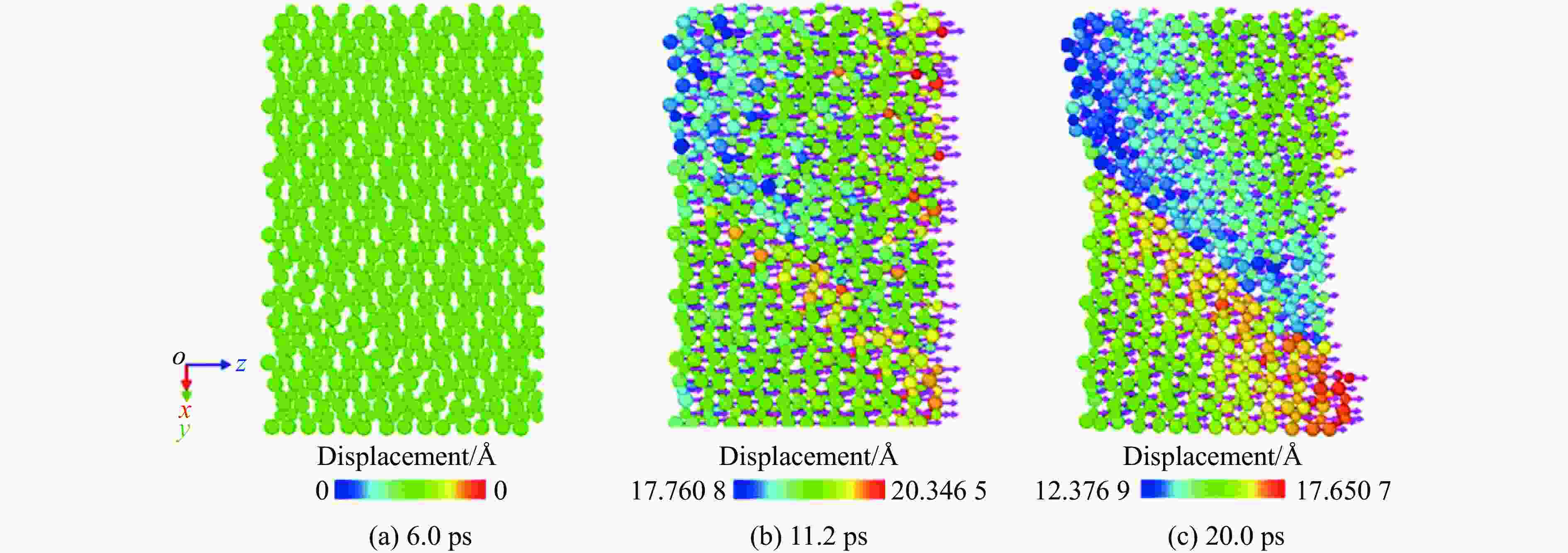
图 8 (a) 11.2 ps时垂直于滑移面截面上的剪切应变分布，(b) (a)中红框的放大（黑圈内2个氧原子的剪切应变大于0.18），(c) 20.0 ps时红框内的应变分布（黑圈内的原子对应(b)中的2个氧原子）
Figure 8. (a) Distribution of shear strain in the cross-section vertical to the later shear plane at t =11.2 ps; (b) zoomed-in view of the red box region in (a) (The shear strains of the two oxygen atoms highlighted by black circles are greater than 0.18.); (c) distributionof shear strain at t=20.0 ps (The two atoms highlighted by black circles correspond to that shown in (b).)
图 9 图8中放大区域的冲击压缩过程
Figure 9. Impact compression process of the enlarged region in Fig.8
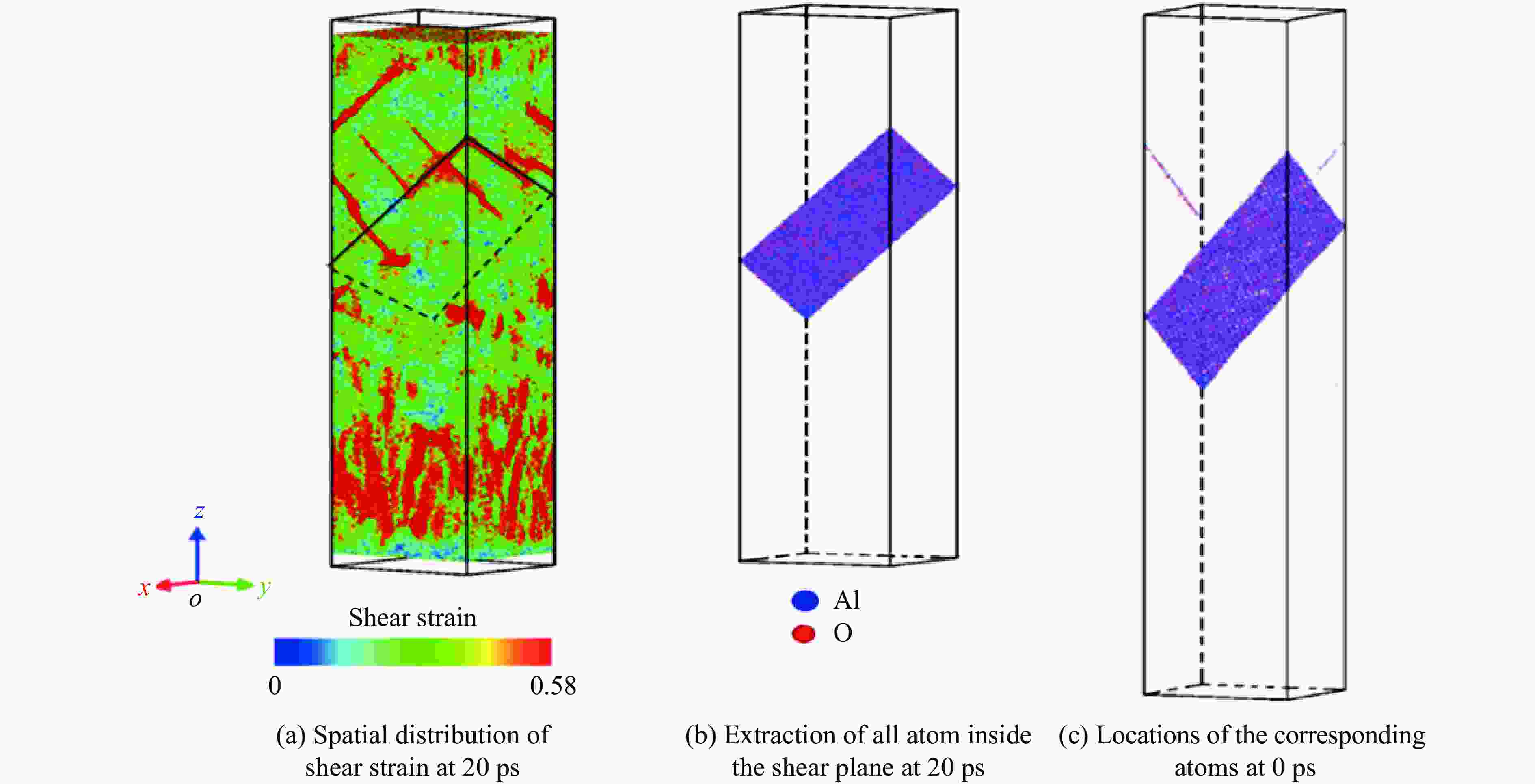
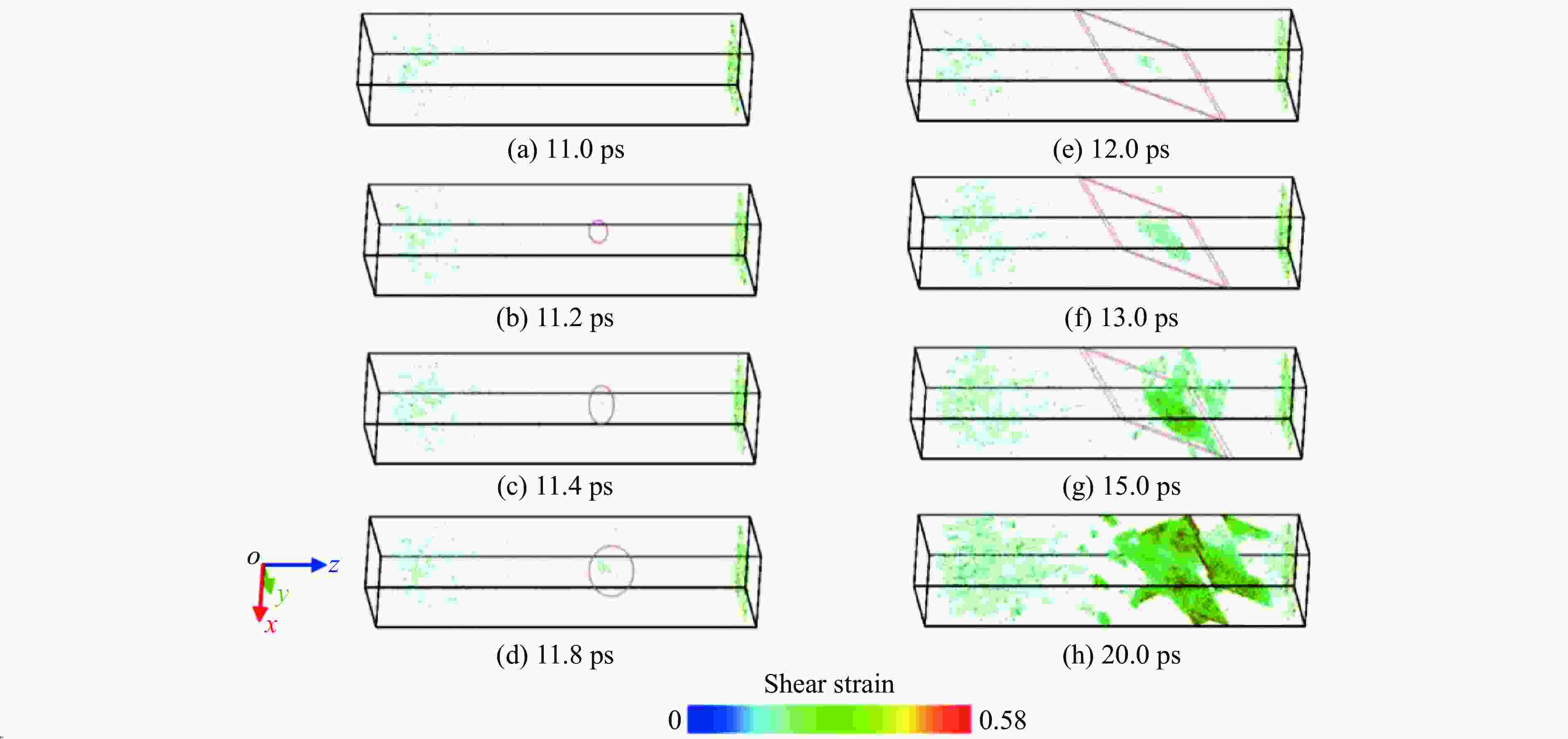
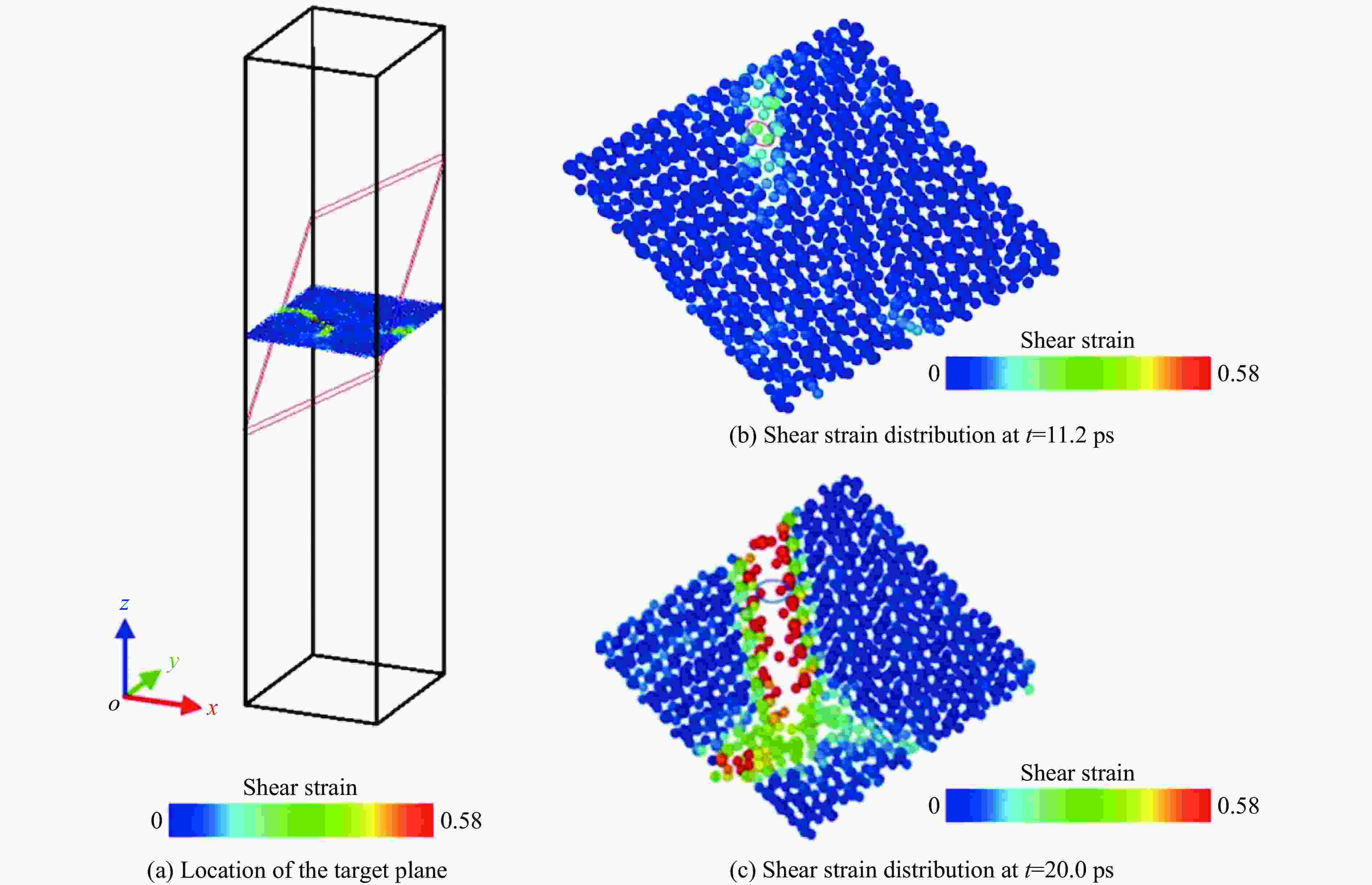
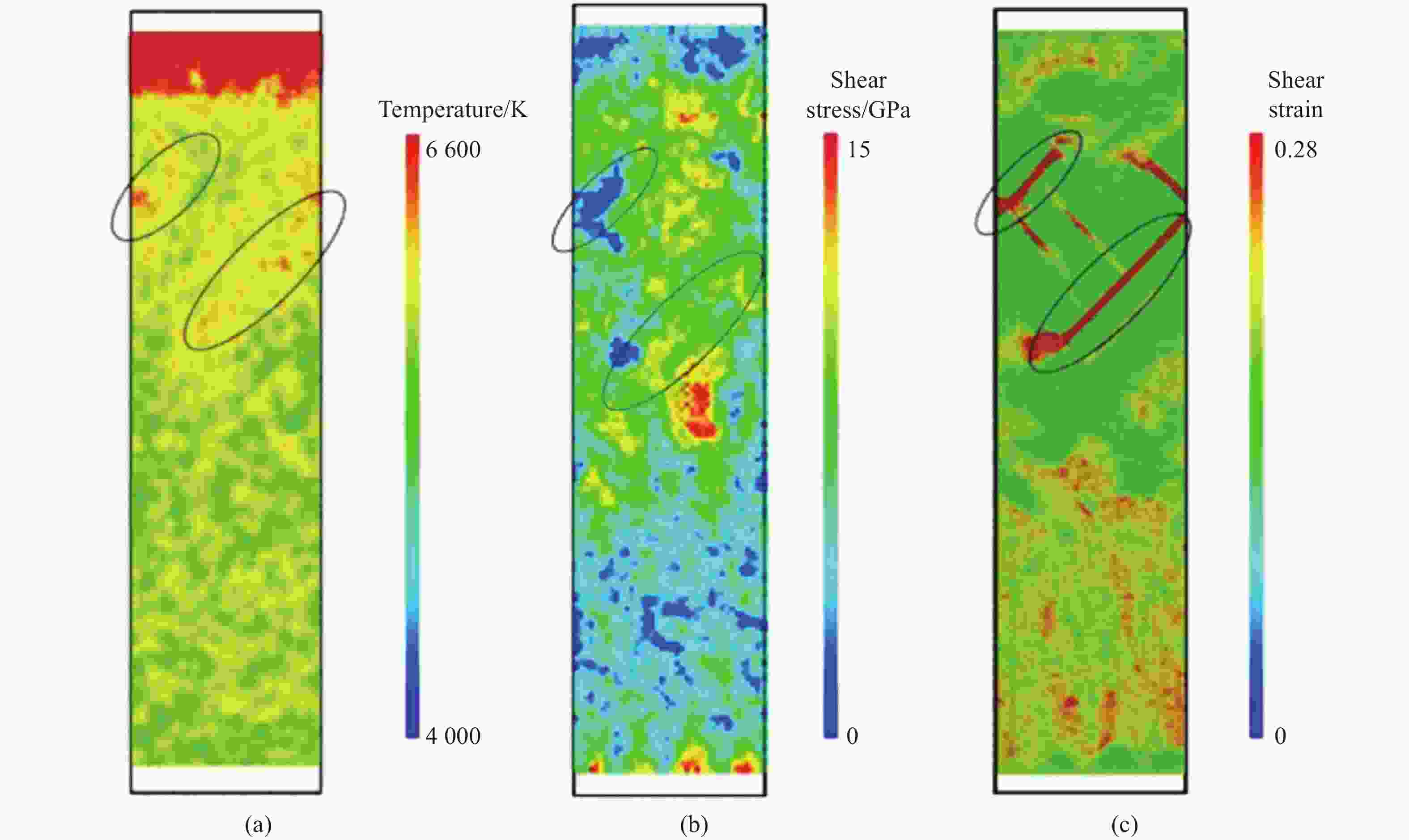
图 12 垂直于冲击方向截面的剪切应变分布：(a)截面位置，(b) 11.2 ps时剪切应变的分布，(c) 20.0 ps时剪切应变的分布
Figure 12. Shear strain distributions in the cross-section plane perpendicular to the impact direction: (a) schematic diagram of the location of the target plane; (b) shear strain distribution at t=11.2 ps; (c) shear strain distribution at t=20.0 ps
图 13 (a) t=16.0 ps时的缺陷分析结果（粉色箭头为伯格斯矢量），(b) 位错分析结果（蓝线为位错线，灰色区域为缺陷）
Figure 13. (a) Defect analysis result at t=16.0 ps (Pink arrows denote the Burgers vectors.); (b) the dislocation analysis result (The blue line represents the dislocation line, and the gray area represents the defect.)
图 14 4 km/s冲击速度下5.6 ps时试样内剪切应变等高图以及剪切应力和温度沿z轴的分布
Figure 14. Contour of shear strain inside the sample and the distributions of shear stress and temperature along the z-axis at 5.6 ps under an impact velocity of 4 km/s
-
[1] OCKENFELS T, VEWINGER F, WEITZ M. Sapphire optical viewport for high pressure and temperature applications [J]. Review of Scientific Instruments, 2021, 92(6): 065109. doi: 10.1063/5.0047609 [2] HARE D E, HOLMES N C, WEBB D J. Shock-wave-induced optical emission from sapphire in the stress range 12 to 45 GPa: images and spectra [J]. Physical Review B, 2002, 66(1): 014108. doi: 10.1103/PhysRevB.66.014108 [3] ZHANG N C, LI D, LI Y Q, et al. The radiation temperature characteristics of sapphire under shock loading [J]. Crystals, 2022, 12(10): 1364. doi: 10.3390/cryst12101364 [4] 张宁超, 王鹏, 华翔, 等. 兆巴压力下蓝宝石发光辐射特性与结构相变 [J]. 光学学报, 2019, 39(7): 0730002. doi: 10.3788/AOS201939.0730002ZHANG N C, WANG P, HUA X, et al. Optical radiation characteristics and structural phase transition of sapphire under Megabar pressure [J]. Acta Optica Sinica, 2019, 39(7): 0730002. doi: 10.3788/AOS201939.0730002 [5] LE C T, NGUYEN T T, NGUYEN T T, et al. Molecular dynamics simulation of phase transformation and mechanical behavior in Al2O3 model [J]. Vacuum, 2019, 167: 175–181. doi: 10.1016/j.vacuum.2019.06.010 [6] ZHANG C, KALIA R K, NAKANO A, et al. Hypervelocity impact induced deformation modes in α-alumina [J]. Applied Physics Letters, 2007, 91(7): 071906. doi: 10.1063/1.2753092 [7] ZHANG C, KALIA R K, NAKANO A, et al. Deformation mechanisms and damage in α-alumina under hypervelocity impact loading [J]. Journal of Applied Physics, 2008, 103(8): 083508. doi: 10.1063/1.2891797 [8] ZHANG C, KALIA R K, NAKANO A, et al. Fracture initiation mechanisms in α-alumina under hypervelocity impact [J]. Applied Physics Letters, 2007, 91(12): 121911. doi: 10.1063/1.2786865 [9] VASHISHTA P, KALIA R K, NAKANO A, et al. Interaction potentials for alumina and molecular dynamics simulations of amorphous and liquid alumina [J]. Journal of Applied Physics, 2008, 103(8): 083504. doi: 10.1063/1.2901171 [10] XU Q Q, SALLES N, CHEVALIER J, et al. Atomistic simulation and interatomic potential comparison in α-Al2O3: lattice, surface and extended-defects properties [J]. Modelling and Simulation in Materials Science and Engineering, 2022, 30(3): 035008. doi: 10.1088/1361-651X/ac4d76 [11] BRANICIO P S, KALIA R K, NAKANO A, et al. Atomistic damage mechanisms during hypervelocity projectile impact on AlN: a large-scale parallel molecular dynamics simulation study [J]. Journal of the Mechanics and Physics of Solids, 2008, 56(5): 1955–1988. doi: 10.1016/j.jmps.2007.11.004 [12] BRANICIO P S, NAKANO A, KALIA R K, et al. Shock loading on AlN ceramics: a large scale molecular dynamics study [J]. International Journal of Plasticity, 2013, 51: 122–131. doi: 10.1016/j.ijplas.2013.06.002 [13] BRANICIO P S, KALIA R K, NAKANO A, et al. Nanoductility induced brittle fracture in shocked high performance ceramics [J]. Applied Physics Letters, 2010, 97(11): 111903. doi: 10.1063/1.3478003 [14] MAKEEV M A, SRIVASTAVA D. Hypersonic velocity impact on a-SiC target: a diagram of damage characteristics via molecular dynamics simulations [J]. Applied Physics Letters, 2008, 92(15): 151909. doi: 10.1063/1.2894188 [15] MAKEEV M A, SRIVASTAVA D. Molecular dynamics simulations of hypersonic velocity impact protection properties of CNT/a-SiC composites [J]. Composites Science and Technology, 2008, 68(12): 2451–2455. doi: 10.1016/j.compscitech.2008.04.040 [16] MAKEEV M A, SUNDARESH S, SRIVASTAVA D. Shock-wave propagation through pristine a-SiC and carbon-nanotube-reinforced a-SiC matrix composites [J]. Journal of Applied Physics, 2009, 106(1): 014311. doi: 10.1063/1.3152587 [17] FENG L X, LI W H, HAHN E N, et al. Structural phase transition and amorphization in hexagonal SiC subjected to dynamic loading [J]. Mechanics of Materials, 2022, 164: 104139. doi: 10.1016/j.mechmat.2021.104139 [18] JIANG T L, YU Y, HE H L, et al. Macroscopic shock plasticity of brittle material through designed void patterns [J]. Journal of Applied Physics, 2016, 119(9): 095905. doi: 10.1063/1.4943227 [19] YU Y, WANG W Q, CHEN K G, et al. Controllable fracture in shocked ceramics: shielding one region from severely fractured state with the sacrifice of another region [J]. International Journal of Solids and Structures, 2018, 135: 137–147. doi: 10.1016/j.ijsolstr.2017.11.016 [20] 喻寅, 王文强, 杨佳, 等. 多孔脆性介质冲击波压缩破坏的细观机理和图像 [J]. 物理学报, 2012, 61(4): 048103. doi: 10.7498/aps.61.048103YU Y, WANG W Q, YANG J, et al. Mesoscopic picture of fracture in porous brittle material under shock wave compression [J]. Acta Physica Sinica, 2012, 61(4): 048103. doi: 10.7498/aps.61.048103 [21] THOMPSON A P, PLIMPTON S J, MATTSON W. General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions [J]. The Journal of Chemical Physics, 2009, 131(15): 154107. doi: 10.1063/1.3245303 [22] HAHN E N, GERMANN T C, RAVELO R, et al. On the ultimate tensile strength of tantalum [J]. Acta Materialia, 2017, 126: 313–328. doi: 10.1016/j.actamat.2016.12.033 [23] MA C, WANG G X, YE C, et al. Shocking of metallic glass to induce microstructure heterogeneity: a molecular dynamics study [J]. Journal of Applied Physics, 2017, 122(9): 095102. doi: 10.1063/1.5000366 [24] 郭志越. 单晶蓝宝石湿法刻蚀机理及表面形貌研究 [D]. 南京: 东南大学, 2019: 11–13.GUO Z Y. The anisotropic mechanism and topography research of wet etching of single-crystal sapphire [D]. Nanjing: Southeast University, 2019: 11–13. [25] 胡博, 郭亚洲, 魏秋明, 等. 绝热剪切变形中温升现象的研究进展 [J]. 高压物理学报, 2021, 35(4): 040106. doi: 10.11858/gywlxb.20210728HU B, GUO Y Z, WEI Q M, et al. Temperature rise during adiabatic shear deformation [J]. Chinese Journal of High Pressure Physics, 2021, 35(4): 040106. doi: 10.11858/gywlxb.20210728 -
下载:
点击查看大图
计量
- 文章访问数: 57
- HTML全文浏览量: 12
- PDF下载量: 13
