-
延性金属在强动载荷下的动态破坏是冲击波物理中重要的基础科学问题之一，在武器制造和装甲防护等特殊环境中具有广泛应用。层裂是延性金属在强动载荷下的一种典型动态破坏形式，不仅包含了金属材料在动态破坏过程中的丰富信息，而且层裂实验原理简单、理论分析成熟，因此一直作为研究材料动态破坏过程的主要方法[1]。Curran等[2]通过对大量实验结果进行观察，提出延性金属的层裂是由于内部的孔洞（或微损伤）成核、长大以及聚集，最后导致材料内部发生断裂，产生层裂飞片的动力学过程，这也是目前得到广泛认可的延性金属层裂的基本物理内涵。
平板撞击实验具有能够在加载过程中保持一维、平面应变载荷条件以及便于测量和分析回收的特点，是研究材料层裂的常用方式，在层裂实验中，自由面速度曲线是研究层裂演化过程最重要的参考数据之一[3]。图1为平板撞击实验原理示意图。飞片在t0时刻以一定速度撞击样片，二者相撞时会分别传入冲击波，当冲击波到达样片自由面和飞片后表面时会形成反射稀疏波，由于飞片厚度比样片厚度小，两束稀疏波会在样片内部相遇并形成拉伸区域，如果拉伸应力超过材料的动态承载极限，材料便会发生层裂[2]。通过VISAR（Velocity interferometer system for any reflector）、DISAR（Displacement interferometer system for any reflector）等诊断技术，可以得到样片的自由面速度曲线，从中可以分析得到延性金属材料动态损伤宏观响应的一系列重要信息，如加载应力幅值、拉伸应变率、层裂强度和层裂片厚度等[4]。
图 1 平板撞击实验原理及自由面速度曲线示意图
Figure 1. Theoretical illustration of the flat plate impact test and the schematic diagram of the free surface velocity curves
Meyers等[5]系统地总结和评述了20世纪80年代之前关于层裂的主要研究结果。2003年，Antoun等[3]在其著作中对21世纪以来的层裂研究历史和现状作了权威性总结。近年来，国内外学者通过实验、理论和数值模拟方法对层裂开展了深入研究。陈永涛等[6]采用等厚对称碰撞实验，对纯铁在冲击压力超过相变阈值下的层裂特性进行了研究，发现样品出现2次层裂现象。Thomas等[7]采用对称碰撞的方式对铁在低于冲击相变阈值下的层裂特性进行了研究，碰撞速度在0.2～0.4 km/s范围内，获得了铁在低速冲击下的Hugoniot弹性极限与层裂强度数据。翟少栋等[8]利用轻气炮与激光加载等方式对铝的层裂特性进行了研究，分析表明层裂强度具有明显的应变率效应。Koller等[9]研究了无氧铜在不同冲击波作用下的层裂特性，结果表明冲击波波形与峰值应力以及拉伸脉冲的持续时间对层裂损伤有显著影响。张林等[10]开展了钽在30 GPa以内冲击波加载下的层裂实验，并对不同的层裂强度计算模型进行了分析讨论。实验研究由于其自身的特点，难以直接获得样品内部物理量随时间的变化数据，只能通过自由面速度等间接获得样品内部层裂信息。而通过数值模拟方法可以提供完整的层裂演化信息，是实验研究的有力补充。目前关于层裂现象的数值仿真技术主要有有限元方法和分子动力学方法。张凤国等[11]基于应力瞬时断裂判据和Tuler-Butcher判据对延性金属在三角波加载下的多次层裂破坏问题进行了研究，分析表明延性金属层裂片厚度主要由材料本身的物理性质和加载条件决定。种涛等[12]使用一维流体动力学软件模拟了铁的冲击相变与层裂损伤之间的相互影响。贺年丰等[13]采用光滑粒子流体动力学（Smoothed particle hydrodynamics, SPH）方法对爆轰加载下锡的层裂进行了数值模拟，得到的结果与实验结果基本吻合。席涛等[14]通过分子动力学方法研究了超高应变率下铜的层裂特性，获得了铜在109～1010 s−1时的层裂强度。Glam等[15]采用数值模拟方法研究了铝在不同温度下的层裂强度与Hugonoit弹性极限，结果表明预加热的铝有更高的层裂强度。
实验研究成本高、周期长、得到的实验数据有限，数值模拟的加载范围与条件更加灵活，并且计算快速、结果直观，已经逐渐成为实验研究的重要补充。基于网格的计算方法对弹塑性材料在中低速冲击下比较可靠，但金属在高速冲击产生的高温高压环境下会表现出流体的性质，在利用传统网格方法进行数值模拟时会遇到一些困难，网格可能会发生严重扭曲，甚至会导致计算无法正常进行。SPH方法[16]是一种无网格粒子算法，相较于传统网格方法，具有精确追踪自由表面、变形边界等优势。SPH方法不依赖网格，而是将材料离散为带有质量、能量、动量的运动粒子进行计算，非常适合模拟层裂、剥落及碎片等现象。Libersky等[17]率先将材料强度效应引入SPH方法，成功地进行了高速碰撞的数值模拟计算。徐志宏等[18]利用改进的SPH方法研究了超高速碰撞问题，分析了靶板厚度、弹丸速度和形状对碎片云的影响。Zhou等[19]则利用SPH方法开展了铝球超高速撞击铝板的数值模拟，并与实验结果进行了对比。综上所述，SPH方法在模拟高速冲击中是一种有效、可行的数值方法。数值模拟结果受状态方程、本构模型和失效模型等因素的影响很大，准确合理的模型选择至关重要。
利用平板撞击实验研究金属材料在高速冲击下的动态损伤时，对冲击波的分析一般采用流体力学近似的方法，忽略固体材料抗剪切能力。要想准确地描述金属材料的复杂力学行为，就必须考虑冲击过程中非各向同性应力状态下的应力、应变、应变率和温度的变化，以及它们之间的相互关系。迄今为止，已经有一些材料模型用来描述延性金属在强动载荷下的动态破坏现象，其中被商用有限元软件广泛采用的主要有3种：Johnson-Cook（JC）模型[20]、Steinberg-Cochran-Guinan（SCG）模型[21]以及Zerilli-Armstrong（ZA）模型[22]。ZA模型基于不同微观结构（FCC、BCC结构）特点建立，参数的物理意义明确。JC模型是一种获得广泛应用的动态本构模型。在JC模型中假定材料的屈服强度与应变率相关而与压力无关，其模型参数较少，通过一维应力实验可快速获得，一般认为JC模型在应变率低于104 s−1时有较好的适用性。SCG模型则考虑了材料在强动载荷下压力和温度对剪切模量与屈服强度的影响，忽略材料在高压下的应变率效应，常用于描述高压状态下材料的动态破坏，例如铝在10 GPa以上时的应变率效应可以忽略，屈服强度和剪切模量只与温度、压力相关[21]，除此之外，SCG模型在延性金属层裂的数值模拟中也得到广泛应用[4, 13, 23-24]。
钽具有高密度、高熔点、良好的延展性和热传导性以及耐腐蚀、可焊接性好、高冲击阻抗与高断裂韧性等特点，在国防领域具有广泛应用。本研究选取钽作为研究对象，利用AUTODYN软件中的Lagrange模块与SPH模块，对钽在高速冲击下的层裂行为进行研究，对比JC、ZA、SCG模型在层裂数值模拟中的结果以及SPH方法与Lagrange方法在层裂模拟中的差异，分析自由面速度曲线的物理意义与获得的物理量之间的关系。得到的结果可以为延性金属层裂的数值模拟方法中材料模型的选择和实际工程应用提供参考。
-
JC模型[20]考虑了延性金属在强动载荷下的应变、应变率硬化和温升软化等因素，假设材料为各向同性，将应变、应变率硬化效应和温升软化效应解耦，广泛应用于表征材料在冲击作用下的动态力学行为[25-26]。JC模型的表达式为
$ \sigma =\left(A+B{\varepsilon }^{n}\right)\left(1+C\mathrm{ln}\frac{\dot{\varepsilon }}{\dot{{\varepsilon }_{0}}}\right)\left({1-{T}^{*}}^{m}\right) $ $ {T}^{*}=\frac{T-{T}_{\rm{{r}}}}{{T}_{\rm{{m}}}-{T}_{\rm{{r}}}} $ 式中：
$\sigma $ 为应力；$\varepsilon $ 为塑性应变；A、B、C、n、m为材料常数，通过试验确定；$\dot\varepsilon$ 为应变率；$ \dot{{\varepsilon }_{0}} $ 为参考应变率；Tr为参考温度；Tm为材料熔化温度。式(1)中$ \left(A+B{\varepsilon }^{n}\right) $ 描述应变硬化效应，$\left(1+C\mathrm{ln}\displaystyle\frac{\dot{\varepsilon }}{\dot{{\varepsilon }_{0}}}\right)$ 描述应变率硬化效应，$\left({1-{T}^{*}}^{m}\right)$ 描述温升软化效应。本研究中计算所采用的JC模型参数如表1[27]所示。 -
Zerilli等[22]基于热激活和位错动力学理论，建立了面心立方金属（FCC）与体心立方金属（BCC）的本构模型，ZA模型具有明确的物理意义，综合考虑了应变率与温度的影响，能够准确地描述多种延性金属的动力学行为[28-29]。对于FCC金属，ZA模型的表达式为
$ \sigma ={C}_{1}+{k}_{1}{\lambda }^{-1/2}+{C}_{2}{\varepsilon }^{1/2}\mathrm{e}\mathrm{x}\mathrm{p}(-{C}_{3}T+{C}_{4}T\mathrm{ln}\,\dot{\varepsilon }) $ 对于BCC金属，ZA模型的表达式为
$\sigma ={C}_{1}+{k}_{1}{\lambda }^{-1/2}+{C}_{2}\mathrm{exp}\left(-{C}_{3}T+{C}_{4}T\mathrm{ln}\,\dot{\varepsilon }\right)+{C}_{5}{\varepsilon }^{n} $ 式中：C1、k1、C2、C3、C4、C5为材料常数，T为温度，
$\lambda $ 为晶粒尺寸。本研究中计算所采用的ZA模型参数如表2[22]所示。 -
金属材料的屈服强度Y与剪切模量G之间存在比例关系[21, 30]，Steinberg等[21]通过研究发现，对于应变率不敏感的材料，屈服强度Y与剪切模量G成正比，即Y与G的比值为常数。基于此，Steinberg、Cochran和Guinan提出了一种适用于金属材料在高压高应变率下的本构模型，考虑了静水压力对剪切模量和屈服强度的强化效应以及温度软化效应，同时忽略了应变率效应，并假设金属在熔化状态下可以忽略材料强度。SCG模型中屈服强度Y和剪切模量G的关系表示为
$ G={G}_{0}\left[1+\left(\frac{{G}_{p}^{'}}{{G}_{0}}\right)\frac{p}{{\eta }^{1/3}}+\left(\frac{{G}_{T}^{'}}{{G}_{0}}\right)(T-300)\right] $ $ Y={Y}_{0}{\left[1+\beta {\varepsilon }_{\rm{{p}}}\right]}^{n}\frac{G}{{G}_{0}} $ 式中：
$\eta $ 为压缩比，$\varepsilon_{\rm{p}}$ 为等效塑性应变，T为温度，p为压强，G0和Y0分别为初始状态下的剪切模量和屈服强度（T = 300 K，p = 0，$\varepsilon $ = 0），$\;\beta $ 和n为材料常数。屈服强度满足
$ {Y}_{0}{\left[1+\beta {\varepsilon }_{\rm{{p}}}\right]}^{n}\leqslant {Y}_{\mathrm{m}\mathrm{a}x} $ 式中：Ymax为最大屈服强度。本研究中计算所采用的SCG模型参数如表3[21]所示。JC模型与ZA模型中采用的剪切模量、屈服强度、熔点等材料参数与SCG模型相同。
-
Mie-Grüneisen状态方程广泛应用于冲击动力学相关问题的数值模拟研究中，内嵌在AUTODYN与LS-DYNA等商业软件中，可以较为准确地描述绝大部分金属固体在冲击载荷下的动力学行为。常用于有限元软件中的形式为[13]
$ p=\frac{{\rho }_{0}{C}_{0}^{2}\mu \left(1+\mu \right)}{\left[1-\left({S}_{1}-1\right)\mu \right]}+\gamma {\rho }_{0}e $ $ \mu =\frac{\rho }{{\rho }_{0}}-1 $ 式中：
$\;\rho $ 为冲击后材料密度，$\;\rho_{0}$ 为初始材料密度，C0为初始波速，S1为材料常数，$\gamma $ 为Grüneisen系数，e为质量内能。本研究中计算所采用的Mie-Grüneisen状态方程参数如表4[31]所示。在计算中，材料密度均选用表4中给出的数值。 -
在层裂的数值模拟中，常用最大主应力失效模型与Grady失效模型。Rinehart[32]将材料静态拉伸断裂模型推广到动态断裂中，提出了最大拉应力失效模型：当材料内部拉应力
$\sigma $ 达到层裂强度$\sigma_{\rm{spall}}$ 时，材料发生层裂。最大主应力失效模型需预设层裂强度，而层裂强度是一个与冲击过程相关的物理量。Grady[33]基于断裂力学理论提出了层裂的能量平衡破碎模型，将层裂强度$\sigma_{\rm{spall}}$ 与层裂碎片平均尺寸和应变率联系起来，层裂强度随冲击加载过程而改变。对于延性金属，层裂强度$\sigma_{\rm{spall}}$ 的表达式为[34]$ {\sigma }_{\rm{{spall}}}={\left(2\rho {C}_{\rm{{b}}}^{2}Y{\varepsilon }_{\rm{{c}}}\right)}^{1/2} $ 式中：Cb为材料体积声速，
$\varepsilon_{\rm{c}}$ 为材料临界失效应变，金属材料一般取0.15[33]。 -
层裂强度是表征材料在强动载荷下性能的一个重要指标，在工程应用中具有重要参考意义，但其在实验中难以直接测量。目前关于如何计算层裂强度还没有统一的方法，常用的方法是通过样片自由面速度曲线来进行计算。Novikov[35]基于声学近似的方法给出了计算层裂强度的公式
$ {\sigma }_{\rm{{spall}}}=\frac{1}{2}{\rho }_{0}{C}_{\rm{{b}}}\Delta {u}_{\rm{{s}}} $ 式中：Δus为自由面速度曲线最大值与第一次速度拉回时的差值。
通过自由面速度曲线，可以得到样片在层裂过程中的平均拉伸应变率
$\dot{\varepsilon }_{\rm{s}}$ ，计算公式为[36]$ {\dot{\varepsilon }}_{\rm{{s}}}=\frac{\Delta {u}_{\rm{{s}}}}{\Delta {t}_{\rm{{s}}}}\frac{1}{2{C}_{\rm{{b}}}} $ 式中：Δts分别为自由面上速度最大值和第一个极小值之间的时间差。
为了能够更系统地了解自由面速度曲线，计算了自由面速度回跳速率，即极小值到峰值速度之间的斜率。回跳速率
${\dot{\varepsilon }}_{\rm{{r}}} $ 的计算公式为${\dot{\varepsilon }}_{\rm{{r}}}=\frac{\Delta {u}_{\rm{{r}}}}{\Delta {t}_{\rm{{r}}}}\frac{1}{2{C}_{\rm{{b}}}} $ 式中：Δur与Δtr分别为自由面上速度第一个极小值与其后峰值之间的速度差和时间差。
通过自由面速度曲线可以获得层裂片厚度dsp，计算公式为
$ {d}_{\rm{{sp}}}=\Delta t\frac{{C}_{\rm{{L}}}}{2} $ 式中：Δt为第一个层裂振荡周期持续时间，CL为弹性纵波声速。
-
数值模拟采用在冲击动力学研究中广泛应用的有限元软件AUTODYN[34, 37-41]。AUTODYN包含欧拉（Euler）求解器、拉格朗日(Lagrange)求解器、任意拉格朗日欧拉（ALE）求解器以及SPH求解器。相对于其他同类软件，AUTODYN中内嵌了丰富的材料模型及对应参数，便于快速部署应用。本研究中采用Lagrange与SPH两种求解器对延性金属在平板撞击下的层裂问题进行分析。Lagrange求解器对于侵彻、碰撞类低速、中速以下变形问题的模拟具有很好的适应性和精确性。SPH求解器是近年来快速发展的一种粒子类方法，没有网格束缚，可以有效地避免网格畸变问题，能方便地处理断裂、层裂、破碎等材料破坏问题[13, 34, 42]。本研究中算例的模型尺寸参数如表5所示。其中：df为飞片厚度，ds为样片厚度，Ds为样片直径，v为撞击速度。采用二维轴对称方式建模，有限元网格尺寸为0.05 mm，SPH粒子尺寸为0.10 mm。平板撞击模型与306 m/s撞击速度下的结果如图2所示。由图2可以看出，层裂区域内的材料已经完全分离，分离界面如图2中白色区域所示，这表明钽靶板在306 m/s的撞击速度下发生了完全层裂。
No. df/mm ds/mm Ds/mm v/(m·s−1) Model Module V-01 3.00 4.95 50.00 306 JC Lagrange V-02 3.00 4.95 50.00 306 JC SPH V-03 3.00 4.95 50.00 306 ZA Lagrange V-04 3.00 4.95 50.00 306 ZA SPH V-05 3.00 4.95 50.00 306 SCG Lagrange V-06 3.00 4.95 50.00 306 SCG SPH 表 5 验证模型参数设置
Table 5. Parameter settings of simulation validation cases
图 2 306 m/s撞击速度下平板撞击模型与模拟结果
Figure 2. Configuration of the plate impact simulations and simulation results at 306 m/s
-
为了分析不同本构模型与求解器对模拟结果的影响，分别采用JC、ZA、SCG模型与Lagrange和SPH求解器对撞击速度为306 m/s、飞片厚度为3.00 mm的情况进行了模拟计算，得到的自由面速度曲线与实验数据[43]的对比如图3所示。从图3中可以看出，（1）在0～2 μs内，即碰撞初始到自由面速度达到最大值阶段，Lagrange求解器的模拟结果与实验数据吻合较好，SPH求解器由于其粒子特性在速度上升段与实验数据稍有不同；二者的区别还体现在，Lagrange求解器的结果可以观察到明显的Hugoniot弹性极限信号，而SPH求解器的结果中Hugoniot弹性极限信号不是特别明显，可见SCG与ZA本构模型对钽的弹塑性行为有较好的描述。除SPH求解器结合ZA本构模型得到的自由面速度曲线最大值稍低之外，其他模拟结果都与实验数据非常接近。（2）对比层裂信号出现时的自由面速度，Lagrange求解器结合JC模型的偏差最大，差值达到65%，Lagrange求解器结合ZA、SCG模型的偏差在25%左右。SPH求解器得到的结果中，JC模型偏差最大，约为55%，而ZA、SCG模型得到的结果与实验数据基本相同。（3）对比层裂信号出现后速度回拉曲线与振荡周期，Lagrange求解器得到的模拟结果中速度回跳速率快于实验数据。具体来看，SCG模型的振荡周期与实验数据较为一致，但回跳速率最大值过高，JC、ZA模型的振荡周期均小于实验数据。SPH求解器的结果中，JC模型偏差较大，ZA模型速度回跳的最大值低于实验数据，SCG模型与实验数据比较吻合。
为了进一步验证SPH方法结合SCG本构模型的准确性，分别对比了撞击速度为212与412 m/s下的实验数据，结果如图4所示。从图4中可以看出，SPH求解器结合SCG本构模型得到的模拟结果与实验数据在各个阶段都有较好的一致性。因此，本研究采用SPH求解器与SCG模型开展钽在平板撞击下的层裂行为模拟。为了探究不同拉伸应变率下钽的层裂行为，保持样片厚度4.95 mm、直径50.00 mm不变，通过改变飞片的厚度来改变飞片自由面反射的稀疏波到达样片自由面的距离，改变样片中的冲击波卸载时间，以此达到不同的拉伸应变率，模拟参数和结果如表6所示。其中：ps为冲击压力，umax为峰值层裂速度。
图 4 不同速度下SCG-SPH模型模拟结果与实验数据对比
Figure 4. Comparison of SCG-SPH model simulation results and experimental data with different velocities
No. df/mm v/(m·s−1) ps/GPa $\dot{\varepsilon } $ 
${\sigma}{_{\rm{ {spall} } } } $ 
umax/(m·s−1) ${\dot{\varepsilon } }{_{\rm{ {r} } }}$ 
S-01 2.00 306 8.84 5.40 4.92 304.12 3.57 S-02 2.00 250 7.05 4.69 4.70 242.03 3.25 S-03 3.00 410 12.25 3.92 4.14 405.61 2.32 S-04 3.00 306 8.84 3.28 3.97 305.62 1.74 S-05 3.00 210 6.19 2.68 3.71 208.75 1.69 S-06 4.00 306 8.84 2.31 3.34 298.19 1.34 表 6 层裂模型参数与结果
Table 6. Parameters of plate impact simulations and results
按照模型参数开展了不同拉伸应变率下的层裂行为模拟，模拟结果如图5所示，拉伸应变率范围为2.13 × 104～5.40 × 104 s−1。从图5中可以看出，在相同的加载速度下，样片自由面速度曲线峰值平台持续时间逐渐延长。这是由于随着飞片厚度的增大，其自由面反射稀疏波到达样片自由面的距离增大，导致自由面速度衰减的稀疏波波头到达自由面的时间延长，自由面速度的衰减时间逐渐延后；在飞片厚度相同时，自由面速度曲线随加载速度增大而升高，峰值速度平台持续时间基本相同。
图 5 数值模拟得到的不同加载情况下的自由面速度曲线
Figure 5. Numerical simulation of free surface velocity profiles with different loading conditions
-
层裂强度是金属材料动态损伤行为的重要参数之一，本研究采用式(11)来计算钽在不同拉应变率下的层裂强度。现有研究表明，在不同加载条件下，金属材料会表现出不同的强度性质[44]。图6给出了钽的层裂强度随拉伸应变率的变化情况，从图6中可以看出，层裂强度与加载速度之间没有明确的对应关系，表明层裂强度不是一个仅受加载速度影响的物理量。进一步分析可以发现，层裂强度随拉伸应变率的增长而增加，结合式(12)，可以推断出层裂强度受冲击加载速度和应力脉冲持续时间等因素的综合作用。这表明层裂强度不是一个特定的材料常数，而是随加载情况的不同而改变。
图 6 层裂强度与拉伸应变率的关系
Figure 6. Relationship between spall strength and tensile strain rate
文献[3]给出了某铜材料的层裂强度与拉伸应变率的拟合关系
$ {\sigma }_{\rm{{spall}}}=0.15\times {\dot{\varepsilon }}^{0.2} $ 通过数值分析方法，对数值模拟得到的数据进行拟合，得到钽的层裂强度与拉伸应变率之间的关系为
$ {\sigma }_{\rm{{spall}}}=0.042\times {\dot{\varepsilon }}^{0.44} $ 图7给出了对数坐标下层裂强度与拉伸应变率之间的关系。从图7可以看出，在对数坐标下钽的层裂强度随拉伸应变率的变化呈线性增长趋势。由于本研究中数值模拟的最高拉伸应变率为5.4 × 104 s−1，在图7中还对比了更高拉伸应变率下的实验数据[45]。更高拉伸应变率下层裂强度与模拟结果呈现相同的增长趋势，并且位于模拟结果的线性拟合曲线上，这再次验证了数值模拟结果的准确性。
图 7 对数坐标下层裂强度与拉伸应变率的关系
Figure 7. Relationship between spall strength andtensile strain rate in logarithmic coordinates
除分析层裂强度与拉伸应变率的关系外，图8给出了层裂强度与回跳速率之间的关系。由图8可知，层裂强度与回跳速率之间近似呈线性增长关系，表明回跳速率与层裂强度存在一定的内在联系。
图 8 层裂强度与回跳速率的关系
Figure 8. Relationship between spall strength and bounce rate
本研究中的层裂强度根据式(11)进行计算，这也是目前研究中广泛采用的声学近似计算方法。式(11)进行了一定的简化，并未考虑塑性波和层裂片厚度等因素的影响。Stepanov等[46]指出，对于弹塑性材料，层裂冲击应以弹性纵波速度CL传播。而在它前面的入射稀疏塑性波应以体积声速Cb传播，当弹性波重要时，可以采用有效声速Ce
$ {C}_{\rm{{e}}}=2{C}_{\rm{{L}}}{C}_{\rm{{b}}}/\left({C}_{\rm{{L}}}+{C}_{\rm{{b}}}\right) $ 将式(11)修正为
$ {\sigma }_{\rm{{m}}1}={\rho }_{0}{C}_{\rm{{b}}}\Delta {u}_{\rm{{s}}}\left(\frac{1}{1+{C}_{\rm{{b}}}/{C}_{\rm{{L}}}}\right) $ 在式(11)基础上，Kanel[47]指出层裂强度的计算应考虑层裂片厚度的影响，并给出了一种考虑层裂片厚度影响的修正公式
$ {\sigma }_{\rm{{m2}}}=\frac{1}{2}{\rho }_{0}{C}_{\rm{{b}}}\Delta {u}_{\rm{{s}}}+{\delta }_{2} $ $ {\delta }_{2}=\left(\frac{{d}_{\rm{{sp}}}}{{C}_{\rm{{b}}}}-\frac{{d}_{\rm{{sp}}}}{{C}_{\rm{{L}}}}\right) \cdot \frac{\left|\dot{{u}_{1}}\dot{{u}_{2}}\right|}{\left|\dot{{u}_{1}}\right|+\dot{{u}_{2}}} \cdot \frac{1}{2}{\rho }_{0}{C}_{\rm{{b}}} $ 式中：
$ \dot{{u}_{1}} $ 为样品自由面粒子速度-时间曲线上层裂信号出现前的速度变化率，$ \dot{{u}_{2}} $ 为层裂反弹信号的速度变化率。3种方法得到的层裂强度计算结果如表7所示。从表7可以发现，第2种方法对第1种方法的修正可达8%，第3种方法的计算结果与第2种相差不大。这表明通过自由面速度曲线来计算层裂强度与选用的计算方法相关，而且不同计算模型之间存在一定差异，差异对结果的影响应该得到关注。
No. df/mm ds/mm Ds/mm v/(m·s−1) ${\sigma }{_{\rm{ {spall} }}}$ 
${\sigma }{_{\rm{ {m1} } }}$ 
${\sigma }{_{\rm{ {m2} } }}$ 
S-01 2.00 4.95 50.00 306 4.92 5.25 5.36 S-02 2.00 4.95 50.00 250 4.71 5.02 5.32 S-03 3.00 4.95 50.00 410 4.13 4.40 4.48 S-04 3.00 4.95 50.00 306 3.97 4.23 4.32 S-05 3.00 4.95 50.00 210 3.72 3.96 4.07 S-06 4.00 4.95 50.00 306 3.35 3.57 3.58 表 7 不同计算层裂强度的公式得到的数据对比
Table 7. Comparison of data obtained by different formulas for calculating the fracture strength
通过式(14)计算得到样片中的层裂片厚度dsp，结果如表8所示，其中
$\delta $ 为误差。由表8可以看出，通过计算得到的层裂片厚度与飞片厚度基本相同，表明样片发生了完全层裂，这与模拟得到的结果相同，同时也验证了所选模型的准确性。样片发生完全层裂时，自由面速度曲线表现出规则的振荡，如图5中所示，自由面速度曲线振幅逐渐减小，表明层裂片中的脉冲在往返过程中逐渐衰减。完全层裂的应力波传播过程如图1所示。No. df/mm ds/mm v/(m·s−1) dsp/mm $\delta $ 
S-01 2.00 4.95 306 1.96 2.0 S-02 2.00 4.95 250 1.92 4.0 S-03 3.00 4.95 410 3.05 2.7 S-04 3.00 4.95 306 2.89 3.4 S-05 3.00 4.95 210 2.92 2.7 S-06 4.00 4.95 306 3.91 2.3 表 8 不同撞击速度下层裂片厚度
Table 8. Spall scab thickness at different impact velocities
-
Hugoniot弹性极限描述了在一维应变压缩条件下，金属材料发生非弹性变形时的纵向应力值，是应力-体积状态转折点，也是重要的评价金属材料抵抗动态破坏能力的指标[48]。从自由面速度曲线可以得到钽的Hugoniot弹性极限
$ {\sigma }_{\rm{{HEL}}}=\frac{1}{2}{\rho }_{0}{C}_{\rm{{L}}}{u}_{\rm{{HEL}}} $ 式中：uHEL为Hugoniot弹性极限出现时对应的自由面速度，对应自由面速度曲线中出现的第一个短平台。表9给出了由式(21)计算得到的Hugoniot弹性极限。从表9中可以看出，Hugoniot弹性极限随加载条件的改变而改变，
$\sigma_{\rm{{HEL}}}$ 的范围为1.77～2.09 GPa，张林[45]通过实验数据得到钽在冲击压力范围8.9～22.6 GPa下的$\sigma_{\rm{{HEL}}}$ 为1.8～2.6 GPa，表明通过数值模拟得到的Hugoniot弹性极限是合理的，当然在更高的冲击压力下，钽有更高的Hugoniot弹性极限。No. v/(m·s−1) ps/GPa $\sigma{_{\rm{HEL} }}$ 
S-01 306 8.84 1.96 S-02 250 7.05 1.89 S-03 410 12.25 2.09 S-04 306 8.84 1.95 S-05 210 6.19 1.77 S-06 306 8.84 1.95 表 9 不同撞击速度下的Hugoniot弹性极限
Table 9. Hugoniot elastic limit at different impact velocities
Hugoniot弹性极限与冲击压力的关系如图9所示。通过数值分析，采用指数形式拟合σHEL与冲击压力数据，得到
图 9 不同冲击压力下Hugoniot弹性极限
Figure 9. Hugoniot elastic limit under different impact pressures
$ {\sigma }_{\rm{{HEL}}}=1.198{{p}_{\rm{{s}}}^{0.224}} $ 将式(21)扩展到17 GPa后，与实验数据进行对比，发现有较好的吻合性。这表明冲击压力越大，钽发生非弹性变形时的纵向应力值越高，即动态屈服强度越高。
-
以自由面速度曲线中第一个极小值为起点，至其后第一个峰值速度平台，分析自由面速度曲线的变化情况，如图10所示。从图10中可以看出，自由面速度回跳曲线随加载速度和飞片厚度的变化没有明显的变化趋势，结合表6中计算的加载应变率信息，发现随着加载应变率的提高，曲线逐渐变得陡峭，斜率逐渐增大。
图 10 自由面速度曲线第一个极小值之后的速度曲线
Figure 10. Free surface velocity profiles afterthe first minimal speed
利用式(13)计算了钽的自由面速度回跳速率，图11给出了回跳速率与拉伸应变率的关系。从图11可知，回跳速率随着拉伸应变率的升高而增长，二者近似呈线性变化趋势。Kanel等[49]在对铝和镁的层裂特性分析中，发现了自由面速度回跳速率与损伤演化之间存在正相关的特点，二者呈线性关系
图 11 应变率对钽样品回跳速率的影响
Figure 11. Influence of strain rate on bounce rate of tantalum samples
$ D\propto {\dot{\varepsilon }}_{\rm{{r}}} $ 式中：D为样片中孔隙率的增长速率。结合本研究中钽的数值模拟数据，可以推断钽在层裂过程中样片内部的损伤演化速率同样随着拉伸应变率的增长而增加，与其他延性金属具有相似的动态损伤演化特点。
-
以延性金属钽为研究对象，通过对不同本构模型结合Lagrange以及SPH求解器，对钽在平面冲击下的层裂行为进行了数值模拟，分析了JC、ZA、SCG本构模型以及Lagrange和SPH求解器在数值模拟中的差异，通过改变飞片厚度与加载速度来改变冲击加载应变率，对不同加载条件下的自由面速度曲线特性进行了分析，得到以下主要结论。
（1）JC模型在模拟中与实验数据相差较大，ZA与SCG模型在模拟弹塑性转变过程中有较好的表现，综合对比，SCG模型得到的模拟结果与实验数据有更好的一致性。
（2）Lagrange求解器在模拟钽的弹塑性转变过程有较好的表现，能够观测到明显的Hugoniot弹性极限信号。SPH求解器得到的结果与实验数据更符合，能够更全面地描述层裂全过程中的自由面速度曲线变化情况，表明利用SPH方法研究钽的层裂行为是可行的。
（3）钽的层裂强度与加载速度没有明确的对应关系，层裂强度随拉伸应变率的增加而增大，二者近似呈指数关系。进一步对比层裂强度随自由面速度回跳速率的关系，结果表明自由面速度回跳速率也是层裂行为的一种反映，应该得到关注。通过观察发现自由面速度回跳速率与拉伸应变率之间近似为线性关系，随拉伸应变率的增加而增大。
钽靶板在冲击下层裂过程的数值模拟
Numerical Simulation of Spalling Process of Tantalum Target under Impacts
-
摘要: 对平面冲击加载下延性金属钽的层裂行为开展了数值模拟研究。利用AUTODYN软件中的Lagrange与SPH求解模块，考察了3种本构模型Johnson-Cook、Steinberg-Cochran-Guinan与Zerilli-Armstrong的模拟结果，结合实验数据对模拟结果进行了验证；在此基础上，通过改变撞击速度与飞片厚度，获得了不同应变率下的自由面速度曲线，分析了不同应变率下的层裂特性。结果表明：在2.31×104～5.40×104 s−1应变率范围内，SPH求解器结合Steinberg-Cochran-Guinan本构模型的结果与实验数据具有较好的一致性；金属钽的层裂强度随拉伸应变率的增加而增大，在对数坐标系下近似呈线性关系；不同层裂强度计算方法得到的结果差异可达8%；随着拉伸应变率的增加，自由面速度回跳速率随之增长。最后，对自由面速度曲线中的特征参量的物理意义进行了解读。Abstract: In this paper, the spallation characteristics of tantalum (Ta) under plate-impact loading are studied through numerical simulation. The feasibility and reliability of the Lagrange and smooth particle hydrodynamics (SPH) methods and several constitutive models (the Johnson-Cook, Steinberg-Cochran-Guinan and Zerilli-Armstrong model) are discussed. Comparison between the simulation results with experimental data, it is found that using the SPH method combined with the Steinberg-Cochran-Guinan constitutive model could produce the best consistency in the strain rate range from 2.31 × 104 s−1 to 5.40 × 104 s−1 for Ta. In addition, by changing the impact velocity and the thickness of the flyer, the free surface velocity curves under different strain rates are obtained, and the spalling characteristics under different strain rates are calculated and discussed. Characteristic parameters of spallation are calculated by using the free surface velocity data. The results have shown that the spalling strength of Ta increases with the strain rate, and is approximately linear in the logarithmic coordinate. Several computation methods of spall strength are considered in this work, and the difference between the results obtained by different methods are within the range of 8%. On the other side of the spectrum, the bounce rate of the free surface velocity increases with increasing strain rate. Finally, the physical meaning of the characteristic parameters in the free surface velocity curve is also discussed.
-
Key words:
- spallation /
- ductile metal /
- plate impact /
- tantalum /
- free surface velocity
-
图 1 平板撞击实验原理及自由面速度曲线示意图
Figure 1. Theoretical illustration of the flat plate impact test and the schematic diagram of the free surface velocity curves
图 2 306 m/s撞击速度下平板撞击模型与模拟结果
Figure 2. Configuration of the plate impact simulations and simulation results at 306 m/s
图 4 不同速度下SCG-SPH模型模拟结果与实验数据对比
Figure 4. Comparison of SCG-SPH model simulation results and experimental data with different velocities
图 5 数值模拟得到的不同加载情况下的自由面速度曲线
Figure 5. Numerical simulation of free surface velocity profiles with different loading conditions
图 6 层裂强度与拉伸应变率的关系
Figure 6. Relationship between spall strength and tensile strain rate
图 7 对数坐标下层裂强度与拉伸应变率的关系
Figure 7. Relationship between spall strength andtensile strain rate in logarithmic coordinates
图 9 不同冲击压力下Hugoniot弹性极限
Figure 9. Hugoniot elastic limit under different impact pressures
图 10 自由面速度曲线第一个极小值之后的速度曲线
Figure 10. Free surface velocity profiles afterthe first minimal speed
图 11 应变率对钽样品回跳速率的影响
Figure 11. Influence of strain rate on bounce rate of tantalum samples
Material A/MPa B/MPa n C m Tantalum 142 164 0.31 0.057 0.88 
下载: 导出CSV
Material C1/MPa k1/(MPa·mm1/2) C2/MPa C3/(10−3 K−1) C4/(10−3 K−1) C5/MPa n Tantalum 1 125 10 178 5.35 0.327 310 0.44
下载: 导出CSV
Material G0/MPa Y0/GPa Ymax/GPa β n $G{_p}^{'}$ $G{_T}^{'}/(\rm{MPa\text{·}K}{^{-1} } )$ $T {\rm{_m}}/\rm{K} $ Tantalum 69 0.77 1.10 10 0.1 1.005 −8.97 4 340
下载: 导出CSV
Material $\;\rho $0/(kg·m−3) C0/(m·s−1) S1 $\gamma $ Tantalum 16 690 3 340 1.20 1.67
下载: 导出CSV
表 5 验证模型参数设置
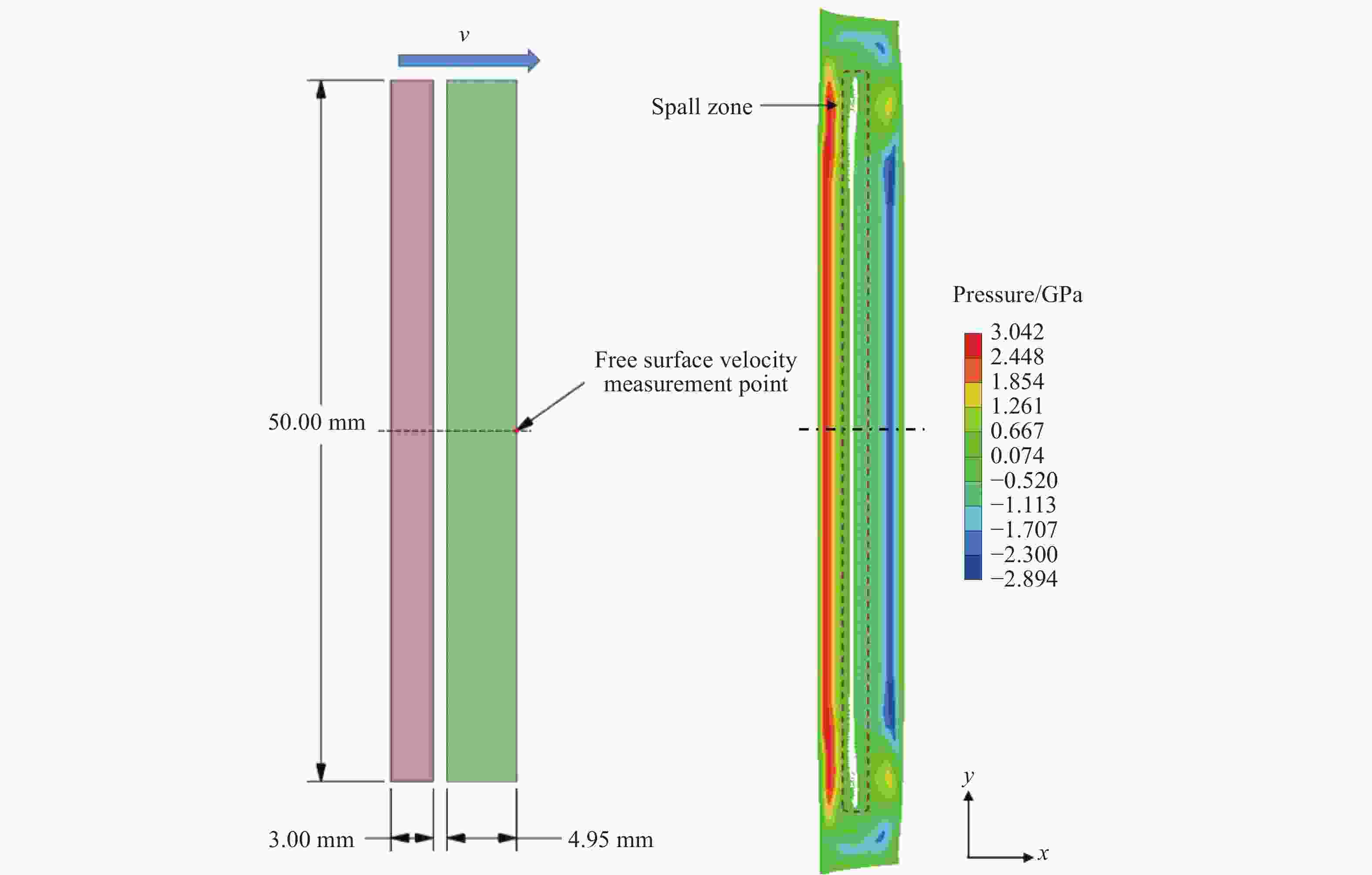
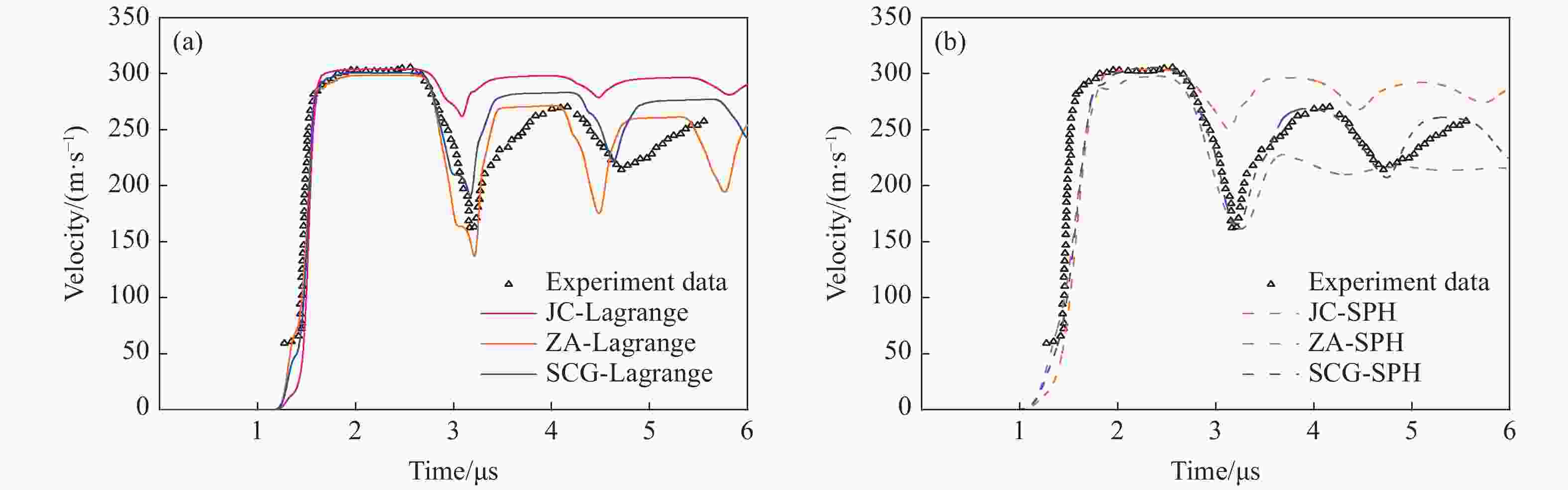
Table 5. Parameter settings of simulation validation cases
No. df/mm ds/mm Ds/mm v/(m·s−1) Model Module V-01 3.00 4.95 50.00 306 JC Lagrange V-02 3.00 4.95 50.00 306 JC SPH V-03 3.00 4.95 50.00 306 ZA Lagrange V-04 3.00 4.95 50.00 306 ZA SPH V-05 3.00 4.95 50.00 306 SCG Lagrange V-06 3.00 4.95 50.00 306 SCG SPH
下载: 导出CSV
表 6 层裂模型参数与结果
Table 6. Parameters of plate impact simulations and results
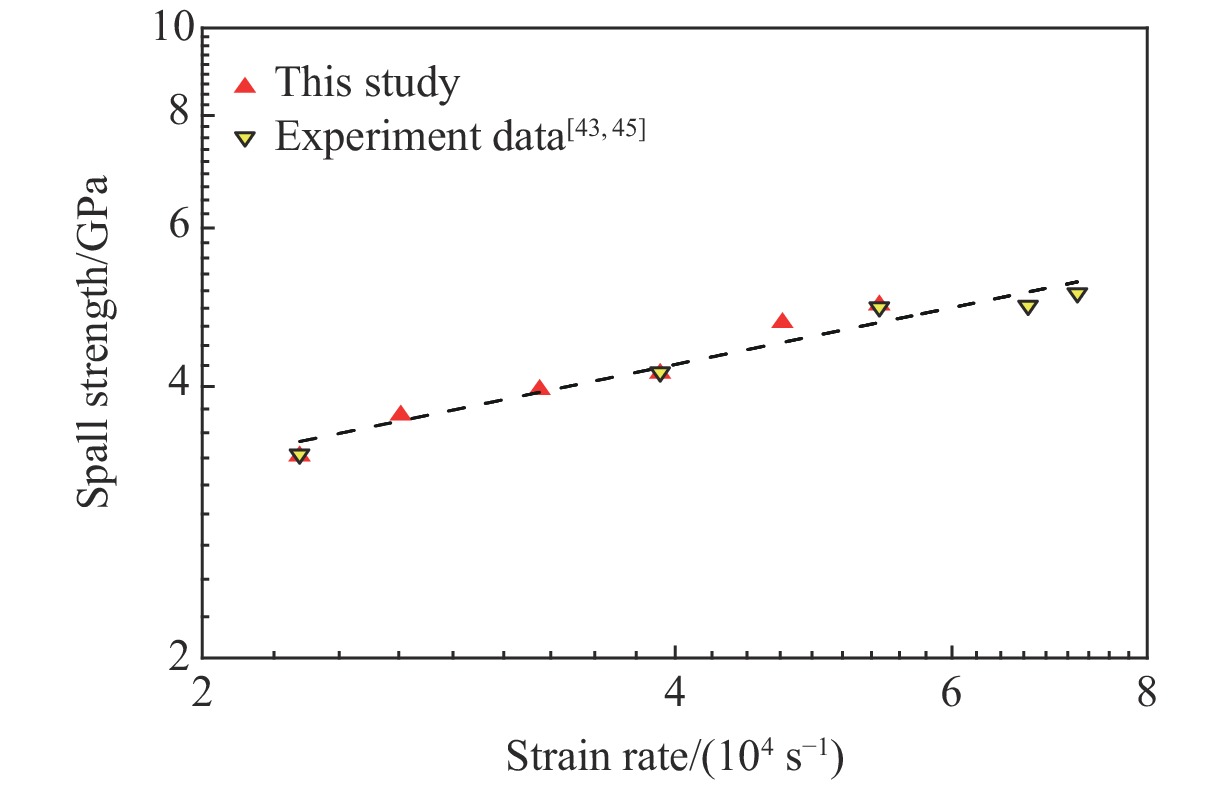
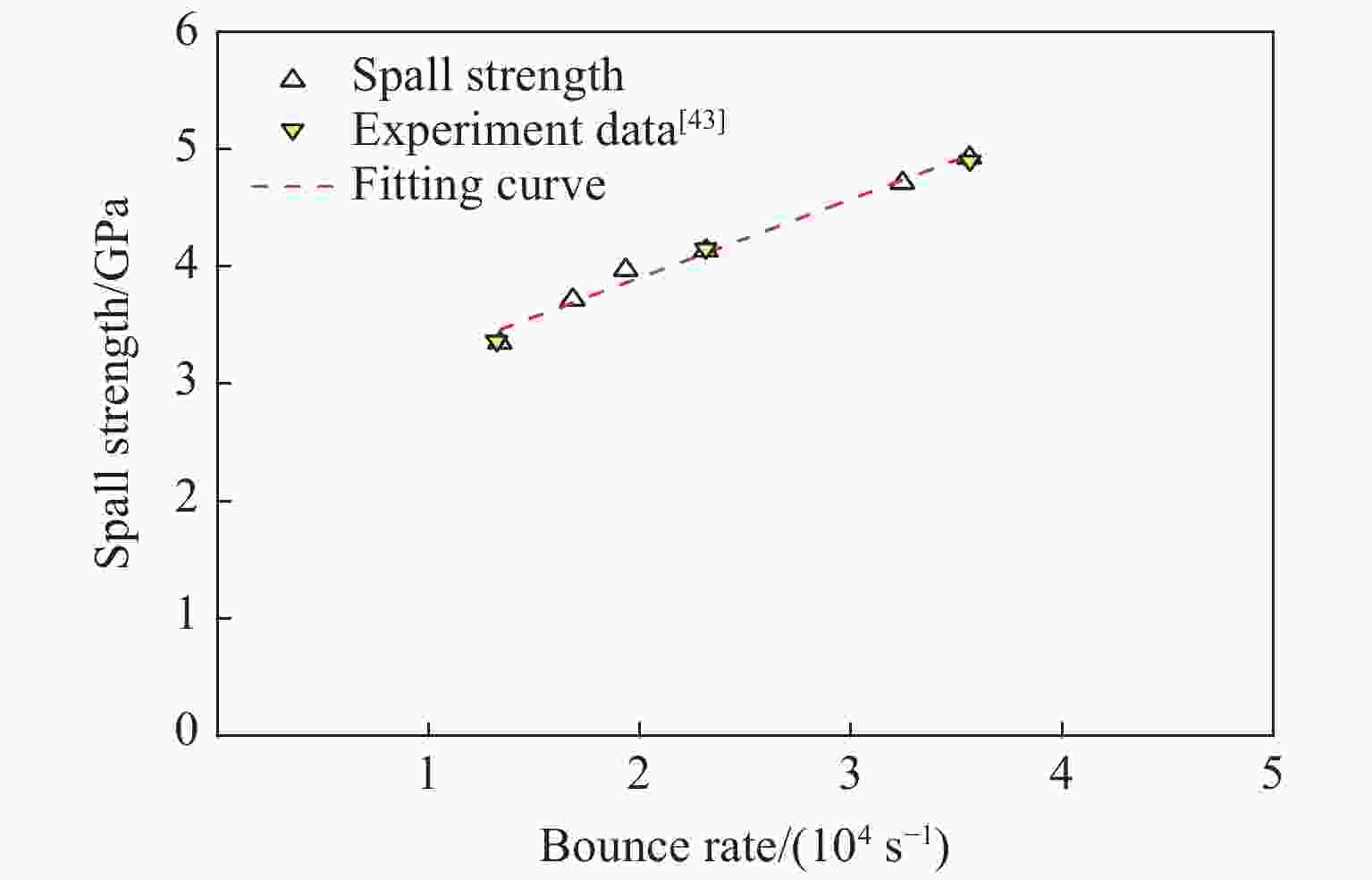
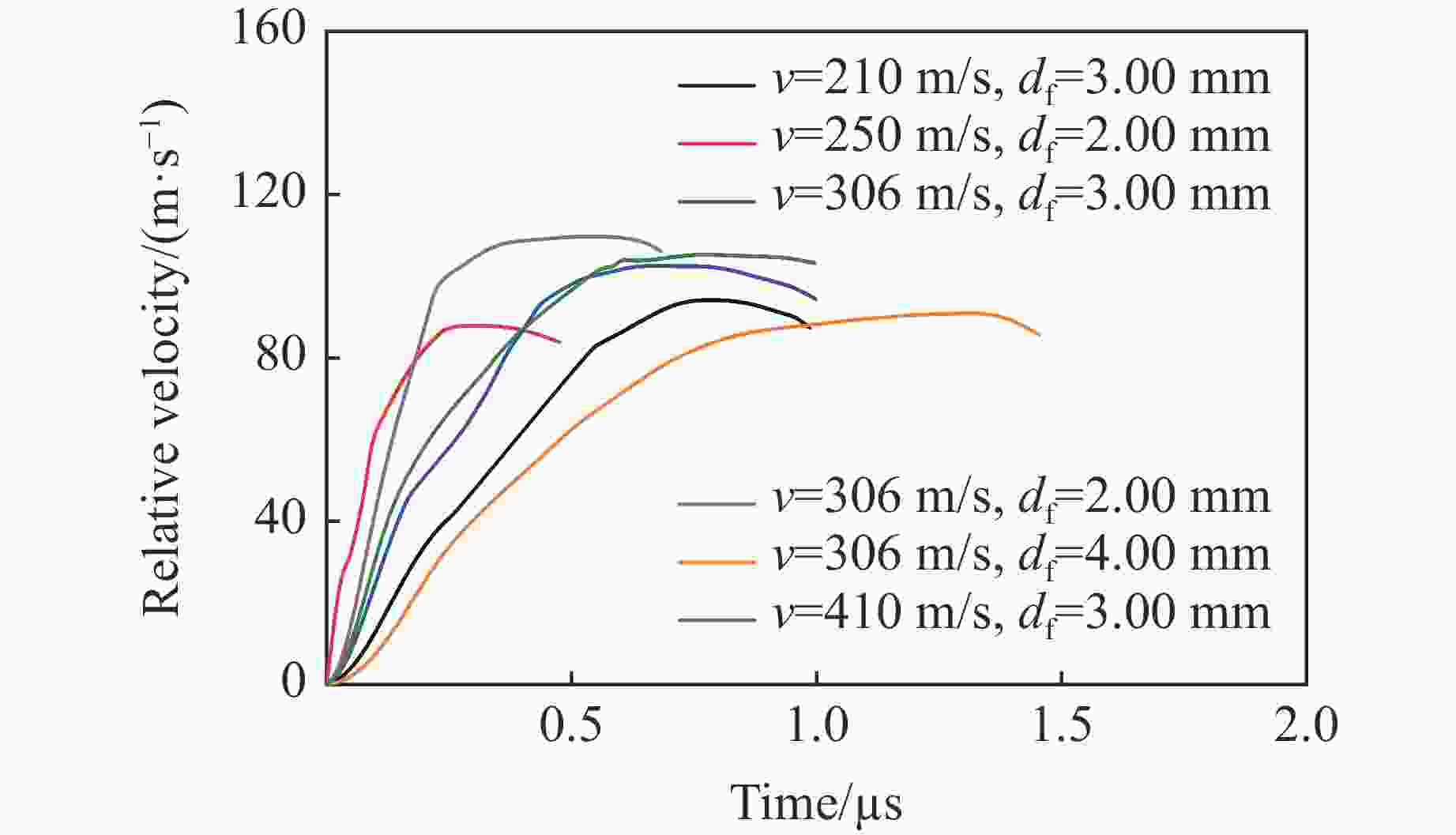
No. df/mm v/(m·s−1) ps/GPa $\dot{\varepsilon } $/(104 s−1) ${\sigma}{_{\rm{ {spall} } } } $/GPa umax/(m·s−1) ${\dot{\varepsilon } }{_{\rm{ {r} } }}$/(104 s−1) S-01 2.00 306 8.84 5.40 4.92 304.12 3.57 S-02 2.00 250 7.05 4.69 4.70 242.03 3.25 S-03 3.00 410 12.25 3.92 4.14 405.61 2.32 S-04 3.00 306 8.84 3.28 3.97 305.62 1.74 S-05 3.00 210 6.19 2.68 3.71 208.75 1.69 S-06 4.00 306 8.84 2.31 3.34 298.19 1.34
下载: 导出CSV
表 7 不同计算层裂强度的公式得到的数据对比
Table 7. Comparison of data obtained by different formulas for calculating the fracture strength
No. df/mm ds/mm Ds/mm v/(m·s−1) ${\sigma }{_{\rm{ {spall} }}}$/GPa ${\sigma }{_{\rm{ {m1} } }}$/GPa ${\sigma }{_{\rm{ {m2} } }}$/GPa S-01 2.00 4.95 50.00 306 4.92 5.25 5.36 S-02 2.00 4.95 50.00 250 4.71 5.02 5.32 S-03 3.00 4.95 50.00 410 4.13 4.40 4.48 S-04 3.00 4.95 50.00 306 3.97 4.23 4.32 S-05 3.00 4.95 50.00 210 3.72 3.96 4.07 S-06 4.00 4.95 50.00 306 3.35 3.57 3.58
下载: 导出CSV
表 8 不同撞击速度下层裂片厚度
Table 8. Spall scab thickness at different impact velocities
No. df/mm ds/mm v/(m·s−1) dsp/mm $\delta $/% S-01 2.00 4.95 306 1.96 2.0 S-02 2.00 4.95 250 1.92 4.0 S-03 3.00 4.95 410 3.05 2.7 S-04 3.00 4.95 306 2.89 3.4 S-05 3.00 4.95 210 2.92 2.7 S-06 4.00 4.95 306 3.91 2.3
下载: 导出CSV
表 9 不同撞击速度下的Hugoniot弹性极限
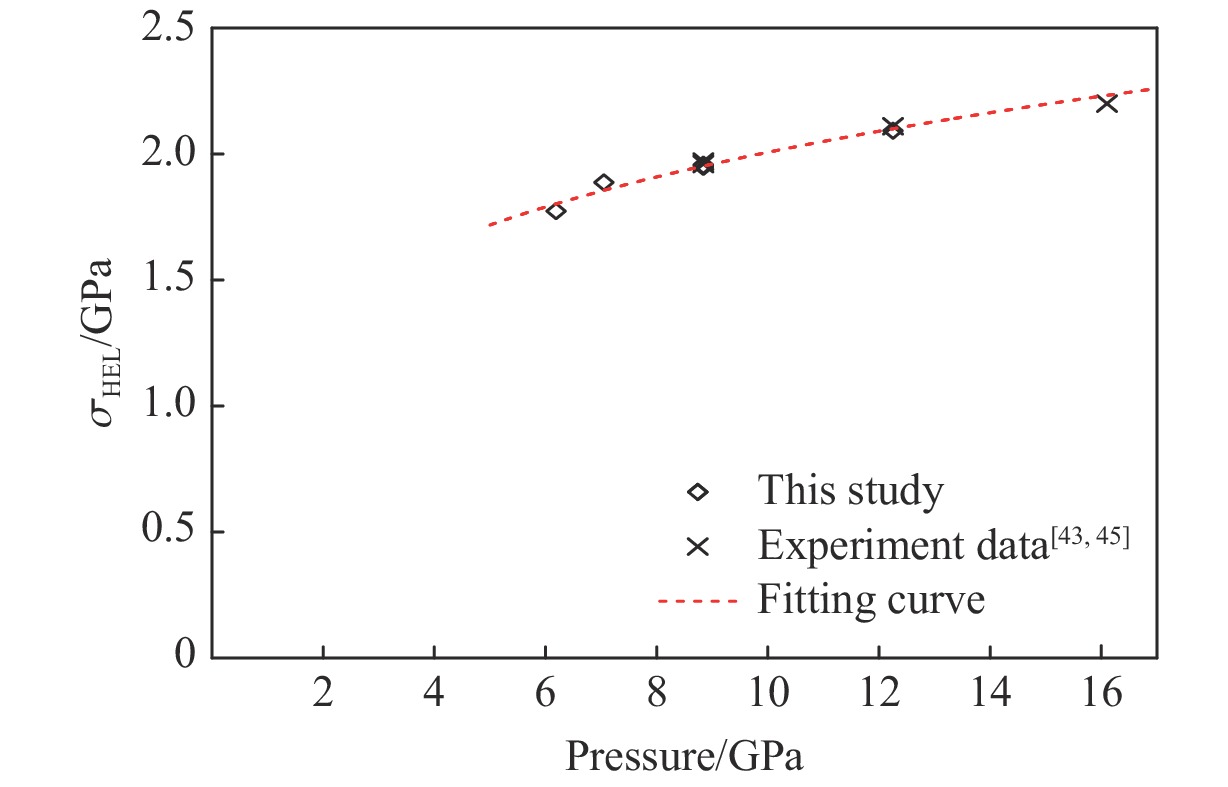
Table 9. Hugoniot elastic limit at different impact velocities
No. v/(m·s−1) ps/GPa $\sigma{_{\rm{HEL} }}$/GPa S-01 306 8.84 1.96 S-02 250 7.05 1.89 S-03 410 12.25 2.09 S-04 306 8.84 1.95 S-05 210 6.19 1.77 S-06 306 8.84 1.95
下载: 导出CSV
-
[1] 裴晓阳, 彭辉, 贺红亮, 等. 延性金属层裂自由面速度曲线物理涵义解读 [J]. 物理学报, 2015, 64(3): 034601. doi: 10.7498/aps.64.034601
PEI X Y, PENG H, HE H L, et al. Discussion on the physical meaning of free surface velocity curve in ductile spallation [J]. Acta Physica Sinica, 2015, 64(3): 034601. doi: 10.7498/aps.64.034601[2] CURRAN D R, SEAMAN L, SHOCKEY D A. Dynamic failure of solids [J]. Physics Reports, 1987, 147(5/6): 253–388. [3] ANTOUN T H, CURRAN D R, RAZORENOV S V, et al. Spall fracture [M]. New York: Springer-Verlag Press, 2003: 93–94. [4] CHEN D N, FAN C L, XIE S G, et al. Study on constitutive relations and spall models for oxygen-free high-conductivity copper under planar shock tests [J]. Journal of Applied Physics, 2007, 101(6): 063532. doi: 10.1063/1.2711405 [5] MEYERS M A, AIMONE C T. Dynamic fracture (spalling) of metals [J]. Progress in Materials Science, 1983, 28(1): 1–96. doi: 10.1016/0079-6425(83)90003-8 [6] 陈永涛, 唐小军, 李庆忠, 等. 纯铁材料的冲击相变与“反常”层裂 [J]. 爆炸与冲击, 2009, 29(6): 637–641. doi: 10.3321/j.issn:1001-1455.2009.06.014
CHEN Y T, TANG X J, LI Q Z, et al. Phase transition and abnormal spallation in pure iron [J]. Explosion and Shock Waves, 2009, 29(6): 637–641. doi: 10.3321/j.issn:1001-1455.2009.06.014[7] THOMAS S A, HAWKINS M, MATTHES M K, et al. Dynamic strength properties and alpha-phase shock Hugoniot of iron and steel [J]. Journal of Applied Physics, 2018, 123(17): 175902. doi: 10.1063/1.5019484 [8] 翟少栋, 李英华, 彭建祥, 等. 平面碰撞与强激光加载下金属铝的层裂行为 [J]. 爆炸与冲击, 2016, 36(6): 767–773. doi: 10.11883/1001-1455(2016)06-0767-07
ZHAI S D, LI Y H, PENG J X, et al. Spall behavior of pure aluminum under plate-impact and high energy laser shock loadings [J]. Explosion and Shock Waves, 2016, 36(6): 767–773. doi: 10.11883/1001-1455(2016)06-0767-07[9] KOLLER D D, HIXSON R S, GRAY G T, et al. Influence of shock-wave profile shape on dynamically induced damage in high-purity copper [J]. Journal of Applied Physics, 2005, 98(10): 103518. doi: 10.1063/1.2128493 [10] 张林, 蔡灵仓, 王悟, 等. 钽在冲击载荷下的动态力学特性 [J]. 高压物理学报, 2001, 15(4): 265–270. doi: 10.3969/j.issn.1000-5773.2001.04.005
ZHANG L, CAI L C, WANG W, et al. The dynamic mechanic characteristics of Tantalum under shock loading [J]. Chinese Journal of High Pressure Physic, 2001, 15(4): 265–270. doi: 10.3969/j.issn.1000-5773.2001.04.005[11] 张凤国, 刘军, 王裴, 等. 三角波强加载下延性金属多次层裂破坏问题 [J]. 爆炸与冲击, 2018, 38(3): 659–664.
ZHANG F G, LIU J, WANG P, et al. Multi-spall in ductile metal under triangular impulse loading [J]. Explosion and Shock Waves, 2018, 38(3): 659–664.[12] 种涛, 唐志平, 谭福利, 等. 纯铁相变和层裂损伤的数值模拟 [J]. 高压物理学报, 2018, 32(1): 014102.
CHONG T, TANG Z P, TAN F L, et al. Numerical simulation of phase transition and spall of iron [J]. Chinese Journal of High Pressure Physics, 2018, 32(1): 014102.[13] 贺年丰, 任国武, 陈永涛, 等. 爆轰加载下金属锡层裂破碎数值模拟 [J]. 爆炸与冲击, 2019, 39(4): 042101.
HE N F, REN G W, CHEN Y T, et al. Numerical simulation on spallation and fragmentation of tin under explosive loading [J]. Explosion and Shock Waves, 2019, 39(4): 042101.[14] 席涛, 范伟, 储根柏, 等. 超高应变率载荷下铜材料层裂特性研究 [J]. 物理学报, 2017, 66(4): 040202. doi: 10.7498/aps.66.040202
XI T, FAN W, CHU G B, et al. Spall behavior of copper under ultra-high strain rate loading [J]. Acta Physica Sinica, 2017, 66(4): 040202. doi: 10.7498/aps.66.040202[15] GLAM B, STRAUSS M, ELIEZER S, et al. Shock compression and spall formation in aluminum containing helium bubbles at room temperature and near the melting temperature: experiments and simulations [J]. International Journal of Impact Engineering, 2014, 65: 1–12. doi: 10.1016/j.ijimpeng.2013.10.010 [16] LIU M B, LIU G R. Smoothed particle hydrodynamics (SPH): an overview and recent developments [J]. Archives of Computational Methods in Engineering, 2010, 17(1): 25–76. doi: 10.1007/s11831-010-9040-7 [17] LIBERSKY L D, PETSCHEK A G. Smooth particle hydrodynamics with strength of materials [M]//TREASE H E, FRITTS M F, CROWLEY W P. Advances in the free-Lagrange method: Springer-Verlag Berlin Heidelberg GmbH, 1991: 248–257. [18] 徐志宏, 汤文辉, 罗永. 光滑粒子模拟方法在超高速碰撞现象中的应用 [J]. 爆炸与冲击, 2006, 26(1): 53–58. doi: 10.3321/j.issn:1001-1455.2006.01.009
XU Z H, TANG W H, LUO Y. Applications of the smoothed particle hydrodynamics method to hypervelocity impact simulations [J]. Explosion and Shock Waves, 2006, 26(1): 53–58. doi: 10.3321/j.issn:1001-1455.2006.01.009[19] ZHOU C E, LIU G R, LOU K Y. Three-dimensional penetration simulation using smoothed particle hydrodynamics [J]. International Journal of Computational Methods, 2007, 4(4): 671–691. doi: 10.1142/S0219876207000972 [20] JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures [J]. Engineering Fracture Mechanics, 1985, 21(1): 31–48. doi: 10.1016/0013-7944(85)90052-9 [21] STEINBERG D J, COCHRAN S G, GUINAN M W. A constitutive model for metals applicable at high-strain rate [J]. Journal of Applied Physics, 1980, 51(3): 1498–1504. doi: 10.1063/1.327799 [22] ZERILLI F J, ARMSTRONG R W. Dislocation-mechanics-based constitutive relations for material dynamics calculations [J]. Journal of Applied Physics, 1987, 61(5): 1816–1825. doi: 10.1063/1.338024 [23] 王泽平, 恽寿榕. 延性材料层裂的数值模拟 [J]. 爆炸与冲击, 1991, 11(1): 20–25.
WANG Z P, YUN S R. Numerical calculations of spallation in ductile solids [J]. Explosion and Shock Waves, 1991, 11(1): 20–25.[24] EAKINS D E, THADHANI N N. Instrumented Taylor anvil-on-rod impact tests for validating applicability of standard strength models to transient deformation states [J]. Journal of Applied Physics, 2006, 100(7): 073503. doi: 10.1063/1.2354326 [25] TENG X, WIERZBICKI T. Evaluation of six fracture models in high velocity perforation [J]. Engineering Fracture Mechanics, 2006, 73(12): 1653–1678. doi: 10.1016/j.engfracmech.2006.01.009 [26] WANG X M, SHI J. Validation of Johnson-Cook plasticity and damage model using impact experiment [J]. International Journal of Impact Engineering, 2013, 60: 67–75. doi: 10.1016/j.ijimpeng.2013.04.010 [27] 樊雪飞, 李伟兵, 王晓鸣, 等. 药型罩材料性能参数对双模毁伤元成型的影响 [J]. 含能材料, 2017, 25(11): 888–895. doi: 10.11943/j.issn.1006-9941.2017.11.002
FAN X F, LI W B, WANG X M, et al. Effects of liner’s material properties on the forming of dual mode damage elements [J]. Chinese Journal of Energetic Materials, 2017, 25(11): 888–895. doi: 10.11943/j.issn.1006-9941.2017.11.002[28] MIRZAIE T, MIRZADEH H, CABRERA J M. A simple Zerilli-Armstrong constitutive equation for modeling and prediction of hot deformation flow stress of steels [J]. Mechanics of Materials, 2016, 94: 38–45. doi: 10.1016/j.mechmat.2015.11.013 [29] ABED F H, VOYIADJIS G Z. A consistent modified Zerilli-Armstrong flow stress model for BCC and FCC metals for elevated temperatures [J]. Acta Mechanica, 2005, 175(1/2/3/4): 1–18. [30] PRESTON D L, TONKS D L, WALLACE D C. Model of plastic deformation for extreme loading conditions [J]. Journal of Applied Physics, 2003, 93(1): 211–220. doi: 10.1063/1.1524706 [31] MARSH S P. LASL shock Hugoniot data [M]. Berkeley: University of California Press, 1980: 136. [32] RINEHART J S. Some quantitative data bearing on the scabbing of metals under explosive attack [J]. Journal of Applied Physics, 1951, 22(5): 555–560. doi: 10.1063/1.1700005 [33] GRADY D E. The spall strength of condensed matter [J]. Journal of the Mechanics and Physics of Solids, 1988, 36(3): 353–384. doi: 10.1016/0022-5096(88)90015-4 [34] 邸德宁, 陈小伟. 碎片云SPH方法数值模拟中的材料失效模型 [J]. 爆炸与冲击, 2018, 38(5): 948–956. doi: 10.11883/bzycj-2017-0328
DI D N, CHEN X W. Material failure models in SPH simulation of debris cloud [J]. Explosion and Shock Waves, 2018, 38(5): 948–956. doi: 10.11883/bzycj-2017-0328[35] NOVIKOV S A. Spall strength of materials under shock load [J]. Journal of Applied Mechanics and Technical Physics, 1967, 3: 109–120. [36] DALTON D A, BREWER J L, BERNSTEIN A C, et al. Laser-induced spallation of aluminum and Al alloys at strain rates above 2 × 106 s−1 [J]. Journal of Applied Physics, 2008, 104(1): 013526. doi: 10.1063/1.2949276 [37] THAM C Y. Reinforced concrete perforation and penetration simulation using AUTODYN-3D [J]. Finite Elements in Analysis and Design, 2005, 41(14): 1401–1410. doi: 10.1016/j.finel.2004.08.003 [38] 石永相, 施冬梅, 李文钊, 等. ZrCuNiAlAg块体非晶合金JH-2模型研究 [J]. 爆炸与冲击, 2019, 39(9): 093104. doi: 10.11883/bzycj-2018-0221
SHI Y X, SHI D M, LI W Z, YU Z T, et al. Study on JH-2 model of the ZrCuNiAlAg bulk amorphous alloy [J]. Explosion and Shock Waves, 2019, 39(9): 093104. doi: 10.11883/bzycj-2018-0221[39] 陈龙明, 李志斌, 陈荣. 装药动爆冲击波特性研究 [J]. 爆炸与冲击, 2020, 40(1): 013201. doi: 10.11883/bzycj-2019-0029
CHEN L M, LI Z B, CHEN R. Characteristics of dynamic explosive shock wave of moving charge [J]. Explosion and Shock Waves, 2020, 40(1): 013201. doi: 10.11883/bzycj-2019-0029[40] 王韫泽, 王树山, 魏平亮, 等. 穿甲弹异物阻滞膛炸机理数值仿真分析 [J]. 兵工学报, 2018, 39(5): 859–866. doi: 10.3969/j.issn.1000-1093.2018.05.004
WANG Y Z, WANG S S, WEI P L, et al. Numerical simulation and analysis of bore premature of armor piercer caused by foreign matter obstruction [J]. Acta Armamentarii, 2018, 39(5): 859–866. doi: 10.3969/j.issn.1000-1093.2018.05.004[41] HUANG H, JIAO Q J, NIE J X, et al. Numerical modeling of underwater explosion by one-dimensional ANSYS-AUTODYN [J]. Journal of Energetic Materials, 2011, 29(4): 292–325. doi: 10.1080/07370652.2010.527898 [42] 孙晓旺, 章杰, 王肖钧, 等. 应力波数值计算中的SPH方法 [J]. 爆炸与冲击, 2017, 37(1): 21–26. doi: 10.11883/1001-1455(2017)01-0021-06
SUN X W, ZHANG J, WANG X J, et al. Application of SPH in stress wave simulation [J]. Explosion and Shock Waves, 2017, 37(1): 21–26. doi: 10.11883/1001-1455(2017)01-0021-06[43] CZARNOTA C, JACQUES N, MERCIER S, et al. Modelling of dynamic ductile fracture and application to the simulation of plate impact tests on tantalum [J]. Journal of the Mechanics and Physics of Solid, 2008, 56(4): 1624–1650. doi: 10.1016/j.jmps.2007.07.017 [44] ARMSTRONG R W, WALLEY S M. High strain rate properties of metals and alloys [J]. International Materials Reviews, 2008, 53(3): 105–128. doi: 10.1179/174328008X277795 [45] 张林. 延性材料冲击响应: 动态损伤与断裂、结构相变的新模型 [D]. 绵阳: 中国工程物理研究院, 2005.
[46] STEPANOV G V, ROMANCHENKO V I, ASTANIN V V. Experimental determination of failure stresses under spallation in elastic-plastic waves [J]. Probl Strength, 1977, 8: 96–99. [47] KANEL G I. Dynamic strength of materials [J]. Fatigue & Fracture of Engineering Materials & Structures, 1999, 22(11): 1011–1020. [48] KANEL G I, FORTOV V E, RAZORENOV S V. Shock-wave phenomena and the properties of condensed matter [M]. New York: Springer, 2004. [49] KANEL G I, RAZORENOV S V, BOGATCH A, et al. Simulation of spall fracture of aluminum and magnesium over a wide range of load duration and temperature [J]. International Journal of Impact Engineering, 1997, 20(6/7/8/9/10): 467–478. -
点击查看大图
图(11)表(9)
计量
- 文章访问数: 931
- 阅读全文浏览量: 178
- PDF下载量: 8
