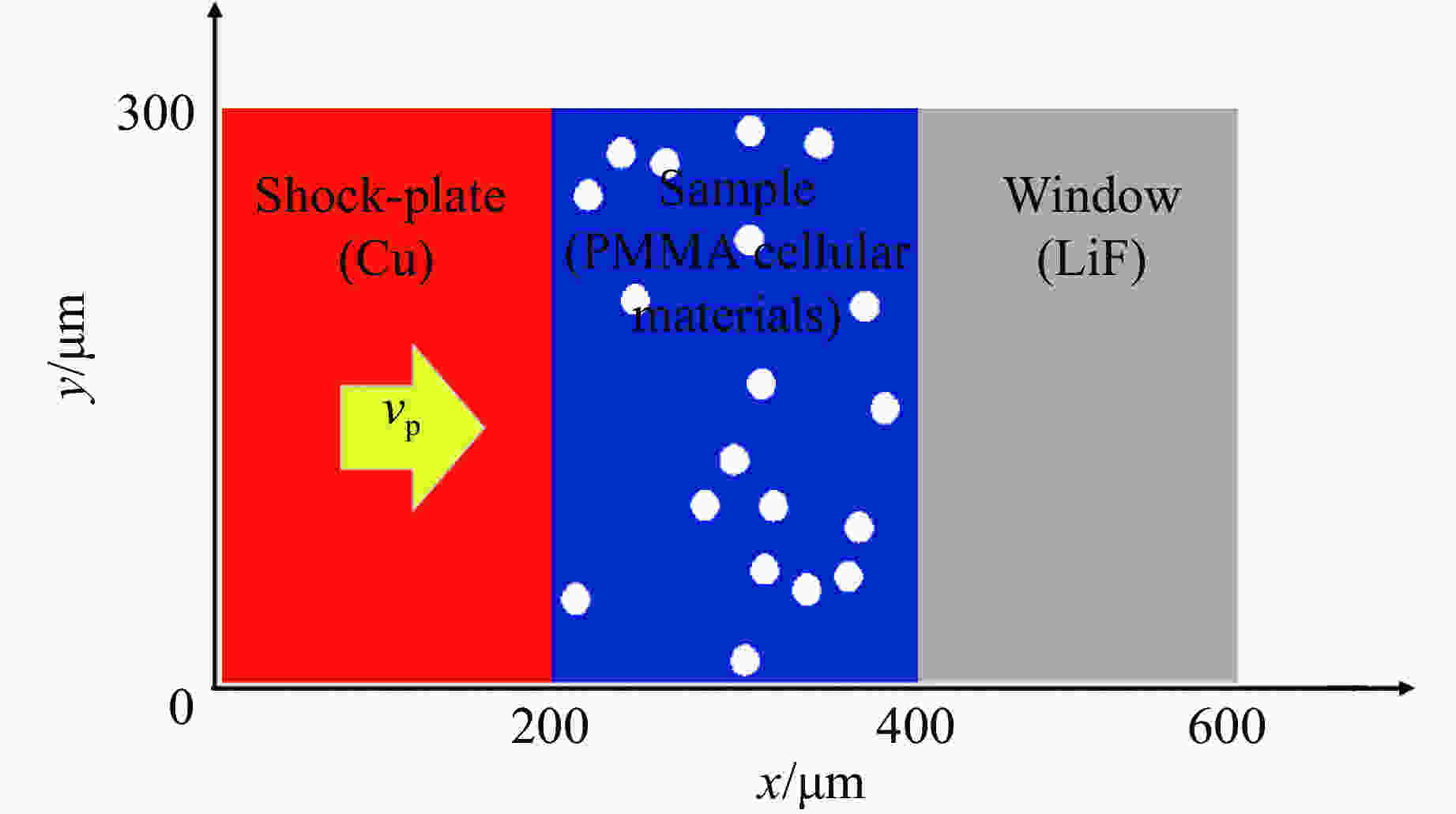
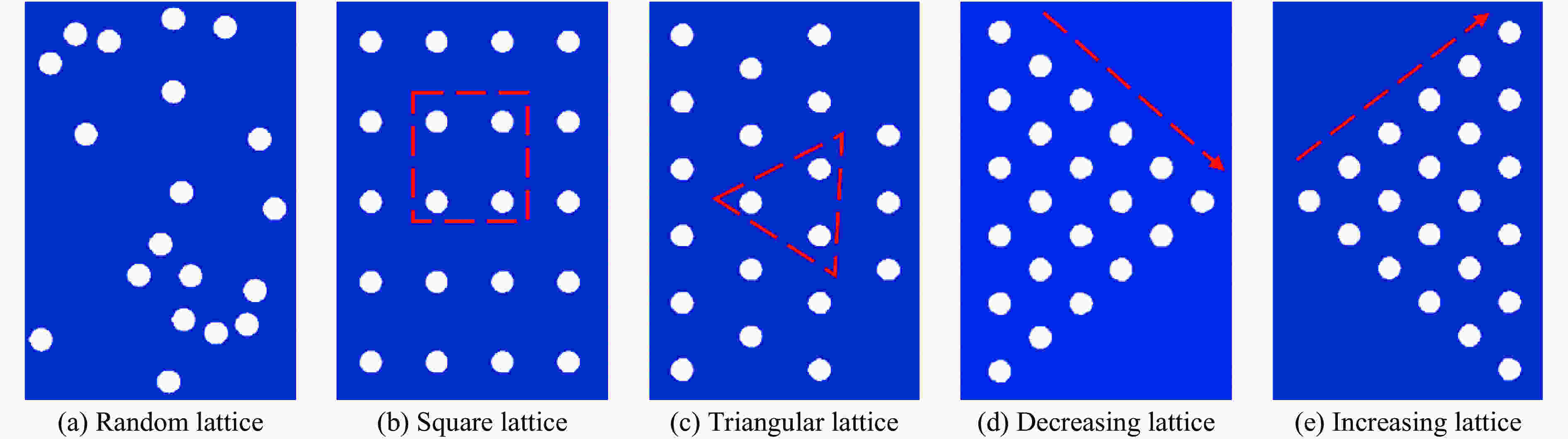
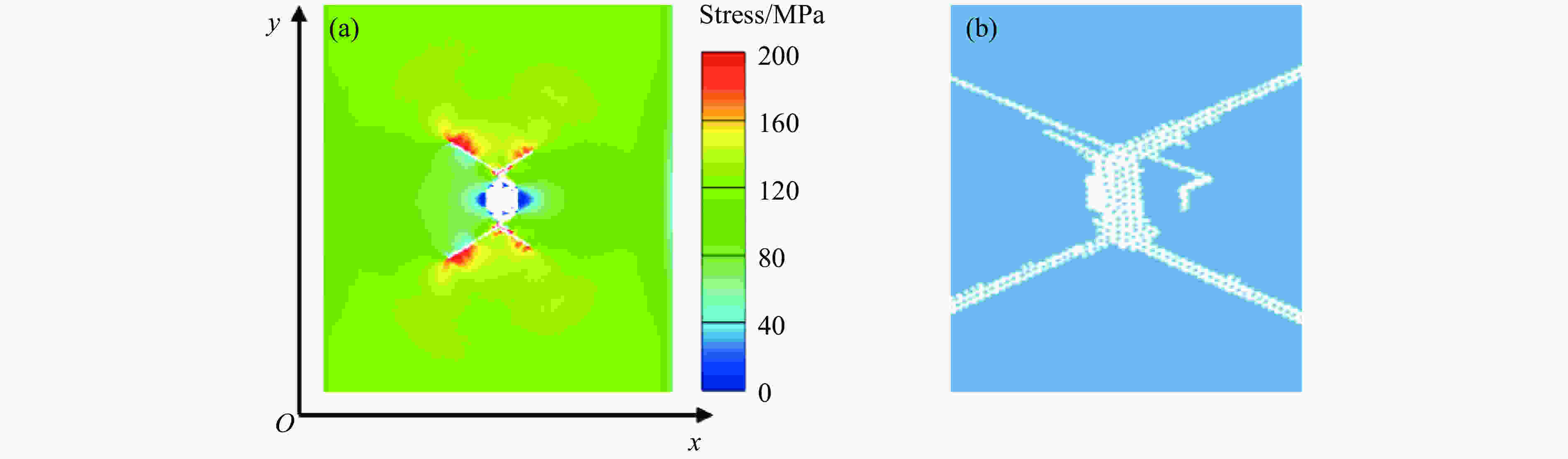
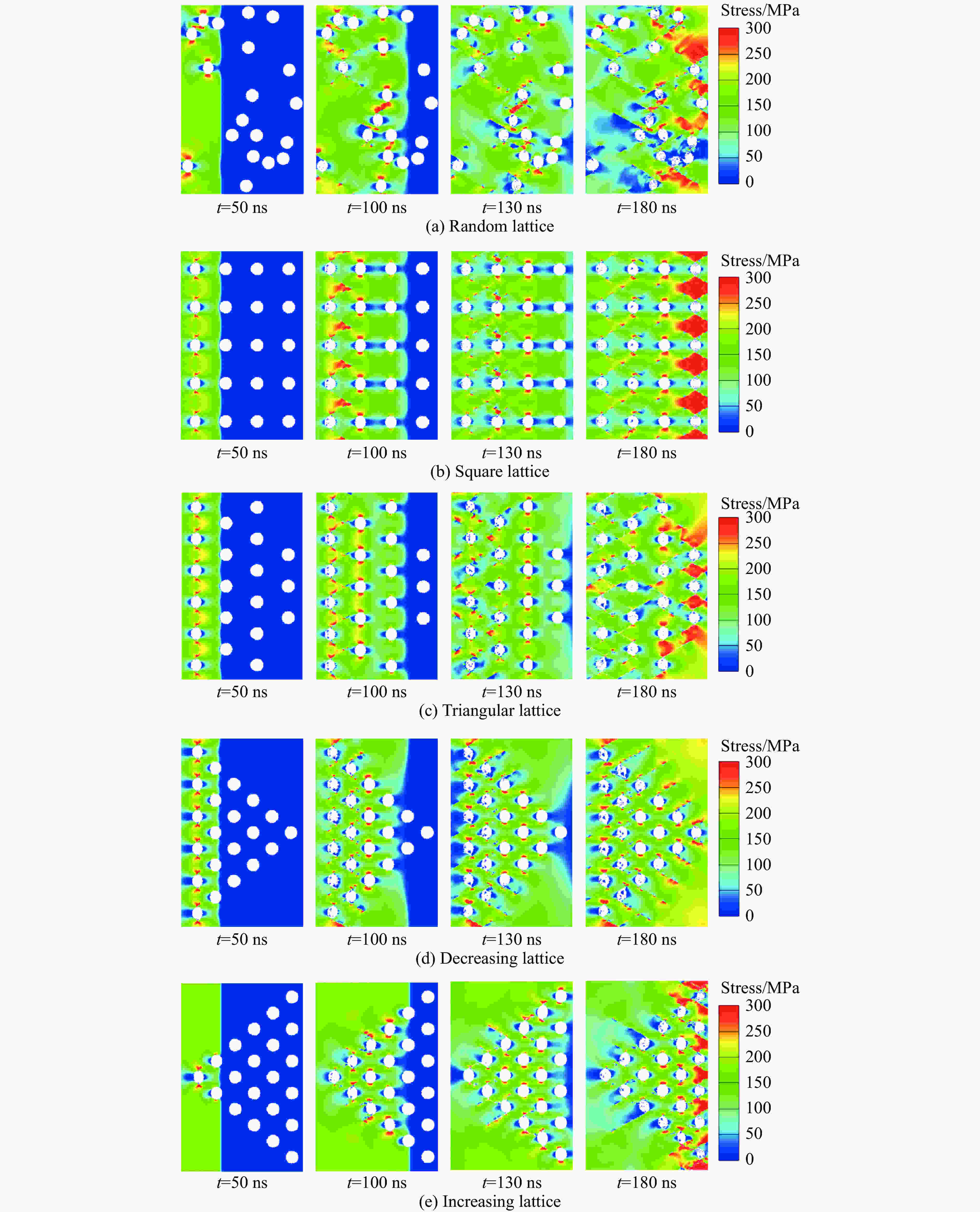
Effect of Voids Arrangement on Behavior of PMMA Cellular Materials on Impact Loading
-
摘要: 多孔材料具有轻质、缓冲减震、吸能等特点,在加载路径调控、爆炸或冲击防护领域具有广泛的应用前景。采用格点-弹簧模型(离散元方法),模拟多种孔洞排布方式的PMMA多孔材料在冲击加载过程中的早期孔洞塌缩破坏、应力分布与粒子速度等冲击响应行为。结果表明:在冲击加载过程中,裂纹萌发于孔洞侧向(垂直于冲击波方向)附近区域,孔洞破坏形式以剪切断裂为主;在不同的孔洞排列模型中,孔洞与孔洞之间均存在剪切裂纹相互贯通现象,促进孔洞体积压缩致密化,且孔洞排列方式不影响冲击波传播速度;四角点阵模型有效减缓孔洞附近区域的应力集中;四角点阵、三角点阵、锥形递减排列、锥形递增排列模型都显著影响PMMA多孔材料的冲击波阵面平整性;孔洞的随机排列模型对降低粒子速度最有效,四角点阵排列模型对降低波阵面后压力贡献最大。Abstract: Cellular materials, characterized by their light weight and energy absorbing, etc., have broad potential applications in the fields of loading-path control, explosion and impact protection. In this paper, the discrete element method of lattice-spring model is utilized to simulate the early impact response of PMMA cellular materials with different arrangement models of voids during the impact loading process. The early void collapse failure, stress distribution and particle velocity of materials with various arrangement models are investigated. Our results show that the arrangement of voids affect the particle velocity but not the shock wave velocity. The cracks are germinated in the area near the longitudinal direction of the void, and the failure mode of the void is mainly shear failure. In different arrangement models of voids, there is a phenomenon of shear cracks interpenetrating between the holes, which promotes the compression of the volume. The square lattice and triangular lattice arrangement models prominently slow the stress concentration and plastic deformation rate of voids in the nearby area. The square lattice, triangular lattice, decreasing arrangement and increasing arrangement significantly have a remarkable influence on the flatness of the shock wave front of PMMA cellular materials. The random arrangement is the most effective one to reduce the particle velocity, and the square lattice contributes most to the post-pressure reduction of the wave front.
-
Key words:
- cellular materials /
- arrangement model of voids /
- shock wave /
- impact loading
-
表 1 模型各部分材料的物性参数
Table 1. Specific physical parameters of each part of the model
Material R/μm $\delta $/μm E/GPa $\;\mu$ $\;\rho$/(kg·m−3) $\gamma $/(J·m−2) Cu 200 110 0.25 8 960 50 000 PMMA 10 200 3 0.20 1 180 10 LiF 200 65 0.10 2 640 表 2 5种孔洞排列模型中的粒子速度与波阵面后应力
Table 2. Particle velocities and stresses in the five arrangements modes of void
Modes Particle velocity/(m·s−1) Stress/MPa Random lattice 142.6 56.11 Square lattice 155.0 29.74 Triangular lattice 151.5 62.84 Decreasing lattice 161.7 58.13 Increasing lattice 158.9 55.39 -
[1] HU L L, YU T X. Dynamic crushing strength of hexagonal honeycombs [J]. International Journal of Impact Engineering, 2010, 37(5): 467–474. doi: 10.1016/j.ijimpeng.2009.12.001 [2] SUN Y L, LI Q M. Dynamic compressive behaviour of cellular materials: a review of phenomenon, mechanism and modelling [J]. International Journal of Impact Engineering, 2018, 112: 74–115. doi: 10.1016/j.ijimpeng.2017.10.006 [3] DUAN Y, ZHAO X H, LIU Z Y, et al. Dynamic response of additively manufactured graded foams [J]. Composites Part B: Engineering, 2020, 183: 107630. doi: 10.1016/j.compositesb.2019.107630 [4] STAPF S. Porous materials: how molecules huddle in holes [J]. Nature Physics, 2006, 2(11): 731–732. doi: 10.1038/nphys441 [5] GUILLARD F, GOLSHAN P, SHEN L M, et al. Dynamic patterns of compaction in brittle porousmedia [J]. Nature Physics, 2015, 11(10): 835–838. doi: 10.1038/nphys3424 [6] 许爱国, 张广财, 蔚喜军, 等. 冲击作用下多孔材料热力学特征的模拟与分析 [J]. 中国工程科学, 2009, 11(9): 13–19. doi: 10.3969/j.issn.1009-1742.2009.09.003XU A G, ZHANG G C, YU X J, et al. Simulation study of shock wave reaction on porous material [J]. Engineering Sciences, 2009, 11(9): 13–19. doi: 10.3969/j.issn.1009-1742.2009.09.003 [7] SETCHELL R E. Shock wave compression of the ferroelectric ceramic Pb0.99(Zr0.95Ti0.05)0.98Nb0.02O3: microstructural effects [J]. Journal of Applied Physics, 2007, 101(5): 053525. doi: 10.1063/1.2697428 [8] BRANCH B, IONITA A, PATTERSON B M, et al. A comparison of shockwave dynamics in stochastic and periodic porous polymer architectures [J]. Polymer, 2019, 160: 325–337. doi: 10.1016/j.polymer.2018.10.074 [9] BRANCH B, IONITA A, CLEMENTS B E, et al. Controlling shockwave dynamics using architecture in periodic porous materials [J]. Journal of Applied Physics, 2017, 121(13): 135102. doi: 10.1063/1.4978910 [10] LIU Y, ZHANG X C. The influence of cell micro-topology on the in-plane dynamic crushing of honeycombs [J]. International Journal of Impact Engineering, 2009, 36(1): 98–109. doi: 10.1016/j.ijimpeng.2008.03.001 [11] ZHENG Z J, YU J L, LI J R. Dynamic crushing of 2D cellular structures: a finite element study [J]. International Journal of Impact Engineering, 2005, 32(1/2/3/4): 650–664. doi: 10.1016/j.ijimpeng.2005.05.007 [12] ZHAO F P, WU H A, LUO S N. Microstructure effects on shock response of Cu nanofoams [J]. Journal of Applied Physics, 2013, 114(7): 073501. doi: 10.1063/1.4818487 [13] HERRING S D, GERMANN T C, GRØNBECH-JENSEN N. Effects of void size, density, and arrangement on deflagration and detonation sensitivity of a reactive empirical bond order high explosive [J]. Physical Review B, 2010, 82(21): 214108. doi: 10.1103/PhysRevB.82.214108 [14] 姜太龙, 喻寅, 宦强, 等. 设计脆性材料的冲击塑性 [J]. 物理学报, 2015, 64(18): 188301. doi: 10.7498/aps.64.188301JIANG T L, YU Y, HUAN Q, et al. Shock plasticity design of brittle material [J]. Acta Physica Sinica, 2015, 64(18): 188301. doi: 10.7498/aps.64.188301 [15] 黄海军, 沈强, 罗国强, 等. 利用多层阻抗梯度飞片产生准等熵压缩的理论解析 [C]//第四届全国爆炸力学实验技术学术会议论文集. 武夷山: 中国力学学会, 2006. [16] 杜艾, 周斌, 沈洋, 等. 激光准等熵压缩实验中阻抗梯度飞片的制备技术简介 [J]. 原子能科学技术, 2014, 48(11): 2158–2164. doi: 10.7538/yzk.2014.48.11.2158DU A, ZHOU B, SHEN Y, et al. Brief introduction of fabrication technique for flier-plate with gradient wave impedance in laser-induced quasi-isentropic compression [J]. Atomic Energy Science and Technology, 2014, 48(11): 2158–2164. doi: 10.7538/yzk.2014.48.11.2158 [17] 朱婷. 基于ABAQUS软件的PMMA材料裂纹及其扩展研究 [D]. 长沙: 湖南大学, 2016: 2–3.ZHU T. Research on crack and propagation of PMMA material based on ABAQUS [D]. Changsha: Hunan University, 2016: 2–3. [18] 喻寅, 李媛媛, 贺红亮, 等. 脆性材料动态断裂的介观格子模型 [J]. 高压物理学报, 2019, 33(3): 030106. doi: 10.11858/gywlxb.20190707YU Y, LI Y Y, HE H L, et al. Mesoscale lattice model for dynamic fracture of brittle materials [J]. Chinese Journal of High Pressure Physics, 2019, 33(3): 030106. doi: 10.11858/gywlxb.20190707 [19] YU Y, WANG W Q, CHEN K G, et al. Controllable fracture in shocked ceramics: shielding one region from severely fractured state with the sacrifice of another region [J]. International Journal of Solids and Structures, 2018, 135: 137–147. doi: 10.1016/j.ijsolstr.2017.11.016 [20] SULSKY D, ZHOU S J, SCHREYER H L. Application of a particle-in-cell method to solid mechanics [J]. Computer Physics Communications, 1995, 87(1/2): 236–252. doi: 10.1016/0010-4655(94)00170-7 [21] SILLING S A. Reformulation of elasticity theory for discontinuities and long-range forces [J]. Journal of the Mechanics and Physics of Solids, 2000, 48(1): 175–209. doi: 10.1016/S0022-5096(99)00029-0 [22] GUSEV A A. Finite element mapping for spring network representations of the mechanics of solids [J]. Physical Review Letters, 2004, 93(3): 034302. doi: 10.1103/PhysRevLett.93.034302 [23] YU Y, WANG W Q, HE H L, et al. Mesoscopic deformation features of shocked porous ceramic: polycrystalline modeling and experimental observations [J]. Journal of Applied Physics, 2015, 117(12): 125901. doi: 10.1063/1.4916244 [24] LAWN B. 脆性固体断裂力学 [M]. 龚江宏, 译. 2版. 北京: 高等教育出版社, 2010: 4–5. [25] PHILLIPS D C, TETELMAN A S. The fracture toughness of fibre composites [J]. Composites, 1972, 3(5): 216–223. doi: 10.1016/0010-4361(72)90630-1 [26] 喻寅, 王文强, 杨佳, 等. 多孔脆性介质冲击波压缩破坏的细观机理和图像 [J]. 物理学报, 2012, 61(4): 048103. doi: 10.7498/aps.61.048103YU Y, WANG W Q, YANG J, et al. Mesoscopic picture of fracture in porous brittle material under shock wave compression [J]. Acta Physica Sinica, 2012, 61(4): 048103. doi: 10.7498/aps.61.048103 [27] 谭华. 实验冲击波物理 [M]. 2版. 北京: 国防工业出版社, 2018: 67–68. [28] 徐之纶. 弹性力学简明教程 [M]. 3版. 北京: 高等教育出版社, 2002: 145–147. -






 下载:
下载: