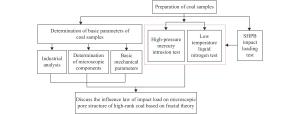
Fractal Study on Influence of Impact Load on Microscopic Pore of Anthracite
-
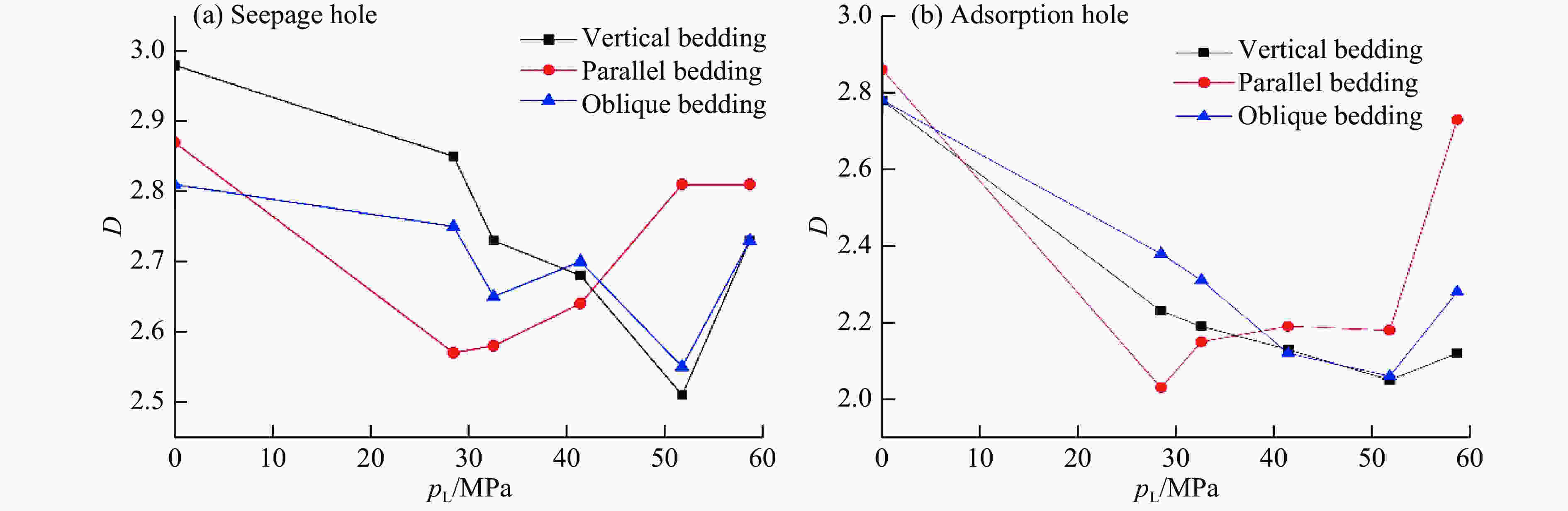
摘要: 为了揭示冲击荷载对无烟煤微观孔隙结构的影响规律,利用分离式霍普金森压杆(SHPB)冲击实验系统模拟了冲击应力在不同衰减过程中的冲击波和应力波,基于冲击前后压汞实验及低温液氮实验测试数据,运用分形理论,研究了赵固二矿不同方向煤体(与层理方向分别呈垂直、平行、45°斜交)冲击前后孔隙结构的分形特征。结果表明:对于渗流孔,冲击荷载提高了瓦斯的渗流与运移速度,对于吸附孔,冲击荷载减小了吸附孔的吸附能力,促进了瓦斯的解吸;分形维数具有明显的冲击方向性,且吸附孔的分形维数明显小于渗流孔;不同方向无烟煤的最佳冲击荷载不同,垂直和斜交层理方向的最佳冲击荷载为51.80 MPa,平行层理方向的最佳冲击荷载为28.46 MPa。研究结果可为冲击荷载促进瓦斯抽采机理的探讨提供参考。Abstract: In order to reveal the influence of impact loading on the microscopic pore structure of anthracite, the shock and stress waves of the impact stress in different attenuation processes were simulated by using the split Hopkinson pressure bar (SHPB) impact loading system, and the fractal characteristics of the pore structures of anthracite in different directions of Zhaogu No.2 Mine (vertical, parallel and 45° oblique to the bedding direction) were studied by using the fractal theory based on the test data of mercury intrusion and low-temperature liquid nitrogen before and after impacting. The results show that for the seepage hole, the impact loading increases the gas seepage and migration velocity. For the adsorption hole, the impact loading reduces the adsorption capacity of the adsorption hole, which promotes the desorption of gas. Fractal dimension has obvious impact directionality, and the fractal dimension of the adsorption hole is obviously smaller than that of the seepage hole; the optimal impact loadings of anthracite in different directions are different. The optimal loading in the vertical bedding direction and the oblique bedding direction is 51.80 MPa, and the optimal impact loading in the parallel bedding direction is 28.46 MPa. The research results can provide support for the discussion of the mechanism of impact loading to promote gas drainage.
-
表 1 煤样基本参数
Table 1. Basic parameters of coal samples
No. $\;\rho $/(g·cm−3) fc/MPa CL/(km·s−1) R0,max/% Mass fraction/% Ash Volatile
componentFixed carbon Exinite Vitrinite Inertinite C0 1.423 17.29 1.381 3.32 5.62 6.05 83.98 1 98 1 P0 1.461 15.13 1.852 X0 1.422 11.65 1.653 表 2 实验数据表
Table 2. Impact test data
Direction pI/MPa pL/MPa No. Size/mm × mm $ D_{\rm{s} }$ $\bar D_{\rm{s} }$ $R_{\rm{s} }^2$ $ D_{\rm{x} }$ $\bar D_{\rm{x} }$ $R_{\rm{x}}^2$ $d $ $\bar d$ Vertical
bedding0 0 YC1 2.99 2.98 0.97 2.75 2.78 0.95 YC2 2.99 0.99 2.78 0.96 YC3 2.95 0.98 2.81 0.98 0.10 28.46 C1 $ \varnothing $49.75 × 50.33 2.85 2.85 0.95 2.31 2.23 0.95 0.14 0.14 C2 $ \varnothing $49.33 × 49.89 2.92 0.96 2.21 0.93 0.16 C3 $ \varnothing $49.34 × 50.42 2.79 0.95 2.17 0.96 0.12 0.15 32.59 C4 $ \varnothing $49.42 × 49.57 2.73 2.73 0.99 2.19 2.19 0.95 0.18 0.16 C5 $ \varnothing $49.66 × 49.93 2.78 0.97 2.23 0.96 0.12 C6 $ \varnothing $49.42 × 50.84 2.69 0.94 2.15 0.95 0.18 0.20 41.43 C7 $ \varnothing $49.39 × 49.93 2.63 2.68 2.05 2.13 0.96 0.18 0.17 C8 $ \varnothing $49.42 × 49.76 2.71 0.98 2.21 0.97 0.17 C9 $ \varnothing $49.45 × 50.28 2.69 0.99 2.13 0.98 0.15 0.30 51.80 C10 $ \varnothing $49.52 × 50.47 2.56 2.51 0.99 2.05 2.05 0.99 0.17 0.19 C11 $ \varnothing $49.36 × 49.78 2.64 0.96 2.09 0.96 0.19 C12 $ \varnothing $49.27 × 50.27 2.34 0.94 2.01 0.96 0.22 0.50 58.70 C13 $ \varnothing $49.38 × 50.47 2.74 2.73 0.92 2.11 2.12 0.92 0.33 0.44 C14 $ \varnothing $49.45 × 50.21 2.79 0.94 2.17 0.93 0.57 C15 $ \varnothing $49.49 × 49.44 2.67 0.95 2.07 0.98 0.42 Parallel
bedding0 0 YP1 2.84 2.87 0.99 2.89 2.86 0.95 YP2 2.91 0.96 2.86 0.94 YP3 2.87 0.97 2.83 0.96 0.10 28.46 P1 $ \varnothing $49.29 × 50.11 2.57 2.57 0.99 2.03 2.03 0.98 0.13 0.13 P2 $ \varnothing $49.36 × 50.37 2.65 0.98 2.05 0.95 0.11 P3 $ \varnothing $49.47 × 49.88 2.50 0.99 2.02 0.96 0.15 0.15 32.59 P4 $ \varnothing $49.31 × 49.32 2.58 2.58 0.97 2.15 2.15 1.00 0.31 0.25 P5 $ \varnothing $49.33 × 50.28 2.61 0.98 2.19 0.95 0.22 P6 $ \varnothing $49.31 × 49.16 2.56 0.95 2.11 0.97 0.22 Parallel
bedding0.20 41.43 P7 $ \varnothing $49.33 × 50.33 2.64 2.64 0.92 2.20 2.19 0.95 0.18 0.28 P8 $ \varnothing $49.60 × 49.85 2.68 0.93 2.14 0.96 0.22 P9 $ \varnothing $49.31 × 50.11 2.61 0.95 2.24 0.98 0.44 0.30 51.80 P10 $ \varnothing $49.31 × 50.40 2.81 2.81 0.94 2.21 2.18 0.95 0.37 0.34 P11 $ \varnothing $49.05 × 49.87 2.85 0.95 2.16 0.97 0.30 P12 $ \varnothing $49.42 × 49.87 2.78 0.94 2.18 0.96 0.35 0.50 58.70 P13 $ \varnothing $49.40 × 49.93 2.89 2.81 0.95 2.82 2.73 0.97 0.54 0.50 P14 $ \varnothing $49.62 × 49.96 2.81 0.99 2.73 0.96 0.49 P15 $ \varnothing $49.32 × 49.79 2.73 0.95 2.63 0.96 0.47 45° oblique bedding 0 0 YX1 2.81 2.81 0.94 2.77 2.78 0.95 YX2 2.85 0.95 2.71 0.95 YX3 2.78 0.97 2.85 0.96 0.10 28.46 X1 $ \varnothing $49.49 × 50.03 2.75 2.75 0.99 2.38 2.38 0.97 0.17 0.16 X2 $ \varnothing $49.27 × 49.63 2.81 0.98 2.28 0.95 0.19 X3 $ \varnothing $49.31 × 49.30 2.68 0.97 2.47 0.96 0.12 0.15 32.59 X4 $ \varnothing $49.24 × 49.93 2.67 2.65 0.99 2.39 2.31 0.98 0.29 0.24 X5 $ \varnothing $49.27 × 49.33 2.75 0.95 2.31 0.96 0.21 X6 $ \varnothing $49.27 × 49.82 2.54 0.98 2.23 0.95 0.22 0.20 41.43 X7 $ \varnothing $49.25 × 49.90 2.76 2.70 0.95 2.08 2.12 0.94 0.20 0.22 X8 $ \varnothing $49.60 × 49.38 2.71 0.92 2.17 0.92 0.21 X9 $ \varnothing $49.29 × 49.05 2.64 0.93 2.12 0.93 0.25 0.30 51.80 X10 $ \varnothing $49.40 × 50.28 2.47 2.55 0.98 2.01 2.06 0.93 0.21 0.18 X11 $ \varnothing $49.38 × 50.88 2.61 0.96 2.07 0.92 0.17 X12 $ \varnothing $49.71 × 50.02 2.58 0.97 2.11 0.95 0.16 0.50 58.70 X13 $ \varnothing $49.66 × 50.44 2.79 2.73 0.98 2.26 2.28 0.96 0.63 0.71 X14 $ \varnothing $49.73 × 49.91 2.75 0.97 2.31 0.94 0.72 X15 $ \varnothing $49.46 × 50.05 2.64 0.96 2.28 0.93 0.78 -
[1] 高为, 易同生, 金军, 等. 黔西地区煤样孔隙综合分形特征及对孔渗性的影响 [J]. 煤炭学报, 2017, 42(5): 1258–1265.GAO W, YI T S, JIN J, et al. Pore integrated fractal characteristics of coal sample in western Guizhou and its impact to porosity and permeability [J]. Journal of China Coal Society, 2017, 42(5): 1258–1265. [2] 秦勇, 邱爱慈, 张永民. 高聚能重复强脉冲波煤储层增渗新技术试验与探索 [J]. 煤炭科学技术, 2014, 42(6): 1–7.QIN Y, QIU A C, ZHANG Y M. Experiment and discovery on permeability improved technology of coal reservoir based on repeated strong pulse waves of high energy accumulation [J]. Coal Science and Technology, 2014, 42(6): 1–7. [3] WEI G Y, SHAN Z Y, ZHANG Z M. Research on hydraulic slotting technology controlling coal-gas outbursts [J]. Journal of Coal Science and Engineering, 2008, 14(1): 67–72. doi: 10.1007/s12404-008-0014-4 [4] 姜永东, 李业, 崔悦震, 等. 声场作用下煤储层渗透性试验研究 [J]. 煤炭学报, 2017, 42(S1): 154–159.JIANG Y D, LI Y, CUI Y Z, et al. Experimental study on characteristics of coal reservoir permeability under acoustic wave [J]. Journal of China Coal Society, 2017, 42(S1): 154–159. [5] 赵丽娟, 秦勇. 超声波作用对改善煤储层渗透性的试验分析 [J]. 天然气地球科学, 2014, 25(5): 747–752.ZHAO L J, QIN Y. Experiment on improving the permeability of coal reservoir under ultrasound [J]. Natural Gas Geoscience, 2014, 25(5): 747–752. [6] FORRESTAL M J, FREW D J, HANCHAK S J, et al. Penetration of grout and concrete targets with ogive-nose steel projectiles [J]. International Journal of Impacting Engineering, 1996, 18(5): 465–476. doi: 10.1016/0734-743X(95)00048-F [7] 穆朝民, 王海露, 黄文尧, 等. 高瓦斯低透气性煤体定向聚能爆破增透机制 [J]. 岩土力学, 2013, 34(9): 2496–2500.MU C M, WANG H L, HUANG W Y, et al. Increasing permeability mechanism using directional cumulative blasting in coal seams with high concentration of gas and low permeability [J]. Rock and Siol Mechanics, 2013, 34(9): 2496–2500. [8] 李恒乐, 秦勇, 张永民, 等. 重复脉冲强冲击波对肥煤结构影响的实验研究 [J]. 煤炭学报, 2015, 40(4): 915–921.LI H L, QIN Y, ZHANG Y M, et al. Experimental study on the effect of strong repetitive pulse shockwave on the pore structure of fat coal [J]. Journal of China Coal Society, 2015, 40(4): 915–921. [9] CAI Y D, LIU D M, PAN Z J, et al. Pore structure and its impact on CH4 adsorption capacity and flow capability of bituminous and subbituminous coals from Northeast China [J]. Fuel, 2013, 103: 258–268. doi: 10.1016/j.fuel.2012.06.055 [10] MANDELBROT B B. The fractal geometry of nature [M]. San Francisco: Freeman, 1982: 35. [11] BIRD N, DÍAZ M C, SAA A, et al. Fractal and multifractal analysis of pore-scale images of soil [J]. Journal of Hydrology, 2006, 322(1/2/3/4): 211–219. [12] DATHE A, EINS S, NIEMEYER J, et al. The surface fractal dimension of the soil-pore interface as measured by image analysis [J]. Geoderma, 2001, 103(1/2): 203–229. [13] HUANG S J, YU Y C, LEE T Y, et al. Correlations and characterization of porous solids by fractal dimension and porosity [J]. Physica A: Statistical Mechanics and Its Applications, 1999, 274(3/4): 419–432. [14] HILDGEN P, NEKKA F, HILDGEN F, et al. Macroporosity measurement by fractal analysis [J]. Physica A: Statistical Mechanics and Its Applications, 1997, 234(3/4): 593–603. [15] YANG F, NING Z F, LIU H Q. Fractal characteristics of shales from a shale gas reservoir in the Sichuan Basin, China [J]. Fuel, 2014, 115: 378–384. doi: 10.1016/j.fuel.2013.07.040 [16] LIU X J, XIONG J, LIANG L X. Investigation of pore structure and fractal characteristics of organic-rich Yanchang formation shale in central China by nitrogen adsorption/desorption analysis [J]. Journal of Natural Gas Science and Engineering, 2015, 22(1): 62–72. [17] 朱汉卿, 贾爱林, 位云生, 等. 蜀南地区五峰-龙马溪组页岩微观孔隙结构及分形特 [J]. 科学技术与工程, 2018, 18(10): 12–19. doi: 10.3969/j.issn.1671-1815.2018.10.003ZHU H Q, JIA A L, WEI Y S, et al. Microscopic pore structure and fractal characteristics of Wufeng-Longmaxi shale, south Sichuan [J]. Science Technology and Engineering, 2018, 18(10): 12–19. doi: 10.3969/j.issn.1671-1815.2018.10.003 [18] GARBACZ J K. Fractal description of partially mobile single gas adsorption on energetically homogeneous solid adsorbent [J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 1998, 143(1): 95–101. [19] LEE G J, PYUN S Ⅰ, RHEE C K. Characterization of geometric and structural properties of pore surfaces of reactivated microporous carbons based upon image analysis and gas adsorption [J]. Microporous and Mesoporous Materials, 2006, 93(1/2/3): 217–225. [20] YAO Y B, LIU D M, TANG D Z, et al. Fractal characterization of adsorption-pores of coals from North China: an investigation on CH4 adsorption capacity of coals [J]. International Journal of Coal Geology, 2008, 73(1): 27–42. doi: 10.1016/j.coal.2007.07.003 [21] XU L J, ZHANG D J, XIAN X F. Fractal dimensions of coals and cokes [J]. Journal of Colloid and Interface Science, 1997, 190(2): 357–359. doi: 10.1006/jcis.1997.4885 [22] 宋昱, 姜波, 李凤丽, 等. 低-中煤级构造煤纳米孔分形模型适用性及分形特征 [J]. 地球科学, 2018, 43(5): 1611–1622.SONG Y, JIANG B, LI F L, et al. Applicability of fractal models and nanopores’ fractal characteristics for low-middle rank tectonic deformed coals [J]. Earth Science, 2018, 43(5): 1611–1622. [23] 王登科, 刘淑敏, 魏建平, 等. 冲击载荷作用下煤的破坏特性试验研究 [J]. 采矿与安全工程学报, 2017, 34(3): 594–600.WANG D K, LIU S M, WEI J P, et al. The failure characteristics of coal under impact load in laboratory [J]. Journal of Mining & Safety Engineering, 2017, 34(3): 594–600. [24] 刘晓辉, 张茹, 刘建锋. 不同应变率下煤岩冲击动力试验研究 [J]. 煤炭学报, 2012, 37(9): 1528–1534.LIU X H, ZHANG R, LIU J F. Dynamic test study of coal rock under different strain rates [J]. Journal of China Coal Society, 2012, 37(9): 1528–1534. [25] XODOT B B. 煤与瓦斯突出 [M]. 宋世钊, 王佑安, 译. 北京: 中国工业出版社, 1966: 310–318. [26] YUAN J, TAKEDA N, WAAS A M. A note on data processing in the split Hopkinson pressure bar tests [J]. Experimental Techniques, 1998, 22(5): 21–24. doi: 10.1111/j.1747-1567.1998.tb02317.x [27] SHAN R L, JIANG Y S, LI B Q. Obtaining dynamic complete stress-strain curves for rock using the split Hopkinson pressure bar technique [J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(6): 983–992. doi: 10.1016/S1365-1609(00)00031-9 [28] 陈俊宇, 裴向军, 杜瑞锋, 等. 冲击载荷作用下砂岩的动力学特性及能耗规律 [J]. 科学技术与工程, 2019, 19(31): 304–310. doi: 10.3969/j.issn.1671-1815.2019.31.045CHEN J Y, PEI X J, DU R F, et al. Dynamic characteristics and energy consumption of sandstone under impact loading [J]. Science Technology and Engineering, 2019, 19(31): 304–310. doi: 10.3969/j.issn.1671-1815.2019.31.045 [29] KOLSKY H. An investigation of the mechanical properties of materials at very high rates of loading [J]. Proceedings of the Physical Society (Section B), 1949, 62: 676–700. doi: 10.1088/0370-1301/62/11/302 [30] LUNDBERG B. A split Hopkinson bar study of energy absorption in dynamic rock fragmentation [J]. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstracts, 1976, 13(6): 187–197. [31] 赵迪斐, 郭英海, WANG G, 等. 基于分形建模的高煤级煤孔隙结构特征量化表征-以阳泉矿区山西组煤样为例 [J]. 东北石油大学学报, 2019, 43(3): 53–67. doi: 10.3969/j.issn.2095-4107.2019.03.006ZHAO D F, GUO Y H, WANG G, et al. Quantitative characterization of pore structure characteristics of high quality coal based on fractal modeling: taking coal samples from Shanxi Formation in Yangquan Mining Area as an example [J]. Journal of Northeast Petroleum University, 2019, 43(3): 53–67. doi: 10.3969/j.issn.2095-4107.2019.03.006 [32] RIGBY S P. Predicting surface diffusivities of molecules from equilibrium adsorption isotherms [J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2005, 262(1/2/3): 139–149. [33] 杨峰, 宁正福, 张世栋, 等. 基于氮气吸附实验的页岩孔隙结构表征 [J]. 天然气工业, 2013, 33(4): 135–140. doi: 10.3787/j.issn.1000-0976.2013.04.025YANG F, NING Z F, ZHANG S D, et al. Characterization of pore structures in shales through nitrogen adsorption experiment [J]. Natural Gas Industry, 2013, 33(4): 135–140. doi: 10.3787/j.issn.1000-0976.2013.04.025 [34] 吉小峰. 煤中纳米孔隙发育特征及其对气体运移的控制机理研究 [D]. 焦作: 河南理工大学, 2018.JI X F. Development characteristics of nanopores in coal and its controlling mechanism on gas migration [D]. Jiaozuo: Henan Polytechnic University, 2018. [35] YAO Y B, LIU D M, TANG D Z, et al. Fractal characterization of seepage-pores of coals from China: an investigation on permeability of coals [J]. Computers & Geosciences, 2009, 35(6): 1159–1166. [36] 宋晓夏, 唐跃刚, 李伟, 等. 中梁山南矿构造煤吸附孔分形特征 [J]. 煤炭学报, 2013, 38(1): 134–139.SONG X X, TANG Y G, LI W, et al. Fractal characteristics of adsorption pores of tectonic coal from Zhongliangshan southern coalmine [J]. Journal of China Coal Society, 2013, 38(1): 134–139. [37] 林海飞, 刘静波, 严敏, 等. CO2/CH4在煤储层中扩散规律的分子动力学模型 [J]. 中国安全生产科学技术, 2017, 13(1): 84–89.LIN H F, LIU J B, YAN M, et al. Molecular dynamics simulation on diffusion rules of CO2/CH4 in coal reservoir [J]. Journal of Safety Science and Technology, 2017, 13(1): 84–89. [38] 董怡静, 韩雨桢, 候泉林, 等. 煤变形产气的力化学机理探讨 [J]. 煤炭学报, 2017, 42(4): 942–949.DONG Y J, HAN Y Z, HOU Q L, et al. Mechanochemistry mechanism of gas generation during coal deformation [J]. Journal of China Coal Society, 2017, 42(4): 942–949. [39] 刘运通, 高文学. 爆炸荷载下岩石损伤的数值模拟研究 [J]. 岩石力学与工程学报, 2001, 20(6): 789–792. doi: 10.3321/j.issn:1000-6915.2001.06.007LIU Y T, GAO W X. Numerical simulation on rock damage under explosion loading [J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(6): 789–792. doi: 10.3321/j.issn:1000-6915.2001.06.007 [40] 唐红梅, 周云涛, 廖云平. 地下工程施工爆破围岩损伤分区研究 [J]. 振动与冲击, 2015, 34(23): 202–206.TANG H M, ZHOU Y T, LIAO Y P. Damage zone of surrounding rock of underground engineering under construction blasting [J]. Journal of Vibration and Shock, 2015, 34(23): 202–206. -







 下载:
下载: