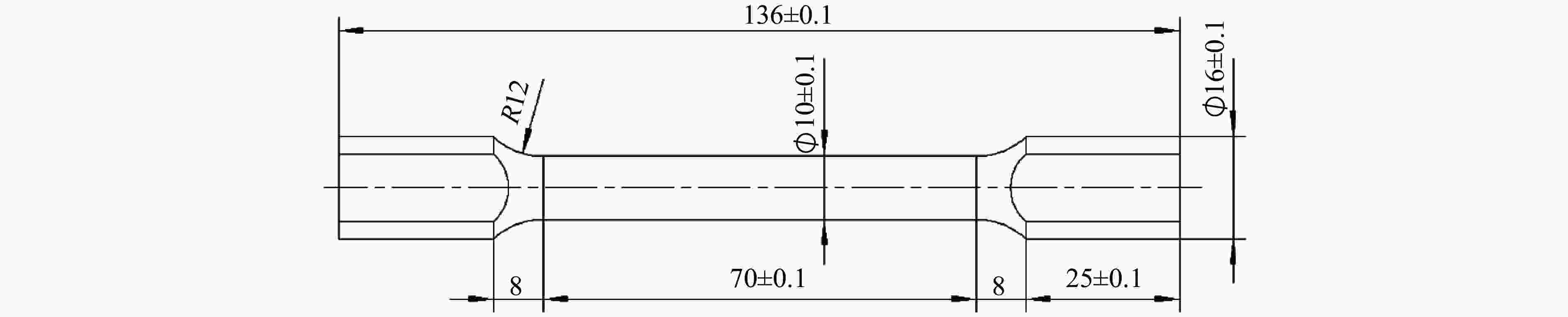
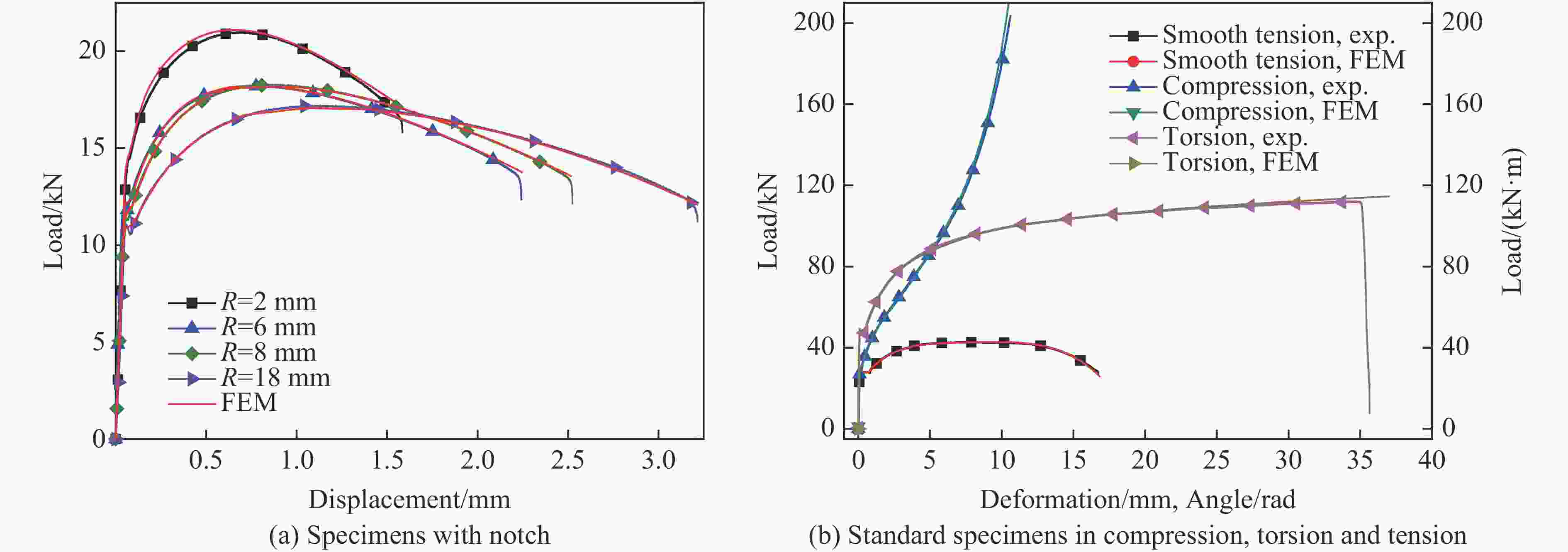
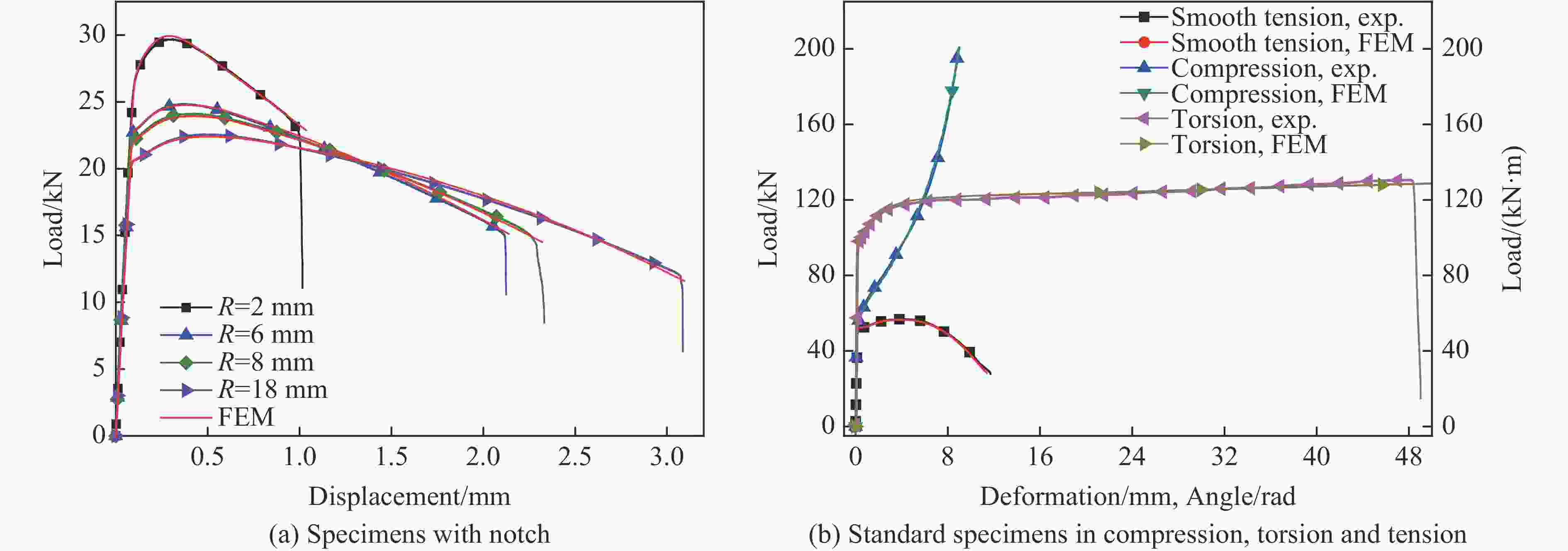
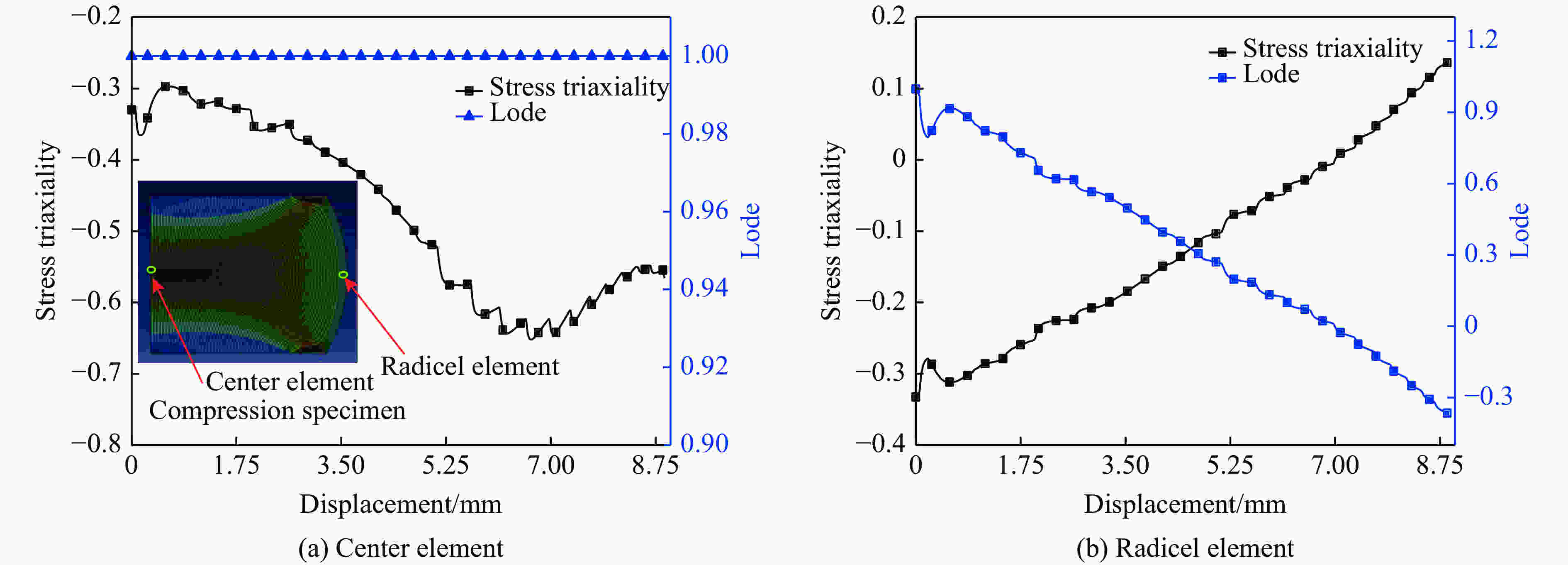
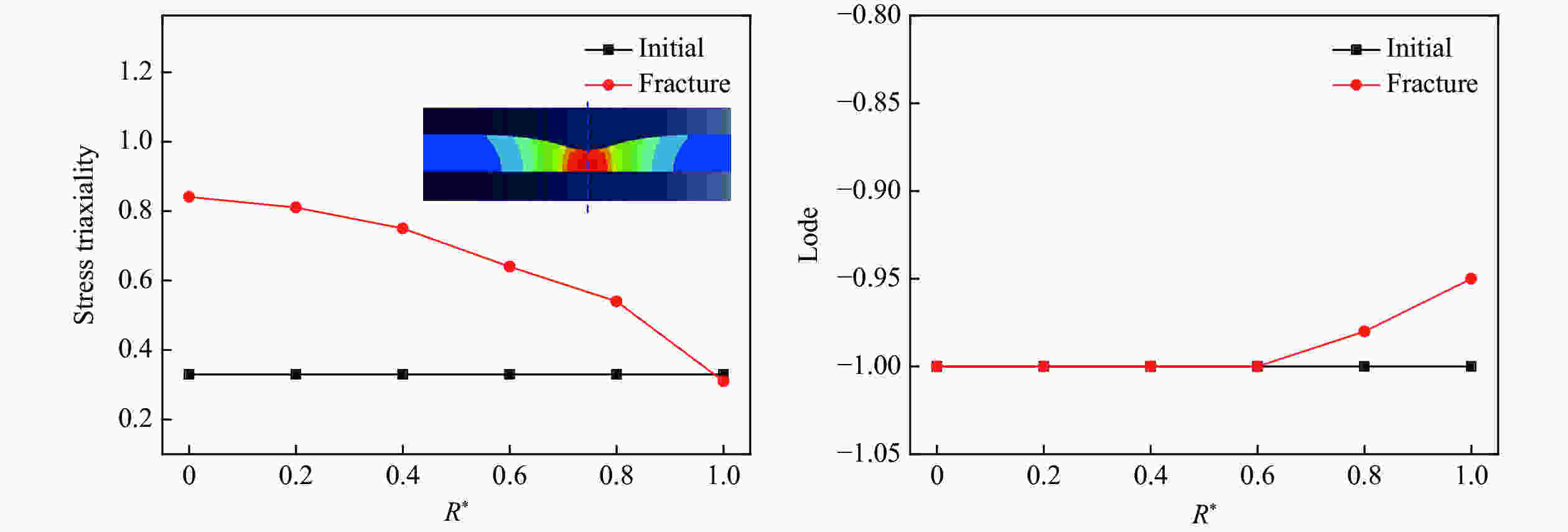
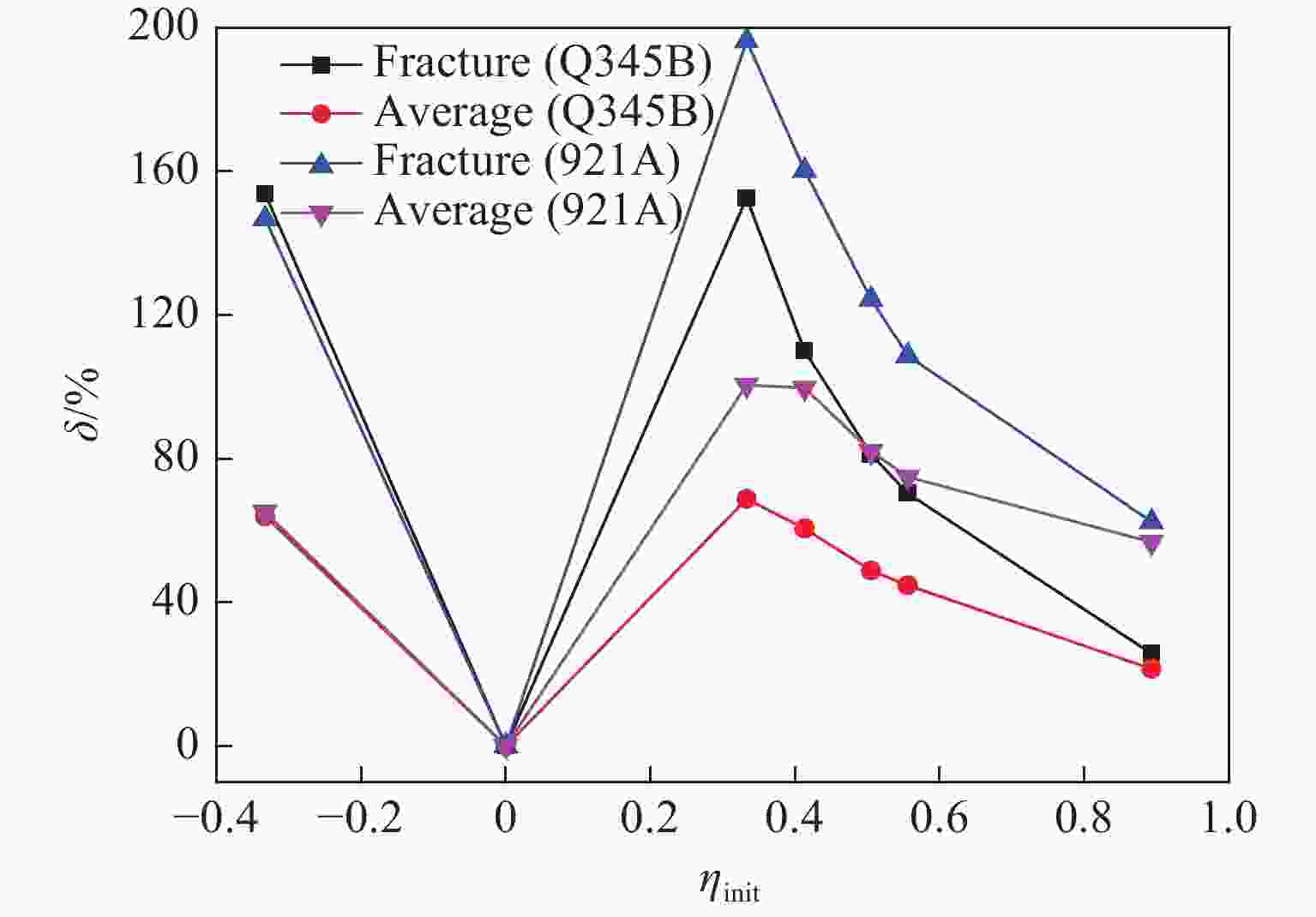
Variation of Stress Distribution in Metal Fracture Process under Compressive, Torsional, and Tensile Loading
-
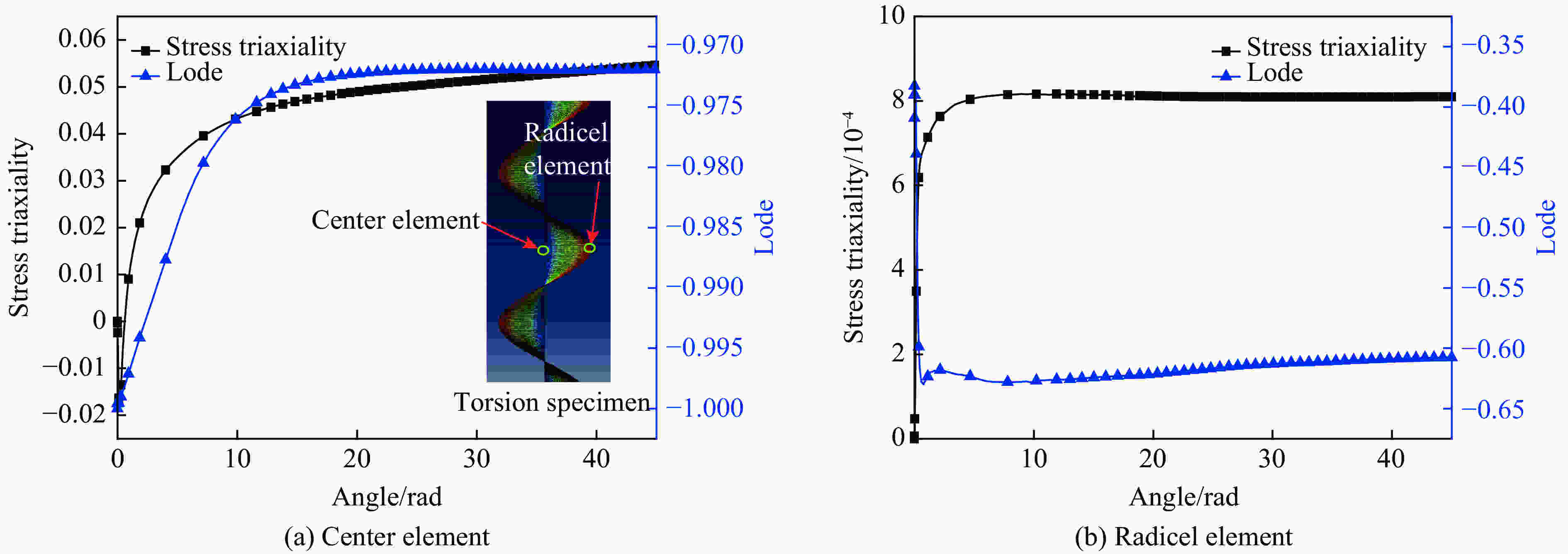
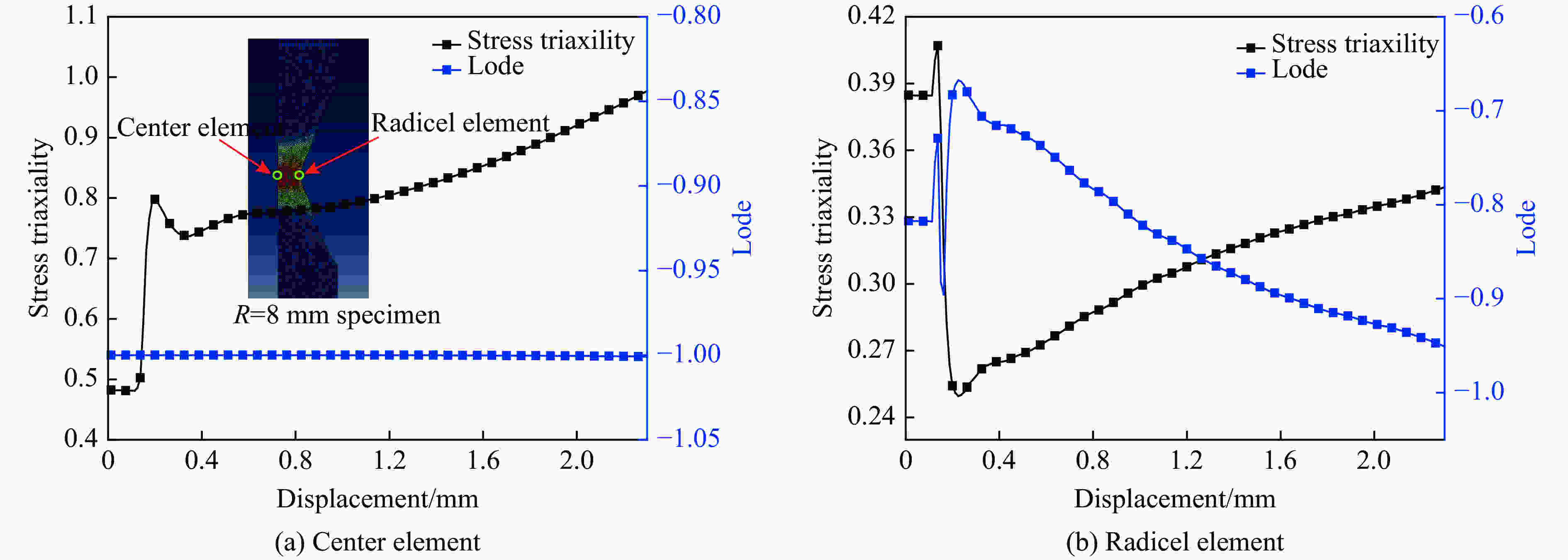
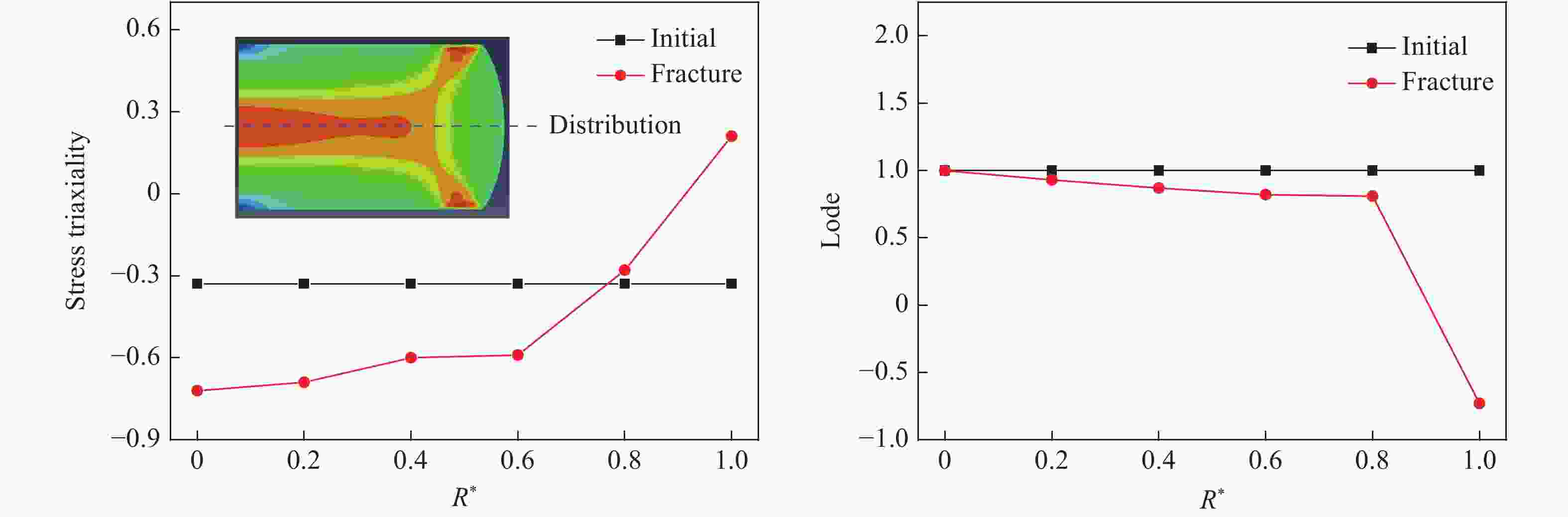
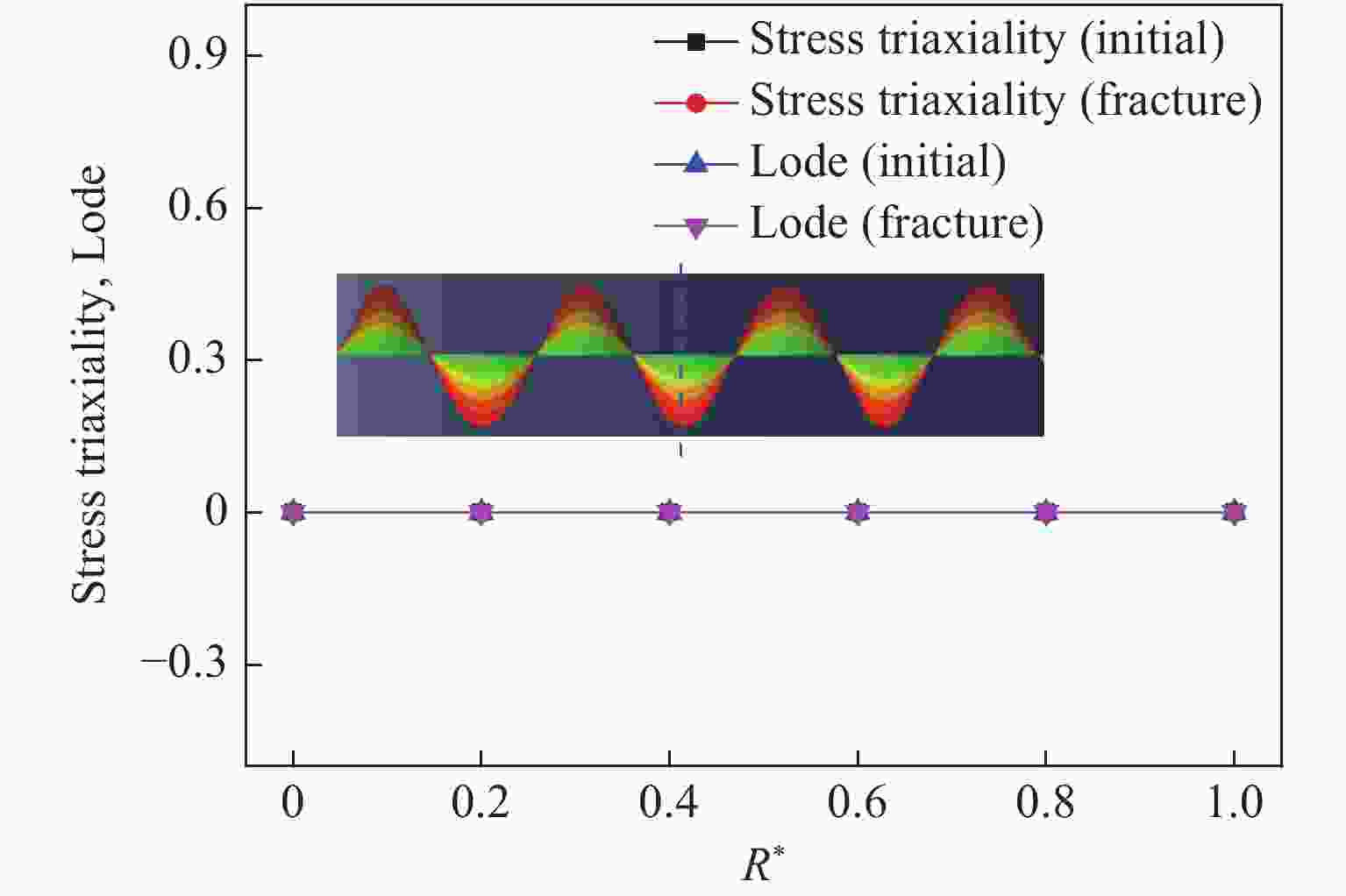
摘要: 为更好地拟合断裂准则(JC、BW、MMC)参数,借助数值模拟手段,对Q345B和921A钢的压缩、扭转、拉伸试件的断裂过程进行了模拟,以应力三轴度、Lode参数作为衡量应力状态变化的重要指标,分析了两种金属材料断裂过程中试件典型位置的变化过程及断裂时刻试件的径向分布趋势,对比分析了Q345B和921A钢的不同类型试件在不同应力三轴度、不同Lode参数表征下的结果。计算结果表明:(1)除扭转试件外,压缩、拉伸试件在断裂过程中的应力状态不断发生变化,试件断裂时刻端口剖面的应力状态分布也不一致;(2)试件断裂过程是一个应力状态不断变化的过程,采用平均应力三轴度、平均Lode参数进行描述更加妥当;(3)对于同一尺寸的拉伸试件,不同金属材料断裂过程中的平均应力三轴度不尽相同。研究成果可为后续断裂准则(JC、BW、MMC)参数的拟合及材料断裂力学性能试验的开展提供指导。Abstract: In order to accurately fit the failure criteria in JC failure model, BW failure model, and MMC failure model, numerical simulations for metal materials Q345B and 921A under various loading conditions of compression, torsion, tension were performed in this work. The variation of stresses, indicated by stress triaxiality and Lode parameter, was investigated during the fracture progress. The results indicated: (1) exclusive of torsional loading, the stress distribution varied in the cracking plane as the crack growth; (2) the average stress triaxiality and Lode parameter are more suitable for describing the stress status; (3) for specimens having the same size, the value of average stress triaxiality was dependent on metal properties. This work would provide useful knowledge for obtaining the failure criterion from material failure experiments.
-
Key words:
- failure experiments /
- stress triaxiality /
- Lode parameter /
- stress status
-
表 1 JC强度模型参数
Table 1. Parameters of JC strength model
Material A/MPa B/MPa n C $\dot \varepsilon $/s−1 Q345B steel 360 700 0.547 0.046 0.002 921A steel 700 706 0.580 0.013 0.002 表 2 各类试件应力三轴度不同表征方法对比
Table 2. Comparison of the stress triaxiality among different specimens
Specimen type Stress triaxiality (Q345B steel) Stress triaxiality (921A steel) Initial Fracture Average Initial Fracture Average Compression −0.333 0.179 −0.120 −0.333 0.156 −0.116 Torsion 0 0 0 0 0 0 Smooth tension 0.333 0.841 0.562 0.333 0.987 0.668 With a 18 mm notch 0.413 0.867 0.663 0.413 1.075 0.825 With a 8 mm notch 0.505 0.915 0.752 0.505 1.133 0.919 With a 6 mm notch 0.556 0.947 0.805 0.556 1.160 0.973 With a 2 mm notch 0.893 1.123 1.085 0.893 1.451 1.400 表 3 各类试件Lode参数不同表征方法对比
Table 3. Comparison of the Lode parameter among different specimens
Specimen type Lode (Q345B steel) Lode (921A steel) Initial Fracture Average Initial Fracture Average Compression 1.00 −0.73 0.24 1.00 −0.22 0.45 Torsion 0 0 0 0 0 0 Smooth tension −1.00 −1.00 −1.00 −1.00 −1.00 −1.00 With a 18 mm notch −1.00 −1.00 −1.00 −1.00 −1.00 −1.00 With a 8 mm notch −1.00 −1.00 −1.00 −1.00 −1.00 −1.00 With a 6 mm notch −1.00 −1.00 −1.00 −1.00 −1.00 −1.00 With a 2 mm notch −1.00 −1.00 −1.00 −1.00 −1.00 −1.00 表 4 拟合JC参数取值
Table 4. JC failure model constant
Material D1 D2 D3 Q345B steel 1.816 −0.353 1.056 921A steel 2.475 −0.661 0.650 -
[1] JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures [C]//Proceeding of the 7th International Symposium on Ballistic. The Hague, Netherlands, 1983: 541–547. [2] BAO Y B, WIERZBICKI T. A comparative study on various ductile crack formation criteria [J]. Journal of Engineering Material and Technology, 2004, 126: 314–324. doi: 10.1115/1.1755244 [3] BAO Y B, WIERZBICKI T. Application of extended Mohr-Coulomb criterion to ductile fracture [J]. International Journal of Fracture, 2010, 161(1): 1–20. doi: 10.1007/s10704-009-9422-8 [4] BORVIK T, HOPPERSTAD O S. A computational model of viscoplasticity and ductile damage for impact and penetration [J]. European Journal of Mechanics Solids, 2001, 20(5): 685–712. doi: 10.1016/S0997-7538(01)01157-3 [5] GUPTA N K, IQBAL M A. Experiment and numerical studies on the behavior of thin aluminum plates subjected to impact by blunt and hemispherical-nosed projectile [J]. International Journal of Impact Engineering, 2006, 32(12): 1921–1944. doi: 10.1016/j.ijimpeng.2005.06.007 [6] 肖新科, 王要沛, 王爽, 等. 应力状态在球形弹丸撞击6061-T6铝薄靶弹道行为数值预报中的作用 [J]. 振动与冲击, 2015, 34(22): 87–91.XIAO X K, WANG Y P, WANG S, et al. Effect of stress state on the numerical prediction of ballistic resistance of thin 6061-T6 aluminum alloy targets against sphere projectile impacts [J]. Journal of Vibration and Shock, 2015, 34(22): 87–91. [7] 肖新科, 王要沛, 张伟. 应力状态在2024-T351 Taylor杆断裂行为数值预报中的作用 [J]. 北京理工大学学报, 2016, 36(1): 157–161.XIAO X K, WANG Y P, ZHANG W. Effect of stress state on the numerical prediction of the fracture behavior of 2064-T351 aluminium alloy Taylor rods [J]. Transactions of Beijing Institute of Technology, 2016, 36(1): 157–161. [8] BORVIK T, HOPPERSTAD O S. Numerical simulation of plugging failure in ballistic penentrtion [J]. International Journal of Solids and Structures, 2001, 38(25): 6241–6264. [9] BAO Y B, WIERZBICKI T. On fracture locus in the equivalent strain and stress triaxiality space [J]. International Journal of Mechanical Sciences, 2004, 46(12): 81–98. [10] GILIOLI A, WIERZBICKI T. Predicting ballistic impact failure of aluminium 6061-T6 with the rate-independent Bao-Wierzbicki fracture model [J]. International Journal of Impact Engineering, 2015, 76(15): 207–220. [11] TENG X, WIERZBICKI T. Evaluation of six fracture models in high velocity perforation [J]. Engineering Fracture Mechanics, 2006, 73(12): 1653–1678. [12] 李营. 液舱防爆炸破片侵彻作用机理研究 [D]. 武汉: 武汉理工大学, 2014.LI Y. Fragment resistant mechanism research of safety liquid cabin [D]. Wuhan: Wuhan University of Technology, 2014. [13] 孟利平. 应变率和应力三轴度对船用钢变形和断裂的影响研究 [D]. 无锡: 中国船舶科学研究中心, 2016.MENG L P. Influence of strain rate and stress triaxiality on the deformation and fracture behavior of ship hull steel [D]. Wuxi: China Ship Scientific Research Center, 2016. [14] BAO Y B, WIERZBICKI T. On fracture locus in the equivalent strain and stress triaxiality space [J]. International Journal of Mechanical Sciences, 2004, 46(1): 81–98. doi: 10.1016/j.ijmecsci.2004.02.006 [15] BAO Y B, WIERZBICKI T. On the cut-off value of negative triaxiality for fracture [J]. Engineering Fracture Mechanics, 2005, 72(7): 1049–1069. doi: 10.1016/j.engfracmech.2004.07.011 -







 下载:
下载: