Deformation and Destruction of TC4 Titanium Alloy Plate under the Bird Impact
-
摘要: 为了分析航空用TC4钛合金板材在鸟撞冲击下的动态响应,通过3D-DIC动态变形场测试技术,研究了鸟撞冲击过程中TC4钛合金平板变形场,并基于显式有限元分析软件ABAQUS,建立了鸟撞数值计算模型。将考虑拉压不对称性的修正von Mises屈服准则引入TC4钛合金材料的Johnson-Cook动态本构模型和动态损伤模型中,采用光滑粒子流体动力学方法(SPH)建立了鸟体模型。数值计算和鸟撞实验的对比结果表明,计算应变与实验结果吻合很好,验证了TC4钛合金鸟撞冲击数值分析模型的合理性和可靠性。
-
关键词:
- TC4钛合金 /
- 鸟撞 /
- 光滑粒子流体动力学方法 /
- 剪切破坏
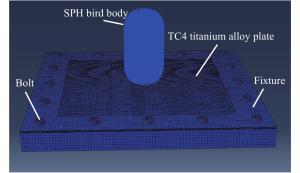
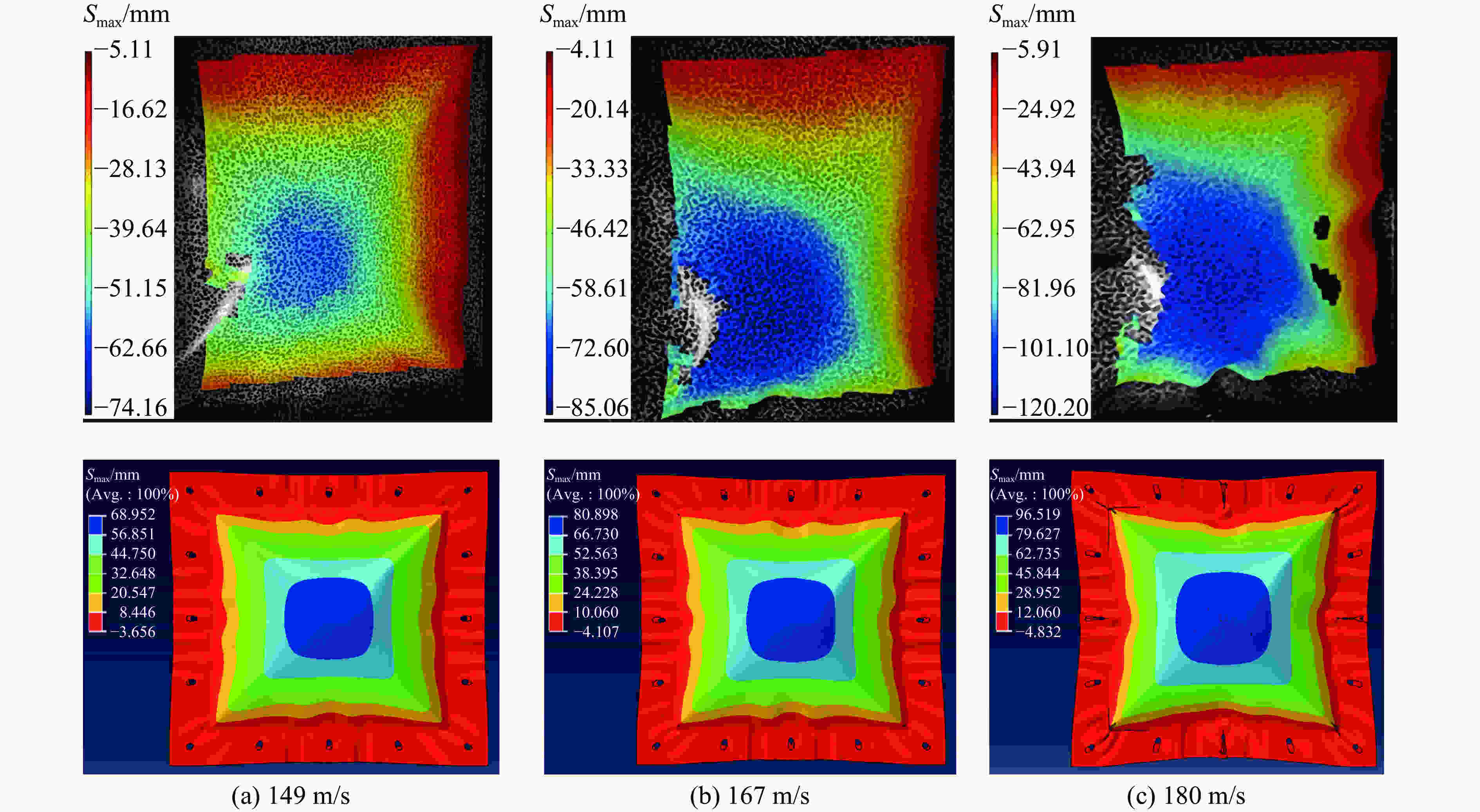
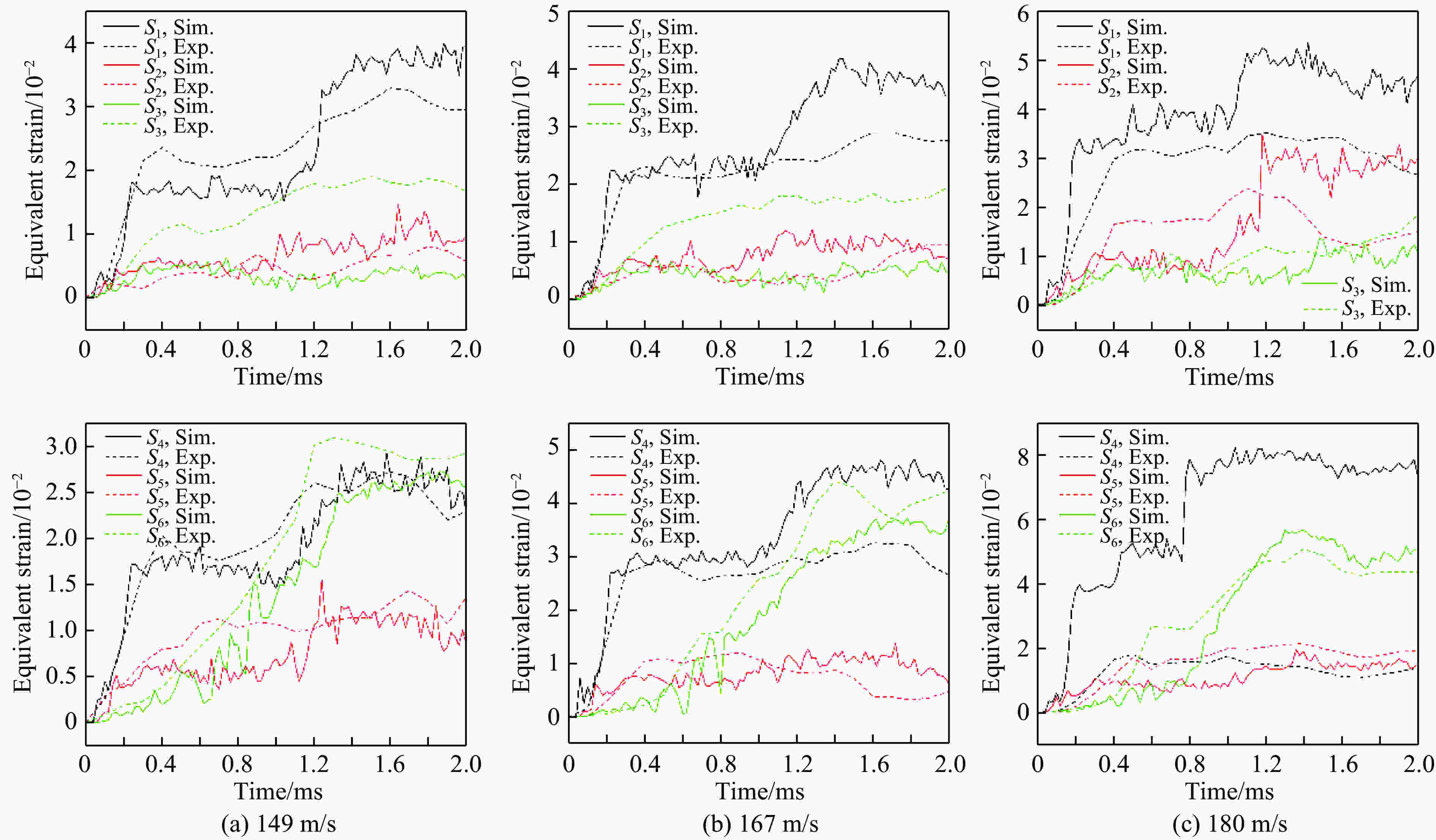
Abstract: In order to analyze the dynamic behavior of aerospace TC4 titanium alloy plane under the bird impact, the deformation field of TC4 titanium alloy plate subjected to the bird impact was studied by 3D-DIC dynamic deformation field test technology. Meanwhile, a numerical simulation model was established based on explicit finite element analysis software ABAQUS. In this model the Johnson-Cook dynamic constitutive relations was used to describe the property of TC4 titanium alloy, and the bird model was established with smooth particle method (SPH). Comparing the numerical and experimental results, it is concluded that the calculated strain can match the experimental results well. The rationality and reliability of numerical analysis of the bird impact on the TC4 titanium alloy model are verified.-
Key words:
- TC4 titanium alloy /
- bird impact /
- smoothed particle hydrodynamics method /
- shear failure
-
表 1 鸟体材料参数
Table 1. Material parameters of bird body
Density/(kg·m−3) Elastic modulus/GPa Poisson’s ratio Yield stress/MPa Failure strain Tangent modulus/MPa 928 0.068 0.49 0.69 1.25 5 ρ/(g·cm−3) μ Tm/K A/MPa B/MPa n C m 4.430 0.33 1 878 1060 1090 0.884 0.0117 1.1 E/GPa ${\dot \varepsilon _{{0}}}$/s−1 D1 D2 D3 D4 D5 135 4 × 10−4 −0.090 0.270 0.480 0.014 3.870 表 3 TC4钛合金平板鸟撞最大位移
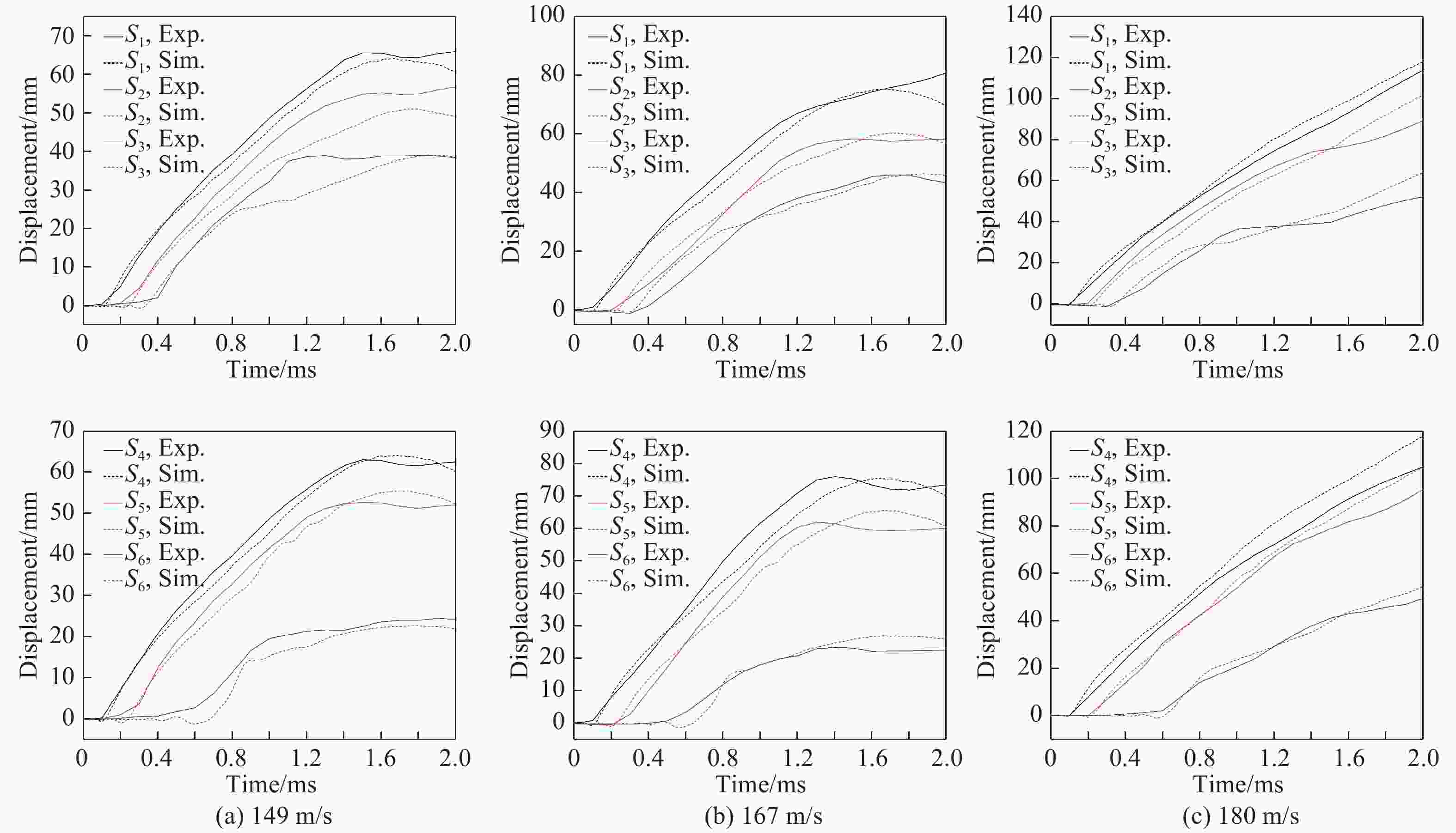
Table 3. Maximum displacement of titanium alloy plate impacted by a bird
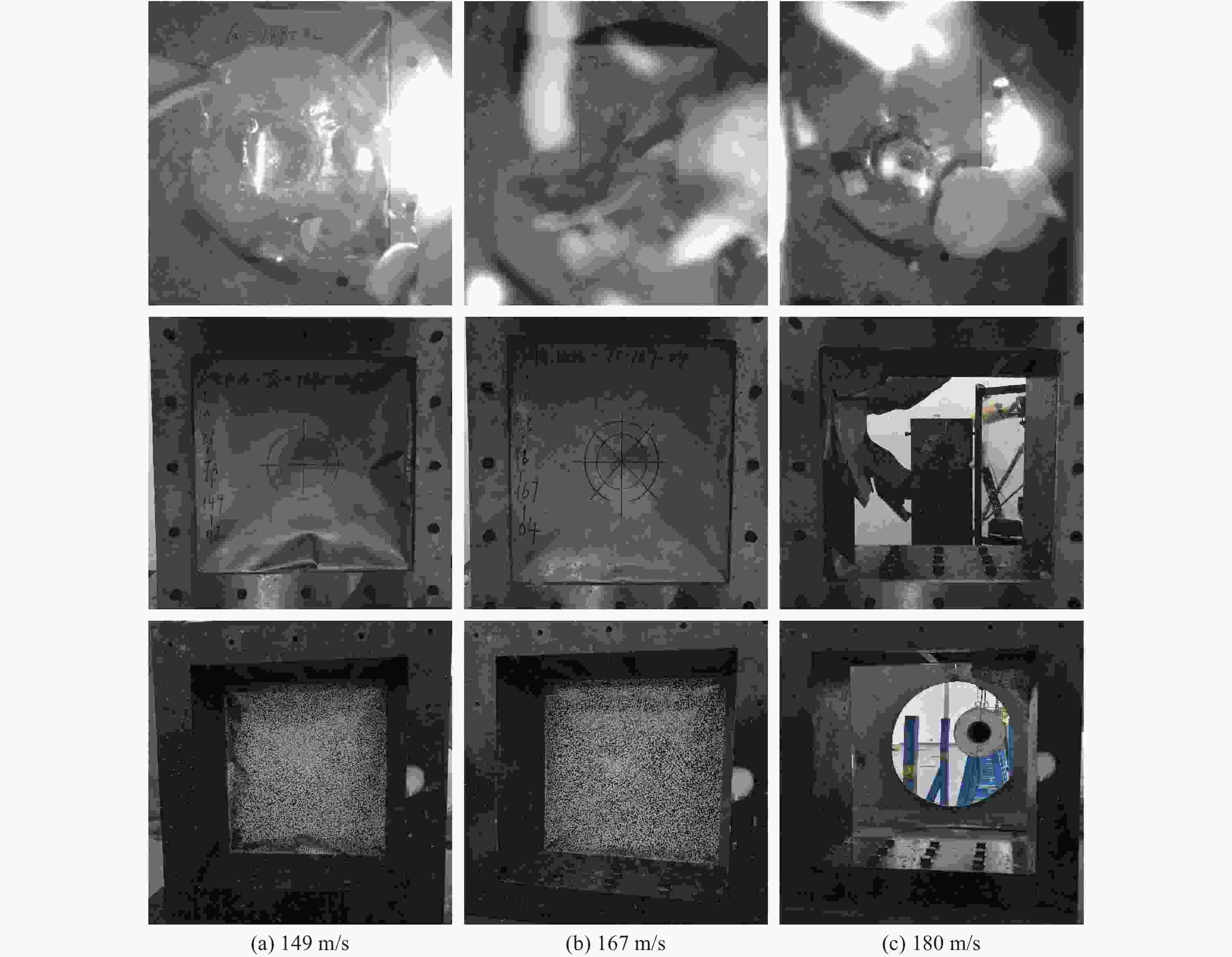
Velocity/(m·s−1) Method Maximum displacement/mm S1 S2 S3 S4 S5 S6 149 Sim. 65 51 36 64 55 23 Exp. 68 60 38 63 53 25 167 Sim. 75 60 48 76 65 27 Exp. 80 59 47 76 63 24 180 Sim. 119 101 63 118 103 54 Exp. 117 90 53 103 95 50 -
[1] 黄旭, 朱知寿, 王红红. 先进航空钛合金材料与应用 [M]. 北京: 国防工业出版社, 2012.HUANG X, ZHU Z S, WANG H H. Advanced aeronautical titanium alloys and applications [M]. Beijing: National Defense Industry Press, 2012. [2] GUIDA M, MARULO F, MEO M, et al. SPH-Lagrangian study of bird impact on leading edge wing [J]. Composite Structures, 2011, 93(3): 1060–1071. doi: 10.1016/j.compstruct.2010.10.001 [3] DE VUYST T, VIGNJEVIC R, CAMPBELL J C. Coupling between meshless and finite element methods [J]. International Journal of Impact Engineering, 2005, 31(8): 1054–1064. doi: 10.1016/j.ijimpeng.2004.04.017 [4] 张鼎逆, 上官倩芡, 刘富. 基于SPH方法的LY12-CZ铝合金平板鸟撞模型 [J]. 江苏大学学报: 自然科学版, 2016, 37(4): 418–422. doi: 10.3969/j.issn.1671-7775.2016.04.008ZHANG D N, SHANGGUAN Q Q, LIU F. Model of bird impact on LY12-CZ aluminum alloy plate based on SPH [J]. Journal of Jiangsu University (Natural Science Edition), 2016, 37(4): 418–422. doi: 10.3969/j.issn.1671-7775.2016.04.008 [5] 刘军, 李玉龙, 刘元镛. 基于SPH方法的叶片鸟撞数值模拟研究 [J]. 振动与冲击, 2008, 27(9): 90–93. doi: 10.3969/j.issn.1000-3835.2008.09.022LIU J, LI Y L, LIU Y Y. Numerical simulation study of bird-impact on a blade using SPH method [J]. Journal of Vibration and Shock, 2008, 27(9): 90–93. doi: 10.3969/j.issn.1000-3835.2008.09.022 [6] 刘富, 张嘉振, 童明波, 等. 2024-T3铝合金动力学实验及其平板鸟撞动态响应分析 [J]. 振动与冲击, 2014, 33(4): 113–118. doi: 10.3969/j.issn.1000-3835.2014.04.021LIU F, ZHANG J Z, TONG M B, et al. Dynamic tests and bird impact dynamic response analysis for a 2024-T3 aluminum alloy plate [J]. Journal of Vibration and Shock, 2014, 33(4): 113–118. doi: 10.3969/j.issn.1000-3835.2014.04.021 [7] LIU J, LI Y L, GAO X S. Bird strike on a flat plate: experiments and numerical simulations [J]. International Journal of Impact Engineering, 2014, 70: 21–37. doi: 10.1016/j.ijimpeng.2014.03.006 [8] 姚小虎, 韩强, 赵隆茂, 等. 飞机圆弧风挡的抗鸟撞击问题研究 [J]. 华南理工大学学报(自然科学版), 2007, 35(2): 6–12. doi: 10.3321/j.issn:1000-565X.2007.02.002YAO X H, HAN Q, ZHAO L M, et al. Investigation into arc windshield of aircraft subjected to bird impact [J]. Journal of South China University of Technology (Natural Science Edition), 2007, 35(2): 6–12. doi: 10.3321/j.issn:1000-565X.2007.02.002 [9] 邹学韬, 张晓晴, 姚小虎. 压剪载荷作用下TB6钛合金的动态力学性能 [J]. 高压物理学报, 2019, 33(2): 024206. doi: 10.11858/gywlxb.20190713ZOU X T, ZHANG X Q, YAO X H. Dynamic behavior of TB6 titanium alloy under shear-compression loading [J]. Chinese Journal of High Pressure Physics, 2019, 33(2): 024206. doi: 10.11858/gywlxb.20190713 [10] 惠旭龙, 牟让科, 白春玉, 等. TC4钛合金动态力学性能及本构模型研究 [J]. 振动与冲击, 2016, 35(22): 161–168. doi: 10.13465/j.cnki.jvs.2016.22.024HUI X L, MU R K, BAI C Y, et al. Dynamic mechanical property and constitutive model for TC4 titanium alloy [J]. Journal of Vibration and Shock, 2016, 35(22): 161–168. doi: 10.13465/j.cnki.jvs.2016.22.024 [11] KAY G. Failure modeling of titanium 6Al-4V and aluminum 2024-T3 with the Johnson-Cook material model: DOT/FAA/AR-03/57 [R]. Washington: U.S. Department of Transportation, Federal Aviation Administration, 2003: 1–11. -







 下载:
下载: