Attenuation Law of Stress Wave in Granular Particles
-
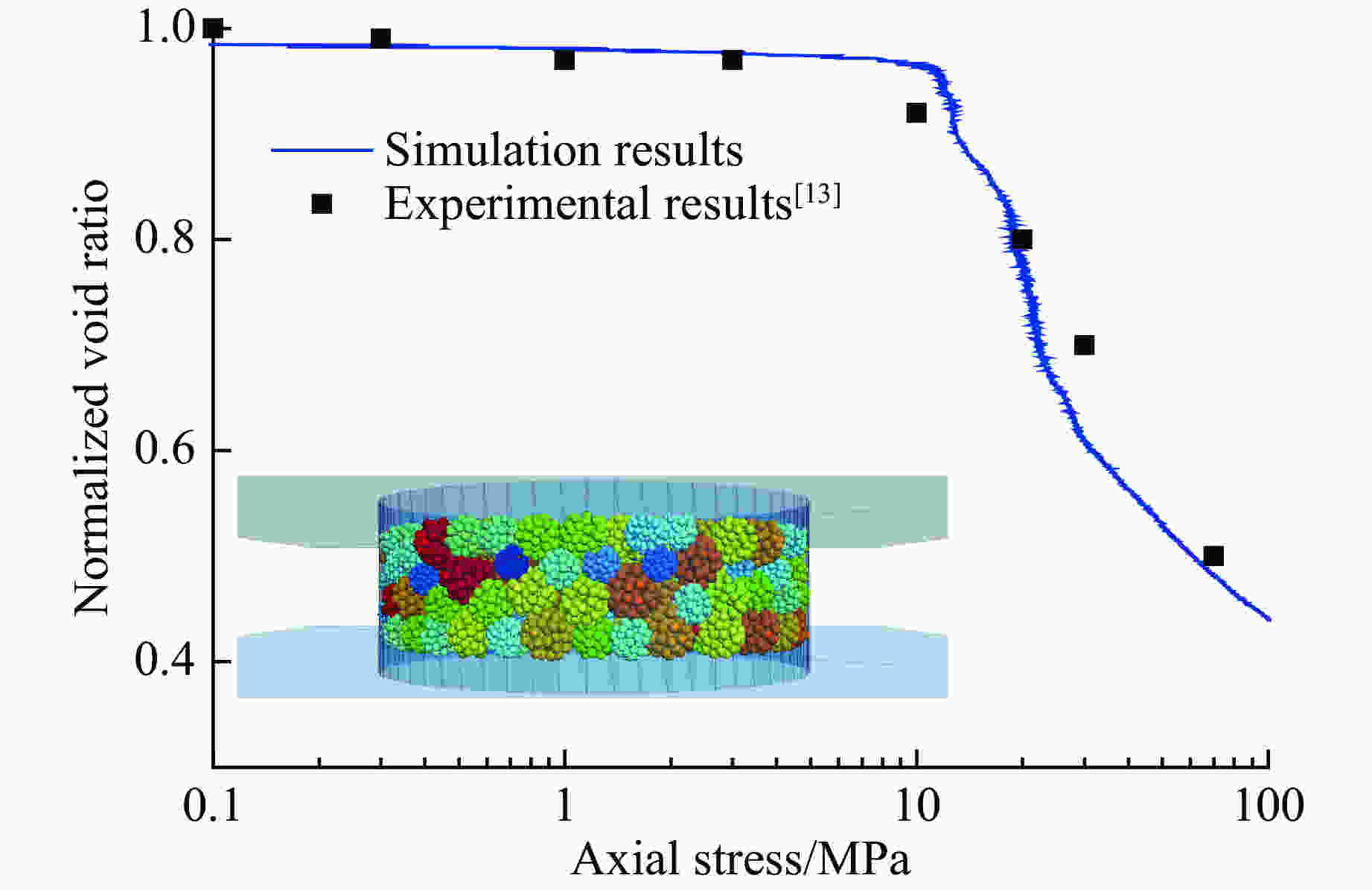
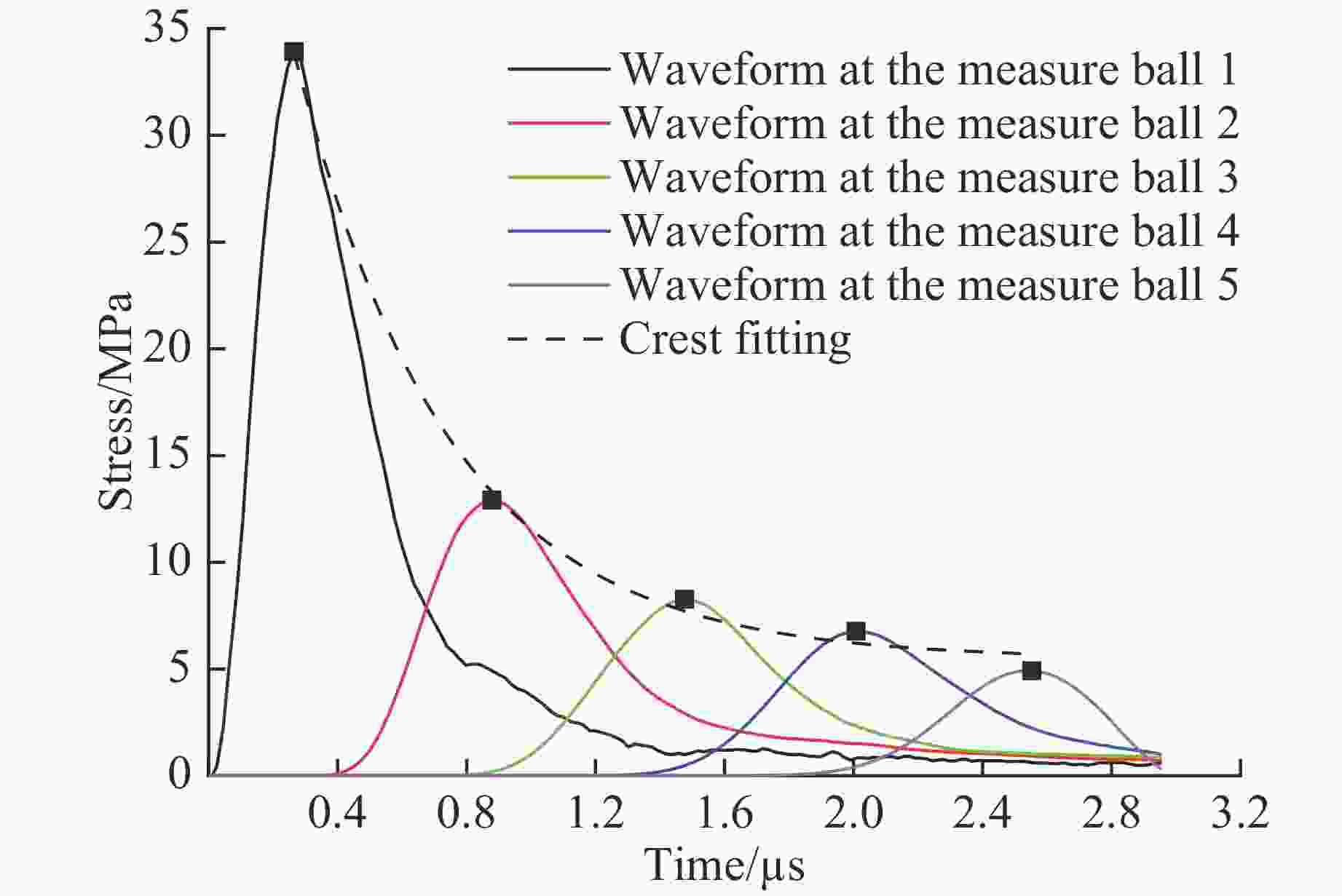
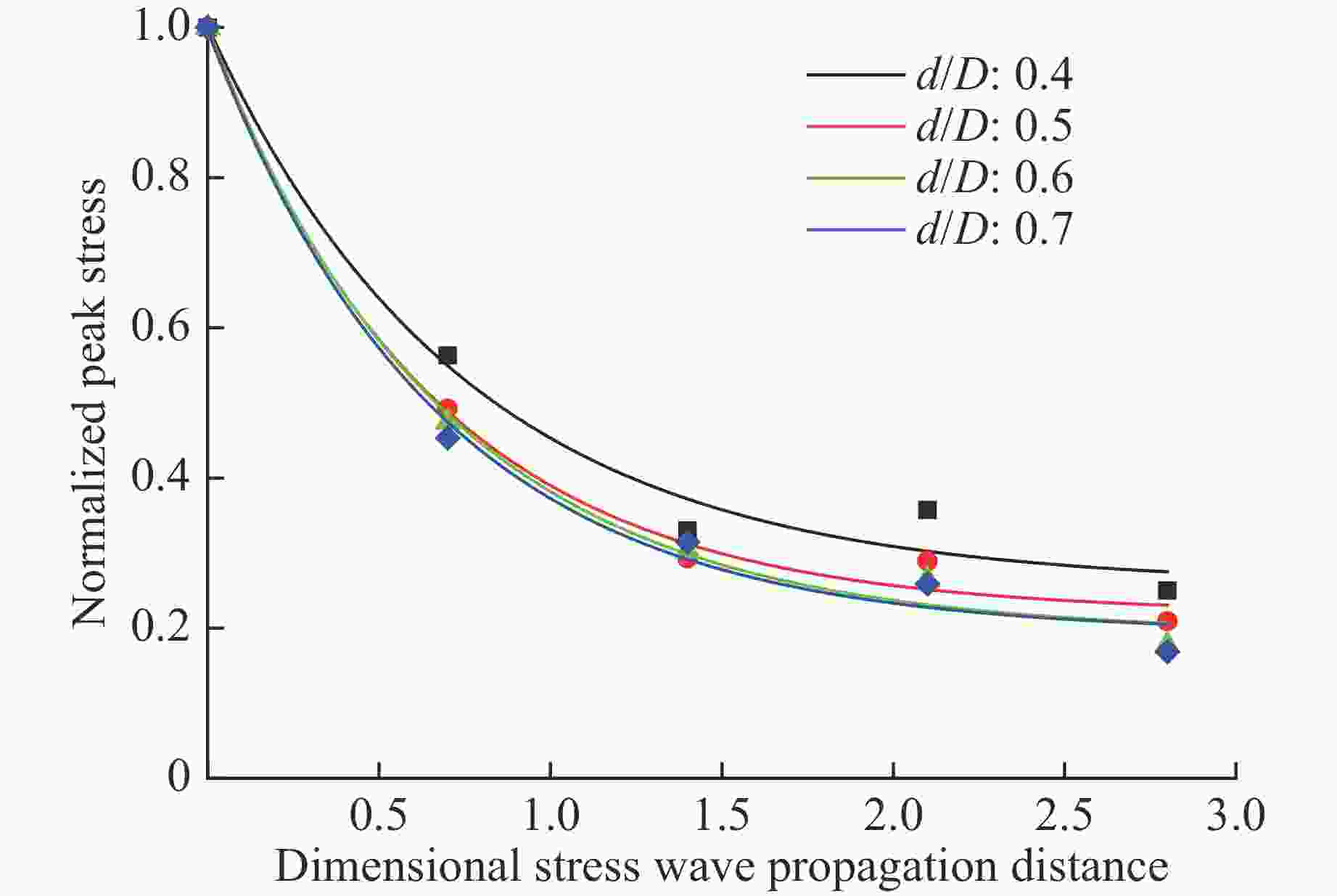
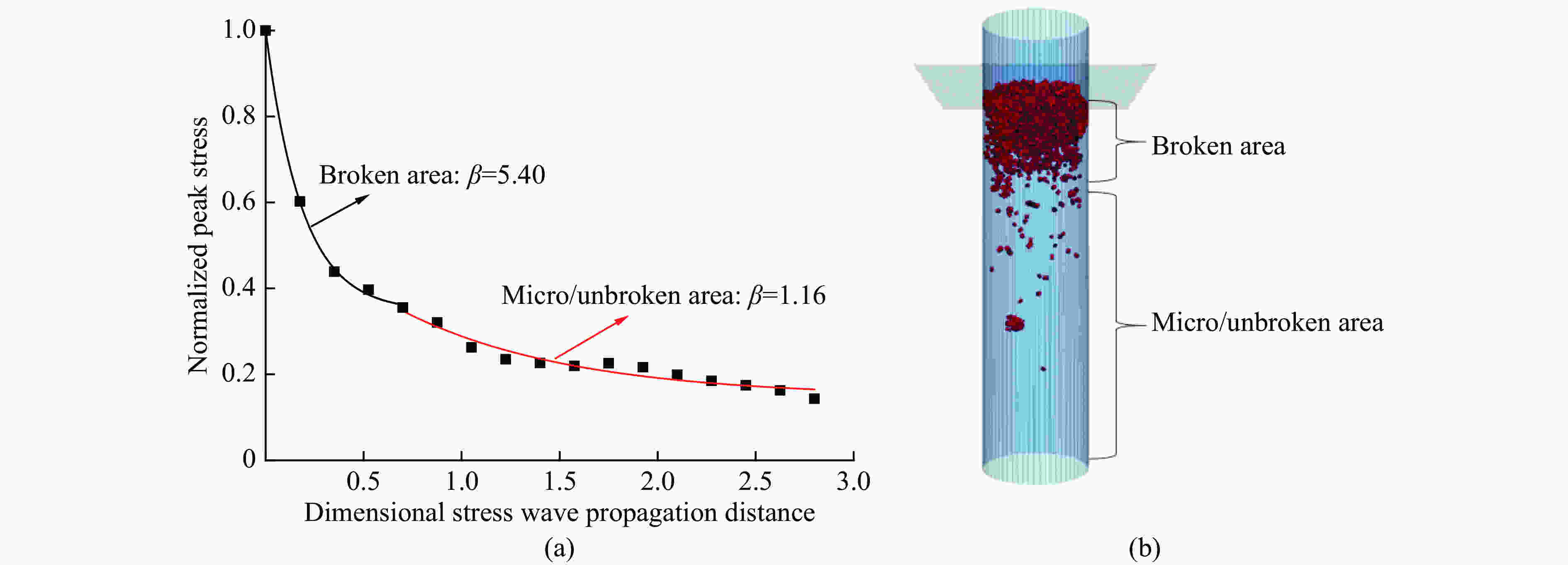
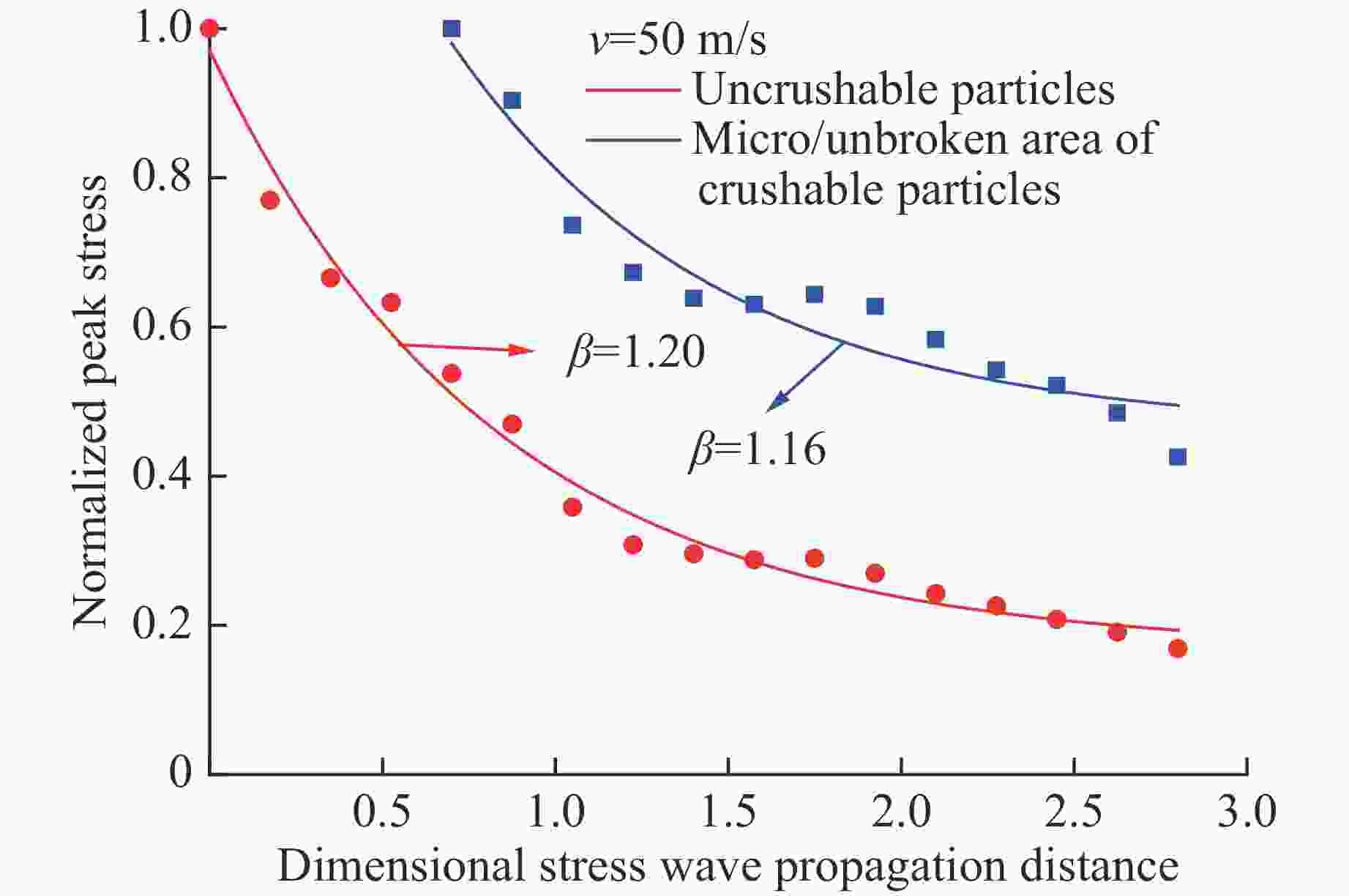
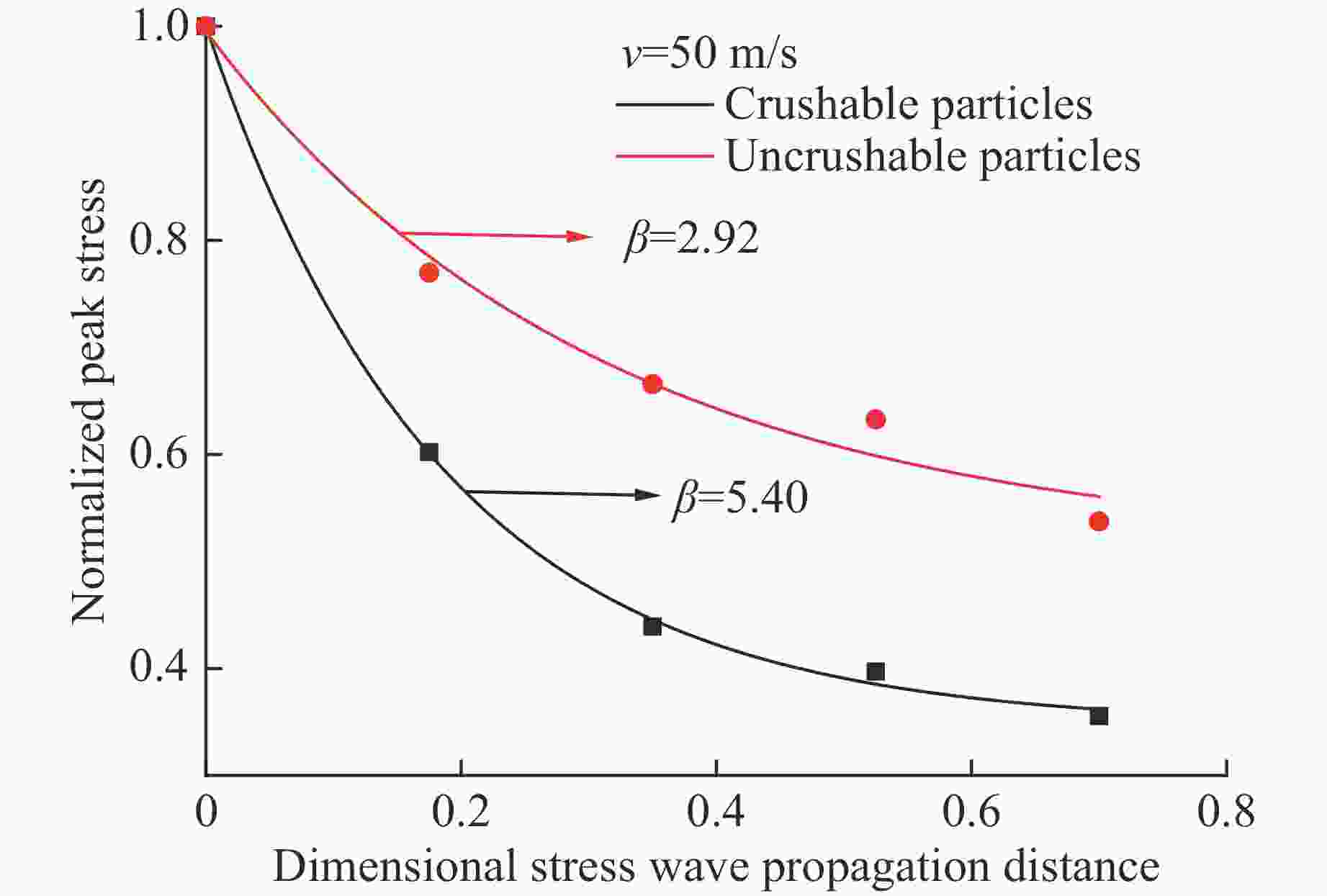
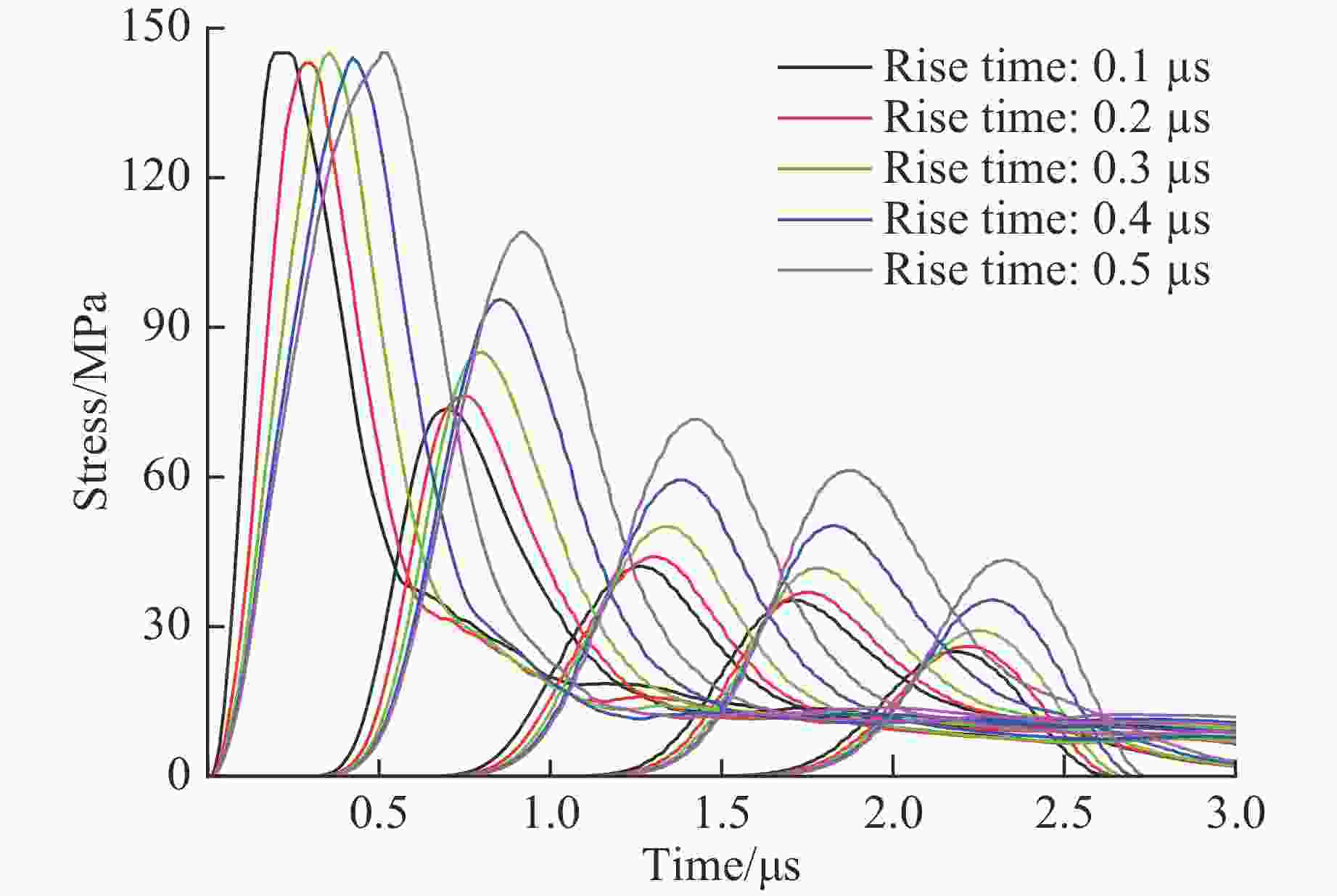
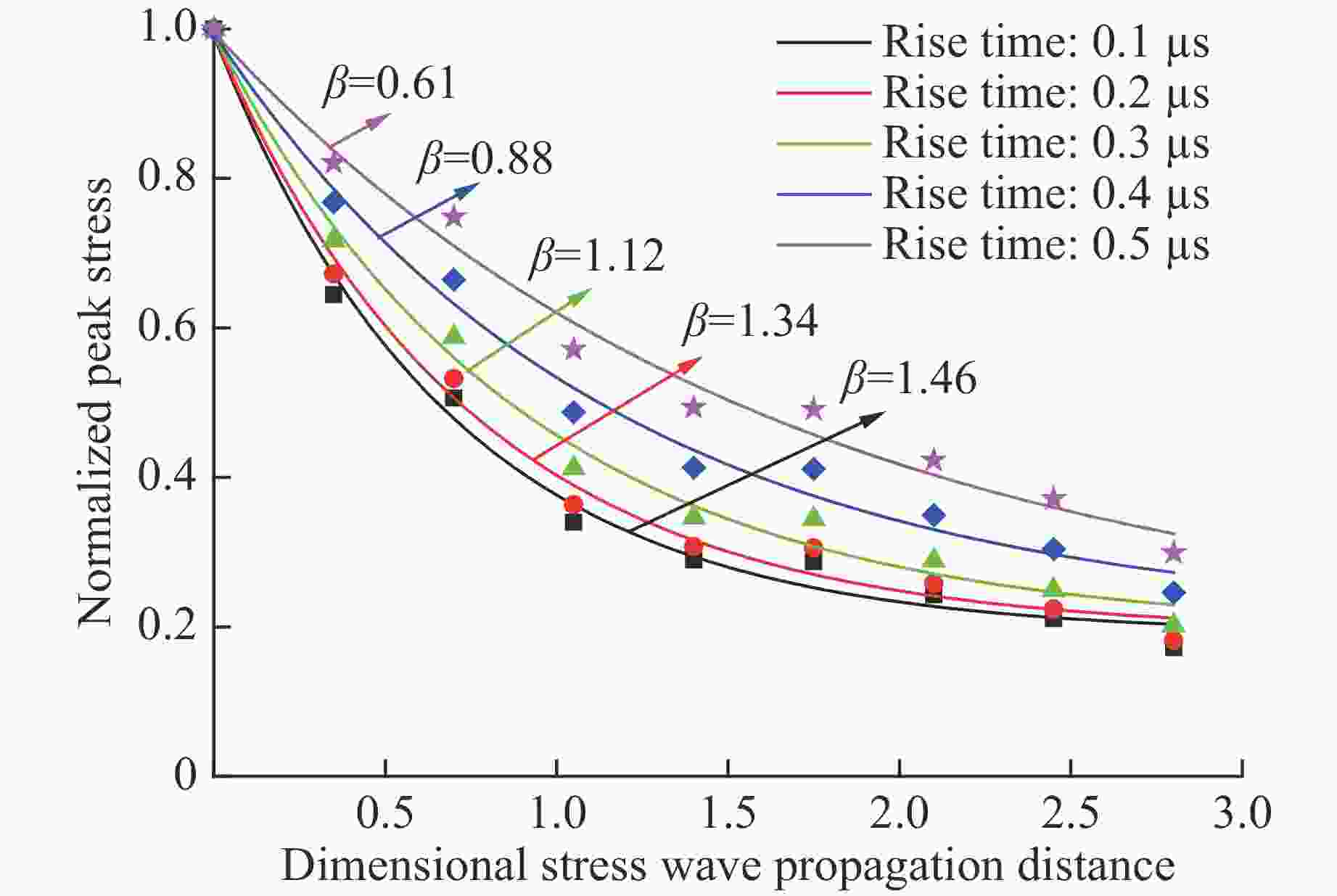
摘要: 脆性散体颗粒在受到冲击加载时,会对应力波传播产生显著的衰减作用。基于离散元颗粒流软件PFC3D建立了散体颗粒模型,通过不同加载速率下的数值模拟,研究应力波在散体颗粒中的传播规律和影响因素。结果表明:在冲击加载下,散体颗粒中传播的应力波峰值整体呈指数型衰减,随着传播距离的增大,应力波衰减程度逐渐减小,颗粒破碎程度也逐渐减小;应力波在散体颗粒中传播时会发生显著的波形弥散,并且应力波波长越短,传播过程中的衰减越大;应力波衰减的率相关性本质上是由散体颗粒的冲击破碎引起的,加载速度越大,颗粒破坏程度越大,应力波的衰减程度越大,而在颗粒不破碎的情况下,加载速度增大时,应力波的衰减程度变化不明显。Abstract: Brittle loose particles exhibit very complex mechanical behavior during the crushing process and have a significant attenuation effect on the stress wave propagation. In order to explore the attenuation law, this paper builds a brittle loose particle model based on the discrete element software PFC3D, and studies the attenuation of stress wave on the microscopic scale. The results show that: under shock loading, the peak value of the stress wave propagating in the granular particles decays exponentially. As the propagation distance increases, the degree of stress wave attenuation gradually decreases, and the degree of particle fragmentation also decreases. Stress wave propagation in granular particles will cause significant wave dispersion, and the shorter the wavelength of the stress wave, the greater the attenuation during propagation. The rate dependence of the stress wave attenuation is essentially caused by the impact fragmentation of the granular particles. The faster the loading speed, the greater degree of particle damage, and the greater the attenuation of stress wave. When the particle is not broken, the degree of attenuation does not change significantly with the increase of the loading velocity.
-
Key words:
- brittle particles /
- discrete element model /
- degree of fracture /
- stress wave /
- attenuation law
-
表 1 Flat-Joint模型微观参数
Table 1. Micro-parameters of the Flat-Joint model
Model Emod/GPa Fj-Kn/GPa Fj-Ks/GPa Fj-Coh/GPa Fj-Ten/GPa Damp Flat-Joint 50 5.25 × 105 9.37 × 105 0.2 0.05 0.15 -
[1] JAEGER H M, NAGEL S R. Granular solids, liquids, and gases [J]. Reviews of Modern Physics, 1996, 68(4): 1259–1273. doi: 10.1103/RevModPhys.68.1259 [2] 张家铭, 汪稔, 张阳明, 等. 土体颗粒破碎研究进展 [J]. 岩土力学, 2003(S2): 661–665.ZHANG J M, WANG R, ZHANG Y M, et al. Advance in studies of soil grain crush [J]. Rock and Soil Mechanics, 2003(S2): 661–665. [3] 王礼立. 应力波基础 [M]. 北京: 国防工业出版社, 1985: 45–47.WANG L L. Foundation of stress waves [M]. Beijing: National Defense Industry Press, 1985: 45–47. [4] 王肖钧. 分层人防工程防护结构对地下爆炸波的阻尼、耗散和导向作用研究 [R]. 合肥: 中国科学技术大学近代力学系, 2008.WANG X J. Research on the damping, dissipation and guiding effect of layered civil air defense engineering structure on underground explosion waves [R]. Hefei: University of Science and Technology of China, 2008. [5] LI J C, MA G W. Experimental study of stress wave propagation across a filled rock joint [J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(3): 471–478. doi: 10.1016/j.ijrmms.2008.11.006 [6] 季顺迎, 李鹏飞, 陈晓东. 冲击荷载下颗粒物质缓冲性能的试验研究 [J]. 物理学报, 2012, 61(18): 184703. doi: 10.7498/aps.61.184703JI S Y, LI P F, CHEN X D. Experiments on shock-absorbing capacity of granular matter under impact load [J]. Acta Physica Sinica, 2012, 61(18): 184703. doi: 10.7498/aps.61.184703 [7] 赵跃堂, 郑守军, 郑大亮, 等. 爆炸波在饱和土介质中传播时压力变化规律的试验研究 [J]. 防灾减灾工程学报, 2004, 24(1): 60–65.ZHAO Y T, ZHENG S J, ZHENG D L, et al. Experimental investigation on pressure variation during explosion wave propagation in saturated soils [J]. Journal of Disaster Prevention and Mitigation Engineering, 2004, 24(1): 60–65. [8] 赵凯. 分层防护层对爆炸波的衰减和弥散作用研究 [D]. 合肥: 中国科学技术大学, 2007: 25–40.ZHAO K. The attenuation and dispersion effects on explosive wave of layered protective engineering [D]. Hefei: University of Science and Technology of China, 2007: 25–40. [9] 魏久淇, 吕亚茹, 刘国权, 等. 钙质砂一维冲击响应及吸能特性试验 [J]. 岩土力学, 2019, 40(1): 191–198.WEI J Q, LÜ Y R, LIU G Q, et al. One-dimensional impact responses and energy absorption of calcareous sand [J]. Rock and Soil Mechanics, 2019, 40(1): 191–198. [10] YU X, CHEN L, FANG Q, et al. Determination of attenuation effects of coral sand on the propagation of impact-induced stress wave [J]. International Journal of Impact Engineering, 2019, 125(1): 63–82. [11] 祁原, 黄俊杰, 陈明祥. 可破碎颗粒体在动力载荷下的耗能特性 [J]. 力学学报, 2015, 47(2): 254–259.QI Y, HUANG J J, CHEN M X. Energy dissipation characteristics of crushable granules under dynamic excitations [J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(2): 254–259. [12] 郑文. 颗粒物质体系复杂动力学行为研究 [D]. 合肥: 中国科学技术大学, 2013: 17–36.ZHENG W. A study on complex dynamic properties of granular material [D]. Hefei: University of Science and Technology of China, 2013: 17–36. [13] 黄俊宇. 冲击载荷下脆性颗粒材料多尺度变形破碎特性研究 [D]. 合肥: 中国科学技术大学, 2016: 19–40.HUANG J Y. Dynamic multiscale deformation behavior and particle-breakage properties of granular materials subjected to impact loading [D]. Hefei: University of Science and Technology of China, 2016: 19–40. [14] 王刚, 叶沁果, 查京京. 珊瑚礁砂砾料力学行为与颗粒破碎的试验研究 [J]. 岩土工程学报, 2018, 40(5): 802–810. doi: 10.11779/CJGE201805004WANG G, YE Q G, ZHA J J. Experimental study on mechanical behavior and particle crushing of coral sand-gravel fill [J]. Chinese Journal of Geotechnical Engineering, 2018, 40(5): 802–810. doi: 10.11779/CJGE201805004 [15] 张科芬, 张升, 滕继东, 等. 颗粒破碎的三维离散元模拟研究 [J]. 岩土力学, 2017, 38(7): 2119–2127.ZHANG K F, ZHANG S, TENG J D, et al. 3D numerical simulation of particle breaking using discrete element [J]. Rock and Soil Mechanics, 2017, 38(7): 2119–2127. [16] 张家铭, 汪稔, 石祥锋, 等. 侧限条件下钙质砂压缩和破碎特性试验研究 [J]. 岩石力学与工程学报, 2005, 24(18): 3327–3331. doi: 10.3321/j.issn:1000-6915.2005.18.022ZHANG J M, WANG R, SHI X F, et al. Compression and crushing behavior of calcareous sand under confined compression [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(18): 3327–3331. doi: 10.3321/j.issn:1000-6915.2005.18.022 [17] POTYONDY D O, CUNDALL P A. A bonded-particle model for rock [J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1329–1364. doi: 10.1016/j.ijrmms.2004.09.011 [18] ZHANG S, ZHANG F. A thermo-elasto-viscoplastic model for soft sedimentary rock [J]. Soils and Foundations, 2009, 49(4): 583–595. doi: 10.3208/sandf.49.583 [19] WNG J F, LI Y L, GAO Y B, et al. Experimental study on structural properties influencing on compressibility of soft clay [J]. Advanced Materials Research, 2011, 261/262/263: 767–1772. [20] YAN W M, LI X S. Mechanical response of a medium-fine-grained decomposed granite in Hong Kong [J]. Engineering Geology, 2012, 129/130: 1–8. [21] HUANG J Y, XU S L, HU S S. Influence of particle breakage on the dynamic compression responses of brittle granular materials [J]. Mechanics of Materials, 2014, 68: 15–28. doi: 10.1016/j.mechmat.2013.08.002 -







 下载:
下载: