Damage Evolution in Concrete Interfacial Transition Zone with Ultrasonic Dynamic Load
-
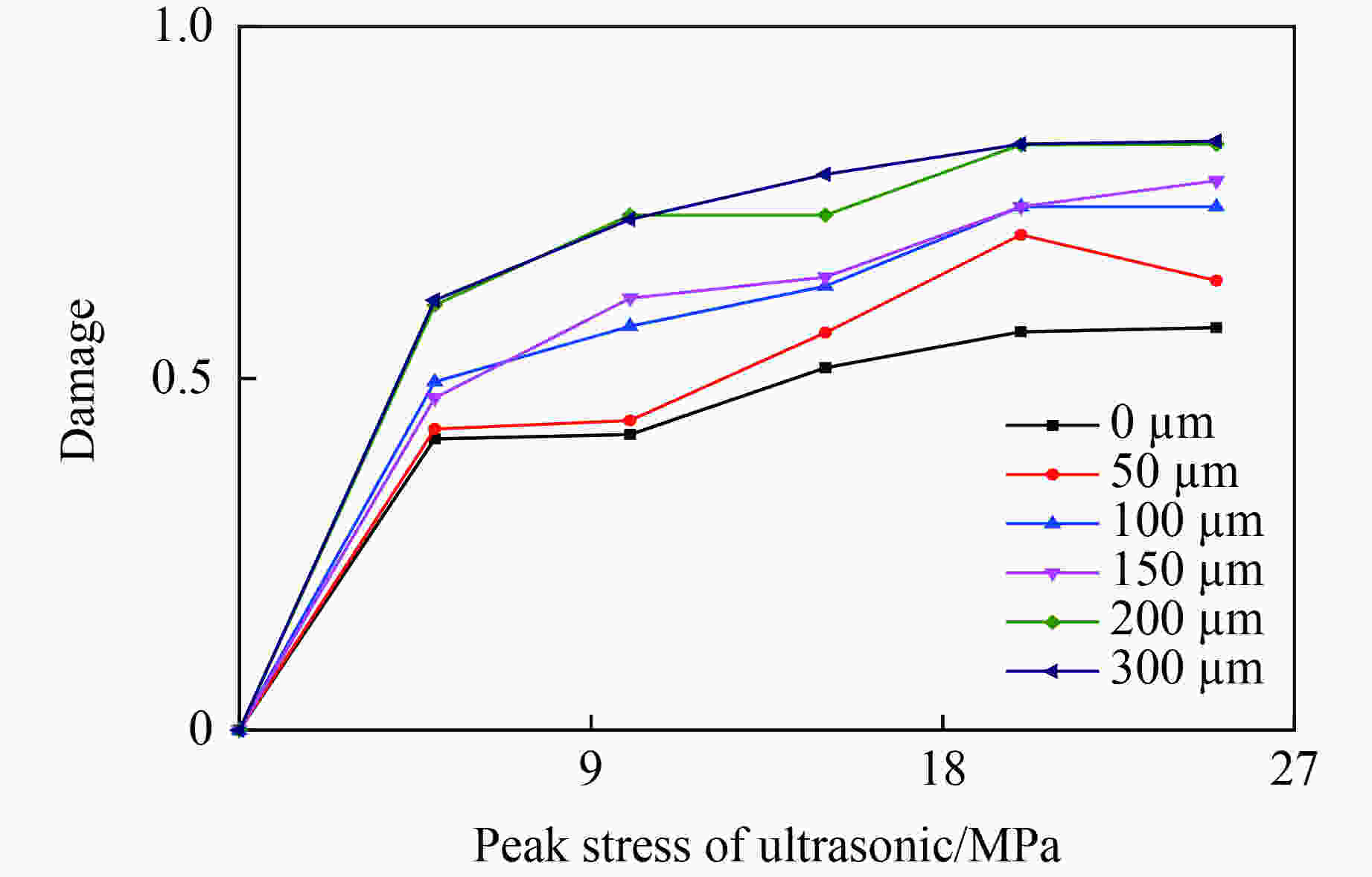
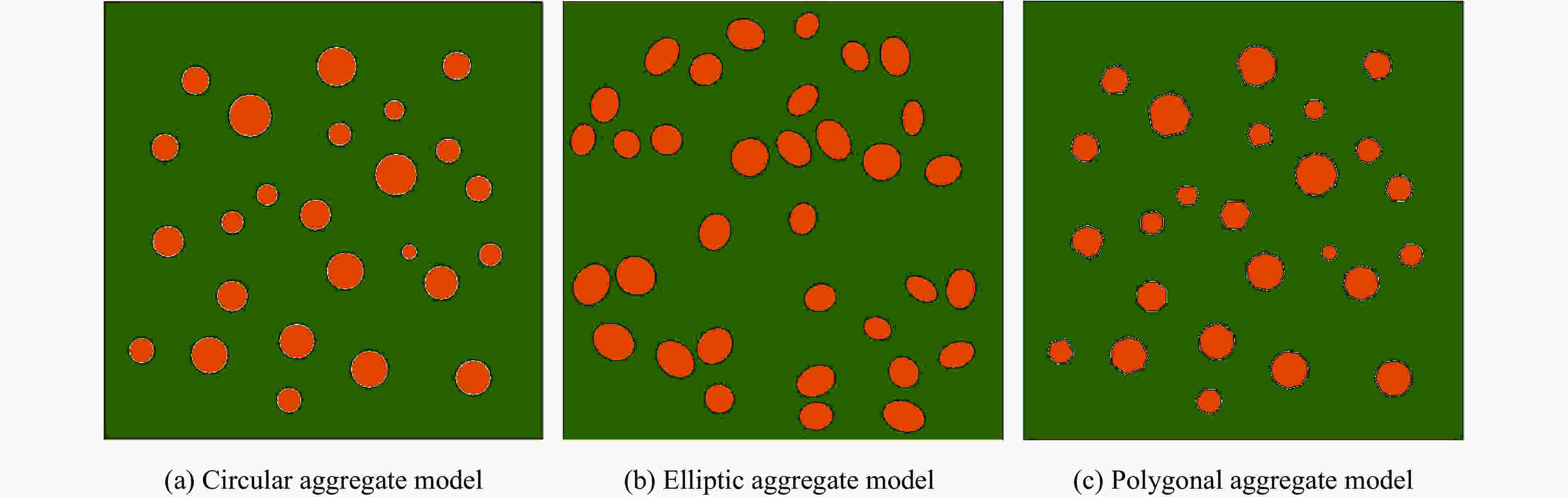
摘要: 混凝土是由粗骨料、水泥砂浆以及过渡区域组成的三相非均质复合材料。混凝土过渡区域(Interfacial transition zone, ITZ)是三相中最薄弱的环节,且难以观测,对混凝土的宏观力学性能有着重要影响。基于ABAQUS的Dynamic/Explicit模块,建立了能反映混凝土基质、骨料形状和 ITZ等真实细观结构的有限元模型,并应用该模型研究了过渡区域对混凝土损伤破坏的影响。研究结果表明:粗骨料的形状对混凝土损伤性能有一定影响,当骨料形状为凸多边形时,其抗损伤性能最弱;混凝土的抗损伤性能随着ITZ强度的降低而减弱,当ITZ的强度高于砂浆的60%时,抗损伤性能逐渐增强;随着ITZ厚度的增加,混凝土的抗损伤能力减弱。Abstract: Concrete is a three-phase material composed of coarse aggregate, cement mortar and interfacial transition zone (ITZ). The ITZ is the weakest of the three phases and difficult to observe, but it has a significant impact on the efficiency of concrete crushing. In order to study the impact of ITZ on the damage performance of concrete crushing, the finite element model that reflects real mesoscopic structure of concrete matrix, aggregate shape, and ITZ was established on the Dynamic/Explicit model in ABAQUS. The results showed that the shape of coarse aggregate has a certain influence on the damage performance of concrete, and when the shape is convex polygonal, its damage resistance is the weakest. The damage resistance ability of concrete decreases with the decrease of ITZ strength. When ITZ strength is higher than 60% of mortar, the damage resistance ability gradually increases. As the thickness of the ITZ area increases, the damage resistance ability decreases.
-
Key words:
- concrete /
- interfacial transition zone /
- damage performance /
- ultrasonic crushing
-
表 1 混凝土各相材料参数
Table 1. Concrete material parameters of each phase
Material Elastic model/GPa Poisson′s ratio μ Bulk density t/m3 Expansion angle/(°) Flow potential offset ε Ratio of double and uniaxial compressive strength αf Constant stress ratio Kc Aggregate 30.00 0.167 2.6 Mortar 10.66 0.167 2.1 30 0.1 1.16 0.666 7 ITZ 0.167 2.1 30 0.1 1.16 0.666 7 -
[1] 陈惠苏, 孙伟, STROEVEN P. 水泥基复合材料集料与浆体界面研究综述(二):界面微观结构的形成、劣化机理及其影响因素 [J]. 硅酸盐学报, 2004, 32(1): 70–79. doi: 10.3321/j.issn:0454-5648.2004.01.013CHEN H S, SUN W, STROEVEN P. Interfacial transition zone between aggregate and paste in cementitious composites (Ⅱ): mechanism of formation and degradation of interfacial transition zone microstructure, and its influence factors [J]. Journal of the Chinese Ceramic Society, 2004, 32(1): 70–79. doi: 10.3321/j.issn:0454-5648.2004.01.013 [2] 徐晶, 王先志. 纳米二氧化硅对混凝土界面过渡区的改性机制及其多尺度模型 [J]. 硅酸盐学报, 2018, 46(8): 1053–1058.XU J, WANG X Z. Effect of nano-silica modification on interfacial transition zone in concrete and its multiscale modelling [J]. Journal of the Chinese Ceramic Society, 2018, 46(8): 1053–1058. [3] YANG C C, CHO S W. Approximate migration coefficient of percolated interfacial transition zone by using the accelerated chloride migration test [J]. Cement and Concrete Research, 2005, 35: 344–350. doi: 10.1016/j.cemconres.2004.05.038 [4] AQUINO M J, LI Z, SHAH S P. Mechanical properties of the aggregate and cement interface [J]. Advanced Cement Based Materials, 1995, 2(6): 211–223. doi: 10.1016/1065-7355(95)90040-3 [5] LEE K M, PARK J H. A numerical model for elastic modulus of concrete considering interfacial transition zone [J]. Cement and Concrete Research, 2008, 38(3): 396–402. doi: 10.1016/j.cemconres.2007.09.019 [6] 王怀亮, 宋玉普. 多轴应力状态下混凝土的动态强度准则 [J]. 哈尔滨工业大学学报, 2014, 46(4): 93–97.WANG H L, SONG Y P. A dynamic strength criterion of concrete under multiaxial stress state [J]. Journal of Harbin Institute of Technology, 2014, 46(4): 93–97. [7] 杜修力, 金浏. 考虑过渡区界面影响的混凝土宏观力学性质研究 [J]. 工程力学, 2012, 29(12): 72–79. doi: 10.6052/j.issn.1000-4750.2011.04.0216DU X L, JIN L. Research on the influence of interfacial transition zone on the macro-mechanical properties of concrete [J]. Engineering Mechanics, 2012, 29(12): 72–79. doi: 10.6052/j.issn.1000-4750.2011.04.0216 [8] 王哲. 沿应变路径准静态加载时混凝土的极限状态现象 [J]. 北京交通大学学报, 2010, 34(1): 30–34. doi: 10.3969/j.issn.1673-0291.2010.01.007WANG Z. Phenomena of concrete limit state under quasi-static loading along strain paths [J]. Journal of Beijing Jiaotong University, 2010, 34(1): 30–34. doi: 10.3969/j.issn.1673-0291.2010.01.007 [9] GUINEA G V, EL-SAYED K, ROCCO C G, et al. The effect of the bond between the matrix and the aggregates on the cracking mechanism and fracture parameters of concrete [J]. Cement and Concrete Research, 2002, 32(12): 1961–1970. doi: 10.1016/S0008-8846(02)00902-X [10] 马巍, 任建伟, 胡俊, 等. 基于不同加载制度的轻骨料混凝土动态冲击性能 [J]. 硅酸盐通报, 2019, 38(4): 974–982.MA W, REN J W, HU J, et al. Dynamical shocking property of light-weighting aggregates concrete based on impact loading regimes [J]. Bulletin of the Chinese Ceramic Society, 2019, 38(4): 974–982. [11] 阮欣, 李越, 金泽人, 等. 混凝土二维细观骨料建模方法综述 [J]. 同济大学学报(自然科学版), 2018, 46(5): 604–612.RUAN X, LI Y, JIN Z R, et al. Review of two-dimensional meso-modeling methods of concrete aggregate [J]. Journal of Tongji University (Natural Science), 2018, 46(5): 604–612. [12] 刘建南, 张昌锁. 过渡区界面对混凝土劈裂性能影响的试验与数值模拟 [J]. 科学技术与工程, 2018, 18(18): 269–274. doi: 10.3969/j.issn.1671-1815.2018.18.044LIU J N, ZHANG C S. Experiment and numerical simulation on the influence of interfacial transition zone on concrete splitting performance [J]. Science Technology and Engineering, 2018, 18(18): 269–274. doi: 10.3969/j.issn.1671-1815.2018.18.044 [13] YANG C C. Effect of the interfacial transition zone on the transport and the elastic properties of mortar [J]. Magazine of Concrete Research, 2003, 55(4): 305–312. doi: 10.1680/macr.2003.55.4.305 [14] 过镇海, 李卫. 混凝土在不同应力-温度途径下的变形试验和本构关系 [J]. 土木工程学报, 1993, 26(5): 58–69. doi: 10.3321/j.issn:1000-131X.1993.05.001GUO Z H, LI W. Deformation testing and constitutive relationship of concrete under different stress-temperature paths [J]. China Civil Engineering Journal, 1993, 26(5): 58–69. doi: 10.3321/j.issn:1000-131X.1993.05.001 [15] 刘海峰, 韩莉. 二维骨料随机分布混凝土的动态力学性能数值模拟 [J]. 高压物理学报, 2016, 30(3): 191–199. doi: 10.11858/gywlxb.2016.03.003LIU H F, HAN L. Numerical simulation of dynamic mechanical behavior of concrete with two-dimensional random distribution of coarse aggregate [J]. Chinese Journal of High Pressure Physics, 2016, 30(3): 191–199. doi: 10.11858/gywlxb.2016.03.003 [16] 蒋橙炜, 陈启东, 顾泽堃. 超声破碎混凝土的力学模型与仿真分析 [J]. 机械制造与自动化, 2019, 48(2): 84–88.JIANG C W, CHEN Q D, GU Z K. Mechanical model and simulation analysis of ultrasonic crushed concrete [J]. Machine Building & Automation, 2019, 48(2): 84–88. [17] WEIBULL W. A statistical distributions function of wide applicability [J]. Journal of Applied Mechanics, 1951, 18: 293–297. -






 下载:
下载: