Mechanical Properties of AlCrFeCuNi High Entropy Alloy: A Molecular Dynamics Study
-
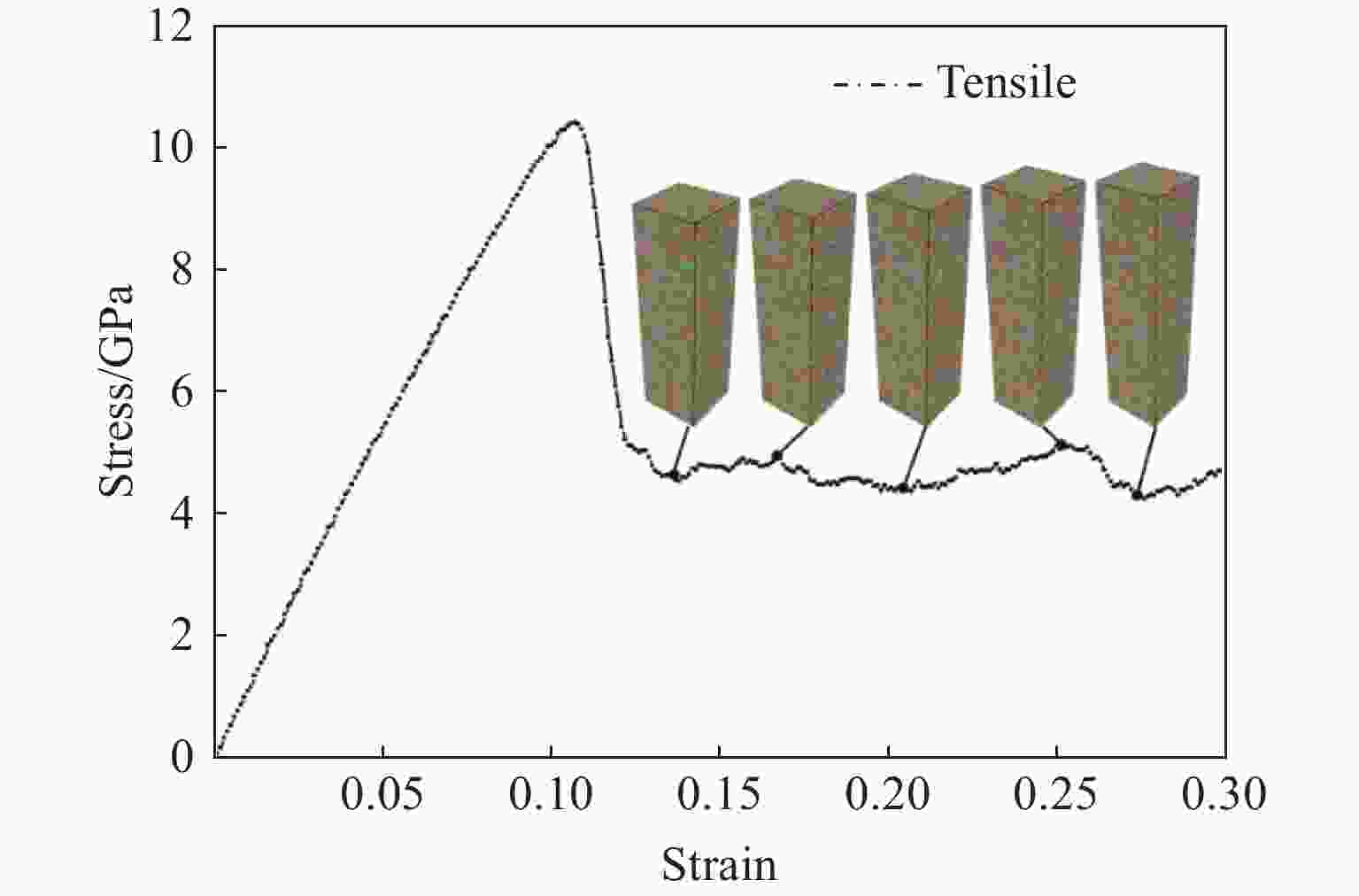
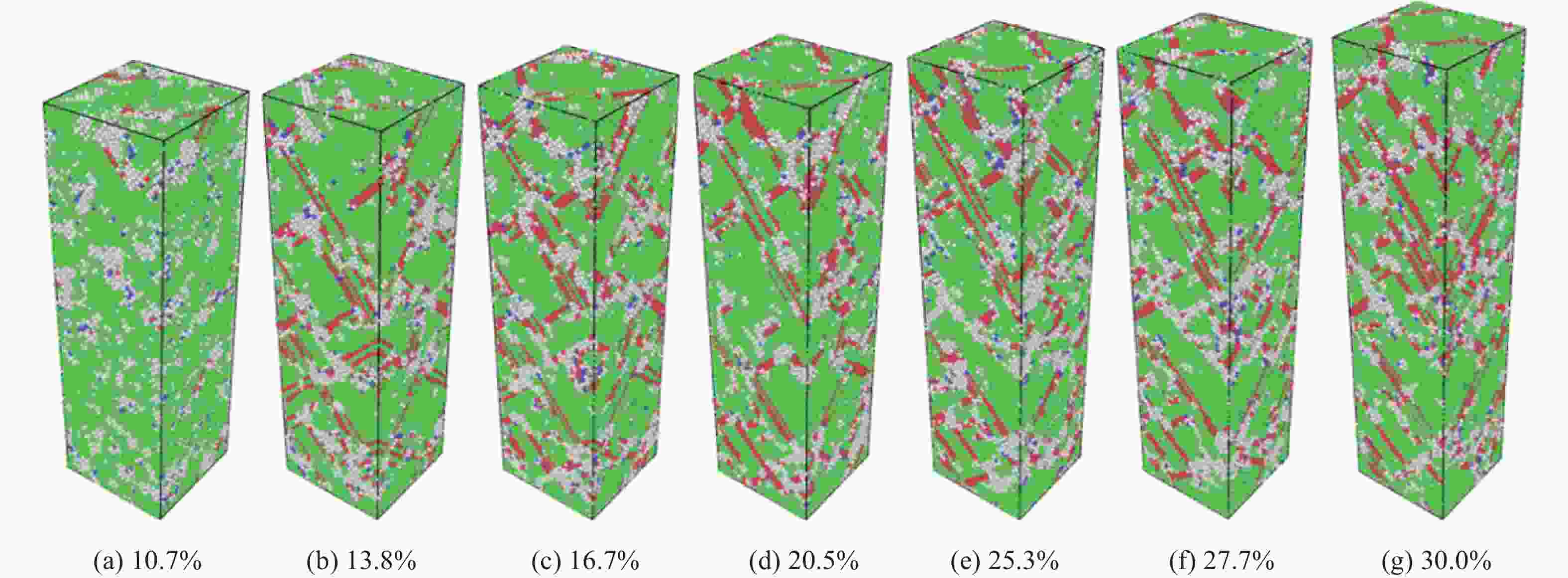
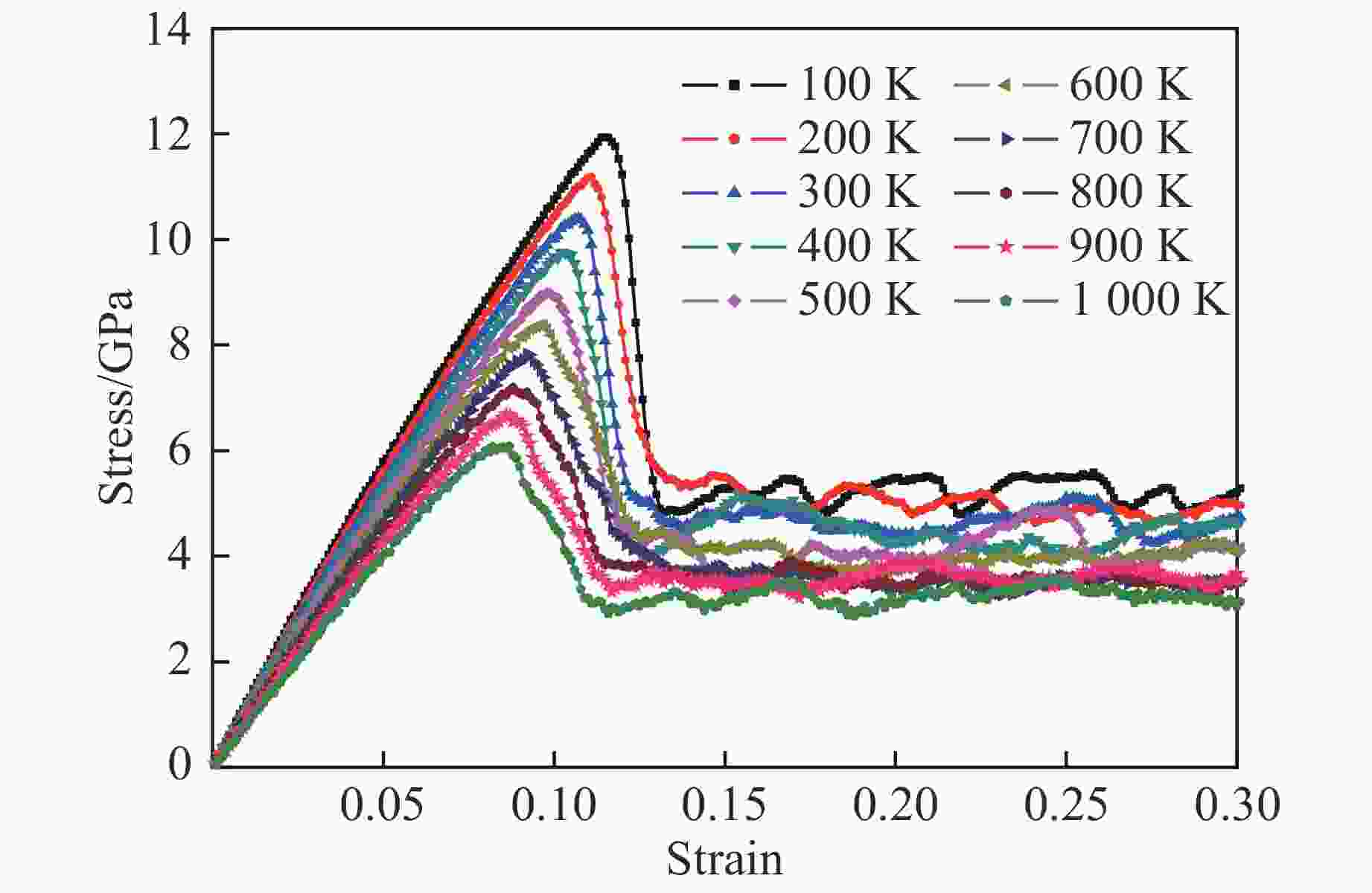
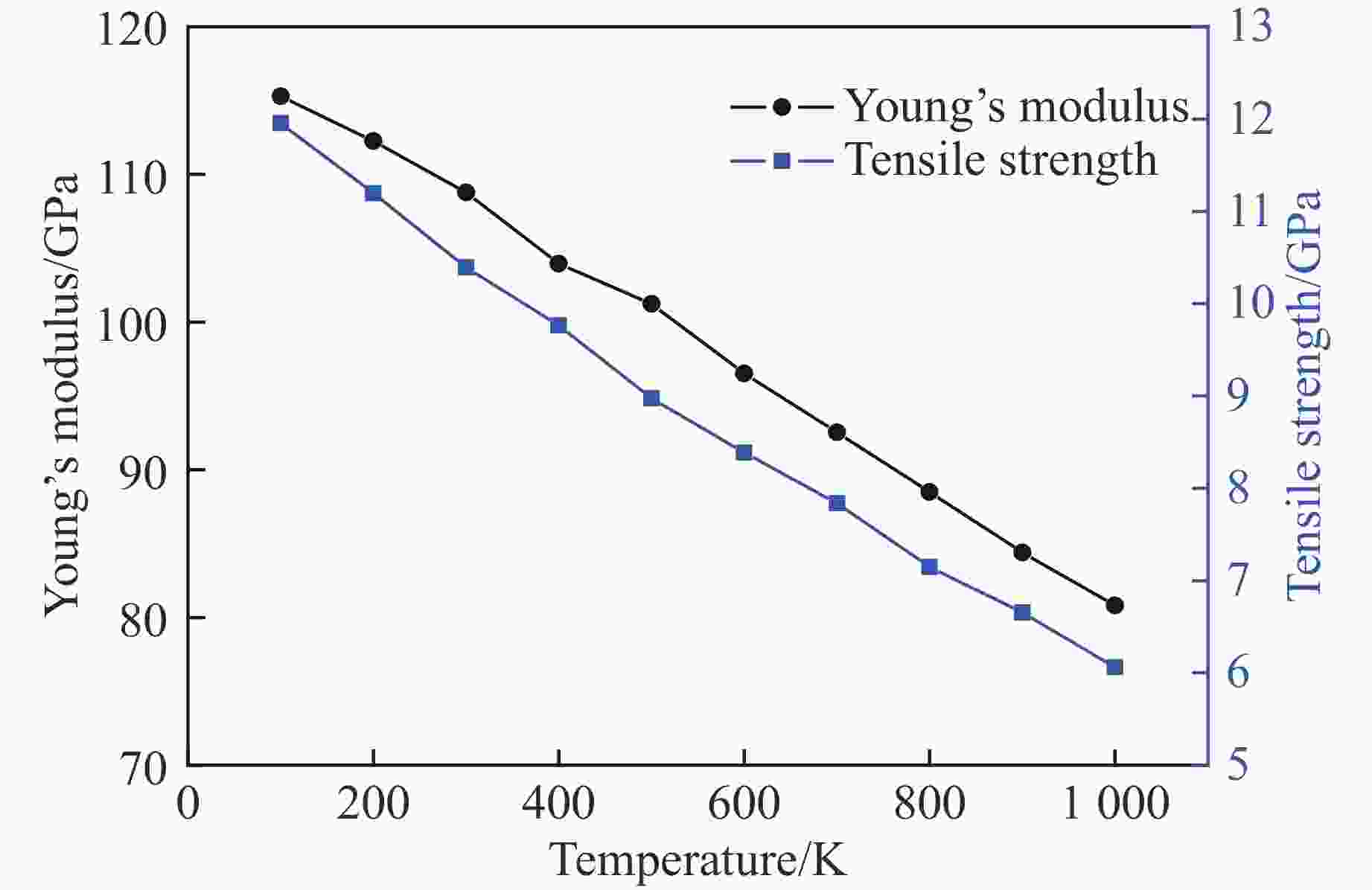
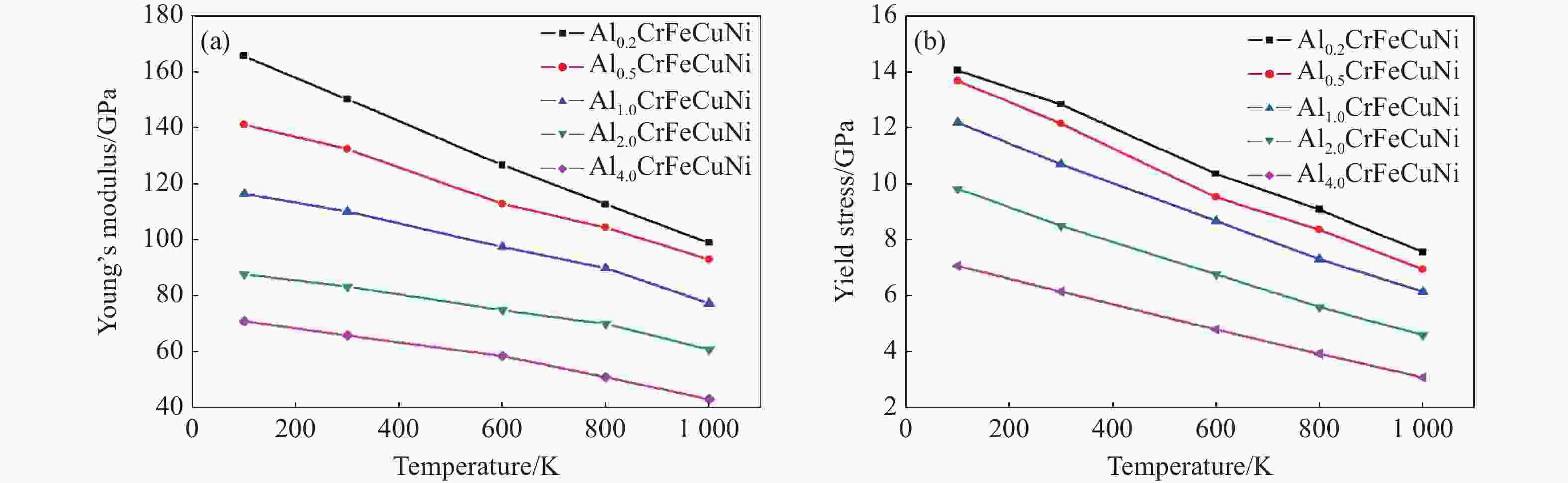
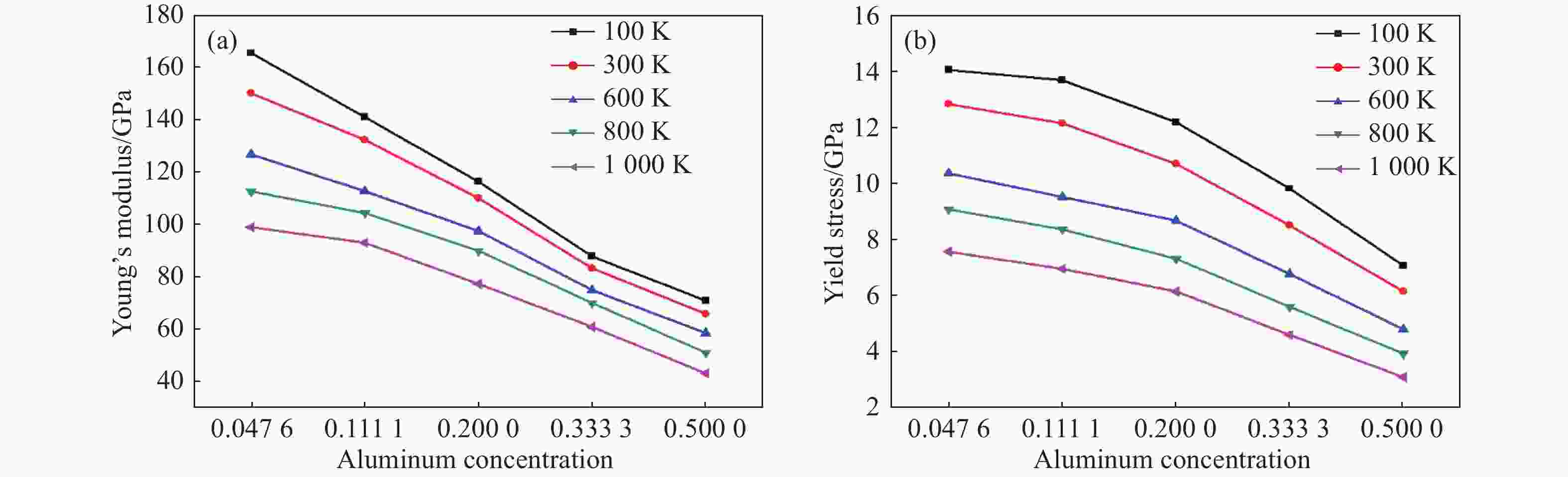
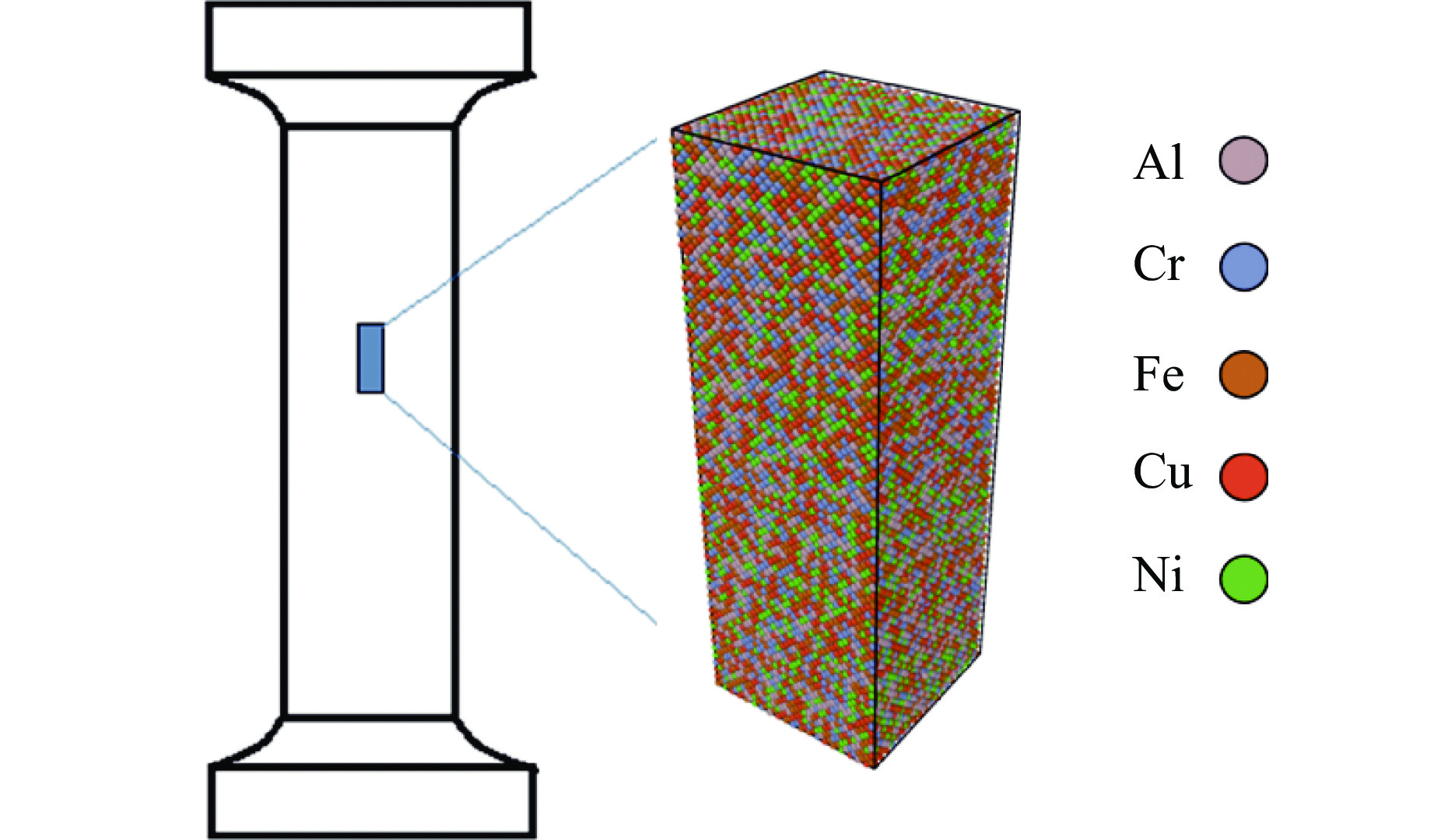
摘要: 高熵合金具有传统合金无法比拟的高强度、高硬度和高耐磨耐腐蚀性,具有广阔的应用前景。为研究AlCrFeCuNi高熵合金(High entropy alloy, HEA)在轴向载荷作用下的力学性能,采用分子动力学方法,模拟高熵合金的实验制备过程并建立原子模型,研究温度和Al的含量对AlCrFeCuNi高熵合金力学性能的影响,从材料学角度分析了变形过程及其具有高塑性的原因。模拟结果表明,AlCrFeCuNi高熵合金在拉伸载荷作用下依次经历弹性、屈服、塑性3个变形阶段。在屈服阶段,开始出现孪晶和层错,孪晶和层错的产生和生长是合金产生不均匀塑性变形的主要原因之一。高熵合金的杨氏模量和屈服应力随着Al含量的增加近似线性降低,同时具有很强的温度效应,温度越低,Al含量越小,其杨氏模量和屈服应力的下降幅度越大。Abstract: High entropy alloy (HEA) has high strength, high hardness, high wear resistance and corrosion resistance which traditional alloys do not have, and has broad application prospects. The mechanical properties of AlCrFeCuNi high Entropy Alloy (HEA) under axial loading were also studied in this paper. Molecular dynamics method was used to simulate the experimental preparation process of HEA and establish an atomic model. The mechanical properties of AlCrFeCuNi HEA at different temperatures and Al concentrations were studied. The deformation process and the reasons for its high plasticity were analyzed from the point of view of material science. The simulation results show that the AlCrFeCuNi HEA undergoes elastic deformation, yield and plastic deformation stages under tension loads. In the yield stage, the appearance and growth of twins and stacking faults are one of the main reasons for the uneven plastic deformation of the alloy. The analysis shows that the Young’s modulus and yield stress of the HEA decrease linearly with the increase of Al concentration. The HEA have strong temperature effect. The lower the temperature, the smaller the Al concentration, and the greater the decrease in Young’s modulus and yield stress.
-
Atom pair D/eV $\alpha $/Å–1 r0/Å Cr-Cu 0.389 04 1.465 4 2.628 9 Fe-Cu 0.378 32 1.373 6 2.645 4 Ni-Cu 0.379 72 1.389 3 2.618 2 Cr-Al 0.345 41 1.368 5 2.819 9 Fe-Al 0.335 89 1.276 7 2.837 6 Ni-Al 0.337 13 1.292 4 2.808 3 表 2 不同温度下的拉伸力学性能
Table 2. Mechanical properties under uniaxial tensile loading at different temperatures
Temperature/K Young’s modulus/
GPaYield stress/
GPaYield strain Temperature/K Young’s modulus/
GPaYield stress/
GPaYield strain 100 115.273 11.954 0.115 600 96.507 8.383 0.097 200 112.251 11.197 0.111 700 92.532 7.838 0.092 300 108.768 10.390 0.107 800 88.503 7.147 0.088 400 103.950 9.765 0.103 900 84.382 6.652 0.087 500 101.228 8.975 0.099 1 000 80.808 6.060 0.086 表 3 AlxCrFeCuNi高熵合金中Al百分含量和各元素原子个数
Table 3. The number of different kinds of atoms of AlxCrFeCuNi
x ${\eta _{{\rm{Al}}}}$/% n(Al) n(Cr) n(Fe) n(Cu) n(Ni) 0.2 4.76 4 515 23 151 22 920 22 980 22 434 0.5 11.11 10 929 21 528 21 423 21 165 20 955 1.0 20.00 19 428 19 338 19 419 18 870 18 945 2.0 33.33 32 238 16 071 16 284 15 666 15 741 4.0 50.00 47 988 12 000 12 336 12 078 11 598 表 4 AlxCrFeCuNi高熵合金在不同温度下的杨氏模量和屈服应力
Table 4. Young’s modulus and yield stress of AlxCrFeCuNi at different temperatures and different Al concentrations
T/K Young’s modulus/GPa Yield stress/GPa x=0.2 x=0.5 x=1.0 x=2.0 x=4.0 x=0.2 x=0.5 x=1.0 x=2.0 x=4.0 100 165.61 141.06 116.39 87.83 70.94 14.05 13.68 12.19 9.82 7.08 300 150.16 132.42 110.13 83.28 65.87 12.83 12.15 10.70 8.51 6.16 600 126.82 112.77 97.55 74.98 58.55 10.36 9.52 8.68 6.78 4.81 800 112.70 104.47 89.96 70.05 51.08 9.08 8.37 7.32 5.61 3.94 1 000 99.06 93.09 77.37 60.94 43.13 7.57 6.96 6.16 4.61 3.10 -
[1] YEH J W, CHEN S K, LIN S J, et al. Nanostructured high-entropy alloys with multiple principal elements: novel alloy design concepts and outcomes [J]. Advanced Engineering Materials, 2004, 6(5): 299–303. doi: 10.1002/adem.200300567 [2] CHEN W, FU Z, FANG S, et al. Alloying behavior, microstructure and mechanical properties in a FeNiCrCo0.3Al0.7 high entropy alloy [J]. Materials & Design, 2013, 51(5): 854–860. [3] CHUANG M H, TSAI M H, WANG W R, et al. Microstructure and wear behavior of Al xCo1.5CrFeNi1.5Ti high-entropy alloys [J]. Acta Materialia, 2011, 59(16): 6308–6317. doi: 10.1016/j.actamat.2011.06.041 [4] LEE C P, CHEN Y Y, HSU C Y, et al. Enhancing pitting corrosion resistance of Al xCrFe1.5MnNi0.5 high-entropy alloys by anodic treatment in sulfuric acid [J]. Thin Solid Films, 2008, 517(3): 1301–1305. doi: 10.1016/j.tsf.2008.06.014 [5] GREER A L. Confusion by design [J]. Nature, 1993, 366(6453): 303–304. doi: 10.1038/366303a0 [6] KO J Y, SONG J S, HONG S I. Effect of carbon addition and recrystallization on the microstructure and mechanical properties of CoCrFeMnNi high entropy alloys [J]. Korean Journal of Metals and Materials, 2018, 56(1): 26–33. doi: 10.3365/KJMM.2018.56.1.26 [7] XIE L, BRAULT P, THOMANN A L, et al. Molecular dynamics simulation of Al-Co-Cr-Cu-Fe-Ni high entropy alloy thin film growth [J]. Intermetallics, 2016, 68: 78–86. doi: 10.1016/j.intermet.2015.09.008 [8] AFKHAMA Y, BAHRAMYANA M, MOUSAVIANA R T, et al. Tensile properties of AlCrCoFeCuNi glassy alloys: a molecular dynamics simulation study [J]. Materials Science & Engineering, 2017, 698: 143–151. [9] CHOI W M, JO Y H, SOHN S S, et al. Understanding the physical metallurgy of the CoCrFeMnNi high-entropy alloy: an atomistic simulation study [J/OL]. NPJ Computational Materials, 2018. [2019–04–18]. https://www_nature.xilesou.top/articles/s41524-017-0060-9 [10] ZHANG Y, WANG X, LI J, et al. Deformation mechanism during high-temperature tensile test in an eutectic high-entropy alloy AlCoCrFeNi2.1 [J]. Materials Science & Engineering A, 2018, 724: 148–155. [11] 吴树森, 柳玉起. 材料成型原理 [M]. 北京: 机械工业出版社, 2008. [12] PI J H, PAN Y, ZHANG H, et al. Microstructure and properties of AlCrFeCuNi x (0.6≤x≤1.4) high-entropy alloys [J]. Materials Science & Engineering A, 2012, 534: 228–233. [13] HU W Y, ZHANG B W, HUANG B Y, et al. Analytic modified embedded atom potentials for HCP metals [J]. Journal of Physics Condensed Matter, 2001, 13(6): 1193. doi: 10.1088/0953-8984/13/6/302 [14] JIA L, FANG Q H, LIU B. Mechanical behaviors of AlCrFeCuNi high-entropy alloys under uniaxial tensile via molecular dynamics simulation [J]. Rsc Advances, 2016, 6(80): 76409–76419. doi: 10.1039/C6RA16503F [15] IMAFUKU M, SASAJIMA Y, YAMAMOTO R, et al. Computer simulations of the structures of the metallic superlattices Au/Ni and Cu/Ni and their elastic moduli [J]. Journal of Physics F: Metal Physics, 1986, 16(7): 823–829. doi: 10.1088/0305-4608/16/7/009 -







 下载:
下载: