Advances in the Study of Dynamic Response of Crystalline Materials by Crystal Plasticity Finite Element Modeling
-
摘要: 作为连续尺度上描述各向异性非均质材料弹塑性变形的重要模拟工具,晶体塑性有限元能够有效预测材料的宏观力学性能,在工程设计方面起着重要的作用。在实际工程应用中,许多晶体材料在高应力、高变形率、高温等极端条件下服役,此时各向异性非均匀的微介观结构演化是理解材料动态响应的关键,这给晶体塑性有限元带来了巨大的机遇和挑战。首先简要综述了晶体塑性有限元的原理和方法,然后着重介绍其在材料动态响应中的应用,最后展望其在材料动态响应模拟方面的发展方向。Abstract: As an important simulation tool for describing the elastoplastic deformation of anisotropic heterogeneous materials on continuum scales, crystal plasticity finite element (CPFE) modeling can effectively predict macroscopic mechanical properties of materials, thus plays a critical role in engineering design. In the practical engineering applications, many crystalline materials work at extreme conditions such as high stress, high deformation rate, and high temperature. The anisotropic heterogeneous microstructure evolutions under such conditions are the key factors to understanding the dynamic response of materials, and it brings great opportunities and challenges for CPFE. In this paper, we firstly review the theory and model of CPFE, and then introduce the applications of this method in study of dynamic response of crystalline materials, and discuss the challenges and open questions of CPFE in modeling material dynamic response at last.
-
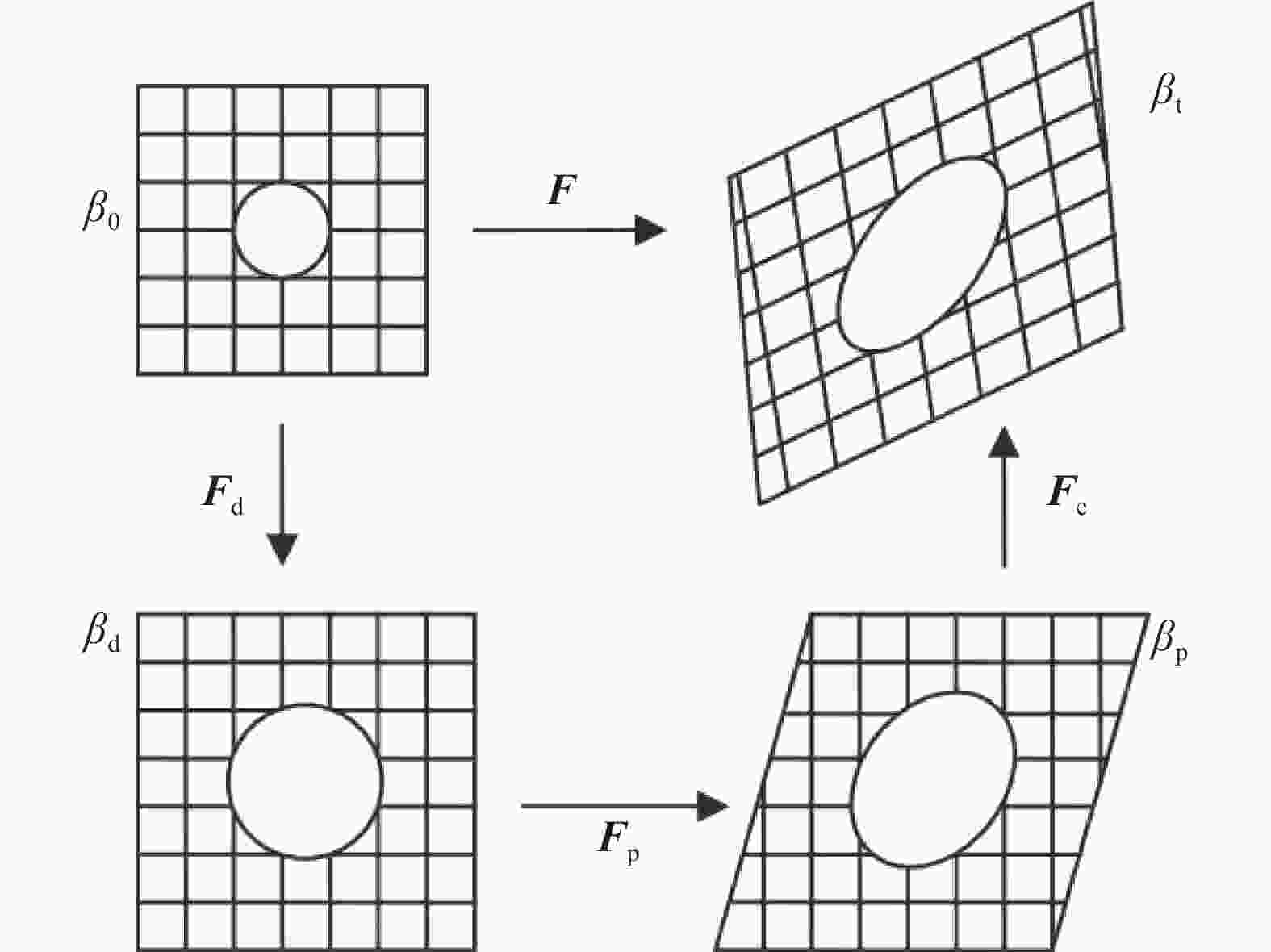
图 1 一般多孔单晶的变形梯度分解
${{F}} = {{{F}}_{\rm{e}}}{{{F}}_{\rm{p}}}{{{F}}_{\rm{d}}}$ ,包含可逆弹性部分${{{F}}_{\rm{e}}}$ 、不可逆偏量部分${{{F}}_{\rm{p}}}$ 以及不可逆体变部分${{{F}}_{\rm{d}}}$ [91]Figure 1. Schematic of a multiplicative decomposition of total macroscopic deformation gradient tensor
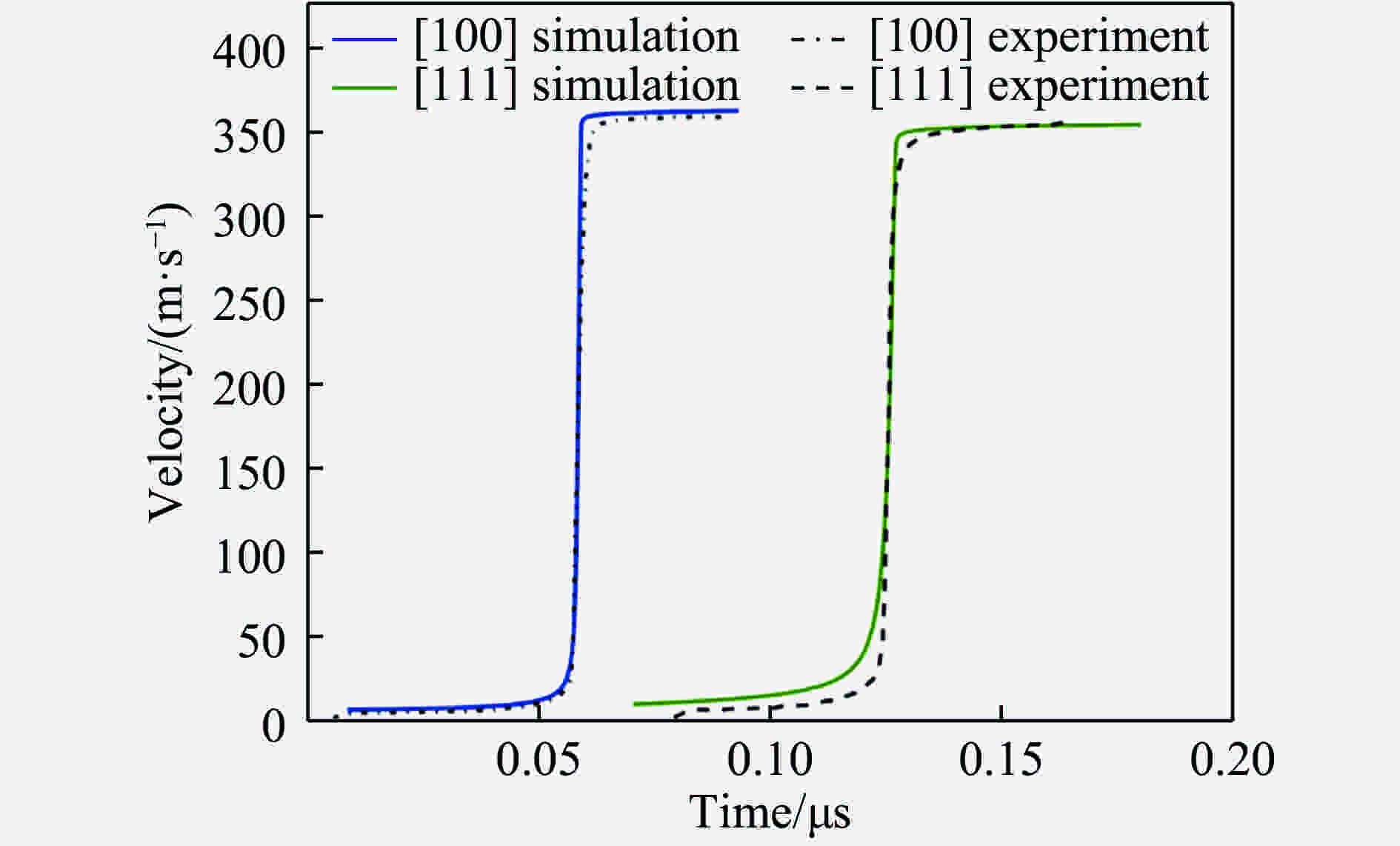
${{F}}$ into elastic${{{F}}_{\rm{e}}}$ , irreversible deviatoric${{{F}}_{\rm{p}}}$ , and irreversible volumetric parts${{{F}}_{\rm{d}}}$ [91]图 4 RDX在[111]方向受到1.25 GPa加载时粒子速度剖面[100](实线是实验结果[101],虚线为模拟结果)
Figure 4. Particle velocity profile of
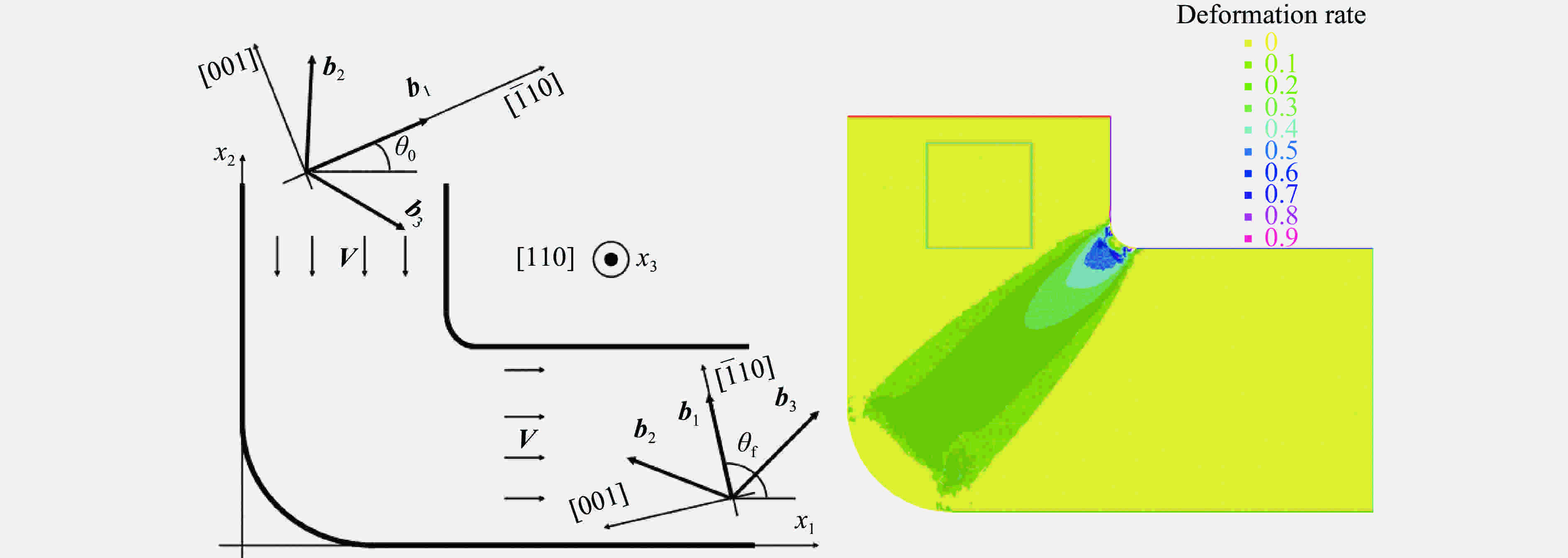
$ \alpha $ -RDX single crystal loaded up to 1.25 GPa along the [111] crystallographic direction (Solid lines correspond to the experimental results [101] while dashed lines correspond to the model predictions [100].)图 5 利用Lagrangean框架建立的唯象CPFE模拟等径角板牙的高应变率变形:(a)几何构型,其中V为此区域外加的速度场;(b)变形率分布[102]
Figure 5. High strain rate deformation of equal-diameter dies simulated by the phenomenological CPFE within the Lagrangean framework. (a) shows the geometry configuration where V is the imposed velocity in the specified domains, and (b) is the deformation rate distribution [102]
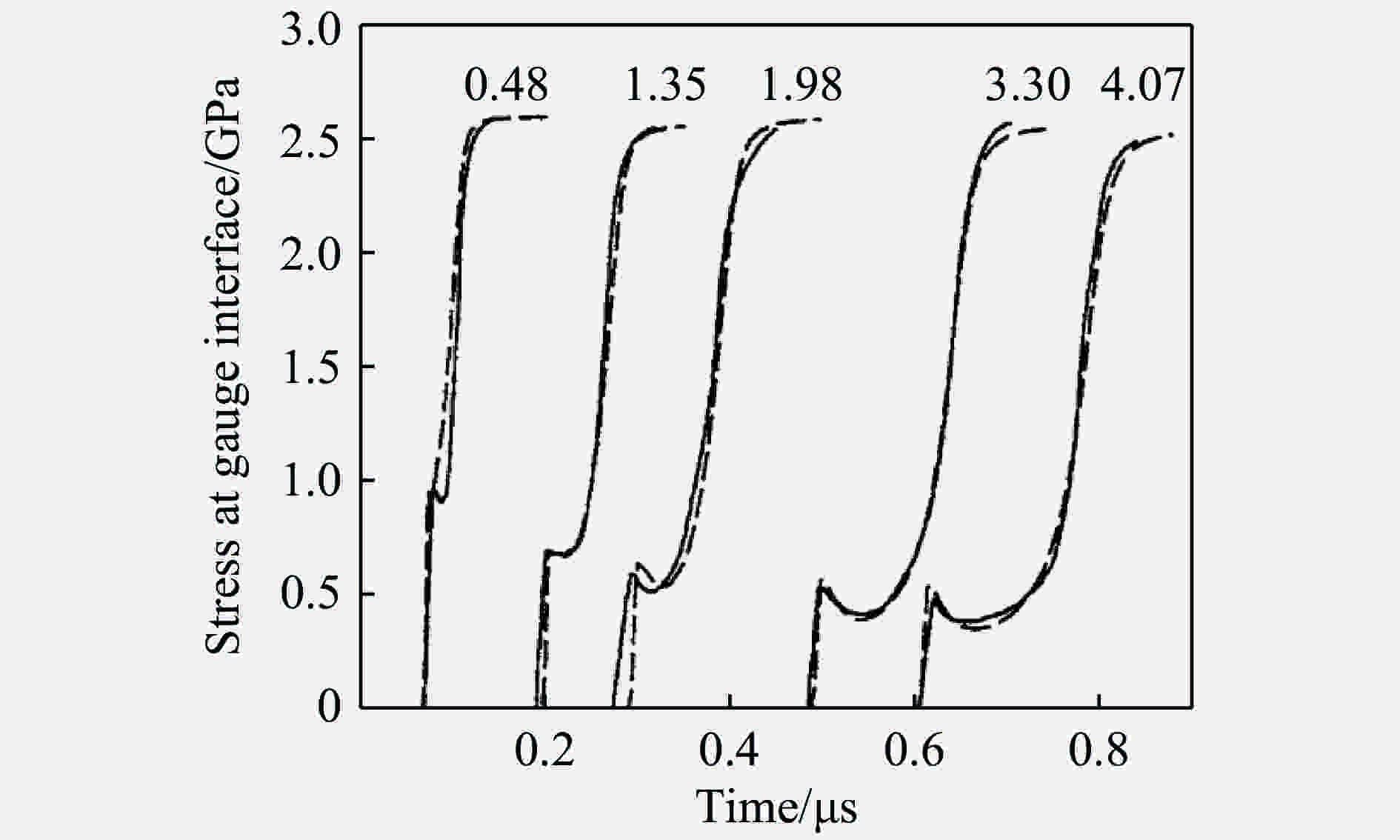
图 6 利用Winey-Gupta模型模拟LiF受[100]方向冲击时的纵波历史(实线为实验测量值,虚线为模拟值;曲线上方数字表示试样的厚度,单位为毫米[105])
Figure 6. Measured and simulated longitudinal stress histories for LiF single crystals shocked along the [100] orientation by Winey-Gupta model [105] (The solid lines are the experimental data and the dashed lines are the simulations. The numbers above the curves indicate the sample thickness in mm. Time is relative to the moment of impact.)
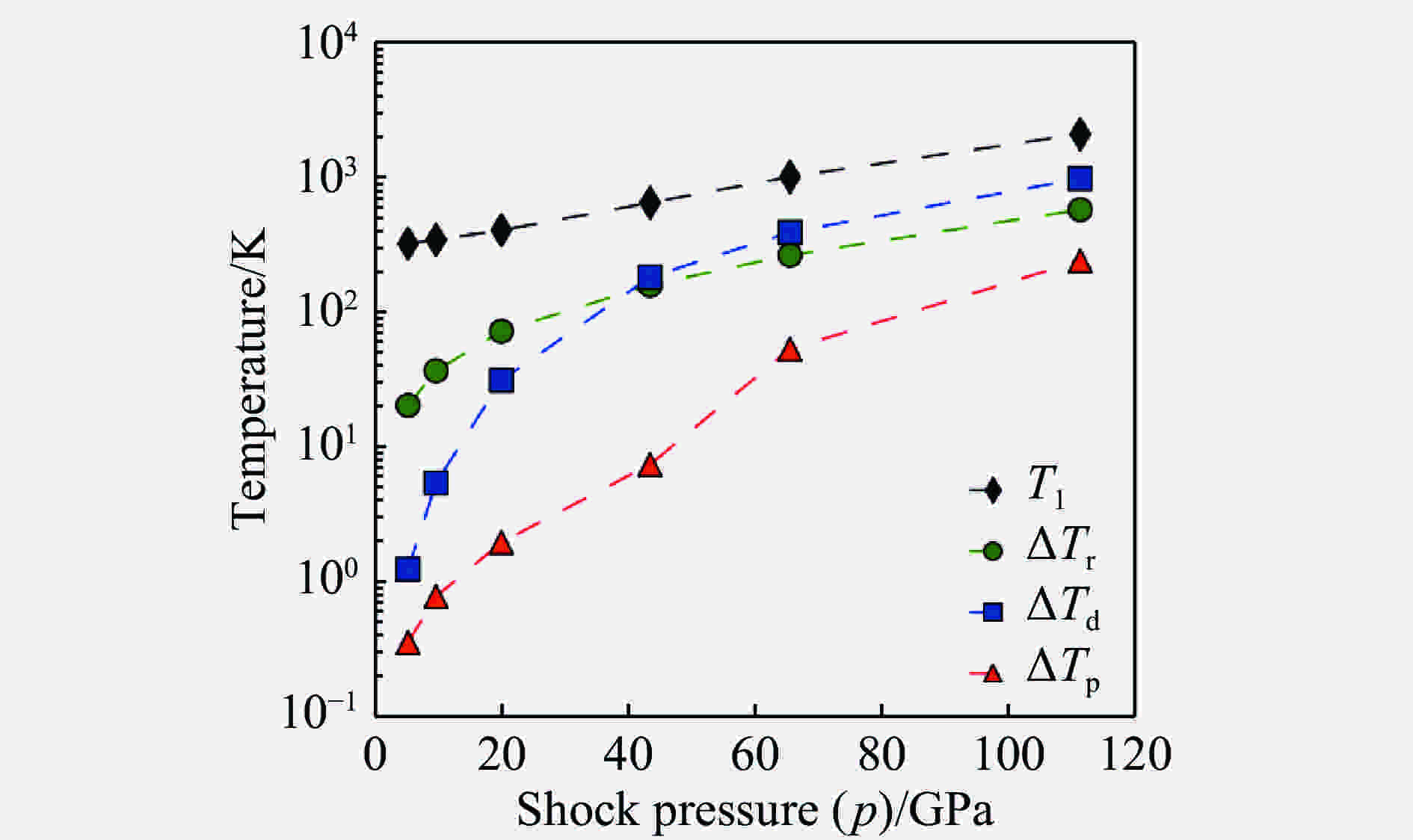
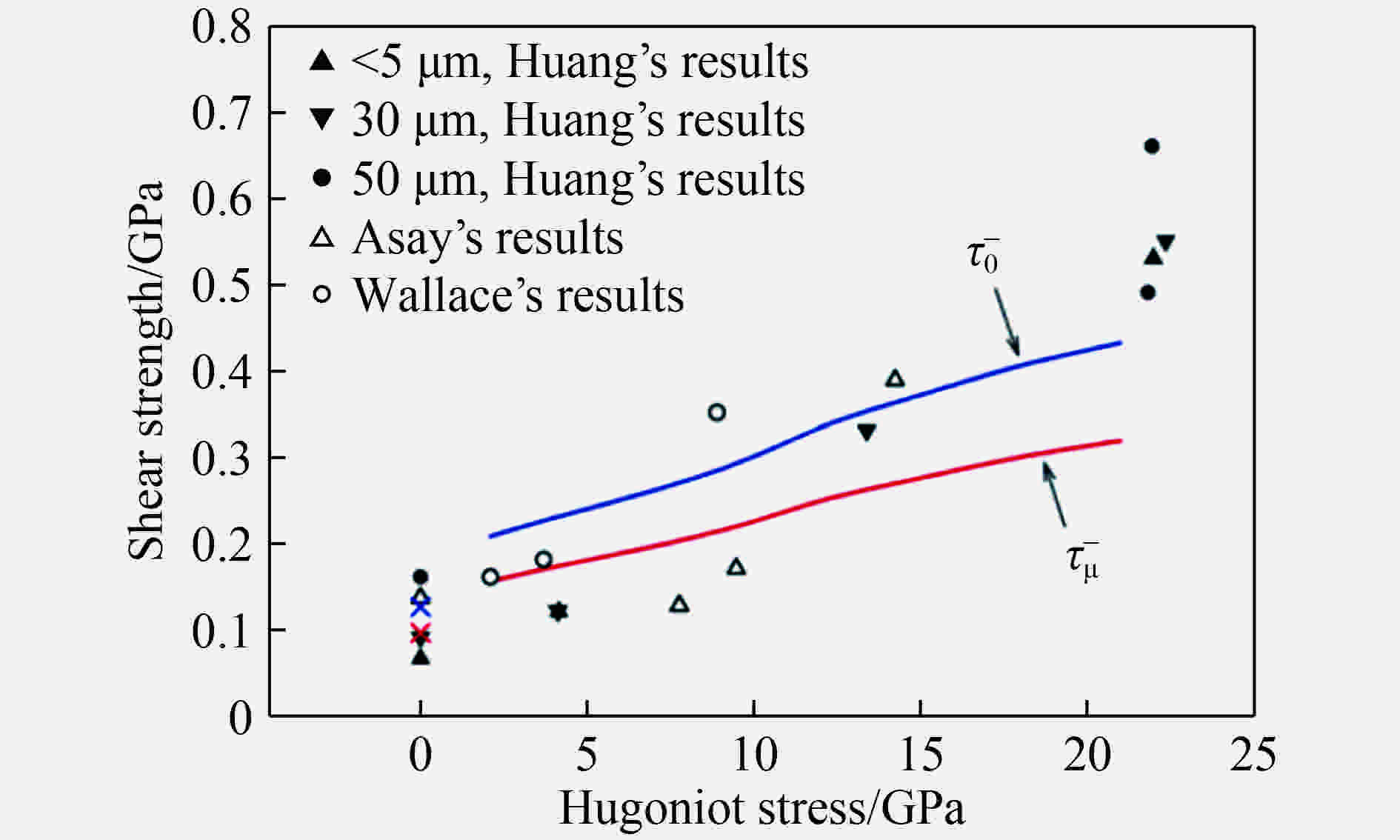
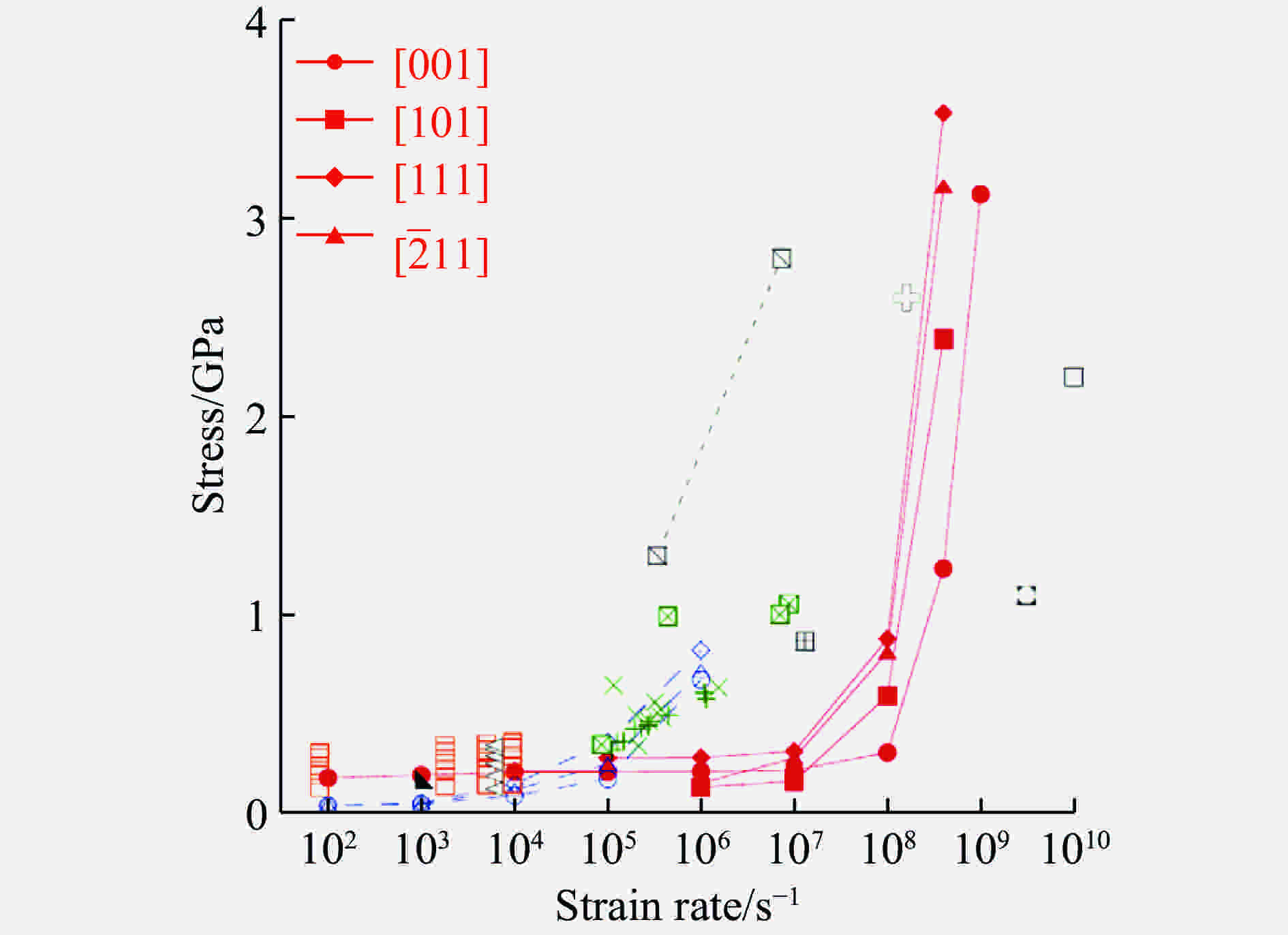
图 7 利用Austin- McDowell模型模拟6061-T6的Hugoniot塑性变形的临界剪切应力(数据点为实验结果;左上角给出了数据点的来源,尺寸参数表示晶粒尺寸,具体信息见文献[106])
Figure 7. The critical shear stress of Hugoniot plastic deformation of 6061-T6 simulated by the Austin-McDowell model (The symbols show the experimental results. The legend gives the sources of the experimental data, and the measurements show the grain sizes, please see Ref.[106] for the detail information.)
-
[1] TAYLOR G I. Plastic strain in metals [J]. Journal of the Institute of Metals, 1938, 62: 307–324. [2] BISHOP J F W, HILL R. A theory of the plastic distortion of a polycrystalline aggregate under combined stresses [J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1951, 42(327): 414–427. doi: 10.1080/14786445108561065 [3] BISHOP J F W, HILL R. A theoretical derivation of the plastic properties of a polycrystalline face-centered metal [J]. Philosophical Magazine, 1951, 42(334): 1298–1307. [4] KRONER E. On the plastic deformation of polycrystals [J]. Acta Metallurgica, 1961, 9(2): 155–161. doi: 10.1016/0001-6160(61)90060-8 [5] CURTIN W A, MILLER R E. Atomistic/continuum coupling in computational materials science [J]. Modelling and Simulation in Materials Science and Engineering, 2003, 11(3): R33. doi: 10.1088/0965-0393/11/3/201 [6] ARSENLIS A, PARKS D M, BECKER R, et al. On the evolution of crystallographic dislocation density in non-homogeneously deforming crystals [J]. Journal of the Mechanics and Physics of Solids, 2004, 52(6): 1213–1246. doi: 10.1016/j.jmps.2003.12.007 [7] VITEK V, MROVEC M, BASSANI J L. Influence of non-glide stresses on plastic flow: from atomistic to continuum modeling [J]. Materials Science and Engineering: A, 2004, 365(1/2): 31–37. [8] ZIENKIEWICZ O C, CHEUNG Y K. The finite element method in structural and continuum mechanics [M]. London: McGraw-Hill, 1967. [9] ZIENKIEWICZ O C, TAYLOR R L. The finite element method for solid and structural mechanics [M]. Elsevier Ltd, 2005. [10] ZHAO Z, MAO W, ROTERS F, et al. A texture optimization study for minimum earing in aluminium by use of a texture component crystal plasticity finite element method [J]. Acta Materialia, 2004, 52(4): 1003–1012. doi: 10.1016/j.actamat.2003.03.001 [11] RICE J R. Inelastic constitutive relations for solids: an internal-variable theory and its application to metal plasticity [J]. Journal of the Mechanics and Physics of Solids, 1971, 19(6): 433–455. doi: 10.1016/0022-5096(71)90010-X [12] ASARO R J, RICE J R. Strain localization in ductile single crystals [J]. Journal of the Mechanics and Physics of Solids, 1977, 25(5): 309–338. doi: 10.1016/0022-5096(77)90001-1 [13] ARSENLIS A, PARKS D M. Crystallographic aspects of geometrically-necessary and statistically-stored dislocation density [J]. Acta Materialia, 1999, 47(5): 1597–1611. doi: 10.1016/S1359-6454(99)00020-8 [14] ARSENLIS A, PARKS D M. Modeling the evolution of crystallographic dislocation density in crystal plasticity [J]. Journal of the Mechanics and Physics of Solids, 2002, 50(9): 1979–2009. doi: 10.1016/S0022-5096(01)00134-X [15] EVERS L P, PARKS D M, BREKELMANS W A M, et al. Crystal plasticity model with enhanced hardening by geometrically necessary dislocation accumulation [J]. Journal of the Mechanics and Physics of Solids, 2002, 50(11): 2403–2424. doi: 10.1016/S0022-5096(02)00032-7 [16] EVERS L P, BREKELMANS W A M, GEERS M G D. Scale dependent crystal plasticity framework with dislocation density and grain boundary effects [J]. International Journal of Solids and Structures, 2004, 41(18/19): 5209–5230. [17] CHEONG K S, BUSSO E P. Discrete dislocation density modelling of single phase FCC polycrystal aggregates [J]. Acta Materialia, 2004, 52(19): 5665–5675. doi: 10.1016/j.actamat.2004.08.044 [18] MA A, ROTERS F. A constitutive model for fcc single crystals based on dislocation densities and its application to uniaxial compression of aluminium single crystals [J]. Acta Materialia, 2004, 52(12): 3603–3612. doi: 10.1016/j.actamat.2004.04.012 [19] MA A, ROTERS F, RAABE D. A dislocation density based constitutive model for crystal plasticity FEM including geometrically necessary dislocations [J]. Acta Materialia, 2006, 54(8): 2169–2179. doi: 10.1016/j.actamat.2006.01.005 [20] MA A, ROTERS F, RAABE D. On the consideration of interactions between dislocations and grain boundaries in crystal plasticity finite element modeling-theory, experiments, and simulations [J]. Acta Materialia, 2006, 54(8): 2181–2194. doi: 10.1016/j.actamat.2006.01.004 [21] EVERS L P, BREKELMANS W A M, GEERS M G D. Non-local crystal plasticity model with intrinsic SSD and GND effects [J]. Journal of the Mechanics and Physics of Solids, 2004, 52(10): 2379–2401. doi: 10.1016/j.jmps.2004.03.007 [22] THAMBURAJA P, ANAND L. Polycrystalline shape-memory materials: effect of crystallographic texture [J]. Journal of the Mechanics and Physics of Solids, 2001, 49(4): 709–737. doi: 10.1016/S0022-5096(00)00061-2 [23] LAN Y J, XIAO N M, LI D Z, et al. Mesoscale simulation of deformed austenite decomposition into ferrite by coupling a cellular automaton method with a crystal plasticity finite element model [J]. Acta Materialia, 2005, 53(4): 991–1003. doi: 10.1016/j.actamat.2004.10.045 [24] KALIDINDI S R. Incorporation of deformation twinning in crystal plasticity models [J]. Journal of the Mechanics and Physics of Solids, 1998, 46(2): 267–290. doi: 10.1016/S0022-5096(97)00051-3 [25] STAROSELSKY A, ANAND L. Inelastic deformation of polycrystalline face centered cubic materials by slip and twinning [J]. Journal of the Mechanics and Physics of Solids, 1998, 46(4): 671–696. doi: 10.1016/S0022-5096(97)00071-9 [26] MARKETZ W T, FISCHER F D, KAUFFMANN F, et al. On the role of twinning during room temperature deformation of γ-TiAl based alloys [J]. Materials Science & Engineering A, 2002, 329: 177–183. [27] SALEM A A, KALIDINDI S R, SEMIATIN S L. Strain hardening due to deformation twinning in α-titanium: constitutive relations and crystal-plasticity modeling [J]. Acta Materialia, 2005, 53(12): 3495–3502. doi: 10.1016/j.actamat.2005.04.014 [28] WEI Y J, ANAND L. Grain-boundary sliding and separation in polycrystalline metals: application to nanocrystalline fcc metals [J]. Journal of the Mechanics and Physics of Solids, 2004, 52(11): 2587–2616. doi: 10.1016/j.jmps.2004.04.006 [29] WEI Y, SU C, ANAND L. A computational study of the mechanical behavior of nanocrystalline fcc metals [J]. Acta Materialia, 2006, 54(12): 3177–3190. doi: 10.1016/j.actamat.2006.03.007 [30] RAABE D, KLOSE P, ENGL B, et al. Concepts for integrating plastic anisotropy into metal forming simulations [J]. Advanced Engineering Materials, 2002, 4(4): 169–180. doi: 10.1002/1527-2648(200204)4:4<>1.0.CO;2-G [31] SACHTLEBER M, ZHAO Z, RAABE D. Experimental investigation of plastic grain interaction [J]. Materials Science and Engineering A, 2002, 336(1/2): 81–87. [32] RAABE D, SACHTLEBER M, WEILAND H, et al. Grain-scale micromechanics of polycrystal surfaces during plastic straining [J]. Acta Materialia, 2003, 51(6): 1539–1560. doi: 10.1016/S1359-6454(02)00557-8 [33] ROTERS F, EISENLOHR P, HANTCHERLI L, et al. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: theory, experiments, applications [J]. Acta Materialia, 2010, 58(4): 1152–1211. doi: 10.1016/j.actamat.2009.10.058 [34] SALVADO F C, TEIXEIRA-DIAS F, WALLEY S M, et al. A review on the strain rate dependency of the dynamic viscoplastic response of FCC metals [J]. Progress in Materials Science, 2017, 88: 186–231. doi: 10.1016/j.pmatsci.2017.04.004 [35] MOLINARI A, RAVICHANDRAN G. Constitutive modeling of high-strain-rate deformation in metals based on the evolution of an effective microstructural length [J]. Mechanics of Materials, 2005, 37(7): 737–752. doi: 10.1016/j.mechmat.2004.07.005 [36] JOHNSON G R. A constitutive model and data for metals subjected to large strains, high strain rates, and high temperatures [C]. Proceedings of the 7th International Symposium on Ballistics, 1983: 541-547. [37] KHAN A S, HUANG S. Experimental and theoretical study of mechanical behavior of 1100 aluminum in the strain rate range 10-5–104 s-1 [J]. International Journal of Plasticity, 1992, 8(4): 397–424. doi: 10.1016/0749-6419(92)90057-J [38] LIN Y C, CHEN X M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working [J]. Materials & Design, 2011, 32(4): 1733–1759. [39] KOCKS U F. Laws for work-hardening and low-temperature creep [J]. Journal of Engineering Materials and Technology, 1976, 98(1): 76–85. doi: 10.1115/1.3443340 [40] LIN Y C, CHEN M S, ZHONG J. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel [J]. Computational Materials Science, 2008, 42(3): 470–477. doi: 10.1016/j.commatsci.2007.08.011 [41] BODNER S R, PARTOM Y. Constitutive equations for elastic-viscoplastic strain-hardening materials [J]. Journal of Applied Mechanics, 1975, 42(2): 385–389. doi: 10.1115/1.3423586 [42] STEINBERG D J, COCHRAN S G, GUINAN M W. A constitutive model for metals applicable at high-strain rate [J]. Journal of Applied Physics, 1980, 51(3): 1498–1504. doi: 10.1063/1.327799 [43] ZERILLI F J, ARMSTRONG R W. Dislocation-mechanics-based constitutive relations for material dynamics calculations [J]. Journal of Applied Physics, 1987, 61(5): 1816–1825. doi: 10.1063/1.338024 [44] MEYER H W JR. A modified Zerilli-Armstrong constitutive model describing the strength and localizing behavior of Ti-6A1-4V: ARL-CR-0578 [R]. Aberdeen, MD: Dynamic Science Inc., 2006. [45] MECKING H, KOCKS U F. Kinetics of flow and strain-hardening [J]. Acta Metallurgica, 1981, 29(11): 1865–1875. doi: 10.1016/0001-6160(81)90112-7 [46] NEMAT-NASSER S, LI Y. Flow stress of fcc polycrystals with application to OFHC Cu [J]. Acta Materialia, 1998, 46(2): 565–577. doi: 10.1016/S1359-6454(97)00230-9 [47] TAYLOR G I. The mechanism of plastic deformation of crystals. Part I. theoretical [J]. Proceedings of the Royal Society of London A, 1934, 145(855): 362–387. doi: 10.1098/rspa.1934.0106 [48] Taylor G I. The mechanism of plastic deformation of crystals. Part II. comparison with observations [J]. Proceedings of the Royal Society of London A, 1934, 145(855): 388–404. doi: 10.1098/rspa.1934.0107 [49] OROWAN E. Zur Kristall Plastizität IIII [J]. Zeitschrift für Physik, 1934, 89: 605–659. doi: 10.1007/BF01341478 [50] POLANYI M. Über eine Art Gitterstörung, die einen Kristall plastisch machen könnte [J]. Zeitschrift für Physik, 1934, 89(9/10): 660–664. [51] PEIRCE D, ASARO R J, NEEDLEMAN A. An analysis of nonuniform and localized deformation in ductile single crystals [J]. Acta Metallurgica, 1982, 30(6): 1087–1119. doi: 10.1016/0001-6160(82)90005-0 [52] HARREN S V, DEVE H E, ASARO R J. Shear band formation in plane strain compression [J]. Acta Metallurgica, 1988, 36(9): 2435–2480. doi: 10.1016/0001-6160(88)90193-9 [53] HARREN S V, ASARO R J. Nonuniform deformations in polycrystals and aspects of the validity of the Taylor model [J]. Journal of the Mechanics and Physics of Solids, 1989, 37(2): 191–232. doi: 10.1016/0022-5096(89)90010-0 [54] BECKER R. Analysis of texture evolution in channel die compression-I. effects of grain interaction [J]. Acta Metallurgica et Materialia, 1991, 39(6): 1211–1230. doi: 10.1016/0956-7151(91)90209-J [55] BECKER R, BUTLER J F, HU H, et al. Analysis of an aluminum single crystal with unstable initial orientation (001)[110] in channel die compression [J]. Metallurgical Transactions A, 1991, 22(1): 45–58. doi: 10.1007/BF03350948 [56] ZHAO Z, RAMESH M, RAABE D, et al. Investigation of three-dimensional aspects of grain-scale plastic surface deformation of an aluminum oligocrystal [J]. International Journal of Plasticity, 2008, 24(12): 2278–2297. doi: 10.1016/j.ijplas.2008.01.002 [57] MIKA D P, DAWSON P R. Effects of grain interaction on deformation in polycrystals [J]. Materials Science and Engineering: A, 1998, 257(1): 62–76. doi: 10.1016/S0921-5093(98)00824-7 [58] SARMA G B, DAWSON P R. Texture predictions using a polycrystal plasticity model incorporating neighbor interactions [J]. International Journal of Plasticity, 1996, 12(8): 1023–1054. doi: 10.1016/S0749-6419(96)00040-X [59] SARMA G B, RADHAKRISHNAN B, ZACHARIA T. Finite element simulations of cold deformation at the mesoscale [J]. Computational Materials Science, 1998, 12(2): 105–123. doi: 10.1016/S0927-0256(98)00036-6 [60] BEAUDOIN A J JR, MECKING H, KOCKS U F. Development of localized orientation gradients in fcc polycrystals [J]. Philosophical Magazine A, 1996, 73(6): 1503–1517. doi: 10.1080/01418619608242998 [61] BACHU V, KALIDINDI S R. On the accuracy of the predictions of texture evolution by the finite element technique for fcc polycrystals [J]. Materials Science and Engineering A, 1998, 257(1): 108–117. doi: 10.1016/S0921-5093(98)00828-4 [62] ZHAO Z, KUCHNICKI S, RADOVITZKY R, et al. Influence of in-grain mesh resolution on the prediction of deformation textures in fcc polycrystals by crystal plasticity FEM [J]. Acta Materialia, 2007, 55(7): 2361–2373. doi: 10.1016/j.actamat.2006.11.035 [63] ZHAO Z, ROTERS F, MAO W, et al. Introduction of a texture component crystal plasticity finite element method for anisotropy simulations [J]. Advanced Engineering Materials, 2001, 3(12): 984–990. doi: 10.1002/1527-2648(200112)3:12<984::AID-ADEM984>3.0.CO;2-L [64] RAABE D, ROTERS F. Using texture components in crystal plasticity finite element simulations [J]. International Journal of Plasticity, 2004, 20(3): 339–361. doi: 10.1016/S0749-6419(03)00092-5 [65] MELCHIOR M A, DELANNAY L. A texture discretization technique adapted to polycrystalline aggregates with non-uniform grain size [J]. Computational Materials Science, 2006, 37(4): 557–564. doi: 10.1016/j.commatsci.2005.12.002 [66] TÓTH L S, VAN HOUTTE P. Discretization techniques for orientation distribution functions [J]. Texture, Stress, and Microstructure, 1992, 19(4): 229–244. doi: 10.1155/TSM.19.229 [67] EISENLOHR P, ROTERS F. Selecting a set of discrete orientations for accurate texture reconstruction [J]. Computational Materials Science, 2008, 42(4): 670–678. doi: 10.1016/j.commatsci.2007.09.015 [68] FLECK N A, MULLER G M, ASHBY M F, et al. Strain gradient plasticity: theory and experiment [J]. Acta Metallurgica et Materialia, 1994, 42(2): 475–487. doi: 10.1016/0956-7151(94)90502-9 [69] FLECK N A, HUTCHINSON J W. Strain gradient plasticity [J]. Advances in Applied Mechanics, 1997, 33: 296–361. [70] NIX W D, GAO H. Indentation size effects in crystalline materials: a law for strain gradient plasticity [J]. Journal of the Mechanics and Physics of Solids, 1998, 46(3): 411–425. doi: 10.1016/S0022-5096(97)00086-0 [71] GAO H, HUANG Y. Geometrically necessary dislocation and size-dependent plasticity [J]. Scripta Materialia, 2003, 48(2): 113–118. doi: 10.1016/S1359-6462(02)00329-9 [72] BIELER T R, EISENLOHR P, ROTERS F, et al. The role of heterogeneous deformation on damage nucleation at grain boundaries in single phase metals [J]. International Journal of Plasticity, 2009, 25(9): 1655–1683. doi: 10.1016/j.ijplas.2008.09.002 [73] STAROSELSKY A, ANAND L. A constitutive model for hcp materials deforming by slip and twinning: application to magnesium alloy AZ31B [J]. International Journal of Plasticity, 2003, 19(10): 1843–1864. doi: 10.1016/S0749-6419(03)00039-1 [74] SUIKER A S J, TURTELTAUB S. Computational modelling of plasticity induced by martensitic phase transformations [J]. International Journal for Numerical Methods in Engineering, 2005, 63(12): 1655–1693. doi: 10.1002/(ISSN)1097-0207 [75] HUTCHINSON J W. Bounds and self-consistent estimates for creep of polycrystalline materials [J]. Proceedings of the Royal Society of London A, 1976, 348(1652): 101–127. doi: 10.1098/rspa.1976.0027 [76] PEIRCE D, ASARO R J, NEEDLEMAN A. Material rate dependence and localized deformation in crystalline solids [J]. Acta Metallurgica, 1983, 31(12): 1951–1976. doi: 10.1016/0001-6160(83)90014-7 [77] VOCE E. The relationship between stress and strain for homogeneous deformation [J]. Journal of the Institute of Metals, 1948, 74: 537–562. [78] BRONKHORST C A, KALIDINDI S R, ANAND L. Polycrystalline plasticity and the evolution of crystallographic texture in FCC metals [J]. Philosophical Transactions of the Royal Society A, 1992, 341(1662): 443–477. [79] HALL E O. The deformation and ageing of mild steel: III. discussion of results [J]. Proceedings of the Physical Society: Section B, 1951, 64(9): 747. doi: 10.1088/0370-1301/64/9/303 [80] PETCH N J. The cleavage strength of polycrystals [J]. Journal of the Iron and Steel Institute, 1953, 174: 25–28. [81] NYE J F. Some geometrical relations in dislocated crystals [J]. Acta Metallurgica, 1953, 1(2): 153–162. doi: 10.1016/0001-6160(53)90054-6 [82] GREENWOOD G W, JOHNSON R H. The deformation of metals under small stresses during phase transformations [J]. Proceedings of the Royal Society of London A, 1965, 283(1394): 403–422. doi: 10.1098/rspa.1965.0029 [83] PATEL J R, COHEN M. Criterion for the action of applied stress in the martensitic transformation [J]. Acta Metallurgica, 1953, 1(5): 531–538. doi: 10.1016/0001-6160(53)90083-2 [84] TURTELTAUB S, SUIKER A S J. Transformation-induced plasticity in ferrous alloys [J]. Journal of the Mechanics and Physics of Solids, 2005, 53(8): 1747–1788. doi: 10.1016/j.jmps.2005.03.004 [85] TURTELTAUB S, SUIKER A S J. A multiscale thermomechanical model for cubic to tetragonal martensitic phase transformations [J]. International Journal of Solids and Structures, 2006, 43(14/15): 4509–4545. [86] DOQUET V. Twinning and multiaxial cyclic plasticity of a low stacking-fault-energy fcc alloy [J]. Acta Metallurgica et Materialia, 1993, 41(8): 2451–2459. doi: 10.1016/0956-7151(93)90325-M [87] SCHLÖGL S M, FISCHER F D. The role of slip and twinning in the deformation behaviour of polysynthetically twinned crystals of TiAl: a micromechanical model [J]. Philosophical Magazine A, 1997, 75(3): 621–636. doi: 10.1080/01418619708207193 [88] MECKING H, HARTIG C, KOCKS U F. Deformation modes in γ-TiAl as derived from the single crystal yield surface [J]. Acta Materialia, 1996, 44(4): 1309–1321. doi: 10.1016/1359-6454(95)00308-8 [89] VASUDEVAN A K, DOHERTY R D. Grain boundary ductile fracture in precipitation hardened aluminum alloys [J]. Acta Metallurgica, 1987, 35(6): 1193–1219. doi: 10.1016/0001-6160(87)90001-0 [90] SURESH S, VASUDEVAN A K, TOSTEN M, et al. Microscopic and macroscopic aspects of fracture in lithium-containing aluminum alloys [J]. Acta Metallurgica, 1987, 35(1): 25–46. doi: 10.1016/0001-6160(87)90210-0 [91] NGUYEN T, LUSCHER D J, WILKERSON J W. A dislocation-based crystal plasticity framework for dynamic ductile failure of single crystals [J]. Journal of the Mechanics and Physics of Solids, 2017, 108: 1–29. [92] ZIKRY M A, NEMAT-NASSER S. High strain-rate localization and failure of crystalline materials [J]. Mechanics of Materials, 1990, 10(3): 215–237. doi: 10.1016/0167-6636(90)90044-G [93] SCHOENFELD S E. Dynamic behaviour of polycrystalline tantalum [J]. International Journal of Plasticity, 1998, 14(9): 871–890. doi: 10.1016/S0749-6419(98)00034-5 [94] KNEZEVIC M, BEYERLEIN I J, LOVATO M L, et al. A strain-rate and temperature dependent constitutive model for BCC metals incorporating non-Schmid effects: application to tantalum-tungsten alloys [J]. International Journal of Plasticity, 2014, 62: 93–104. doi: 10.1016/j.ijplas.2014.07.007 [95] LIM H, BATTAILE C C, CARROLL J D, et al. A physically based model of temperature and strain rate dependent yield in BCC metals: implementation into crystal plasticity [J]. Journal of the Mechanics and Physics of Solids, 2015, 74: 80–96. doi: 10.1016/j.jmps.2014.10.003 [96] LIM H, HALE L M, ZIMMERMAN J A, et al. A multi-scale model of dislocation plasticity in α-Fe: incorporating temperature, strain rate and non-Schmid effects [J]. International Journal of Plasticity, 2015, 73: 100–118. doi: 10.1016/j.ijplas.2014.12.005 [97] BECKER R. Effects of crystal plasticity on materials loaded at high pressures and strain rates [J]. International Journal of Plasticity, 2004, 20(11): 1983–2006. doi: 10.1016/j.ijplas.2003.09.002 [98] SIMMONS G, WANG H. A handbook of single crystal elastic constants and calculated aggregate properties [M]. Cambridge, Mass: MIT Press, 1971. [99] LUSCHER D J, BRONKHORST C A, ALLEMAN C N, et al. A model for finite-deformation nonlinear thermomechanical response of single crystal copper under shock conditions [J]. Journal of the Mechanics and Physics of Solids, 2013, 61(9): 1877–1894. doi: 10.1016/j.jmps.2013.05.002 [100] DE S, ZAMIRI A R. A fully anisotropic single crystal model for high strain rate loading conditions with an application to α-RDX [J]. Journal of the Mechanics and Physics of Solids, 2014, 64: 287–301. doi: 10.1016/j.jmps.2013.10.012 [101] CAWKWELL M J, RAMOS K J, HOOKS D E, et al. Homogeneous dislocation nucleation in cyclotrimethylene trinitramine under shock loading [J]. Journal of Applied Physics, 2010, 107(6): 063512. doi: 10.1063/1.3305630 [102] CAZACU O, IONESCU I R. Dynamic crystal plasticity: an Eulerian approach [J]. Journal of the Mechanics and Physics of Solids, 2010, 58(6): 844–859. doi: 10.1016/j.jmps.2010.04.001 [103] CLAYTON J D. Analysis of shock compression of strong single crystals with logarithmic thermoelastic-plastic theory [J]. International Journal of Engineering Science, 2014, 79: 1–20. doi: 10.1016/j.ijengsci.2014.02.016 [104] WINEY J M, GUPTA Y M. Nonlinear anisotropic description for shocked single crystals: thermoelastic response and pure mode wave propagation [J]. Journal of Applied Physics, 2004, 96(4): 1993–1999. doi: 10.1063/1.1767294 [105] WINEY J M, GUPTA Y M. Nonlinear anisotropic description for the thermomechanical response of shocked single crystals: inelastic deformation [J]. Journal of Applied Physics, 2006, 99(2): 023510. doi: 10.1063/1.2161414 [106] AUSTIN R A, MCDOWELL D L. A dislocation-based constitutive model for viscoplastic deformation of fcc metals at very high strain rates [J]. International Journal of Plasticity, 2011, 27(1): 1–24. doi: 10.1016/j.ijplas.2010.03.002 [107] CLIFTON R J. Analysis of the laser velocity interferometer [J]. Journal of Applied Physics, 1970, 41(13): 5335–5337. doi: 10.1063/1.1658673 [108] LLOYD J T, CLAYTON J D, AUSTIN R A, et al. Plane wave simulation of elastic-viscoplastic single crystals [J]. Journal of the Mechanics and Physics of Solids, 2014, 69: 14–32. doi: 10.1016/j.jmps.2014.04.009 [109] LUSCHER D J, MAYEUR J R, MOURAD H M, et al. Coupling continuum dislocation transport with crystal plasticity for application to shock loading conditions [J]. International Journal of Plasticity, 2016, 76: 111–129. doi: 10.1016/j.ijplas.2015.07.007 [110] LUSCHER D J, ADDESSIO F L, CAWKWELL M J, et al. A dislocation density-based continuum model of the anisotropic shock response of single crystal α-cyclotrimethylene trinitramine [J]. Journal of the Mechanics and Physics of Solids, 2017, 98: 63–86. doi: 10.1016/j.jmps.2016.09.005 [111] HANSEN B L, BEYERLEIN I J, BRONKHORST C A, et al. A dislocation-based multi-rate single crystal plasticity model [J]. International Journal of Plasticity, 2013, 44: 129–146. doi: 10.1016/j.ijplas.2012.12.006 [112] SHAHBA A, GHOSH S. Crystal plasticity FE modeling of Ti alloys for a range of strain-rates. Part I: a unified constitutive model and flow rule [J]. International Journal of Plasticity, 2016, 87: 48–68. doi: 10.1016/j.ijplas.2016.09.002 [113] LLOYD J T, CLAYTON J D, BECKER R, et al. Simulation of shock wave propagation in single crystal and polycrystalline aluminum [J]. International Journal of Plasticity, 2014, 60: 118–144. doi: 10.1016/j.ijplas.2014.04.012 [114] BARTON N R, BENSON D J, BECKER R. Crystal level continuum modelling of phase transformations: the α↔ϵ transformation in iron [J]. Modelling and Simulation in Materials Science and Engineering, 2005, 13(5): 707. doi: 10.1088/0965-0393/13/5/006 [115] ADDESSIO F L, LUSCHER D J, CAWKWELL M J, et al. A single-crystal model for the high-strain rate deformation of cyclotrimethylene trinitramine including phase transformations and plastic slip [J]. Journal of Applied Physics, 2017, 121(18): 185902. doi: 10.1063/1.4983009 [116] KNEZEVIC M, ZECEVIC M, BEYERLEIN I J, et al. Strain rate and temperature effects on the selection of primary and secondary slip and twinning systems in HCP Zr [J]. Acta Materialia, 2015, 88: 55–73. doi: 10.1016/j.actamat.2015.01.037 [117] ARDELJAN M, BEYERLEIN I J, MCWILLIAMS B A, et al. Strain rate and temperature sensitive multi-level crystal plasticity model for large plastic deformation behavior: application to AZ31 magnesium alloy [J]. International Journal of Plasticity, 2016, 83: 90–109. doi: 10.1016/j.ijplas.2016.04.005 [118] MEREDITH C S, LLOYD J T, SANO T. The quasi-static and dynamic response of fine-grained Mg alloy AMX602: an experimental and computational study [J]. Materials Science and Engineering A, 2016, 673: 73–82. doi: 10.1016/j.msea.2016.07.035 [119] GARCÍA-GRAJALES J A, FERNÁNDEZ A, LEARY D, et al. A new strain rate dependent continuum framework for Mg alloys [J]. Computational Materials Science, 2016, 115: 41–50. doi: 10.1016/j.commatsci.2015.12.046 [120] 潘昊, 王升涛, 吴子辉, 等. 孪晶对Be材料冲击加-卸载动力学影响的数值模拟研究 [J]. 物理学报, 2018, 67(16): 164601. doi: 10.7498/aps.67.20180451PAN H, WANG S T, WU Z H, et al. Effect of twining on dynamic behaviors of beryllium materials under impact loading and unloading [J]. Acta Physica Sinica, 2018, 67(16): 164601. doi: 10.7498/aps.67.20180451 [121] CLAYTON J D. Dynamic plasticity and fracture in high density polycrystals: constitutive modeling and numerical simulation [J]. Journal of the Mechanics and Physics of Solids, 2005, 53(2): 261–301. doi: 10.1016/j.jmps.2004.06.009 [122] VOGLER T J, CLAYTON J D. Heterogeneous deformation and spall of an extruded tungsten alloy: plate impact experiments and crystal plasticity modeling [J]. Journal of the Mechanics and Physics of Solids, 2008, 56(2): 297–335. doi: 10.1016/j.jmps.2007.06.013 [123] DEMIR E, RAABE D, ZAAFARANI N, et al. Investigation of the indentation size effect through the measurement of the geometrically necessary dislocations beneath small indents of different depths using EBSD tomography [J]. Acta Materialia, 2009, 57(2): 559–569. doi: 10.1016/j.actamat.2008.09.039 [124] DMITRIEVA O, DONDL P W, MÜLLER S, et al. Lamination microstructure in shear deformed copper single crystals [J]. Acta Materialia, 2009, 57(12): 3439–3449. doi: 10.1016/j.actamat.2009.03.035 [125] HUANG H, VAN SWYGENHOVEN H. Atomistic simulations of mechanics of nanostructures [J]. MRS bulletin, 2009, 34(3): 160–166. doi: 10.1557/mrs2009.46 -














 下载:
下载: