Dynamic Behavior of TB6 Titanium Alloy under Shear-Compression Loading
-
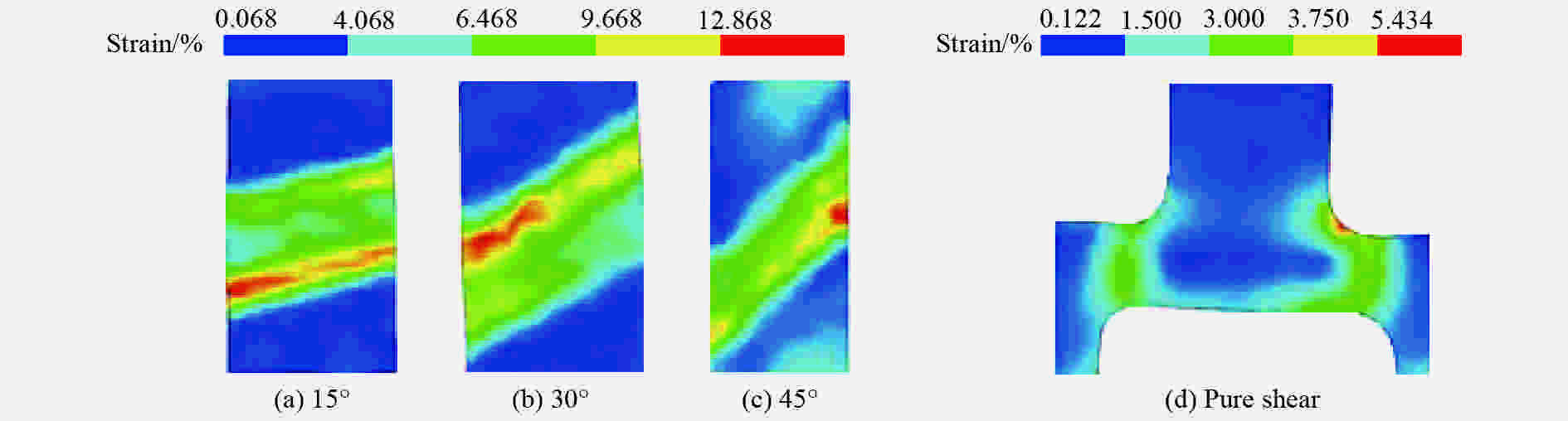
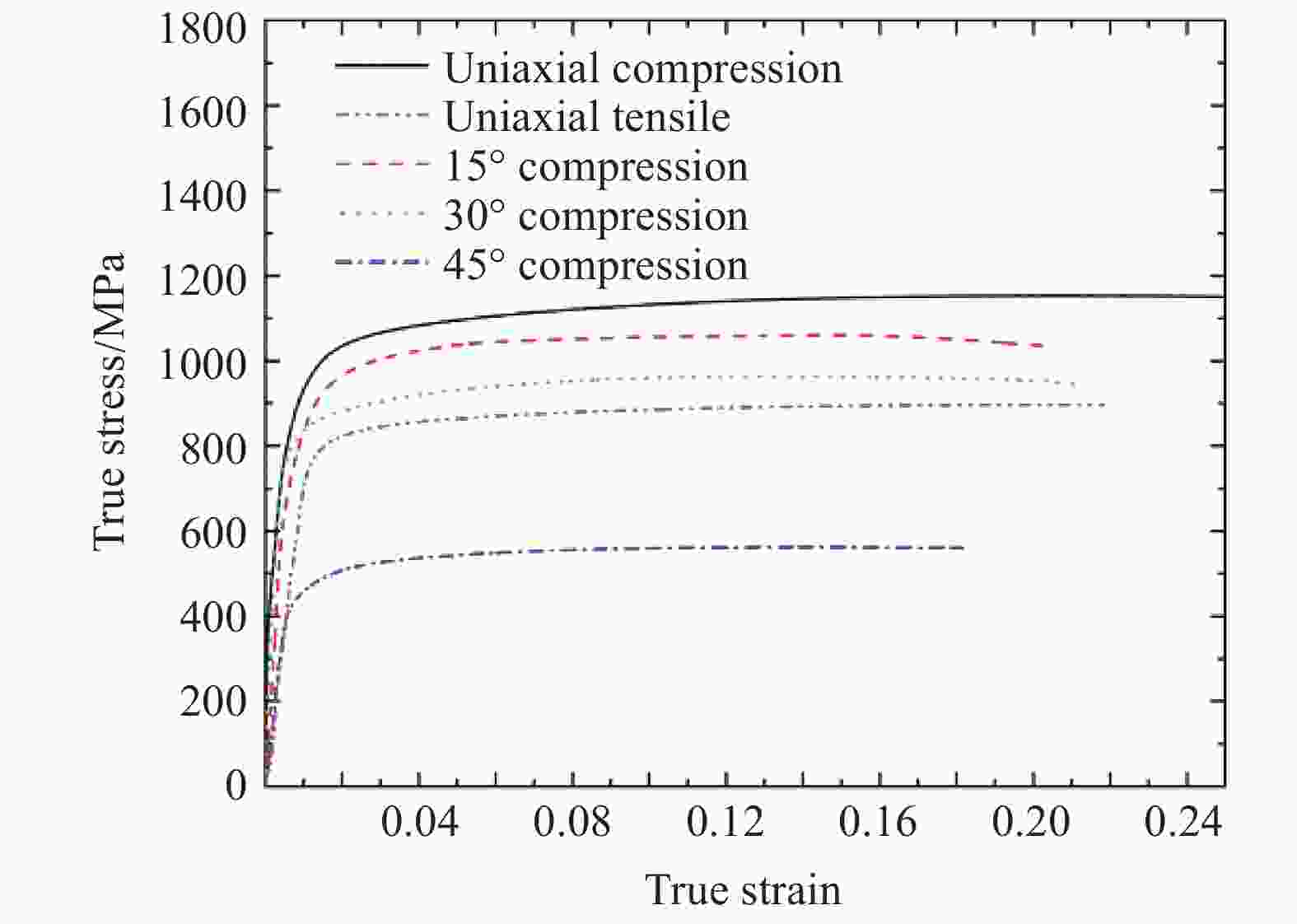
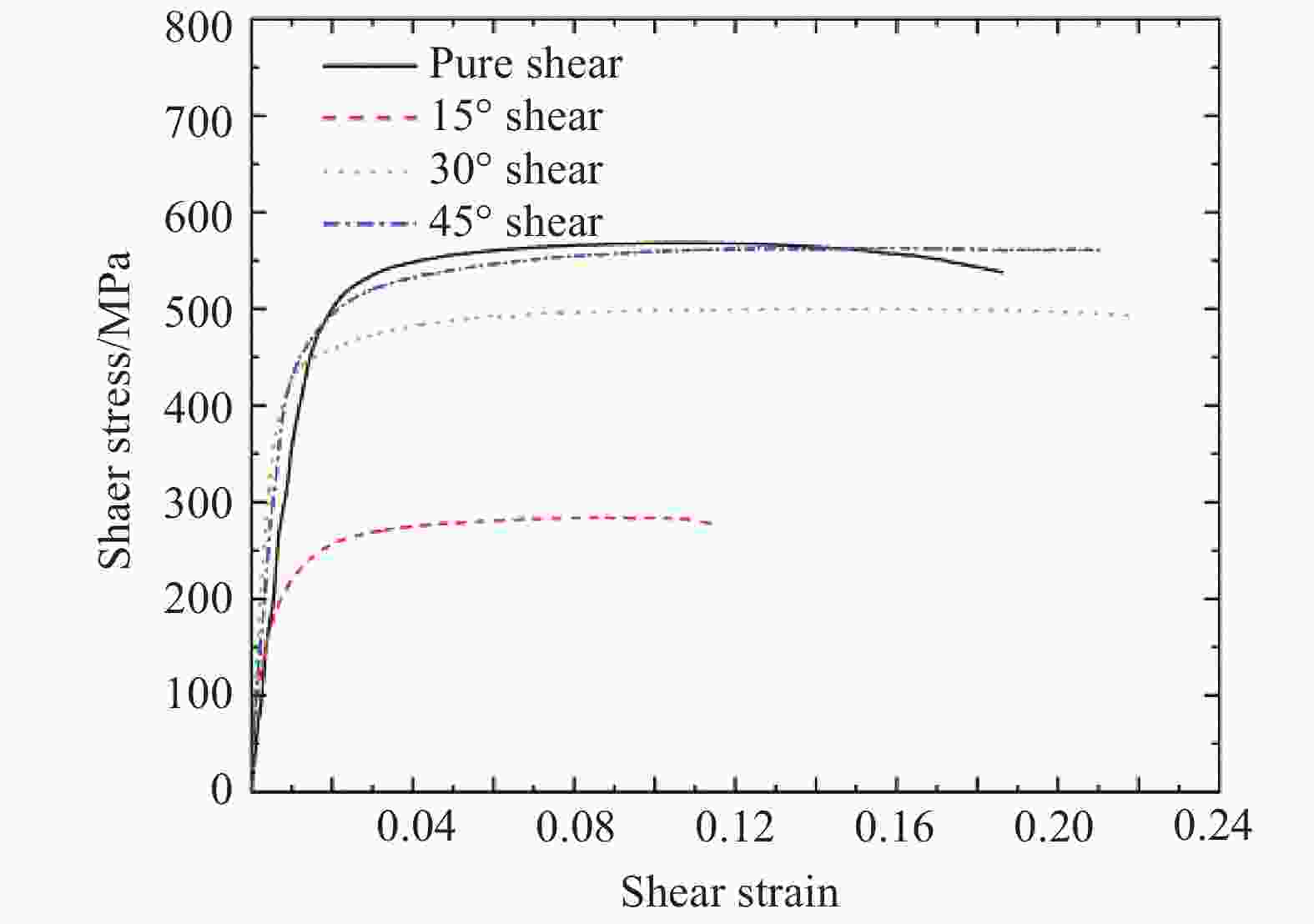
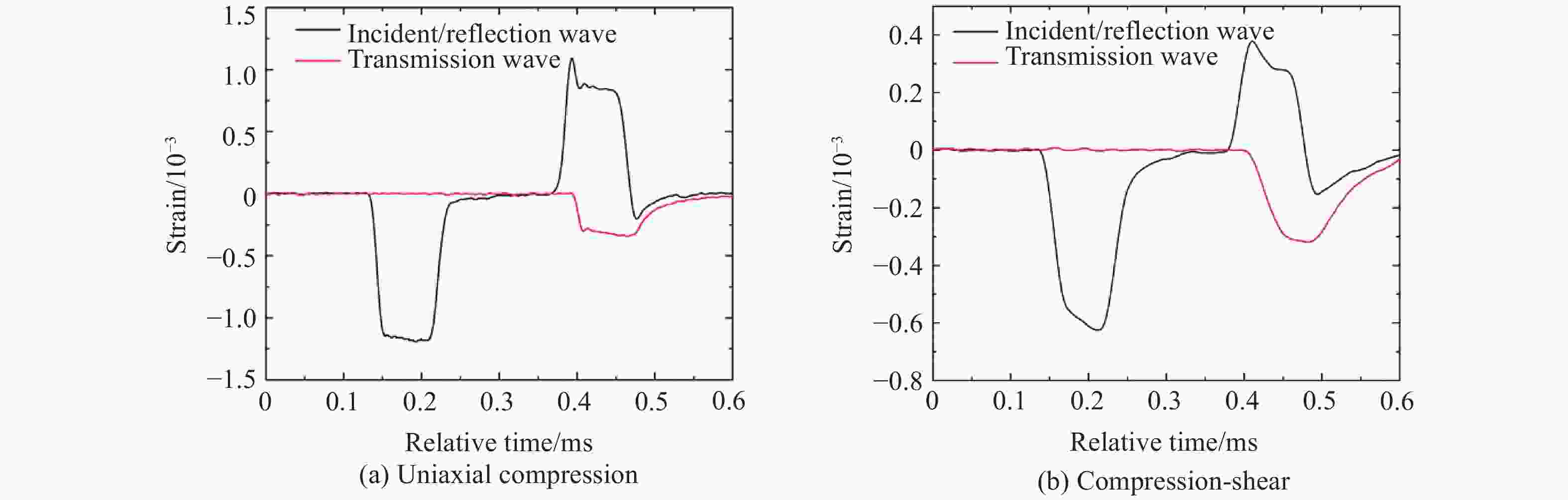
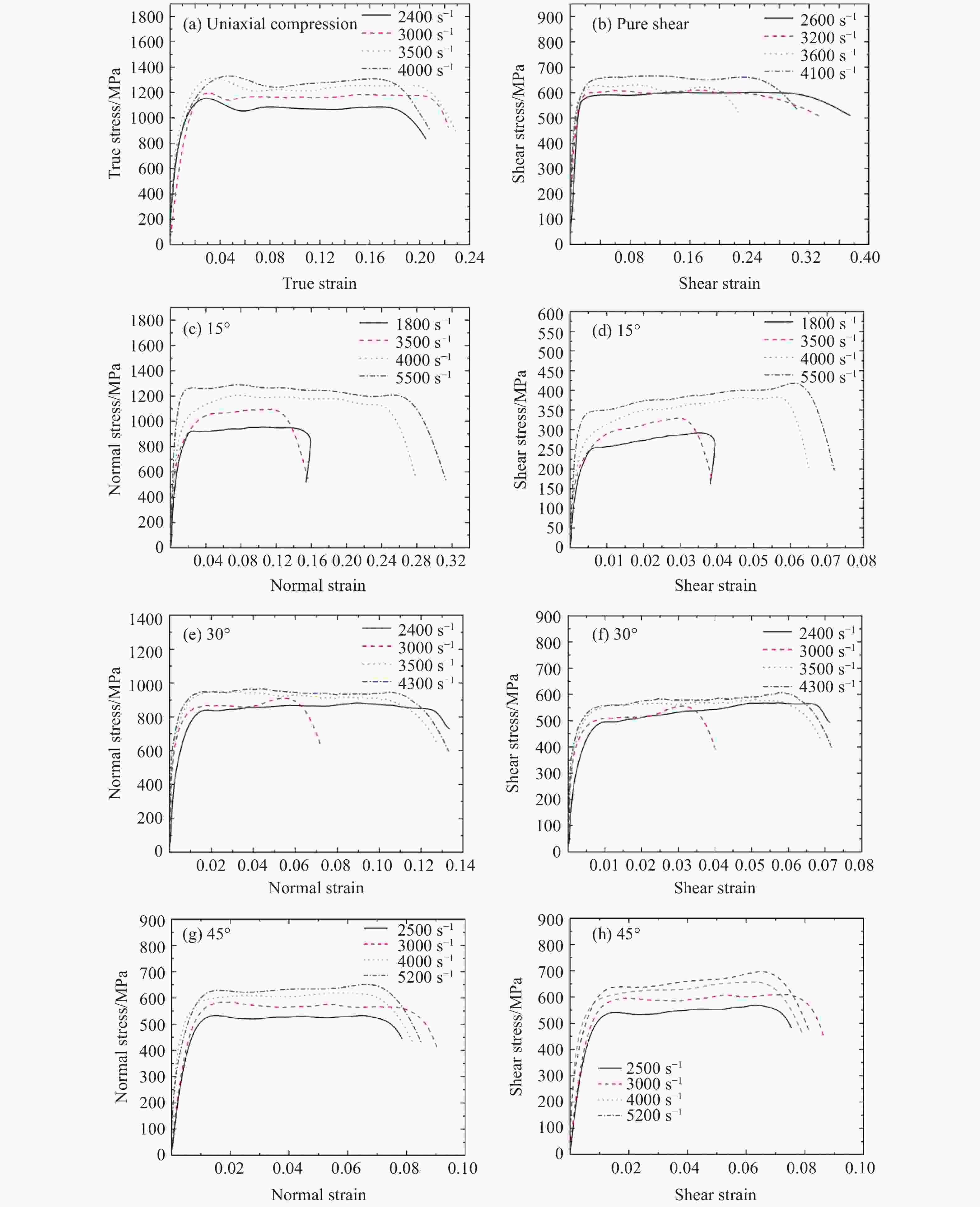
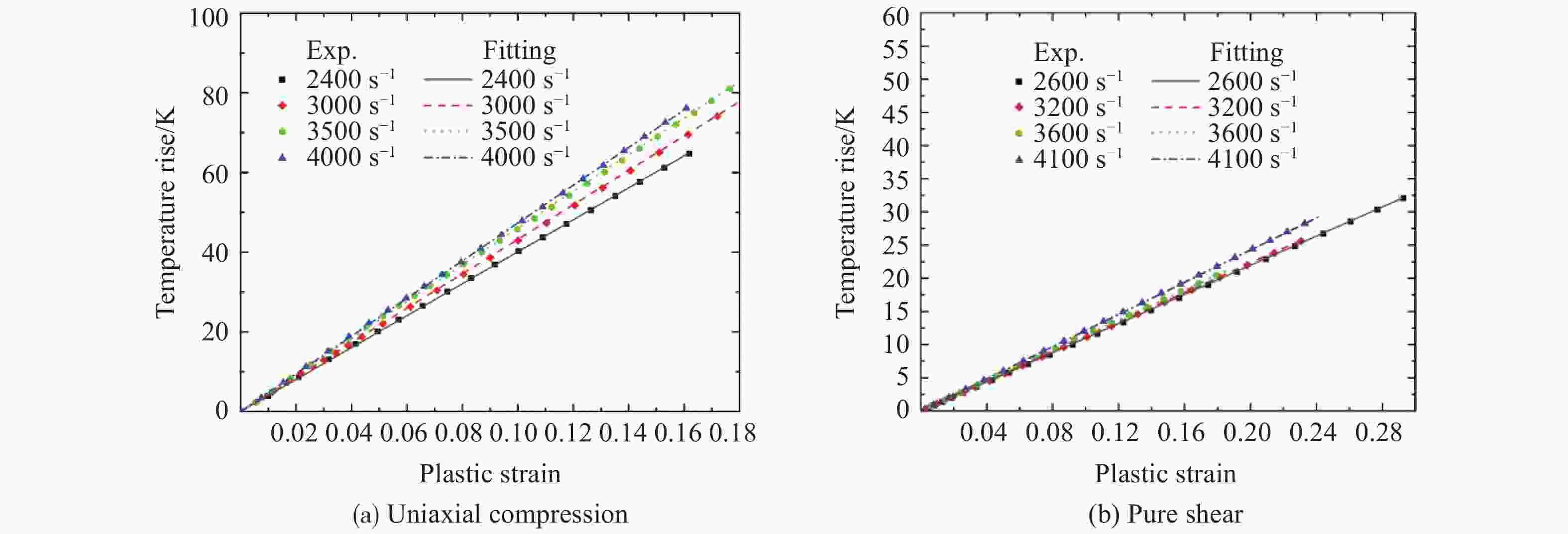
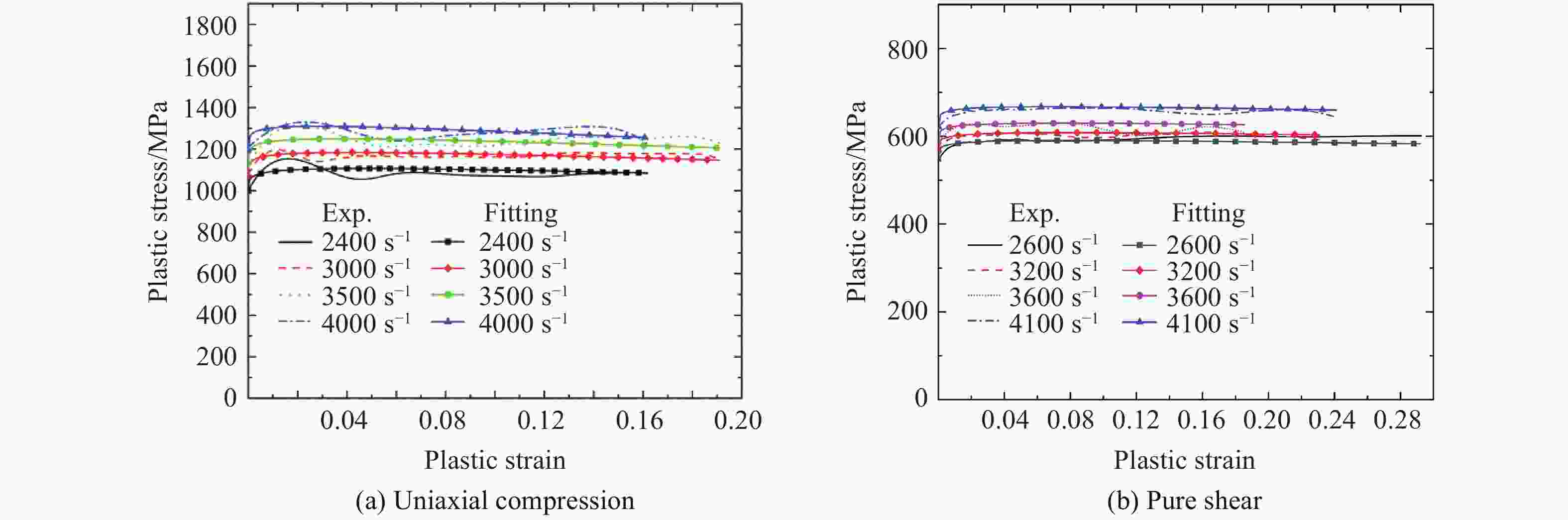
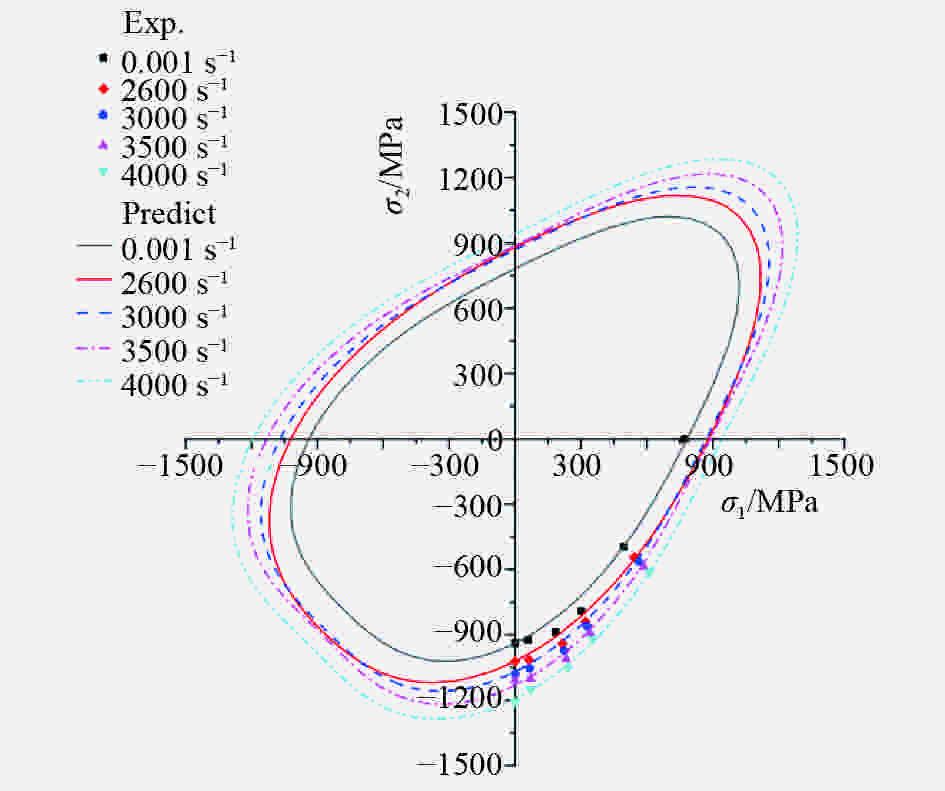
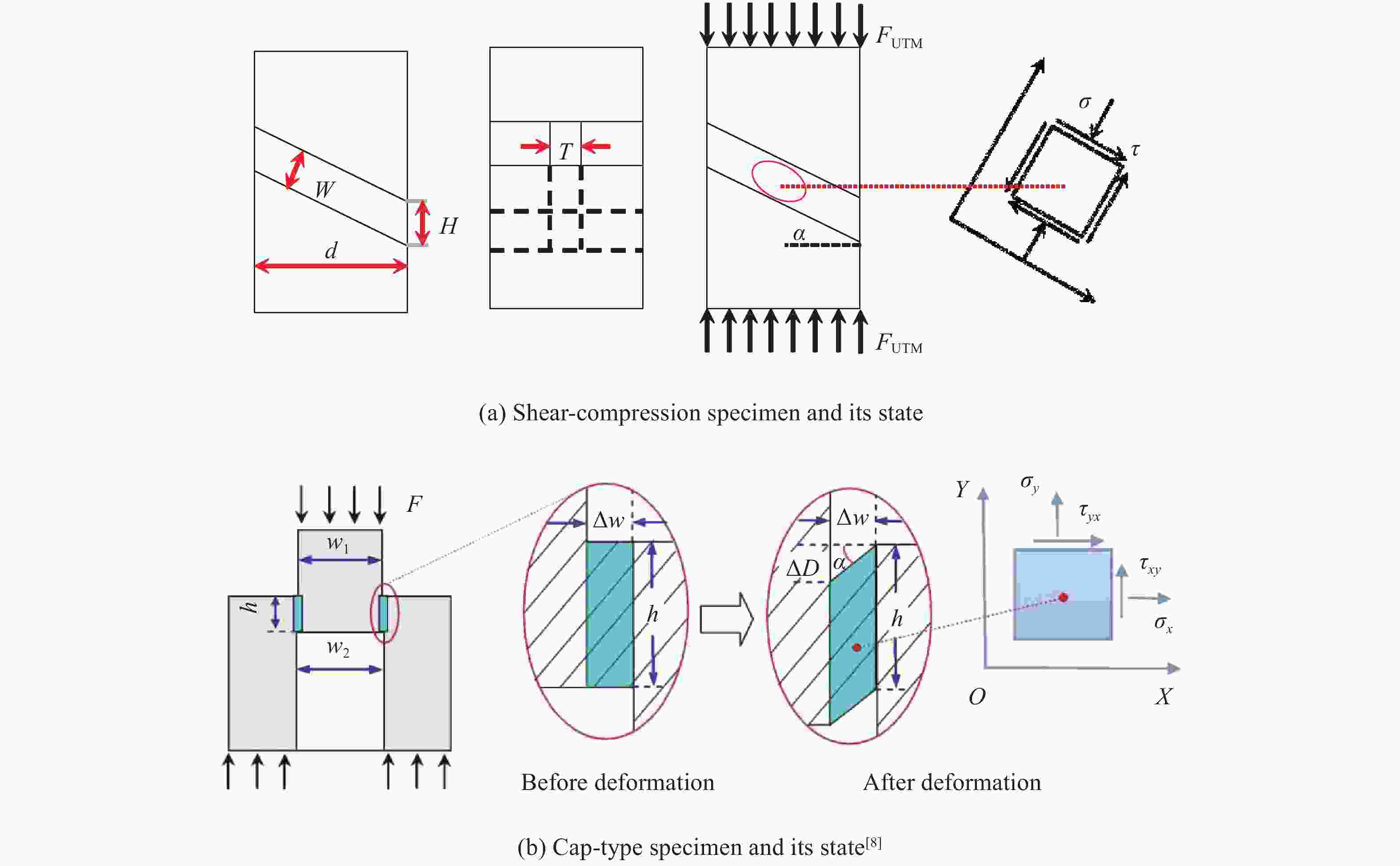
摘要: 钛合金以其轻质高强的优异力学性能被广泛应用于航空航天领域。使用Instron万能材料试验机和分离式霍普金森压杆,对TB6钛合金进行准静态和动态力学性能实验,得到了压缩、拉伸和压剪载荷作用下TB6钛合金的准静态和动态应力-应变曲线,构建了单轴压缩和纯剪切两种应力状态下的Johnson-Cook动态本构模型。结果表明,TB6钛合金的屈服应力表现出明显的拉压不对称性、应变率强化和热软化效应。使用拉压不对称因子,修正了von Mises屈服准则,修正的屈服准则可很好地预测TB6钛合金的准静态和动态屈服行为。Abstract: Titanium alloy is widely used in aerospace industry due to its excellent mechanical properties of high strength and light weight. In this paper, a quasi-static and dynamic tests of TB6 titanium alloy has been implemented with an Instron universal material testing machine and a split Hopkinson pressure bar (SHPB). Quasi-static and dynamic stress-strain curves of TB6 titanium alloy under compression, tension and shear-compression loads were obtained. Based on the data of experiment, we have established Johnson-Cook dynamic constitutive model under uniaxial compression and pure shear. The results show that, the yield stress of TB6 titanium alloy exhibits obvious tension-compression asymmetry, strain rate hardening and thermal softening effects. The von Mises yield criterion is modified by considering the asymmetric factor of tension and compression. The modified yield criterion has been proved to be accurate and suitable for predicting the quasi-static and dynamic yield behaviors of TB6 titanium alloy.
-
表 1 J-C模型参数拟合结果
Table 1. Fitting results of J-C model parameters
Condition A/MPa B/MPa n m Uniaxial compression 939 326.6 0.24 0.661 18 Pure shear 495 92.5 0.21 0.655 48 -
[1] 欧阳德来. TB6和TA15钛合金β锻组织演变及动态再结晶行为研究 [D]. 南京: 南京航空航天大学, 2011: 1-2 [2] 吴琳, 王克鲁, 鲁世强. 基于逐步回归法的TB6钛合金本构关系研究 [J]. 热加工工艺, 2010, 39(8): 29–35 doi: 10.3969/j.issn.1001-3814.2010.08.010WU L, WANG K L, LU S Q. Study on constitutive relationship of TB6 alloy based on stepwise regression method [J]. Hot Working Technology, 2010, 39(8): 29–35 doi: 10.3969/j.issn.1001-3814.2010.08.010 [3] 雷力明, 黄旭, 黄利军. 铸态TB6钛合金热变形行为及本构关系 [J]. 中国有色金属学报, 2010, 20(Suppl 1): 377–380LEI L M, HUANG X, HUANG L J. Hot deformation behavior and constitutive relationship of as-cast TB6 alloy [J]. The Chinese Journal of Nonferrous Metals, 2010, 20(Suppl 1): 377–380 [4] 段园培, 黄仲佳, 余小鲁. 基于摩擦修正的TB6合金流变应力行为研究及本构模型建立 [J]. 稀有金属, 2014, 38(2): 202–209DUAN Y P, HUANG Z J, YU X L. Flow stress behavior and constitutive model of as-cast TB6 titanium alloy based on friction correction [J]. Chinese Journal of Rare Metals, 2014, 38(2): 202–209 [5] WU Y, LIU J, WANG H, et al. Effect of stress ratio on very high cycle fatigue properties of Ti-10V-2Fe-3Al alloy with duplex microstructure [J]. Journal of Materials Science & Technology, 2018, 34(7): 1189–1195. [6] LI J, LI F G, MA X K, et al. Micromechanical study of the forged Ti-1023 titanium alloy by micro-indentation [C]//Key Engineering Materials. Trans Tech Publications, 2018, 765: 160-165. [7] RITTEL D, LEE S, RAVICHANDRAN G. A shear-compression specimen for large strain testing [J]. Experimental Mechanics, 2002, 42(1): 58–64. doi: 10.1007/BF02411052 [8] 周刚毅, 董新龙, 付应乾. 不同加载状态下TA2钛合金绝热剪切破坏响应特性 [J]. 力学学报, 2016, 48(6): 1353–1361ZHOU G Y, DONG X L, FU Y Q. An experimental study on adiabatic shear behavior of TA2 titanium alloy subject to different loading condition [J]. Chinese Journal of Theoretical & Applied Mechanics, 2016, 48(6): 1353–1361 [9] JIN T, ZHOU Z, SHU X, et al. Effects of strain rate on PMMA failure behavior [J]. Applied Physics A, 2016, 122(1): 7. doi: 10.1007/s00339-015-9526-0 [10] 宋立, 胡时胜. SHPB数据处理中的二波法与三波法 [J]. 爆炸与冲击, 2005, 25(4): 368–373 doi: 10.3321/j.issn:1001-1455.2005.04.014SONG L, HU S S. Two-wave and three-wave method in SHPB data processing [J]. Explosion and Shock Waves, 2005, 25(4): 368–373 doi: 10.3321/j.issn:1001-1455.2005.04.014 [11] JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures [C]//Proceedings of the 7th International Symposium on Ballistic, 1983: 541-547. [12] 徐天平, 王礼立, 卢维娴. 高应变率下钛合金Ti-6AI-4V的热-粘塑性特性和绝热剪切变形 [J]. 爆炸与冲击, 1987, 7(1): 1–8XU T P, WANG L L, LU W X. The thermo-visco plasticity and adiabatic shear deformation for a titanium alloy Ti-6Al-4V under high strain rates [J]. Explosion and Shock Waves, 1987, 7(1): 1–8 [13] CAZACU O, PLUNKETT B, BARLAT F. Orthotropic yield criterion for hexagonal closed packed metals [J]. International Journal of Plasticity, 2006, 22(7): 1171–1194. doi: 10.1016/j.ijplas.2005.06.001 [14] KHAN A S, YU S, LIU H. Deformation induced anisotropic responses of Ti-6Al-4V alloy Part II: a strain rate and temperature dependent anisotropic yield criterion [J]. International Journal of Plasticity, 2012, 38(4): 14–26. -






 下载:
下载: