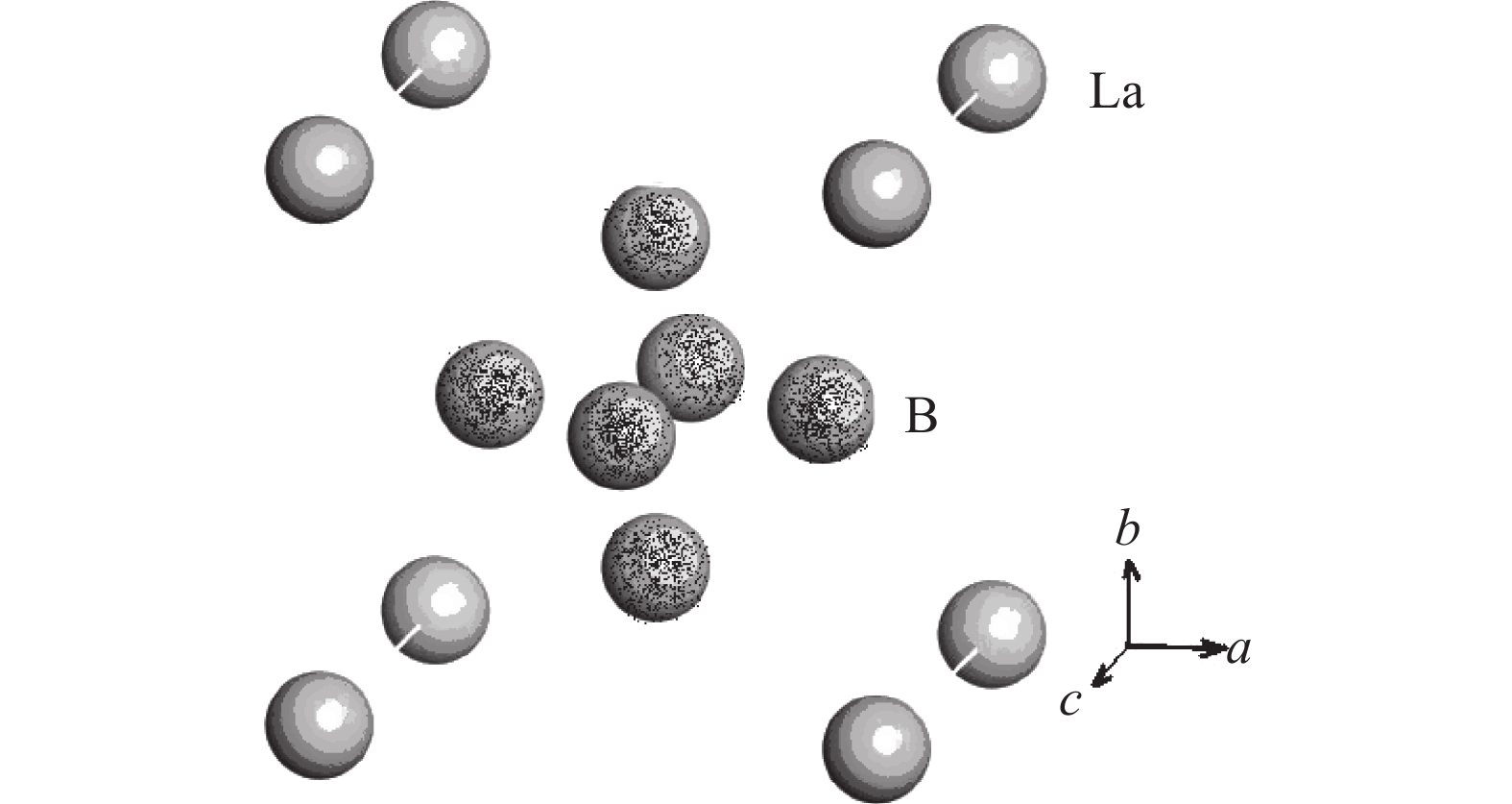
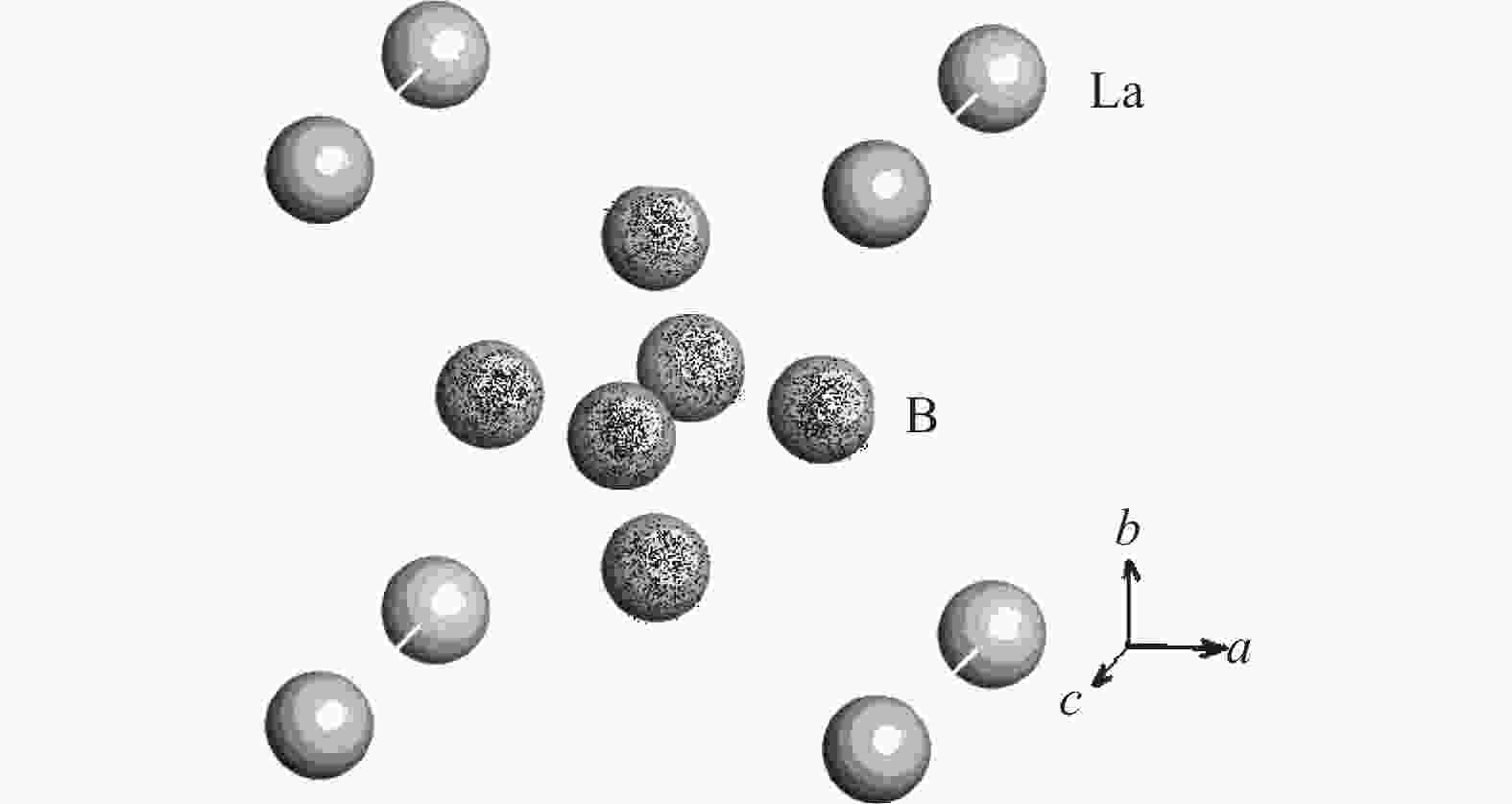
Elastic and Mechanical Properties of Rare Earth Boride LaB6 Crystalline Material
-
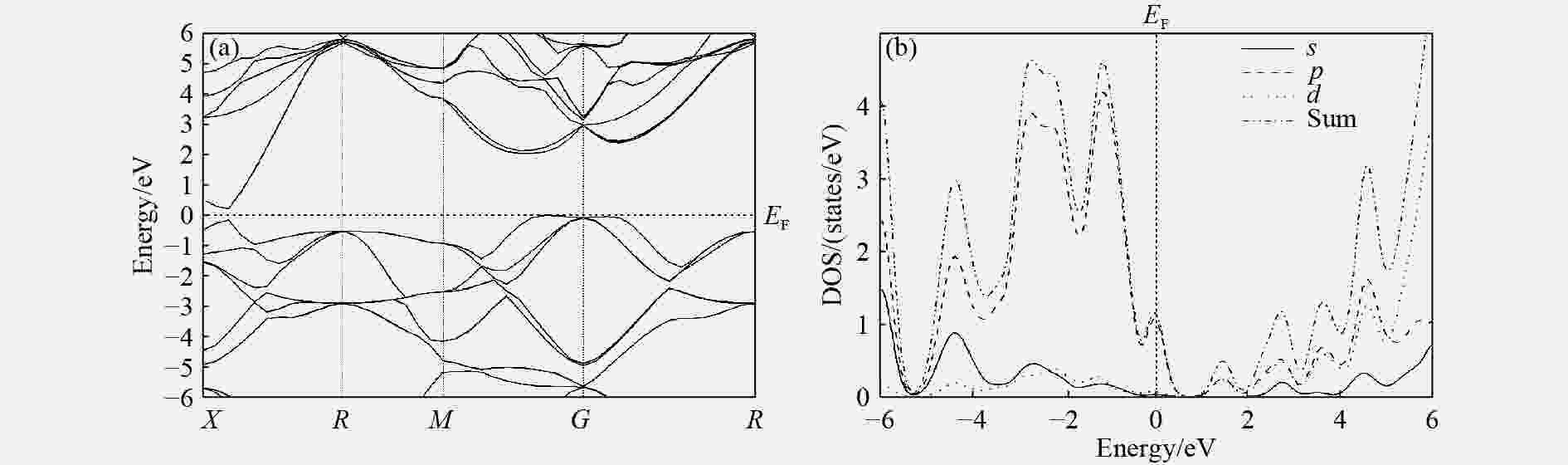
摘要: 利用密度泛函理论和Birch-Murnaghan物态方程,系统分析了LaB6晶体材料的弹性常数参数、体弹性模量、剪切弹性模量及其他力学性能。结果表明:LaB6晶体具有较大的弹性常数参数C11,说明在此主轴应力方向上具有较大的弹性常数;同时它还具有较大的体弹性模量,并且体弹性模量具有各向同性,剪切弹性模量具有各向异性;LaB6晶体的杨氏模量为227.85 GPa,泊松比为0.26,体剪弹性模量比值达到1.44,表明其脆性较强,不易发生弹性形变;LaB6晶体的硬度达到11.56 GPa,平均弹性波速达4.87 km/s。LaB6的带隙宽度为0.20 eV,呈金属性,内部电子具有较强的局域性,La和B之间具有较强的共价键成分。Abstract: The elastic constants parameters, bulk modulus, shear modulus and mechanical properties of the LaB6 crystalline material have been systematically studied with density functional theory and the Birch-Murnaghan formation. The results show that the LaB6 has larger C11, indicating its larger elastic constant along this direction. The LaB6 also has large bulk modulus, and the bulk modulus is isotropic, whereas the shear modulus is moderately anisotropic. The LaB6 crystalline material has large Young’s modulus of 227.85 GPa, so it is hard for elastic deformation. The Poisson’s ratio is 0.26 and the B/G value is 1.44, these values indicate the moderate brittleness of this material. The hardness of LaB6 is 11.56 GPa and the mean elastic velocity is 4.87 km/s. The LaB6 has narrow band gap of 0.20 eV, showing that it is metallic type material. The electrons of LaB6 have strong localization interaction, and there is covalent bond between La and B.
-
Key words:
- LaB6 /
- elastic properties /
- mechanical properties /
- elastic constant
-
表 1 LaB6晶体材料的晶格参数
Table 1. Structural parameters of LaB6 crystalline material
Method a/nm b/nm c/nm α/(°) β/(°) γ/(°) Experiment 0.415 49 0.415 49 0.415 49 90 90 90 Calculation 0.420 205 0.420 205 0.420 205 90 90 90 表 2 LaB6晶体材料的体弹性模量和剪切弹性模量
Table 2. Bulk modulus and shear modulus of LaB6 crystalline material
BV/GPa BR/GPa BH/GPa GV/GPa GR/GPa GH/GPa 160.55 160.55 160.55 111.49 68.85 90.17 表 3 LaB6晶体材料的力学性能参数和弹性波速
Table 3. Mechanical parameters and elastic velocities of LaB6 crystalline material
E/GPa γ λ AB AG H/GPa vl/(km·s–1) vt/(km·s–1) vm/(km·s–1) 227.85 0.26 1.44 0 0.24 11.56 7.72 4.38 4.87 表 4 LaB6晶体材料的电荷转移
Table 4. Charge distributions of LaB6 crystalline material
Atom Charge distribution/e s orbital p orbital d orbital Total charge B 0.88 2.54 0.00 –0.42 La 1.50 5.46 1.51 2.53 -
[1] LAFFERTY J M. Boride cathodes [J]. Journal of Applied Physics, 1951, 22(3): 299–309. doi: 10.1063/1.1699946 [2] HOSSAIN F M, RILEY D P, MURCH G E. Ab initio calculations of the electronic structure and bonding characteristics of LaB6 [J]. Physical Review B, 2005, 72(23): 235101. doi: 10.1103/PhysRevB.72.235101 [3] CHEN C H, AIZAWA T, IYI N, et al. Structural refinement and thermal expansion of hexaborides [J]. Journal of Alloys and Compounds, 2004, 366(1/2): L6–L8. [4] 张宁, 张玖兴, 包黎红. 悬浮区域熔炼法制备REB6(LaB6、CeB6)单晶体及其表征 [J]. 功能材料, 2012, 43(2): 178–180 doi: 10.3969/j.issn.1007-4252.2012.02.016ZHANG N, ZHANG J X, BAO L H, et al. Floating zone growth and characterization of single crystal REB3 (LaB6, CeB6) cathode [J]. Chinese Journal of Functional Materials, 2012, 43(2): 178–180 doi: 10.3969/j.issn.1007-4252.2012.02.016 [5] 包黎红, 那仁格日乐, 特古斯, 等. 放电等离子烧结原位合成La xCe1- xB6化合物及性能研究 [J]. 物理学报, 2013, 62: 196105 doi: 10.7498/aps.62.196105BAO L H, NARENGERILE, TEGUS O, et al. Synthesis and properties of LaxCe1–xB6 compounds by in-situ spark plasma sintering [J]. Acta Physica Sinica, 2013, 62: 196105 doi: 10.7498/aps.62.196105 [6] 刘洪亮, 张忻, 王杨, 等. 单晶LaB6阴极材料典型晶面的电子结构和发射性能研究 [J]. 物理学报, 2018, 67: 048101 doi: 10.7498/aps.67.20172187LIU H L, ZHANG X, WANG Y, et al. Surface electronic structures and emission property of single crystal LaB6 typical surfaces [J]. Acta Physica Sinica, 2018, 67: 048101 doi: 10.7498/aps.67.20172187 [7] 高瑞兰, 于化顺, 于普涟, 等. LaB6多晶材料的制备工艺研究 [J]. 山东大学学报(工学版), 2002, 32(6): 593–596 doi: 10.3969/j.issn.1672-3961.2002.06.024GAO R L, YU H S, YU P L, et al. Preparation of LaB6 polycrystalline materials [J]. Journal of Shandong University (Engineering Science), 2002, 32(6): 593–596 doi: 10.3969/j.issn.1672-3961.2002.06.024 [8] NYE J F. Physical properties of crystals: their representation by tensors and matrices [M]. Oxford: Oxford University Press, 1957. [9] HILL R. The elastic behaviour of a crystalline aggregate [J]. Proceedings of the Physical Society Section A, 1952, 65(5): 349. doi: 10.1088/0370-1298/65/5/307 [10] TIAN Y, XU B, ZHAO Z. Microscopic theory of hardness and design of novel superhard crystals [J]. International Journal of Refractory Metals and Hard Materials, 2012, 33: 93–106. doi: 10.1016/j.ijrmhm.2012.02.021 [11] BORN M, HUANG K. Dynamical theory of crystal lattices [M]. Oxford: Clarendon Press, 1968. [12] HAINES J, LEGER J M, BOCQUILLON G. Synthesis and design of superhard materials [J]. Annual Review of Materials Research, 2001, 31(1): 1–23. doi: 10.1146/annurev.matsci.31.1.1 [13] PANDA K B, CHANDRAN K S R. Determination of elastic constants of titanium diboride (TiB2) from first principles using FLAPW implementation of the density functional theory [J]. Computational Materials Science, 2006, 35(2): 134–150. doi: 10.1016/j.commatsci.2005.03.012 [14] ANDERSON O L. A simplified method for calculating the Debye temperature from elastic constants [J]. Journal of Physics and Chemistry of Solids, 1963, 24(7): 909–917. doi: 10.1016/0022-3697(63)90067-2 -






 下载:
下载: