Elastic Properties of ReN2 under High Pressure
-
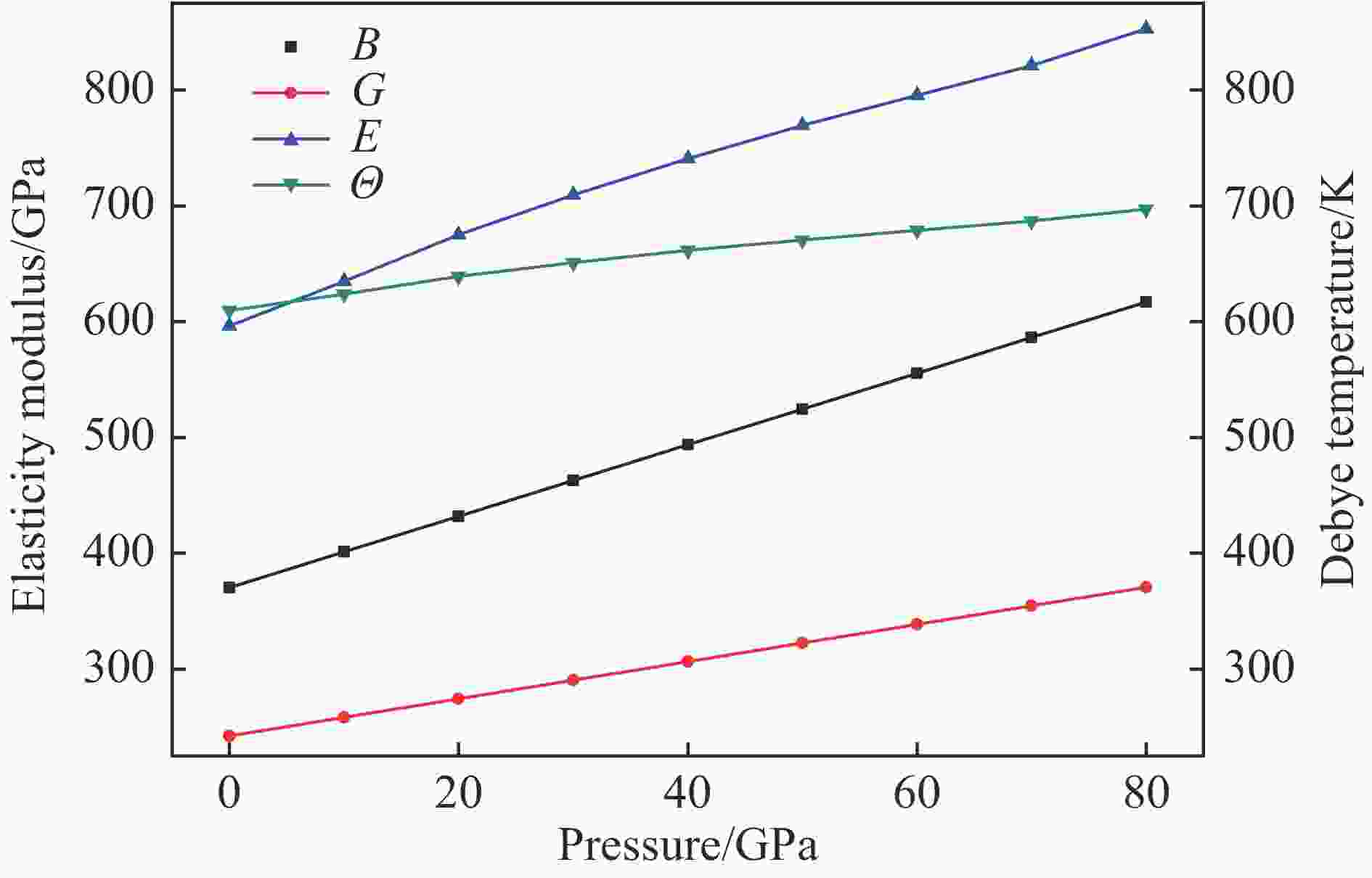
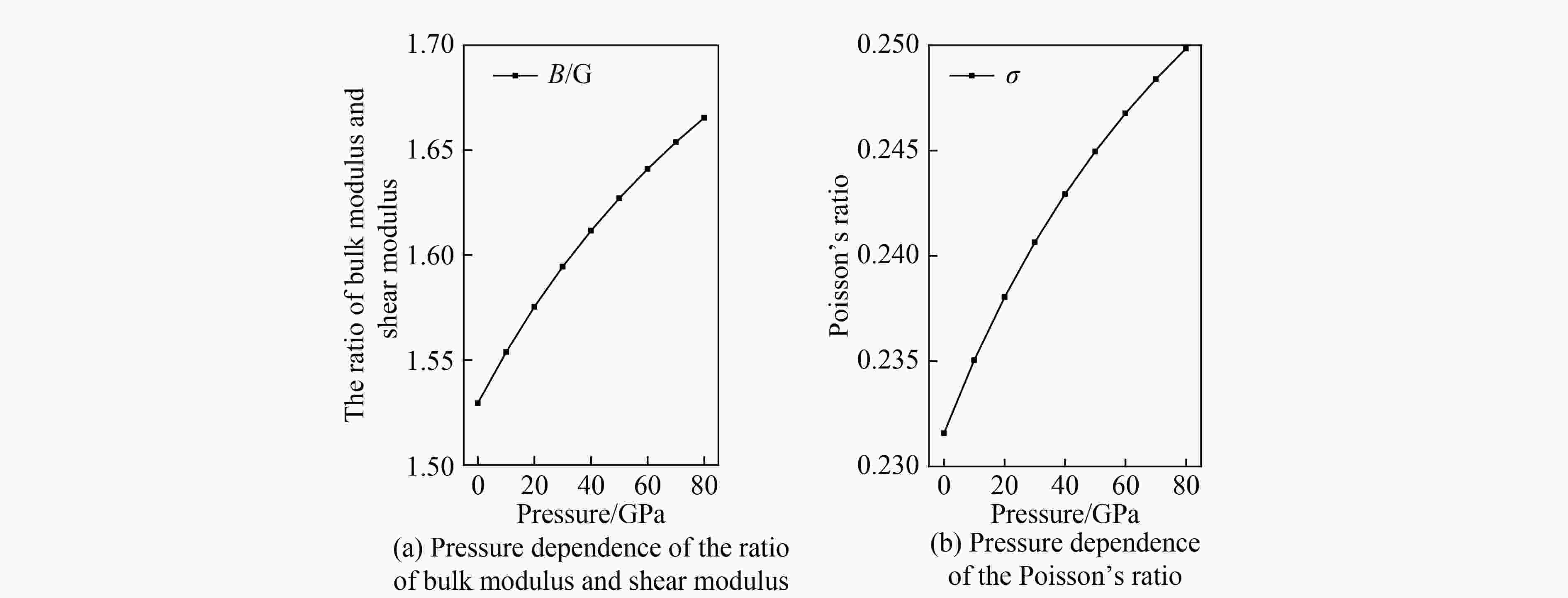
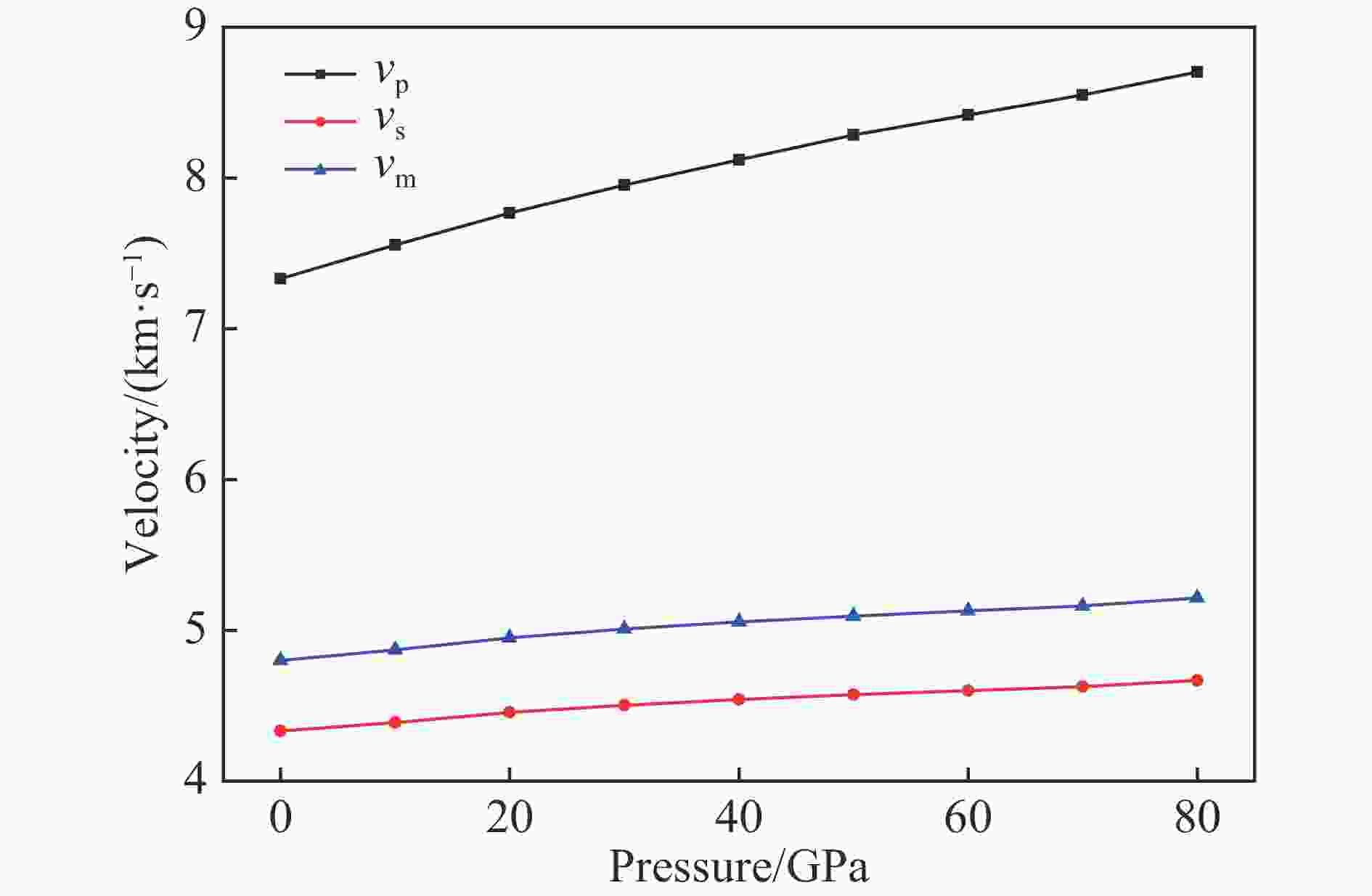
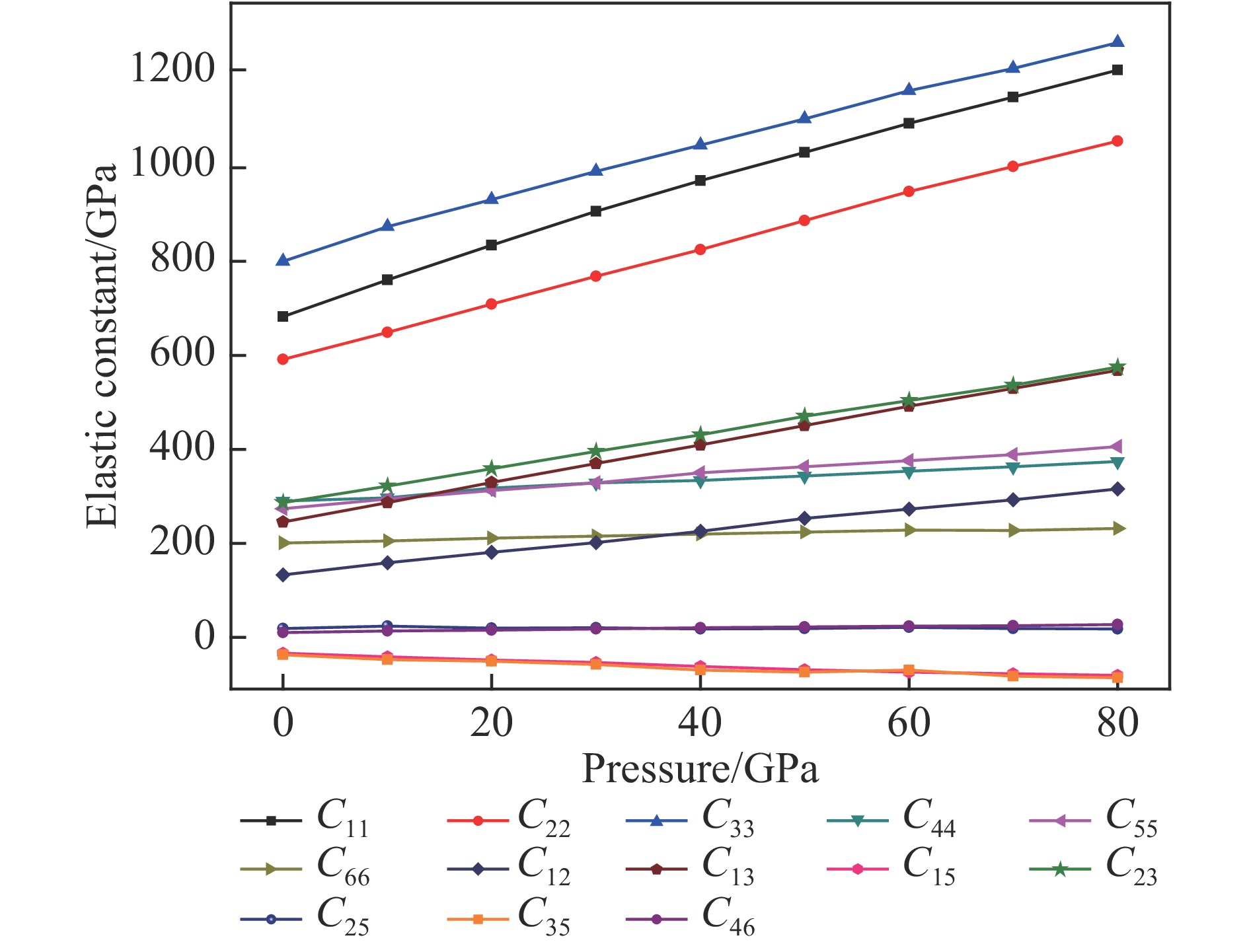
摘要: 超硬材料在工业上具有广泛的应用前景,如切割器具、研磨材料及耐磨涂层等。作为5d过渡金属双氮化合物之一的ReN2由共价键、离子键及金属键混合而成,因而具有诸多如高硬度、高熔点、耐腐蚀等优异的物理性质,进而具有潜在的研究价值。采用密度泛函理论中的平面波赝势法计算了零温零压下C2/m-ReN2的结构性质,并首次研究了高压下C2/m-ReN2的力学结构稳定性及弹性性质。研究得出了C2/m-ReN2的弹性常数、弹性模量、德拜温度、声速随压强的变化关系,除个别弹性常数,这些物理量皆随压强的增加而增加。还预测了C2/m-ReN2的韧脆性,并估算了C2/m-ReN2的维氏硬度。Abstract: Super hard materials have wide applications in industry, such as cutting tools, abrasive materials, wear resistant coatings. As one of the 5d transition metals double nitrogen compound, ReN2 contains both covalent bond, ionic bond and metallic bonding. In view of its many excellent physical properties, such as high hardness, high melting point and corrosion resistance, ReN2 earns much research interests. This article has calculated the structural properties of C2/m-ReN2 under zero temperature and zero pressure using the plane wave pseudo-potential method of density functional theory, and has studied the mechanical structure stability and elastic properties of C2/m-ReN2 under high pressure for the first time. The relations of the elastic constants, various modulus of elasticity, Debye temperature and the sound speed of C2/m-ReN2 with the pressure have obtained. In addition to the individual elastic constants, these quantities increase with the increase in pressure. In addition, we have also predicted the toughness and brittleness of C2/m-ReN2, and have estimated the Vickers hardness of C2/m-ReN2.
-
Key words:
- ReN2 /
- mechanical structure /
- elastic property /
- hardness
-
表 1 在p=0 GPa和T=0 K下的平衡晶格参数a、b、c及
${\;\beta}$ ,平衡体积V0,体模量B0,体模量对压强的一阶导数${B_0'}$ 及其他理论值[13, 27]Table 1. Equilibrium lattice parameters a, b, c and
${\;\beta}$ , equilibrium volume V0, bulk modulus B0, and its pressure derivation${B_0'}$ at p=0 GPa and T=0 K, together with other theoretical results [13, 27]Method a/nm b/nm c/nm $\beta$/(°) V0/nm3 B0/GPa B0′/GPa This work 0.682 0.282 0.939 142.38 0.027 59 361 4.78 Ref. [13] 0.682 0.284 0.936 142.30 0.027 60 Ref. [27] 0.683 0.284 0.939 0.027 77 表 2 在p=0 GPa和T=0 K下的体模量B、剪切模量G、杨氏模量E、泊松比
$\sigma $ 、维氏硬度HV及其他理论值[13, 27]Table 2. Bulk modulus B, shear modulus G, Young’s modulus E, Poisson’s ratio
$\sigma $ and Vickers hardness HV at p=0 GPa and T=0 K, together with other theoretical results[13, 27]Method B/GPa G/GPa E/GPa $\sigma $ Hv /GPa This work 370 242 596 0.23 27.66 Ref. [13] 369 217 Ref. [27] 376 210 531 0.26 -
[1] OYAMA S T. Crystal structure and chemical reactivity of transition metal carbides and nitrides [J]. Journal of Solid State Chemistry, 1992, 96(2): 442–445. doi: 10.1016/S0022-4596(05)80279-8 [2] LÉVY F, HONES P, SCHMID P E, et al. Electronic states and mechanical properties in transition metal nitrides [J]. Surface and Coatings Technology, 1999, 120/121: 284–290. doi: 10.1016/S0257-8972(99)00498-3 [3] IVANOVSKII A L. Platinum group metal nitrides and carbides: synthesis, properties and simulation [J]. Russian Chemical Reviews, 2009, 78(4): 303–318. doi: 10.1070/RC2009v078n04ABEH004036 [4] GILMAN J J, CUMBERLAND R W, KANER R B. Design of hard crystals [J]. International Journal of Refractory Metals and Hard Materials, 2006, 24(1/2): 1–5. [5] HAINES J, LEGER J M, BOCQUILLON G. Synthesis and design of superhard materials [J]. Annual Review of Materials Research, 2001, 31(1): 1–23. doi: 10.1146/annurev.matsci.31.1.1 [6] CROWHURST J C, GONCHAROV A F, SADIGH B, et al. Synthesis and characterization of the nitrides of platinum and iridium [J]. Science, 2006, 311(5765): 1275–1278. doi: 10.1126/science.1121813 [7] GREGORYANZ E, SANLOUP C, SOMAYAZULU M, et al. Synthesis and characterization of a binary noble metal nitride [J]. Nature Materials, 2004, 3(5): 294–297. doi: 10.1038/nmat1115 [8] YOUNG A F, SANLOUP C, GREGORYANZ E, et al. Synthesis of novel transition metal nitrides IrN2 and OsN2 [J]. Physical Review Letters, 2006, 96(15): 155501. doi: 10.1103/PhysRevLett.96.155501 [9] ZHAO E, WU Z. Structural, electronic and mechanical properties of ReN2 from first principles [J]. Computational Materials Science, 2008, 44(2): 531–535. doi: 10.1016/j.commatsci.2008.04.016 [10] LI Y, ZENG Z. New potential super-incompressible phase of ReN2 [J]. Chemical Physics Letters, 2009, 474(1/2/3): 93–96. [11] DU X P, WANG Y X, LO V C. Investigation of tetragonal ReN2 and WN2 with high shear moduli from first-principles calculations [J]. Physics Letters A, 2010, 374(25): 2569–2574. doi: 10.1016/j.physleta.2010.04.020 [12] KAWAMURA F, YUSA H, TANIGUCHI T. Synthesis of rhenium nitride crystals with MoS2 structure [J]. Applied Physics Letters, 2012, 100(25): 251910. doi: 10.1063/1.4729586 [13] WANG Y, YAO T, YAO J L, et al. Does the real ReN2 have the MoS2 structure? [J]. Physical Chemistry Chemical Physics, 2013, 15(1): 183–187. doi: 10.1039/C2CP43010J [14] WANG Y, LV J, ZHU L, et al. Crystal structure prediction via particle-swarm optimization [J]. Physical Review B, 2010, 82(9): 094116. doi: 10.1103/PhysRevB.82.094116 [15] BOUHEMADOU A, KHENATA R. Pseudo-potential calculations of structural and elastic properties of spinel oxides ZnX2O4 (X= Al, Ga, In) under pressure effect [J]. Physics Letters A, 2006, 360(2): 339–343. doi: 10.1016/j.physleta.2006.08.008 [16] LOUAIL L, MAOUCHE D, ROUMILI A, et al. Calculation of elastic constants of 4d transition metals [J]. Materials Letters, 2004, 58(24): 2975–2978. doi: 10.1016/j.matlet.2004.04.033 [17] SEGALL M D, LINDAN P J D, PROBERT M J, et al. First-principles simulation:ideas, illustrations and the CASTEP code [J]. Journal of Physics: Condensed Matter, 2002, 14(11): 2717–2744. doi: 10.1088/0953-8984/14/11/301 [18] VANDERBILT D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism [J]. Physical Review B, 1990, 41(11): 7892–7895. doi: 10.1103/PhysRevB.41.7892 [19] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Physical Review Letters, 1996, 77(18): 3865–3868. doi: 10.1103/PhysRevLett.77.3865 [20] PERDEW J P, CHEVARY J A, VOSKO S H, et al. Atoms, molecules, solids, and surfaces:Applications of the generalized gradient approximation for exchange and correlation [J]. Physical Review B, 1992, 46(11): 6671–6687. doi: 10.1103/PhysRevB.46.6671 [21] PFROMMER B G, COTE M, LOUIE S G, et al. Relaxation of crystals with the quasi-Newton method [J]. Journal of Computational Physics, 1997, 131(1): 233–240. doi: 10.1006/jcph.1996.5612 [22] MONKHORST H J, PACK J D. Special points for Brillouin-zone integrations [J]. Physical Review B, 1976, 13(12): 5188–5192. doi: 10.1103/PhysRevB.13.5188 [23] WALLACE D C. Thermodynamics of crystals [M]. New York: Wiley, 1972: 582. [24] WANG J, LI J, YIP S, et al. Mechanical instabilities of homogeneous crystals [J]. Physical Review B, 1995, 52(17): 12627–12635. doi: 10.1103/PhysRevB.52.12627 [25] BARRON T H K, KLEIN M L. Second-order elastic constants of a solid under stress [J]. Proceedings of the Physical Society, 1965, 85(3): 523–532. doi: 10.1088/0370-1328/85/3/313 [26] BIRCH F. Finite elastic strain of cubic crystals [J]. Physical Review, 1947, 71(11): 809–824. doi: 10.1103/PhysRev.71.809 [27] ZHAO Z L, BAO K, LI D, et al. Nitrogen concentration driving the hardness of rhenium nitrides [J]. Scientific Reports, 2014, 4(1): 4797. [28] WATT J P. Hashin-Shtrikman bounds on the effective elastic moduli of polycrystals with orthorhombic symmetry [J]. Journal of Applied Physics, 1979, 50(10): 6290–6295. doi: 10.1063/1.325768 [29] HILL R. The elastic behaviour of a crystalline aggregate [J]. Proceedings of the Physical Society, Section A, 1952, 65(5): 349. doi: 10.1088/0370-1298/65/5/307 [30] PUGH S F.XCII Relations between the elastic moduli and the plastic properties of polycrystalline pure metals [J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1954, 45(367): 823–843. doi: 10.1080/14786440808520496 [31] FRANTSEVICH I N, VORONOV F F, BOKUTA S A. Elastic constants and elastic moduli of metals and insulators [M]. Kiev: Naukova Dumka, 1983: 60–180. [32] IVANOVSKII A L. Microhardness of compounds of rhenium with boron, carbon, and nitrogen [J]. Journal of Superhard Materials, 2012, 34(2): 75–80. doi: 10.3103/S1063457612020013 [33] TIAN Y J, XU B, ZHAO Z S. Microscopic theory of hardness and design of novel superhard crystals [J]. International Journal of Refractory Metals and Hard Materials, 2012, 33: 93–106. doi: 10.1016/j.ijrmhm.2012.02.021 -







 下载:
下载: