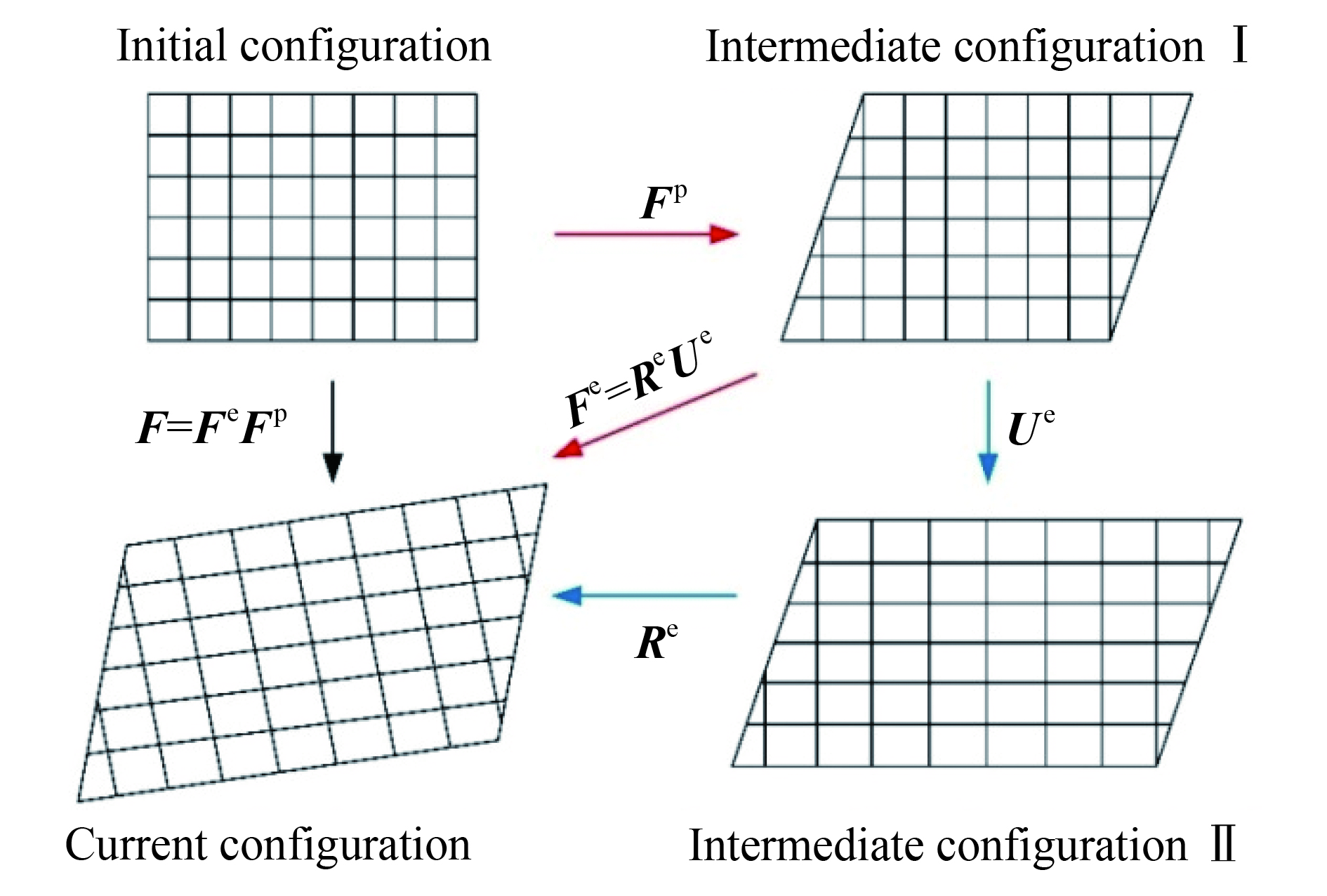
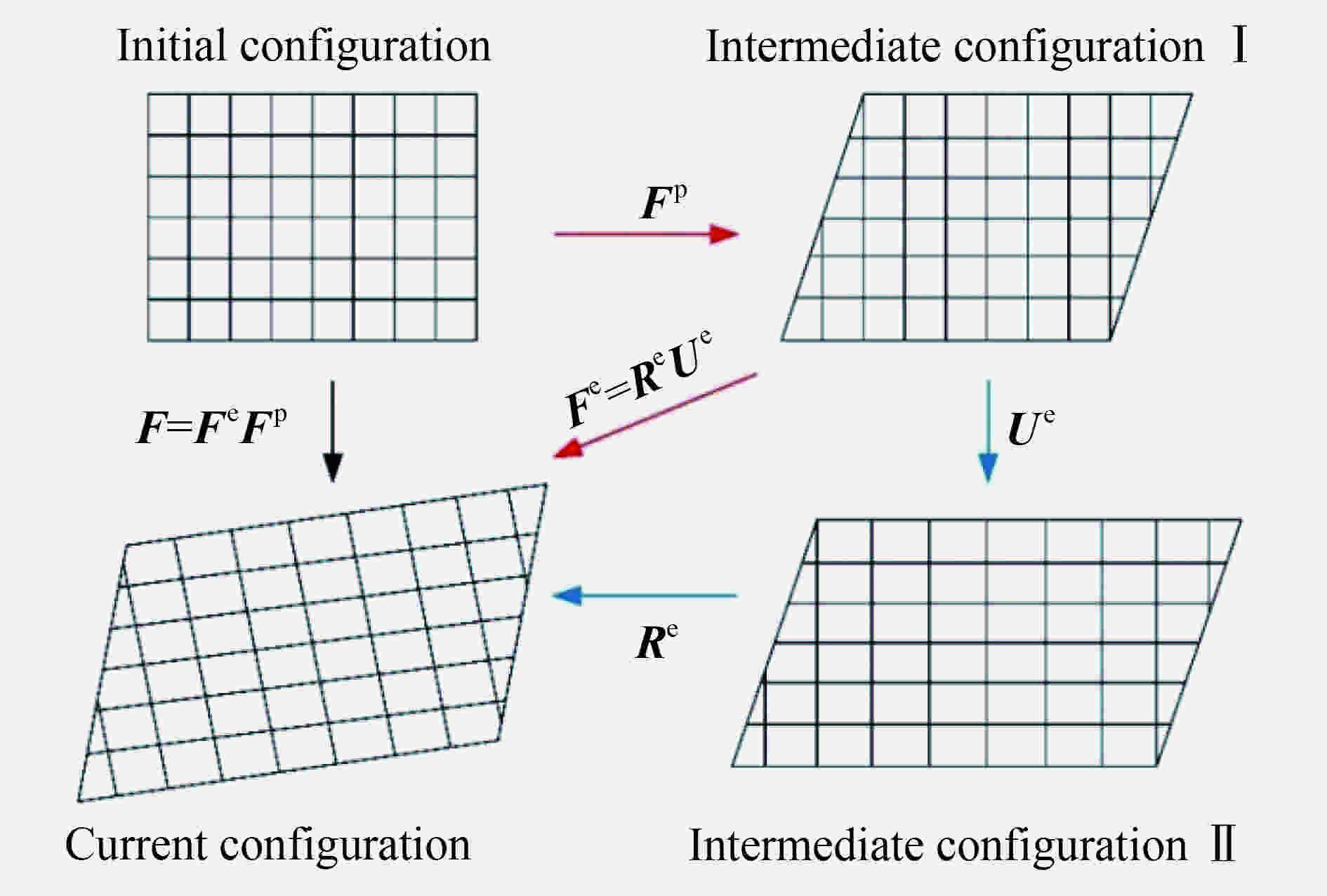
Crystal Plasticity Finite Element Simulation of High-Rate Shock Deformation Process of <100> LiF
-
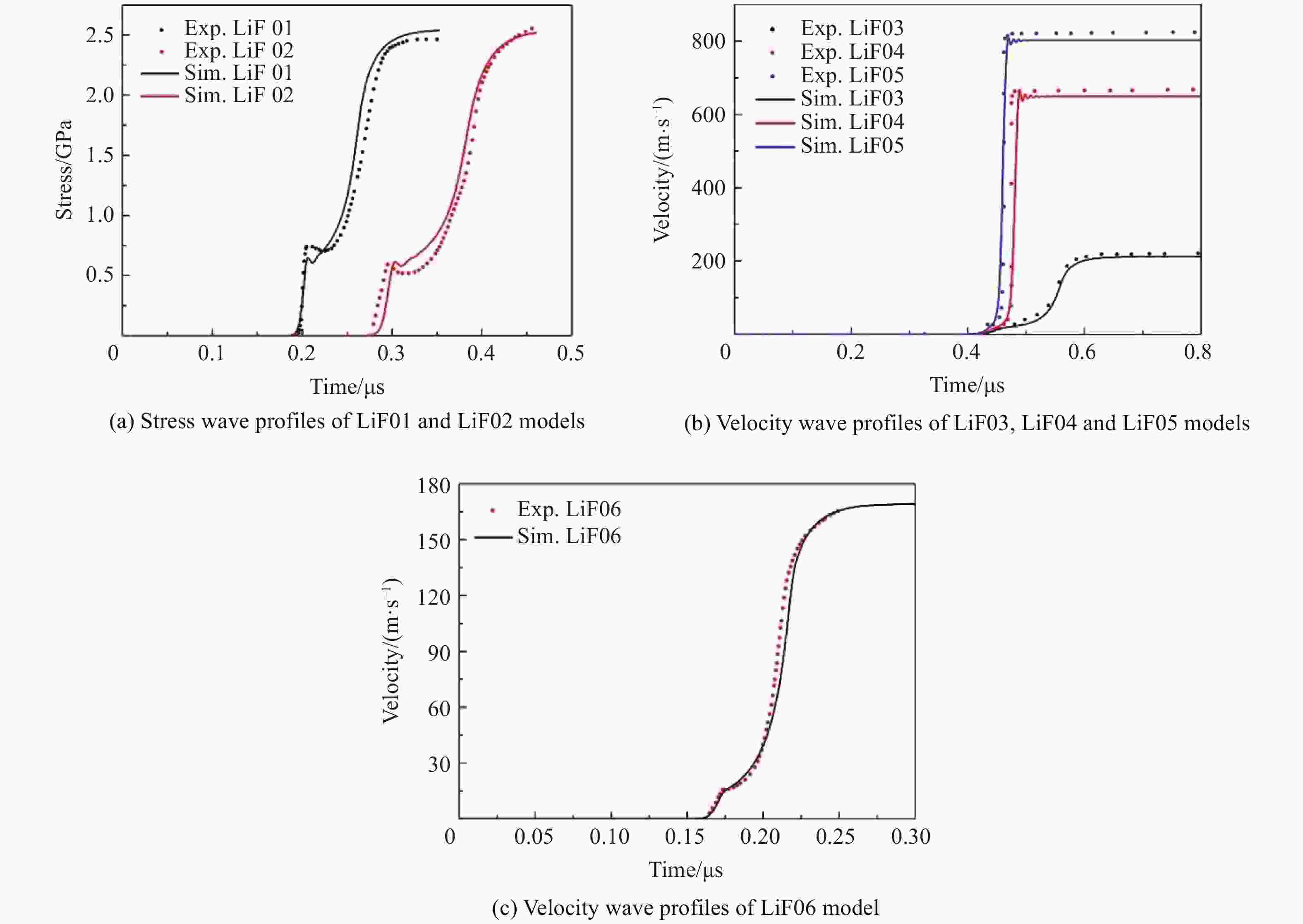
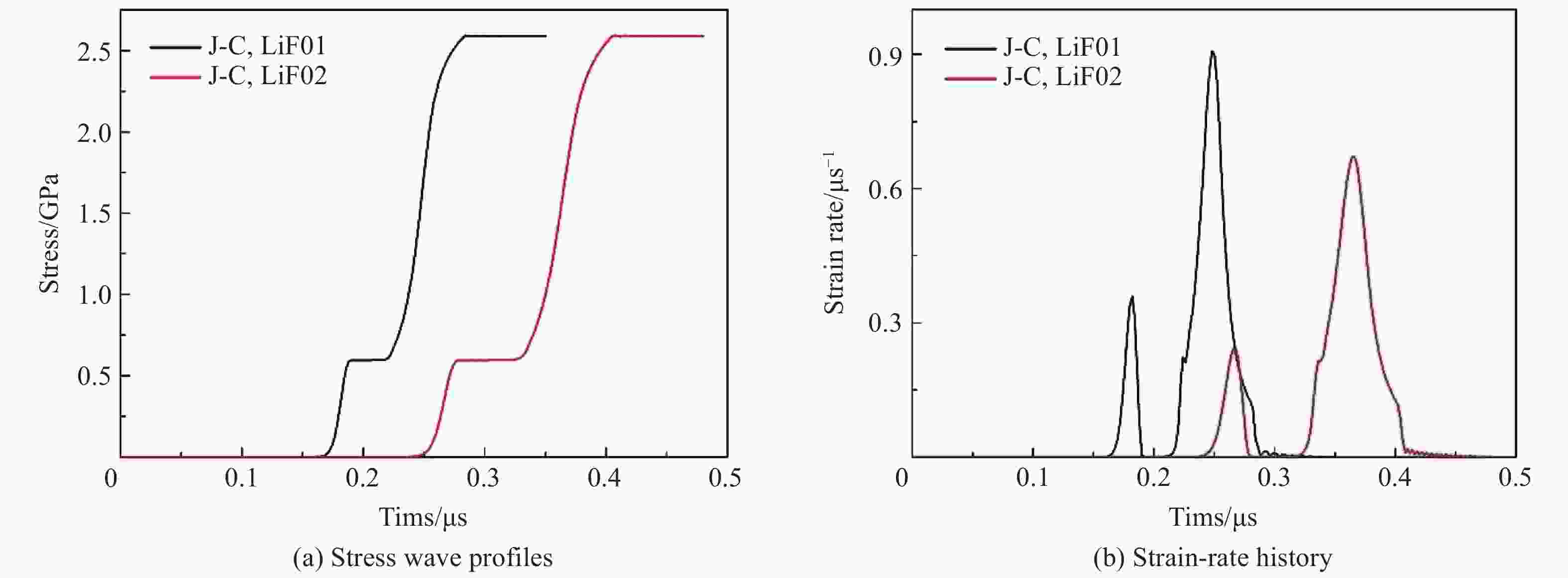
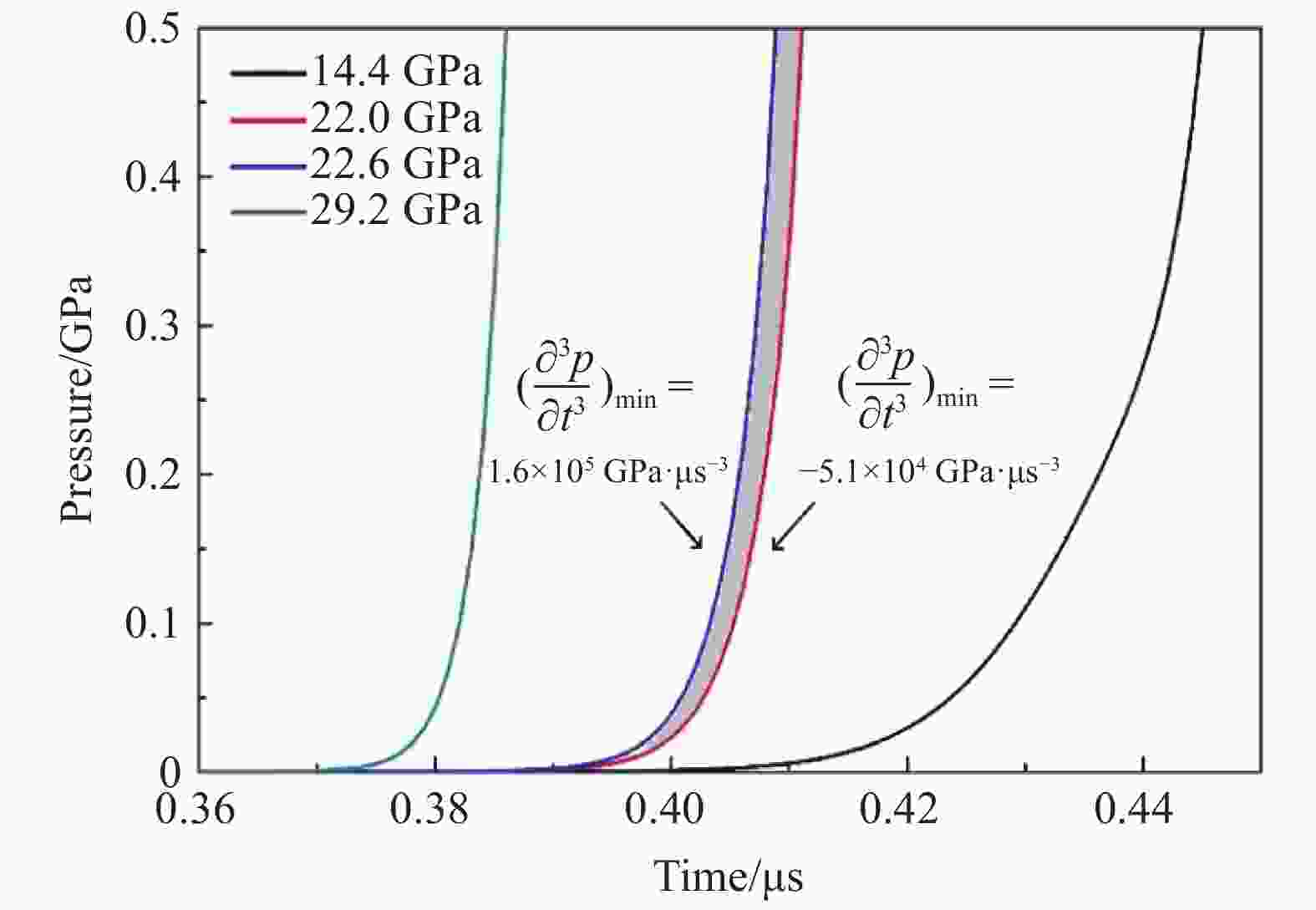
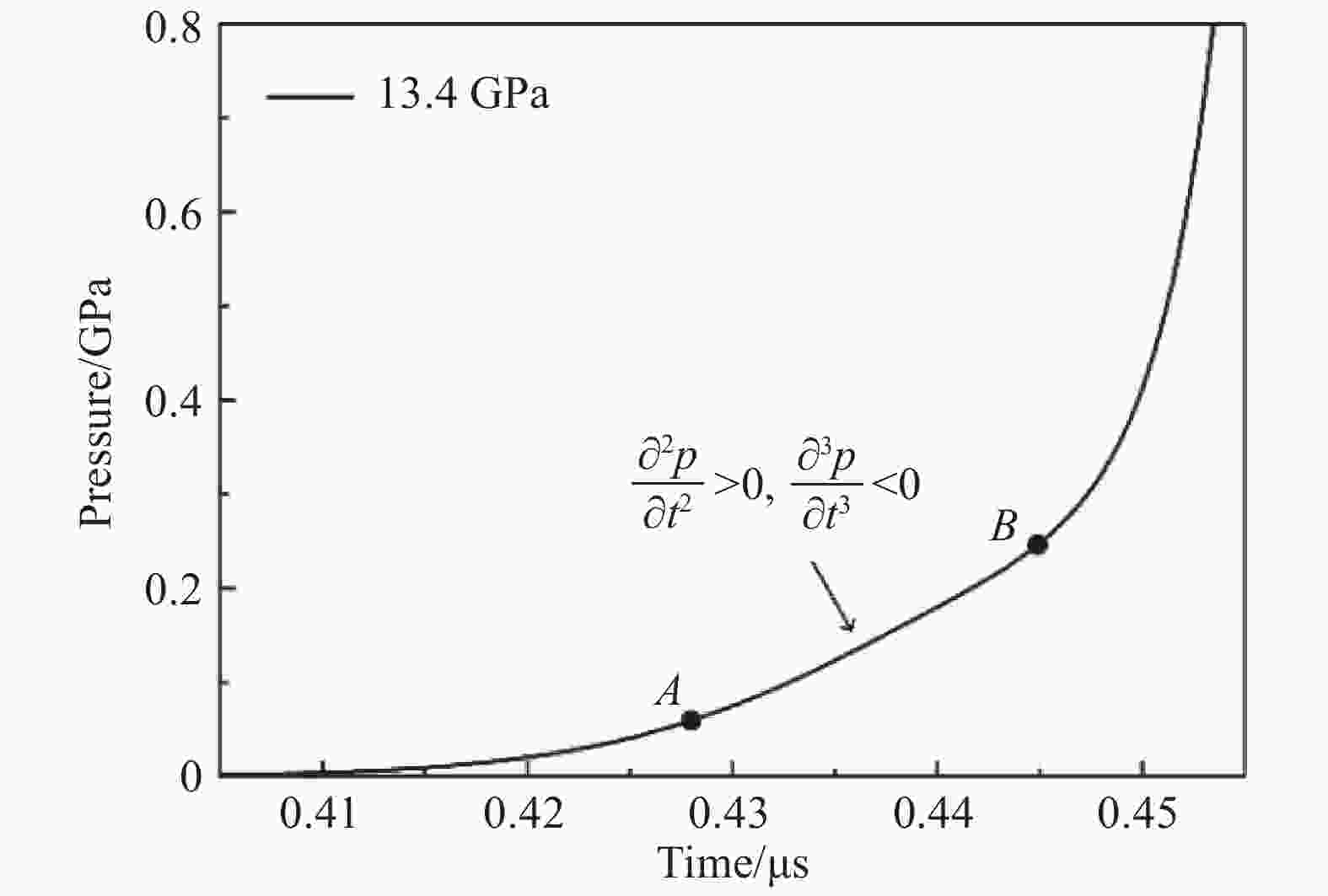
摘要: 结合状态方程建立晶体塑性有限元模型，模拟高速冲击加载条件下<100> LiF的动态弹塑性大变形行为，得到应力波剖面特征、动态力学演化规律及其连续介质力学根源。结果表明：毫米级样品经约15 GPa以内的低压冲击，波剖面具有弹塑性双波响应、弹性前驱衰减和应力松弛现象，其决定性因素包括样品厚度、外加压力和材料本构；从连续介质力学角度分析得到,应力松弛本质上是由于黏性塑性流动，导致总应变增速小于塑性应变增速，从而使弹性应变减小、压力降低；提出用压力关于时间的三阶导数大于零作为判断条件，对应力波剖面上双波和单波响应的临界压力进行估测，发现随着样品掺杂浓度的增加，临界压力增大；高速冲击变形的温升效应不可忽略，且温升绝大部分来自弹性体积变形的贡献。Abstract: A crystal plasticity finite element model combined with equation of state was built to simulate the dynamic elastic-plastic large deformation behavior of <100> LiF under high-rate shock loading. The characterization of the stress wave profile, the patterns of the dynamic mechanical evolution and their essential causes in view of the continuum mechanics were obtained through simulations, with the following results achieved: (1) the wave profiles of millimeter-sized specimens exhibit elastic-plastic two-wave response, elastic precursor decay and stress relaxation below 15 GPa; (2) in view of continuum mechanics, the stress relaxation is essentially due to the viscous plastic flow which accounts for the increase rate of the total strain being less than that of the plastic strain, and which further reduces the elastic strain and pressure; (3) the third derivative of pressure to time being greater than zero was proposed as a criterion for estimating the critical pressure of the two-wave and the one-wave response of the stress wave profile, and the estimation result indicated that the critical pressure increased with the increase of the doping concentration in specimen; (4) the effect of temperature rise during the high-rate shock deformation is non-negligible, and the elastic volumetric deformation contributes to most of the temperature rise.
-
Key words:
- LiF /
- crystal plasticity /
- equation of state /
- stress relaxation /
- two-wave response
-
图 3 CPFEM模拟的<100> LiF波剖面与实验的比对结果
Figure 3. Comparison of wave profiles of <100> LiF from CPFEM simulations and experiments
图 4 加载条件和样品厚度相同、样品掺杂浓度不同（LiF11～LiF13，掺杂浓度依次减小）时模拟的应力波剖面
Figure 4. Stress wave profiles from models with same loading condition, specimen thickness and different doping concentrations (LiF11–LiF13, with doping concentration decreasing in order)
图 5 采用Johnson-Cook本构方程对LiF01、LiF02模型的模拟结果
Figure 5. Simulation results of LiF01 and LiF02 models using Johnson-Cook constitutive equation
图 6 LiF03、LiF04、LiF05和LiF12双波和 单波响应的临界压力
Figure 6. Critical pressure of two-wave and one-wave response of LiF03–LiF05 and LiF12 models
图 7 模拟LiF03、LiF04、LiF05和LiF12在13.4 GPa压力下的双波响应
Figure 7. Two-wave response of LiF03–LiF05 and LiF12 models under 13.4 GPa pressure by simulation
图 8 模拟LiF03、LiF04、LiF05、LiF12在0～40 GPa 冲击压力范围内温度随压力的响应
Figure 8. Temperature responding to pressure ranging from 0 to 40 GPa of LiF03–LiF05 and LiF12 models by simulation
表 1 模拟中采用的模型信息
Table 1. Model information in simulations
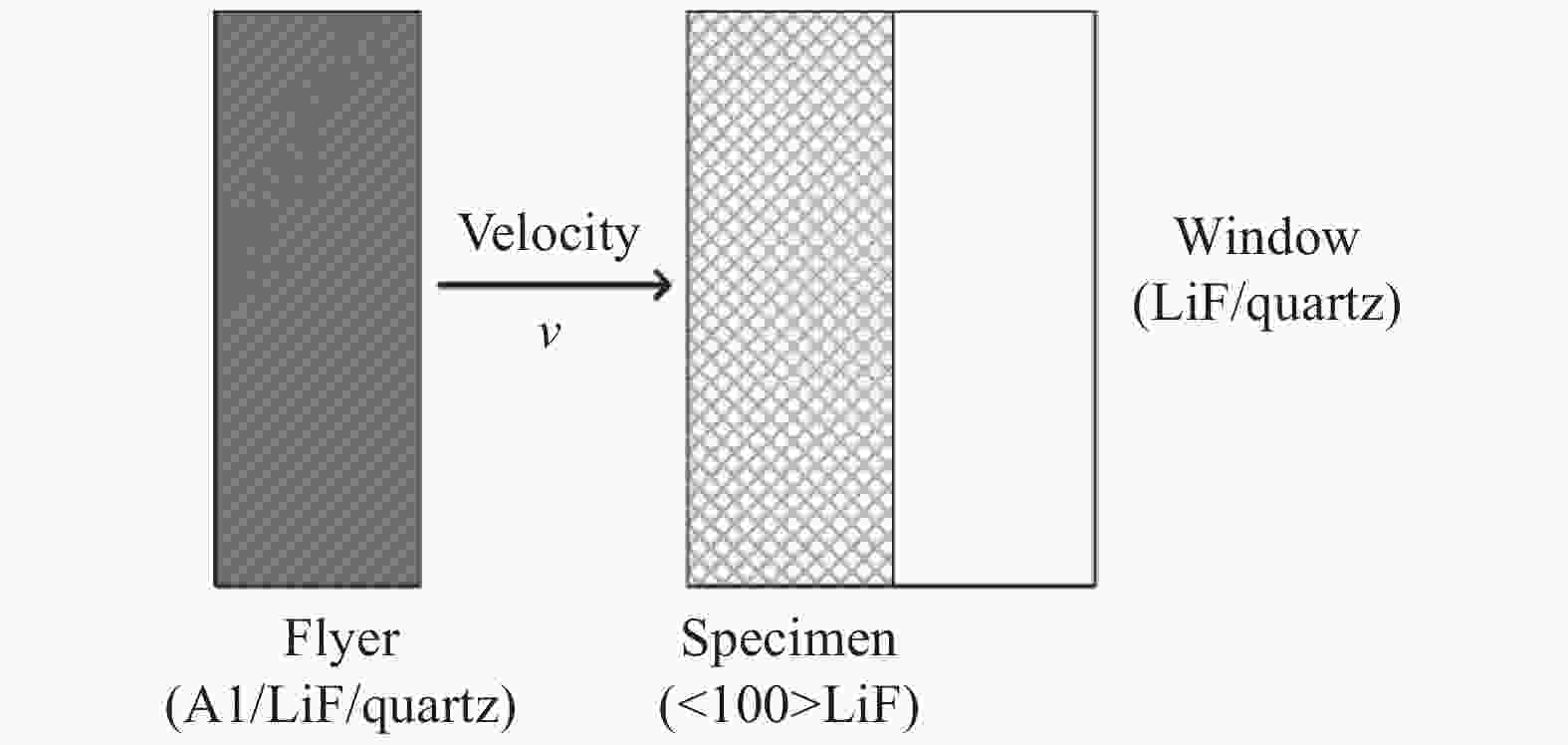
Sample No. Flyer material Window material v/(m·s–1) Sample’s thickness/mm Ref. LiF01 Al Quartz 340.0 1.35 [6] LiF02 Al Quartz 340.0 1.98 [6] LiF03 LiF LiF 423.8 3.0 [17] LiF04 LiF LiF 1 321.6 3.0 [17] LiF05 LiF LiF 1 641.5 3.0 [17] LiF06 Fused sillica Fused sillica 340.9 1.143 [18] LiF11, LiF12, LiF13 LiF LiF 340.0 3.0 Note: LiF01–LiF06 models were built based on the parameters of specimens and experiments in references, while LiF11–
LiF13 models were designed for comparison of profile characteristic differences with successively increased specimen
doping concentration.
下载: 导出CSV
表 2 <100> LiF的超弹性本构参数
Table 2. Hyperelastic constitutive parameters of <100> LiF
Subscript Cij/GPa $\dfrac{{{\rm{d}}{{C}_{ij}}}}{{{\rm{d}}{p}}}$ $\dfrac{{{\rm{d}}{{C}_{ij}}}}{{{\rm{d}}{T}}}/(\rm MPa \cdot K^{-1})$ K0/GPa $ K_0^{\prime}$ ρ0/(g·cm–3) cV/(J·kg–1·K–1) Γm 11 113.97 9.97 –75.56 69.97 4.43 2.64 1 612.02 1.68 12 47.67 2.73 –28.39 44 63.64 1.38 –13.94
下载: 导出CSV
表 3 <100> LiF的晶体塑性本构参数
Table 3. Crystal plasticity constitutive parameters of <100> LiF
Sample No. τ0/MPa B n ${\dot \gamma _{{\rm{off}}}}$/μs–1 ${\dot \gamma _{\rm{0}}}$/μs–1 m λ $\dfrac{{{\tau _{\rm T}}}}{\theta}/{\rm μs}^{-1}$ LiF01, LiF02, LiF11 121.0 4.0 0.08 3.5×10–9 0.12 0.09 4.7×10–2 0.15 LiF03, LiF04, LiF05, LiF12 113.9 0.30 LiF06, LiF13 86.4 0.40
下载: 导出CSV
-
[1] 王礼立, 胡时胜, 杨黎明, 等. 材料动力学 [M]. 合肥:中国科学技术大学出版社, 2017: 7-9, 111-113. [2] 经福谦. 实验物态方程导引 [M]. 2版. 北京: 科学出版社, 1999: 7-26. [3] BECKER R. Effects of crystal plasticity on materials loaded at high pressures and strain rates [J]. International Journal of Plasticity, 2004, 20(11): 1983–2006. doi: 10.1016/j.ijplas.2003.09.002 [4] DE S, ZAMIRI A R. A fully anisotropic single crystal model for high strain rate loading conditions with an application to α-RDX [J]. Journal of the Mechanics and Physics of Solids, 2014, 64: 287–301. doi: 10.1016/j.jmps.2013.10.012 [5] GILMAN J J. Plastic anisotropy of LiF and other rocksalt-type crystals [J]. Acta Metallurgica, 1959, 7(9): 608–613. doi: 10.1016/0001-6160(59)90130-0 [6] ASAY J R, FOWLES G R, DURALL G E, et al. Effects of point defects on elastic precursor decay in LiF [J]. Journal of Applied Physics, 1972, 43(5): 2132–2145. doi: 10.1063/1.1661464 [7] ROSENBERG G, DUVALL G E. Precursor amplitudes in LiF from shocks propagating in <111> directions [J]. Journal of Applied Physics, 1980, 51(1): 319–330. doi: 10.1063/1.327375 [8] WINEY J M, GUPTA Y M. Nonlinear anisotropic description for the thermomechanical response of shocked single crystals: inelastic deformation [J]. Journal of Applied Physics, 2006, 99(2): 023510. doi: 10.1063/1.2161414 [9] ASARO R J. Micromechanics of crystals and polycrystals [J]. Advances in Applied Mechanics, 1983, 23(8): 1–115. [10] HOGER A. The stress conjugate to logarithmic strain [J]. International Journal of Solids and Structures, 1987, 23(12): 1645–1656. doi: 10.1016/0020-7683(87)90115-6 [11] 黄克智. 固体本构关系 [M]. 北京: 清华大学出版社, 1999: 205-208. [12] LEMAITRE J, CHABOCHE J L. Mechanics of solids materials [M]. Cambrige: Cambridge University Press, 1990: 311-313. [13] ASARO R J, RICE J R. Strain localization in ductile single crystals [J]. Journal of the Mechanics and Physics of Solids, 1977, 25(5): 309–338. doi: 10.1016/0022-5096(77)90001-1 [14] KUMAR A, HAUSER F E, DORN J E. Viscous drag on dislocations in aluminum at high strain rates [J]. Acta Metallurgica, 1968, 16(9): 1189–1197. doi: 10.1016/0001-6160(68)90054-0 [15] STEINBERG D J, COCHRAN S G, GUINAN M W. A constitutive model for metals applicable at high-strain rate [J]. Journal of Applied Physics, 1980, 51(3): 1498–1504. doi: 10.1063/1.327799 [16] NEMAT-NASSER S, GUO W G, KIHL D P. Thermomechanical response of AL-6XN stainless steel over a wide range of strain rates and temperatures [J]. Journal of the Mechanics and Physics of Solids, 2001, 49(8): 1823–1846. doi: 10.1016/S0022-5096(00)00069-7 [17] 李雪梅, 俞宇颖, 张林, 等. <100>LiF的低压冲击响应和1 550 nm波长下的窗口速度修正 [J]. 物理学报, 2012, 61(15): 156202 doi: 10.7498/aps.61.156202LI X M, YU Y Y, ZHANG L, et al. Elastic-plastic response of shocked (100) LiF and its window correction at 1 550 nm wavelength [J]. Acta Physica Sinica, 2012, 61(15): 156202 doi: 10.7498/aps.61.156202 [18] ASAY J R, HICKS D L, HOLDRIDGE D B. Comparison of experimental and calculated elastic-plastic wave profiles in LiF [J]. Journal of Applied Physics, 1975, 46(10): 4316–4322. doi: 10.1063/1.321454 [19] MILLER R A, SMITH C S. Pressure derivatives of the elastic constants of LiF and NaF [J]. Journal of Physics and Chemistry of Solids, 1964, 25(12): 1279–1292. doi: 10.1016/0022-3697(64)90043-5 [20] 于锦泉, 肖亚斌, 周显明, 等. 冲击压缩下单晶 LiF 高压声速及卸载路径研究 [J]. 高压物理学报, 2005, 19(3): 206–212 doi: 10.3969/j.issn.1000-5773.2005.03.003YU J Q, XIAO Y B, ZHOU X M, et al. Study on sound velocity and unloading path for single crystal LiF under shock compression [J]. Chinese Journal of High Pressure Physics, 2005, 19(3): 206–212 doi: 10.3969/j.issn.1000-5773.2005.03.003 [21] ANDERSSON S, BACKSTROM G. Thermal conductivity and heat capacity of single-crystal LiF and CaF2 under hydrostatic pressure [J]. Journal of Physics C: Solid State Physics, 1987, 20(35): 5951. doi: 10.1088/0022-3719/20/35/011 [22] NELDER J A, MEAD R. A simplex method for function minimization [J]. The Computer Journal, 1965, 7(4): 308–313. doi: 10.1093/comjnl/7.4.308 [23] YAO S L, PEI X Y, YU J D, et al. A dislocation-based explanation of quasi-elastic release in shock-loaded aluminum [J]. Journal of Applied Physics, 2017, 121(3): 035101. doi: 10.1063/1.4974055 [24] NEWTON M D, O'KEEFFE M, GIBBS G V. Ab initio calculation of interatomic force constants in H6Si2O7 and the bulk modulus of α quartz and α cristobalite [J]. Physics and Chemistry of Minerals, 1980, 6(4): 305–312. doi: 10.1007/BF00307620 [25] GRAHAM R A. Shock-wave compression of x-cut quartz as determined by electrical response measurements [J]. Journal of Physics and Chemistry of Solids, 1974, 35(3): 355–372. doi: 10.1016/S0022-3697(74)80029-6 [26] RAMMO N N, FARID S B. Thermal expansion coefficients and Grüneisen parameters of quartz at high temperature by X-ray method [J]. Powder Diffraction, 1994, 9(2): 148–150. doi: 10.1017/S0885715600014147 [27] MEADE C, JEANLOZ R. Frequency-dependent equation of state of fused silica to 10 GPa [J]. Physical Review B, 1987, 35(1): 236. doi: 10.1103/PhysRevB.35.236 [28] BOGARDUS E H. Third-order elastic constants of Ge, MgO, and fused SiO2 [J]. Journal of Applied Physics, 1965, 36(8): 2504–2513. doi: 10.1063/1.1714520 [29] JOHNSON J N, JONES O E, MICHAELS T E. Dislocation dynamics and single-crystal constitutive relations: shock-wave propagation and precursor decay [J]. Journal of Applied Physics, 1970, 41(6): 2330–2339. doi: 10.1063/1.1659227 [30] DING J L, ASAY J R, AO T. Modeling of the elastic precursor behavior and dynamic inelasticity of tantalum under ramp wave loading to 17 GPa [J]. Journal of Applied Physics, 2010, 107(8): 083508. doi: 10.1063/1.3373388 -
下载:
点击查看大图
计量
- 文章访问数: 8684
- HTML全文浏览量: 3018
- PDF下载量: 52
