Influence of Plexiglass-Air Interlayer Structure on Foundation Vibration of Small Pool Underwater Explosion
-
摘要: 为了研究有机玻璃-空气层结构对水下爆炸振动的影响, 采用NUBOX-6016爆破振动测试仪监测小水池(直径5.5 m、高3.62 m)中该结构下水下爆炸引起的地基振动信号, 研究不同空气层厚度对最大振动速度的影响; 基于Matlab软件编写相关程序对测得的振动信号进行Hilbert-Huang变换(HHT), 分析不同空气层厚度对振动信号全局频率的影响。结果表明:对于有机玻璃-空气层结构, 随着空气层厚度的增加, 最大振动速度呈先减小后增大的趋势, 当空气层厚度为120 mm时隔振效果最佳; 通过对振动信号的HHT分析得到全局频率所对应的幅值, 5~15 Hz低频区间段的幅值衰减较明显, 且振动作用时间缩短, 能够有效防止水下爆炸与建/构筑物之间产生共振现象。所得试验结果及分析对水下爆破工程防护及军事舰艇防雷仓结构设计等具有一定参考价值。
-
关键词:
- 水下爆炸 /
- 有机玻璃-空气层结构 /
- 爆炸振动 /
- Hilbert-Huang变换
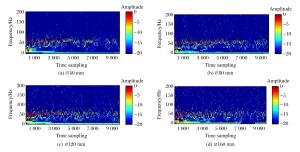
Abstract: To study the influence of the plexiglass-air interlayer structure on underwater explosion vibration, the foundation vibration signals for this structure caused by underwater explosion in the small pool (5.5 m in diameter and 3.62 m in height), the influence of different air interlayer thicknesses on the maximum vibration velocity was studied, HHT (Hilbert-Huang Transform) was used to analyze the vibration test signals by writing relevant programs based on Matlab software, studying the influence of different air interlayer thickness on the global frequency of vibration signals.Experimental results show that:under the condition of plexiglass-air interlayer structure, with the increase of air interlayer thickness, the maximum vibration velocity decreases first and then increases, and the vibration isolation effect is the best when the thickness is 120 mm.The amplitude corresponding to the global frequency can be obtained by means of HHT analysis, the amplitude attenuation of the 5-15 Hz low frequency section is obvious, the action time is shortened, which can effectively prevent the resonance phenomenon between the building and structure.The experimental results and analysis have certain theoretical reference value for underwater blasting engineering protection and structural design of lightning protection bunker for military ship. -
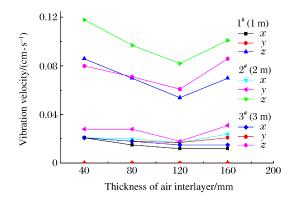
表 1 不同距离、不同厚度空气层对水下爆炸振动的影响
Table 1. Influence of distances and thickness of air interlayer on underwater explosion vibration
Distance/m Direction Main vibration frequency/Hz Maximum vibration velocity/(cm·s-1) ∅40 mm ∅80 mm ∅120 mm ∅160 mm ∅40 mm ∅80 mm ∅120 mm ∅160 mm 1 z 56.763 56.763 56.763 56.763 0.086 0.070 0.054 0.070 2 z 56.763 56.763 56.763 44.556 0.118 0.097 0.082 0.101 3 z 56.763 56.763 56.763 56.763 0.080 0.071 0.061 0.086 表 2 不同距离、不同厚度水隔层对水下爆炸振动的影响
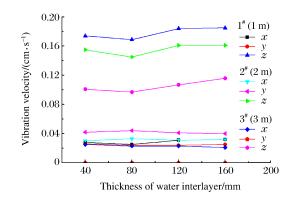
Table 2. Influence of distances and thickness of water interlayer on underwater explosion vibration
Distance/m Direction Main vibration frequency/Hz Maximum vibration velocity/(cm·s-1) ∅40 mm ∅80 mm ∅120 mm ∅160 mm ∅40 mm ∅80 mm ∅120 mm ∅160 mm 1 z 62.256 62.256 62.256 56.763 0.086 0.169 0.184 0.185 2 z 62.256 62.256 62.256 62.256 0.155 0.145 0.160 0.161 3 z 62.256 62.256 62.256 62.256 0.101 0.097 0.107 0.116 表 3 信号经EMD分解后相关参数
Table 3. Related parameters of the signal by EMD decomposition
IMF Variance Proportion/% C1 0 1.646 3 C2 0 0.862 9 C3 0 0.626 8 C4 0.000 1 70.307 9 C5 0 20.200 7 C6 0 2.208 9 C7 0 1.254 8 C8 0 1.081 4 C9 0 1.719 6 C10 0 0.015 0 C11 0 0.060 6 C12 0 0.015 0 -
[1] 库尔·P. 水中爆炸[M]. 罗耀杰, 等译. 北京: 国防工业出版社, 1960.COLE P. Underwater explosion[M]. Translated by LUO Y J, et al. Beijing: National Defense Industry Press, 1960. [2] RAJENDRAN R, LEE J M.Blast loaded plates[J].Marine Structures, 2009, 22(2):99-127. doi: 10.1016/j.marstruc.2008.04.001 [3] 张社荣, 孔源, 王高辉.水下和空中爆炸冲击波传播特性对比分析[J].振动与冲击, 2014, 33(13):148-153. http://www.cnki.com.cn/Article/CJFDTotal-ZDCJ201413027.htmZHANG S R, KONG Y, WANG G H.Comparative analysis on propagation characteristics of shock wave induced by underwater and air explosions[J].Journal of Vibration and Shock, 2014, 33(13):148-153. http://www.cnki.com.cn/Article/CJFDTotal-ZDCJ201413027.htm [4] 高建华, 陆林, 何洋扬.浅水中爆炸及其破坏效应[M].北京:国防工业出版社, 2010.Gao J H, LU L, HE Y Y.Explosion and its damage effect in shallow water[M].Beijing:National Defense Industry Press, 2010. [5] WANG G H, ZHANG S R, YU M, et al.Investigation of the shock wave propagation characteristics and cavitation effects of underwater explosion near boundaries[J].Applied Ocean Research, 2014, 46(2):40-53. https://www.sciencedirect.com/science/article/pii/S014111871400011X [6] PETROV N V, SCHMIDT A A.Multiphase phenomena in underwater explosion[J].Experimental Thermal and Fluid Science, 2015, 60:367-373. doi: 10.1016/j.expthermflusci.2014.05.008 [7] 樊自建, 沈兆武, 马宏昊, 等.空气隔层对水中冲击波衰减效果的实验研究[J].中国科学技术大学学报, 2007, 37(10):1306-1311. doi: 10.3969/j.issn.0253-2778.2007.10.025FAN Z J, SHEN Z W, MA H H, et al.Experimental study on attenuation of underwater shock wave by air interlayer[J].Journal of University of Science and Technology of China, 2007, 37(10):1306-1311. doi: 10.3969/j.issn.0253-2778.2007.10.025 [8] 贾虎, 郑伟花, 罗强, 等.爆炸气泡帷幕对水中冲击波能量的衰减特性[J].含能材料, 2015, 23(10):1015-1019. doi: 10.11943/j.issn.1006-9941.2015.10.018JIA H, ZHENG W H, LUO Q, et al.Attenuation characteristics of underwater explosion bubble curtain on the shock[J].Chinese Journal of Energetic Materials, 2015, 23(10):1015-1019. doi: 10.11943/j.issn.1006-9941.2015.10.018 [9] 贾虎, 沈兆武.空气隔层对水中冲击波的衰减特性[J].爆炸与冲击, 2012, 32(1):61-66. doi: 10.11883/1001-1455(2012)01-0061-06JIA H, SHEN Z W.An investigation into attenuation of underwater shockwave by air interlayer[J].Explosion and Shock Waves, 2012, 32(1):61-66. doi: 10.11883/1001-1455(2012)01-0061-06 [10] 寇晓枫, 王高辉, 卢文波, 等.空气隔层对水下爆炸冲击波的缓冲效应[J].振动与冲击, 2017, 36(3):7-13. http://d.old.wanfangdata.com.cn/Periodical/zdycj201703002KOU X F, WANG G H, LU W B, et al.Mitigation effects of air interlayer on underwater explosion shock wave[J].Journal of Vibration and Shock, 2017, 36(3):7-13. http://d.old.wanfangdata.com.cn/Periodical/zdycj201703002 [11] 姚熊亮, 杨文山, 初文华, 等.水中空气隔层衰减冲击波性能研究[J].高压物理学报, 2011, 25(2):165-172. doi: 10.11858/gywlxb.2011.02.013YAO X L, YANG W S, CHU W H, et al.Research on performance of the underwater air buffer weakening shock wave[J].Chinese Journal of High Pressure Physics, 2011, 25(2):165-172. doi: 10.11858/gywlxb.2011.02.013 [12] 姚熊亮, 刘文韬, 张阿漫, 等.水下爆炸气泡及其对结构毁伤研究综述[J].中国舰船研究, 2016, 11(1):36-45. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjcyj201601006YAO X L, LIU W T, ZHANG A M, et al.Review of the research on underwater explosion bubbles and the corresponding structural damage[J].Chinese Journal of Ship Research, 2016, 11(1):36-45. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjcyj201601006 [13] 刘欣, 顾文彬, 陈学平.气泡帷幕对水中冲击波衰减特性的数值模拟研究[J].爆破, 2015, 32(3):79-84. doi: 10.3963/j.issn.1001-487X.2015.03.014LIU X, GU W B, CHEN X P.Numerical simulation study of attenuation characteristics of water shock wave under bubble curtain[J].Blasting, 2015, 32(3):79-84. doi: 10.3963/j.issn.1001-487X.2015.03.014 [14] 汤有富, 汪泉, 朱恺波, 等.基于HHT变换的小水池水下爆炸振动分析[J].工程爆破, 2017, 23(1):29-33.TANG Y F, WANG Q, ZHU K B, et al.Underwater explosion vibration analysis based on HHT transform in small pond[J].Engineering Blasting, 2017, 23(1):29-33. [15] 张义平. 爆破震动信号的HHT分析与应用研究[D]. 长沙: 中南大学, 2006.ZHANG Y P. HHT analysis and its application of blasting vibration signals[D]. Changsha: Central South University, 2006. [16] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C]//Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. The Royal Society, 1998, 454(1971): 903-995. [17] PENG Z K, PETER W T, CHU F L.An improved Hilbert-Huang transform and its application in vibration signal analysis[J].Journal of Sound and Vibration, 2005, 286(1):187-205. https://www.sciencedirect.com/science/article/pii/S0022460X04007928 [18] 张立, 汪大立.水下爆炸炸药能测量消除边界效应的研究[J].爆破器材, 1995(2):1-6.ZHANG L, WANG D L.A study on elimination of boundary effects in underwater explosion testing of explosive[J].Explosive Materials, 1995(2):1-6. -







 下载:
下载: