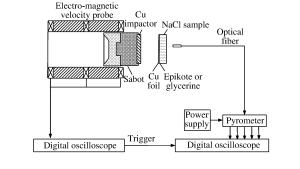
Simultaneous Measurement of Sound Velocity and Temperature of Single Crystal NaCl under Shock Loading
-
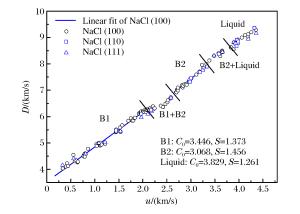
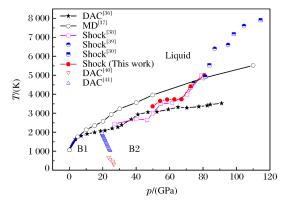
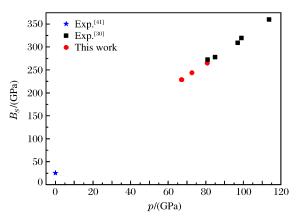
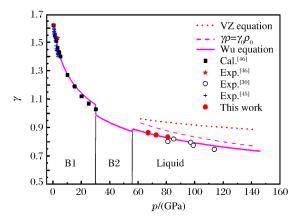
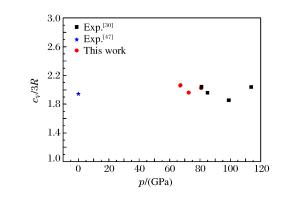
摘要: 基于二级轻气炮和多通道辐射高温计,测量了45~85 GPa压力范围内NaCl单晶的B2相区、B2-液相混合相区和液相区的高压声速和温度。通过高压声速数据,确定了NaCl单晶的冲击熔化压力区间为58~67 GPa。当压力为67 GPa时,NaCl单晶的冲击熔化温度为3 740 K。计算了NaCl单晶的等熵体模量、Grüneisen系数和定容比热容,对比分析了多种模型对Grüneisen系数高压演化特性的描述。结果显示,根据吴强模型计算的Grüneisen系数不但在液相区与冲击压缩实验结果吻合得非常好,而且在低压区也与金刚石压砧实验结果及有限应变计算结果吻合得非常好。
-
关键词:
- 冲击加载 /
- NaCl /
- 声速 /
- 冲击温度 /
- Grüneisen系数
Abstract: Based on a two-stage light gas gun and a multi-channel time-resolved pyrometer, we simultaneously measured the shock temperatures and sound velocities of B2, B2-liquid and liquid phase NaCl single crystal in the pressure range from 45 GPa to 85 GPa.According to these sound velocities, the shock melting pressure region was determined to be 58-67 GPa, and the shock melting point obtained was 3 740 K at 67 GPa.Furthermore, we calculated the isentropic bulk modulus, the Grüneisen parameter, and the specific heat capacity under constant pressure and compared the experimental results with the previously published data.The Grüneisen parameter calculated by Wuqiang model has an excellent agreement with both the shock compression experiment data in the liquid region and the diamond anvil cell experiment data and the finite strain theory calculation results in the low pressure region.-
Key words:
- shock loading /
- NaCl /
- sound velocity /
- shock temperature /
- Grüneisen parameter
-
表 1 实验参数
Table 1. Experimental parameters
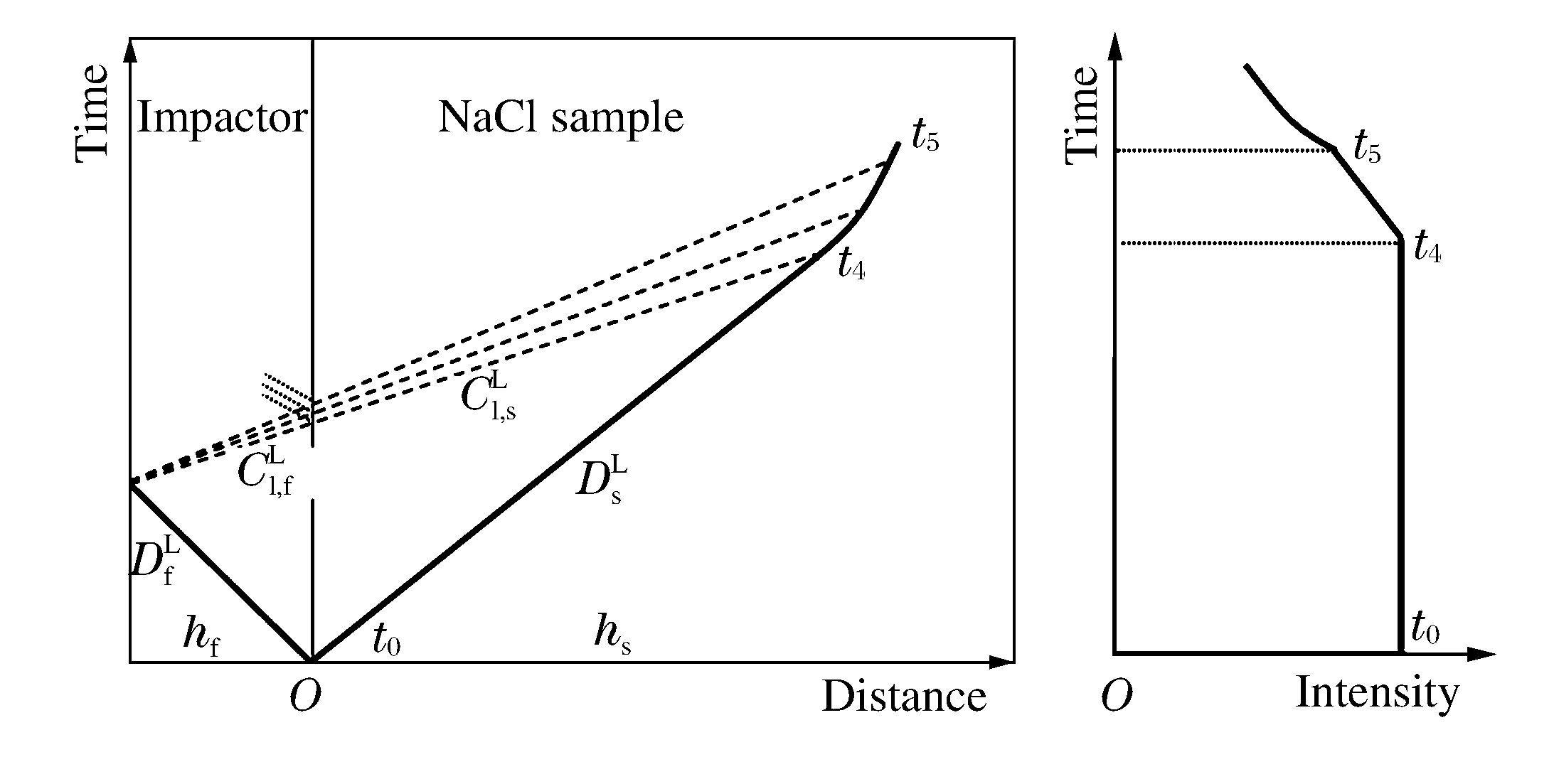
Exp.No. w/(km/s) hf/(mm) hs/(mm) NaCl-01 4.537 1.186±0.001 10.038±0.010 NaCl-03 5.218 1.216±0.001 10.035±0.005 NaCl-04 4.943 1.217±0.001 10.001±0.006 NaCl-05 4.945 1.218±0.001 10.055±0.003 NaCl-06 5.605 1.218±0.001 10.070±0.002 NaCl-07 4.754 1.242±0.001 10.041±0.005 NaCl-08 4.320 1.231±0.001 10.031±0.012 NaCl-09 4.079 1.240±0.001 10.103±0.010 表 2 NaCl的高压声速实验结果
Table 2. High pressure sound velocity measurement results of NaCl
Exp.No. w/(km/s) p/(GPa) Cl, sL/(km/s) Cl, sE/(km/s) CbE/(km/s) δCbE/(%) NaCl-01 4.537 58.5 13.993±0.385 7.970±0.224 NaCl-03 5.218 72.6 14.230±0.335 7.915±0.200 7.954 0.5 NaCl-04 4.943 67.0 13.656±0.317 7.735±0.180 7.758 0.3 NaCl-05 4.945 67.1 13.654±0.317 7.733±0.179 7.775 0.6 NaCl-06 5.605 80.8 15.013±0.361 8.150±0.194 8.201 0.6 NaCl-07 4.754 62.8 13.882±0.379 7.909±0.219 NaCl-08 4.320 54.3 13.310±0.379 7.779±0.219 NaCl-09 4.079 49.8 12.874±0.341 7.639±0.202 表 3 NaCl的冲击温度实验结果
Table 3. Shock temperature measurement results of NaCl
Exp.No. w/(km/s) p/(GPa) T/(K) ε δT/(%) NaCl-01 4.537 58.5 3 724 0.24 12.7 NaCl-03 5.218 72.6 4 420 1.00 5.8 NaCl-04 4.943 67.0 3 742 0.95 8.2 NaCl-05 4.945 67.1 3 738 0.96 5.0 NaCl-06 5.605 80.8 5 000 0.92 9.5 NaCl-07 4.754 62.8 3 735 0.30 13.5 NaCl-08 4.320 54.3 3 649 0.36 9.0 NaCl-09 4.079 49.8 3 366 0.41 8.5 表 4 液相区NaCl的等熵体模量和Grüneisen系数
Table 4. Isentropic bulk modulus and Grüneisen parameter of liquid NaCl
Exp.No. p/(GPa) BS/(GPa) γ δγ/(%) This study (Eq.(10)) Wu model (Eq.(20)) NaCl-03 72.6 243.8 0.851 0.827 2.8 NaCl-04 67.0 228.7 0.865 0.841 2.8 NaCl-05 67.1 228.6 0.868 0.841 3.1 NaCl-06 80.8 264.9 0.841 0.810 3.7 -
[1] LIU L, BASSETT W A.Compression of Ag and phase transformation of NaCl[J]. J Appl Phys, 1973, 44(4):1475-1479. doi: 10.1063/1.1662396 [2] SATA N, SHEN G, RIVERS M L, et al.Pressure-volume equation of state of the high-pressure B2 phase of NaCl[J]. Phys Rev B, 2002, 65(10):104114. doi: 10.1103/PhysRevB.65.104114 [3] ONO S, KIKEGAWA T, OHISHI Y.Structural property of CsCl-type sodium chloride under pressure[J]. Solid State Commun, 2006, 137(10):517-521. doi: 10.1016/j.ssc.2006.01.022 [4] FEI Y W, RICOLLEAU A, FRANK M, et al.Toward an internally consistent pressure scale[J]. Proc Natl Acad Sci, 2007, 104(22):9182-9186. doi: 10.1073/pnas.0609013104 [5] FROYEN S, COHEN M L.Structural properties of NaCl[J]. Phys Rev B, 1984, 29(6):3770-3772. doi: 10.1103/PhysRevB.29.3770 [6] HEMLEY R J, GORDON R G.Theoretical study of solid NaF and NaCl at high pressures and temperatures[J]. J Geophys Res, 1985, 90(B9):7803-7813. doi: 10.1029/JB090iB09p07803 [7] ZHANG H Y, BUKOWINSKI M S T.Modified potential-induced-breathing model of potentials between close-shell ions[J]. Phys Rev B, 1991, 44(6):2495-2503. doi: 10.1103/PhysRevB.44.2495 [8] RECIO J M, PENDÁS A M, FRANCISCO E, et al.Low- and high-pressure ab initio equations of state for the alkali chlorides[J]. Phys Rev B, 1993, 48(9):5891-5901. doi: 10.1103/PhysRevB.48.5891 [9] FELDMAN J L, MEHL M J, KRAKAUER H.Sodium chloride structural properties:linearized augmented-plane-wave calculations and pressure calibration[J]. Phys Rev B, 1987, 35(12):6395-6398. doi: 10.1103/PhysRevB.35.6395 [10] BUKOWINSKI M S T, AIDUN J.First principles versus spherical ion models of the B1 and B2 phases of NaCl[J]. J Geophys Res, 1985, 90(B2):1794-1800. doi: 10.1029/JB090iB02p01794 [11] DECKER D L.High-pressure equation of state for NaCl, KCl, and CsCl[J]. J Appl Phys, 1971, 42(8):3239-3244. doi: 10.1063/1.1660714 [12] BROWN J M.The NaCl pressure standard[J]. J Appl Phys, 1999, 86(10):5801-5808. doi: 10.1063/1.371596 [13] ONO S, BRODHOLT J P, ALFÈ D, et al.Ab initio molecular dynamics simulations for thermal equation of state of B2-type NaCl[J]. J Appl Phys, 2008, 103(2):023510. doi: 10.1063/1.2832632 [14] UEDA Y, MATSUI M, YOKOYAMA A, et al.Temperature-pressure-volume equation of state of the B2 phase of sodium chloride[J]. J Appl Phys, 2008, 103(11):113513. doi: 10.1063/1.2939254 [15] BIRCH F.Finite strain isotherm and velocities for single-crystal and polycrystalline NaCl at high pressures and 300 K[J]. J Geophys Res, 1978, 83(B3):1257-1268. doi: 10.1029/JB083iB03p01257 [16] 吴强.金属材料高压状态方程及Grüneisen系数的研究[D].绵阳: 中国工程物理研究院, 2004. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y662944 [17] 王金贵.冲击压缩性的高精度测量技术[J].高压物理学报, 1995, 9(4):289-295. http://www.gywlxb.cn/CN/abstract/abstract983.shtmlWANG J G.An accrate measurement technique for shock Hugoniot[J]. Chinese Journal of High Pressure Physics, 1995, 9(4):289-295. http://www.gywlxb.cn/CN/abstract/abstract983.shtml [18] MITCHELL A C, NELLIS W J.Shock compression of aluminum, copper, and tantalum[J]. J Appl Phys, 1981, 52(5):3363-3374. doi: 10.1063/1.329160 [19] CHHABILDAS L C, ASAY J R.Time-resolved wave profile measurements in copper to megabar pressures: SAND-81-1358C[R]. Albuquerque: Sandia National Labs, 1981: 183. http://adsabs.harvard.edu/abs/1981aira.conf.....C [20] MORRIS C E, FRITZ J N, HOLIAN B.Quasi-elastic high pressure waves in 2024 A1 and Cu[C]//Shock Waves in Condensed Matter-1981.New York: American Institute of Physics, 1982: 382-386. [21] BROBERG K B.弹性及弹-塑性介质中的冲击波[M].尹祥础, 译.北京: 科学出版社, 1965: 21. [22] HAYES D, HIXSON R S, MCQUEEN R G.High pressure elastic properties, solid-liquid phase boundary and liquid equation of state from release wave measurements in shock-loaded copper[C]//Shock Compression of Condensed Matter-1999.New York: American Institute of Physics, 2000: 483-488. https://digital.library.unt.edu/ark:/67531/metadc723353/ [23] 宋萍.无氧铜的高压卸载研究[D].绵阳: 中国工程物理研究院, 2003. http://cdmd.cnki.com.cn/Article/CDMD-82818-2003113016.htm [24] MARSH S P.LASL shock Hugoniot data[M]. Berkeley:University of Califonia Press, 1980:335. [25] SCHMITT D R, AHRENS T J, SVENDSEN B.Shock-induced melting and shear banding in single-crystal NaCl[J]. J Appl Phys, 1988, 63(1):99-106. doi: 10.1063/1.340469 [26] FRITZ J N, MARSH S P, CARTER W J, et al.The Hugoniot equation of state of sodium chloride in the sodium chloride[C]//Accurate Characterization of the High-pressure Environment.Washington D C: National Bureau of Standards Publications, 1968: 201. [27] FRANKEL J, RICH F J, HOMAN C G.Acoustic velocities in polycrystalline NaCl at 300 K measured at static pressures from 25 to 270 kbar[J]. J Geophys Res, 1976, 81(35):6357-6363. doi: 10.1029/JB081i035p06357 [28] VORONOV F F, GRIGOREV S B.Velocity of sound in cesium chloride and sodium chloride at pressures up to 100 kbars[J]. Sov Phys Dokl, 1971, 15:1126. http://adsabs.harvard.edu/abs/1971SPhD...15.1126V [29] ПАВЛОВСКUǓ M N.Измерения скоростм звука в ударно-сЖатых кварците, доломите, ангидрите, полиэтилене и фторопласте-4[J]. Z Prik Mek TeK, 1976, 17:136. [30] BONESS D A, BROWN J M.Time-resolved optical spectroscopy of shock-compressed fluid alkali halides[C]//Shock Compression of Condensed Matter-1989.New York: American Institute of Physics, 1989: 863-866. [31] SLATER J C.Introduction to chemical physics[M]. New York:McGraw-Hill, 1939. [32] DUGDALE J S, MACDONALD D K C.The thermal expansion of solids[J]. Phys Rev, 1953, 89(4):832-834. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_0904.4015 [33] VASCHENKO V Y, ZUBAREV V N.Concerning the Grüneisen constant[J]. Sov Phys Solid State, 1963, 5:653-655. [34] ANDERSON O L.Evidence supporting the approximation γρ=const for the Grüneisen parameter of the Earth's lower mantle[J]. J Geophys Res, 1979, 84(B7):3537-3542. doi: 10.1029/JB084iB07p03537 [35] MORRIS C E, JAMIESON J C, YARGER F L.Ultrasonic measurements at elevated pressures (9 GPa) to determine Poisson's ratio and other elastic moduli of NaCl and NaF[J]. J Appl Phys, 1976, 47(9):3979-3986. doi: 10.1063/1.323220 [36] BOEHLER R, ROSS M, BOERCKER D B.Melting of LiF and NaCl to 1 Mbar:systematics of ionic solids at extreme conditions[J]. Phys Rev Lett, 1997, 78(24):4589-4592. doi: 10.1103/PhysRevLett.78.4589 [37] AN Q, ZHENG L Q, FU R S, et al.Solid-liquid transitions of sodium chloride at high pressures[J]. J Chem Phys, 2006, 125(15):154510. doi: 10.1063/1.2357737 [38] KORMER S B.Optical study of the characteristics of shock-compressed condensed dielectrics[J]. Sov Phys-Uspekhi, 1968, 11(2):229-254. doi: 10.1070/PU1968v011n02ABEH003814 [39] AHRENS T J.Temperatures induced by shock waves in minerals: applications to geophysics[C]//High Pressure Research in Geophysics.Tokyo: Center for Academic Publications, 1982: 579-594. https://core.ac.uk/display/33118044 [40] LI X Y, JEANLOZ R.Measurement of the B1-B2 transition pressure in NaCl at high temperatures[J]. Phys Rev B, 1987, 36(1):474-479. doi: 10.1103/PhysRevB.36.474 [41] NISHIYAMA N, KATSURA T, FUNAKOSHI K, et al.Determination of the phase boundary between the B1 and B2 phases in NaCl by in situ X-ray diffraction[J]. Phys Rev B, 2003, 68(13):134109. doi: 10.1103/PhysRevB.68.134109 [42] RADOUSKY H B, ROSS M, MITCHELL A C, et al.Shock temperatures and melting in CsI[J]. Phys Rev B, 1985, 31(3):1457-1462. doi: 10.1103/PhysRevB.31.1457 [43] SWENSON C A, SHANER J W, BROWN J M.Hugoniot overtake sound-velocity measurements on CsI[J]. Phys Rev B, 1986, 34(11):7924-7935. doi: 10.1103/PhysRevB.34.7924 [44] MCQUEEN R G.Laboratory technique for very high pressures and the behavior of metals under dynamic loading[C]//Conference on Metallurgy at High Pressure.New York: Gordon and Breach, 1964: 44. https://www.osti.gov/biblio/4013771/ [45] BOEHLER R, GETTING I C, KENNEDY G C.Grüneisen parameter of NaCl at high compressions[J]. J Phys Chem Solids, 1977, 38(3):233-236. doi: 10.1016-0022-3697(77)90095-6/ [46] BIRCH F.Equation of state and thermodynamic parameters of NaCl to 300 kbar in the high-temperature domain[J]. J Geophys Res, 1986, 91(B5):4949-4954. doi: 10.1029/JB091iB05p04949 [47] BROWN J M.The NaCl pressure standard[J]. J Appl Phys, 1999, 86(10):5801-5808. doi: 10.1063/1.371596 -






 下载:
下载: