Dynamic Mechanical Behavior of Concrete with Different Sizes of Interface Transition Zone
-
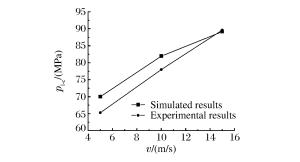
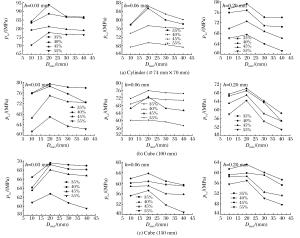
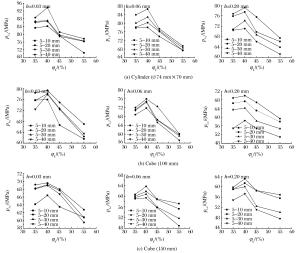
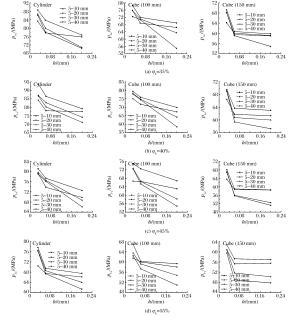
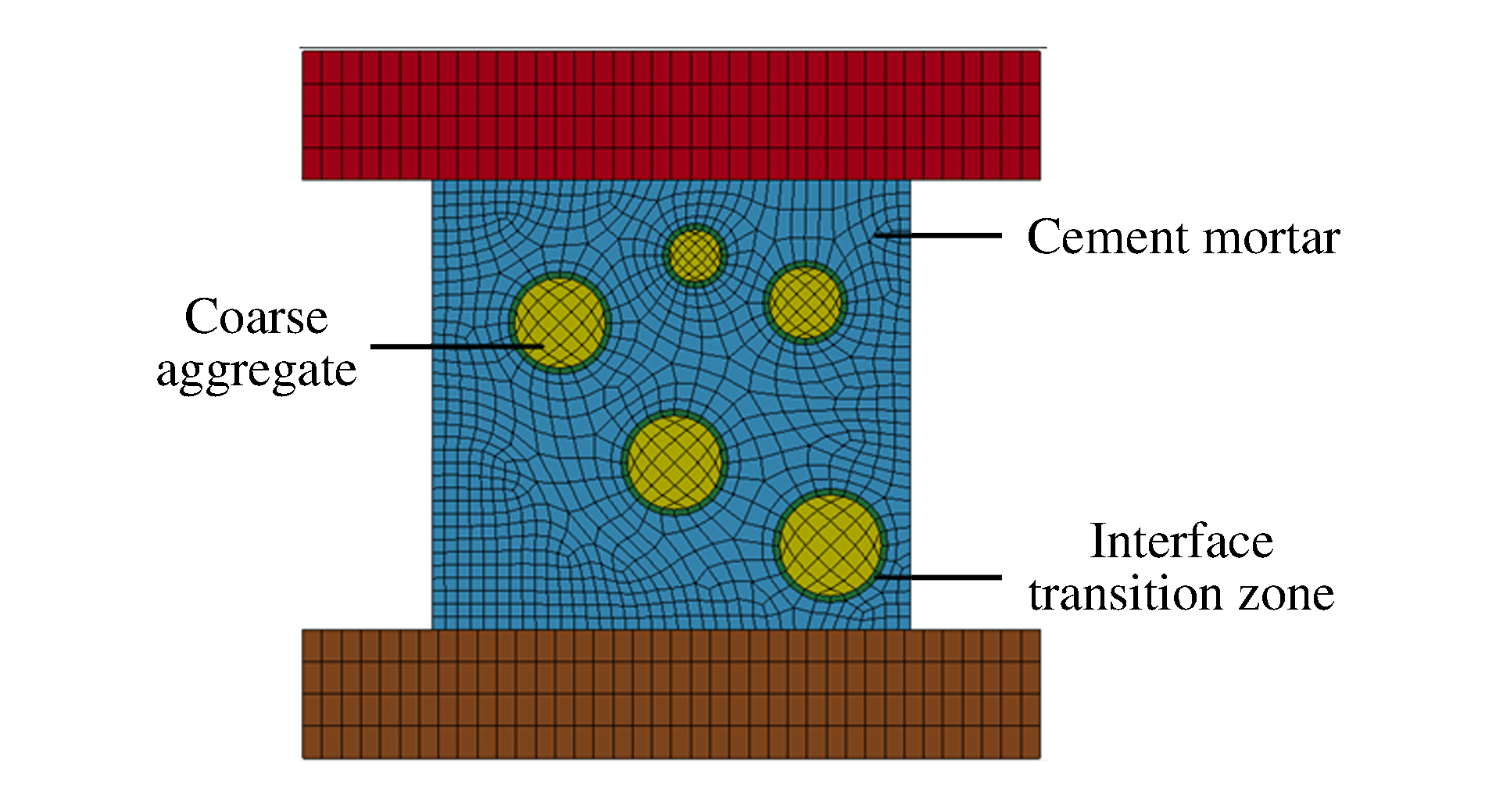
摘要: 在细观层次上，可将混凝土看作由水泥砂浆、粗骨料和界面相组成的三相复合材料。为探讨界面相对混凝土动态力学特性的影响，编写了含界面相的圆形骨料随机分布程序，并对具有不同界面相厚度的混凝土动态破坏过程进行模拟，揭示界面相厚度、粗骨料大小、粗骨料体积分数和试件尺寸对混凝土动态特性的影响规律。研究表明：与普通混凝土相同，含界面相的混凝土表现出明显的尺寸效应；随着界面相厚度的增大，混凝土承载能力逐渐减小；保持界面相厚度和粗骨料尺寸不变时，随着粗骨料体积分数的增加，混凝土承载能力呈先增大后减小趋势；保持粗骨料最小粒径和界面相厚度不变时，随着粗骨料最大粒径的增大，混凝土承载能力呈先增大后减小趋势。Abstract: From a micromechanical point of view, concrete was considered as a three-phase composite composed of cement mortar, coarse aggregate and interface transition zone (ITZ) between them.In order to study the influence of ITZ on the dynamic mechanical behavior of concrete, we designed a two dimensional circular coarse aggregate random distribution program to simulate the dynamic failure process of concrete with different ITZ sizes, and analyzed the influences of the ITZ size, the specimen size, and the particle size and the volume fraction of coarse aggregate on the load-carrying capacity of concrete.Numerical simulation showed that the concrete with different ITZ sizes has an obvious size effect.The load-carrying capacity of the concrete with different ITZ sizes decreases with the size of ITZ.When the ITZ size and the particle size of the coarse aggregate are kept unchanged, the load-carrying capacity of the concrete increases at first and then decreases with the volume fraction of the coarse aggregate; when the minimum particle diameter of the coarse aggregate and the ITZ size are kept constant, the load-carrying capacity of the concrete increases at first and then decreases with the increase of the maximum particle diameter of the coarse aggregate.
-
图 3 在15 m/s的冲击速度下混凝土破坏模式的数值模拟结果与实验结果
Figure 3. Experimental and simulated failure modes of concrete at impact speed of 15 m/s
图 4 界面相厚度不同的混凝土冲击破坏过程
Figure 4. Impact failure process of concrete with different ITZ sizes
图 5 混凝土承载能力与粗骨料最大粒径的关系
Figure 5. Load-carrying capacity of concrete vs.maximum particle diameter of coarse aggregate
图 6 混凝土承载能力与粗骨料体积分数的关系
Figure 6. Load-carrying capacity of concrete vs.volume fraction of coarse aggregate
表 1 模型参数
Table 1. Model parameters
Material ρ0/(g/cm3) G/(GPa) fc′/(MPa) A B C N Smax p1/(MPa) pc/(MPa) K1/(MPa) K2/(MPa) K3/(MPa) D1 D2 εf，min μ1 μc T/(MPa) fs Cement mortar 2.10 10.66 32 0.79 1.80 0.007 0.61 7 700 10.67 85 -171 208 0.04 1.0 0.01 0.10 0.0007 2.656 0.002 Interface phase 2.40 7.25 19 0.79 1.80 0.007 0.61 7 1000 6.33 85 -171 208 0.04 1.0 0.01 0.01 0.0008 1.577 0.002 Aggregate 2.60 23.00 70 0.79 1.80 0.007 0.61 7 1000 23.33 85 -171 208 0.04 1.0 0.01 0.01 0.0008 5.810 0.002 
下载: 导出CSV
表 2 粗骨料最大粒径不同的混凝土的承载能力
Table 2. Load-carrying capacity of concrete with different maximum sizes of coarse aggregate
Specimen h/(mm) D0/(mm) φk/(%) {[pl-c-pl-c(Dmax=10 mm)]/pl-c(Dmax=10 mm)}/(%) Dmax=10 mm Dmax=20 mm Dmax=30 mm Dmax=40 mm Cylinder
(Ø74 mm×70 mm)0.03 5 35
40
45
550
0
0
06.33
11.40
2.45
10.304.07
3.37
0.59
8.643.37
2.97
-0.30
8.350.06 5 35
40
45
550
0
0
07.77
10.80
4.81
3.012.87
6.07
3.67
1.700.45
2.85
3.12
-0.100.20 5 35
40
45
550
0
0
01.16
2.22
3.91
2.06-6.60
-4.30
-1.60
-0.05-7.20
-8.20
-5.30
-7.30Cube
(100 mm)0.03 5 35
40
45
550
0
0
03.55
4.50
12.50
8.93-0.20
2.88
9.13
3.17-4.40
2.50
8.72
1.460.06 5 35
40
45
550
0
0
04.65
5.81
9.00
0.323.30
4.22
-0.10
-1.302.85
3.69
-1.80
-4.600.20 5 35
40
45
550
0
0
03.66
3.85
6.00
2.38-4.50
-4.60
-7.60
-5.60-17.40
-13.20
-13.10
-12.20Cube
(150 mm)0.03 5 35
40
45
550
0
0
07.90
4.76
7.13
3.196.41
4.12
5.62
-0.106.21
3.84
5.17
-2.200.06 5 35
40
45
550
0
0
01.08
3.11
0.34
3.58-0.90
-1.70
-4.80
-6.50-1.60
-3.90
-5.20
-11.000.20 5 35
40
45
550
0
0
01.15
2.76
0.15
2.47-0.20
-2.20
-10.00
-9.70-7.24
-6.67
-12.40
-14.00
下载: 导出CSV
表 3 粗骨料体积分数不同时混凝土的承载能力
Table 3. Load-carrying capacity of concrete with various volume fractions of coarse aggregate
Specimen h/(mm) D/(mm) {[pl-c-pl-c(φk=35%)]/pl-c(φk=35%)}/(%) φk=35% φk=40% φk=45% φk=55% Cylinder
(Ø74 mm×70 mm)0.03 5-10
5-20
5-30
5-400
0
0
01.03
5.87
0.36
0.64-4.97
-8.43
-8.14
-8.32-15.43
-12.27
-11.72
-11.370.06 5-10
5-20
5-30
5-400
0
0
00.28
3.15
3.40
2.68-5.09
-7.70
-4.35
-2.57-13.26
-17.09
-14.24
-13.760.20 5-10
5-20
5-30
5-400
0
0
02.07
3.14
4.59
0.92-8.01
-5.51
-3.06
-6.16-12.84
-12.07
-6.73
-12.99Cube
(100 mm)0.03 5-10
5-20
5-30
5-400
0
0
00.22
1.15
3.29
7.50-12.11
-4.51
-3.92
-0.01-18.85
-14.64
-16.14
-13.850.06 5-10
5-20
5-30
5-400
0
0
04.29
5.44
5.22
5.14-3.31
0.71
-6.51
-7.67-12.78
-16.39
-16.69
-19.060.20 5-10
5-20
5-30
5-400
0
0
01.31
1.50
1.15
6.49-5.09
-2.95
-8.23
-0.13-12.72
-13.80
-13.77
-7.29Cube
(150 mm)0.03 5-10
5-20
5-30
5-400
0
0
03.59
0.56
1.36
1.28-1.00
-1.70
-1.73
-1.97-5.19
-9.33
-11.00
-12.670.06 5-10
5-20
5-30
5-400
0
0
02.92
4.98
2.14
0.51-2.07
-2.79
-5.90
-5.66-7.96
-5.69
-13.13
-17.170.20 5-10
5-20
5-30
5-400
0
0
03.77
5.42
1.73
4.41-1.13
-2.11
-10.97
-6.60-6.06
-4.83
-14.93
-12.91
下载: 导出CSV
表 4 界面相厚度不同的混凝土的承载能力
Table 4. Load-carrying capacity of concrete with different sizes of ITZ
Specimen φk/(%) D/(mm) {[pl-c-pl-c(h=0.03 mm)]/pl-c(h=0.03 mm)}/(%) h=0.03 mm h=0.06 mm h=0.20 mm Cylinder
(Ø74 mm×70 mm)35 5-10
5-20
5-30
5-400
0
0
0-6.67
-5.41
-7.75
-9.31-8.95
-13.38
-18.28
-18.2340 5-10
5-20
5-30
5-400
0
0
0-7.37
-7.84
-4.95
-7.48-8.02
-15.61
-14.84
-18.0045 5-10
5-20
5-30
5-400
0
0
0-6.79
-4.65
-3.94
-3.62-11.87
-10.61
-13.76
-16.3055 5-10
5-20
5-30
5-400
0
0
0-4.27
-10.60
-10.39
-11.76-6.16
-13.18
-13.66
-19.73Cube
(100 mm)35 5-10
5-20
5-30
5-400
0
0
0-9.23
-8.27
-6.08
-9.31-12.37
-12.28
-16.14
-18.2340 5-10
5-20
5-30
5-400
0
0
0-5.55
-4.37
-4.32
-7.48-11.43
-11.98
-17.87
-18.0045 5-10
5-20
5-30
5-400
0
0
0-0.15
-3.26
-8.61
-3.62-5.37
-10.85
-19.89
-16.3055 5-10
5-20
5-30
5-400
0
0
0-2.44
-10.15
-6.70
-11.76-5.76
-11.42
-13.77
-19.73Cube
(150 mm)35 5-10
5-20
5-30
5-400
0
0
0-6.41
-12.32
-12.85
-13.30-7.86
-13.63
-13.61
-19.5240 5-10
5-20
5-30
5-400
0
0
0-7.01
-8.48
-12.19
-13.96-7.69
-9.45
-13.30
-17.0345 5-10
5-20
5-30
5-400
0
0
0-7.42
-13.29
-16.55
-16.56-7.98
-13.98
-21.74
-23.3355 5-10
5-20
5-30
5-400
0
0
0-9.14
-8.80
-14.93
-17.77-8.70
-9.34
-17.42
-19.75
下载: 导出CSV
表 5 具有不同试件尺寸的混凝土的承载能力
Table 5. Load-carrying capacity of concrete with different specimen sizes
h/(mm) D/(mm) [(pl-c-pl-c, cylinder)/pl-c, cylinder]/(%) Cylinder (Ø74 mm×70 mm) Cube (100 mm) Cube (150 mm) 0.03 5-10
5-20
5-30
5-400
0
0
0-7.99
-12.17
-9.59
-7.23-20.77
-26.31
-26.55
-25.990.06 5-10
5-20
5-30
5-400
0
0
0-7.99
-12.17
-9.59
-7.23-20.77
-26.31
-26.55
-25.990.20 5-10
5-20
5-30
5-400
0
0
0-13.10
-11.71
-13.39
-17.78-20.79
-20.38
-19.07
-19.47
下载: 导出CSV
-
[1] 王政, 倪玉山, 曹菊珍, 等.冲击载荷下混凝土动态力学性能研究进展[J].爆炸与冲击, 2005, 25(6):519-527. doi: 10.3321/j.issn:1001-1455.2005.06.007WANG Z, NI Y S, CAO J Z, et al.Recent advances of dynamic mechanical behavior of concrete under impact loading[J].Explosion and Shock Waves, 2005, 25(6):519-527. doi: 10.3321/j.issn:1001-1455.2005.06.007 [2] ABRAMS D A.Effect of rate of application of load on the compressive strength of concerete[J].Int J ASTM, 1917, 17:364-377. [3] 胡时胜, 王道荣, 刘剑飞.混凝土材料动态力学性能的实验研究[J].工程力学, 2001, 18(5):115-118. doi: 10.3969/j.issn.1000-4750.2001.05.015HU S S, WANG D R, LIU J F.Experimental study of dynamic mechanical behavior of concrete[J].Engineering Mechanics, 2001, 18(5):115-118. doi: 10.3969/j.issn.1000-4750.2001.05.015 [4] 杜修力, 田瑞俊, 彭一江, 等.冲击荷载作用下混凝土抗压强度的细观力学数值模拟[J].北京工业大学学报, 2009, 35(2):213-217. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK200900160387DU X L, TIAN R J, PENG Y J, et al.Numerical simulation of concrete dynamic compressive strength under impact loading based on mesomechanics[J].Journal of Beijing University of Technology, 2009, 35(2):213-217. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK200900160387 [5] 刘传雄, 李玉龙, 吴子燕, 等.混凝土材料的动态压缩破坏机理及本构关系[J].振动与冲击, 2011, 30(5):1-5. doi: 10.3969/j.issn.1000-3835.2011.05.001LIU C X, LI Y L, WU Z Y, et al.Failure mechanism and constitutive model of a concrete material under dynamic compressive loads[J].Journal of Vibration and Shock, 2011, 30(5):1-5. doi: 10.3969/j.issn.1000-3835.2011.05.001 [6] 刘海峰, 韩莉.冲击荷载作用下混凝土动态力学性能数值模拟研究[J].固体力学学报, 2015, 36(2):145-153. http://d.old.wanfangdata.com.cn/Conference/9123914LIU H F, HAN L.Numerical simulation research on dynamic mechanical behaviors of concrete subjected to impact loading[J].Chinese Journal of Solid Mechanics, 2015, 36(2):145-153. http://d.old.wanfangdata.com.cn/Conference/9123914 [7] 刘海峰, 王亿颖, 宋建夏.沙漠砂混凝土动态力学性能数值模拟[J].水利学报, 2016, 47(4):493-500. http://d.old.wanfangdata.com.cn/Periodical/slxb201604004LIU H F, WANG Y Y, SONG J X.Numerical simulation of dynamic mechanical behaviors of desert sand concrete[J].Journal of Hydraulic Engineering, 2016, 47(4):493-500. http://d.old.wanfangdata.com.cn/Periodical/slxb201604004 [8] 刘海峰, 韩莉.二维骨料随机分布混凝土的动态力学性能数值模拟[J].高压物理学报, 2016, 30(3):191-199. http://www.gywlxb.cn/CN/abstract/abstract1870.shtmlLIU H F, HAN L.Numerical simulation of dynamic mechanical behavior of concrete with two-dimensional random distribution of coarse aggregate[J].Chinese Journal of High Pressure Physics, 2016, 30(3):191-199. http://www.gywlxb.cn/CN/abstract/abstract1870.shtml [9] 韩宇栋, 张君, 高原.粗骨料体积含量对混凝土断裂参数的影响[J].工程力学, 2013, 30(3):191-197. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QKC20132013051500037475HAN Y D, ZHANG J, GAO Y.Effect of coarse aggregate content on fracture parameters of concrete[J].Engineering Mechanics, 2013, 30(3):191-197. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QKC20132013051500037475 [10] 姜璐.界面结构特性及混凝土弹性模量预测[D].杭州: 浙江工业大学, 2005. http://cdmd.cnki.com.cn/article/cdmd-10337-2005103151.htmJIANG L.Structural characteristics of ITZ and prediction of elastic modulus of concrete[D].Hangzhou: Zhejiang University of Technology, 2005. http://cdmd.cnki.com.cn/article/cdmd-10337-2005103151.htm [11] 何锐, 嵇绍华, 黄平明, 等.粗骨料/浆体界面性能对混凝土力学性能影响的数值模拟[J].长安大学学报(自然科学版), 2015, 35(2):31-37. doi: 10.3969/j.issn.1671-8879.2015.02.006HE R, JI S H, HUANG P M, et al.Numerical simulation of the effect of interface transition zone between mortar and aggregates on the mechanics properties of concrete[J].Journal of Chang'an University (Natural Science Edition), 2015, 35(2):31-37. doi: 10.3969/j.issn.1671-8879.2015.02.006 [12] LEE K M, PARK J H.A numerical model for elastic modulus of concrete considering interfacial transition zone[J].Cem Concr Res, 2008, 38(3):396-402. doi: 10.1016/j.cemconres.2007.09.019 [13] DIAMOND S, HUANG J.The ITZ in concrete:a different view based on image analysis and SEM observations[J].Cem Concr Compos, 2001, 23(2):179-188. http://www.sciencedirect.com/science/article/pii/S0958946500000652 [14] GUINEA G V, EL-SAYED K, ROCCO C G, et al.The effect of the bond between the matrix and the aggregates on the cracking mechanism and fracture parameters of concrete[J].Cem Concr Res, 2002, 32(12):1961-1970. doi: 10.1016/S0008-8846(02)00902-X [15] 杜修力, 金浏.界面过渡区对混凝土动态力学行为影响分析[J].地震工程与工程振动, 2015, 35(1):11-19. http://www.cnki.com.cn/Article/CJFDTotal-DGGC201501002.htmDU X L, JIN L.Effect of the interfacial transition zone on the dynamic macroscopic mechanical behavior of concrete[J].Earthquake Engineering and Engineering Dynamics, 2015, 35(1):11-19. http://www.cnki.com.cn/Article/CJFDTotal-DGGC201501002.htm [16] 吕燕红.混凝土开裂在细观层次上的数值模拟研究[D].昆明: 昆明理工大学, 2013.LV Y H.Numerical simulation of concrete cracking from the micro-mechanical viewpoint[D].Kunming: Kunming University of Science and Technology, 2013. [17] FULLER W B, THOMPSON S E.The laws of proportioning concrete[J].Asian J Civil Eng Transp, 1907, 59(1):67-143. doi: 10.1002-jctb.5000531605/ [18] WALRAVEN J C, REINHARDT H W.Theory and experiments on the mechanical behaviour of cracks in plain and reinforced concrete subjected to shear loading[J].HERON, 1981, 26(1A):26-35. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=0520071206690785 [19] HOLMQUIST T J, JOHNSON G R, COOK W H.A computational constitutive model for concrete subjected to large strains, high strain rates and high pressures[C]//JACKSON N, DICKERS S.Proceedings of the 14th International Symposium on Ballistics.Quebec, Canada, 1993. [20] 曹吉星, 陈虬, 张吉萍.混凝土SHPB试验的数值模拟及应力均匀性[J].西南交通大学学报, 2008, 43(1):67-70. doi: 10.3969/j.issn.0258-2724.2008.01.013CAO J X, CHEN Q, ZHANG J P.Simulation of shpb test on concrete and uniformity of stresses[J].Journal of Southwest Jiaotong University, 2008, 43(1):67-70. doi: 10.3969/j.issn.0258-2724.2008.01.013 [21] LIU H F, NING J G.Constitutive model for concrete subjected to impact loading[J].Journal of Southeast University (English Edition), 2012, 25(12):135-140. http://en.cnki.com.cn/Article_en/CJFDTotal-DNDY201201017.htm [22] 陈志源, 李启令.土木工程材料[M].第2版.武汉:武汉理工大学出版社, 2009.CHEN Z Y, LI Q L.Civil engineering materials[M].2nd ed.Wuhan:Wuhan University of Technology Press, 2009. -
下载:
点击查看大图
图(8) / 表(5)
计量
- 文章访问数: 5444
- HTML全文浏览量: 2413
- PDF下载量: 43
