A Particle Image Velocimetry Study of Richtmyer-Meshkov Instability in a Twice-Shocked Heavy Gas Cylinder
-
摘要: 采用粒子图像测速(PIV)技术,实验研究了激波两次冲击空气环境中重气体SF6气柱的Richtmyer-Meshkov(RM)不稳定性,定量表征了流场的速度、涡量和环量。结果表明,激波首次冲击气柱后,界面演化成初始涡对,且在较长时间内涡强度的变化很小。激波二次冲击气柱后:当反射距离较小时,界面衍生出二次涡对,其旋转方向与初始涡对的旋转方向相反,强度显著小于初始涡对的强度;当反射距离较大时,则不衍生大尺度涡结构。初始涡对的环量在激波二次冲击气柱后随时间逐渐减小,说明能量逐渐由流场中的大尺度结构转移至小尺度结构。利用PIV技术得到的初始涡对和二次涡对的环量与理论模型的预测结果吻合较好。
-
关键词:
- Richtmyer-Meshkov不稳定性 /
- 二次冲击 /
- 粒子图像测速 /
- 速度场 /
- 环量
Abstract: The Richtmyer-Meshkov (RM) instability in a twice-shocked heavy gas (SF6) cylinder surrounded by ambient air is experimentally studied using the particle image velocimetry (PIV) technique, and the velocity and vorticity fields as well as the circulation of the flow are quantitatively characterized. The results show that after the first shock-interface interaction, the evolution of the interface is dominated by the formation of a primary vortex pair, whose strength undergoes little change over a relatively long time; but after a reshock, for a short endwall distance, a secondary vortex pair, with its rotation opposite to the primary vortex pair, is formed whose strength is significantly weaker than that of the primary vortex pair, while, for a long endwall distance, no large scale vortex structure is formed. The circulation of the primary vortex pair decreases over time after the reshock, which suggests that the energy is being transferred from the large scale structures to the smaller ones in the flow. The circulations of the primary and secondary vortex pairs are remarkably consistent with the predictions by the theoretical models.-
Key words:
- Richtmyer-Meshkov instability /
- reshock /
- particle image velocimetry /
- velocity field /
- circulation
-
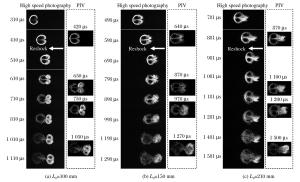
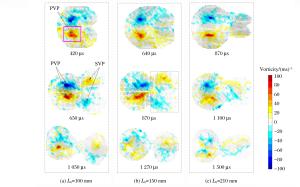
表 1 3种反射距离下PIV的测量时刻
Table 1. Times of PIV measurements for 3 endwall distances
L0/(mm) Reshock time/(μs) Times of PIV measurements/(μs) 100 450 420, 650, 750, 1 050 150 670 640, 870, 970, 1 270 210 900 870, 1 100, 1 200, 1 500 -
[1] RICHTMYER R D.Taylor instability in shock acceleration of compressible fluids[J].Commun Pur Appl Math, 1960, 13(2):297-319. doi: 10.1002/(ISSN)1097-0312 [2] MESHKOV E E.Instability of the interface of two gases accelerated by a shock wave [J].Fluid Dyn, 1969, 4(5):101-104. doi: 10.1007/BF01015969 [3] BROUILLETTE M.The Richtmyer-Meshkov instability[J].Annu Rev Fluid Mech, 2002, 34:445-468. doi: 10.1146/annurev.fluid.34.090101.162238 [4] HAAS J F, STURTEVANT B.Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities[J].J Fluid Mech, 1987, 181:41-76. doi: 10.1017/S0022112087002003 [5] JACOBS J W.Shock-induced mixing of a light-gas cylinder[J].J Fluid Mech, 1992, 234:629-649. doi: 10.1017/S0022112092000946 [6] JACOBS J W.The dynamics of shock accelerated light and heavy gas cylinders[J].Phys Fluids A, 1993, 5(9):2239-2247. doi: 10.1063/1.858562 [7] TOMKINS C, PRESTRIDGE K, RIGHTLEY P, et al.Flow morphologies of two shock-accelerated unstable gas cylinders[J].J Vis, 2002, 5(3):273-283. doi: 10.1007/BF03182335 [8] KUMAR S, ORLICZ G, TOMKINS C, et al.Stretching of material lines in shock-accelerated gaseous flows[J].Phys Fluids, 2005, 17(8):082107. doi: 10.1063/1.2031347 [9] TOMKINS C, KUMAR S, ORLICZ G, et al. An experimental investigation of mixing mechanisms in shock-accelerated flow [J].J Fluid Mech, 2008, 611(3):131-150. doi: 10.1017-S0022112008002723/ [10] KUMAR S, VOROBIEFF P, ORLICZ G, et al.Complex flow morphologies in shock-accelerated gaseous flows[J].Phys D, 2007, 235(1/2):21-28. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=bdbcdf0e0282f4b502c2c68e5b86d83b [11] ZOU L Y, LIU C L, TAN D W, et al.On interaction of shock wave with elliptic gas cylinder[J].J Vis, 2010, 13(4):347-353. doi: 10.1007/s12650-010-0053-y [12] SI T, ZHAI Z, LUO X, et al.Experimental study on a heavy-gas cylinder accelerated by cylindrical converging shock waves[J].Shock Waves, 2014, 24(1):3-9. doi: 10.1007/s00193-013-0450-y [13] PRESTRIDGE K, ORLICZ G, BALASUBRAMANIAN S, et al.Experiments of the Richtmyer-Meshkov instability[J].Phil Trans R Soc A, 2013, 371(2003):20120165. doi: 10.1098/rsta.2012.0165 [14] 陈模军, 王显圣, 翟志刚, 等.平面激波冲击柱形气体界面的实验研究[J].中国科学G辑, 2015, 45(2):024704. http://www.cnki.com.cn/Article/CJFDTotal-JGXK201502007.htmCHEN M J, WANG X S, ZHAI Z G, et al.Experimental investigation on the interaction of planar shock wave with cylindrical gaseous inhomogeneity[J].Scientia Sinica G, 2015, 45(2):024704. http://www.cnki.com.cn/Article/CJFDTotal-JGXK201502007.htm [15] ARNETT W D.Supernova theory and supernova 1987A[J].Astrophys J, 1987, 319:136-142. doi: 10.1086/165439 [16] PFALZNER S.An introduction to inertial confinement fusion[M].Boca Raton:CRC Press, 2006. [17] 王显圣, 司廷, 罗喜胜, 等.反射激波冲击重气柱的RM不稳定性数值研究[J].力学学报, 2012, 44(4):664-672. doi: 10.6052/0459-1879-11-245WANG X S, SI T, LUO X S, et al.Numerical study on the RM instability of a heavy-gas cylinder interacted with reshock[J].Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(4):664-672. doi: 10.6052/0459-1879-11-245 [18] ZHAI Z G, ZHANG F, SI T, et al.Evolution of heavy gas cylinder under reshock conditions[J].J Vis, 2014, 17(2):123-129. doi: 10.1007/s12650-014-0198-1 [19] 何惠琴, 翟志刚, 司廷, 等.反射激波作用下两种重气柱界面不稳定性实验研究[J].实验流体力学, 2014, 28(6):56-60. http://d.old.wanfangdata.com.cn/Periodical/ltlxsyycl201406008HE H Q, ZHAI Z G, SI T, et al.Experimental study on the reshocked RM instability of two kinds of heavy gas cylinder[J].Journal of Experiments in Fluid Mechanics, 2014, 28(6):56-60. http://d.old.wanfangdata.com.cn/Periodical/ltlxsyycl201406008 [20] 张赋, 翟志刚, 司廷, 等.反射激波作用下重气柱界面演化的PIV研究[J].实验流体力学, 2014, 28(5):13-17. http://d.old.wanfangdata.com.cn/Periodical/ltlxsyycl201405003ZHANG F, ZHAI Z G, SI T, et al.Experimental study on the evolution of heavy gas cylinder under reshock condition by PIV method[J].Journal of Experiments in Fluid Mechanics, 2014, 28(5):13-17. http://d.old.wanfangdata.com.cn/Periodical/ltlxsyycl201405003 [21] 廖深飞, 邹立勇, 刘金宏, 等.反射激波作用重气柱的Richtmyer-Meshkov不稳定性的实验研究[J].爆炸与冲击, 2016, 36(1):87-92. http://d.old.wanfangdata.com.cn/Periodical/bzycj201601014LIAO S F, ZOU L Y, LIU J H, et al.Experimental study of Richtmyer-Meshkov instability in a heavy gas cylinder interacting with reflected shock wave[J].Explosion and Shock Waves, 2016, 36(1):87-92. http://d.old.wanfangdata.com.cn/Periodical/bzycj201601014 [22] 邹立勇, 刘金宏, 谭多望, 等.弱激波冲击无膜重气柱和气帘界面的实验研究[J].高压物理学报, 2010, 24(4):241-247. http://www.gywlxb.cn/CN/Y2010/V24/I4/241ZOU L Y, LIU J H, TAN D W, et al.Experimental study on the membraneless heavy gas cylinder and gas curtain interfaces impacted by a weak shock wave[J].Chinese Journal of High Pressure Physics, 2010, 24(4):241-247. http://www.gywlxb.cn/CN/Y2010/V24/I4/241 [23] RIGHTLEY P M, VOROBIEFF P, BENJAMIN R F.Evolution of a shock-accelerated thin fluid layer[J].Phys Fluids, 1997, 9(6):1770-1782. doi: 10.1063/1.869299 [24] PRESTRIDGE K, RIGHTLEY P M, VOROBIEFF P, et al.Simultaneous density-field visualization and PIV of a shock-accelerated gas curtain[J].Exp Fluids, 2000, 29(4):339-346. doi: 10.1007/s003489900091 [25] RAFFEL M, WILLERT C E, KOMPENHANS J.Particle image velocimetry:a practical guide[M].2nd ed.Berlin:Springer, 2007. [26] JEONG J, HUSSAIN F.On the identification of a vortex[J].J Fluid Mech, 1995, 285:69-94. doi: 10.1017/S0022112095000462 [27] RUDINGER G, SOMERS L M.Behaviour of small regions of different gases carried in accelerated gas flows[J].J Fluid Mech, 1960, 7(2):161-176. doi: 10.1017/S0022112060001419 [28] ORLICZ G C, BALASUBRAMANIAN S, PRESTRIDGE K P.Incident shock Mach number effects on Richtmyer-Meshkov mixing in a heavy gas layer[J].Phys Fluids, 2013, 25(11):114101. doi: 10.1063/1.4827435 [29] SAMTANEY R, ZABUSKY N J.Circulation deposition on shock-accelerated planar and curved density-stratified interfaces:models and scaling laws[J].J Fluid Mech, 1994, 269(12):45-78. doi: 10.1017-S0022112094001485/ [30] BAI J S, ZOU L Y, WANG T, et al.Experimental and numerical study of shock-accelerated elliptic heavy gas cylinders[J].Phys Rev E, 2010, 82(5):056318. doi: 10.1103/PhysRevE.82.056318 [31] HAEHN N, WEBER C, OAKLEY J, et al.Experimental investigation of a twice-shocked spherical gas inhomogeneity with particle image velocimetry[J].Shock Waves, 2011, 21(3):225-231. doi: 10.1007/s00193-011-0299-x -







 下载:
下载: