自由边界影响下定向断裂爆破裂纹尖端应力分布与扩展机理

邱鹏; 岳中文

doi:10.11858/gywlxb.20240799

自由边界影响下定向断裂爆破裂纹尖端应力分布与扩展机理

doi: 10.11858/gywlxb.20240799

邱鹏^1,,
岳中文^2,*, ,

1.
太原理工大学原位改性采矿教育部重点实验室, 山西太原　030024
2.
中国矿业大学（北京）力学与土木工程学院, 北京　100083

基金项目: 国家自然科学基金（52204106，52174094）；国家重点研发计划（2021YFC2902103）；山西省基础研究面上项目（202203021211133）

详细信息

作者简介:
邱　鹏（1991－），男，博士，助理研究员，主要从事煤岩爆破断裂研究. E-mail：qiupeng@tyut.edu.cn

通讯作者:
岳中文（1975－），男，博士，教授，主要从事岩土工程、爆破工程、采矿工程研究. E-mail：zwyue75@163.com

中图分类号: O389; O521.9
计量
- 文章访问数: 23
- HTML全文浏览量: 19
- PDF下载量: 8
出版历程
- 收稿日期: 2024-04-22
- 修回日期: 2024-05-15
- 网络出版日期: 2024-08-29
- 刊出日期: 2024-09-29

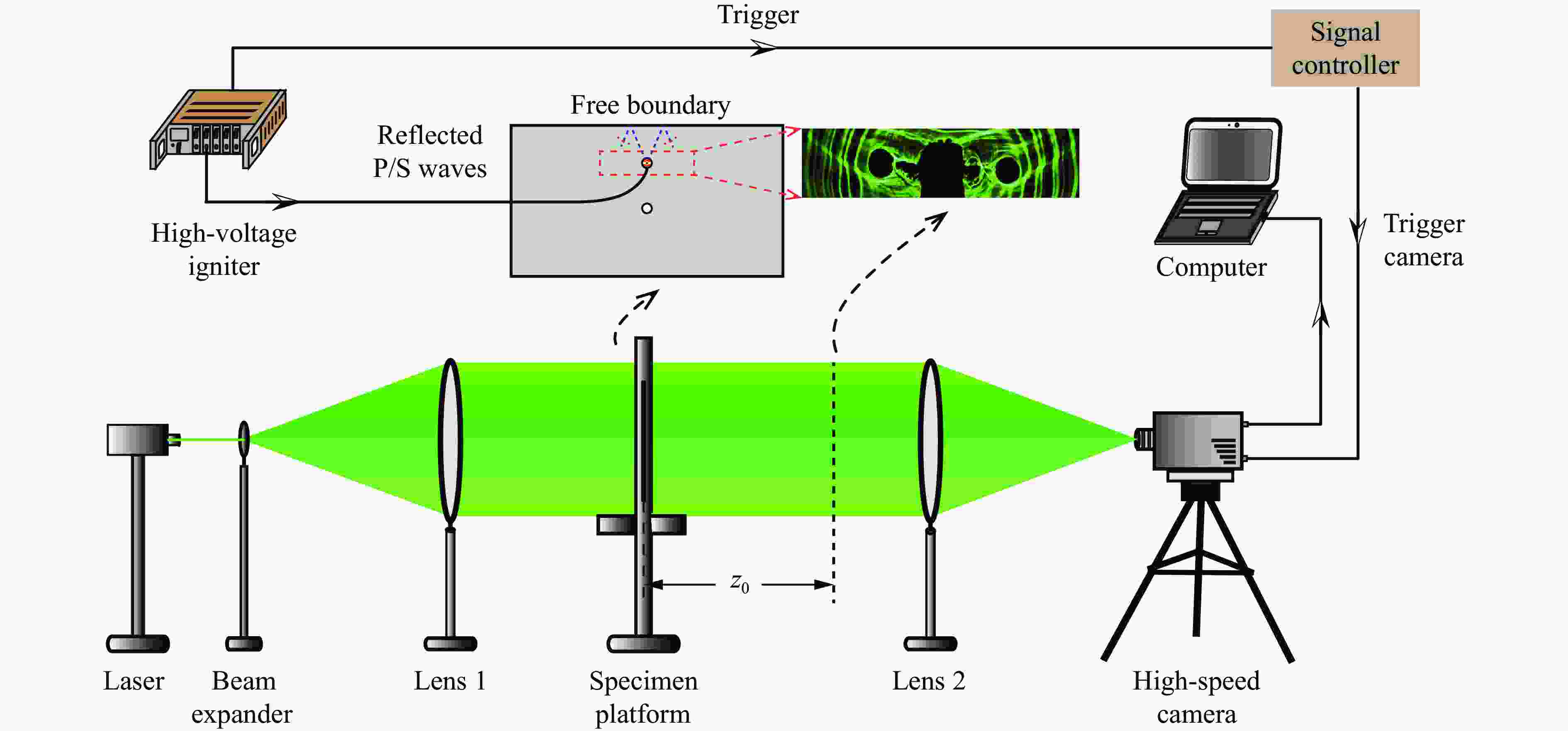
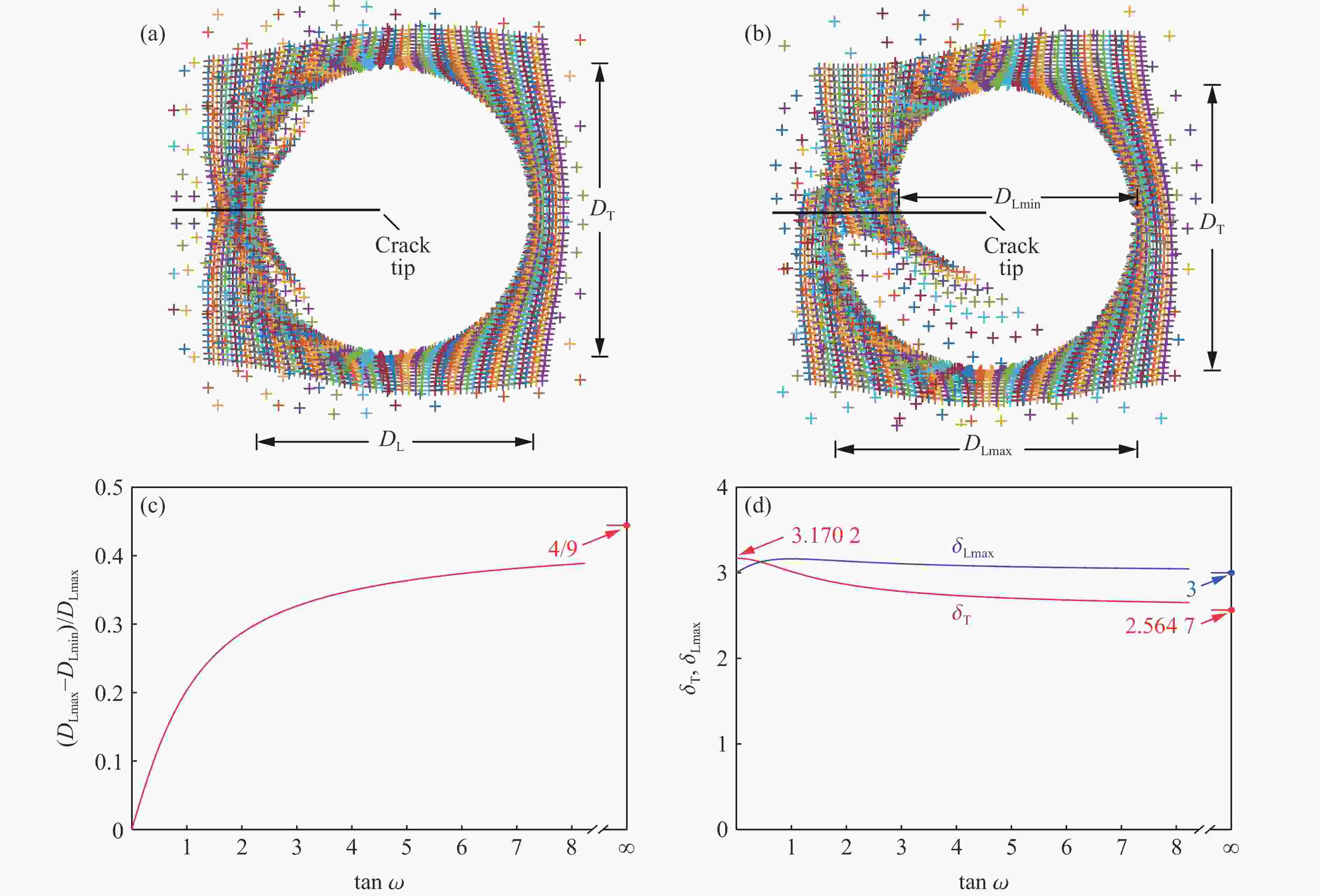
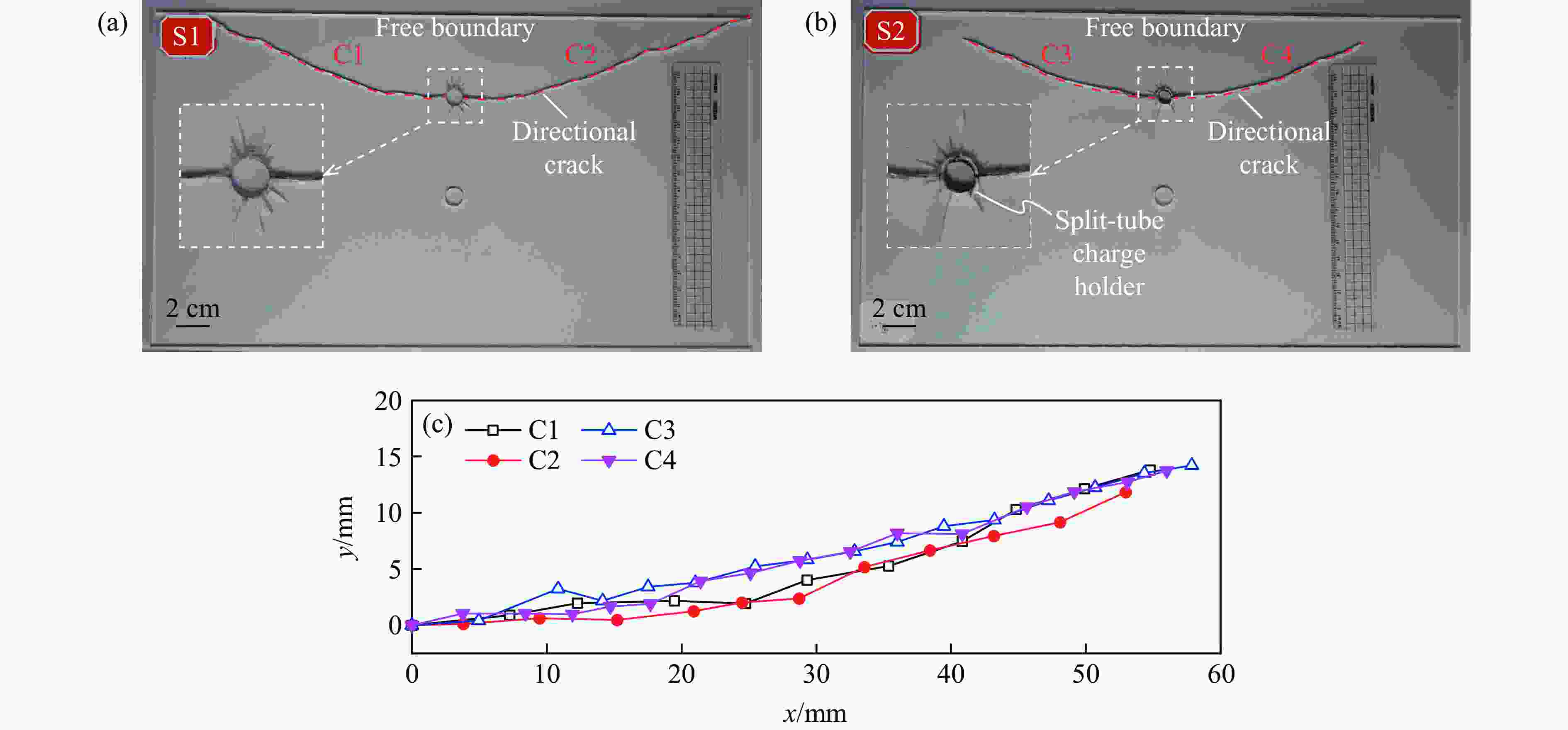
Stress Distribution and Propagation Mechanism of Crack Tip in Directional Fracturing Blasting under the Influence of Free Boundary

QIU Peng^1
,,
YUE Zhongwen^{2,*
, ,}

1.
Key Laboratory of In-Situ Property-Improving Mining of Ministry of Education, Taiyuan University of Technology, Taiyuan 030024, Shanxi, China
2.
School of Mechanics and Civil Engineering, China University of Mining and Technology (Beijing), Beijing 100083, China

摘要

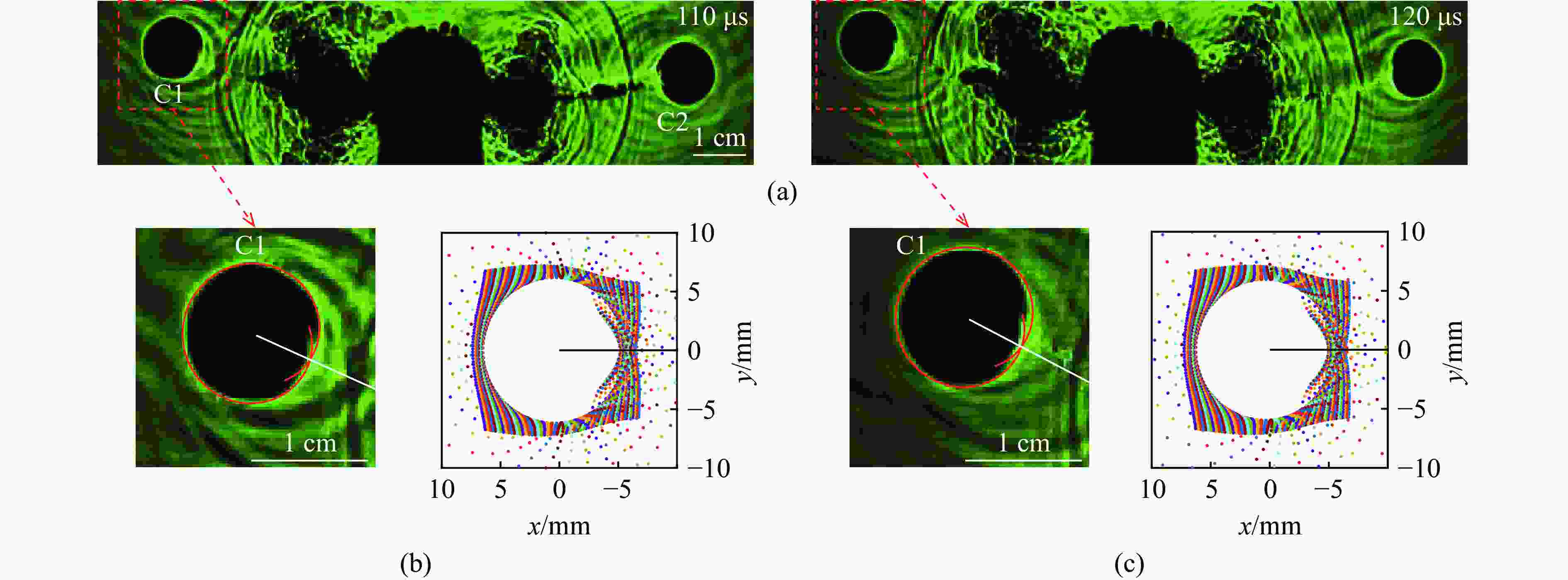
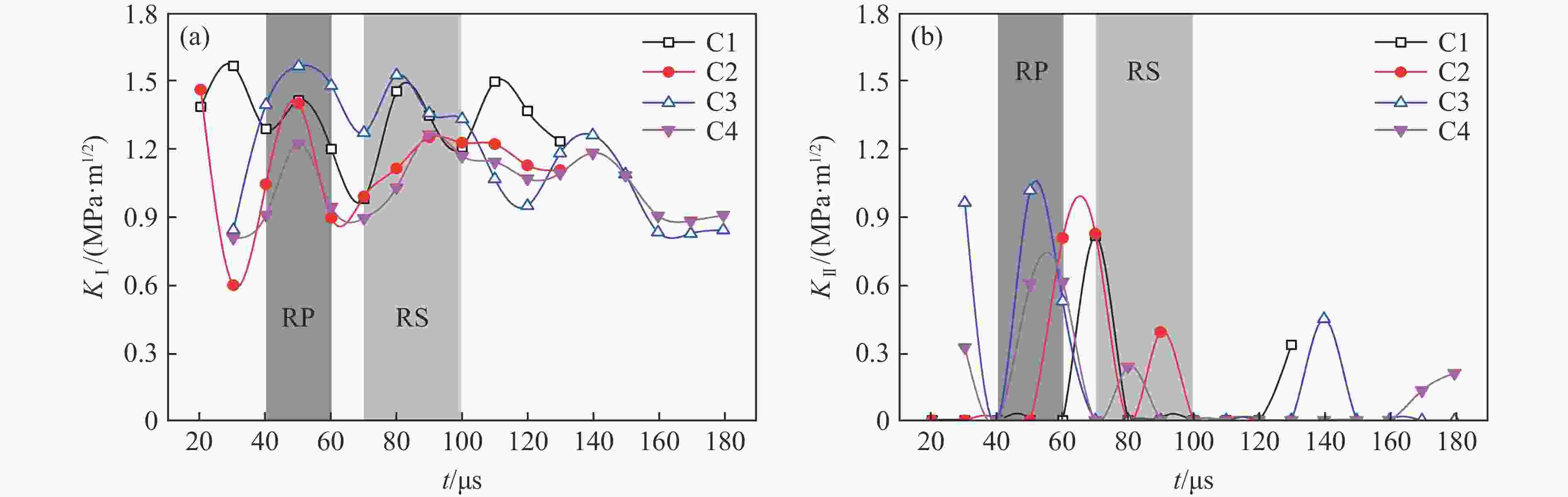
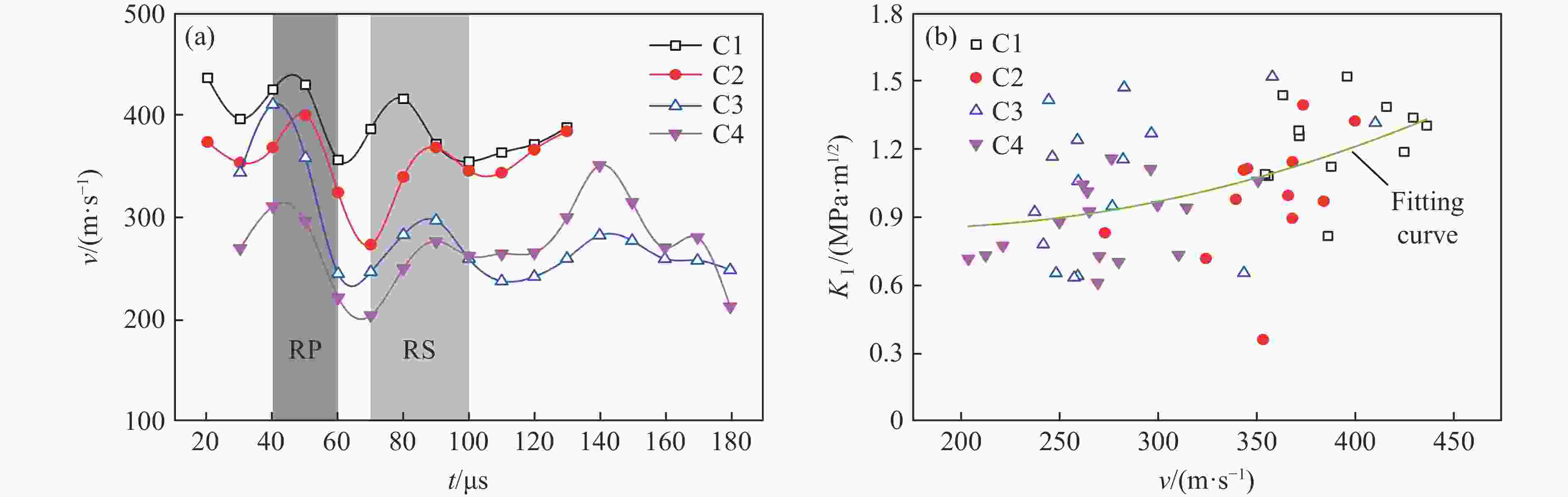
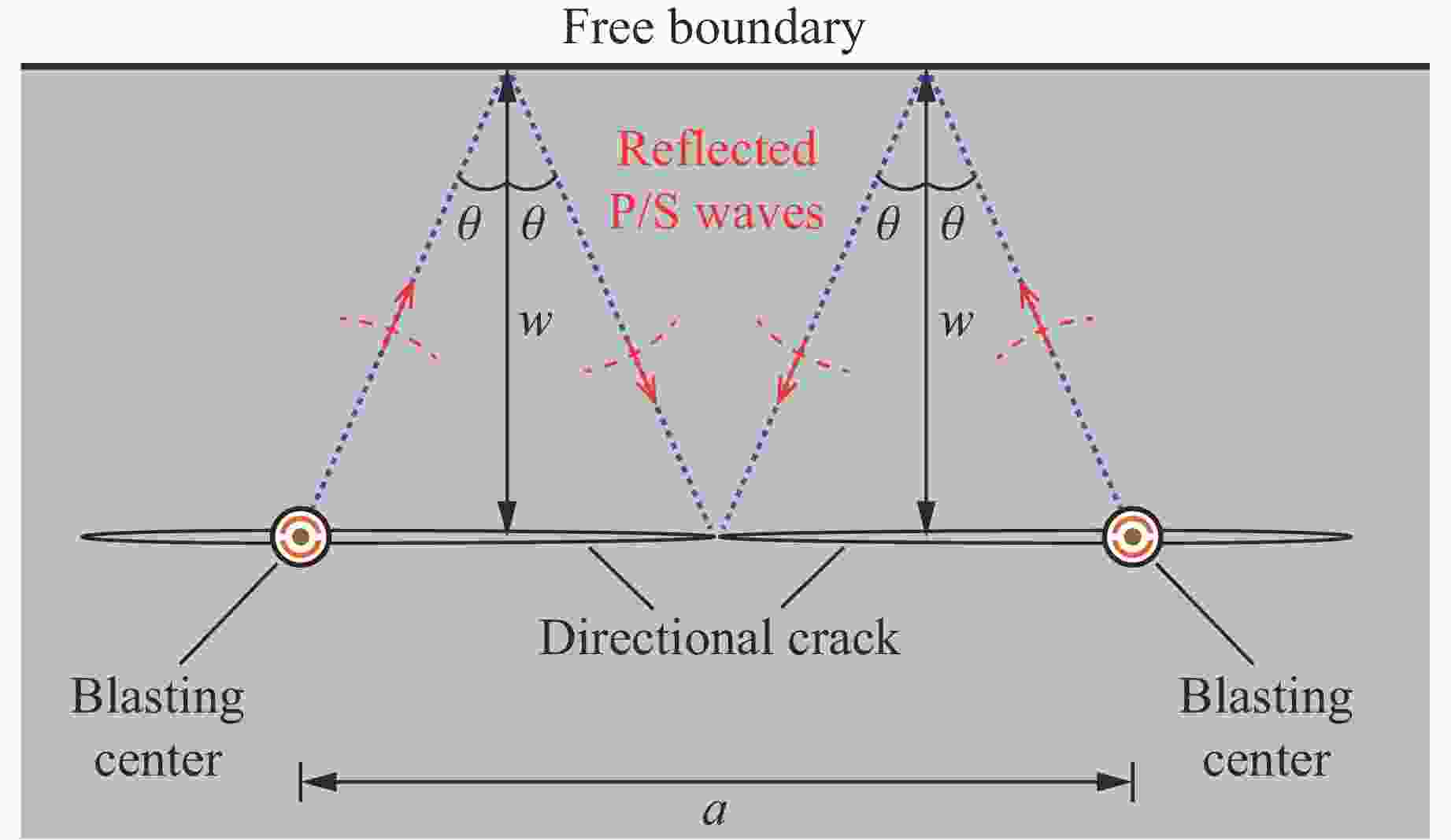
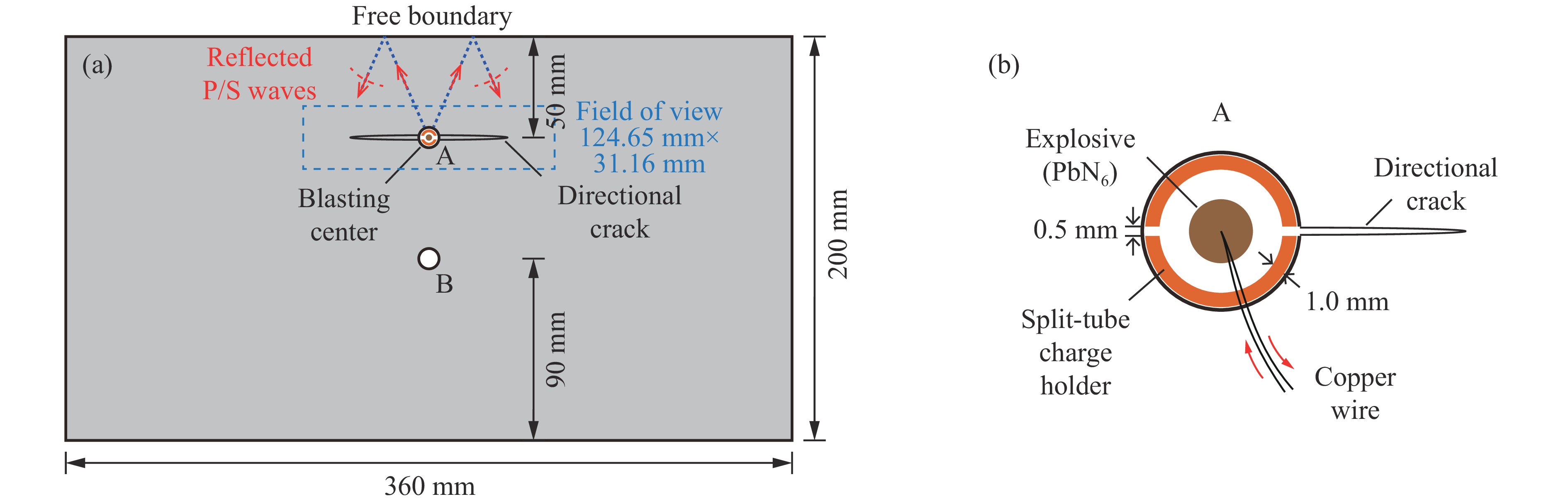
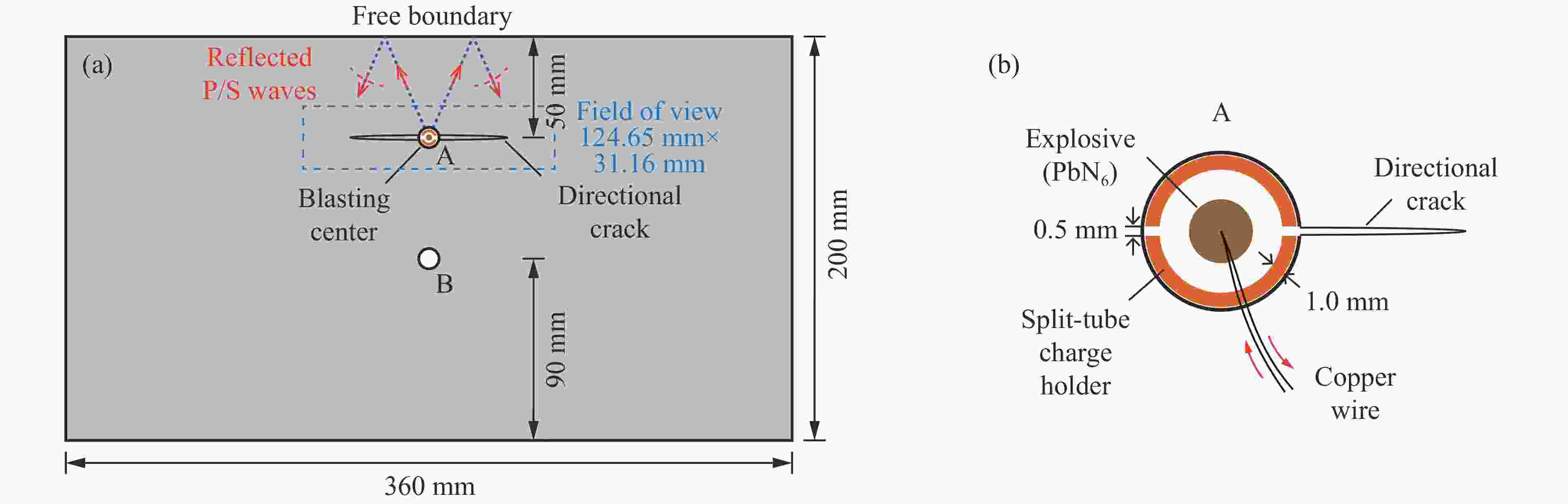
摘要: 天然岩体常含自由边界，对定向断裂爆破产生干扰。为探究自由边界对定向断裂爆破的影响，采用爆炸焦散线方法和高速摄影技术，研究了含自由边界时定向爆炸裂纹尖端的应力分布和扩展机理。自由边界的反射P/S波作用于定向爆炸裂纹，改变了裂尖应力分布，产生了“弧线形”裂纹扩展路径。定向爆炸裂纹扩展可分为3个阶段。(1) 反射波作用前：裂尖受爆生气体“气楔”作用，产生Ⅰ型断裂，并沿直线扩展。(2) 反射波作用时：反射P/S波均使裂尖受张拉-剪切作用，产生Ⅰ-Ⅱ复合型断裂，裂纹偏转趋向自由边界；在反射P波的作用下裂尖产生畸变焦散斑，裂尖应力由K场主导变为非K场主导，而在反射S波的作用下裂尖应力恢复为K场主导。(3) 反射波作用后：裂尖在惯性作用下恢复为Ⅰ型断裂，沿直线扩展。在明确反射P/S波对定向爆炸裂纹作用的基础上，推导了自由边界影响下定向断裂爆破炮孔间距的计算公式，可为精细化定向断裂爆破提供理论参考。
- 自由边界 /
- 定向断裂爆破 /
- 反射P/S波 /
- 裂尖应力分布 /
- 裂纹扩展
Abstract: Natural rock masses often contain free boundaries, which can interfere with directional fracturing blasting. To investigate effects of free boundary on directional fracturing blasting, the caustics method and high-speed photography were used to study the crack-tip stress distribution and propagation of directional blast-induced cracks. The reflected P/S waves from the free boundary act on a directional blast-induced crack, and change the crack-tip stress distribution and generate an “arc shaped” crack path. Directional blast-induced crack propagation can be divided into three stages. Stage one: before the action of reflected waves, the crack tip is subjected to the action of a blast-induced gas wedge, resulting in a mode Ⅰ crack that propagates along a straight line. Stage two: under the action of reflected waves, both reflected P and S waves cause the crack tip to be subjected to tension and shear action, resulting in a mixed mode Ⅰ-Ⅱ crack which deflects towards the free boundary. Under reflected P waves, the crack tip produces distorted caustics, and crack-tip stress changes from K-dominated field to non-K-dominated field, while under reflected S waves, crack-tip stress returns to K-dominated field. Stage three: after the action of reflected waves, the crack tip is subjected to inertial action and then returns to a mode Ⅰ crack which propagates along a straight line. On the basis of clarifying effects of reflected P/S waves on the tip of directional blast-induced cracks, a calculation formula for the distance between two directional fracturing blasting holes under the influence of free boundary is derived, providing a theoretical basis for refined directional fracturing blasting.
- free boundary /
- directional fracturing blasting /
- reflected P/S waves /
- crack-tip stress distribution /
- crack propagation

HTML全文

图 1 试件的示意图：(a) 试件尺寸，(b) 切缝药包

Figure 1. Schematic diagram of the specimen: (a) size of the specimen; (b) slotted cartridge

下载: 全尺寸图片幻灯片

图 2 爆炸焦散线实验系统

Figure 2. Blasting caustics experimental setup

下载: 全尺寸图片幻灯片

图 3 经典的焦散斑方法测量应力强度因子：(a) Ⅰ型焦散斑，(b) Ⅰ-Ⅱ复合型焦散斑，(c) 焦散斑尺寸比例，(d) δ_T和δ_Lmax

Figure 3. Classical stress intensity factor measurement by caustics patterns: (a) mode Ⅰ caustics pattern; (b) mixed Ⅰ-Ⅱ mode caustics pattern; (c) ratio of caustics pattern size; (d) δ_T and δ_Lmax

下载: 全尺寸图片幻灯片

图 4 爆炸后裂纹路径：(a) 爆后试件S1，(b) 爆后试件S2，(c) 4条定向爆炸裂纹路径

Figure 4. Crack path after blasting: (a) specimen S1 after blasting; (a) specimen S2 after blasting;(c) paths of four directional blast-induced cracks

下载: 全尺寸图片幻灯片

图 5 反射波作用前：(a) 爆炸焦散斑图像，(b) t=30 μs时C1裂纹尖端“圆形”焦散斑，(c) t=40 μs时C1裂纹尖端“椭圆形”焦散斑

Figure 5. Before action of reflected waves: (a) blast-induced caustics patterns; (b) circle caustics pattern at the tip of crack C1 at 30 μs; (c) ellipse caustics pattern at the tip of crack C1 at 40 μs

下载: 全尺寸图片幻灯片

图 6 反射P波作用时：(a) 爆炸焦散斑图像，(b) t=50 μs时C1裂纹尖端的“椭圆形”焦散斑，(c) t=60 μs时C2裂纹尖端的Ⅰ-Ⅱ复合型焦散斑

Figure 6. Under action of reflected P wave: (a) blast-induced caustics patterns; (b) ellipse caustics pattern at the tip of crack C1 at 50 μs; (c) mixed Ⅰ-Ⅱ mode caustics pattern at the tip of crack C2 at 60 μs

下载: 全尺寸图片幻灯片

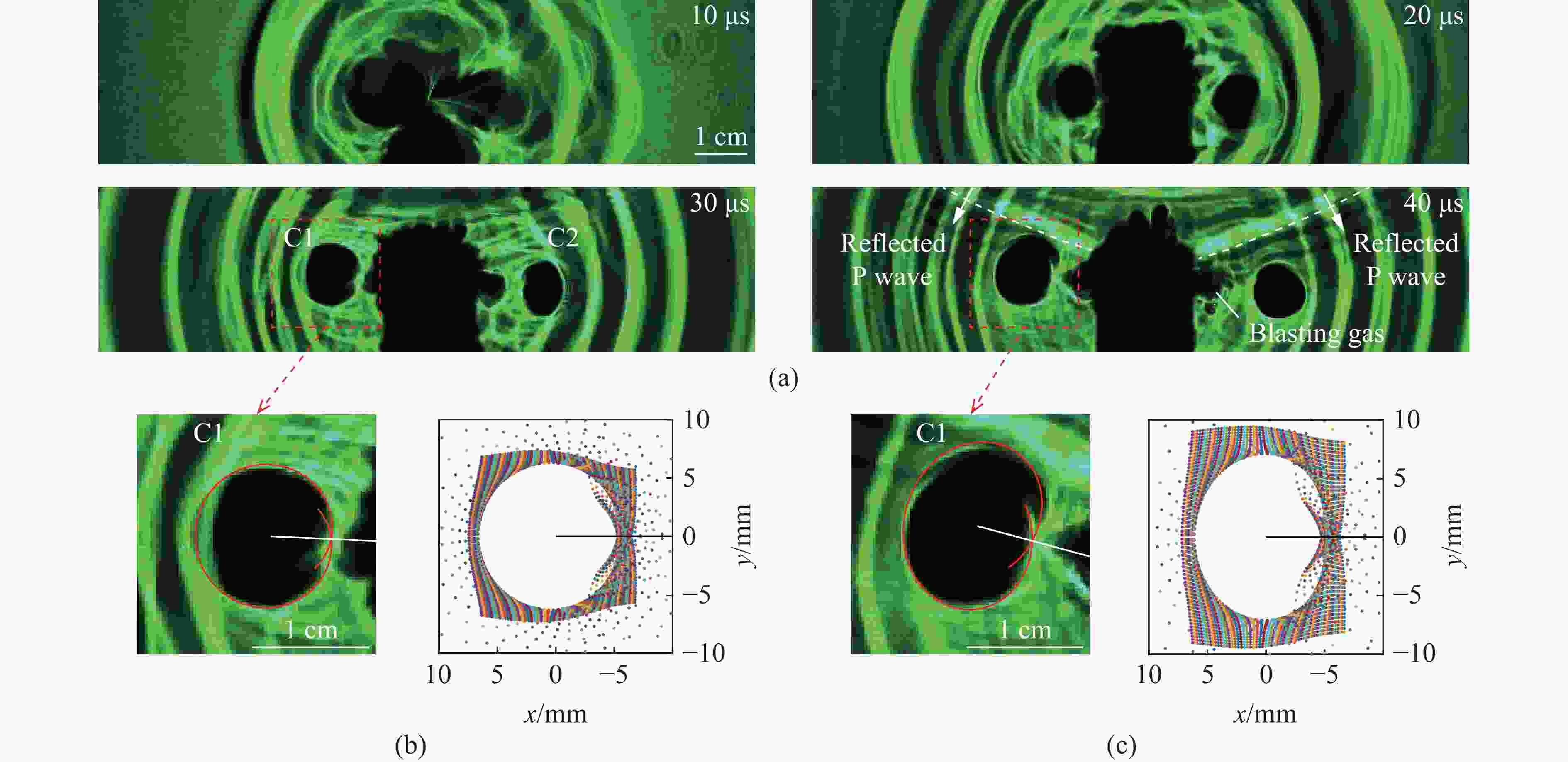
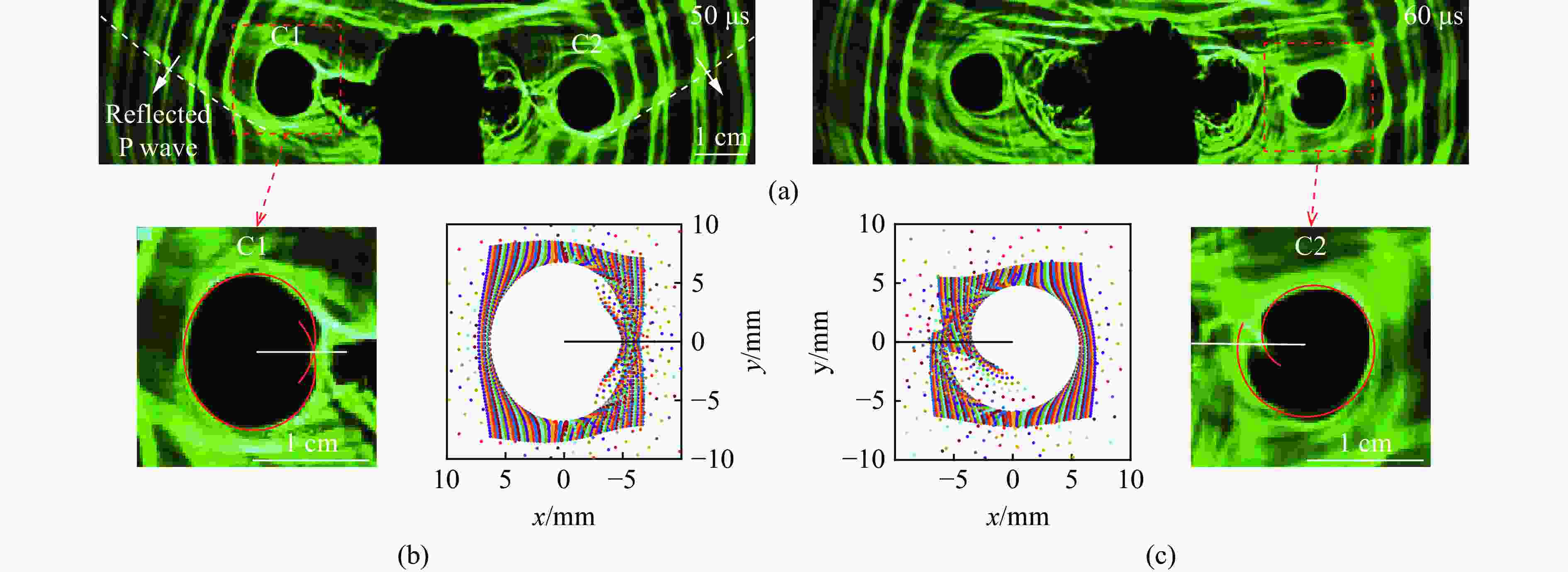
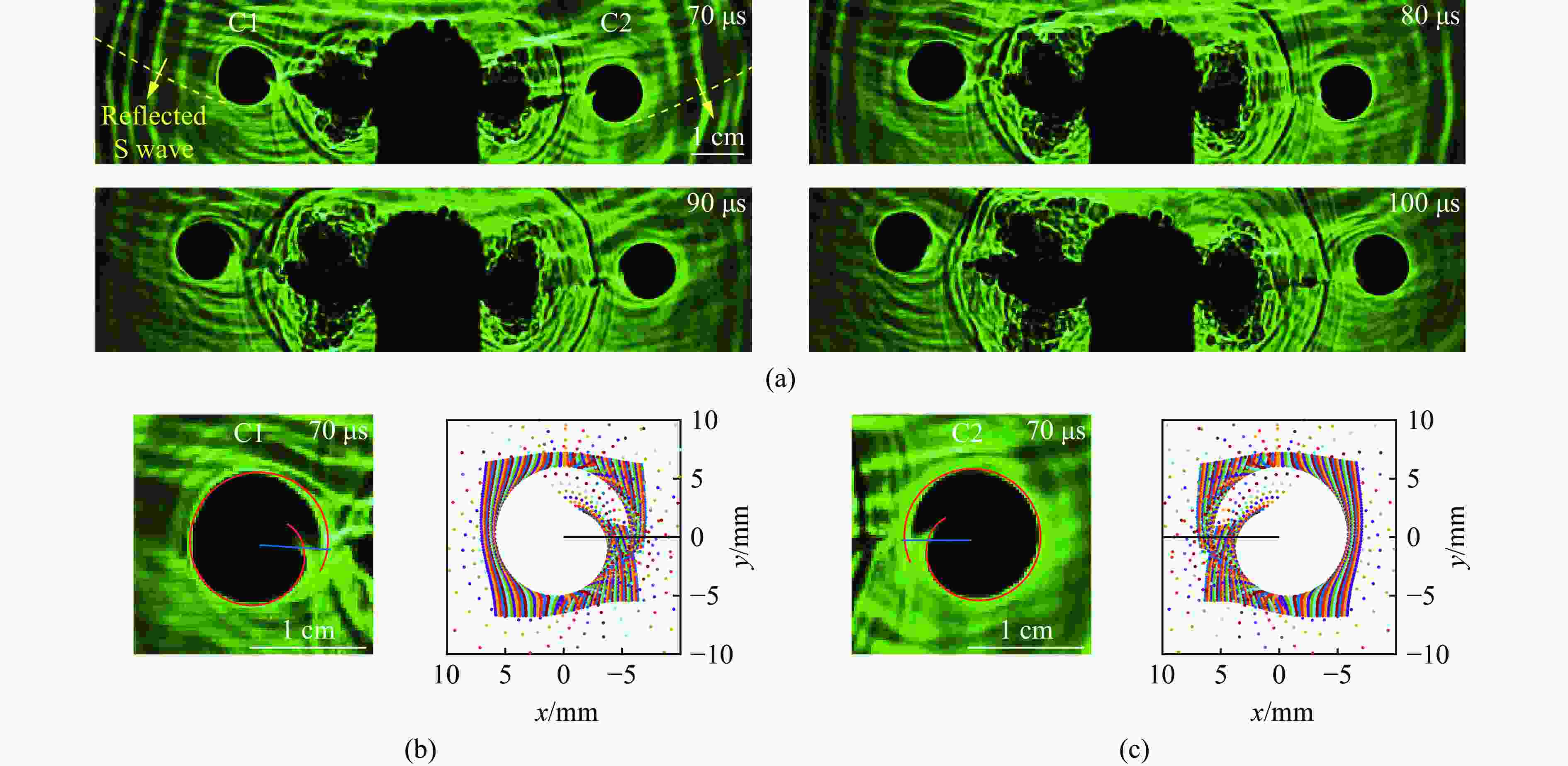
图 7 反射S波作用时：(a) 爆炸焦散斑图像，(b) t=70 μs 时C1裂纹尖端的Ⅰ-Ⅱ复合型焦散斑，(c) t=70 μs时C2裂纹尖端的Ⅰ-Ⅱ复合型焦散斑

Figure 7. Under action of reflected S wave: (a) blast-induced caustics patterns; (b) mixed Ⅰ-Ⅱ mode caustics pattern at the tip of crack C1 at 70 μs; (c) mixed Ⅰ-Ⅱ mode caustics pattern at the tip of crack C2 at 70 μs

下载: 全尺寸图片幻灯片

图 8 反射波作用后：(a) 爆炸焦散斑图像，(b) t=110 μs 时C1裂纹尖端Ⅰ型焦散斑，(c) t=120 μs 时C1裂纹尖端的Ⅰ型焦散斑

Figure 8. After action of reflected waves: (a) blast-induced caustics patterns; (b) mode Ⅰ caustics pattern at the tip of crack C1 at 110 μs; (c) mode Ⅰ caustics pattern at the tip of crack C1 at 120 μs

下载: 全尺寸图片幻灯片

图 9 定向爆炸裂纹尖端应力强度因子：(a) Ⅰ型应力强度因子K_Ⅰ，(b) Ⅱ型应力强度因子K_Ⅱ（RP和RS分别代表反射P波和反射S波）

Figure 9. Stress intensity factors of directional blast-induced cracks: (a) mode Ⅰ stress intensity factor K_Ⅰ; (b) mode Ⅱ stress intensity factor K_Ⅱ (RP and RS represent reflected P and S waves, respectively.)

下载: 全尺寸图片幻灯片

图 10 定向爆炸裂纹扩展结果：(a) 裂纹扩展速度，(b) 裂纹扩展速度与K_Ⅰ的正相关性

Figure 10. Results of directional blast-induced crack propagation : (a) crack propagation velocity; (b) positive correlation between crack propagation velocity and K_Ⅰ

下载: 全尺寸图片幻灯片

图 11 定向断裂爆破炮孔间距计算示意图

Figure 11. Schematic diagram of borehole spacing calculation for directional fracturing blasting

下载: 全尺寸图片幻灯片

参考文献(22)

[1]	赵晓明, 杨玉民, 蒋楠, 等. 深埋引水隧洞光面爆破周边孔装药结构优化试验研究 [J]. 高压物理学报, 2022, 36(4): 045301. doi: 10.11858/gywlxb.20220503 ZHAO X M, YANG Y M, JIANG N, et al. Optimization of charging structure of surrounding holes in smooth blasting of deep diversion tunnel [J]. Chinese Journal of High Pressure Physics, 2022, 36(4): 045301. doi: 10.11858/gywlxb.20220503
[2]	杨仁树, 李成孝, 陈骏, 等. 我国煤矿岩巷爆破掘进发展历程与新技术研究进展 [J]. 煤炭科学技术, 2023, 51(1): 224–241. YANG R S, LI C X, CHEN J, et al. Development history and new technology research progress of rock roadway blasting excavation in coal mines in China [J]. Coal Science and Technology, 2023, 51(1): 224–241.
[3]	何满潮. 无煤柱自成巷开采理论与110工法 [J]. 采矿与安全工程学报, 2023, 40(5): 869–881. HE M C. Theory and engineering practice for non-pillars mining with automagical entry formation and 110 mining method [J]. Journal of Mining & Safety Engineering, 2023, 40(5): 869–881.
[4]	乔国栋, 刘泽功, 高魁, 等. 切缝药包超前预裂爆破厚硬顶板矿压与瓦斯综合防治试验研究 [J]. 中国矿业大学学报, 2024, 53(2): 334–345, 376. QIAO G D, LIU Z G, GAO K, et al. Experimental study on the control of mine pressure and gas governance in thick and hard roof by pre-blasting of slotted cartridge [J]. Journal of China University of Mining & Technology, 2024, 53(2): 334–345, 376.
[5]	杨国梁, 毕京九, 董智文, 等. 定向断裂控制爆破下层理页岩的致裂机理 [J]. 爆炸与冲击, 2024, 44(6): 061001. YANG G L, BI J J, DONG Z W, et al. Fracturing mechanism of bedding shale under directional fracture-controlled blasting [J]. Explosion and Shock Waves, 2024, 44(6): 061001.
[6]	杨仁树, 丁晨曦, 杨立云, 等. 含缺陷PMMA介质的定向断裂控制爆破试验研究 [J]. 岩石力学与工程学报, 2017, 36(3): 690–696. YANG R S, DING C X, YANG L Y, et al. Experimental study on controlled directional fracture blasting on PMMA mediums with flaws [J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(3): 690–696.
[7]	岳中文, 郭洋, 许鹏, 等. 定向断裂控制爆破爆生裂纹扩展机理的实验研究 [J]. 工程力学, 2016, 33(2): 50–58. doi: 10.6052/j.issn.1000-4750.2014.09.0816 YUE Z W, GUO Y, XU P, et al. Controlled blasting experimental study on the mechanism of blast-induced crack propagation under directional fracture [J]. Engineering Mechanics, 2016, 33(2): 50–58. doi: 10.6052/j.issn.1000-4750.2014.09.0816
[8]	岳中文, 郭洋, 许鹏, 等. 定向断裂控制爆破的空孔效应实验分析 [J]. 爆炸与冲击, 2015, 35(3): 304–311. doi: 10.11883/1001-1455-(2015)03-0304-08 YUE Z W, GUO Y, XU P, et al. Analysis of empty hole effect in directional fracture controlled blasting [J]. Explosion and Shock Waves, 2015, 35(3): 304–311. doi: 10.11883/1001-1455-(2015)03-0304-08
[9]	王雁冰, 商禹智, 石震鑫, 等. 定向断裂双孔爆破含缺陷介质裂纹扩展的动焦散试验 [J]. 爆破, 2018, 35(1): 15–20, 48. doi: 10.3963/j.issn.1001-487X.2018.01.003 WANG Y B, SHANG Y Z, SHI Z X, et al. Dynamic caustics experiment on crack propagation in defective medium by directional breaking with double hole blasting [J]. Blasting, 2018, 35(1): 15–20, 48. doi: 10.3963/j.issn.1001-487X.2018.01.003
[10]	许鹏, 陈程, 郭洋, 等. 含垂直层理介质在切缝药包爆破下裂纹扩展行为的试验研究 [J]. 矿业科学学报, 2019, 4(6): 498–505. XU P, CHEN C, GUO Y, et al. Experimental study on crack propagation of slit charge blasting in media with vertical bedding plane [J]. Journal of Mining Science and Technology, 2019, 4(6): 498–505.
[11]	费鸿禄, 山杰, 包士杰, 等. 节理几何特征对爆破裂纹扩展的数值模拟研究 [J]. 工程爆破, 2023, 29(5): 12–21. FEI H L, SHAN J, BAO S J, et al. Numerical simulation study of joint geometric characteristics for explosion crack propagation [J]. Engineering Blasting, 2023, 29(5): 12–21.
[12]	郭德勇, 张慧杰, 吕鹏飞, 等. 断层对深孔聚能爆破煤层增透的影响 [J]. 北京科技大学学报, 2014, 36(10): 1281–1286. GUO D Y, ZHANG H J, LYU P F, et al. Effect of fault on deep-hole cumulative blasting to improve coal bed permeability [J]. Journal of University of Science and Technology Beijing, 2014, 36(10): 1281–1286.
[13]	QIU P, YUE Z W, YANG R S, et al. Effects of vertical and horizontal reflected blast stress waves on running cracks by caustics method [J]. Engineering Fracture Mechanics, 2019, 212: 164–179.
[14]	QIU P, YUE Z W, JU Y, et al. Characterizing dynamic crack-tip stress distribution and evolution under blast gases and reflected stress waves by caustics method [J]. Theoretical and Applied Fracture Mechanics, 2020, 108: 102632.
[15]	QIU P, YUE Z W, YANG R S, et al. Modified mixed-mode caustics interpretation to study a running crack subjected to obliquely incident blast stress waves [J]. International Journal of Impact Engineering, 2021, 150: 103821.
[16]	吴延梦, 李洪伟, 苏洪, 等. 单向围压下切槽爆破裂纹扩展规律研究 [J]. 高压物理学报, 2023, 37(6):129–139. WU Y M, LI H W, SU H, et al. Crack propagation law of notch blasting under unidirectional confining pressure [J]. Chinese Journal of High Pressure Physics, 2023, 37(6):129–139.
[17]	邱鹏. 爆炸应力波与裂纹相互作用机理研究 [D]. 北京:中国矿业大学(北京), 2019. QIU P. Mechanisms of the interaction between blast stress waves and cracks [D]. Beijing: China University of Mining and Technology (Beijing), 2019.
[18]	THEOCARIS P S. Elastic stress intensity factors evaluated by caustics [M]//SIH G C. Experimental evaluation of stress concentration and intensity factors. Netherlands: Springer, 1981: 189–252.
[19]	PAPADOPOULOS G A. Fracture mechanics: the experimental method of caustics and the det.-criterion of fracture [M]. London: Springer-Verlag, 1993.
[20]	李庆扬, 王能超, 易大义. 数值分析 [M]. 北京: 清华大学出版社, 2008. LI Q Y, WANG N C, YI D Y. Numerical analysis [M]. Beijing: Tsinghua University Press, 2008.
[21]	ANDERSON T L. Fracture mechanics: fundamentals and applications [M]. Boca Raton, FL: CRC Press, 2005.
[22]	范天佑. 断裂动力学原理与应用 [M]. 北京: 北京理工大学出版社, 2006. FAN T Y. Principles and applications of fracture dynamics [M]. Beijing: Beijing Institute of Technology Press, 2006.