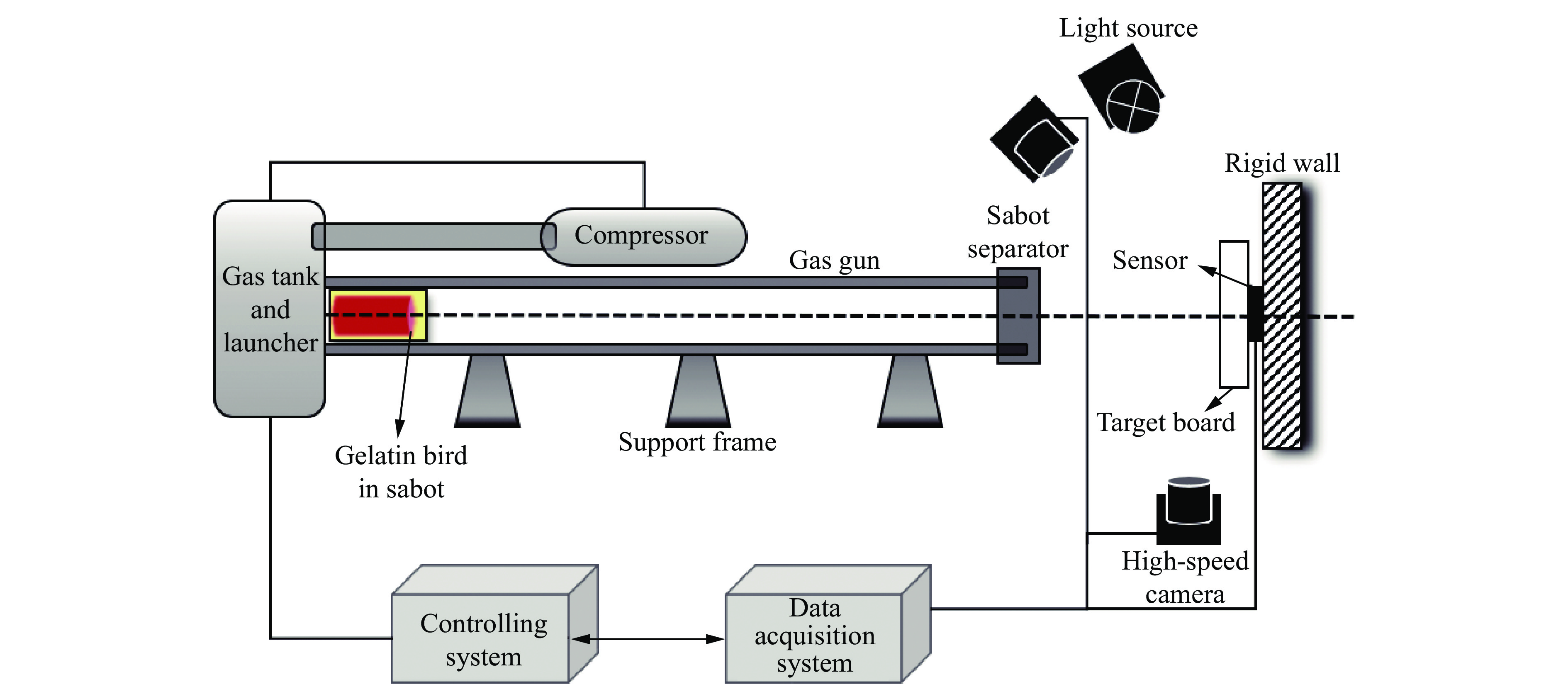
A Numerical Modeling Method of Gelatin Bird Projectile Suitable for Wide-Speed-Range Impact
-
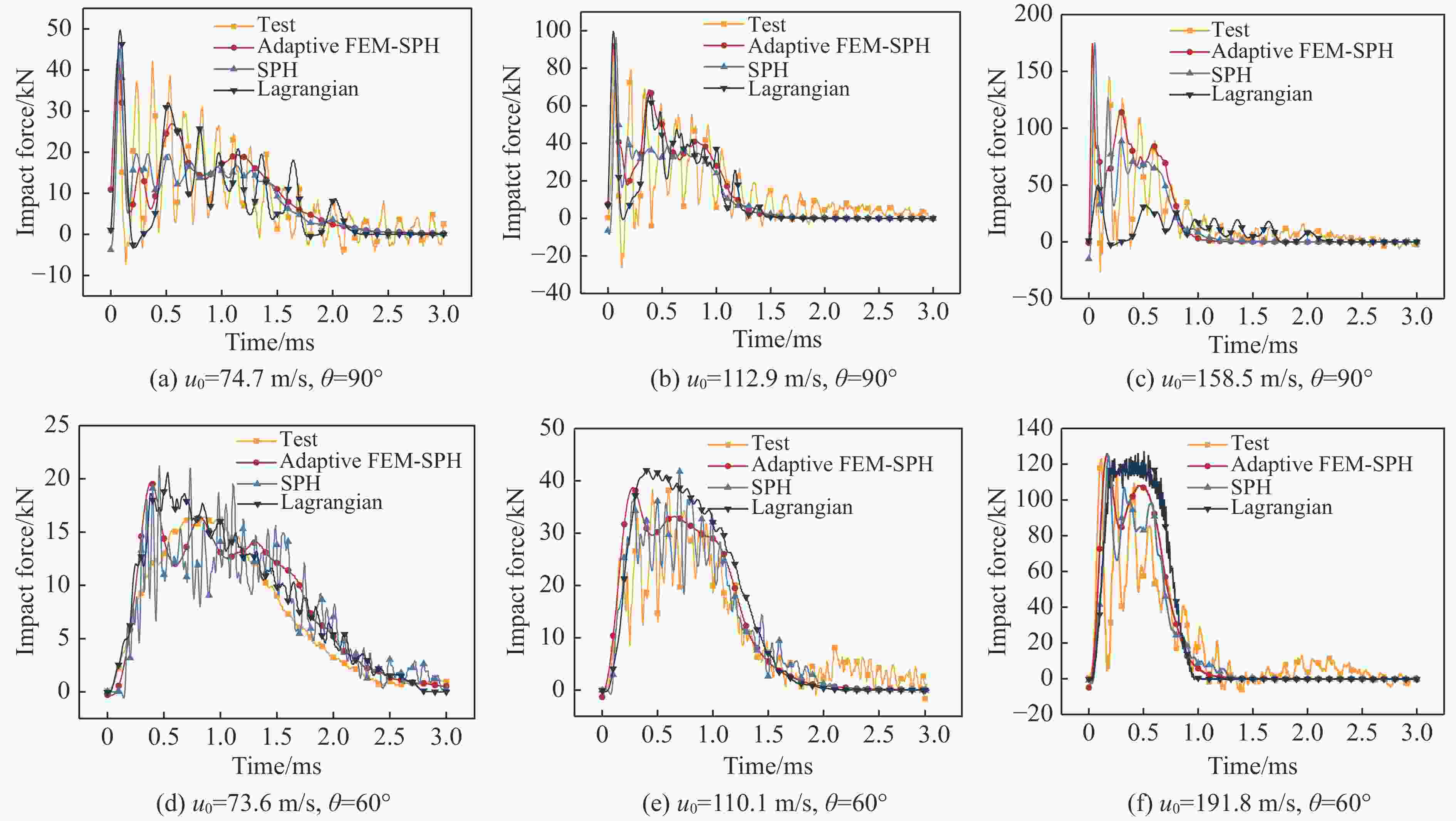
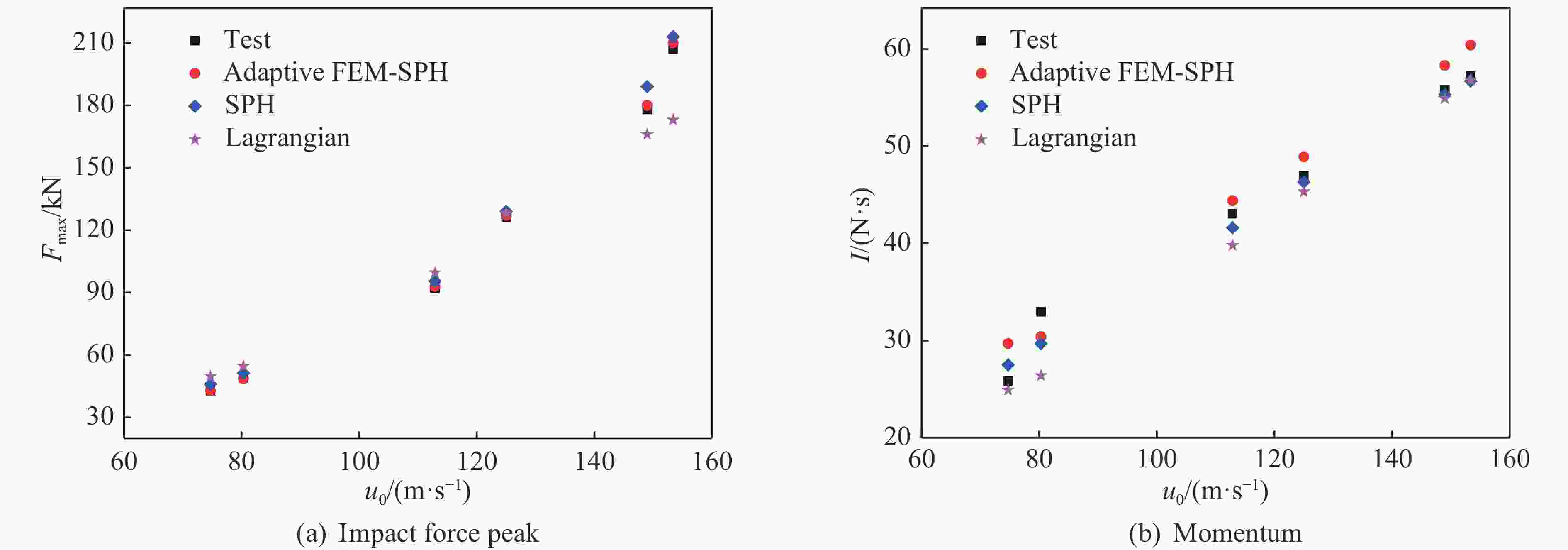
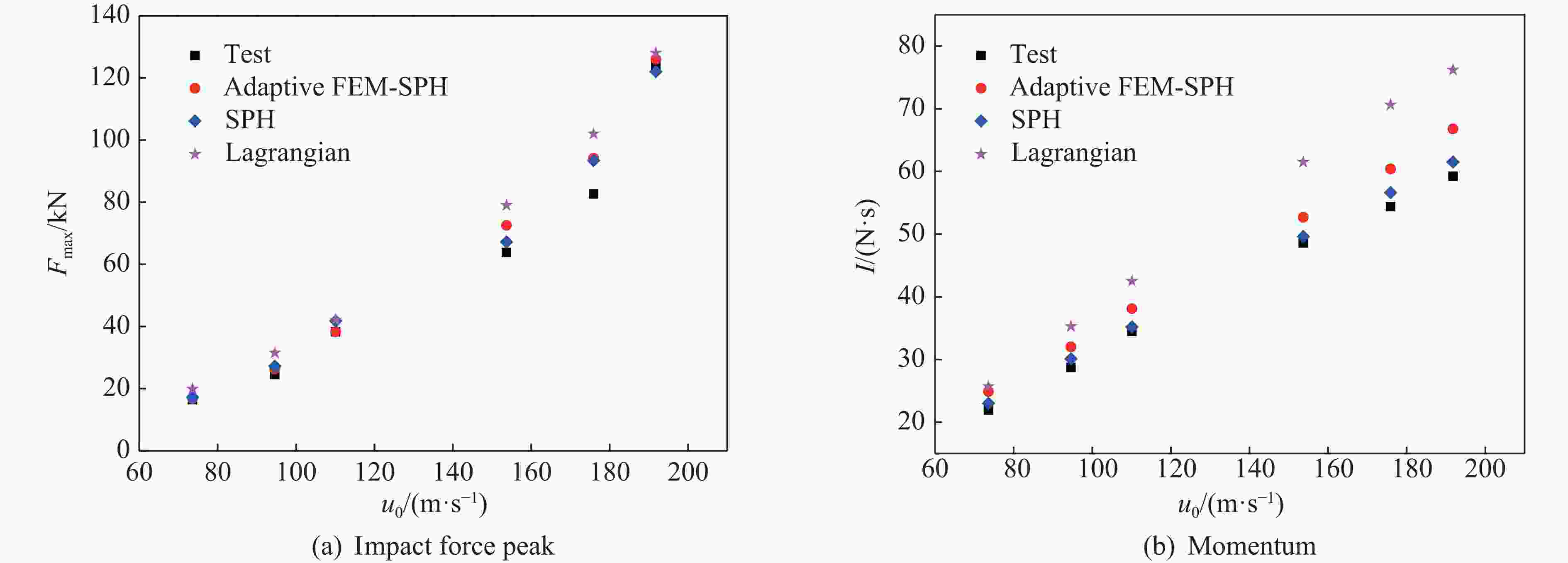
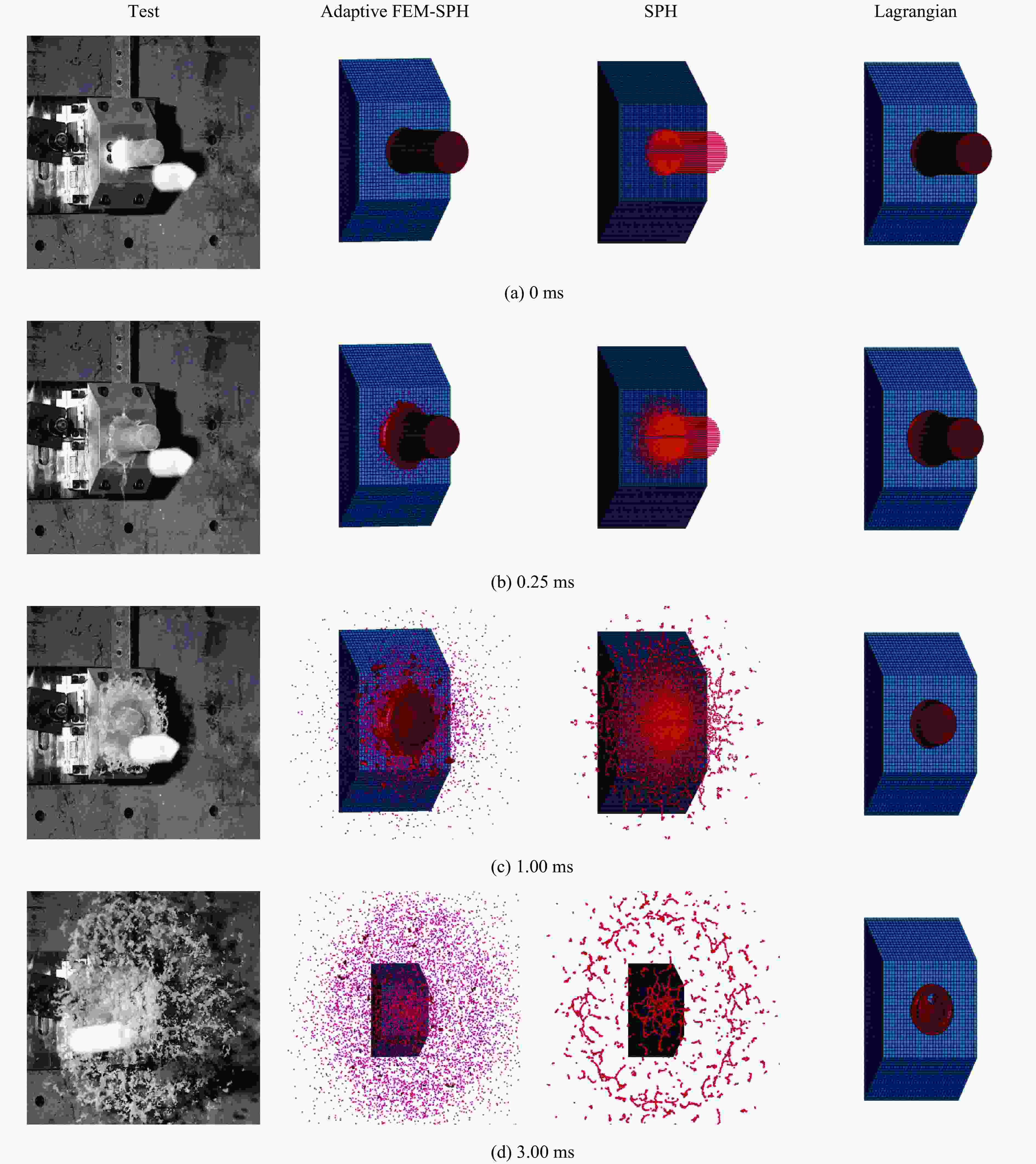
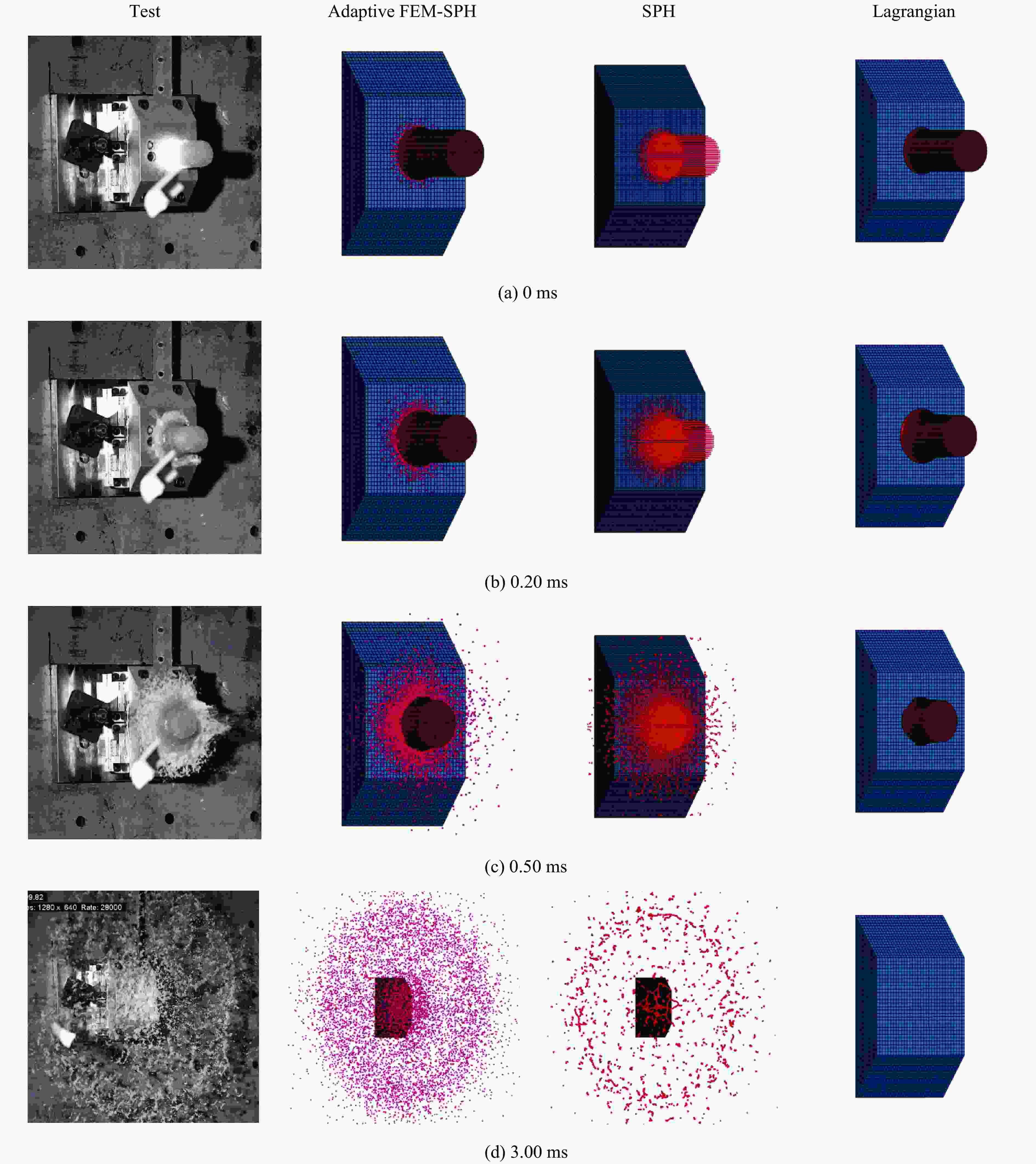
摘要: 明胶鸟弹在不同撞击速度下表现出不同的响应特性。为解决传统明胶鸟弹本构表征方法在不同速度范围内不能通用的问题,开展了330 g明胶鸟弹以70~190 m/s速度、60°或90°入射刚性铝合金平板试验,记录了冲击力数据及撞击形貌。结果表明,随着撞击速度的提高,鸟弹碎裂得更充分,碎块体积减小。利用LS-DYNA建立了自适应FEM-SPH(finite element method-smoothed particle hydrodynamics)鸟体模型。依据试验结果反演得到一组鸟体本构参数:切线模量为1.33 MPa,剪切模量为115.95 MPa,Murnaghan状态方程参数γ为10.49,k0为69.77 MPa,体积模量为246.4 MPa,失效塑性应变为1.15,初始屈服应力为0.21 MPa。仿真结果与试验结果具有很好的一致性,冲击力峰值的相对误差在2%以内,冲量的相对误差在10%以内。自适应FEM-SPH鸟体模型具有比SPH模型和拉格朗日模型更高的精度。由自适应模型得到的Hugoniot压强与理论结果具有相同的变化趋势,滞止压强与理论值较接近。Abstract: Previous studies revealed that gelatin birds show different mechanical behaviors at different impact velocities. In order to solve the problem that the traditional constitutive methods of gelatin bird cannot be universal in different velocity ranges, the tests of 330 g gelatin birds impacting rigid aluminum alloy plate at 60° and 90° incident angles, covering a velocity range of 70−190 m/s were carried out to record the impact force data and impact morphology. With the increase of velocity, the birds were broken more fully and smaller fragments were observed. The adaptive FEM-SPH (finite element method-smoothed particle hydrodynamics) model of bird was established in LS-DYNA, and a set of constitutive parameters were inverted according to the test results: tangent modulus equals to 1.33 MPa, shear modulus equals to 115.95 MPa, the parameters of Murnaghan equation of state γ equals to 10.49, k0 equals to 69.77 MPa, bulk modulus equals to 246.4 MPa, failure plastic strain is 1.15, yield stress is 0.21 MPa. The simulation results were in good agreement with the test results, and had higher accuracy compared to the SPH models and the Lagrangian models. The Hugoniot pressure of the adaptive model had the same change trend as the theoretical value, and the stagnation pressure was close to the theoretical value.
-
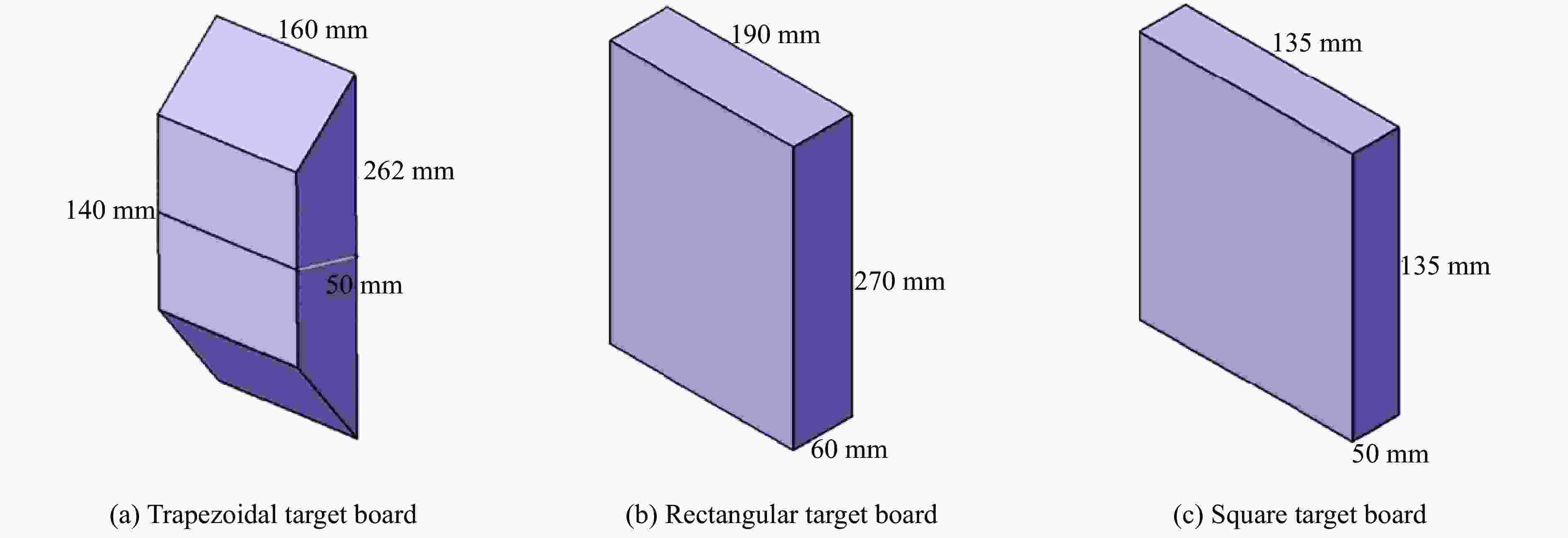
表 1 不同工况下鸟撞试验结果
Table 1. Test results of bird impact under various impact conditions
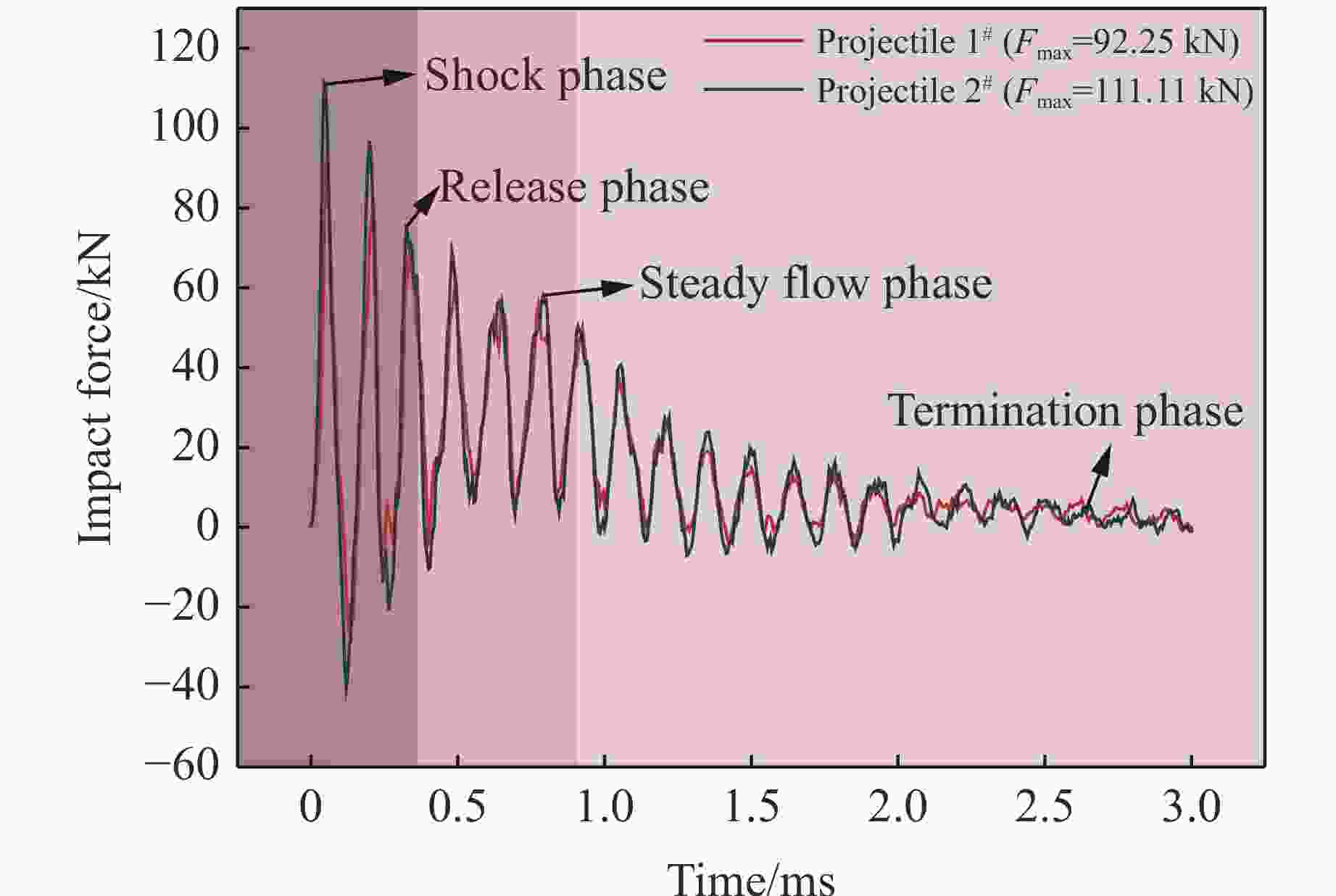
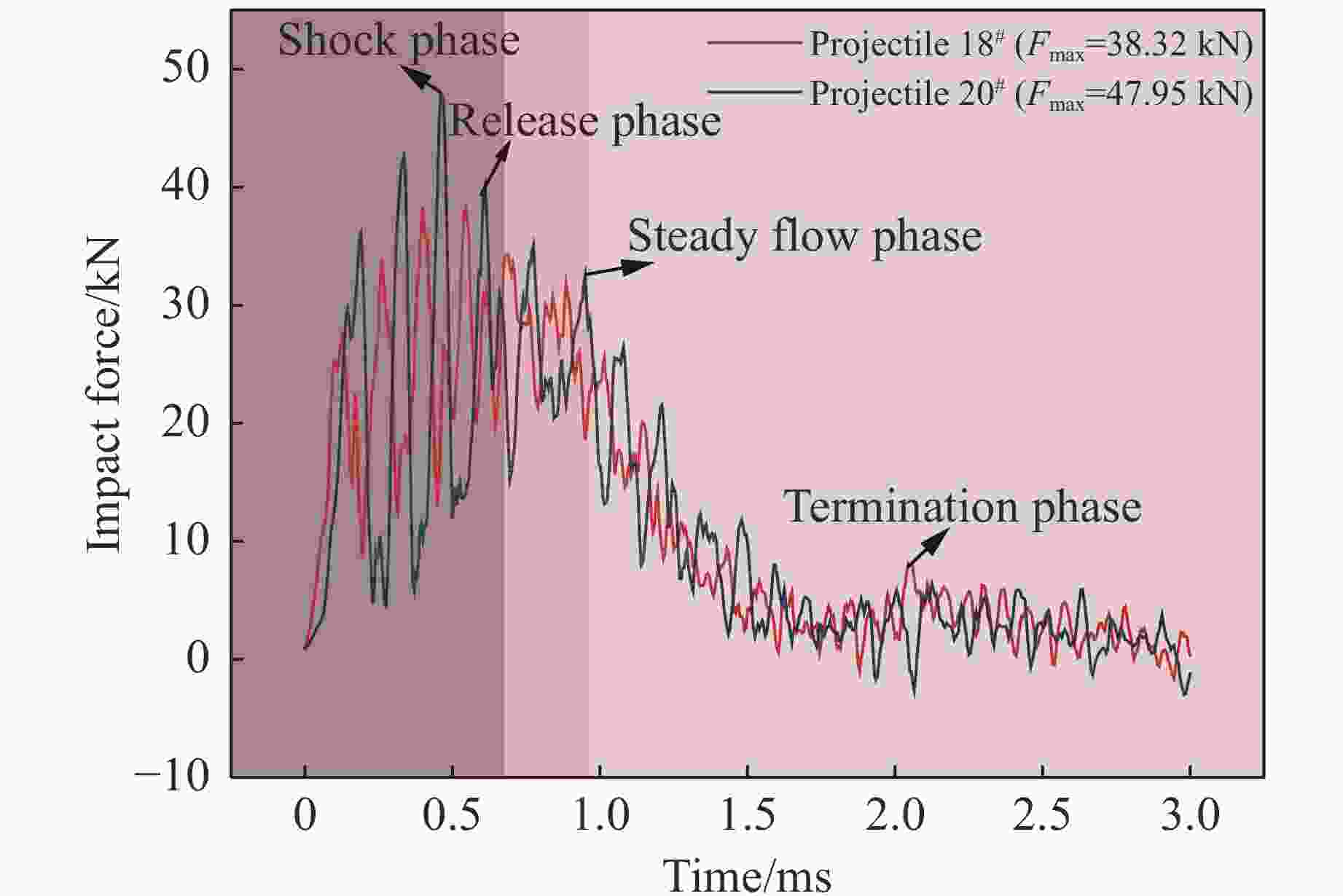
Case u0/(m·s−1) θ/(°) Plate shape Bird projectile No. (m, actual impact velocity) 1 110 60 Rectangular 18# (334 g, 110.1 m/s), 20# (329.5 g, 107.0 m/s) 2 110 60 Rectangular 29# (326 g, 114.7 m/s) 3 120 60 Rectangular 21# (327 g, 124.6 m/s), 22# (328 g, 124.1 m/s) 4 150 60 Rectangular 23# (331 g, 150.1 m/s), 24# (330 g, 153.7 m/s) 5 160 60 Rectangular 25# (331 g, 166.6 m/s) 6 170 60 Rectangular 26# (328 g, 175.9 m/s) 7 180 60 Rectangular 28# (331 g, 185.3 m/s) 8 190 60 Rectangular 27# (332 g, 191.8 m/s) 9 70 60 Square 39# (328 g, 75.2 m/s), 40# (328 g, 73.6 m/s) 10 90 60 Square 37# (328 g, 94.6 m/s) 11 100 60 Square 38# (327 g, 99.6 m/s) 12 110 90 Trapezoidal 1# (336 g, 112.9 m/s), 2# (328 g, 113.1 m/s) 13 120 90 Trapezoidal 5# (333 g, 125.0 m/s), 12# (334 g, 121.8 m/s) 14 150 90 Trapezoidal 6# (332 g, 149.0 m/s), 7# (328 g, 148.8 m/s) 15 150 90 Trapezoidal 8# (332 g, 153.4 m/s), 9# (333 g, 148.8 m/s) 16 160 90 Trapezoidal 10# (325 g, 165.3 m/s), 11# (329 g, 158.5 m/s) 17 80 90 Square 34# (330 g, 84.9 m/s), 35# (329 g, 80.3 m/s) 18 70 90 Square 36# (330.5 g, 74.7 m/s) 表 2 铝合金的材料参数
Table 2. Material parameters of aluminum alloy
Density/(kg·m−3) Young’s modulus/GPa Poisson’s ratio Yield stress/MPa Tangent modulus/GPa 2796 71 0.33 450 5 表 3 SPH鸟体材料参数
Table 3. Material parameters of SPH bird model
Density/(kg·m−3) Cut-off pressure/MPa Dynamic viscosity/(Pa·s) 950 −1 0.001 表 4 自适应FEM-SPH模型的本构参数优化结果
Table 4. Optimization results of constitutive parameters for adaptive FEM-SPH model
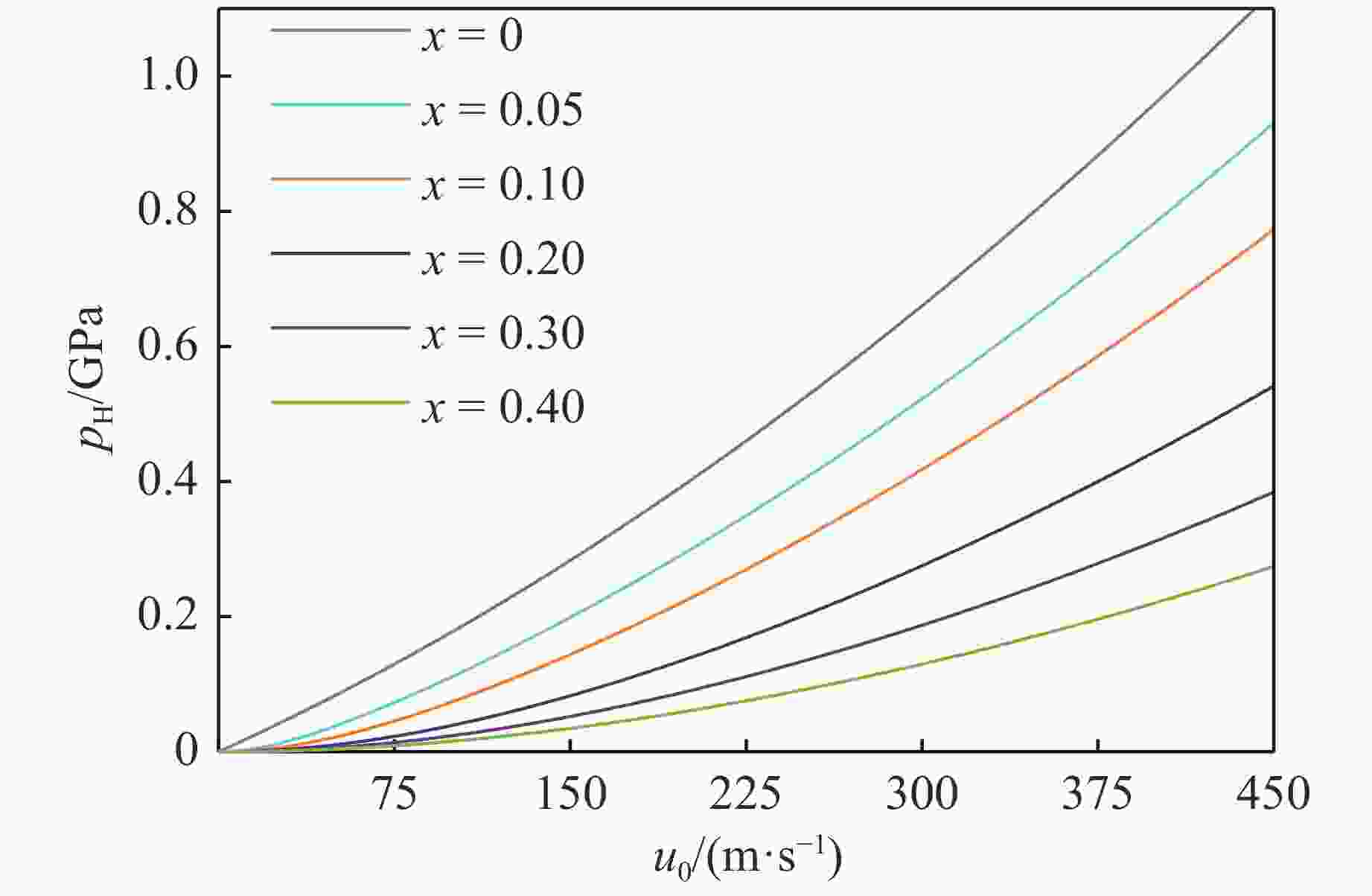
Value Et/MPa G/MPa γ K/MPa k0/MPa εf σs/MPa Range 0.01−2.00 1−300 1−20 1−300 1−300 0.01−1.20 0.01−1.00 Optimal value 1.33 115.95 10.49 246.4 69.77 1.15 0.21 表 5 不同学者通过数值模拟得到的归一化Hugoniot压强和滞止压强[10, 12, 18, 20–27]
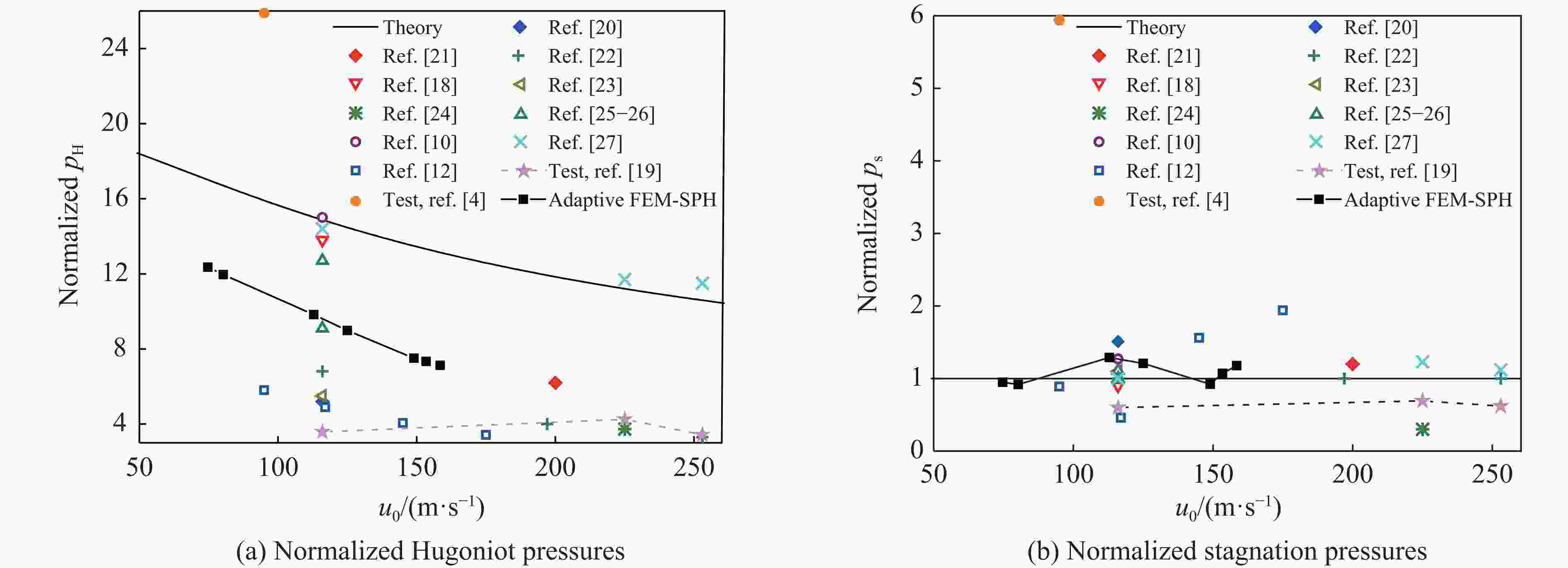
Table 5. Numerical results of normalized Hugoniot and stagnation pressures calculated by different researchers[10, 12, 18, 20–27]
Ref. u0/(m·s−1) Normalized pH Normalized ps m/kg Density/(kg·m−3) Bird model geometry [20] 116 5.2 1.5 1.8 938 Hemispherical-ended [21] 200 6.2 1.2 0.6 930 Cylinder [22] 116 6.8 1.0 1.8 934 Hemispherical-ended [22] 197 4.0 1.0 1.8 934 Hemispherical-ended [22] 253 3.3 1.0 1.8 934 Hemispherical-ended [18] 116 13.8 0.9 1.0 950 Hemispherical-ended [23] 116 5.5 1.1 1.8 950 Hemispherical-ended [24] 225 3.7 0.3 1.8 934 Cylinder [25] 116 12.7 1.1 1.8 938 Hemispherical-ended [26] 116 9.1 1.0 1.7 950 Hemispherical-ended [10] 116 15.0 1.3 0.2 1019 Cylinder [27] 116 14.4 1.0 0.8 938 Hemispherical-ended [27] 225 11.7 1.2 0.8 938 Hemispherical-ended [27] 253 11.5 1.1 0.8 938 Hemispherical-ended [12] 95 5.8 0.9 1.3 968 Cylinder [12] 117 4.9 0.5 1.3 968 Cylinder [12] 145 4.1 1.6 1.3 968 Cylinder [12] 175 3.4 1.9 1.3 968 Cylinder -
[1] GUIDA M, MARULO F, BELKHELFA F Z, et al. A review of the bird impact process and validation of the SPH impact model for aircraft structures [J]. Progress in Aerospace Sciences, 2022, 129: 100787. doi: 10.1016/j.paerosci.2021.100787 [2] 张迎春, 陆晓华, 张柱国. 运输类飞机鸟撞适航要求解析及审定实践 [M]. 北京: 科学出版社, 2023: 39–40.ZHANG Y C, LU X H, ZHANG Z G. Transport category airplane bird-strike airworthiness regulations interpretation and certification practice [M]. Beijing: Science Press, 2023: 39–40. [3] 刘小川, 王计真, 白春玉. 人工鸟研究进展及在飞机结构抗鸟撞中的应用 [J]. 振动与冲击, 2021, 40(12): 80–89. doi: 10.13465/j.cnki.jvs.2021.12.011LIU X C, WANG J Z, BAI C Y. Overview on artificial bird and application on the structural bird-strike [J]. Journal of Vibration and Shock, 2021, 40(12): 80–89. doi: 10.13465/j.cnki.jvs.2021.12.011 [4] LAVOIE M A, GAKWAYA A, ENSAN M N, et al. Bird’s substitute tests results and evaluation of available numerical methods [J]. International Journal of Impact Engineering, 2009, 36(10/11): 1276–1287. doi: 10.1016/j.ijimpeng.2009.03.009 [5] 王富生, 李立州, 王新军, 等. 鸟体材料参数的一种反演方法 [J]. 航空学报, 2007, 28(2): 344–347. doi: 10.3321/j.issn:1000-6893.2007.02.018WANG F S, LI L Z, WANG X J, et al. A method to identify bird’s material parameters [J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(2): 344–347. doi: 10.3321/j.issn:1000-6893.2007.02.018 [6] LIU J, LI Y L, GAO X S. Bird strike on a flat plate: experiments and numerical simulations [J]. International Journal of Impact Engineering, 2014, 70: 21–37. doi: 10.1016/j.ijimpeng.2014.03.006 [7] 王计真, 刘小川. 鸟撞平板试验与鸟体本构参数识别方法 [J]. 航空学报, 2017, 38(Suppl 1): 721550. doi: 10.7527/S1000-6893.2017.721550WANG J Z, LIU X C. Test of bird striking on panel and identification method for bird constitutive parameters [J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(Suppl 1): 721550. doi: 10.7527/S1000-6893.2017.721550 [8] ZHANG Y L, ZHOU Y D. Evaluating constitutive models of smoothed particle hydrodynamics for bird-strike simulation [J]. International Journal of Crashworthiness, 2023: 1–10. doi: 10.1080/13588265.2023.2258650 [9] YU P, YU S L, HE S, et al. Inversion for constitutive model parameters of bird in case of bird striking [J]. Shock and Vibration, 2022: 2456777. doi: 10.1155/2022/2456777 [10] ZAKIR S M, LI Y L. Dynamic response of the leading edge wing under soft body impact [J]. International Journal of Crashworthiness, 2012, 17(4): 357–376. doi: 10.1080/13588265.2012.661239 [11] 冯振宇, 霍雨佳, 裴惠, 等. 明胶鸟弹撞击力传感器试验及数值建模方法研究 [J]. 振动与冲击, 2019, 38(12): 206–212. doi: 10.13465/j.cnki.jvs.2019.12.029FENG Z Y, HUO Y J, PEI H, et al. An experiment and numerical modeling method of gelatin bird striking on force sensors [J]. Journal of Vibration and Shock, 2019, 38(12): 206–212. doi: 10.13465/j.cnki.jvs.2019.12.029 [12] ASLAM M A, RAYHAN S B, KE Z G, et al. Ballistic gelatin Lagrange Mooney-Rivlin material model as a substitute of bird in finite element bird strike case studies [J]. Latin American Journal of Solids and Structures, 2020, 17(6): e298. doi: 10.1590/1679-78256215 [13] PERNAS-SÁNCHEZ J, ARTERO-GUERRERO J, VARAS D, et al. Artificial bird strike on Hopkinson tube device: experimental and numerical analysis [J]. International Journal of Impact Engineering, 2020, 138: 103477. doi: 10.1016/j.ijimpeng.2019.103477 [14] 刘小川, 郭军, 孙侠生, 等. 用于鸟撞试验的仿真鸟弹研究 [J]. 实验力学, 2012, 27(5): 623–629.LIU X C, GUO J, SUN X S, et al. Investigation on the artificial bird projectile used in bird strike test [J]. Journal of Experimental Mechanics, 2012, 27(5): 623–629. [15] YANG X F, LIU M B, PENG S L. Smoothed particle hydrodynamics modeling of viscous liquid drop without tensile instability [J]. Computers & Fluids, 2014, 92: 199–208. doi: 10.1016/j.compfluid.2014.01.002 [16] 刘军, 李玉龙, 郭伟国, 等. 鸟撞45#钢平板动响应试验研究 [J]. 振动与冲击, 2013, 32(4): 15–20. doi: 10.3969/j.issn.1000-3835.2013.04.004LIU J, LI Y L, GUO W G, et al. Tests for bird striking on a plate made of 45# steel [J]. Journal of Vibration and Shock, 2013, 32(4): 15–20. doi: 10.3969/j.issn.1000-3835.2013.04.004 [17] HE Q G, CHEN X W, CHEN J F. Finite element-smoothed particle hydrodynamics adaptive method in simulating debris cloud [J]. Acta Astronautica, 2020, 175: 99–117. doi: 10.1016/j.actaastro.2020.05.056 [18] LAVOIE M A, GAKWAYA A, ENSAN M N, et al. Validation of available approaches for numerical bird strike modeling tools [J]. International Review of Mechanical Engineering, 2007, 1(4): 380–389. [19] WILBECK J S. Impact behavior of low strength projectiles [D]. College Station: Texas A&M University, 1977. [20] JOHNSON A F, HOLZAPFEL M. Modelling soft body impact on composite structures [J]. Composite Structures, 2003, 61(1/2): 103–113. doi: 10.1016/S0263-8223(03)00033-3 [21] AIROLDI A, CACCHIONE B. Modelling of impact forces and pressures in Lagrangian bird strike analyses [J]. International Journal of Impact Engineering, 2006, 32(10): 1651–1677. doi: 10.1016/j.ijimpeng.2005.04.011 [22] JENQ S T, HSIAO F B, LIN I C, et al. Simulation of a rigid plate hit by a cylindrical hemi-spherical tip-ended soft impactor [J]. Computational Materials Science, 2007, 39(3): 518–526. doi: 10.1016/j.commatsci.2006.08.008 [23] THO C H, SMITH M R. Accurate bird strike simulation methodology for BA609 tiltrotor [J]. Journal of the American Helicopter Society, 2011, 56(1): 12007. doi: 10.4050/JAHS.56.012007 [24] MEGUID S A, MAO R H, NG T Y. FE analysis of geometry effects of an artificial bird striking an aeroengine fan blade [J]. International Journal of Impact Engineering, 2008, 35(6): 487–498. doi: 10.1016/j.ijimpeng.2007.04.008 [25] SMOJVER I, IVANČEVIĆ D. Numerical simulation of bird strike damage prediction in airplane flap structure [J]. Composite Structures, 2010, 92(9): 2016–2026. doi: 10.1016/j.compstruct.2009.12.006 [26] SMOJVER I, IVANČEVIĆ D. Advanced modelling of bird strike on high lift devices using hybrid Eulerian-Lagrangian formulation [J]. Aerospace Science and Technology, 2012, 23(1): 224–232. doi: 10.1016/j.ast.2011.07.010 [27] HEDAYATI R, SADIGHI M, MOHAMMADI-AGHDAM M. On the difference of pressure readings from the numerical, experimental and theoretical results in different bird strike studies [J]. Aerospace Science and Technology, 2014, 32(1): 260–266. doi: 10.1016/j.ast.2013.10.008 -






 下载:
下载: