基于神经网络势函数计算地球内核条件下的铁-硫合金黏度

徐云帆; 何宇; 张为; 李和平

doi:10.11858/gywlxb.20251221

基于神经网络势函数计算地球内核条件下的铁-硫合金黏度

doi: 10.11858/gywlxb.20251221

徐云帆^{1, 2, 3,},
何宇^{1, 2, 3,*, ,},
张为⁴,
李和平^{1, 2}

1.
中国科学院地球化学研究所关键矿产成矿与预测全国重点实验室, 贵州贵阳　550081
2.
中国科学院地球化学研究所地球内部物质高温高压重点实验室, 贵州贵阳　550081
3.
中国科学院大学, 北京　100049
4.
贵州师范大学喀斯特研究院, 贵州贵阳　550025

基金项目: 国家自然科学基金（42350002，42074104）；中国科学院青年交叉团队项目（JCTD-2022-1）；中国科学院青年创新促进会项目（2020394）；贵州省2020年科技专项补助项目（NGZ2020SIG）

详细信息

作者简介:
徐云帆（1997－），男，博士研究生，主要从事高温高压下地球内部物质性质的计算模拟研究. E-mail：xuyunfan@mail.gyig.ac.cn

通讯作者:
何　宇（1985－），男，博士，研究员，主要从事高温高压下地球内部物质性质的计算模拟研究. E-mail：heyu@mail.gyig.ac.cn

中图分类号: O521.2
计量
- 文章访问数: 91
- HTML全文浏览量: 33
- PDF下载量: 6
出版历程
- 收稿日期: 2025-10-09
- 修回日期: 2025-12-11
- 录用日期: 2025-12-12
- 网络出版日期: 2025-11-26

Viscosity of Iron-Sulfur Alloy under the Conditions of the Earth Inner Core Calculated Based on the Neural Network Potential

XU Yunfan^{1, 2, 3
,},
HE Yu^{1, 2, 3,*
, ,},
ZHANG Wei⁴,
LI Heping^{1, 2}

1.
State Key Laboratory of Critical Mineral Research and Exploration, Institute of Geochemistry, Chinese Academy of Sciences, Guiyang 550081, Guizhou, China
2.
Key Laboratory of High-Temperature and High-Pressure Study of the Earth’s Interior, Institute of Geochemistry, Chinese Academy of Sciences, Guiyang 550081, Guizhou, China
3.
University of Chinese Academy of Sciences, Beijing 100049, China
4.
School of Karst Science, Guizhou Normal University, Guiyang 550025, Guizhou, China

摘要

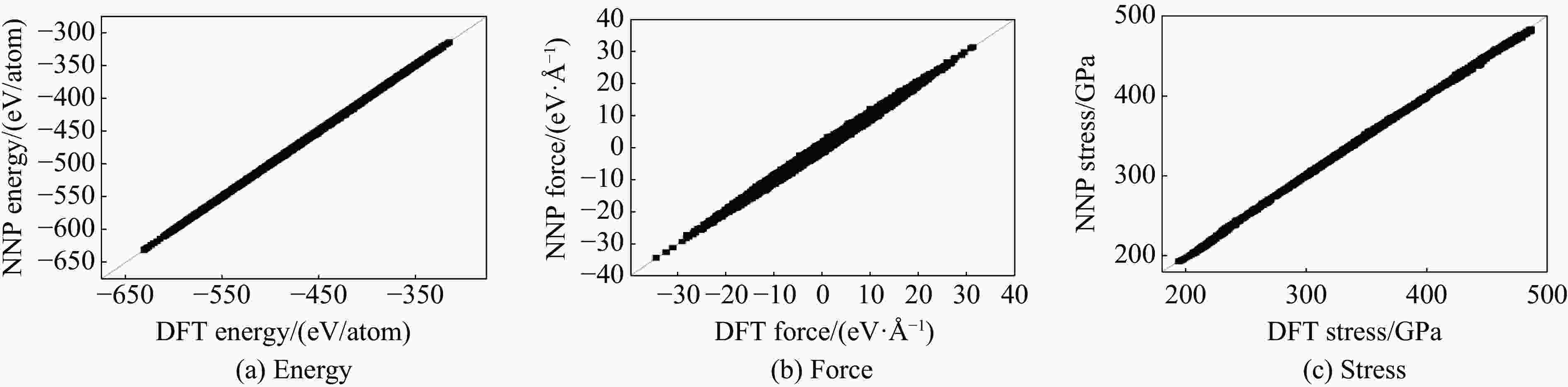
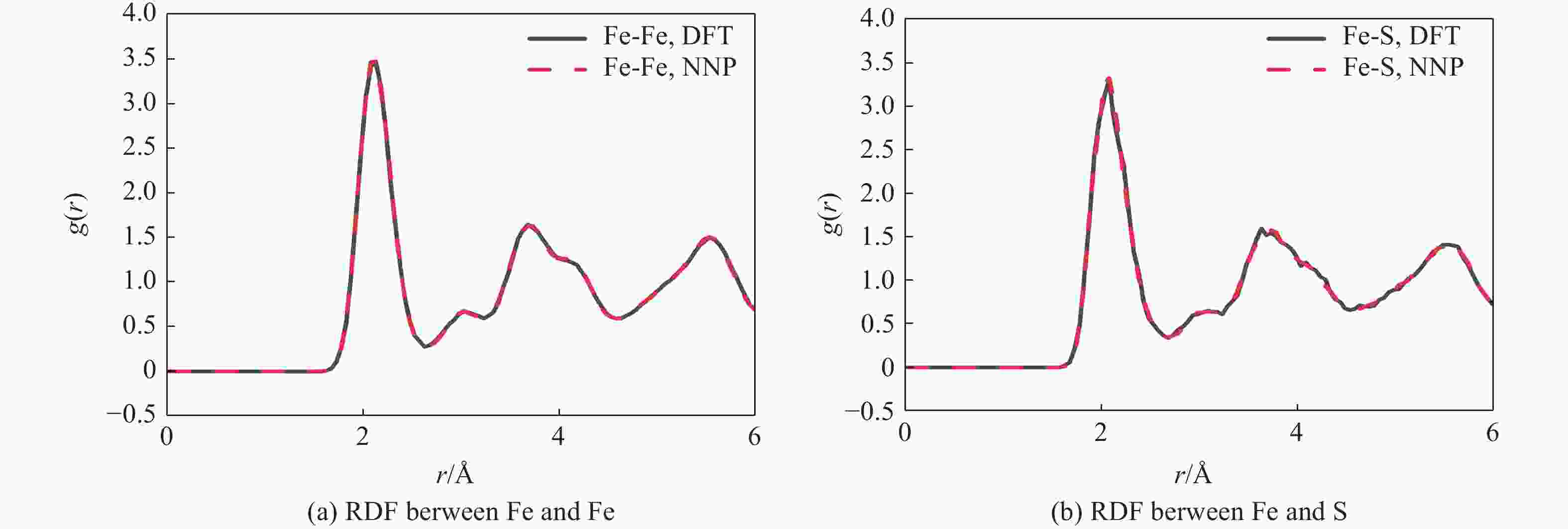
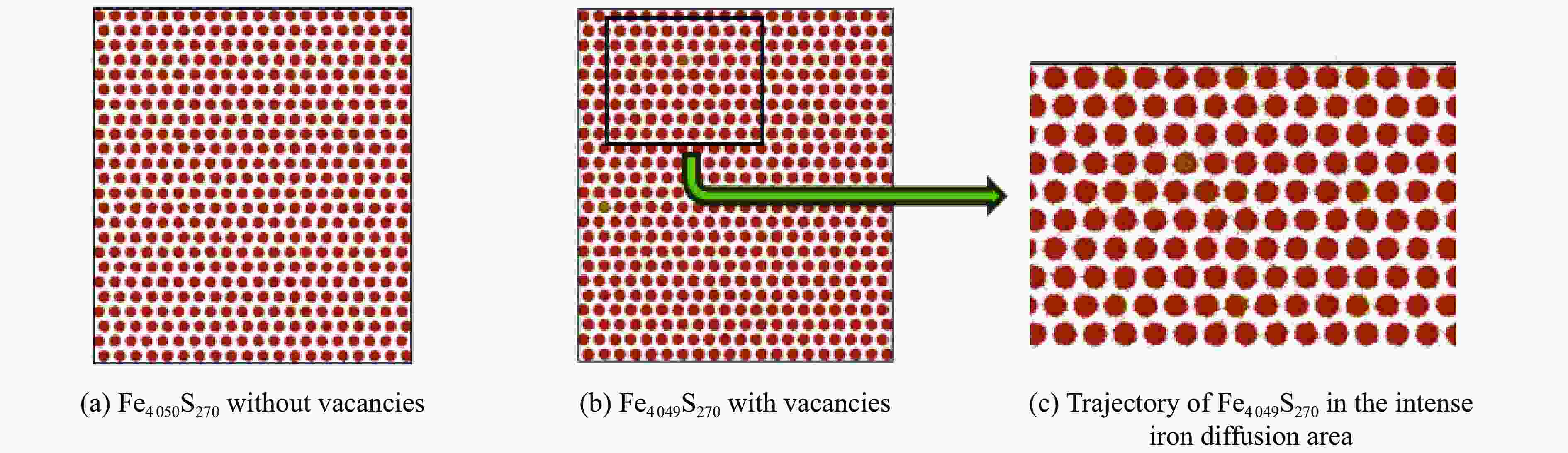
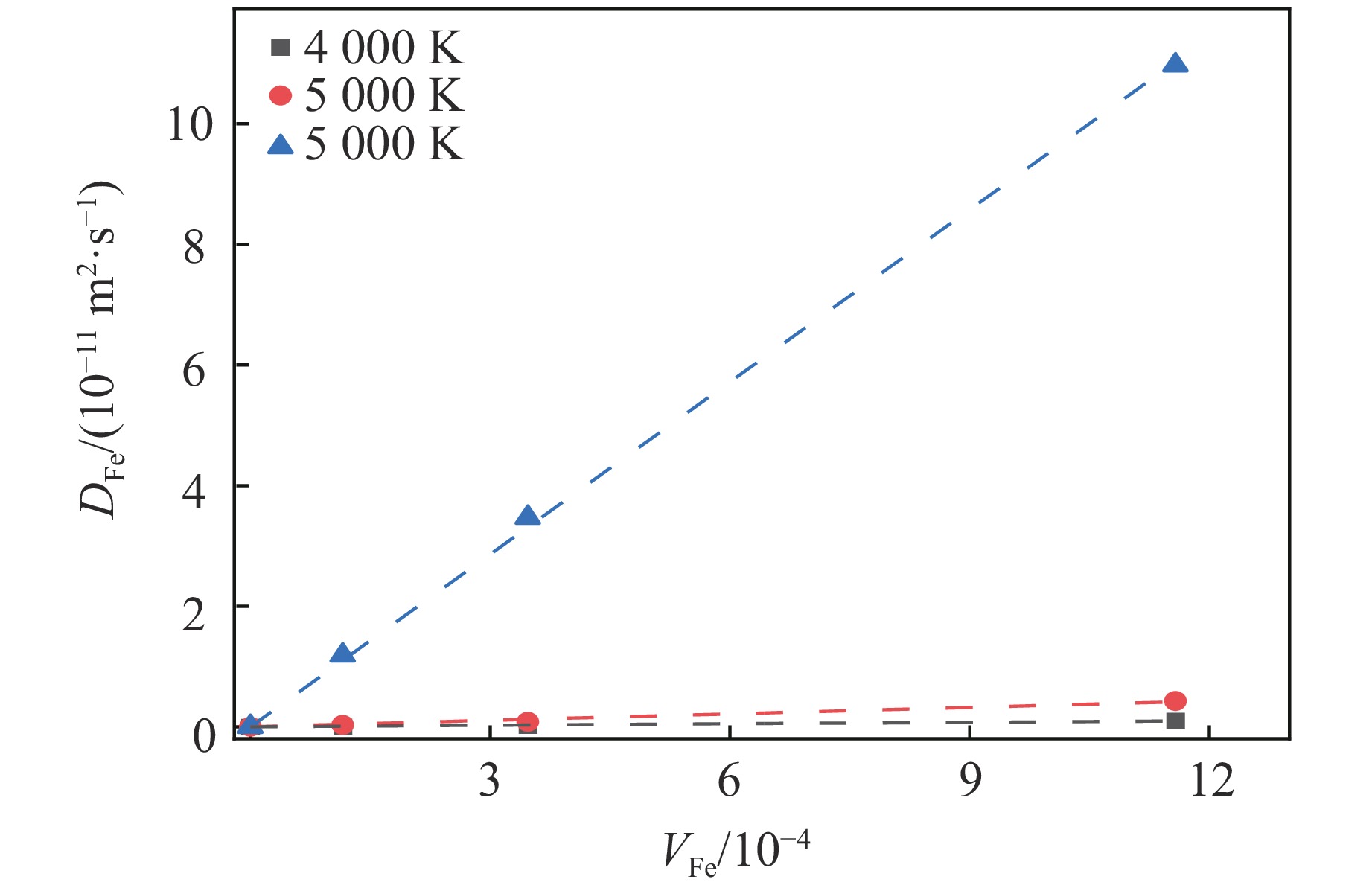
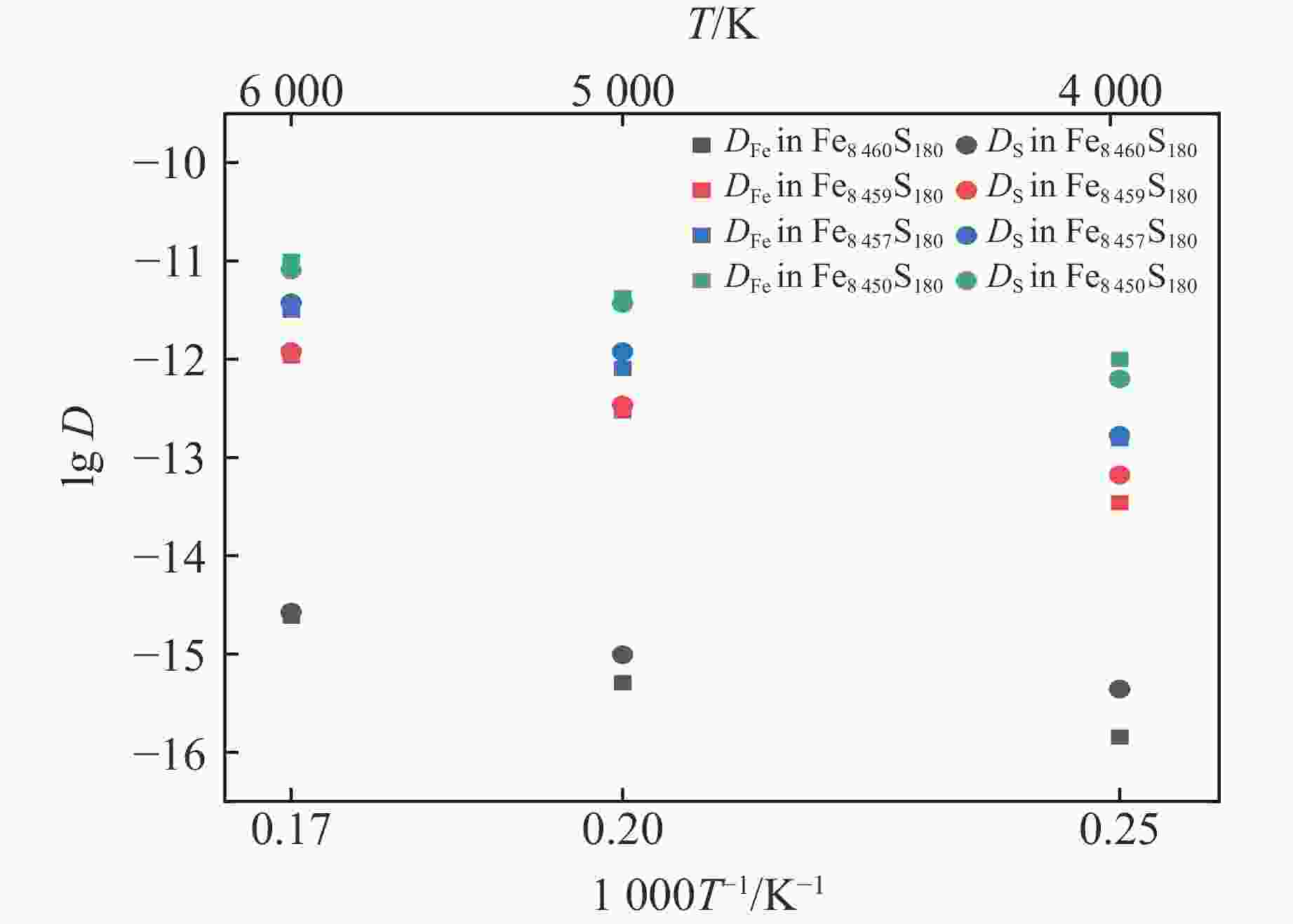
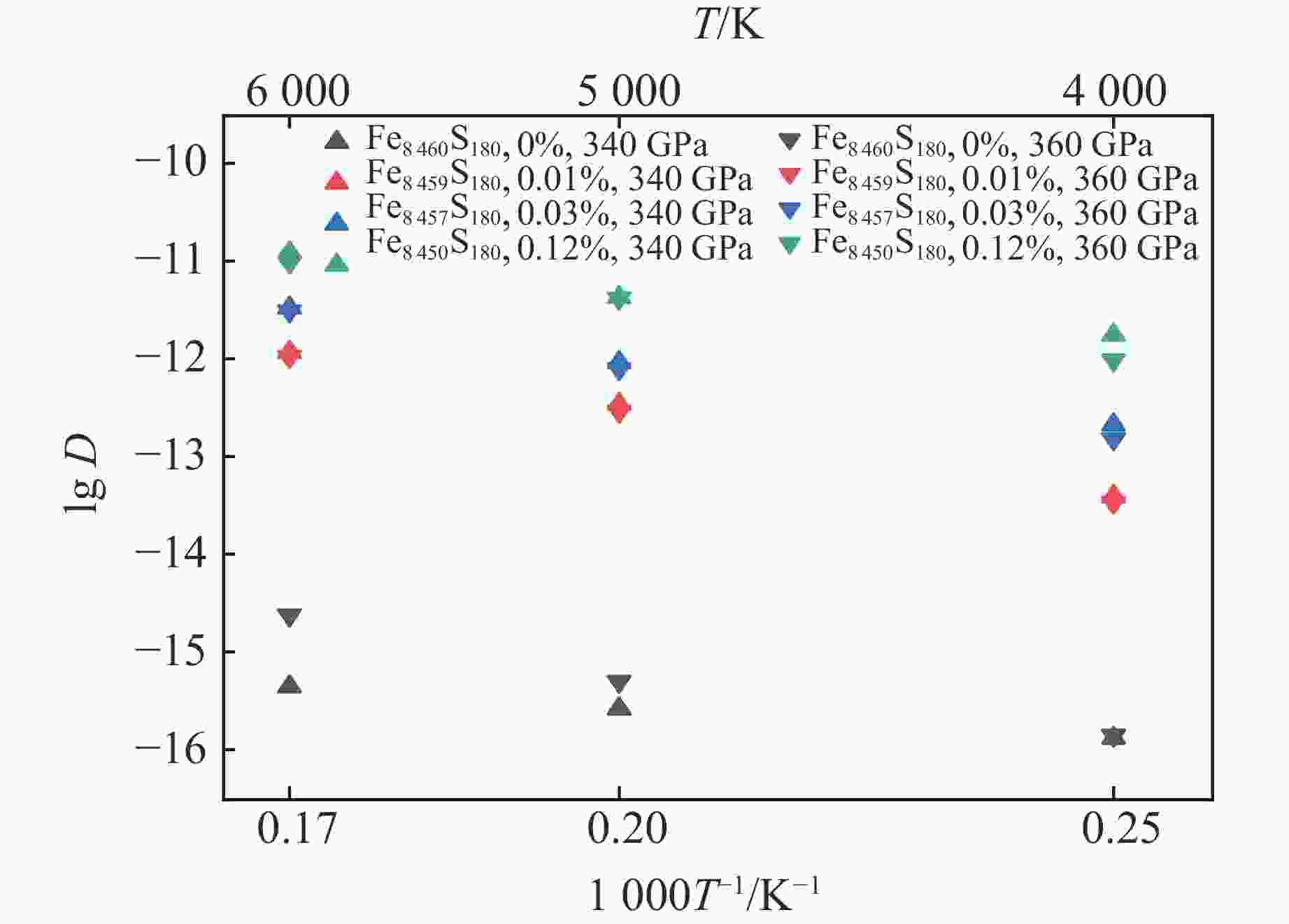
摘要: 地球内核的密度较纯铁低，表明其中存在轻元素。碳、氢、氧、硫、硅被认为是最可能存在于内核的轻元素。黏度是反映地球内核动力学和演化历史的关键物理量，对于地球内核波速各向异性的成因具有重要影响。前人已对内核条件下纯铁的六方密堆积相（hexagonal close-packed, HCP）和体心立方相（body-centered cubic, BCC）的黏度进行了模拟计算。然而，目前仍然缺乏针对地球内核中轻元素对地球内核黏度影响的系统性研究。为此，构建了内核条件下铁-硫合金的神经网络势函数，利用该方法实现了对铁-硫体系的大规模分子动力学模拟，研究了空位浓度低至0.01%时对该合金离子输运性质的影响。利用晶格中铁的自扩散系数研究了内核铁-硫合金的蠕变机制和黏度，将地球内核条件下铁-硫合金的黏度限定为1×10¹⁴～2×10¹⁶ Pa·s，与自由核章动以及地震波观测结果一致。
- 神经网络势函数 /
- 地球内核 /
- 自扩散系数 /
- 黏度 /
- 分子动力学
Abstract: The density of the Earth’s inner core is lower than that of pure iron, indicating the presence of light elements. Among the candidate elements, carbon, hydrogen, oxygen, sulfur, and silicon are considered the most likely. Viscosity is a key physical property controlling the dynamics and evolutionary history of the inner core, and it has significant implications for the origin of seismic anisotropy. Previous studies have investigated the viscosity of pure iron in its hexagonal close-packed (HCP) and body-centered cubic (BCC) phases under inner-core conditions through computational simulations. However, the influence of light elements on the viscosity of the inner core remains insufficiently constrained. In this study, we constructed a neural-network potential (NNP) for Fe-S alloy under inner-core conditions and employed it to perform large-scale molecular dynamics simulations. We systematically examined the impact of vacancy concentrations as low as 0.01% on the ionic transport properties of Fe-S alloy. Based on the self-diffusion coefficients of Fe in the lattice, we further explored the creep mechanisms and viscosity of Fe-S alloy under core conditions. Our results indicate that dislocation creep dominates the rheological behavior, yielding viscosities of 1×10¹⁴–2×10¹⁶ Pa·s, consistent with constraints from free-core nutation and seismic observations.
- neural-network potential /
- Earth’s inner core /
- self-diffusion coefficient /
- viscosity /
- molecular dynamics

HTML全文

图 1 初始结构

Figure 1. Original structure

下载: 全尺寸图片幻灯片

图 2 流程图

Figure 2. Flow chart

下载: 全尺寸图片幻灯片

图 3 势函数模拟的能量、受力、应力的均方根误差

Figure 3. Energy, force and stress root mean squared error of potential function

下载: 全尺寸图片幻灯片

图 4 6 000 K和360 GPa下的神经网络势的RDF^[76]

Figure 4. RDF of neural-network potential at 6 000 K and 360 GPa^[76]

下载: 全尺寸图片幻灯片

图 5 360 GPa和6 000 K条件下空位浓度为0.01%的Fe-S合金经10 ps弛豫后的结构

Figure 5. Structure of the Fe-S alloy with a vacancy concentration of 0.01% after 10 ps relaxation at 360 GPa and 6 000 K

下载: 全尺寸图片幻灯片

图 6 360 GPa和6 000 K条件下Fe₄₀₅₀S₂₇₀无空穴和Fe₄₀₄₉S₂₇₀含空穴体系的轨迹叠加图像

Figure 6. Trajectories of Fe₄₀₅₀S₂₇₀ without vacancies and Fe₄₀₄₉S₂₇₀ with vacancies at 360 GPa and 6 000 K

下载: 全尺寸图片幻灯片

图 7 360 GPa、不同温度下Fe原子的扩散系数随空位浓度的变化

Figure 7. Variation of the diffusion coefficient of Fe iron with vacancy concentrations at different temperatures at 360 GPa

下载: 全尺寸图片幻灯片

图 8 360 GPa下不同空穴浓度下2种组分的自扩散系数

Figure 8. Diffusion coefficients of two elements at different vacancy concentrations at 360 GPa

下载: 全尺寸图片幻灯片

图 9 340和360 GPa下不同空位浓度铁的自扩散系数

Figure 9. Iron diffusion coefficients at 340 and 360 GPa with different vacancy concentrations

下载: 全尺寸图片幻灯片

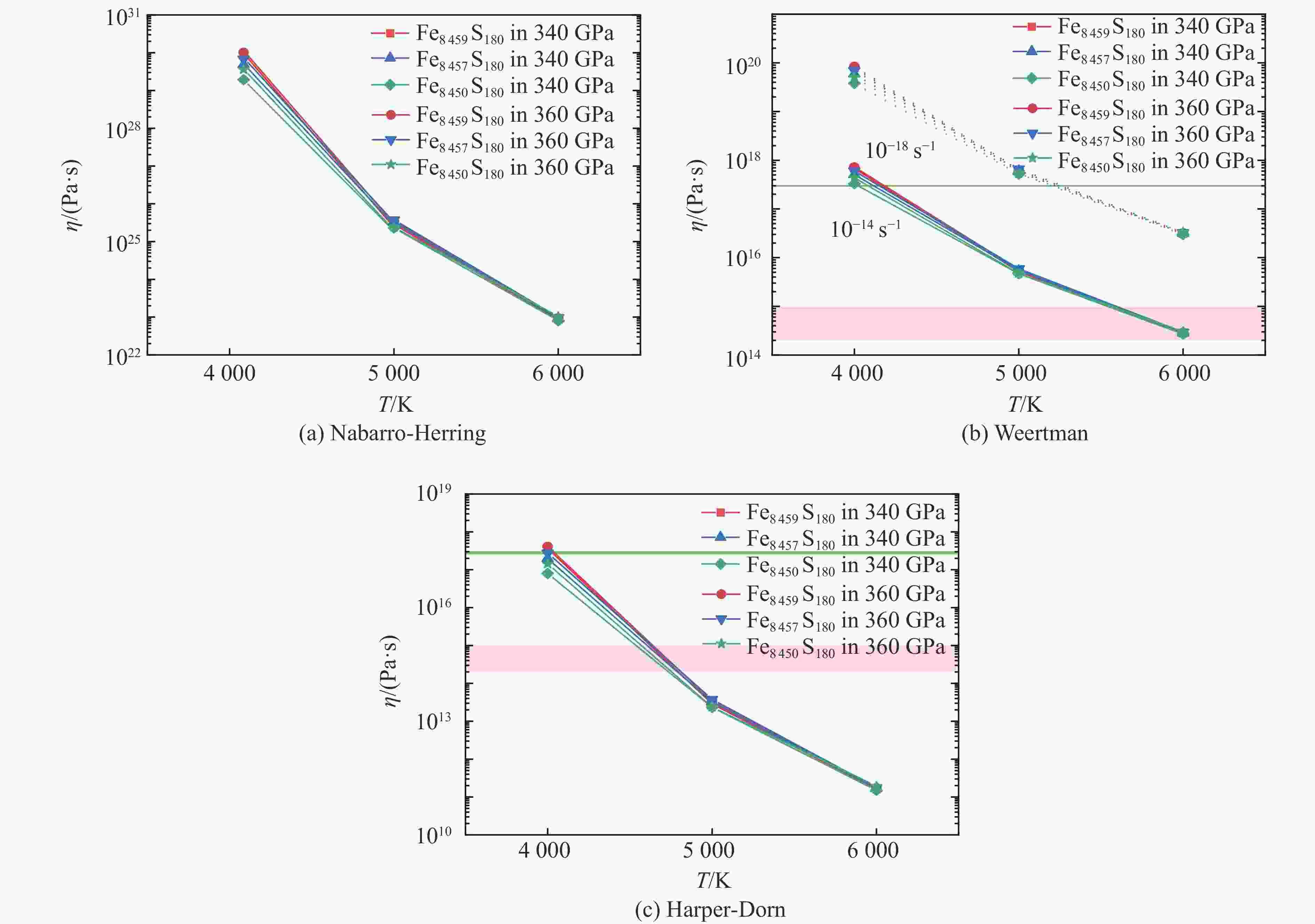
图 10 340和 360 GPa条件下不同蠕变模型预测的黏度结果（粉色区域表示自由核章动对地球内核黏度的约束^[85]，绿色区域表示核幔引力耦合对地球内核黏度的约束^[84]）

Figure 10. Viscosities predicted by different creap models at 340 and 360 GPa (The pink region represents the constraint on inner-core viscosity from free-core nutation^[85], while the green region denotes the constraint from core-mantle gravitational coupling^[84].)

下载: 全尺寸图片幻灯片

表 1 不同训练模型的参数

Table 1. Parameters of different training model

Model	Descriptor	Rcut_smth/Å	Rcut/Å	Neuron	Learning rate type	Start_lr
DP-GEN	se_e2_a	1.5	6.0	[240, 240, 240]	Exp.	0.001
DeePMD-kit	se_e2_a	1.5	6.0	[240, 240, 240]	Exp.	0.001

Model	Stop_lr	Start_pref_e	Limit_pref_e	Start_pref_f	Limit_pref_f	Stop_batch
DP-GEN	3.54×10^–7	0.02	1	1 000	1	8×10⁵
DeePMD-kit	3.54×10^–7	0.02	1	1 000	1	1×10⁷

下载: 导出CSV

参考文献(91)

[1]	ROSENBLATT F. The perceptron: a probabilistic model for information storage and organization in the brain [J]. Psychological Review, 1958, 65(6): 386–408. doi: 10.1037/h0042519
[2]	RUMELHART D E, HINTON G E, WILLIAMS R J. Learning representations by back-propagating errors [J]. Nature, 1986, 323(6088): 533–536. doi: 10.1038/323533a0
[3]	HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks [J]. Science, 2006, 313(5786): 504–507. doi: 10.1126/science.1127647
[4]	朱玉富, 赵春风, 周志航. 基于机器学习的钢筋混凝土板在爆炸作用下的最大位移预测模型 [J]. 高压物理学报, 2023, 37(2): 024205. doi: 10.11858/gywlxb.20220667 ZHU Y F, ZHAO C F, ZHOU Z H. Prediction model of maximum displacement for RC slabs under blast load based on machine learning [J]. Chinese Journal of High Pressure Physics, 2023, 37(2): 024205. doi: 10.11858/gywlxb.20220667
[5]	姬广富. 极端条件下含能材料的模拟研究思考 [J]. 高压物理学报, 2025, 39(1): 010102. doi: 10.11858/gywlxb.20240911 JI G F. Some viewpoints on the simulation research of energetic materials under extreme conditions [J]. Chinese Journal of High Pressure Physics, 2025, 39(1): 010102. doi: 10.11858/gywlxb.20240911
[6]	邓溥, 侯瑞, 赵英亮, 等. 消失的石英-柯石英路径: 基于机器学习模拟的二氧化硅相变机理探究 [J/OL]. 高压物理学报 (2025-08-22)[2025-10-09]. https://link.cnki.net/urlid/51.1147.O4.20250822.1059.004. DENG P, HOU R, ZHAO Y L, et al. The disappearing quartz-coesite path: the phase transition mechanism of silicon dioxide from machine learning simulations [J/OL]. Chinese Journal of High Pressure Physics (2025-08-22)[2025-10-09]. https://link.cnki.net/urlid/51.1147.O4.20250822.1059.004.
[7]	李君, 宋佳和, 季伟, 等. 碳化硼陶瓷动态力学行为与延展性增强机制的深度势能分子动力学研究进展 [J]. 高压物理学报, 2025, 39(11): 110102. doi: 10.11858/gywlxb.20251129 LI J, SONG J H, JI W, et al. Dynamical mechanical behaviors and enhanced ductility mechanisms of boron carbide based on deep potential molecular dynamics simulations [J]. Chinese Journal of High Pressure Physics, 2025, 39(11): 110102. doi: 10.11858/gywlxb.20251129
[8]	何宇, 孙士川, 李和平. 地球内核超离子态铁合金及其效应 [J]. 高压物理学报, 2024, 38(3): 030202. doi: 10.11858/gywlxb.20240707 HE Y, SUN S C, LI H P. Superionic iron alloys in Earth’s inner core and their effects [J]. Chinese Journal of High Pressure Physics, 2024, 38(3): 030202. doi: 10.11858/gywlxb.20240707
[9]	ZHANG Y J, WANG Y, HUANG Y Q, et al. Collective motion in hcp-Fe at Earth’s inner core conditions [J]. Proceedings of the National Academy of Sciences of the United States of America, 2023, 120(41): e2309952120. doi: 10.1073/pnas.2309952120
[10]	曾启昱, 陈博, 康冬冬, 等. 大规模、量子精度的分子动力学模拟: 以极端条件液态铁为例 [J]. 物理学报, 2023, 72(18): 187102. doi: 10.7498/aps.72.20231258 ZENG Q Y, CHEN B, KANG D D, et al. Large scale and quantum accurate molecular dynamics simulation: liquid iron under extreme condition [J]. Acta Physica Sinica, 2023, 72(18): 187102. doi: 10.7498/aps.72.20231258
[11]	UNKE O T, CHMIELA S, GASTEGGER M, et al. SpookyNet: learning force fields with electronic degrees of freedom and nonlocal effects [J]. Nature Communications, 2021, 12(1): 7273. doi: 10.1038/s41467-021-27504-0
[12]	BATATIA I, KOVÁCS D P, SIMM G N C, et al. MACE: higher order equivariant message passing neural networks for fast and accurate force fields [C]//Proceedings of the 36th International Conference on Neural Information Processing Systems. New Orleans: Curran Associates Inc., 2022: 830.
[13]	SMITH J S, ISAYEV O, ROITBERG A E. ANI-1: an extensible neural network potential with DFT accuracy at force field computational cost [J]. Chemical Science, 2017, 8(4): 3192–3203. doi: 10.1039/C6SC05720A
[14]	MUELLER T, HERNANDEZ A, WANG C H. Machine learning for interatomic potential models [J]. The Journal of Chemical Physics, 2020, 152(5): 050902. doi: 10.1063/1.5126336
[15]	SCHÜTT K T, SAUCEDA H E, KINDERMANS P J, et al. SchNet—a deep learning architecture for molecules and materials [J]. The Journal of Chemical Physics, 2018, 148(24): 241722. doi: 10.1063/1.5019779
[16]	BATZNER S, MUSAELIAN A, SUN L X, et al. E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials [J]. Nature Communications, 2022, 13(1): 2453. doi: 10.1038/s41467-022-29939-5
[17]	ZHANG L F, HAN J Q, WANG H, et al. Deep potential molecular dynamics: a scalable model with the accuracy of quantum mechanics [J]. Physical Review Letters, 2018, 120(14): 143001. doi: 10.1103/PhysRevLett.120.143001
[18]	WU F L, WU S Q, WANG C Z, et al. Melting temperature of iron under the Earth’s inner core condition from deep machine learning [J]. Geoscience Frontiers, 2024, 15(6): 101925. doi: 10.1016/j.gsf.2024.101925
[19]	WU F L, SUN Y, WAN T Q, et al. Deep-learning-based prediction of the tetragonal → cubic transition in davemaoite [J]. Geophysical Research Letters, 2024, 51(12): e2023GL108012. doi: 10.1029/2023GL108012
[20]	PENG Y H, DENG J. Thermal conductivity of MgSiO₃-H₂O system determined by machine learning potentials [J]. Geophysical Research Letters, 2024, 51(5): e2023GL107245. doi: 10.1029/2023GL107245
[21]	WAN T Q, LUO C X, SUN Y, et al. Thermoelastic properties of bridgmanite using deep-potential molecular dynamics [J]. Physical Review B, 2024, 109(9): 094101. doi: 10.1103/PhysRevB.109.094101
[22]	DENG J. Large-scale atomistic simulations of magnesium oxide exsolution driven by machine learning potentials: implications for the early geodynamo [J]. Geophysical Research Letters, 2024, 51(16): e2024GL109793. doi: 10.1029/2024GL109793
[23]	YUAN L, STEINLE-NEUMANN G. Hydrogen distribution between the Earth’s inner and outer core [J]. Earth and Planetary Science Letters, 2023, 609: 118084. doi: 10.1016/j.jpgl.2023.118084
[24]	SUN S C, HE Y, YANG J Y, et al. Superionic effect and anisotropic texture in Earth’s inner core driven by geomagnetic field [J]. Nature Communications, 2023, 14(1): 1656. doi: 10.1038/s41467-023-37376-1
[25]	DENG J, NIU H Y, HU J W, et al. Melting of MgSiO₃ determined by machine learning potentials [J]. Physical Review B, 2023, 107: 064103. doi: 10.1103/PhysRevB.107.064103
[26]	LI Z, SCANDOLO S. Elasticity and viscosity of hcp iron at Earth’s inner core conditions from machine learning-based large-scale atomistic simulations [J]. Geophysical Research Letters, 2022, 49(24): e2022GL101161. doi: 10.1029/2022GL101161
[27]	YANG F H, ZENG Q Y, CHEN B, et al. Lattice thermal conductivity of MgSiO₃ perovskite and post-perovskite under lower mantle conditions calculated by deep potential molecular dynamics [J]. Chinese Physics Letters, 2022, 39(11): 116301. doi: 10.1088/0256-307X/39/11/116301
[28]	DENG J, STIXRUDE L. Thermal conductivity of silicate liquid determined by machine learning potentials [J]. Geophysical Research Letters, 2021, 48(17): e2021GL093806. doi: 10.1029/2021GL093806
[29]	LUO H Y, KARKI B B, GHOSH D B, et al. Anomalous behavior of viscosity and electrical conductivity of MgSiO₃ melt at mantle conditions [J]. Geophysical Research Letters, 2021, 48(13): e2021GL093573. doi: 10.1029/2021GL093573
[30]	FU J, CAO L Z, DUAN X M, et al. Density and sound velocity of liquid Fe-S alloys at Earth’s outer core p-T conditions [J]. American Mineralogist, 2020, 105(9): 1349–1354. doi: 10.2138/am-2020-7349
[31]	THOMPSON S, KOMABAYASHI T, BRETON H, et al. Compression experiments to 126 GPa and 2 500 K and thermal equation of state of Fe₃S: implications for sulphur in the Earth’s core [J]. Earth and Planetary Science Letters, 2020, 534: 116080. doi: 10.1016/j.jpgl.2020.116080
[32]	KAMADA S, OHTANI E, FUKUI H, et al. The sound velocity measurements of Fe₃S [J]. American Mineralogist, 2014, 99(1): 98–251. doi: 10.2138/am.2014.4463
[33]	HUANG H J, WU S J, HU X J, et al. Shock compression of Fe-FeS mixture up to 204 GPa [J]. Geophysical Research Letters, 2013, 40(4): 687–691. doi: 10.1002/grl.50180
[34]	SEAGLE C T, CAMPBELL A J, HEINZ D L, et al. Thermal equation of state of Fe₃S and implications for sulfur in Earth’s core [J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B6): B06209. doi: 10.1029/2005JB004091
[35]	DEUSS A. Heterogeneity and anisotropy of Earth’s inner core [J]. Annual Review of Earth and Planetary Sciences, 2014, 42(1): 103–126. doi: 10.1146/annurev-earth-060313-054658
[36]	LI Y G, VOČADLO L, BRODHOLT J P. The elastic properties of hcp-Fe alloys under the conditions of the Earth’s inner core [J]. Earth and Planetary Science Letters, 2018, 493: 118–127. doi: 10.1016/j.jpgl.2018.04.013
[37]	BERENDSEN H J C, VAN DER SPOEL D, VAN DRUNEN R. GROMACS: a message-passing parallel molecular dynamics implementation [J]. Computer Physics Communications, 1995, 91(1/2/3): 43–56. doi: 10.1016/0010-4655(95)00042-E
[38]	THOMPSON A P, AKTULGA H M, BERGER R, et al. LAMMPS—a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales [J]. Computer Physics Communications, 2022, 271: 108171. doi: 10.1016/j.cpc.2021.108171
[39]	LABROSSE S, MACOUIN M. The inner core and the geodynamo La graine et la géodynamo [J]. Comptes Rendus Geoscience, 2003, 335(1): 37–50. doi: 10.1016/S1631-0713(03)00013-0
[40]	FIQUET G, GUYOT F, BADRO J. The Earth’s lower mantle and core [J]. Elements, 2008, 4(3): 177–182. doi: 10.2113/GSELEMENTS.4.3.177
[41]	BELONOSHKO A B, SKORODUMOVA N V, ROSENGREN A, et al. Elastic anisotropy of Earth’s inner core [J]. Science, 2008, 319(5864): 797–800. doi: 10.1126/science.1150302
[42]	TANAKA S. Depth extent of hemispherical inner core from PKP(DF) and PKP(Cdiff) for equatorial paths [J]. Physics of the Earth and Planetary Interiors, 2012, 210/211: 50–62. doi: 10.1016/j.pepi.2012.08.001
[43]	FROST D A, LASBLEIS M, CHANDLER B, et al. Dynamic history of the inner core constrained by seismic anisotropy [J]. Nature Geoscience, 2021, 14(7): 531–535. doi: 10.1038/s41561-021-00761-w
[44]	MONNEREAU M, CALVET M, MARGERIN L, et al. Lopsided growth of Earth’s inner core [J]. Science, 2010, 328(5981): 1014–1017. doi: 10.1126/science.1186212
[45]	MORELLI A, DZIEWOŃSKI A M, WOODHOUSE J H. Anisotropy of the inner core inferred from PKIKP travel times [J]. Geophysical Research Letters, 1986, 13(13): 1545–1548. doi: 10.1029/GL013i013p01545
[46]	SU W J, DZIEWOŃSKI A M. Inner core anisotropy in three dimensions [J]. Journal of Geophysical Research: Solid Earth, 1995, 100(B6): 9831–9852. doi: 10.1029/95JB00746
[47]	ISHII M, DZIEWOŃSKI A M. The innermost inner core of the Earth: evidence for a change in anisotropic behavior at the radius of about 300 km [J]. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(22): 14026–14030. doi: 10.1073/pnas.172508499
[48]	SUN X L, SONG X D. The inner inner core of the Earth: texturing of iron crystals from three-dimensional seismic anisotropy [J]. Earth and Planetary Science Letters, 2008, 269(1/2): 56–65. doi: 10.1016/j.jpgl.2008.01.049
[49]	PHẠM T S, TKALČIĆ H. Up-to-fivefold reverberating waves through the Earth’s center and distinctly anisotropic innermost inner core [J]. Nature Communications, 2023, 14(1): 754. doi: 10.1038/s41467-023-36074-2
[50]	NIU F L, WEN L X. Hemispherical variations in seismic velocity at the top of the Earth’s inner core [J]. Nature, 2001, 410(6832): 1081–1084. doi: 10.1038/35074073
[51]	IRVING J C E, DEUSS A. Hemispherical structure in inner core velocity anisotropy [J]. Journal of Geophysical Research, 2011, 116(B4): B04307. doi: 10.1029/2010JB007942
[52]	WASZEK L, DEUSS A. Distinct layering in the hemispherical seismic velocity structure of Earth’s upper inner core [J]. Journal of Geophysical Research, 2011, 116(B12): B12313. doi: 10.1029/2011JB008650
[53]	BRETT H, DEUSS A. Inner core anisotropy measured using new ultra-polar PKIKP paths [J]. Geophysical Journal International, 2020, 223(2): 1230–1246. doi: 10.1093/gji/ggaa348
[54]	WEN L X, NIU F L. Seismic velocity and attenuation structures in the top of the Earth’s inner core [J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B11): 2273. doi: 10.1029/2001JB000170
[55]	TANAKA S, HAMAGUCHI H. Degree one heterogeneity and hemispherical variation of anisotropy in the inner core from PKP(BC)–PKP(DF) times [J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B2): 2925–2938. doi: 10.1029/96JB03187
[56]	CREAGER K C. Large-scale variations in inner core anisotropy [J]. Journal of Geophysical Research: Solid Earth, 1999, 104(B10): 23127–23139. doi: 10.1029/1999JB900162
[57]	LYTHGOE K H, DEUSS A, RUDGE J F, et al. Earthʼs inner core: innermost inner core or hemispherical variations? [J]. Earth and Planetary Science Letters, 2014, 385: 181–189. doi: 10.1016/j.jpgl.2013.10.049
[58]	GARCIA R, SOURIAU A. Inner core anisotropy and heterogeneity level [J]. Geophysical Research Letters, 2000, 27(19): 3121–3124. doi: 10.1029/2000GL008520
[59]	YU W C, WEN L X. Seismic velocity and attenuation structures in the top 400 km of the Earth’s inner core along equatorial paths [J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B7): B07308. doi: 10.1029/2005JB003995
[60]	ORESHIN S I, VINNIK L P. Heterogeneity and anisotropy of seismic attenuation in the inner core [J]. Geophysical Research Letters, 2004, 31(2): L02613. doi: 10.1029/2003GL018591
[61]	JACKSON I, GERALD J D F, KOKKONEN H. High-temperature viscoelastic relaxation in iron and its implications for the shear modulus and attenuation of the Earth’s inner core [J]. Journal of Geophysical Research: Solid Earth, 2000, 105(B10): 23605–23634. doi: 10.1029/2000JB900131
[62]	GLEASON A E, MAO W L. Strength of iron at core pressures and evidence for a weak Earth’s inner core [J]. Nature Geoscience, 2013, 6(7): 571–574. doi: 10.1038/ngeo1808
[63]	NISHIHARA Y, DOI S, TSUJINO N, et al. Rheology of hexagonal close-packed (hcp) iron [J]. Journal of Geophysical Research: Solid Earth, 2023, 128(6): e2022JB026165. doi: 10.1029/2022JB026165
[64]	VAN ORMAN J A. On the viscosity and creep mechanism of Earth’s inner core [J]. Geophysical Research Letters, 2004, 31(20): L20606. doi: 10.1029/2004GL021209
[65]	REAMAN D M, COLIJN H O, YANG F Y, et al. Interdiffusion of Earth’s core materials to 65 GPa and 2 200 K [J]. Earth and Planetary Science Letters, 2012, 349/350: 8–14. doi: 10.1016/j.jpgl.2012.06.053
[66]	RITTERBEX S, TSUCHIYA T. Viscosity of hcp iron at Earth’s inner core conditions from density functional theory [J]. Scientific Reports, 2020, 10(1): 6311. doi: 10.1038/s41598-020-63166-6
[67]	BELONOSHKO A B, FU J, BRYK T, et al. Low viscosity of the Earth’s inner core [J]. Nature Communications, 2019, 10(1): 2483. doi: 10.1038/s41467-019-10346-2
[68]	SUN Y, ZHANG F, MENDELEV M I, et al. Two-step nucleation of the Earth’s inner core [J]. Proceedings of the National Academy of Sciences of the United States of America, 2022, 119(2): e2113059119. doi: 10.1073/pnas.2113059119
[69]	BOUJIBAR A, ANDRAULT D, BOUHIFD M A, et al. Metal-silicate partitioning of sulphur, new experimental and thermodynamic constraints on planetary accretion [J]. Earth and Planetary Science Letters, 2014, 391: 42–54. doi: 10.1016/j.jpgl.2014.01.021
[70]	ZHANG Z G, CSÁNYI G, ALFÈ D. Partitioning of sulfur between solid and liquid iron under Earth’s core conditions: constraints from atomistic simulations with machine learning potentials [J]. Geochimica et Cosmochimica Acta, 2020, 291: 5–18. doi: 10.1016/j.gca.2020.03.028
[71]	ZURKOWSKI C C, LAVINA B, BRAUSER N M, et al. Pressure-induced C23–C37 transition and compression behavior of orthorhombic Fe₂S to Earth’s core pressures and high temperatures [J]. American Mineralogist, 2022, 107(10): 1878–1885. doi: 10.2138/am-2022-8187
[72]	THOMPSON S, SUGIMURA-KOMABAYASHI E, KOMABAYASHI T, et al. High-pressure melting experiments of Fe₃S and a thermodynamic model of the Fe-S liquids for the Earth’s core [J]. Journal of Physics: Condensed Matter, 2022, 34(39): 394003. doi: 10.1088/1361-648X/ac8263
[73]	ZURKOWSKI C C, LAVINA B, CASE A, et al. Fe₅S₂ identified as a host of sulfur in Earth and planetary cores [J]. Earth and Planetary Science Letters, 2022, 593: 117650. doi: 10.1016/j.jpgl.2022.117650
[74]	OKA K, TATENO S, KUWAYAMA Y, et al. A cotunnite-type new high-pressure phase of Fe₂S [J]. American Mineralogist, 2022, 107(7): 1249–1253. doi: 10.2138/am-2022-7959
[75]	ZHANG Y Z, WANG H D, CHEN W J, et al. DP-GEN: a concurrent learning platform for the generation of reliable deep learning based potential energy models [J]. Computer Physics Communications, 2020, 253: 107206. doi: 10.1016/j.cpc.2020.107206
[76]	XU Y F, HE Y, SUN S C, et al. Viscosities of hcp iron alloys under Earth’s inner core conditions [J]. Geoscience Frontiers, 2025, 16(1): 101935. doi: 10.1016/j.gsf.2024.101935
[77]	HIREL P. Atomsk: a tool for manipulating and converting atomic data files [J]. Computer Physics Communications, 2015, 197: 212–219. doi: 10.1016/j.cpc.2015.07.012
[78]	VIDALE J E, WANG W, WANG R Y, et al. Annual-scale variability in both the rotation rate and near surface of Earth’s inner core [J]. Nature Geoscience, 2025, 18(3): 267–272. doi: 10.1038/s41561-025-01642-2
[79]	BERGMAN M I. Estimates of the Earth’s inner core grain size [J]. Geophysical Research Letters, 1998, 25(10): 1593–1596. doi: 10.1029/98GL01239
[80]	KARATO S I. Seismic anisotropy of the Earth’s inner core resulting from flow induced by Maxwell stresses [J]. Nature, 1999, 402(6764): 871–873. doi: 10.1038/47235
[81]	YAMAZAKI D, TSUJINO N, YONEDA A, et al. Grain growth of ε-iron: implications to grain size and its evolution in the Earth’s inner core [J]. Earth and Planetary Science Letters, 2017, 459: 238–243. doi: 10.1016/j.jpgl.2016.11.049
[82]	REAMAN D M, DAEHN G S, PANERO W R. Predictive mechanism for anisotropy development in the Earth’s inner core [J]. Earth and Planetary Science Letters, 2011, 312(3/4): 437–442. doi: 10.1016/j.jpgl.2011.10.038
[83]	BLUM W, MAIER W. Harper-Dorn creep — a myth? [J]. 3.0.CO;2-8">Physica Status Solidi (A), 1999, 171(2): 467–474. doi: 10.1002/(SICI)1521-396X(199902)171:2<467::AID-PSSA467>3.0.CO;2-8
[84]	DUMBERRY M, BLOXHAM J. Inner core tilt and polar motion [J]. Geophysical Journal International, 2002, 151(2): 377–392. doi: 10.1046/j.1365-246X.2002.01756.x
[85]	KOOT L, DUMBERRY M. Viscosity of the Earth’s inner core: constraints from nutation observations [J]. Earth and Planetary Science Letters, 2011, 308(3/4): 343–349. doi: 10.1016/j.jpgl.2011.06.004
[86]	GLATZMAIERS G A, ROBERTS P H. A three-dimensional self-consistent computer simulation of a geomagnetic field reversal [J]. Nature, 1995, 377(6546): 203–209. doi: 10.1038/377203a0
[87]	SONG X D, RICHARDS P G. Seismological evidence for differential rotation of the Earth’s inner core [J]. Nature, 1996, 382(6588): 221–224. doi: 10.1038/382221a0
[88]	BUFFETT B A. Geodynamic estimates of the viscosity of the Earth’s inner core [J]. Nature, 1997, 388(6642): 571–573. doi: 10.1038/41534
[89]	JEANLOZ R, WENK H R. Convection and anisotropy of the inner core [J]. Geophysical Research Letters, 1988, 15(1): 72–75. doi: 10.1029/GL015i001p00072
[90]	ALBOUSSIÈRE T, DEGUEN R, MELZANI M. Melting-induced stratification above the Earth’s inner core due to convective translation [J]. Nature, 2010, 466(7307): 744–747. doi: 10.1038/nature09257
[91]	GOMI H, HIROSE K. Impurity resistivity of the Earth’s inner core [J]. Journal of Geophysical Research: Solid Earth, 2023, 128(11): e2023JB027097. doi: 10.1029/2023JB027097