高压下SrB<sub>2</sub>C<sub>2</sub>的结构相变与物性

郭华; 王凡; 郑宝兵

doi:10.11858/gywlxb.20251148

高压下SrB₂C₂的结构相变与物性

doi: 10.11858/gywlxb.20251148

宝鸡文理学院物理与光电技术学院, 陕西宝鸡　721016

基金项目: 陕西省自然科学基础研究计划项目（2025JC-YBMS-002）；陕西数理基础科学研究项目（23JSY009）

详细信息

作者简介:
郭　华（2000－），女，硕士研究生，主要从事计算凝聚态物理研究. E-mail：15929081276@163.com

通讯作者:
郑宝兵（1983－），男，博士，教授，主要从事计算凝聚态物理研究. E-mail：scu_zheng@163.com

中图分类号: O521.2
计量
- 文章访问数: 181
- HTML全文浏览量: 41
- PDF下载量: 16
出版历程
- 收稿日期: 2025-07-31
- 修回日期: 2025-08-19
- 网络出版日期: 2025-08-21

High-Pressure Study on Structural Phase Transformation and Physical Properties of SrB₂C₂

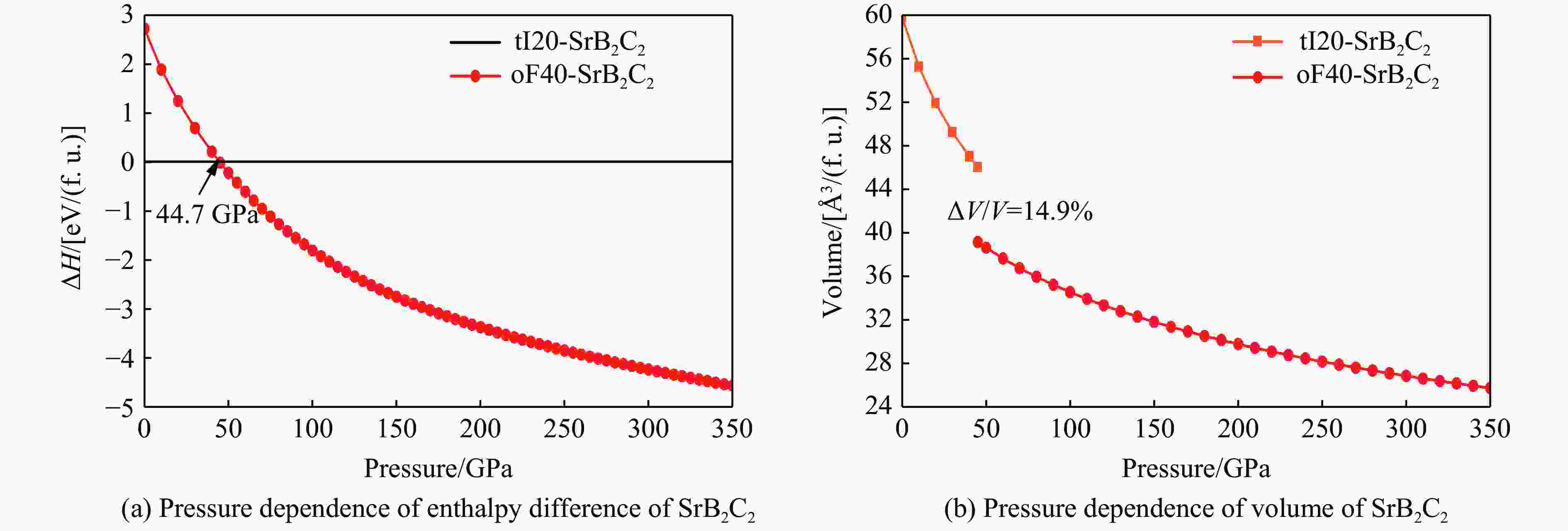
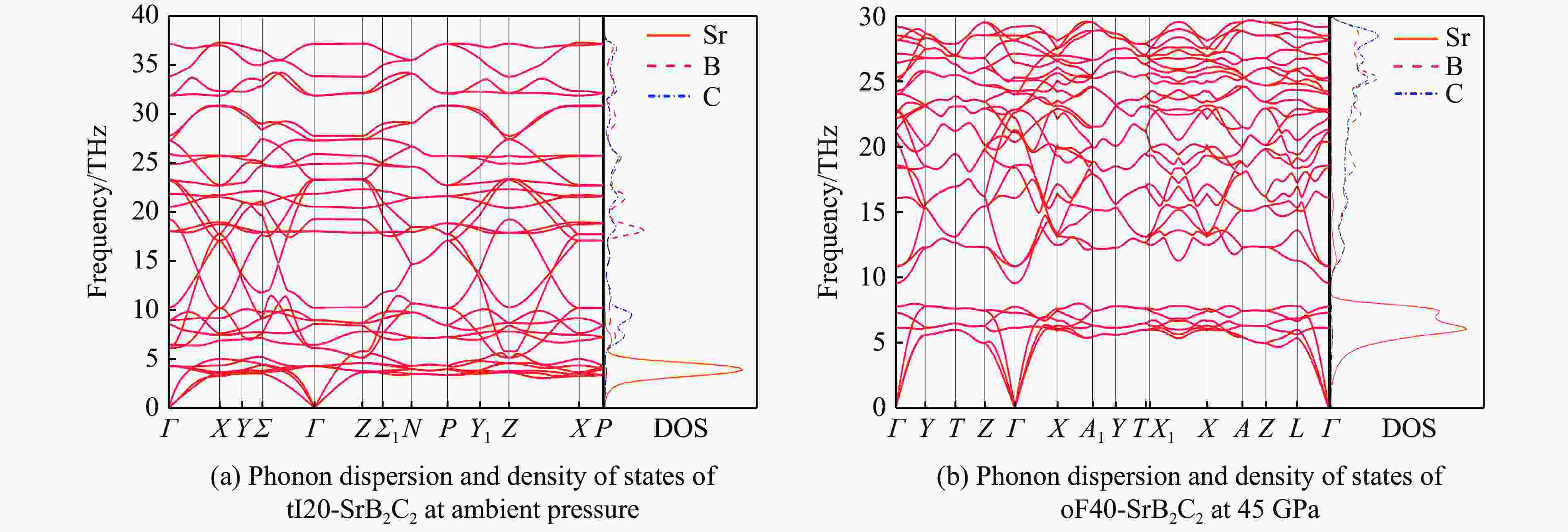
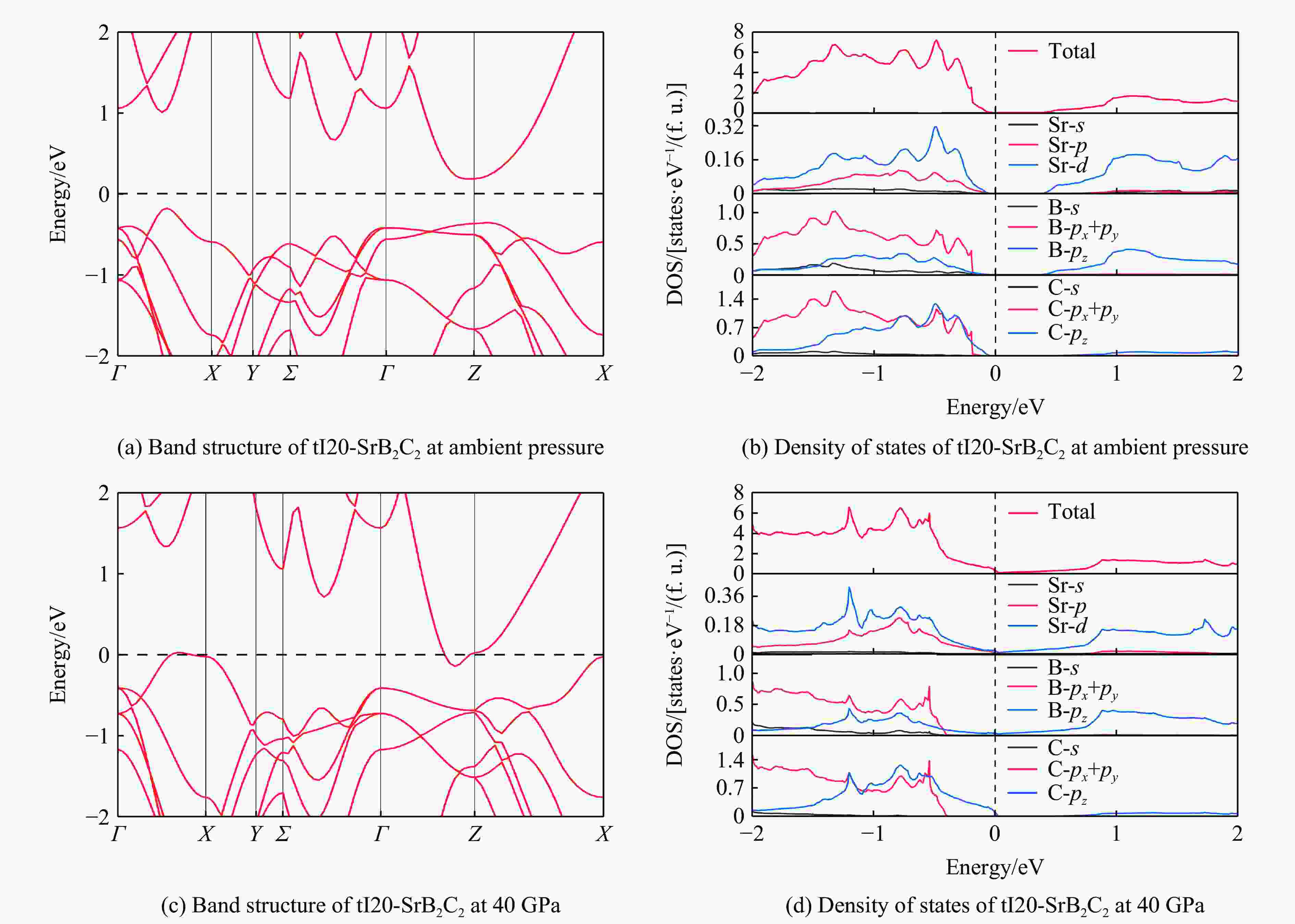
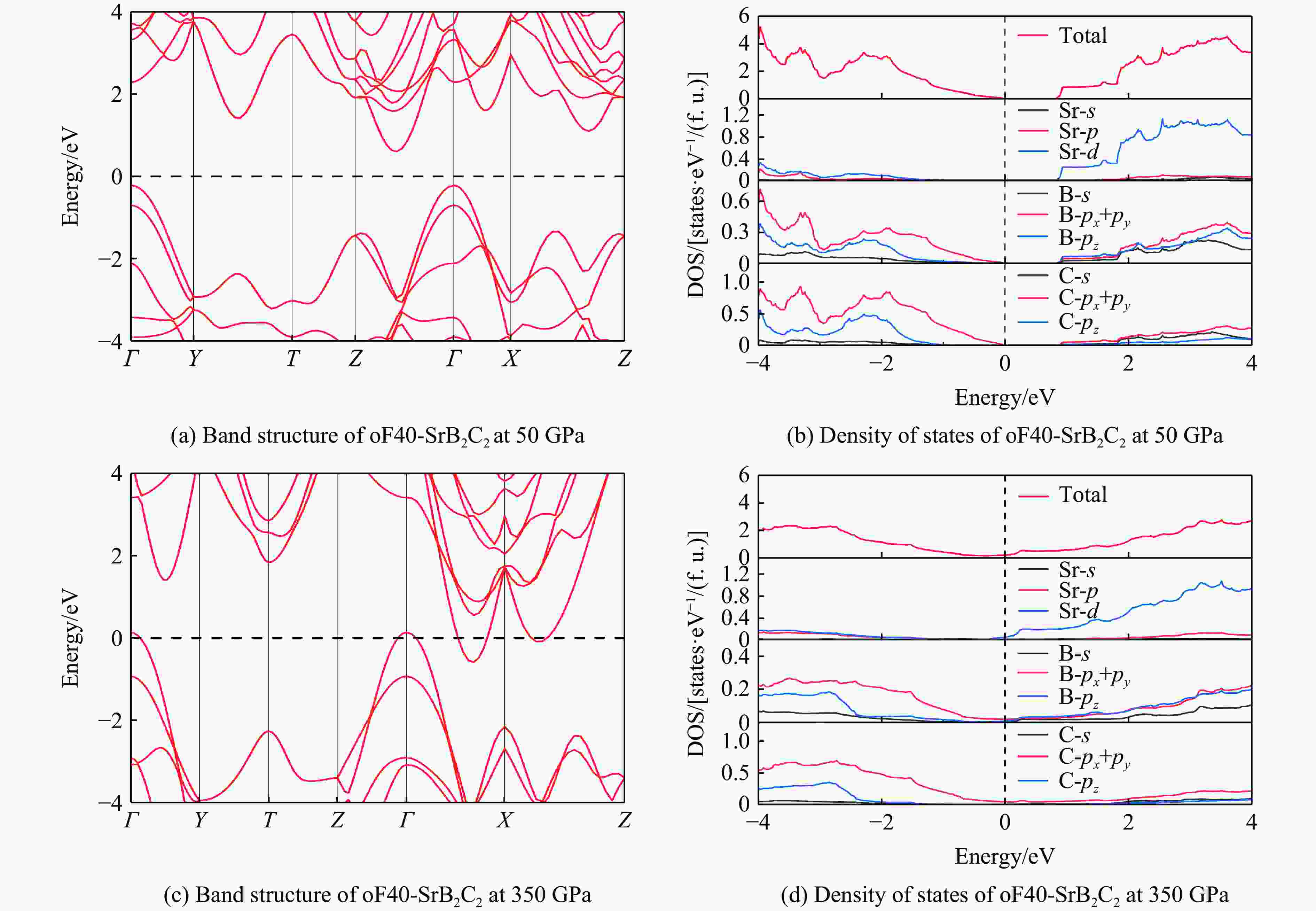
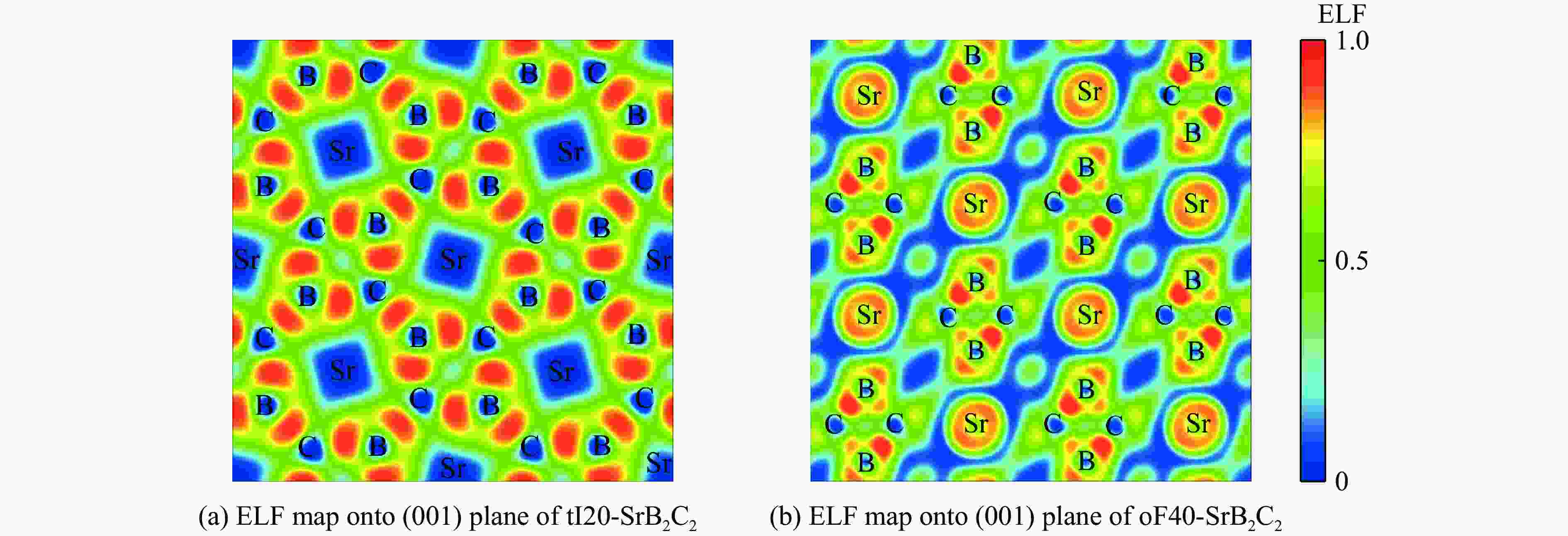
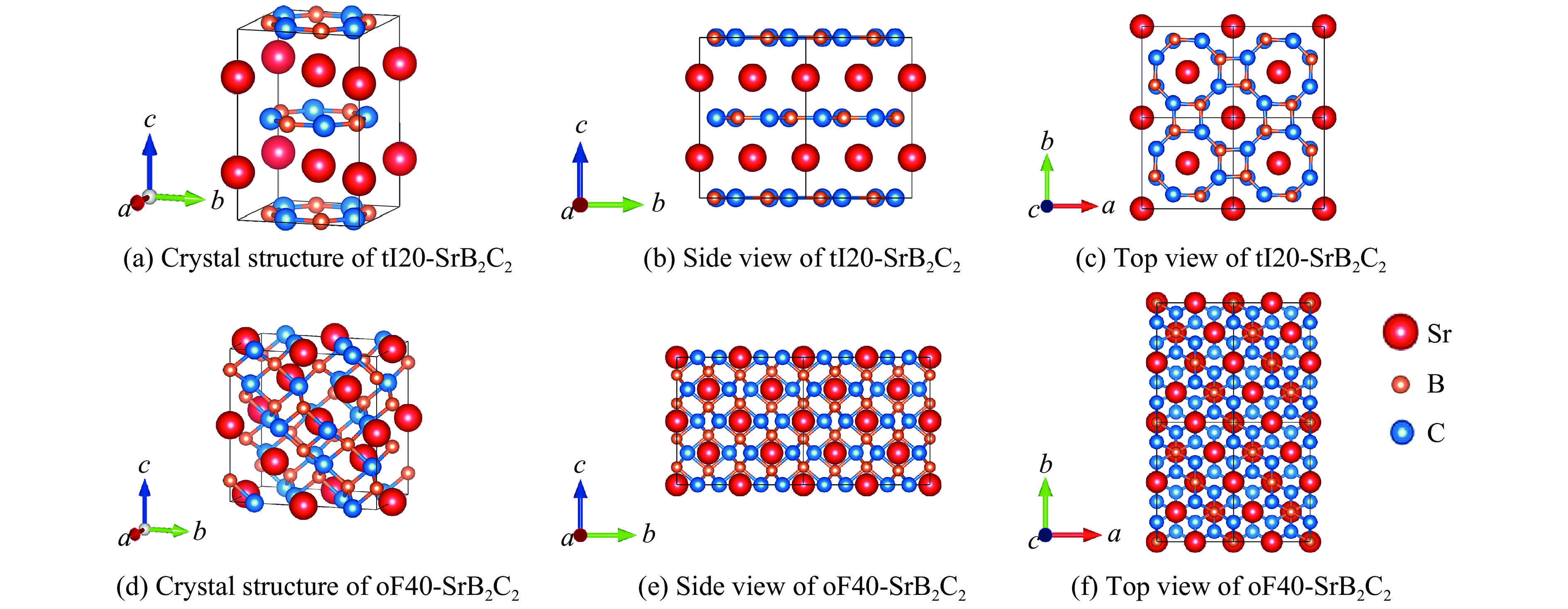
College of Physics and Optoelectronic Technology, Baoji University of Arts and Sciences, Baoji 721016, Shaanxi, China

摘要

摘要: 采用基于密度泛函理论的第一性原理计算方法和基于粒子群优化算法的结构预测方法，在0～350 GPa压力范围内对SrB₂C₂进行结构搜索，成功确定了SrB₂C₂在常压下是属于四方晶系的tI20-SrB₂C₂，在高压下是属于正交晶系的oF40-SrB₂C₂。基于焓差曲线，确定了SrB₂C₂的相变压力为44.7 GPa。通过计算声子谱、弹性常数和形成焓，验证了tI20-SrB₂C₂和oF40-SrB₂C₂在对应压力下的稳定性和实验合成的可能性。由不同方向的杨氏模量和剪切模量可以看出，tI20-SrB₂C₂具有比oF40-SrB₂C₂更明显的力学各向异性，主要是由于sp²杂化的硼碳键组成了层状结构的tI20-SrB₂C₂，而oF40-SrB₂C₂的硼碳键主要是sp³杂化的共价键，形成了更稳定的三维网状四面体结构。电子结构计算表明，SrB₂C₂均为间接带隙半导体，电子局域函数计算说明了tI20-SrB₂C₂和oF40-SrB₂C₂中的硼碳键分别为sp²和sp³共价键。
- SrB₂C₂ /
- 第一性原理计算 /
- 晶体结构预测 /
- 高压
Abstract: By employing the first-principles calculations and the structure prediction method, which are based on density functional theory and particle swarm optimization algorithm respectively, this work conducted a structural search of SrB₂C₂ in the pressure range of 0−350 GPa, and successfully determined the structure of tetragonal phase tI20-SrB₂C₂ at ambient pressure and orthorhombic phase oF40-SrB₂C₂ at high pressures. Based on the enthalpy difference curve of SrB₂C₂, the phase transition pressure was determined to be 44.7 GPa. Moreover, the stability and the possibility of experimental synthesis of tI20-SrB₂C₂ and oF40-SrB₂C₂ at the corresponding pressure were verified by calculating the phonon spectrum, elastic constants and formation enthalpy. In addition, the tI20-SrB₂C₂ has higher degree of mechanical anisotropy than oF40-SrB₂C₂, which can be seen from the Young’s modulus and shear modulus as a function of orientations. It can be ascribed to the fact that the sp²-hybridized boron-carbon bonds form the layered structure of tI20-SrB₂C₂, while the boron-carbon bonds of oF40-SrB₂C₂ are mainly sp³-hybridized covalent bonds, forming a more stable three-dimensional tetrahedral network structure. The electronic structure calculations show that SrB₂C₂ is an indirect band gap semiconductor, and the calculated electronic localization function reveals that the boron-carbon bonds in tI20-SrB₂C₂ and oF40-SrB₂C₂ are sp² and sp³ covalent bonds, respectively.
- SrB₂C₂ /
- first-principles calculations /
- crystal structure prediction /
- high pressure

HTML全文

图 1 tI20-SrB₂C₂的晶体结构(a)及其侧视图(b)和俯视图(c)，oF40-SrB₂C₂的晶体结构(d)及其侧视图(e)和俯视图(f)

Figure 1. Crystal structure of tI20-SrB₂C₂ (a), and side view (b) and top view (c) of it; the crystal structure of oF40-SrB₂C₂ (d), and side view (e) and top view (f) of it

下载: 全尺寸图片幻灯片

图 2 0～350 GPa压力下SrB₂C₂的焓差(a)和体积(b)随压力的变化曲线

Figure 2. Pressure dependence of enthalpy difference (a) and volume (b) of SrB₂C₂ from 0 GPa to 350 GPa

下载: 全尺寸图片幻灯片

图 3 (a) 常压下tI20-SrB₂C₂的声子色散谱和声子态密度，(b) 45 GPa下oF40-SrB₂C₂的声子色散谱和声子态密度

Figure 3. Phonon dispersion and density of states of (a) tI20-SrB₂C₂ at ambient pressure and (b) oF40-SrB₂C₂ at 45 GPa

下载: 全尺寸图片幻灯片

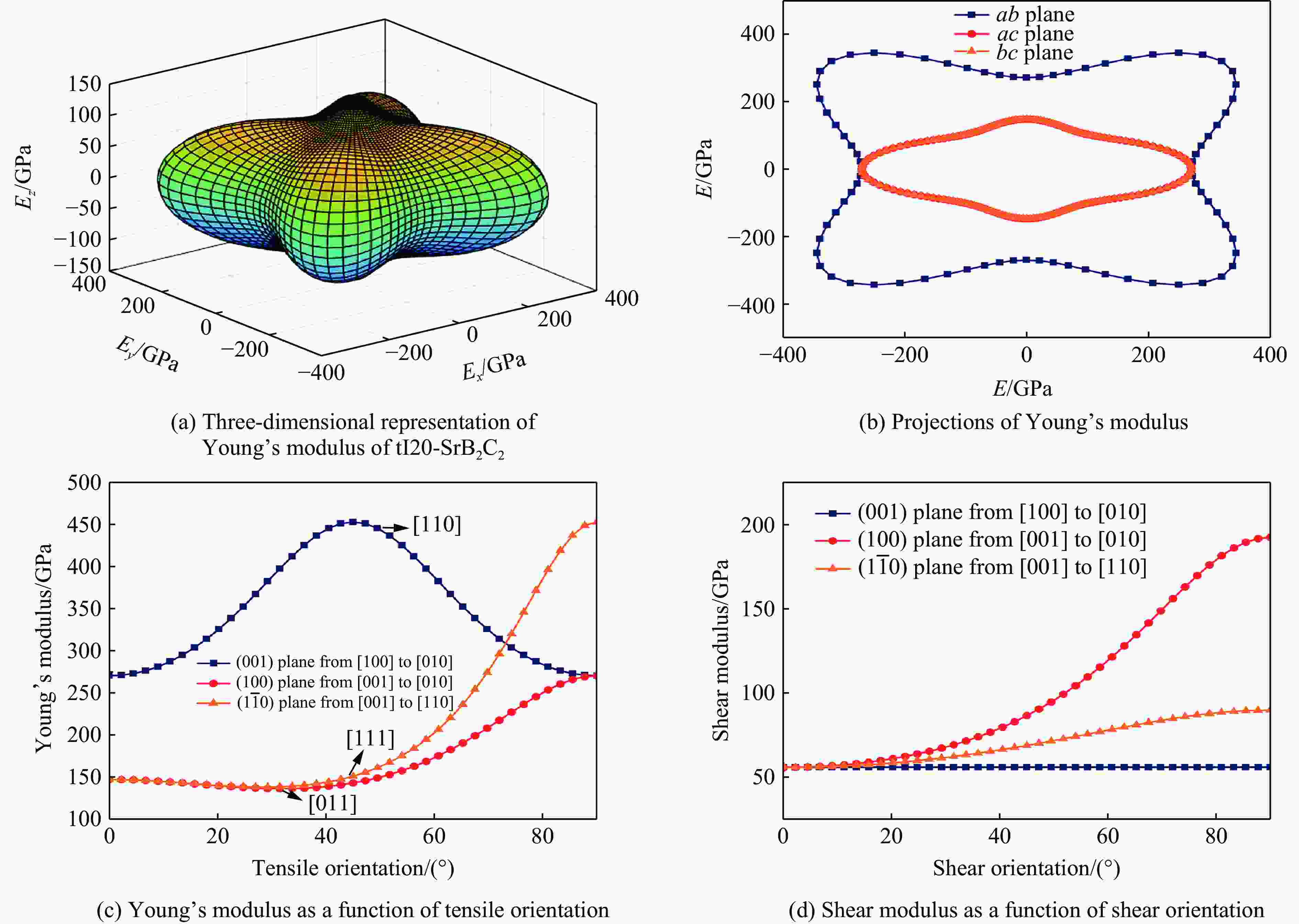
图 4 (a) tI20-SrB₂C₂的杨氏模量的三维表示，(b)杨氏模量在ab、ac和bc平面上的投影，(c) 不同平面的杨氏模量随应力方向的变化，(d) 剪切模量随应力方位的变化

Figure 4. (a) Three-dimensional representation of Young’s modulus of tI20-SrB₂C₂; (b) projections of Young’s modulus on ab, ac, and bc planes; (c) Young’s modulus as a function of tensile orientation in different planes; (d) shear modulus as a function of shear orientation in different planes

下载: 全尺寸图片幻灯片

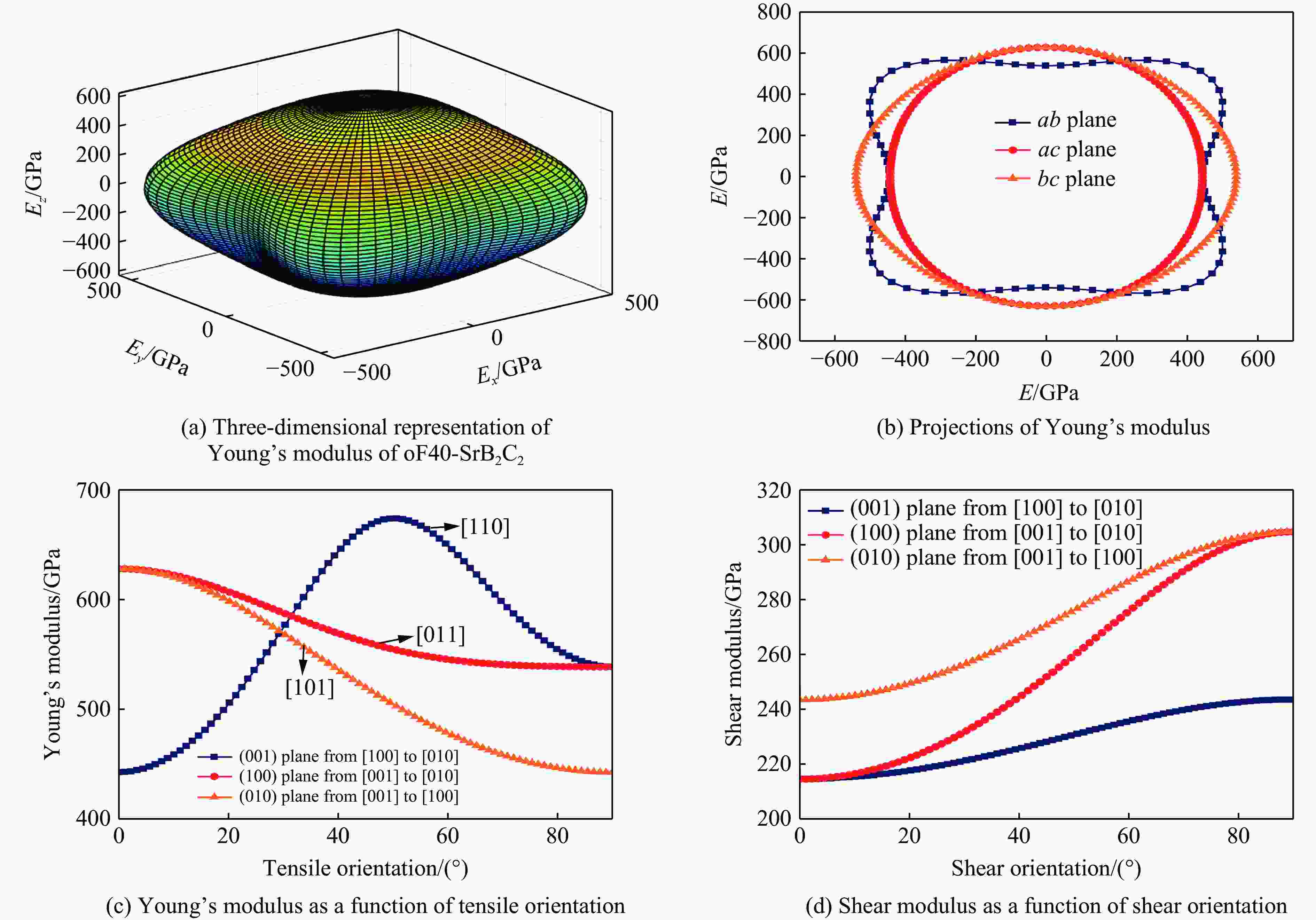
图 5 (a) oF40-SrB₂C₂的杨氏模量的三维表示，(b) 杨氏模量在ab、ac和bc平面的投影，(c) 不同平面的杨氏模量随应力方向的变化，(d) 剪切模量随应力方位的变化

Figure 5. (a) Three-dimensional representation of Young’s modulus of oF40-SrB₂C₂; (b) projections of Young’s modulus on ab, ac, and bc planes; (c) Young’s modulus as a function of tensile orientation in different planes; (d) shear modulus as a function of shear orientation in different planes

下载: 全尺寸图片幻灯片

图 6 常压下tI20-SrB₂C₂的能带(a)和电子态密度(b)以及40 GPa下tI20-SrB₂C₂的能带(c)和电子态密度(d)

Figure 6. Band structure (a) and density of states (b) of tI20-SrB₂C₂ at ambient pressure; band structure (c) and density of states (d) of tI20-SrB₂C₂ at 40 GPa

下载: 全尺寸图片幻灯片

图 7 50 GPa下oF40-SrB₂C₂的能带(a)和电子态密度(b)以及350 GPa下oF40-SrB₂C₂的能带(c)和电子态密度(d)

Figure 7. Band structure (a) and density of states (b) of oF40-SrB₂C₂at 50 GPa; band structure (c) and density of states (d) of oF40-SrB₂C₂ at 350 GPa

下载: 全尺寸图片幻灯片

图 8 常压下tI20-SrB₂C₂ (a)和45 GPa下oF40-SrB₂C₂ (b)在(001)面的电子局域函数图

Figure 8. ELF maps onto (001) plane of tI20-SrB₂C₂ at ambient pressure (a) and oF40-SrB₂C₂ at 45 GPa (b)

下载: 全尺寸图片幻灯片

表 1 tI20-SrB₂C₂ 和oF40-SrB₂C₂的晶格参数和原子位置

Table 1. Lattice parameters and atomic positions of tI20-SrB₂C₂ and oF40-SrB₂C₂

Phase	Pressure/GPa	Space group	Lattice parameters	Wyckoff position
tI20-SrB₂C₂	0	I4/mcm (No.140)	a=5.4139 Å,	Sr: 4a (0.0000, 0.0000, 0.7500)
			b=5.4139 Å,	B: 8h (0.8602, 0.6398, 0.0000)
			c=8.1714 Å	C: 8h (0.3418, 0.1582, 0.0000)
oF40-SrB₂C₂	45	Fddd (No.70)	a=5.0388 Å,	Sr: 8b (0.0000, 0.0000, 0.5000)
			b=7.8600 Å,	B: 16g (0.0000, 0.0000, 0.8617)
			c=7.9122 Å	C: 16f (0.2500, 0.0850, 0.2500)

下载: 导出CSV

表 2 tI20-SrB₂C₂和oF40-SrB₂C₂的独立弹性常数、体弹模量、杨氏模量、剪切模量和泊松比

Table 2. Independent elastic constants, bulk modulus, Young’s modulus, shear modulus and Poisson’s ratio of tI20-SrB₂C₂ at ambient pressure and oF40-SrB₂C₂ at 45 GPa

Compound	Pressure/GPa	C₁₁/GPa	C₁₂/GPa	C₁₃/GPa	C₂₂/GPa	C₂₃/GPa	C₃₃/GPa	C₄₄/GPa
tI20-SrB₂C₂	0	368.0	188.8	22.1			149.3	55.7
oF40-SrB₂C₂	45	541.5	222.2	168.9	638.4	143.3	690.9	243.5

Compound	Pressure/GPa	C₅₅/GPa	C₆₆/GPa	B/GPa	G/GPa	E/GPa	ν
tI20-SrB₂C₂	0		192.2	128.6	222.2	91.7	0.212
oF40-SrB₂C₂	45	214.6	304.7	326.1	573.5	237.6	0.207

下载: 导出CSV

参考文献(40)

[1]	NAGAMATSU J, NAKAGAWA N, MURANAKA T, et al. Superconductivity at 39 K in magnesium diboride [J]. Nature, 2001, 410(6824): 63–64. doi: 10.1038/35065039
[2]	SHAH S, KOLMOGOROV A N. Stability and superconductivity of Ca-B phases at ambient and high pressure [J]. Physical Review B, 2013, 88(1): 014107. doi: 10.1103/PhysRevB.88.014107
[3]	EMERY N, HÉROLD C, D’ASTUTO M, et al. Superconductivity of bulk CaC₆ [J]. Physical Review Letters, 2005, 95(8): 087003. doi: 10.1103/PhysRevLett.95.087003
[4]	GAO M, YAN X W, LU Z Y, et al. Strong-coupling superconductivity in LiB₂C₂ trilayer films [J]. Physical Review B, 2020, 101(9): 094501. doi: 10.1103/PhysRevB.101.094501
[5]	ZHENG B B. Pressure-induced phase transition and electronic properties of MgB₂C₂ [J]. Journal of Applied Physics, 2017, 121(19): 195102. doi: 10.1063/1.4983821
[6]	YAN H Y, ZHANG M G, WEI Q, et al. Ab initio studies of ternary semiconductor BeB₂C₂ [J]. Computational Materials Science, 2013, 68: 174–180. doi: 10.1016/j.commatsci.2012.10.013
[7]	ZHENG B B, ZHANG M G, CHANG S M. Structural, mechanical and electronic properties of CaB₂C₂ at high pressure [J]. Europhysics Letters, 2017, 118(6): 66001. doi: 10.1209/0295-5075/118/66001
[8]	AKIMITSU J, TAKENAWA K, SUZUKI K, et al. High-temperature ferromagnetism in CaB₂C₂ [J]. Science, 2001, 293(5532): 1125–1127. doi: 10.1126/science.1061501
[9]	HAQUE E, HOSSAIN M A, STAMPFL C. First-principles prediction of phonon-mediated superconductivity in XBC (X=Mg, Ca, Sr, Ba) [J]. Physical Chemistry Chemical Physics, 2019, 21(17): 8767–8773. doi: 10.1039/c8cp07634k
[10]	ZHU L, BORSTAD G M, LIU H Y, et al. Carbon-boron clathrates as a new class of sp³-bonded framework materials [J]. Science Advances, 2020, 6(2): eaay8361. doi: 10.1126/sciadv.aay8361
[11]	WANG J N, YAN X W, GAO M. High-temperature superconductivity in SrB₃C₃ and BaB₃C₃ predicted from first-principles anisotropic Migdal-Eliashberg theory [J]. Physical Review B, 2021, 103(14): 144515. doi: 10.1103/PhysRevB.103.144515
[12]	ZHU L, LIU H Y, SOMAYAZULU M, et al. Superconductivity in SrB₃C₃ clathrate [J]. Physical Review Research, 2023, 5(1): 013012. doi: 10.1103/PhysRevResearch.5.013012
[13]	ZHANG Y M, CHEN J Y, HAO J, et al. Conventional high-temperature superconductivity in σ-band driven metallized two-dimensional metal borocarbides [J]. Physical Review B, 2024, 110(6): 064513. doi: 10.1103/PhysRevB.110.064513
[14]	BURDETT J K, LEE S, MCLARNAN T J. Coloring problem [J]. Journal of the American Chemical Society, 1985, 107(11): 3083–3089. doi: 10.1021/ja00297a012
[15]	WHEELER R A, WHANGBO M H, HUGHBANKS T, et al. Symmetric vs. asymmetric linear M-X-M linkages in molecules, polymers, and extended networks [J]. Journal of the American Chemical Society, 1986, 108(9): 2222–2236. doi: 10.1021/ja00269a018
[16]	MILLER G J. The “coloring problem” in solids: how it affects structure, composition and properties [J]. European Journal of Inorganic Chemistry, 1998, 1998(5): 523–536. doi: 10.1002/(SICI)1099-0682(199805)1998:5<523::AID-EJIC523>3.0.CO;2-L
[17]	DOMNICH V, REYNAUD S, HABER R A, et al. Boron carbide: structure, properties, and stability under stress [J]. Journal of the American Ceramic Society, 2011, 94(11): 3605–3628. doi: 10.1111/j.1551-2916.2011.04865.x
[18]	LONIE D C, ZUREK E. XtalOpt: an open-source evolutionary algorithm for crystal structure prediction [J]. Computer Physics Communications, 2011, 182(2): 372–387. doi: 10.1016/j.cpc.2010.07.048
[19]	WANG Y C, LV J, ZHU L, et al. Crystal structure prediction via particle-swarm optimization [J]. Physical Review B, 2010, 82(9): 094116. doi: 10.1103/PhysRevB.82.094116
[20]	WANG Y C, LV J, ZHU L, et al. CALYPSO: a method for crystal structure prediction [J]. Computer Physics Communications, 2012, 183(10): 2063–2070. doi: 10.1016/j.cpc.2012.05.008
[21]	LU C, LI Q, MA Y M, et al. Extraordinary indentation strain stiffening produces superhard tungsten nitrides [J]. Physical Review Letters, 2017, 119(11): 115503. doi: 10.1103/PhysRevLett.119.115503
[22]	LU S H, WANG Y C, LIU H Y, et al. Self-assembled ultrathin nanotubes on diamond (100) surface [J]. Nature Communications, 2014, 5(1): 3666. doi: 10.1038/ncomms4666
[23]	HE X L, ZHAO W B, XIE Y, et al. Predicted hot superconductivity in LaSc₂H₂₄ under pressure [J]. Proceedings of the National Academy of Sciences of the United States of America, 2024, 121(26): e2401840121. doi: 10.1073/pnas.2401840121
[24]	MA C H, MA Y, WANG H, et al. Hydrogen-vacancy-induced stable superconducting niobium hydride at high pressure [J]. Journal of the American Chemical Society, 2025, 147(13): 11028–11035. doi: 10.1021/jacs.4c15868
[25]	LUO X Y, YANG J H, LIU H Y, et al. Predicting two-dimensional boron-carbon compounds by the global optimization method [J]. Journal of the American Chemical Society, 2011, 133(40): 16285–16290. doi: 10.1021/ja2072753
[26]	WANG Y, LI F, LI Y F, et al. Semi-metallic Be₅C₂ monolayer global minimum with quasi-planar pentacoordinate carbons and negative Poisson’s ratio [J]. Nature Communications, 2016, 7(1): 11488. doi: 10.1038/ncomms11488
[27]	TANG C, KOUR G, DU A J. Recent progress on the prediction of two-dimensional materials using CALYPSO [J]. Chinese Physics B, 2019, 28(10): 107306. doi: 10.1088/1674-1056/ab41ea
[28]	MONKHORST H J, PACK J D. Special points for Brillouin-zone integrations [J]. Physical Review B, 1976, 13(12): 5188–5192. doi: 10.1103/PhysRevB.13.5188
[29]	COLLE R, SALVETTI O. Approximate calculation of the correlation energy for the closed shells [J]. Theoretica Chimica Acta, 1975, 37(4): 329–334. doi: 10.1007/BF01028401
[30]	PERDEW J P, CHEVARY J A, VOSKO S H, et al. Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation [J]. Physical Review B, 1992, 46(11): 6671–6687. doi: 10.1103/PhysRevB.46.6671
[31]	METHFESSEL M, PAXTON A T. High-precision sampling for Brillouin-zone integration in metals [J]. Physical Review B, 1989, 40(6): 3616–3621. doi: 10.1103/PhysRevB.40.3616
[32]	NYE J F. Physical properties of crystals: their representation by tensors and matrices [J]. Acta Crystallographica Section A, 1985, 41(6): 624–624.
[33]	WANG V, XU N, LIU J C, et al. VASPKIT: a user-friendly interface facilitating high-throughput computing and analysis using VASP code [J]. Computer Physics Communications, 2021, 267: 108033. doi: 10.1016/j.cpc.2021.108033
[34]	MOUHAT F, COUDERT F X. Necessary and sufficient elastic stability conditions in various crystal systems [J]. Physical Review B, 2014, 90(22): 224104. doi: 10.1103/PhysRevB.90.224104
[35]	方俊鑫, 陆栋. 固体物理学[M]. 上海: 上海科学技术出版社, 1980.
[36]	CHANDRASEKAR S, SANTHANAM S. A calculation of the bulk modulus of polycrystalline materials [J]. Journal of Materials Science, 1989, 24(12): 4265–4267. doi: 10.1007/BF00544497
[37]	PANDA K B, CHANDRAN K S R. Determination of elastic constants of titanium diboride (TiB₂) from first principles using FLAPW implementation of the density functional theory [J]. Computational Materials Science, 2006, 35(2): 134–150. doi: 10.1016/j.commatsci.2005.03.012
[38]	YAN H Y, ZHANG M G, WEI Q, et al. Elastic anisotropy and thermodynamic properties of tetrahedrally bonded dense C₂N₂ (NH) under high pressure and high temperature [J]. Physica Status Solidi B, 2013, 250(7): 1293–1299. doi: 10.1002/pssb.201248225
[39]	CAZZANI A, ROVATI M. Extrema of Young’s modulus for elastic solids with tetragonal symmetry [J]. International Journal of Solids and Structures, 2005, 42(18/19): 5057–5096. doi: 10.1016/j.ijsolstr.2005.02.018
[40]	HE Y, SCHWARZ R B, MIGLIORI A, et al. Elastic constants of single crystal γ-TiAl [J]. Journal of Materials Research, 1995, 10(5): 1187–1195. doi: 10.1557/JMR.1995.1187