基于吉布斯热力学曲面理论的镁橄榄石熔融计算研究

赵轩; 尹坤

doi:10.11858/gywlxb.20251130

基于吉布斯热力学曲面理论的镁橄榄石熔融计算研究

doi: 10.11858/gywlxb.20251130

赵轩^1,,
尹坤^{1, 2,*, ,}

1.
成都理工大学地球与行星科学学院, 四川成都　610059
2.
成都理工大学地质灾害防治与地质环境保护全国重点实验室, 四川成都　610059

基金项目: 国家自然科学基金（41972036）；国家重点研发计划（2024YFF0807500）

详细信息

作者简介:
赵　轩（2000－），男，硕士研究生，主要从事计算矿物物理研究. E-mail：zhaoxuane@outlook.com

通讯作者:
尹　坤（1982－），男，博士，副研究员，主要从事计算矿物物理研究. E-mail：yinkun@cdut.edu.cn

中图分类号: O521.2; P311.9
计量
- 文章访问数: 379
- HTML全文浏览量: 84
- PDF下载量: 57
出版历程
- 收稿日期: 2025-07-15
- 修回日期: 2025-07-23
- 网络出版日期: 2025-07-28
- 刊出日期: 2025-10-05

A Gibbs Thermodynamic Surface Approach to Modeling the Melting of Forsterite

ZHAO Xuan^1
,,
YIN Kun^{1, 2,*
, ,}

1.
College of Earth and Planetary Sciences, Chengdu University of Technology, Chengdu 610059, Sichuan, China
2.
State Key Laboratory of Geohazard Prevention and Geoenvironment Protection, Chengdu University of Technology, Chengdu 610059, Sichuan, China

摘要

摘要: 熔融过程在地球与其他行星的演化中发挥着重要作用。由于行星内部普遍处于高压环境，研究物质在高压条件下的熔融行为对于理解其组成及内部动力学过程至关重要。为此，在吉布斯热力学曲面理论及前人工作的基础上，结合第一性原理分子动力学模拟，通过构建几何模型，获得了镁橄榄石在0～16 GPa压力范围内的熔融数据。该方法能够在有限的计算资源下高效且准确地获取特定压力范围内任意点的熔融数据，包括固相和熔体相各自的吉布斯自由能、亥姆霍兹自由能、焓、内能、熵和体积。同时，使用该方法确定了镁橄榄石和瓦兹利石在1200～2500 K内的相变边界。所有计算结果均与已有实验及计算数据高度一致，验证了该方法在计算高压下物质的熔化行为的可靠性和准确性。该方法突破了现有方法在有限计算资源下难以高效获取完整高压熔融数据的瓶颈。
- 熔化曲线 /
- 吉布斯热力学曲面 /
- 高压 /
- 分子动力学模拟 /
- 镁橄榄石
Abstract: The process of melting is widespread in nature and plays a crucial role in the evolution of magma oceans on Earth and other planetary bodies. Given that planetary interiors are generally subjected to high-pressure conditions, the study of melting behavior under high-pressure conditions is essential for understanding the composition and dynamic evolution of planetary interiors. Based on the theory of the Gibbs thermodynamic surface and previous research, this study employs ab initio molecular dynamics simulation combined with a geometric model to obtain the melting data of forsterite (Mg₂SiO₄) within the pressure range of 0 to 16 GPa. Under limited computational resources, this method enables the efficient and accurate acquisition of melting-related properties at any point within a given pressure range, including the Gibbs free energy, Helmholtz free energy, enthalpy, internal energy, entropy, and volume of solid and liquid phases. This approach is also used to determine the phase boundary between forsterite and wadsleyite within the temperature range of 1200 to 1500 K. The calculated results show high consistency with existing experimental and computational data, validating the reliability and accuracy of this method for obtaining melting data under high pressure. This approach overcomes the bottleneck of existing methods in efficiently obtaining complete high-pressure melting data with limited computational resources.
- melting curve /
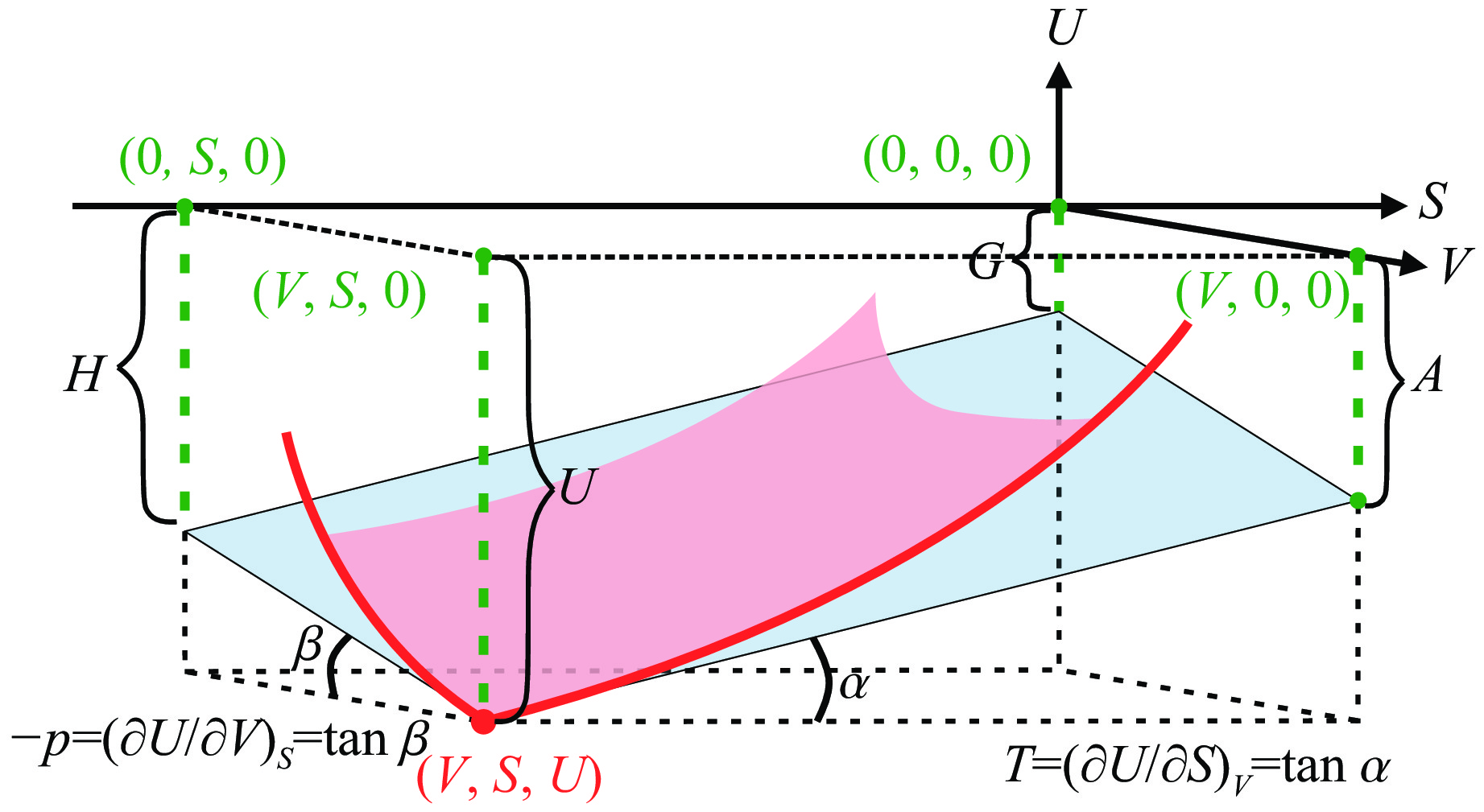
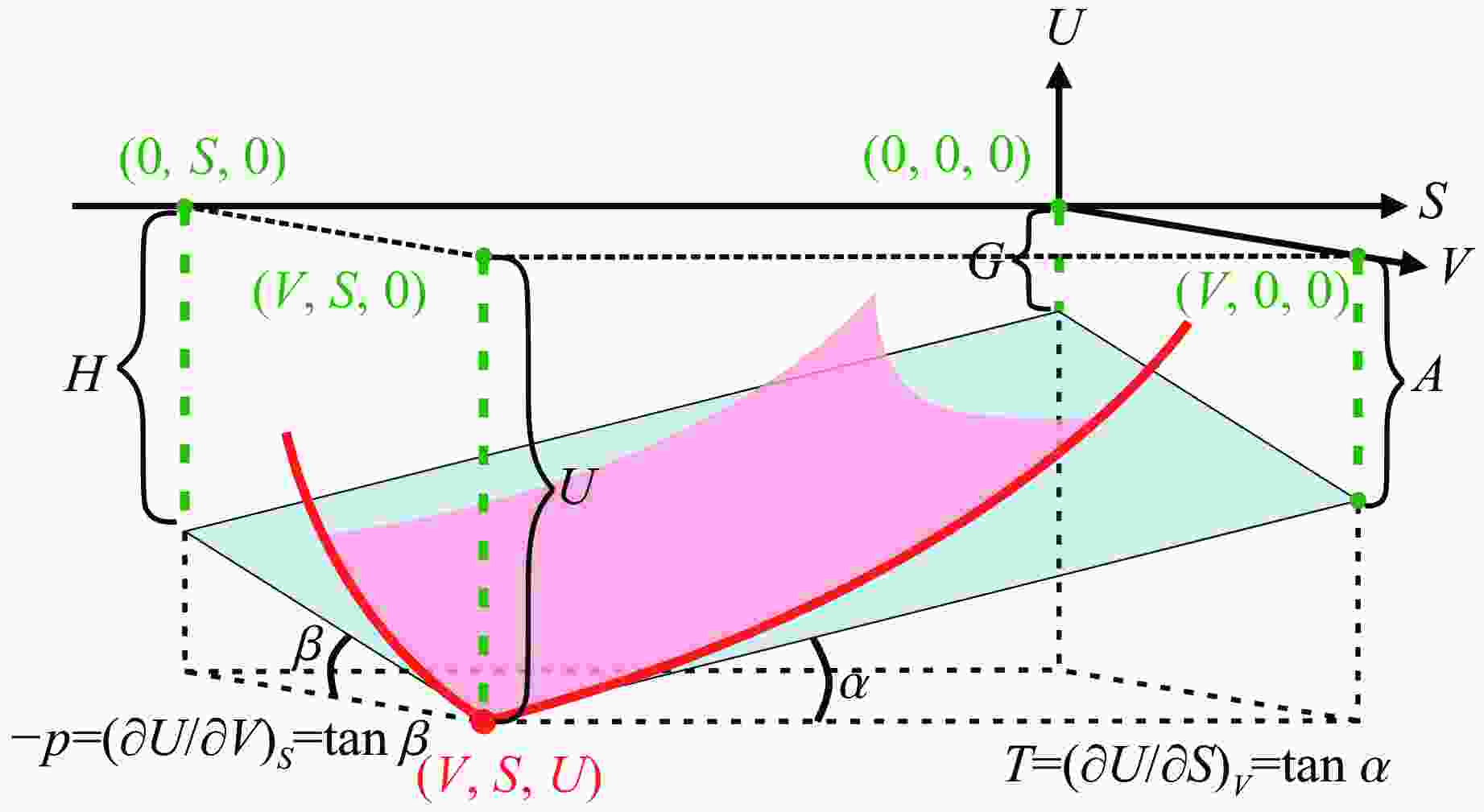
- Gibbs thermodynamic surface /
- high pressure /
- molecular dynamics simulation /
- forsterite

HTML全文

图 1 吉布斯热力学曲面示意图

Figure 1. Schematic diagram of Gibbs thermodynamic surface

下载: 全尺寸图片幻灯片

图 2 橄榄石单胞

Figure 2. Unit cell of olivine

下载: 全尺寸图片幻灯片

图 3 镁橄榄石在不同温度下的径向分布函数（V/V₀=1.0）

Figure 3. Radial distribution functions of forsterite at various temperatures (V/V₀=1.0)

下载: 全尺寸图片幻灯片

图 4 2.0～10.0 GPa压力范围内镁橄榄石的4种热力学势相图

Figure 4. Projection diagrams of four thermodynamic potentials in the range of 2.0 to 12.0 GPa for forsterite

下载: 全尺寸图片幻灯片

图 5 镁橄榄石的熔化曲线

Figure 5. Melting curves of forsterite

下载: 全尺寸图片幻灯片

图 6 镁橄榄石和瓦兹利石的相变边界

Figure 6. Phase boundary between forsterite and wadsleyite

下载: 全尺寸图片幻灯片

表 1 镁橄榄石的熔融数据

Table 1. Melting data of forsterite

p/GPa	T_m/K	Phase	V/(Å³/atom)	G/(eV/atom)	A/(eV/atom)	H/(eV/atom)	U/(eV/atom)	S/(μeV·K⁻¹/atom)
0.5	2195	Solid	11.357	−6.597	−6.633	−6.538	−6.574	27
0.5	2195	Liquid	12.540	−6.583	−6.622	−6.373	−6.412	102
1.0	2232	Solid	11.310	−6.563	−6.634	−6.496	−6.567	30
1.0	2232	Liquid	12.365	−6.550	−6.627	−6.318	−6.395	110
2.0	2295	Solid	11.214	−6.495	−6.635	−6.416	−6.556	34
2.0	2295	Liquid	12.109	−6.487	−6.638	−6.210	−6.361	124
3.0	2363	Solid	11.125	−6.428	−6.636	−6.335	−6.543	39
3.0	2363	Liquid	11.908	−6.425	−6.648	−6.111	−6.334	135
4.0	2411	Solid	11.125	−6.428	−6.636	−6.335	−6.543	39
4.0	2411	Liquid	11.908	−6.425	−6.648	−6.111	−6.334	135
6.0	2469	Solid	10.834	−6.226	−6.632	−6.122	−6.528	42
6.0	2469	Liquid	11.377	−6.225	−6.651	−5.876	−6.302	142
8.0	2529	Solid	10.657	−6.095	−6.627	−5.985	−6.517	43
8.0	2529	Liquid	11.088	−6.094	−6.647	−5.731	−6.285	143
9.0	2555	Solid	10.573	−6.030	−6.623	−5.918	−6.512	44
9.0	2555	Liquid	10.957	−6.029	−6.644	−5.662	−6.277	144
10.0	2579	Solid	10.492	−5.965	−6.620	−5.852	−6.507	44
10.0	2579	Liquid	10.834	−5.964	−6.641	−5.593	−6.270	144
11.0	2630	Solid	10.424	−5.902	−6.618	−5.779	−6.494	47
11.0	2630	Liquid	10.731	−5.905	−6.641	−5.517	−6.254	148
13.0	2634	Solid	10.261	−5.773	−6.606	−5.660	−6.493	43
13.0	2634	Liquid	10.503	−5.773	−6.625	−5.397	−6.249	143
14.0	2649	Solid	10.189	−5.710	−6.600	−5.598	−6.488	42
14.0	2649	Liquid	10.404	−5.710	−6.619	−5.333	−6.242	142
16.0	2672	Solid	10.051	−5.585	−6.588	−5.475	−6.479	41
16.0	2672	Liquid	10.219	−5.585	−6.605	−5.209	−6.230	140

下载: 导出CSV

表 2 镁橄榄石-瓦兹利石相变边界热力学数据

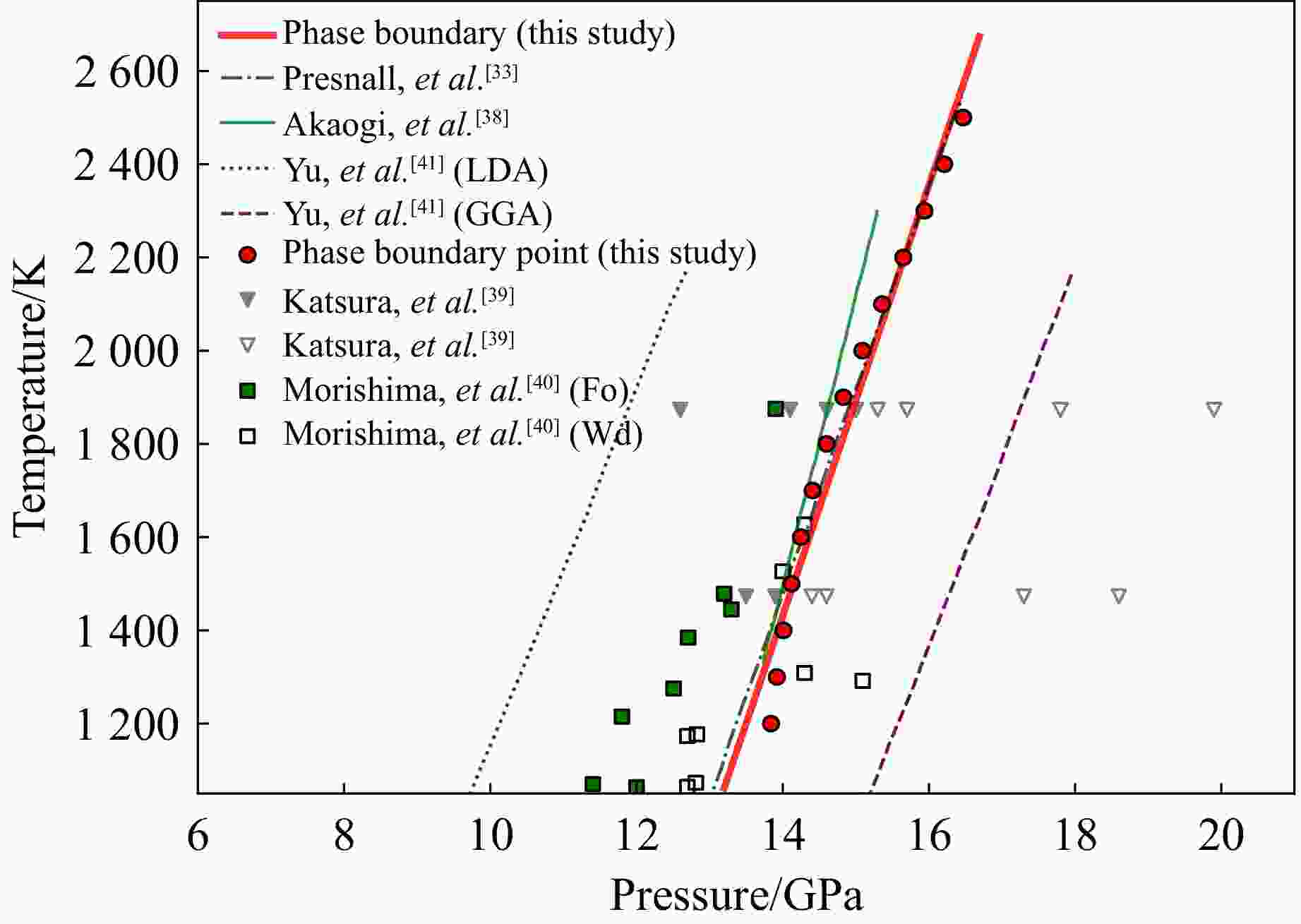
Table 2. Data for phase boundary between forsterite and wadsleyite

p/GPa	T/K	Phase	V/（Å³/atom）	G/(eV/atom)	A/(eV/atom)	H/(eV/atom)	U/(eV/atom)	S/(μeV·K⁻¹/atom)
13.84	1200	Fo	9.850	−5.800	−6.651	−6.010	−6.861	−178
13.84	1200	Wd	9.259	−5.800	−6.600	−6.024	−6.824	−186
13.92	1300	Fo	9.860	−5.778	−6.635	−5.978	−6.834	−156
13.92	1300	Wd	9.277	−5.778	−6.584	−5.992	−6.798	−164
14.01	1400	Fo	9.870	−5.757	−6.621	−5.945	−6.808	−135
14.01	1400	Wd	9.296	−5.757	−6.570	−5.959	−6.772	−144
14.12	1500	Fo	9.882	−5.738	−6.608	−5.911	−6.781	−116
14.12	1500	Wd	9.315	−5.738	−6.558	−5.926	−6.747	−125
14.25	1600	Fo	9.893	−5.718	−6.598	−5.875	−6.755	−98
14.25	1600	Wd	9.333	−5.718	−6.549	−5.891	−6.721	−108
14.41	1700	Fo	9.904	−5.699	−6.590	−5.838	−6.729	−82
14.41	1700	Wd	9.352	−5.699	−6.540	−5.854	−6.695	−91
14.60	1800	Fo	9.913	−5.680	−6.583	−5.799	−6.702	−66
14.60	1800	Wd	9.368	−5.680	−6.534	−5.816	−6.670	−76
14.83	1900	Fo	9.922	−5.660	−6.578	−5.757	−6.676	−51
14.83	1900	Wd	9.383	−5.660	−6.528	−5.776	−6.644	−61
15.09	2000	Fo	9.930	−5.639	−6.574	−5.714	−6.650	−38
15.09	2000	Wd	9.395	−5.639	−6.524	−5.733	−6.618	−47
15.36	2100	Fo	9.937	−5.619	−6.572	−5.670	−6.623	−24
15.36	2100	Wd	9.405	−5.619	−6.521	−5.690	−6.592	−34
15.65	2200	Fo	9.944	−5.599	−6.571	−5.626	−6.597	−12
15.65	2200	Wd	9.413	−5.599	−6.519	−5.647	−6.566	−21
15.94	2300	Fo	9.951	−5.581	−6.571	−5.582	−6.571	0
15.94	2300	Wd	9.419	−5.581	−6.518	−5.603	−6.540	−10
16.21	2400	Fo	9.960	−5.564	−6.572	−5.538	−6.546	11
16.21	2400	Wd	9.425	−5.564	−6.518	−5.560	−6.513	2
16.47	2500	Fo	9.970	−5.550	−6.575	−5.496	−6.520	22
16.47	2500	Wd	9.429	−5.550	−6.519	−5.518	−6.487	13

下载: 导出CSV

参考文献(44)

[1]	MAO H K, CHEN X J, DING Y, et al. Solids, liquids, and gases under high pressure [J]. Reviews of Modern Physics, 2018, 90(1): 015007. doi: 10.1103/RevModPhys.90.015007
[2]	XU M L, LI Y W, MA Y M. Materials by design at high pressures [J]. Chemical Science, 2022, 13(2): 329–344. doi: 10.1039/D1SC04239D
[3]	SAKAIRI T, OHTANI E, KAMADA S, et al. Melting relations in the Fe-S-Si system at high pressure and temperature: implications for the planetary core [J]. Progress in Earth and Planetary Science, 2017, 4(1): 10. doi: 10.1186/s40645-017-0125-x
[4]	HU J P, SHARP T G. Formation, preservation and extinction of high-pressure minerals in meteorites: temperature effects in shock metamorphism and shock classification [J]. Progress in Earth and Planetary Science, 2022, 9(1): 6. doi: 10.1186/s40645-021-00463-2
[5]	贺芝宇, 黄秀光, 舒桦, 等. 冰巨行星内部深处物理与化学过程研究进展 [J]. 高压物理学报, 2023, 37(5): 050105. doi: 10.11858/gywlxb.20230721 HE Z Y, HUANG X G, SHU H, et al. Progress on physical and chemical processes deep inside ice giants [J]. Chinese Journal of High Pressure Physics, 2023, 37(5): 050105. doi: 10.11858/gywlxb.20230721
[6]	YIN K, BELONOSHKO A B, LI Y H, et al. Davemaoite as the mantle mineral with the highest melting temperature [J]. Science Advances, 2023, 9(49): eadj2660. doi: 10.1126/sciadv.adj2660
[7]	KATSURA T. Phase relations of bridgmanite, the most abundant mineral in the Earth’s lower mantle [J]. Communications Chemistry, 2025, 8(1): 28. doi: 10.1038/s42004-024-01389-8
[8]	LI J, WU Q, LI J B, et al. Shock melting curve of iron: a consensus on the temperature at the Earth’s inner core boundary [J]. Geophysical Research Letters, 2020, 47(15): e2020GL087758. doi: 10.1029/2020GL087758
[9]	王宝云, 肖万生, 宋茂双. δ-(Al, Fe)OOH的高压相变 [J]. 高压物理学报, 2021, 35(6): 061201. doi: 10.11858/gywlxb.20210765 WANG B Y, XIAO W S, SONG M S. Pressure-induced phase transitions in δ-(Al, Fe)OOH [J]. Chinese Journal of High Pressure Physics, 2021, 35(6): 061201. doi: 10.11858/gywlxb.20210765
[10]	姜昌国, 谭大勇, 谢亚飞, 等. 高压剪切作用下三水铝石的结构稳定性 [J]. 高压物理学报, 2022, 36(1): 011202. doi: 10.11858/gywlxb.20210766 JIANG C G, TAN D Y, XIE Y F, et al. Investigation on structural stability of γ-Al(OH)₃ under high pressure and shear stress [J]. Chinese Journal of High Pressure Physics, 2022, 36(1): 011202. doi: 10.11858/gywlxb.20210766
[11]	陈炜珊, 谭毅, 谭大勇, 等. NaPO₃高压结构行为的第一性原理理论研究 [J]. 高压物理学报, 2024, 38(5): 050106. doi: 10.11858/gywlxb.20240755 CHEN W S, TAN Y, TAN D Y, et al. First-principles theoretical study on the structure behaviors of NaPO₃ under compression [J]. Chinese Journal of High Pressure Physics, 2024, 38(5): 050106. doi: 10.11858/gywlxb.20240755
[12]	何宇, 孙士川, 李和平. 地球内核超离子态铁合金及其效应 [J]. 高压物理学报, 2024, 38(3): 030202. doi: 10.11858/gywlxb.20240707 HE Y, SUN S C, LI H P. Superionic iron alloys in Earth’s inner core and their effects [J]. Chinese Journal of High Pressure Physics, 2024, 38(3): 030202. doi: 10.11858/gywlxb.20240707
[13]	吴忠庆, 王文忠. 矿物高温高压下弹性的第一性原理计算研究进展 [J]. 中国科学: 地球科学, 2016, 46(5): 582–617. WU Z Q, WANG W Z. First-principles calculations of elasticity of minerals at high temperature and pressure [J]. Science China Earth Sciences, 2016, 59(6): 1107–1137.
[14]	甘波, 李俊, 蒋刚, 等. Fe高压熔化线的实验研究进展 [J]. 高压物理学报, 2021, 35(6): 060101. doi: 10.11858/gywlxb.20210859 GAN B, LI J, JIANG G, et al. A review of the experimental determination of the melting curve of iron at ultrahigh pressures [J]. Chinese Journal of High Pressure Physics, 2021, 35(6): 060101. doi: 10.11858/gywlxb.20210859
[15]	LUO S N, STRACHAN A, SWIFT D C. Nonequilibrium melting and crystallization of a model Lennard-Jones system [J]. The Journal of Chemical Physics, 2004, 120(24): 11640–11649. doi: 10.1063/1.1755655
[16]	BELONOSHKO A B. Molecular dynamics of MgSiO₃ perovskite at high pressures: equation of state, structure, and melting transition [J]. Geochimica et Cosmochimica Acta, 1994, 58(19): 4039–4047. doi: 10.1016/0016-7037(94)90265-8
[17]	BELONOSHKO A B, SKORODUMOVA N V, ROSENGREN A, et al. Melting and critical superheating [J]. Physical Review B, 2006, 73(1): 012201. doi: 10.1103/PhysRevB.73.012201
[18]	SIMON F, GLATZEL G. Bemerkungen zur schmelzdruckkurve [J]. Zeitschrift für Anorganische und Allgemeine Chemie, 1929, 178(1): 309–316. doi: 10.1002/zaac.19291780123
[19]	KECHIN V V. Melting curve equations at high pressure [J]. Physical Review B, 2001, 65(5): 052102. doi: 10.1103/PhysRevB.65.052102
[20]	GIBBS J W. Graphical methods in the thermodynamics of fluids [J]. Transactions of the Connecticut Academy of Arts and Sciences, 1873, 2: 309–342.
[21]	GIBBS J W. A method of geometrical representation of the thermodynamic properties of substances by means of surfaces [J]. Transactions of the Connecticut Academy of Arts and Sciences, 1873, 2: 382–404.
[22]	GIBBS J W. On the equilibrium of heterogeneous substances [J]. Transactions of the Connecticut Academy of Arts and Sciences, 1876, 3: 108–248.
[23]	YIN K, LU X C, ZHOU H Q, et al. Thermodynamic stability limit of the crystalline state from the Gibbs perspective [J]. Physical Review B, 2018, 98(14): 144113. doi: 10.1103/PhysRevB.98.144113
[24]	KATSURA T, YAMADA H, NISHIKAWA O, et al. Olivine-wadsleyite transition in the system (Mg, Fe)₂SiO₄ [J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B2): B02209. doi: 10.1029/2003JB002438
[25]	刘曦, 代立东, 邓力维, 等. 近十年我国在地球内部物质高压物性实验研究方面的主要进展 [J]. 高压物理学报, 2017, 31(6): 657–681. doi: 10.11858/gywlxb.2017.06.001 LIU X, DAI L D, DENG L W, et al. Recent progresses in some fields of high-pressure physics relevant to Earth sciences achieved by Chinese scientists [J]. Chinese Journal of High Pressure Physics, 2017, 31(6): 657–681. doi: 10.11858/gywlxb.2017.06.001
[26]	BOSTROEM D. Single-crystal X-ray diffraction studies of synthetic Ni-Mg olivine solid solutions [J]. American Mineralogist, 1987, 72(9/10): 965–972.
[27]	KRESSE G, FURTHMÜLLER J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set [J]. Physical Review B, 1996, 54(16): 11169–11186. doi: 10.1103/PhysRevB.54.11169
[28]	PERDEW J P, RUZSINSZKY A, CSONKA G I, et al. Restoring the density-gradient expansion for exchange in solids and surfaces [J]. Physical Review Letters, 2008, 100(13): 136406. doi: 10.1103/PhysRevLett.100.136406
[29]	NOSÉ S. A unified formulation of the constant temperature molecular dynamics methods [J]. The Journal of Chemical Physics, 1984, 81(1): 511–519. doi: 10.1063/1.447334
[30]	HOOVER W G. Canonical dynamics: equilibrium phase-space distributions [J]. Physical Review A, 1985, 31(3): 1695–1697. doi: 10.1103/PhysRevA.31.1695
[31]	OHTANI E, KUMAZAWA M. Melting of forsterite Mg₂SiO₄ up to 15 GPa [J]. Physics of the Earth and Planetary Interiors, 1981, 27(1): 32–38. doi: 10.1016/0031-9201(81)90084-4
[32]	DAVIS B T C, ENGLAND J L. The melting of forsterite up to 50 kilobars [J]. Journal of Geophysical Research, 1964, 69(6): 1113–1116. doi: 10.1029/JZ069i006p01113
[33]	PRESNALL D C, WALTER M J. Melting of forsterite, Mg₂SiO₄, from 9.7 to 16.5 GPa [J]. Journal of Geophysical Research: Solid Earth, 1993, 98(B11): 19777–19783. doi: 10.1029/93JB01007
[34]	BOYD F R, ENGLAND J L. The quartz-coesite transition [J]. Journal of Geophysical Research, 1960, 65(2): 749–756. doi: 10.1029/JZ065i002p00749
[35]	BOWEN N L, ANDERSEN O. The binary system MgO-SiO₂ [J]. American Journal of Science, 1914, s4-37(222): 487–500.
[36]	DE KOKER N P, STIXRUDE L, KARKI B B. Thermodynamics, structure, dynamics, and freezing of Mg₂SiO₄ liquid at high pressure [J]. Geochimica et Cosmochimica Acta, 2008, 72(5): 1427–1441. doi: 10.1016/j.gca.2007.12.019
[37]	HORIUCHI H, SAWAMOTO H. β-Mg₂SiO₄: single-crystal X-ray diffraction study [J]. American Mineralogist, 1981, 66(5/6): 568–575.
[38]	AKAOGI M, ITO E, NAVROTSKY A. Olivine-modified spinel-spinel transitions in the system Mg₂SiO₄-Fe₂SiO₄: calorimetric measurements, thermochemical calculation, and geophysical application [J]. Journal of Geophysical Research: Solid Earth, 1989, 94(B11): 15671–15685. doi: 10.1029/JB094iB11p15671
[39]	KATSURA T, ITO E. The system Mg₂SiO₄-Fe₂SiO₄ at high pressures and temperatures: precise determination of stabilities of olivine, modified spinel, and spinel [J]. Journal of Geophysical Research: Solid Earth, 1989, 94(B11): 15663–15670. doi: 10.1029/JB094iB11p15663
[40]	MORISHIMA H, KATO T, SUTO M, et al. The phase boundary between α- and β-Mg₂SiO₄ determined by in situ X-ray observation [J]. Science, 1994, 265(5176): 1202–1203. doi: 10.1126/science.265.5176.1202
[41]	YU Y G, WU Z Q, WENTZCOVITCH R M. α-β-γ transformations in Mg₂SiO₄ in Earth’s transition zone [J]. Earth and Planetary Science Letters, 2008, 273(1/2): 115–122. doi: 10.1016/j.jpgl.2008.06.023
[42]	GASPARIK T. Phase relations in the transition zone [J]. Journal of Geophysical Research: Solid Earth, 1990, 95(B10): 15751–15769. doi: 10.1029/JB095iB10p15751
[43]	PERDEW J P, ZUNGER A. Self-interaction correction to density-functional approximations for many-electron systems [J]. Physical Review B, 1981, 23(10): 5048–5079. doi: 10.1103/PhysRevB.23.5048
[44]	PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Physical Review Letters, 1996, 77(18): 3865–3868. doi: 10.1103/PhysRevLett.77.3865