Tensile Fracture Characteristics and Dynamic Crack Evolution Law of Concrete
-
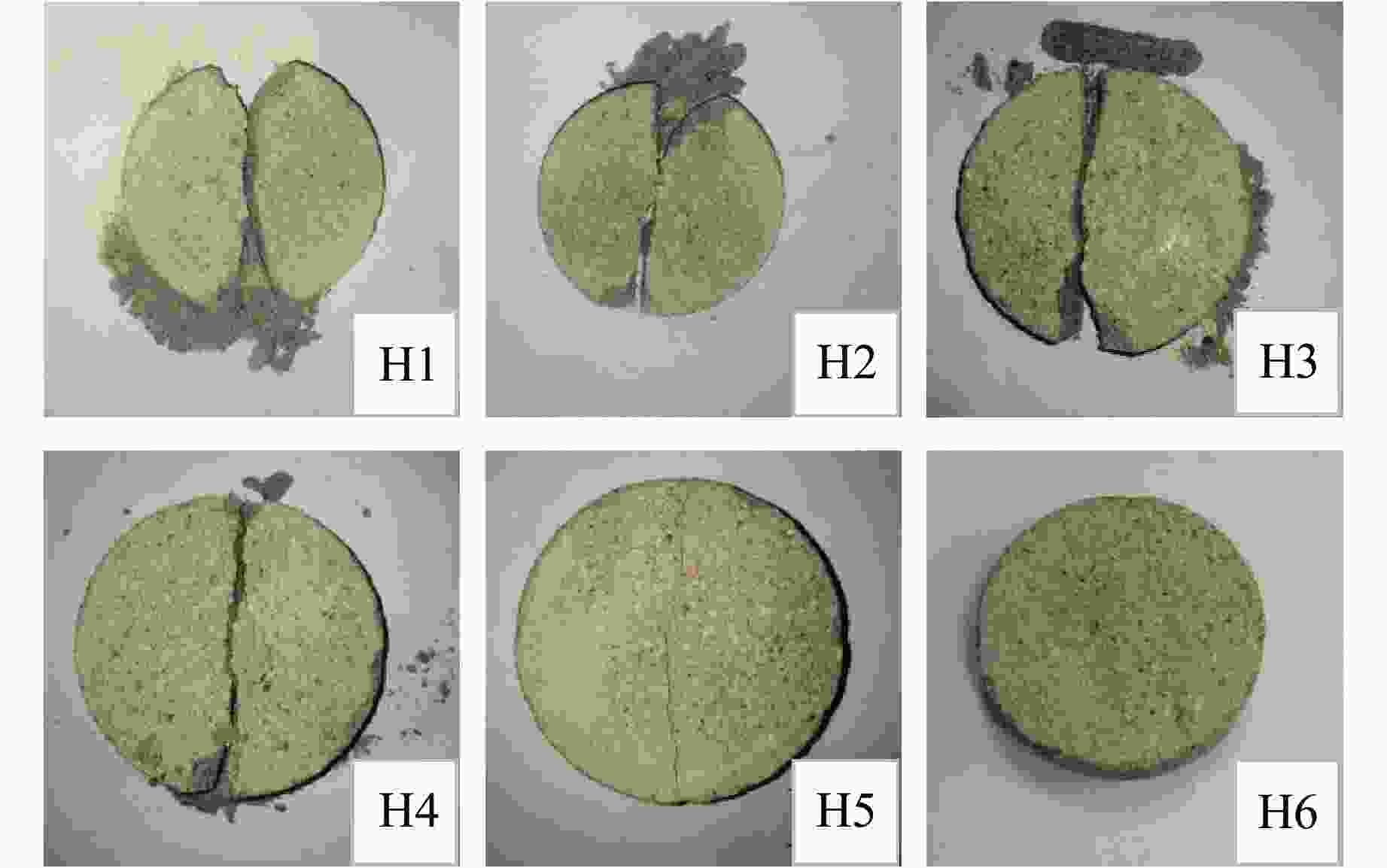
摘要: 为探究混凝土的拉伸断裂特性和裂纹演化规律，开展了巴西圆盘的准静态劈裂试验和落锤冲击动态劈裂试验，结合有限元-黏聚单元耦合法（finite-cohesive element method，FCEM）模拟分析裂纹扩展过程及力学响应。试验结果表明：准静态加载时，混凝土圆盘试件发生拉伸断裂，圆盘中心形成一条沿加载方向贯穿的主裂纹和少量与其平行的次裂纹，裂纹主要在砂浆内部及骨料-砂浆界面扩展；三维圆盘试件的拉伸性能随厚径比的增大而增强。在动态冲击载荷作用下，试件仍为中心起裂模式，即圆盘中心形成一条沿加载方向的主裂纹，边缘则产生三角状破碎区域。随着落锤释放高度的增加，试件的破坏形态依次表现为：未起裂、起裂未贯穿、起裂贯穿和严重破碎。通过高速摄影获得的不同时刻裂纹长度的结果表明，随着落锤释放高度的降低，裂纹扩展时间延长。数值模拟结果显示，试件的起裂时间随落锤释放高度的增加呈非线性递减，并给出了起裂时间与落锤释放高度关系的经验公式。Abstract: To investigate the tensile fracture characteristics and crack evolution mechanisms of concrete, Brazilian disc quasi-static splitting tests and falling weight impact tests were conducted. The crack propagation and mechanical responses were analyzed using the finite cohesive-element method (FCEM). Test results demonstrated that under quasi-static loading, concrete discs exhibited tensile fracture with a primary crack penetrating along the loading direction at the disc center, accompanied by minor parallel secondary cracks. Crack propagation primarily occurred within the mortar matrix and along aggregate-mortar interfaces. The tensile performance of three-dimensional concrete discs exhibited significant enhancement with increasing thickness-diameter ratio. Under dynamic impact loading, specimens maintained a center-initiated fracture pattern, where the main crack propagated along the loading diameter, while triangular crushing zones formed at the edges in contact with testing apparatus. With increasing drop height, the specimens sequentially exhibited four distinct failure modes: no crack initiation, crack initiation without penetration, complete crack penetration, and severe fragmentation. High-speed photography quantified time-dependent crack lengths, demonstrating prolonged crack propagation durations at reduced drop heights. Numerical simulations revealed a nonlinear decreasing trend in crack initiation time versus drop height, with an empirical formula established to describe their relationship.
-
Key words:
- dynamic loading /
- Brazilian disc /
- cohesive zone model /
- tensile fracture /
- crack evolution /
- crack initiation time
-
图 4 不同厚度圆盘试件的载荷-位移曲线
Figure 4. Load-displacement curves of specimens with different thicknesses
图 5 圆盘试件厚径比与抗拉强度的关系曲线
Figure 5. Relationship curve between thickness-diameter ratio and tensile strength of disc specimens
图 6 试件H1裂纹扩展的高速摄影图像
Figure 6. High-speed photographic images of crack propagation in the specimen H1
图 7 试件H1～试件H6的起裂时间与裂纹扩展时间
Figure 7. Crack initiation time and crack propagation time of specimens H1–H6
图 14 数值模拟和试验得到的载荷-位移曲线
Figure 14. Load-displacement curves obtained from numerical simulation and test
图 15 落锤冲击下混凝土试件中裂纹的萌生和扩展
Figure 15. Initiation and propagation of cracks in concrete specimens under falling weight impact
图 16 不同释放高度下落锤的加速度时程曲线
Figure 16. Acceleration-time curves of the falling weight under different release heights
图 17 不同释放高度下接触力的变化情况
Figure 17. Variation of contact forceunder different release heights
图 18 圆盘的起裂时间随落锤释放高度的变化
Figure 18. Variation of crack initiation timewith release height
表 1 混凝土试件的力学性能参数
Table 1. Mechanical property parameters of concrete specimens
ν ρ/(g·cm–3) E/GPa fc/MPa 0.19 2.32 25.5 32 
下载: 导出CSV
表 2 不同厚径比试件的极限载荷与抗拉强度
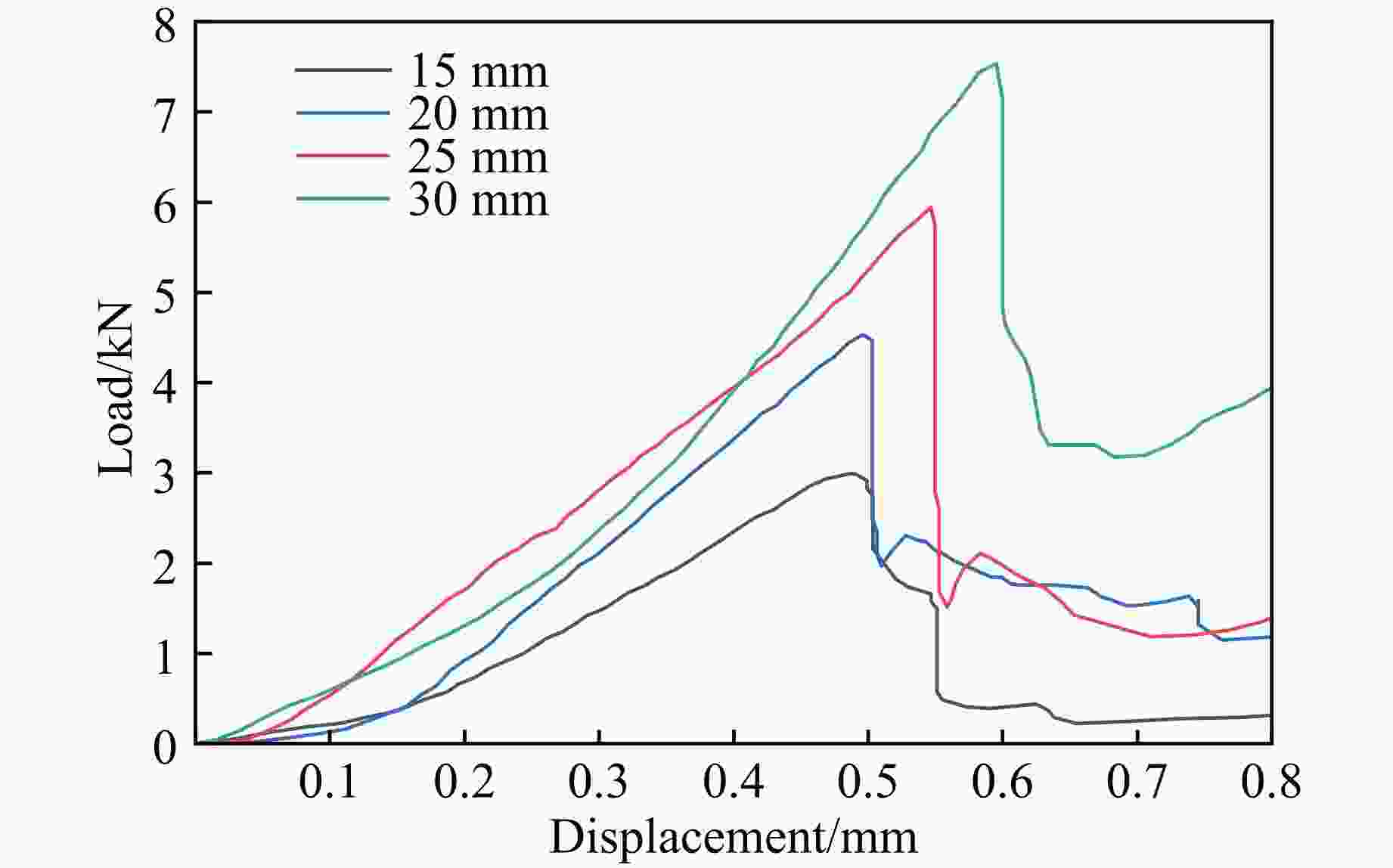
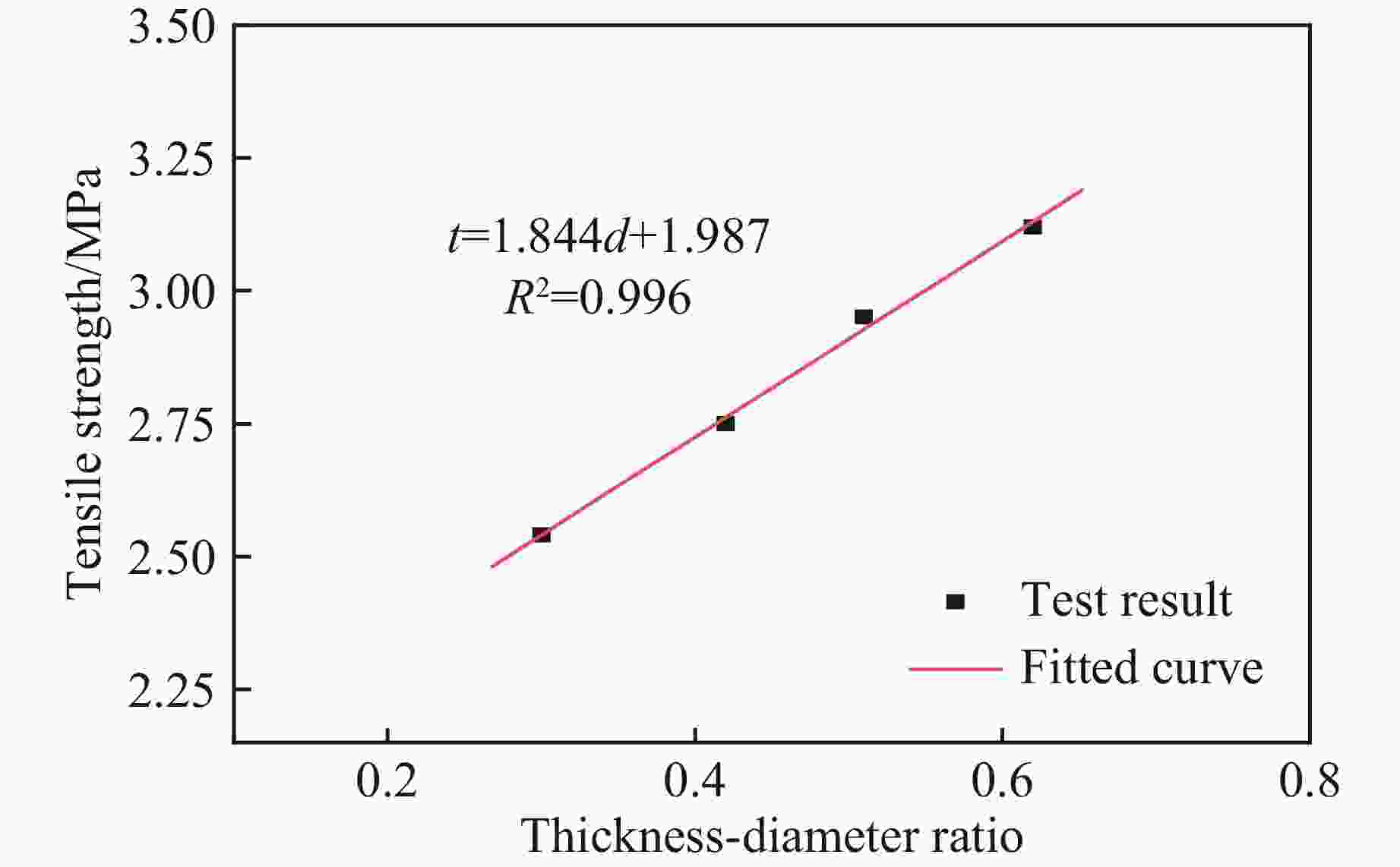
Table 2. Ultimate load and tensile strength of specimens with different thickness-diameter ratio
Thickness/mm Thickness-diameter ratio Ultimate load/kN Tensile strength/MPa 15.0 0.30 2.99 2.54 21.2 0.42 4.58 2.75 25.6 0.51 5.94 2.95 30.8 0.62 7.54 3.12
下载: 导出CSV
表 3 不同释放高度下巴西圆盘试件的落锤冲击试验工况
Table 3. Conditions for the falling weight impact test on Brazilian disc specimens at different release heights
Specimen No. Falling weight mass/kg Height/mm Velocity/(m·s–1) Impact energy/J H1 10 300 2.42 29.40 H2 10 200 1.98 19.60 H3 10 100 1.40 9.80 H4 10 50 0.99 4.90 H5 10 20 0.63 1.96 H6 10 15 0.54 1.47
下载: 导出CSV
表 4 落锤冲击试验得到的圆盘起裂时间与裂纹扩展时间
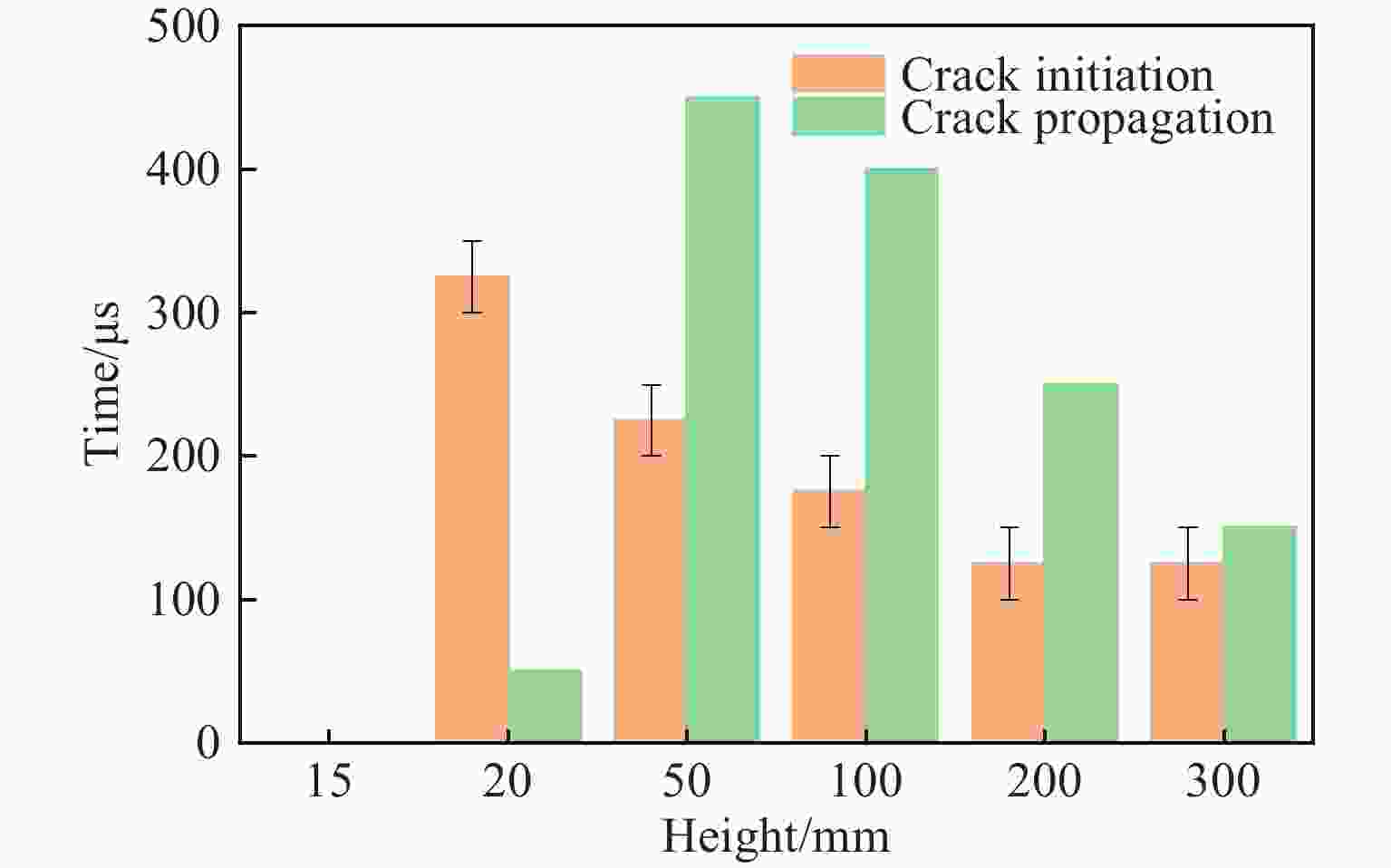
Table 4. Crack initiation time and crack propagation time of disc specimens obtained from the falling weight impact tests
Specimen No. Height/mm Test results Crack initiation time/μs Crack propagation time/μs H1 300 100−150 150 H2 200 100−150 250 H3 100 150−200 400 H4 50 200−250 450 H5 20 300−350 50 H6 15 0 0
下载: 导出CSV
表 5 混凝土的HJC模型参数
Table 5. Parameters of the HJC model for concrete
ρ/(g·cm–3) fc/MPa A B N C D1 D2 2.32 32 0.79 1.62 0.61 0.008 0.04 1.00 K1/GPa K2/GPa K3/GPa pc/MPa μc $ {\dot{\varepsilon }}_{0} $/s–1 εf,min Smax 0.85 −1.71 2.08 10.7 7.8×10–4 1.00 0.01 7.00
下载: 导出CSV
ρ/(g·cm–3) $ \eta $ GⅠ/(N·m–1) GⅡ/(N·m–1) ET/(N·m–3) EN/(N·m–3) 2.32 −2 56.42 282.13 8.3×1010 8.3×1010
下载: 导出CSV
表 7 不同释放高度下圆盘试件的起裂时间
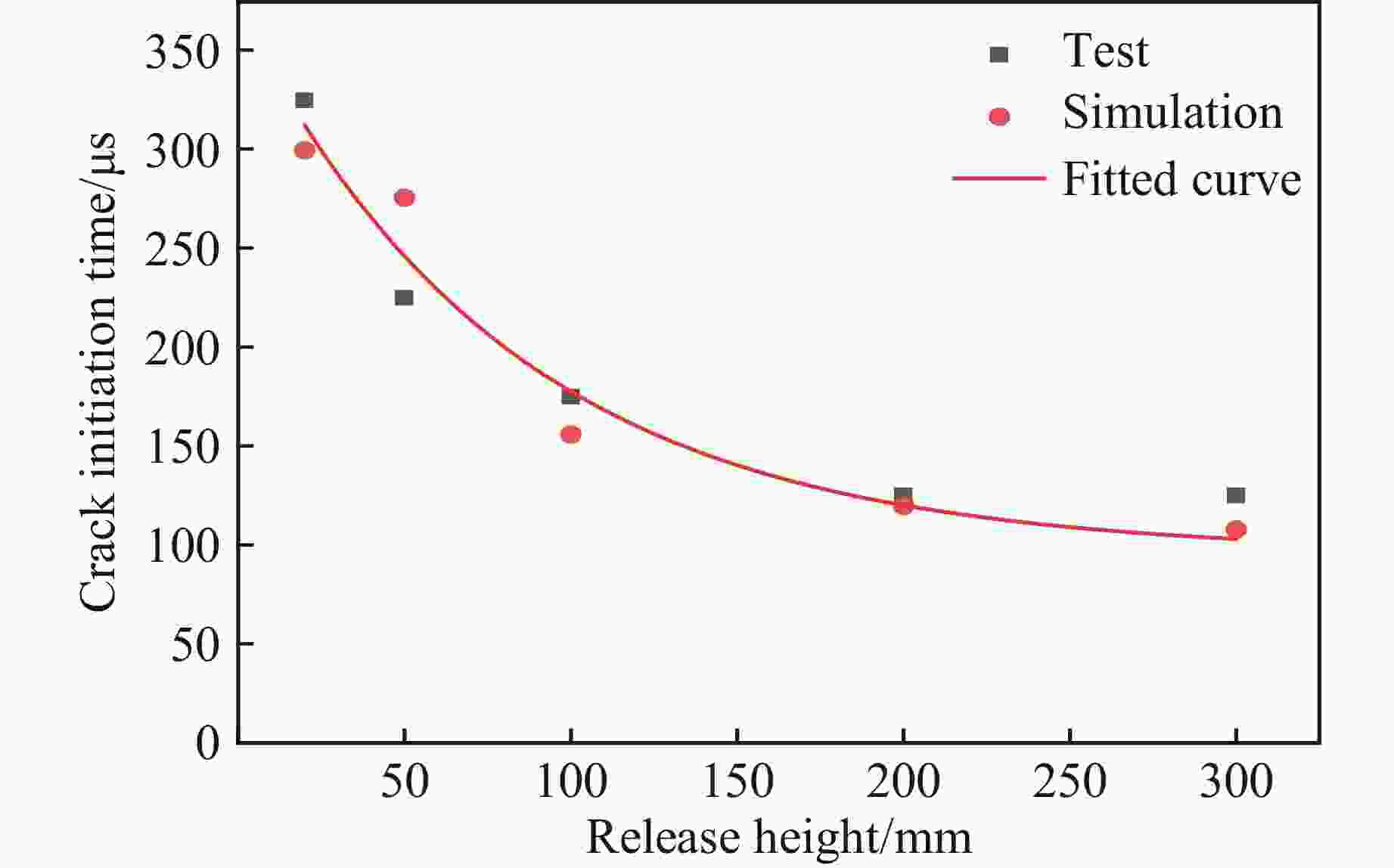
Table 7. Crack initiation time of specimens under different release heights
Specimen No. Height/mm Crack initiation time/μs Test results Simulation results H1 300 100–150 108 H2 200 100–150 120 H3 100 150–200 156 H4 50 200–250 276 H5 20 300–350 300 H6 15 0 0
下载: 导出CSV
-
[1] FENG S W, ZHOU Y, WANG Y, et al. Experimental research on the dynamic mechanical properties and damage characteristics of lightweight foamed concrete under impact loading [J]. International Journal of Impact Engineering, 2020, 140: 103558. doi: 10.1016/j.ijimpeng.2020.103558 [2] 孙雁新, 王成, 王浩宇, 等. 爆炸载荷作用下高强度混凝土毁伤效应的数值模拟及实验研究 [J]. 力学学报, 2024, 56(11): 3243–3261. doi: 10.6052/0459-1879-24-195SUN Y X, WANG C, WANG H Y, et al. Numerical simulation and experimental research on the damage effect of high-strength concrete under explosion load [J]. Chinese Journal of Theoretical and Applied Mechanics, 2024, 56(11): 3243–3261. doi: 10.6052/0459-1879-24-195 [3] BAZANT Z P, PLANAS J. Fracture and size effect in concrete and other quasibrittle materials [M]. New York: Routledge, 1998. [4] CARNEIRO F L L B, BARCELLOS A. Tensile strength of concretes [J]. RILEM Bulletin, 1953, 13: 103–107. [5] CHEN J Y, XIANG D, WANG Z H, et al. Dynamic tensile strength enhancement of concrete in split Hopkinson pressure bar test [J]. Advances in Mechanical Engineering, 2018, 10(6): 1687814018782301. [6] 王智德, 李杰, 武海港, 等. 不同高应变率冲击荷载作用下混凝土试件的能量耗散分析 [J]. 计算力学学报, 2023, 40(4): 621–627. doi: 10.7511/jslx20211226001WANG Z D, LI J, WU H G, et al. Energy dissipation analysis of concrete samples under impact loads of different high strain rates [J]. Chinese Journal of Computational Mechanics, 2023, 40(4): 621–627. doi: 10.7511/jslx20211226001 [7] 崔大顺, 王利民, 薛辉庭, 等. 冲击荷载作用下纤维混凝土动态劈裂试验与分析 [J]. 振动与冲击, 2024, 43(16): 219–226. doi: 10.13465/j.cnki.jvs.2024.16.027CUI D S, WANG L M, XUE H T, et al. A dynamic splitting test and analysis of fiber reinforced concrete under impact load [J]. Journal of Vibration and Shock, 2024, 43(16): 219–226. doi: 10.13465/j.cnki.jvs.2024.16.027 [8] 胡利, 李映春, 唐梓棋, 等. 基于SHPB试验的超高性能混凝土动力性能研究 [J]. 防护工程, 2023, 45(5): 13–21. doi: 10.3969/j.issn.1674-1854.2023.05.003HU L, LI Y C, TANG Z Q, et al. Experimental study on dynamic performance of UHPC based on SHPB [J]. Protective Engineering, 2023, 45(5): 13–21. doi: 10.3969/j.issn.1674-1854.2023.05.003 [9] 徐风, 蒋建伟, 王树有, 等. CL-20基高爆速压装炸药的落锤冲击响应特性 [J]. 爆炸与冲击, 2025, 45(4): 041406. doi: 10.11883/bzycj-2024-0109XU F, JIANG J W, WANG S Y, et al. Response of CL-20-based high-detonation-velocity pressed explosive to drop-hammer impact [J]. Explosion and Shock Waves, 2025, 45(4): 041406. doi: 10.11883/bzycj-2024-0109 [10] 王新颖, 王树山, 王绍慧, 等. 典型水中战斗部炸药装药跌落撞击响应特性 [J]. 兵工学报, 2021, 42(Suppl 1): 33–39. doi: 10.3969/j.issn.1000-1093.2021.S1.004WANG X Y, WANG S S, WANG S H, et al. Drop impact response characteristics of typical explosive charge in underwater warhead [J]. Acta Armamentarii, 2021, 42(Suppl 1): 33–39. doi: 10.3969/j.issn.1000-1093.2021.S1.004 [11] ANAS S M, ALAM M, UMAIR M. Experimental and numerical investigations on performance of reinforced concrete slabs under explosive-induced air-blast loading: a state-of-the-art review [J]. Structures, 2021, 31: 428–461. doi: 10.1016/j.istruc.2021.01.102 [12] 康耕新, 颜海春, 张亚栋, 等. 接触爆炸下混凝土墩破坏效应试验与数值模拟 [J]. 兵工学报, 2024, 45(1): 144–155. doi: 10.12382/bgxb.2022.0397KANG G X, YAN H C, ZHANG Y D, et al. Experimental and numerical investigation on the damage effects of concrete pier under contact explosion [J]. Acta Armamentarii, 2024, 45(1): 144–155. doi: 10.12382/bgxb.2022.0397 [13] BARENBLATT G I. The mathematical theory of equilibrium cracks in brittle fracture [J]. Advances in Applied Mechanics, 1962, 7: 55–129. doi: 10.1016/S0065-2156(08)70121-2 [14] DUGDALE D S. Yielding of steel sheets containing slits [J]. Journal of the Mechanics and Physics of Solids, 1960, 8(2): 100–104. doi: 10.1016/0022-5096(60)90013-2 [15] CHEN B Y, YU H F, ZHANG J H, et al. Effects of the embedding of cohesive zone model on the mesoscopic fracture behavior of concrete: a case study of uniaxial tension and compression tests [J]. Engineering Failure Analysis, 2022, 142: 106709. doi: 10.1016/j.engfailanal.2022.106709 [16] TRAWIŃSKI W, TEJCHMAN J, BOBIŃSKI J. A three-dimensional meso-scale modelling of concrete fracture, based on cohesive elements and X-ray μCT images [J]. Engineering Fracture Mechanics, 2018, 189: 27–50. doi: 10.1016/j.engfracmech.2017.10.003 [17] 丁威, 冷发光, 韦庆东, 等. 《普通混凝土配合比设计规程》(JGJ 55–2011)简介 [J]. 混凝土世界, 2011(12): 76–79. doi: 10.3969/j.issn.1674-7011.2011.12.016DING W, LENG F G, WEI Q D, et al. Brief introduction of specification for mix design of ordinary concrete (JGJ 55–2011) [J]. China Concrete, 2011(12): 76–79. doi: 10.3969/j.issn.1674-7011.2011.12.016 [18] 郭明伟, 邓琴, 李春光, 等. 巴西圆盘试验问题与三维抗拉强度准则 [J]. 岩土力学, 2008, 29(Suppl 1): 545–549,554. doi: 10.3969/j.issn.1000-7598.2008.z1.110GUO M W, DENG Q, LI C G, et al. Brazilian disc test and 3-D tensile strength principle [J]. Rock and Soil Mechanics, 2008, 29(Suppl 1): 545–549,554. doi: 10.3969/j.issn.1000-7598.2008.z1.110 [19] 杜闯, 宋帅, 张江鹏. 爆炸冲击作用下三种混凝土本构模型对比研究 [J]. 兵器装备工程学报, 2022, 43(11): 49–56. doi: 10.11809/bqzbgcxb2022.11.007DU C, SONG S, ZHANG J P. Comparative study on three concrete constitutive models under blast loading [J]. Journal of Ordnance Equipment Engineering, 2022, 43(11): 49–56. doi: 10.11809/bqzbgcxb2022.11.007 [20] 苗春贺, 陈丽娜, 单俊芳, 等. 水泥砂浆抗弹性能研究 [J]. 高压物理学报, 2021, 35(2): 024205. doi: 10.11858/gywlxb.20200609MIAO C H, CHEN L N, SHAN J F, et al. Research on the ballistic performance of cement mortar [J]. Chinese Journal of High Pressure Physics, 2021, 35(2): 024205. doi: 10.11858/gywlxb.20200609 [21] JOHNSON G R, HOLMQUIST T J. A computational constitutive model for brittle materials subjected to large strains, high strain rates, and high pressures [M]//MEYERS M A, MURR L E, STAUDHAMMER K P. Shock Wave and High-Strain-Rate Phenomena in Materials. Boca Raton: CRC Press, 1992: 1075−1082. [22] HILLERBORG A, MODÉER M, PETERSSON P E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements [J]. Cement and Concrete Research, 1976, 6(6): 773–781. doi: 10.1016/0008-8846(76)90007-7 [23] PETERSSON P E. Crack growth and development of fracture zones in plain concrete and similar materials: TVBM 1006 [R]. Lund: Division of Building Materials, Lund University, 1981. [24] GOPALARATNAM V S, SHAH S P. Softening response of plain concrete in direct tension [J]. ACI Materials Journal, 1985, 82(3): 310–323. doi: 10.14359/10338 [25] KARIHALOO B L. Fracture mechanics and structural concrete [M]. New York: Wiley, 1995. [26] CHO K Z, KOBAYASHI A S, HAWKINS N M, et al. Fracture process zone of concrete cracks [J]. Journal of Engineering Mechanics, 1984, 110(8): 1174–1184. doi: 10.1061/(ASCE)0733-9399(1984)110:8(1174 [27] BENZEGGAGH M L, KENANE M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus [J]. Composites Science and Technology, 1996, 56(4): 439–449. doi: 10.1016/0266-3538(96)00005-X [28] ZHANG B, NADIMI S, EISSA A, et al. Modelling fracturing process using cohesive interface elements: theoretical verification and experimental validation [J]. Construction and Building Materials, 2023, 365: 130132. doi: 10.1016/j.conbuildmat.2022.130132 [29] DE MAIO U, CENDÓN D, GRECO F, et al. Investigation of concrete cracking phenomena by using cohesive fracture-based techniques: a comparison between an embedded crack model and a refined diffuse interface model [J]. Theoretical and Applied Fracture Mechanics, 2021, 115: 103062. doi: 10.1016/j.tafmec.2021.103062 [30] DE MAIO U, GRECO F, LEONETTI L, et al. A refined diffuse cohesive approach for the failure analysis in quasibrittle materials—part Ⅱ: application to plain and reinforced concrete structures [J]. Fatigue & Fracture of Engineering Materials & Structures, 2019, 42(12): 2764–2781. doi: 10.1111/ffe.13115 -
下载:
计量
- 文章访问数: 391
- HTML全文浏览量: 108
- PDF下载量: 23
