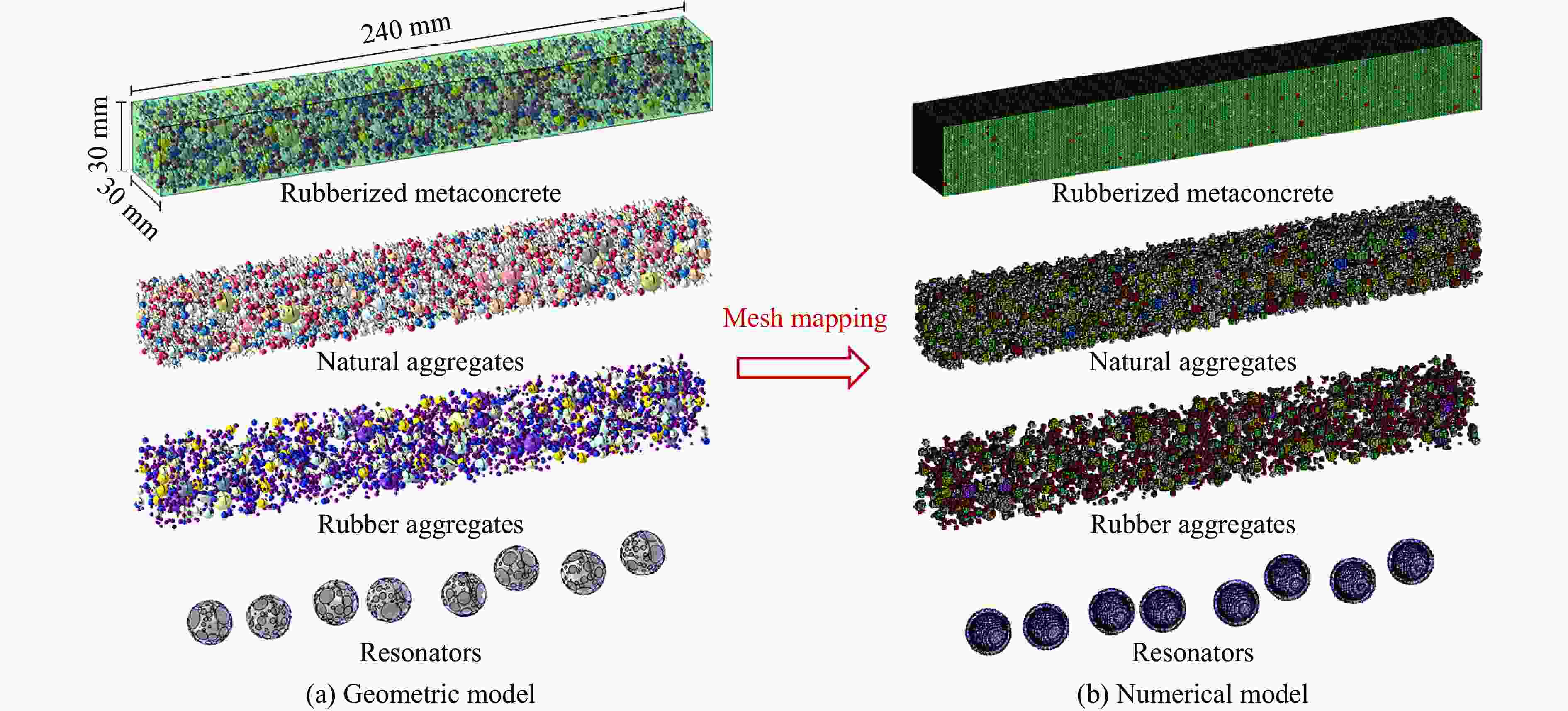
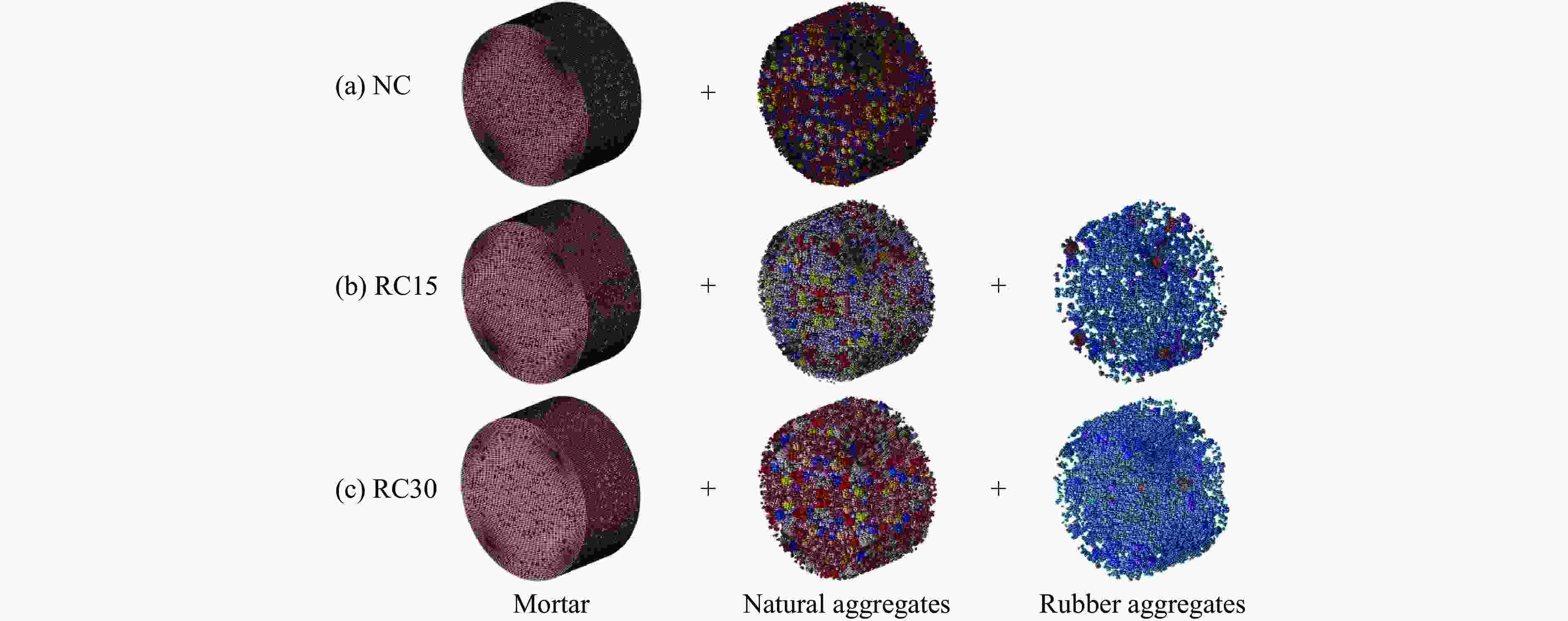
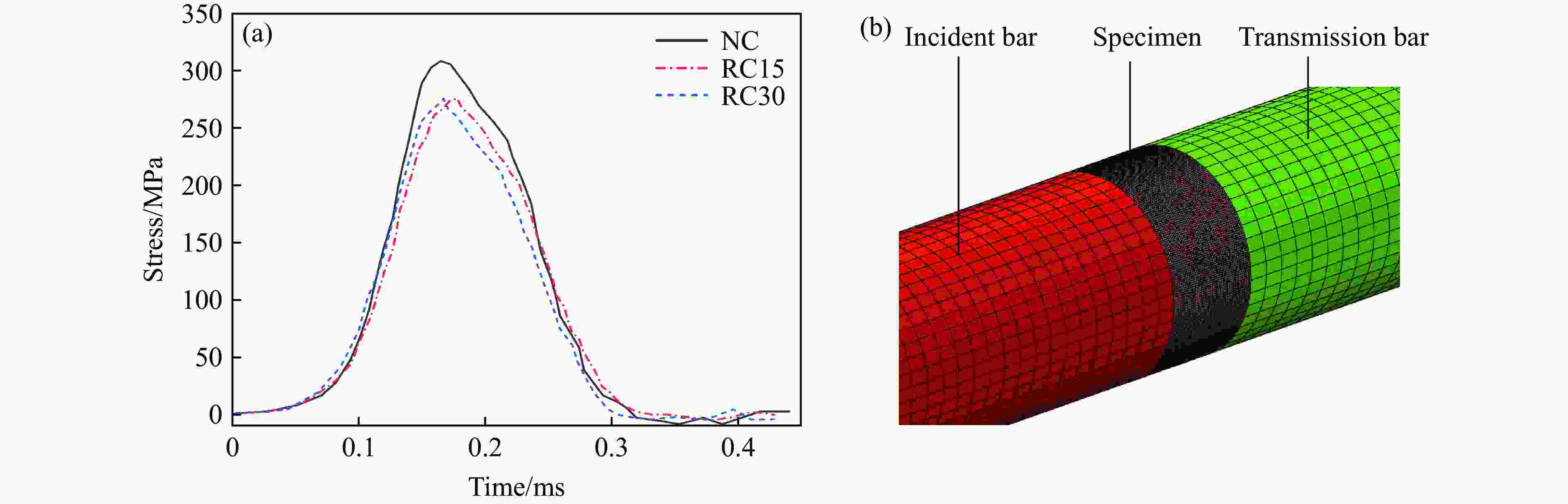
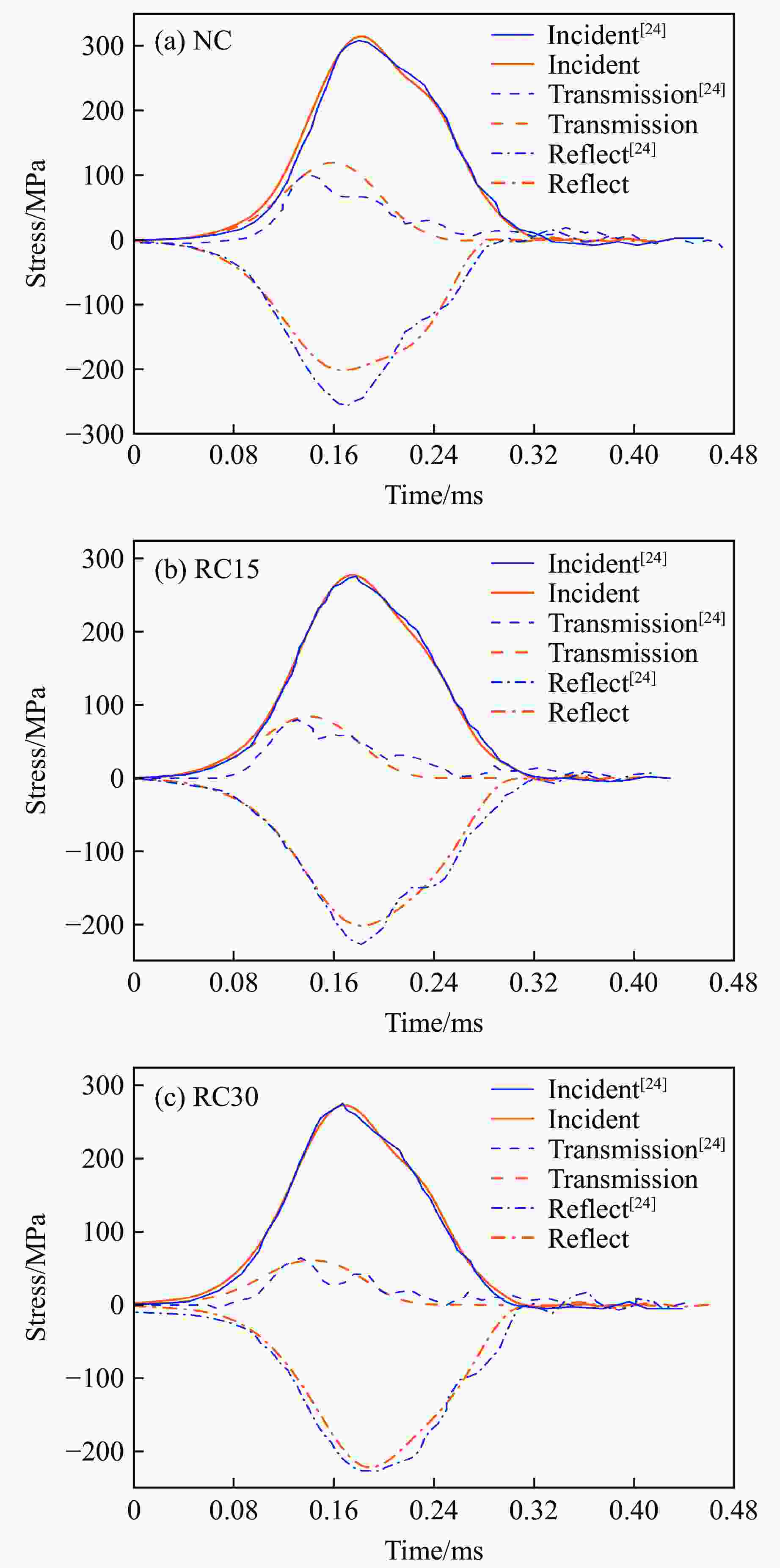
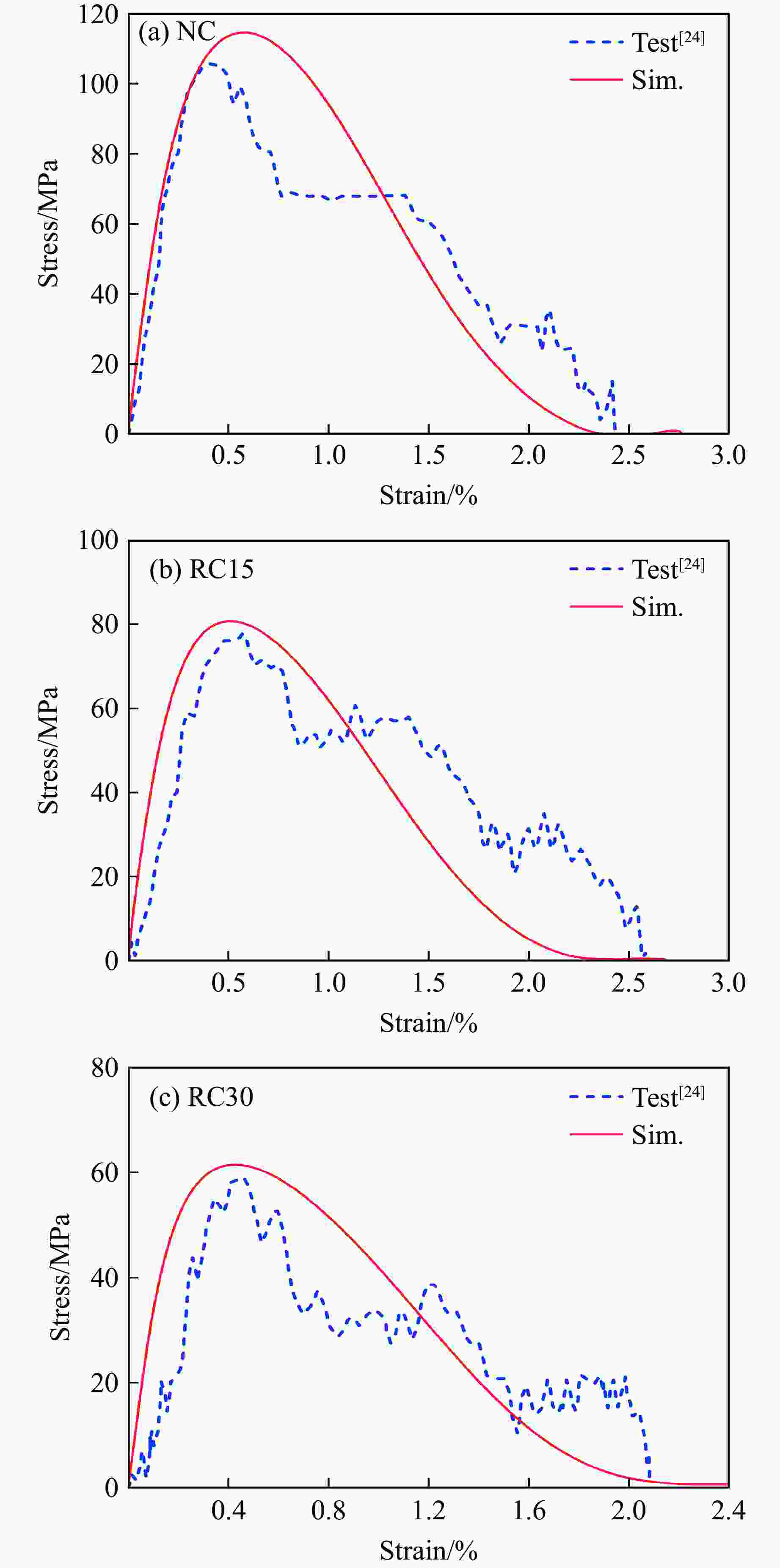
Numerical Simulation of Rubberized Metaconcrete under Impact Load
-
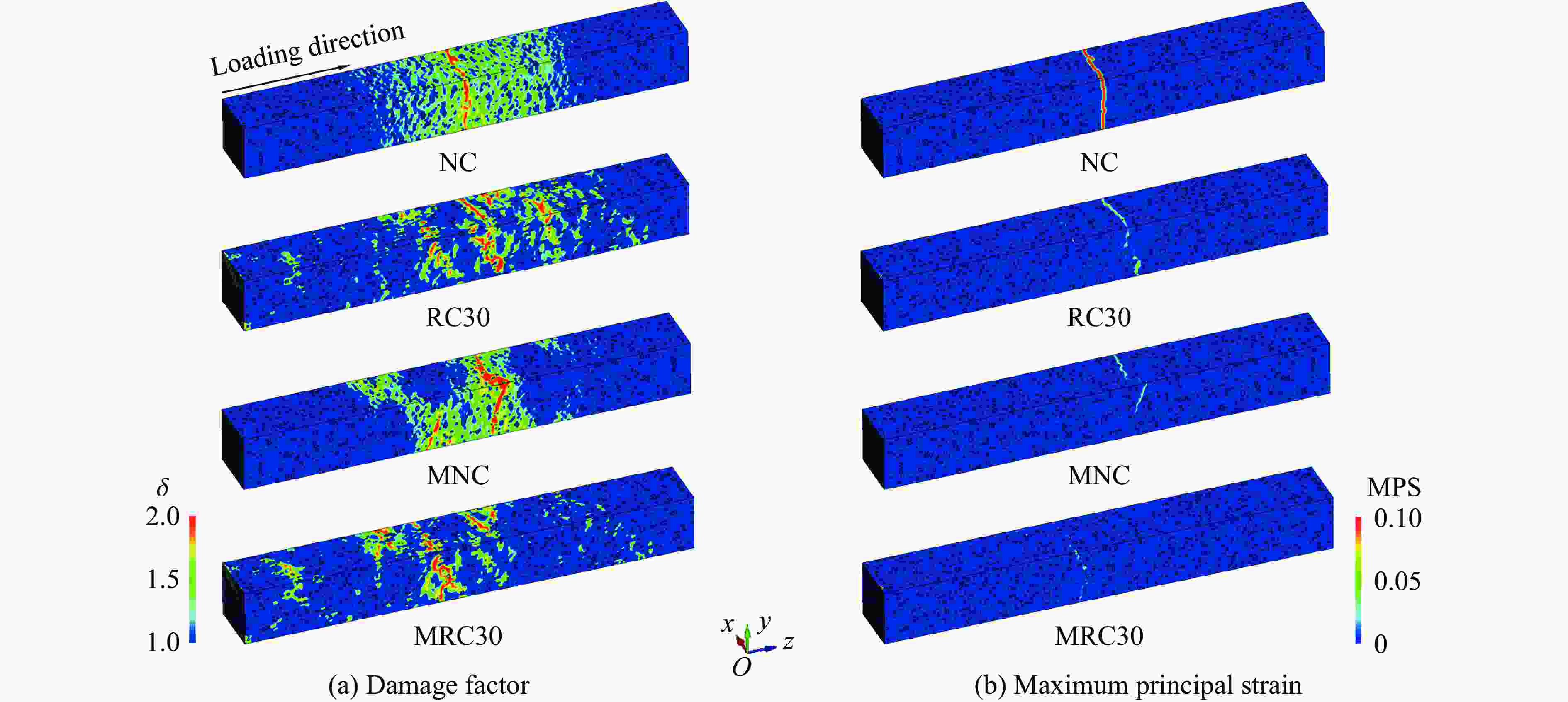
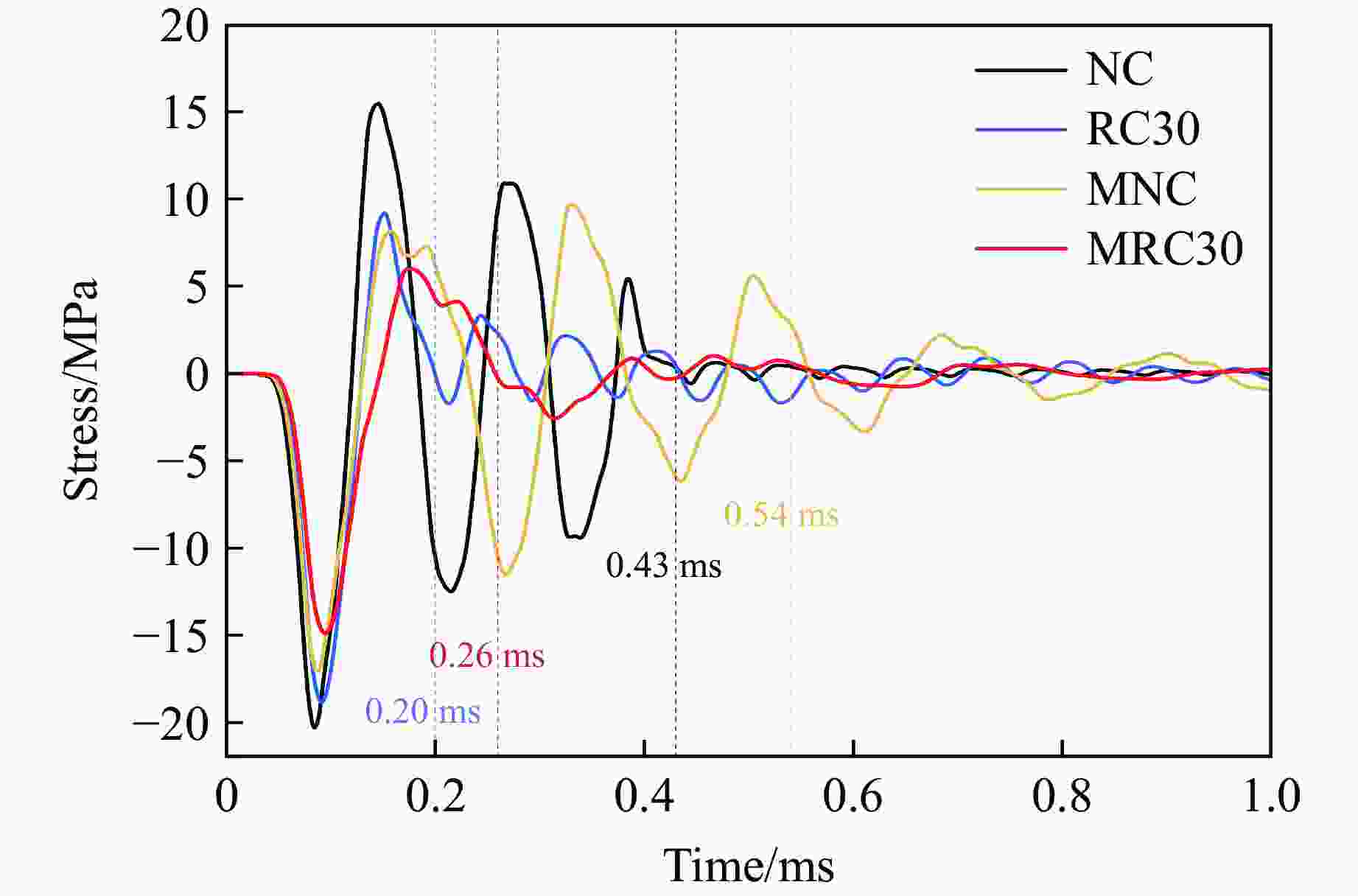
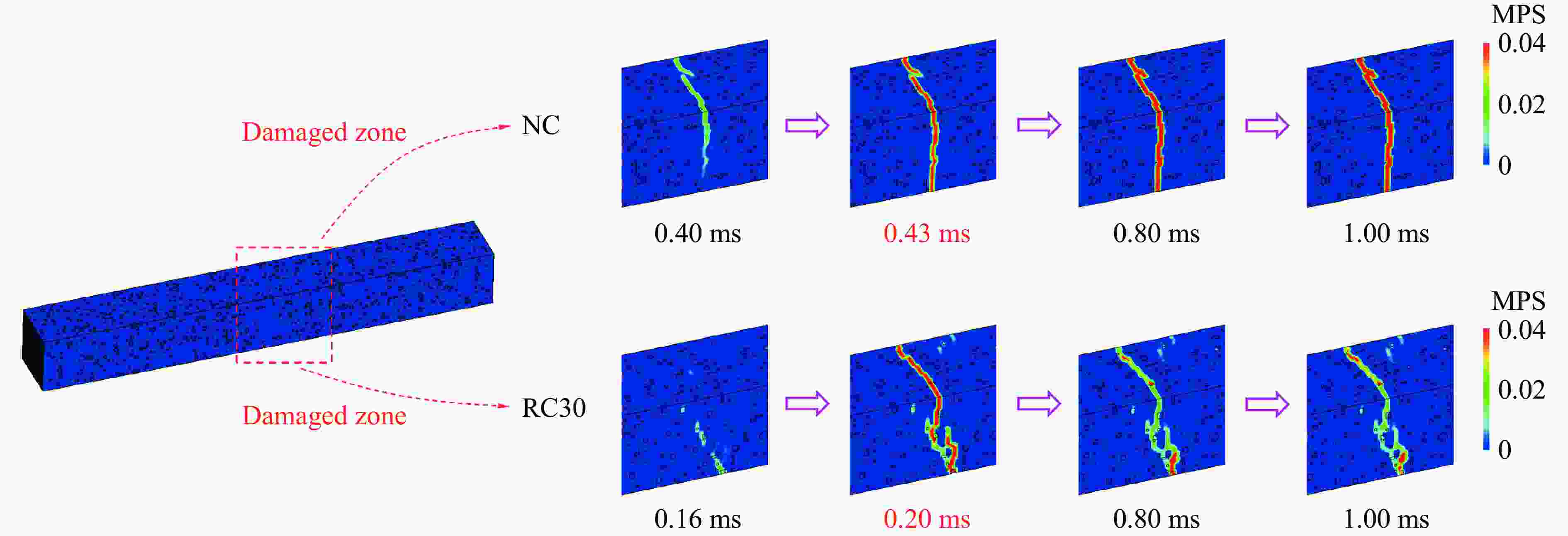
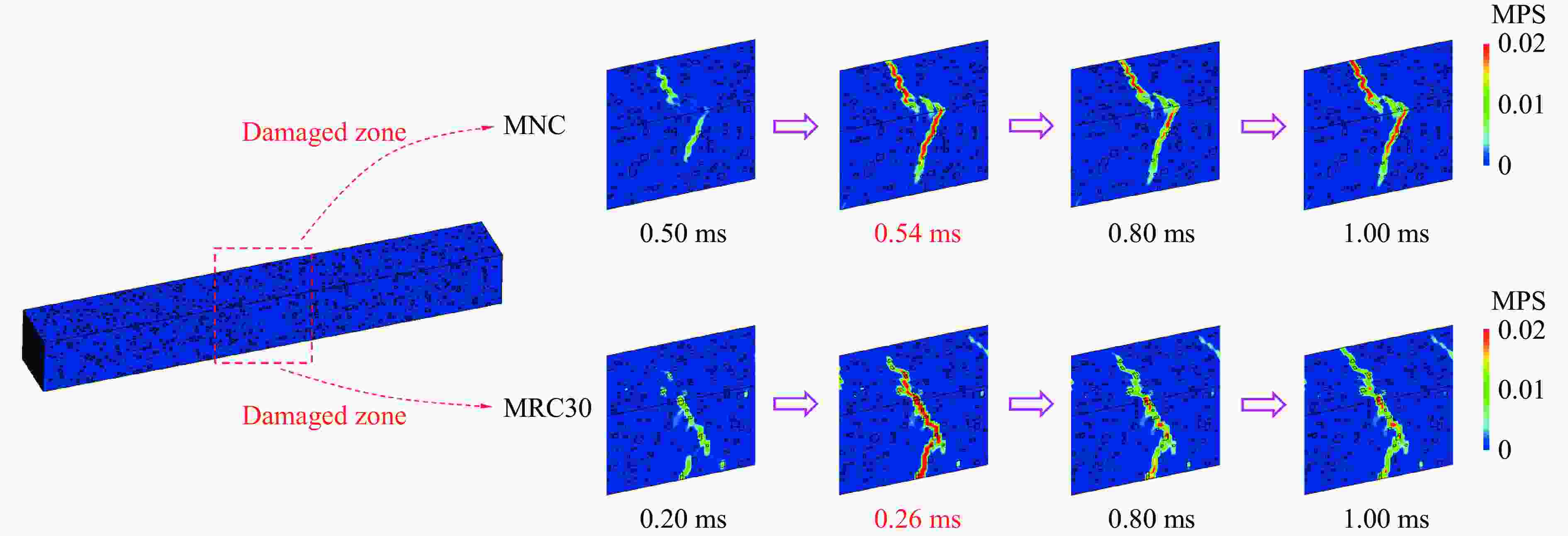
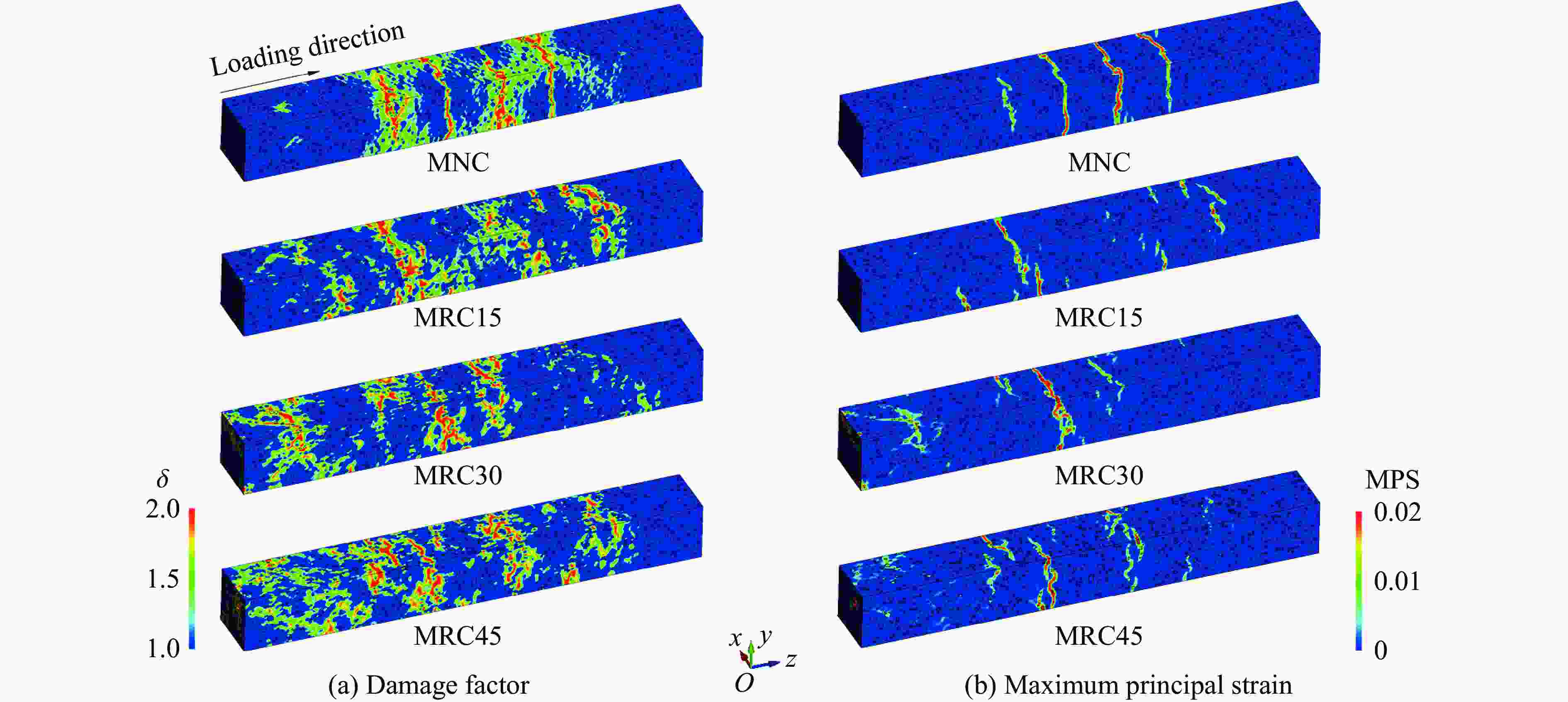
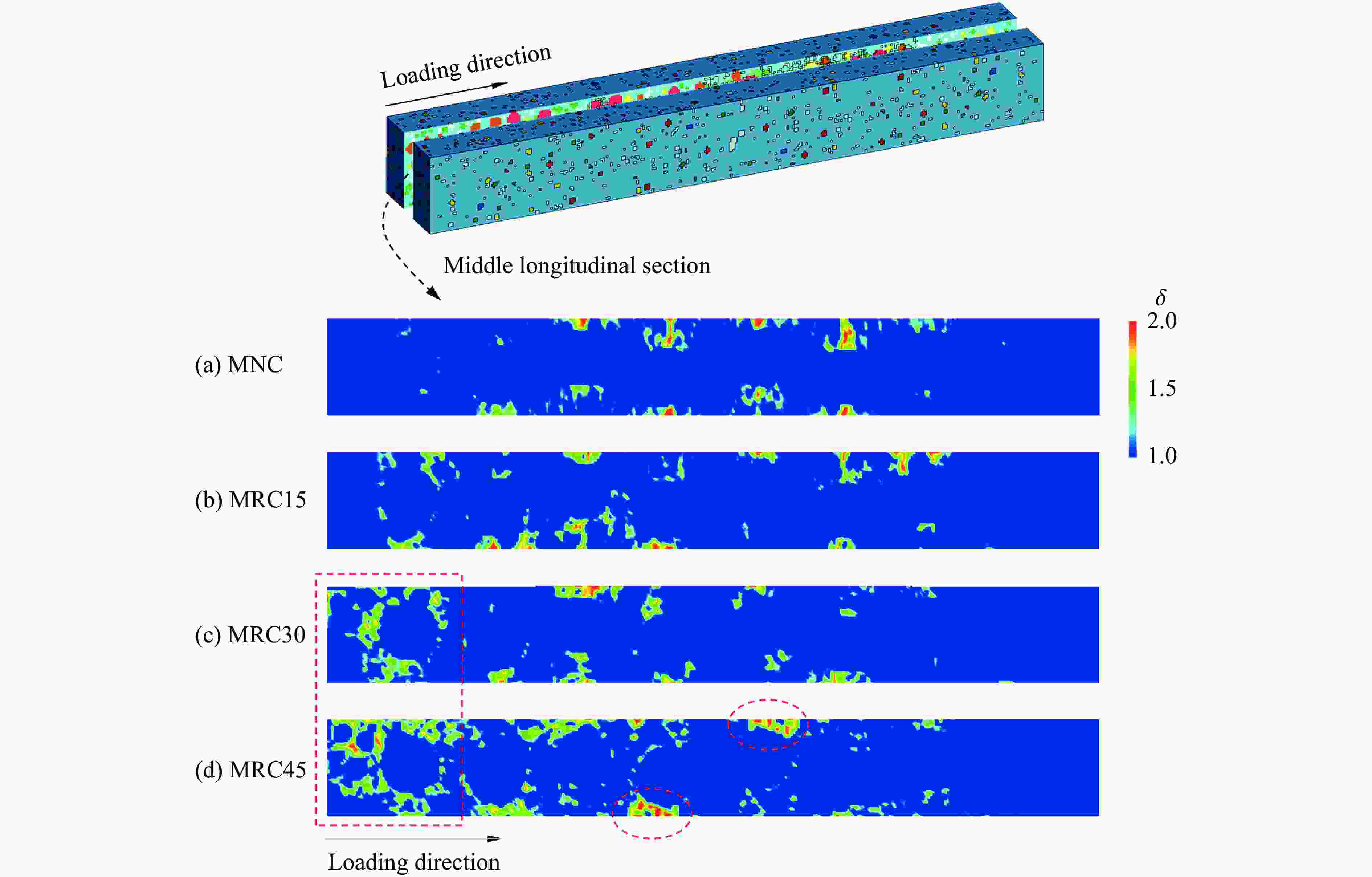
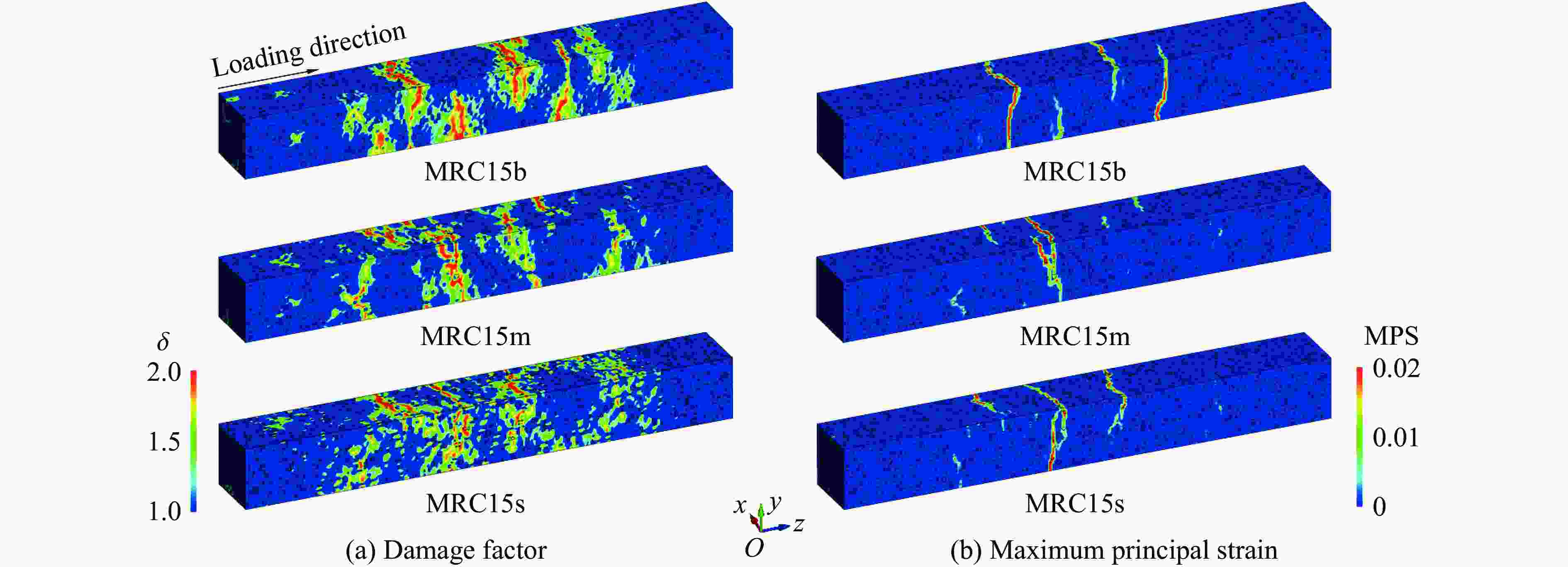
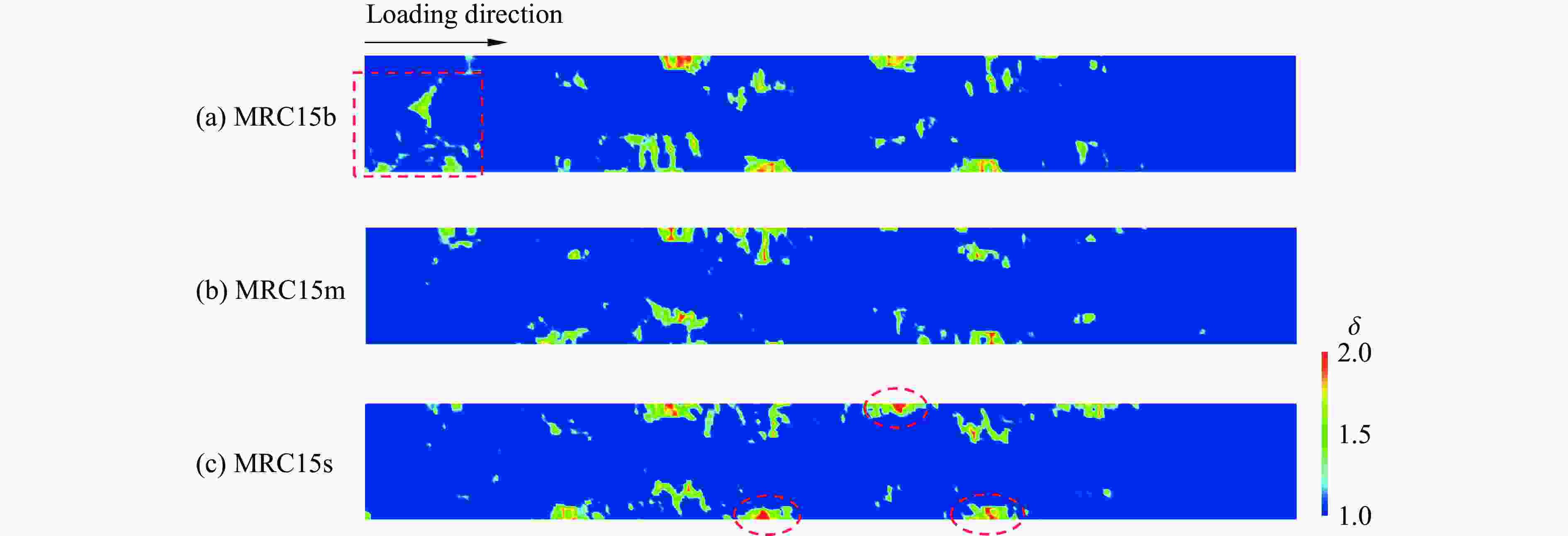
摘要: 为提升现有类混凝土材料的动态性能，在超材料混凝土基质中加入橡胶骨料形成新型抗冲击材料，并对其细观力学模型在冲击荷载作用下的动态响应进行数值模拟。对试件内各组分含量、级配、分布情况及适用材料模型进行系统标定和验证，分析了橡胶超材料混凝土在冲击荷载下的衰波能力及各组分相互作用规律，探讨了橡胶骨料在高幅值荷载下对橡胶超材料混凝土破坏模式、损伤区域及损伤程度的影响，并对橡胶含量及粒径进行了参数分析。数值模拟结果表明：橡胶骨料的加入不仅使混凝土的损伤区域呈现“分散”特征，还能够有效降低试件的损伤程度；橡胶骨料可提升试件韧性，抑制损伤程度的加剧；高橡胶含量对试件强度造成负面影响，形成损伤抑制与损伤加剧之间的矛盾，为确保两者平衡，建议橡胶骨料体积占骨料总体积的15%～30%。以上结果说明，在超材料混凝土中加入橡胶骨料能够有效提升试件的动态性能，为未来抗冲击材料的设计和工程应用提供参考。Abstract: To enhance the dynamic performance of existing concrete-like materials, rubber aggregates were incorporated into a metaconcrete matrix to create a novel impact-resistant material, and the dynamic response of its mesoscopic mechanical model under impact load was simulated. Initially, the content, gradation, distribution, and appropriate material models of the specimen components were systematically calibrated and validated. Subsequently, the wave-damping capacity and the interaction patterns of the components in rubber-based metaconcrete under impact load were analyzed. In particular, the effect of rubber aggregates on the failure modes, damage zones, and extent of damage in metaconcrete under high-amplitude loads was thoroughly examined, and a parameter analysis of the rubber content and particle size was conducted. The numerical results showed that the addition of the rubber aggregates not only makes the damaged area of the concrete show dispersed characteristics, but also effectively reduces the degree of specimen damage. Rubber aggregates enhance the specimen’s toughness and suppress the intensification of damage. However, high rubber content has a detrimental effect on the specimen’s strength, and leads to a trade-off between damage suppression and damage exacerbation. To balance these two effects, it is recommended that rubber aggregates make up 15% to 30% of the total volume of aggregates. These findings demonstrate that incorporating rubber aggregates into metaconcrete can significantly improve its dynamic performance, providing a reference for the design and engineering application of impact-resistant materials in the future.
-
Key words:
- impact-resistant materials /
- rubber /
- metaconcrete /
- dynamic behavior /
- damage /
- resonator
-
图 2 细观橡胶超材料混凝土模型示意图
Figure 2. Schematic diagram of meso-scale rubber metaconcrete model
图 3 K&C模型的本构描述：(a) 强度面子午线，(b) 经典应力-应变曲线
Figure 3. Constitutive description of K&C model: (a) meridians of strength surfaces; (b) typical stress-strain curve
图 6 加载曲线和数值模型示意图(a)以及应力时程曲线(b)
Figure 6. (a) Schematic diagram of the numerical model and loading curve; (b) stress-time curves
图 7 不同橡胶含量的混凝土数值模型
Figure 7. Numerical models of the concrete with varying rubber contents
图 8 NC、RC15和RC30的加载曲线(a)以及SHPB数值模型(b)
Figure 8. (a) Loading curves of NC, RC15 and RC30 and (b) numerical model of SHPB
图 11 试件尺寸及波能集中频带示意图
Figure 11. Schematic diagrams of the specimen size and wave energy concentration bandgap
图 12 (a) 单胞尺寸示意图，(b) 谐振器不同模态的固有频率及位移（S）云图，(c) 单胞能带结构
Figure 12. (a) Schematic diagram of unit cell dimensions; (b) natural frequencies and displacement (S) contour of the resonator’s different modes; (c) band structure of the unit cell
图 14 NC、RC30、MNC和MRC30的应力时程曲线(a)及其FFT 曲线(b)
Figure 14. (a) Stress-time curves and (b) FFT curves for NC, RC30, MNC, and MRC30
图 15 试件内不同组分的能量占比
Figure 15. Energy proportion among different components of specimens
图 18 不同时刻NC和RC30的最大主应变云图
Figure 18. Maximum principal strain contours of NC and RC30 at different time
图 19 不同时刻MNC和MRC30的最大主应变云图
Figure 19. Maximum principal strain contours of MNC and MRC30 at different time
图 21 不同橡胶含量的超材料混凝土中部纵截面损伤云图
Figure 21. Damage contour of the longitudinal cross-section at the center of metaconcrete with different rubber contents
图 22 含不同橡胶骨料尺寸的超材料混凝土数值模型示意图
Figure 22. Schematic diagram of the numerical model of metaconcrete with different rubber aggregate sizes
图 23 含不同橡胶骨料尺寸的超材料混凝土的损伤
Figure 23. Damage of metaconcrete with varying rubber aggregate sizes
图 24 不同橡胶粒径试件中部纵截面损伤因子云图
Figure 24. Damage contour of the longitudinal cross-section at the center of metaconcrete with different rubber aggregate sizes
Component Density/(kg·m−3) Poisson’s ratio Strength/MPa C10 C01 Mortar 2100 0.18 35 Natural aggregate 2600 0.14 90 Rubber aggregate 1000 0.492 0.58643 − 0.038942 
下载: 导出CSV
表 2 谐振器软涂层和内核材料参数
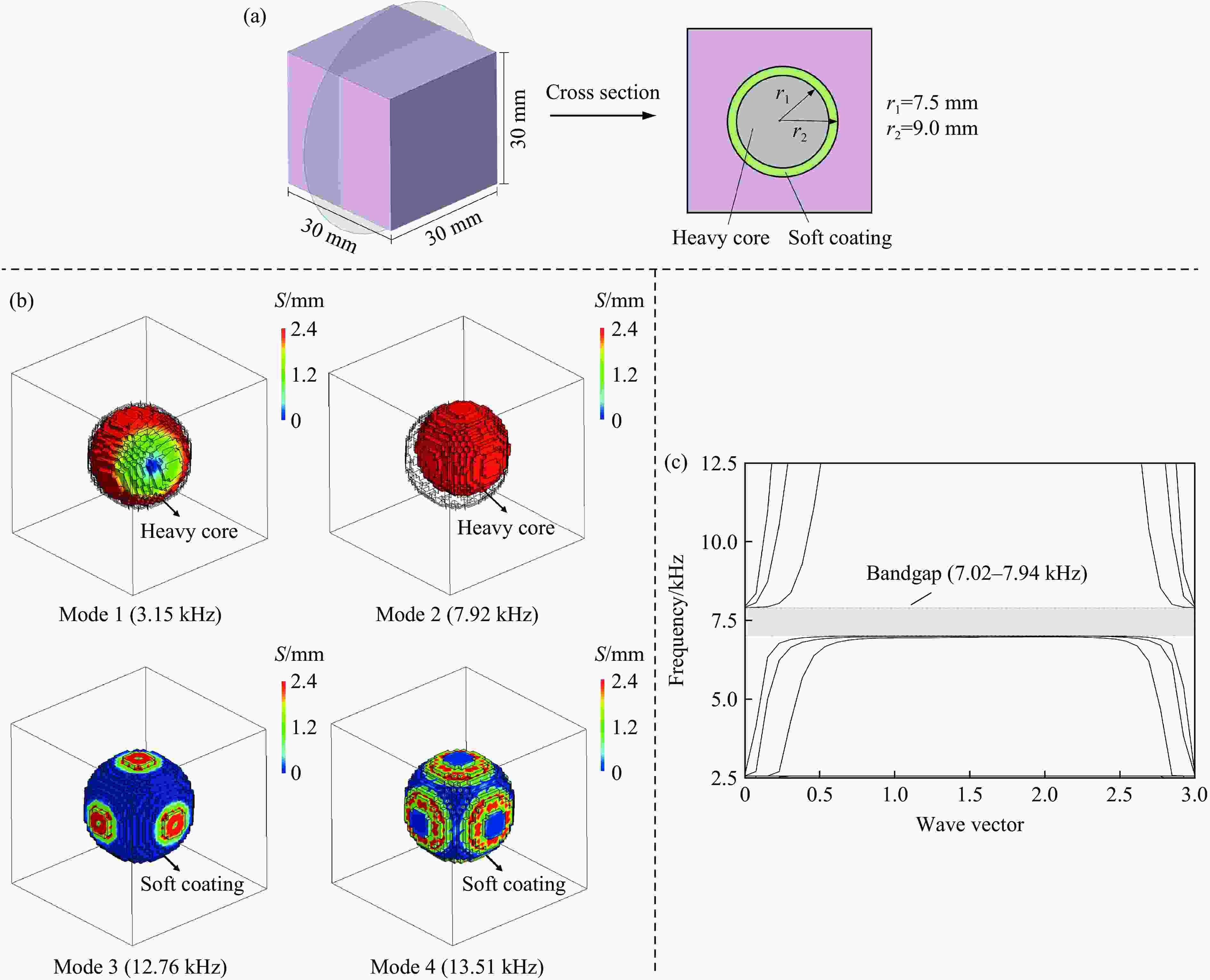
Table 2. Parameters of the resonator soft coating and heavy core
Component Density/(kg·m−3) Poisson’s ratio Young’s modulus/GPa Soft coating 900 0.49 0.01 Heavy core 7850 0.30 210
下载: 导出CSV
-
[1] HERNÁNDEZ-OLIVARES F, BARLUENGA G, BOLLATI M, et al. Static and dynamic behaviour of recycled tyre rubber-filled concrete [J]. Cement and Concrete Research, 2002, 32(10): 1587–1596. doi: 10.1016/S0008-8846(02)00833-5 [2] LI G Q, STUBBLEFIELD M A, GARRICK G, et al. Development of waste tire modified concrete [J]. Cement and Concrete Research, 2004, 34(12): 2283–2289. doi: 10.1016/j.cemconres.2004.04.013 [3] TOPÇU I B, AVCULAR N. Analysis of rubberized concrete as a composite material [J]. Cement and Concrete Research, 1997, 27(8): 1135–1139. doi: 10.1016/S0008-8846(97)00115-4 [4] ELDIN N N, SENOUCI A B. Observations on rubberized concrete behavior [J]. Cement, Concrete and Aggregates, 1993, 15(1): 74–84. doi: 10.1520/CCA10590J [5] TOPCU I B. The properties of rubberized concretes [J]. Cement and Concrete Research, 1995, 25(2): 304–310. doi: 10.1016/0008-8846(95)00014-3 [6] TOUTANJI H A. The use of rubber tire particles in concrete to replace mineral aggregates [J]. Cement and Concrete Composites, 1996, 18(2): 135–139. doi: 10.1016/0958-9465(95)00010-0 [7] ZHENG L, HUO X S, YUAN Y. Experimental investigation on dynamic properties of rubberized concrete [J]. Construction and Building Materials, 2008, 22(5): 939–947. doi: 10.1016/j.conbuildmat.2007.03.005 [8] SEGRE N, JOEKES I. Use of tire rubber particles as addition to cement paste [J]. Cement and Concrete Research, 2000, 30(9): 1421–1425. doi: 10.1016/S0008-8846(00)00373-2 [9] XUE J, SHINOZUKA M. Rubberized concrete: a green structural material with enhanced energy-dissipation capability [J]. Construction and Building Materials, 2013, 42: 196–204. doi: 10.1016/j.conbuildmat.2013.01.005 [10] LIU Z Y, ZHANG X X, MAO Y W, et al. Locally resonant sonic materials [J]. Science, 2000, 289(5485): 1734–1736. doi: 10.1126/science.289.5485.1734 [11] MITCHELL S J. Metaconcrete: engineered aggregates for enhanced dynamic performance [D]. Pasadena: California Institute of Technology, 2016. [12] 张恩, 路国运, 杨会伟, 等. 超材料混凝土的带隙特征及对冲击波的衰减效应 [J]. 爆炸与冲击, 2020, 40(6): 063301. doi: 10.11883/bzycj-2019-0252ZHANG E, LU G Y, YANG H W, et al. Band gap features of metaconcrete and shock wave attenuation in it [J]. Explosion and Shock Waves, 2020, 40(6): 063301. doi: 10.11883/bzycj-2019-0252 [13] XU C, CHEN W S, HAO H, et al. Experimental and numerical assessment of stress wave attenuation of metaconcrete rods subjected to impulsive loads [J]. International Journal of Impact Engineering, 2022, 159: 104052. doi: 10.1016/j.ijimpeng.2021.104052 [14] XU C, CHEN W S, HAO H. The influence of design parameters of engineered aggregate in metaconcrete on bandgap region [J]. Journal of the Mechanics and Physics of Solids, 2020, 139: 103929. doi: 10.1016/j.jmps.2020.103929 [15] KETTENBEIL C, RAVICHANDRAN G. Experimental investigation of the dynamic behavior of metaconcrete [J]. International Journal of Impact Engineering, 2018, 111: 199–207. doi: 10.1016/j.ijimpeng.2017.09.017 [16] XU C, CHEN W S, HAO H, et al. Static mechanical properties and stress wave attenuation of metaconcrete subjected to impulsive loading [J]. Engineering Structures, 2022, 263: 114382. doi: 10.1016/j.engstruct.2022.114382 [17] LIU Y, SHI D Y, HE H G, et al. Double-resonator based metaconcrete composite slabs and vibration attenuation mechanism [J]. Engineering Structures, 2022, 262: 114392. doi: 10.1016/j.engstruct.2022.114392 [18] JIN H X, HAO H, CHEN W S, et al. Spall behaviors of metaconcrete: 3D meso-scale modelling [J]. International Journal of Structural Stability and Dynamics, 2021, 21(9): 2150121. doi: 10.1142/S0219455421501212 [19] FENG W H, CHEN B Y, YANG F, et al. Numerical study on blast responses of rubberized concrete slabs using the Karagozian and Case concrete model [J]. Journal of Building Engineering, 2021, 33: 101610. doi: 10.1016/j.jobe.2020.101610 [20] THILAKARATHNA P S M, BADUGE K S K, MENDIS P, et al. Mesoscale modelling of concrete: a review of geometry generation, placing algorithms, constitutive relations and applications [J]. Engineering Fracture Mechanics, 2020, 231: 106974. doi: 10.1016/j.engfracmech.2020.106974 [21] OLLIVIER J P, MASO J C, BOURDETTE B. Interfacial transition zone in concrete [J]. Advanced Cement Based Materials, 1995, 2(1): 30–38. doi: 10.1016/1065-7355(95)90037-3 [22] WRIGGERS P, MOFTAH S O. Mesoscale models for concrete: homogenisation and damage behaviour [J]. Finite Elements in Analysis and Design, 2006, 42(7): 623–636. doi: 10.1016/j.finel.2005.11.008 [23] CHEN G, HAO Y F, HAO H. 3D meso-scale modelling of concrete material in spall tests [J]. Materials and Structures, 2015, 48(6): 1887–1899. doi: 10.1617/s11527-014-0281-z [24] PHAM T M, CHEN W S, KHAN A M, et al. Dynamic compressive properties of lightweight rubberized concrete [J]. Construction and Building Materials, 2020, 238: 117705. doi: 10.1016/j.conbuildmat.2019.117705 [25] CUI J, HAO H, SHI Y C. Numerical study of the influences of pressure confinement on high-speed impact tests of dynamic material properties of concrete [J]. Construction and Building Materials, 2018, 171: 839–849. doi: 10.1016/j.conbuildmat.2018.03.170 [26] PAN L, HAO H, CUI J, et al. Numerical study on dynamic properties of rubberised concrete with different rubber contents [J]. Defence Technology, 2023, 24: 228–240. doi: 10.1016/j.dt.2022.04.007 [27] MALVAR L J, SIMONS D. Concrete material modeling in explicit computations [C]//Proceedings of Workshop on Recent Advances in Computational Structural Dynamics and High Performance Computing. Vicksburg: USAE Waterways Experiment Station, 1996: 165–194. [28] ZHOU R X, SONG Z H, LU Y. 3D mesoscale finite element modelling of concrete [J]. Computers & Structures, 2017, 192: 96–113. doi: 10.1016/j.compstruc.2017.07.009 [29] ZHOU R X, LU Y. A mesoscale interface approach to modelling fractures in concrete for material investigation [J]. Construction and Building Materials, 2018, 165: 608–620. doi: 10.1016/j.conbuildmat.2018.01.040 [30] CUI J, HAO H, SHI Y C. Discussion on the suitability of concrete constitutive models for high-rate response predictions of RC structures [J]. International Journal of Impact Engineering, 2017, 1016: 202–216. doi: 10.1016/j.ijimpeng.2017.04.003 [31] CRAWFORD J E, WU Y C, MAGALLANES J M, et al. The importance of shear-dilatancy behaviors in RC columns [J]. International Journal of Protective Structures, 2013, 4(3): 341–377. doi: 10.1260/2041-4196.4.3.341 [32] ABEDINI M, ZHANG C W. Performance assessment of concrete and steel material models in LS-DYNA for enhanced numerical simulation, a state of the art review [J]. Archives of Computational Methods in Engineering, 2021, 28(4): 2921–2942. doi: 10.1007/s11831-020-09483-5 [33] CUI J, HAO H, SHI Y C. Study of concrete damage mechanism under hydrostatic pressure by numerical simulations [J]. Construction and Building Materials, 2018, 160: 440–449. doi: 10.1016/j.conbuildmat.2017.11.083 [34] MALVAR L J, CRAWFORD J E, WESEVICH J W, et al. A plasticity concrete material model for DYNA3D [J]. International Journal of Impact Engineering, 1997, 19(9/10): 847–873. doi: 10.1016/S0734-743X(97)00023-7 [35] MOONEY M. A theory of large elastic deformation [J]. Journal of Applied Physics, 1940, 11(9): 582–592. doi: 10.1063/1.1712836 [36] RIVLIN R S, SAUNDERS D W. Large elastic deformations of isotropic materials Ⅶ. experiments on the deformation of rubber [J]. Philosophical Transactions of the Royal Society A, 1951, 243(865): 251–288. doi: 10.1098/rsta.1951.0004 [37] AYHAN B, LALE E. Modeling strain rate effect on tensile strength of concrete using damage plasticity model [J]. International Journal of Impact Engineering, 2022, 162: 104132. doi: 10.1016/j.ijimpeng.2021.104132 [38] LI Q M, MENG H. About the dynamic strength enhancement of concrete-like materials in a split Hopkinson pressure bar test [J]. International Journal of Solids and Structures, 2003, 40(2): 343–360. doi: 10.1016/S0020-7683(02)00526-7 [39] ERZAR B, FORQUIN P. Experiments and mesoscopic modelling of dynamic testing of concrete [J]. Mechanics of Materials, 2011, 43(9): 505–527. doi: 10.1016/j.mechmat.2011.05.002 [40] GROTE D L, PARK S W, ZHOU M. Dynamic behavior of concrete at high strain rates and pressures: Ⅰ. experimental characterization [J]. International Journal of Impact Engineering, 2001, 25(9): 869–886. doi: 10.1016/S0734-743X(01)00020-3 [41] Federation Internationale du Beton. FIB model code for concrete structures 2010 [M]. Berlin: Ernst & Sohn, 2013. [42] HAO Y, HAO H, ZHANG X H. Numerical analysis of concrete material properties at high strain rate under direct tension [J]. International Journal of Impact Engineering, 2012, 39(1): 51–62. doi: 10.1016/j.ijimpeng.2011.08.006 [43] HAO Y F, HAO H. Numerical evaluation of the influence of aggregates on concrete compressive strength at high strain rate [J]. International Journal of Protective Structures, 2011, 2(2): 177–206. doi: 10.1260/2041-4196.2.2.177 [44] Standards Australia Committee on Methods of Testing Concrete. Methods of testing concrete: method 2: preparation of concrete mixes in the laboratory: AS 1012.2—1994 [S]. Australia, 1994. [45] VALAPPIL S V, ARAGÓN A M, GOOSEN H. Phononic crystals’ band gap manipulation via displacement modes [J]. Solid State Communications, 2023, 361: 115061. doi: 10.1016/J.Ssc.2022.115061 -
下载:
点击查看大图
计量
- 文章访问数: 108
- HTML全文浏览量: 32
- PDF下载量: 21
