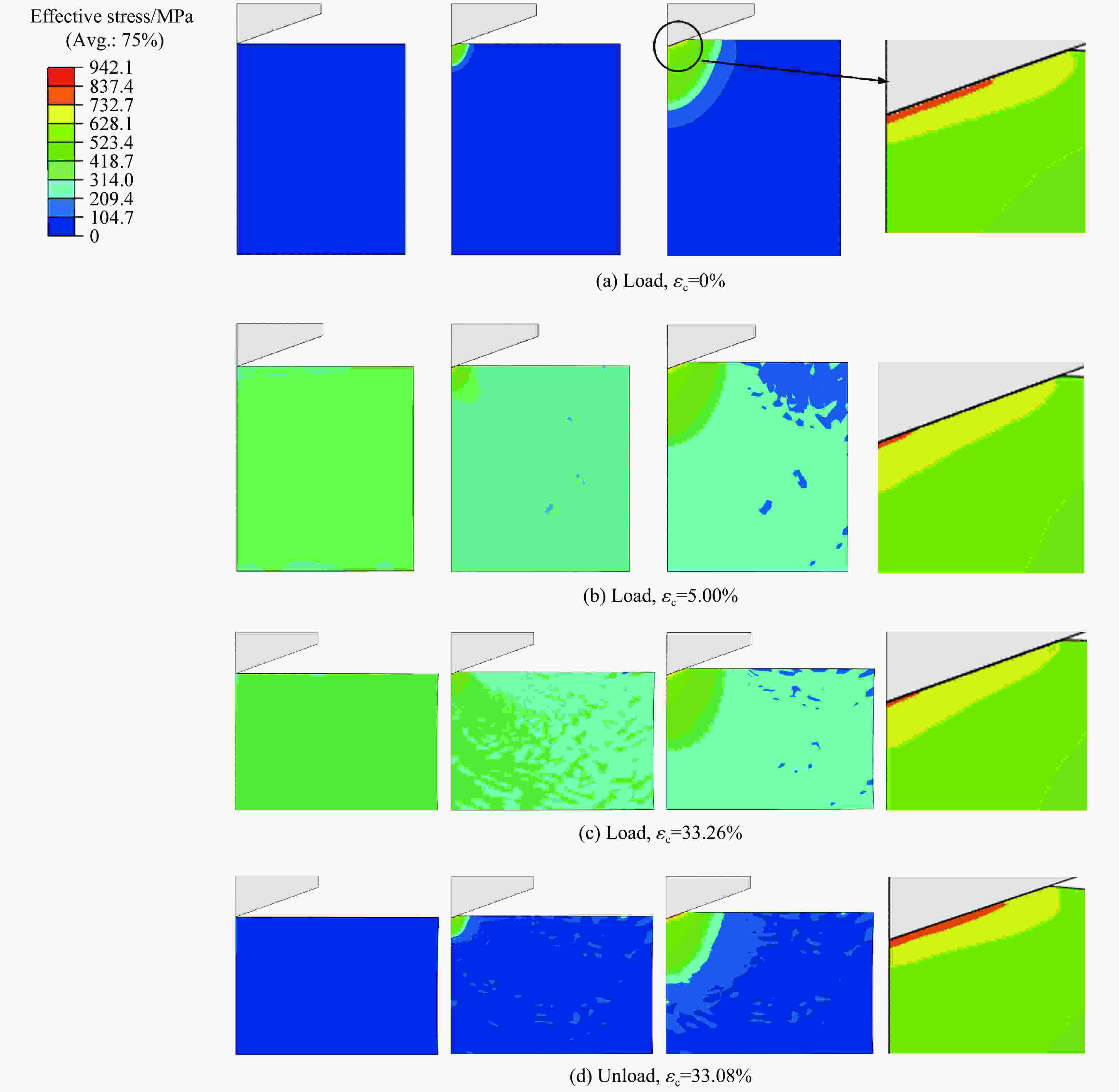
Indentation Behavior of CoCrFeNiMn High-Entropy Alloys under Dynamic Loads
-
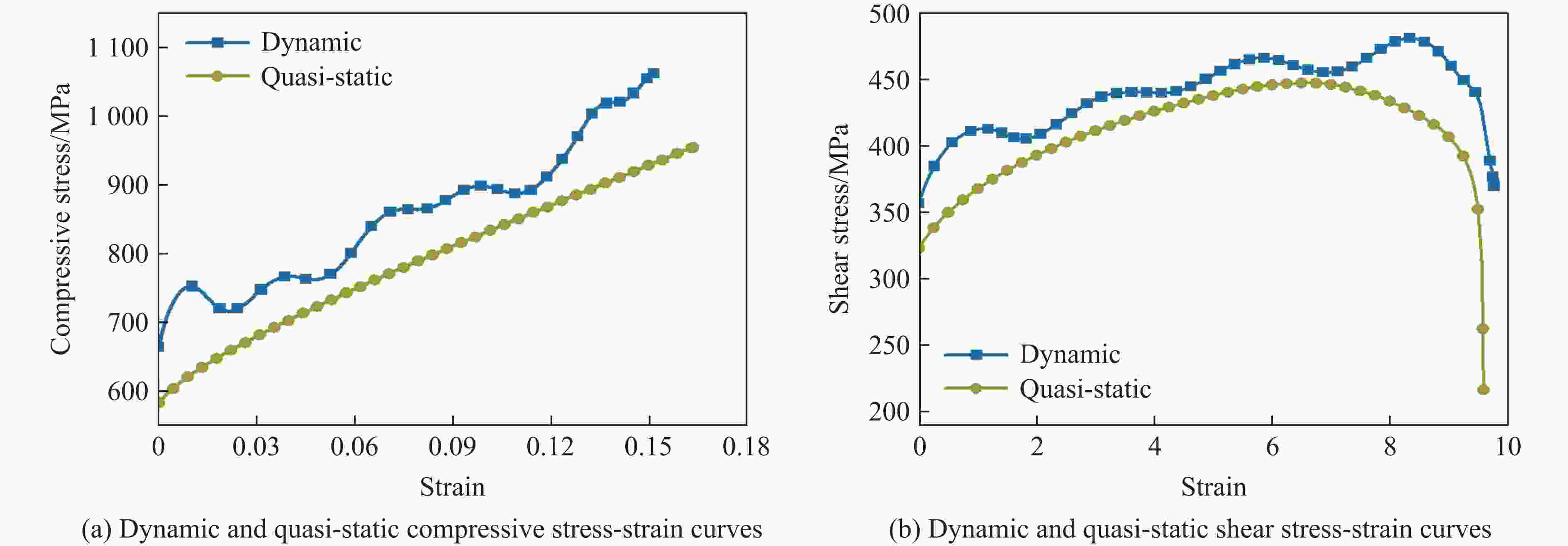
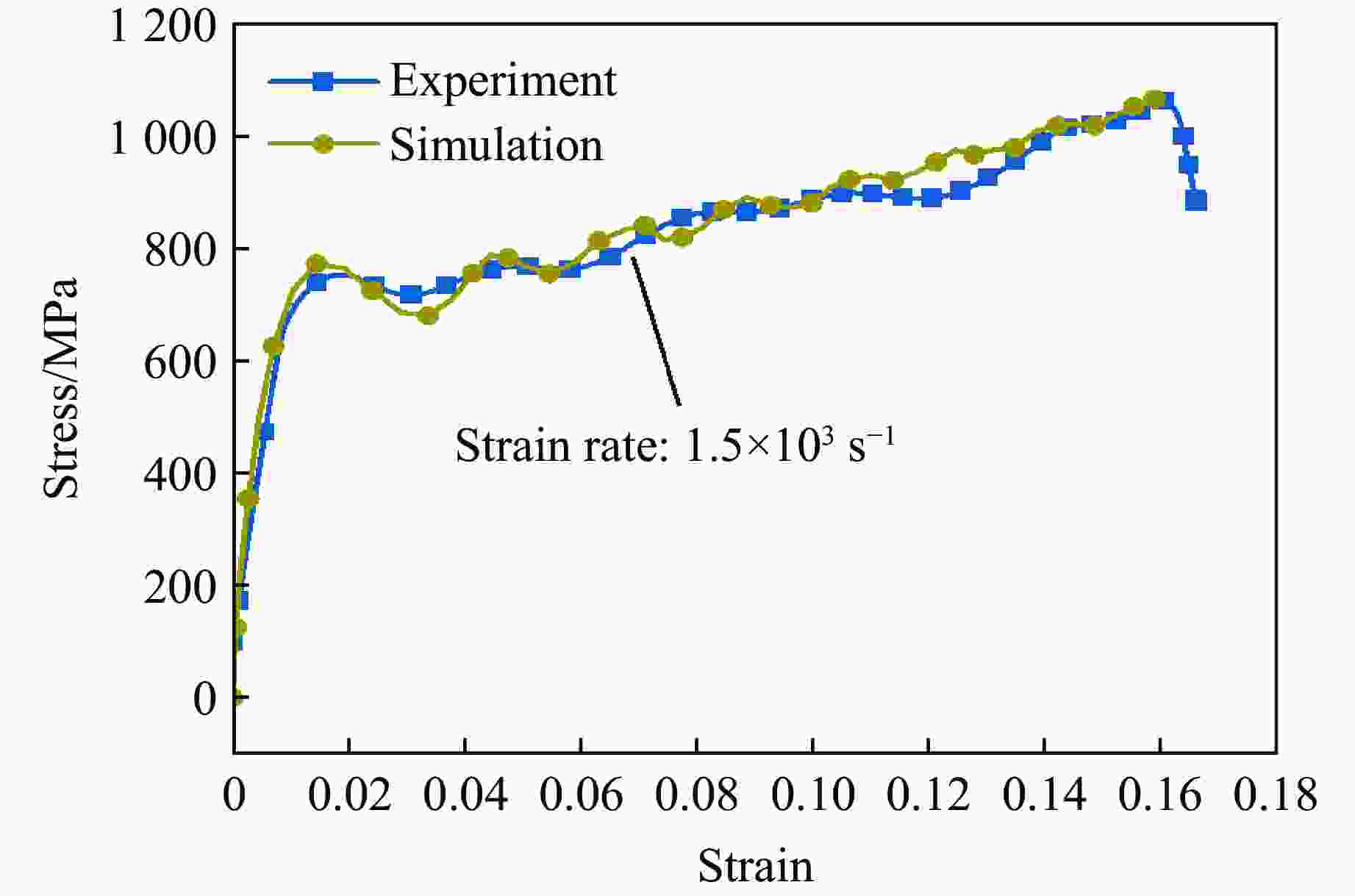
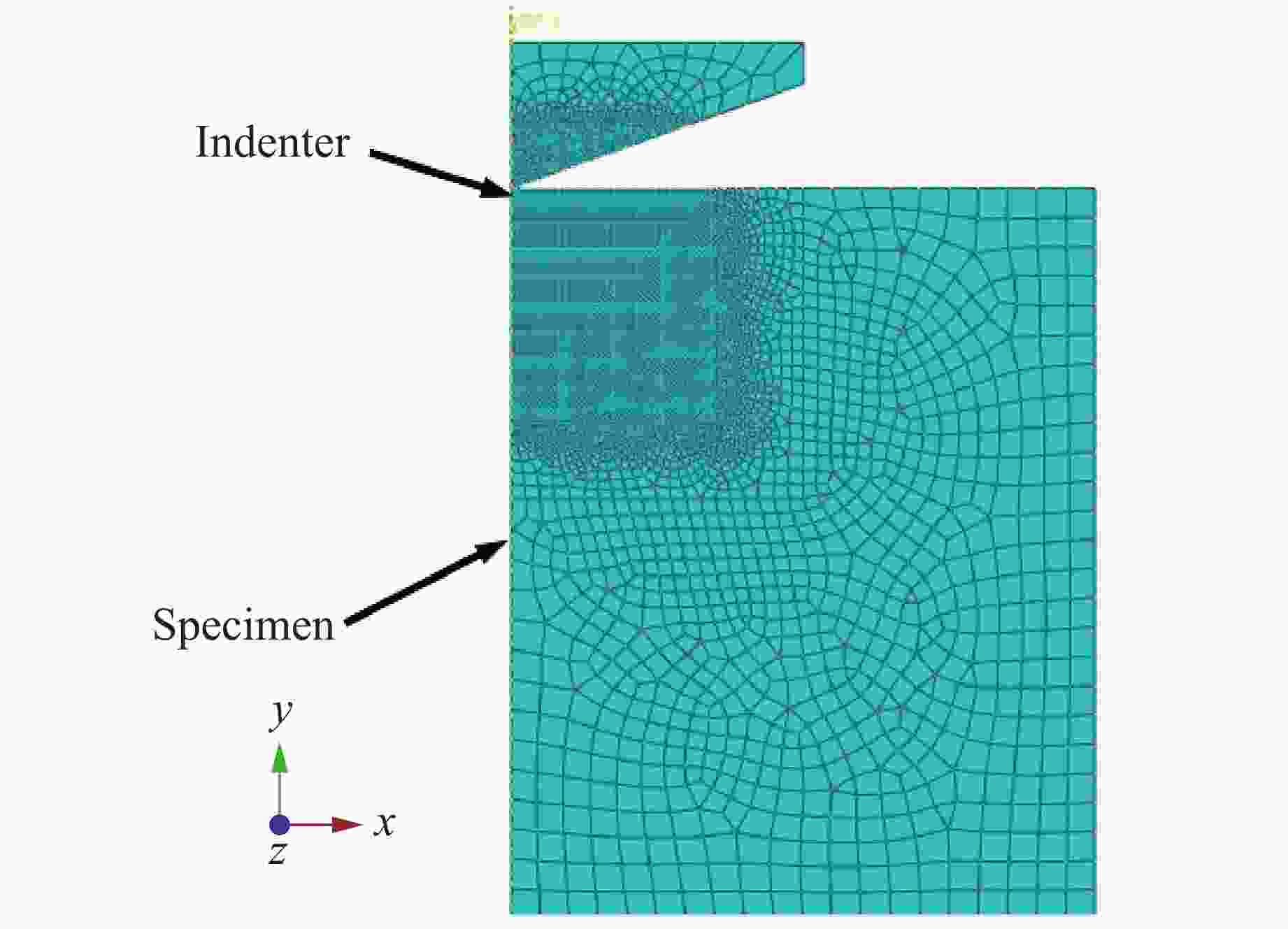
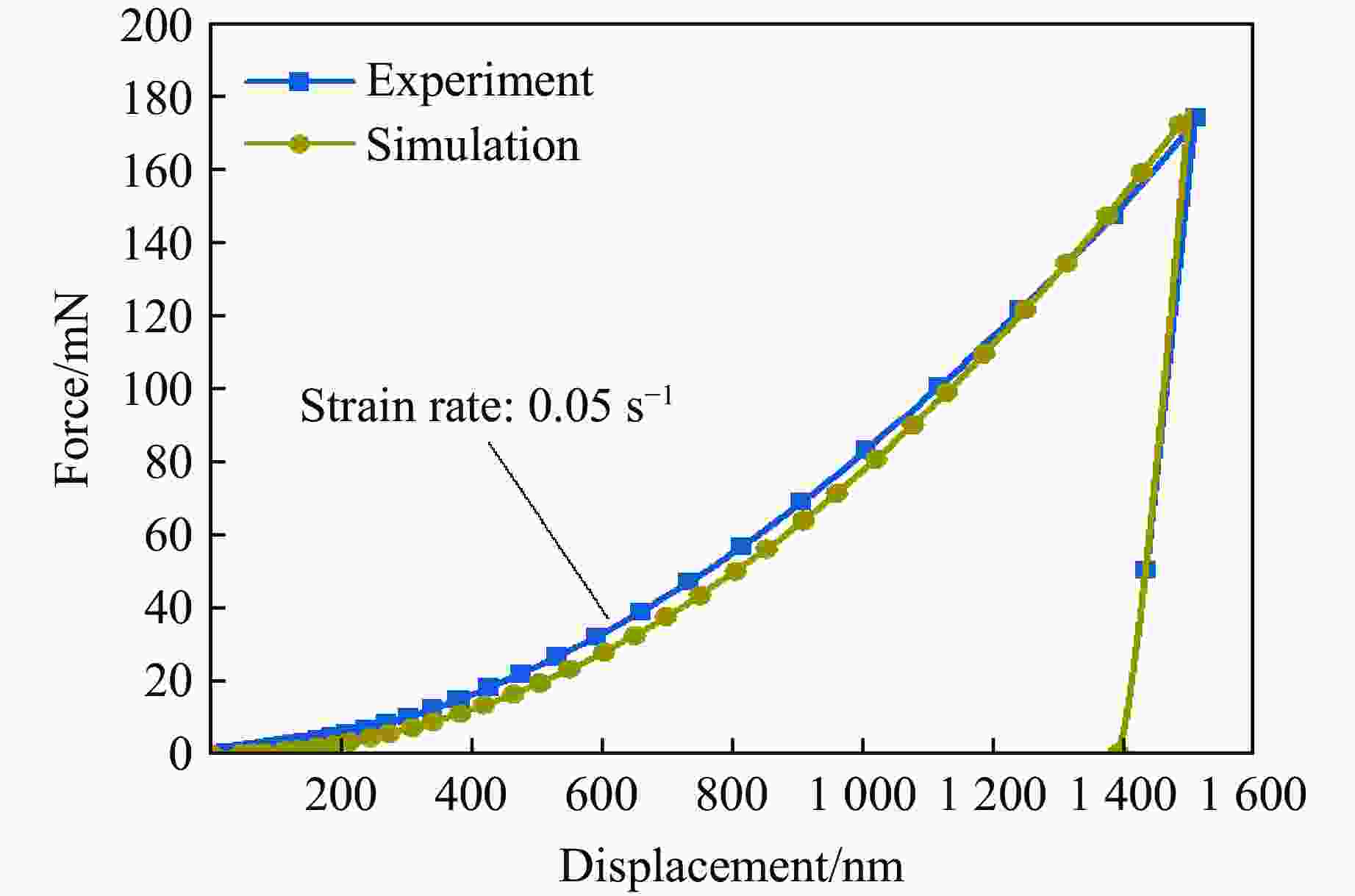
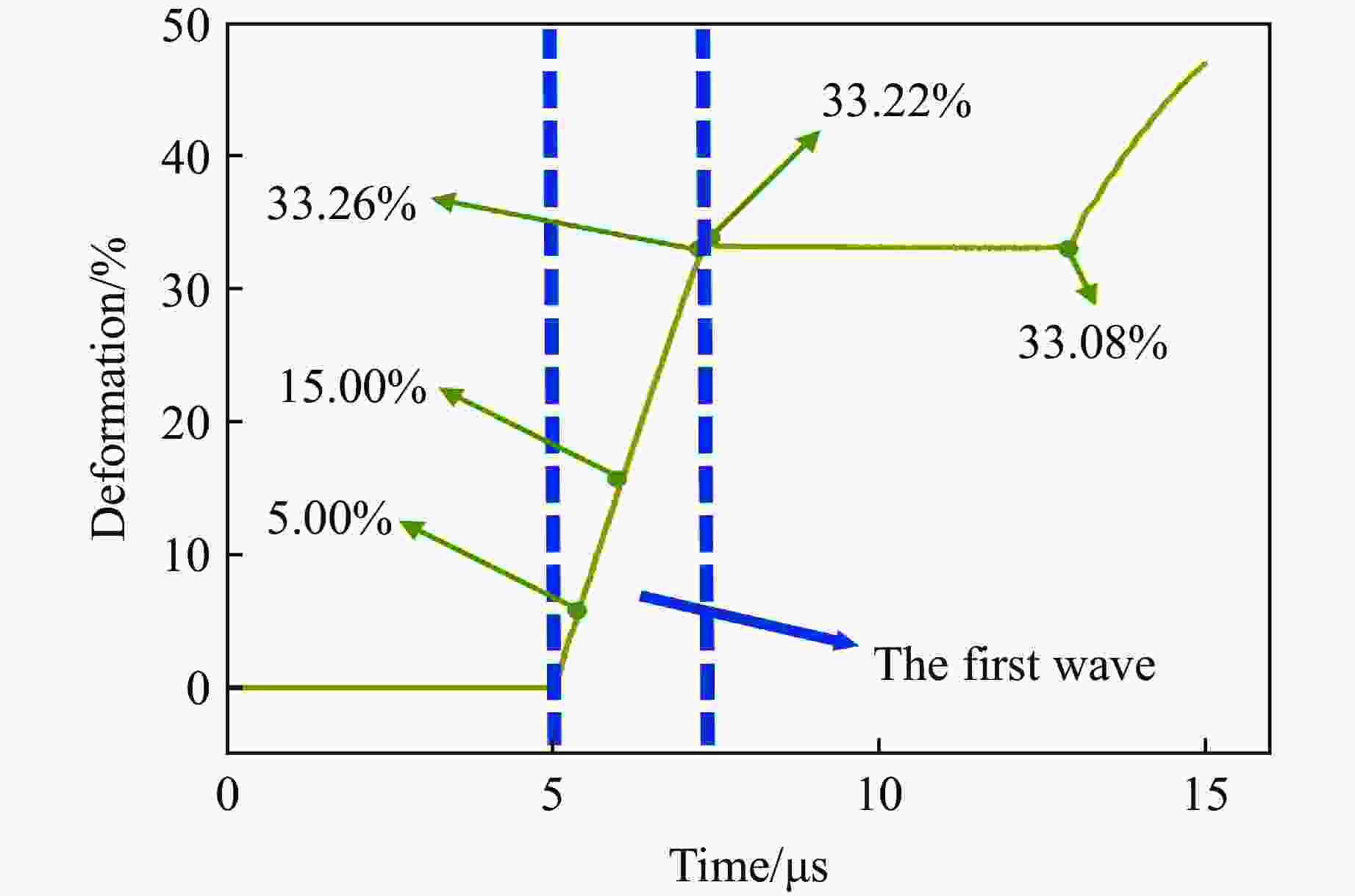
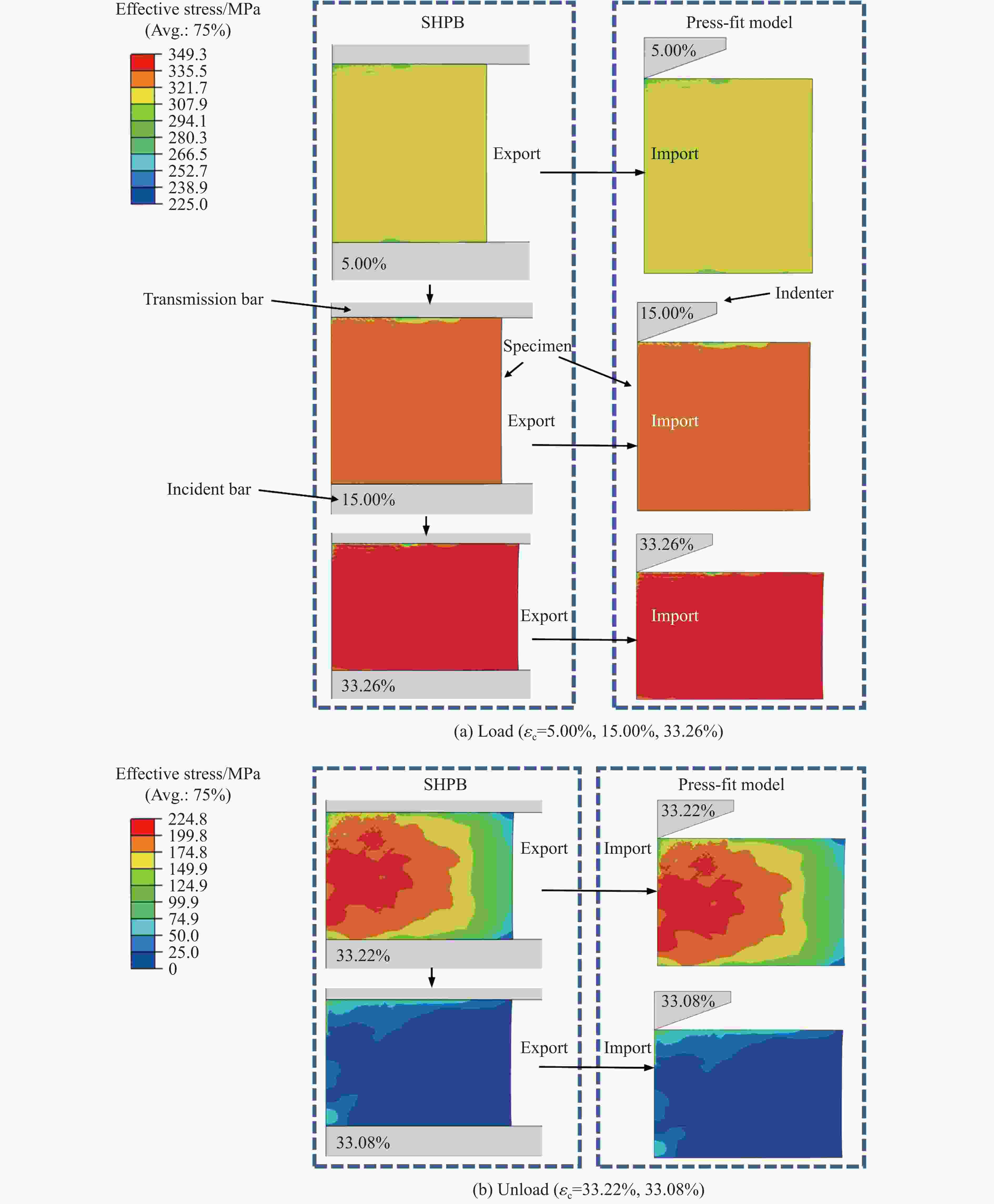
摘要: 为解决材料或结构在服役环境中的内部应力难以评估的问题，提出了一种有限元与微压入测试相结合的方法。以CoCrFeNiMn高熵合金为例，分别在不同加载速度下开展了压缩、剪切和微压入测试，并基于非对称初始屈服函数、Swift硬化与关联流动法则，构建了该材料的弹塑性本构模型。利用应力积分算法将该本构模型程序化，并接入ABAQUS有限元软件中，通过对比分离式霍普金森压杆与压入模型的有限元模拟结果和实验结果，验证了模型的可靠性。基于分离式霍普金森压杆模型，进行了动态压缩实验的数值模拟，并将不同动态变形时刻的应力场作为初始应力场（内部应力）导入压入模型中，进行压入模拟分析。结果表明：加载阶段的初始应力场会显著降低相同压入深度下的压入载荷，且降低幅度随着初始应力的增加而增大；此外，初始应力场的存在会进一步减弱压入过程中的应力集中。通过对不同压缩量下的载荷-压入位移曲线进行定量分析，揭示了不同初始应力条件下材料的压入响应规律。研究结果为服役条件下材料或结构内部应力的评估提供了参考。Abstract: To address the challenge of evaluating the internal stress of materials or structures in service environments, a method combining finite element analysis and micro-indentation testing is proposed. Taking the CoCrFeNiMn high-entropy alloy as the research object, compression, shear and micro-indentation tests were carried out at various loading speeds respectively. Based on an asymmetric initial yield function, Swift hardening and the associated flow rule, an elastoplastic constitutive model for this material was established. The constitutive model was programmed by using the stress integration algorithm and interfaced with the ABAQUS finite element software. Furthermore, by comparing the finite element simulation results with the experimental results from the split Hopkinson pressure bar (SHPB) tests and the indentation model, the reliability of the model was verified. Using the SHPB model, the numerical simulation of the dynamic compression experiment was carried out, and the stress fields at different dynamic deformation moments were imported into the indentation model as the initial stress (internal stress) fields for indentation simulation analysis. The results indicated that the initial stress field in the loading stage significantly reduces the indentation load at the same indentation depth, and the reduction amplitude increases with the increase of stress. In addition, the existence of the initial stress field will further weaken the stress concentration during the indentation process. Through the quantitative analysis of the load-indentation displacement curves under different compression amounts, the indentation response laws of the materials under different initial stress conditions were revealed. The research results provide a reference for the evaluation of the internal stress of materials or structures under service conditions.
-
图 2 CoCrFeNiMn高熵合金的动态及准静态压缩和剪切应力-应变曲线
Figure 2. Dynamic and quasi-static compressive and shear stress-strain curves of CoCrFeNiMn high-entropy alloy
图 4 CoCrFeNiMn高熵合金动态压缩实验与模拟得到的应力-应变曲线
Figure 4. Stress-strain curves from dynamic compression experiments and simulations of CoCrFeNiMn high-entropy alloy
图 6 CoCrFeNiMn高熵合金压入实验与数值模拟得到的载荷-位移曲线
Figure 6. Force-displacement curves from indentation experiments and simulations of CoCrFeNiMn high-entropy alloy
图 7 动态加载过程中CoCrFeNiMn高熵合金的变形历程
Figure 7. Deformation history of CoCrFeNiMn high-entropy alloy during dynamic loading
图 9 不同初始应力下的载荷-压入深度曲线
Figure 9. Force-indentation displacement curves under different initial stress conditions
图 11 不同初始应力下压入过程的等效应力云图
Figure 11. Equivalent stress nephogram during indentation process under different initial stresses
表 1 本构方程参数
Table 1. Constitutive equation parameters
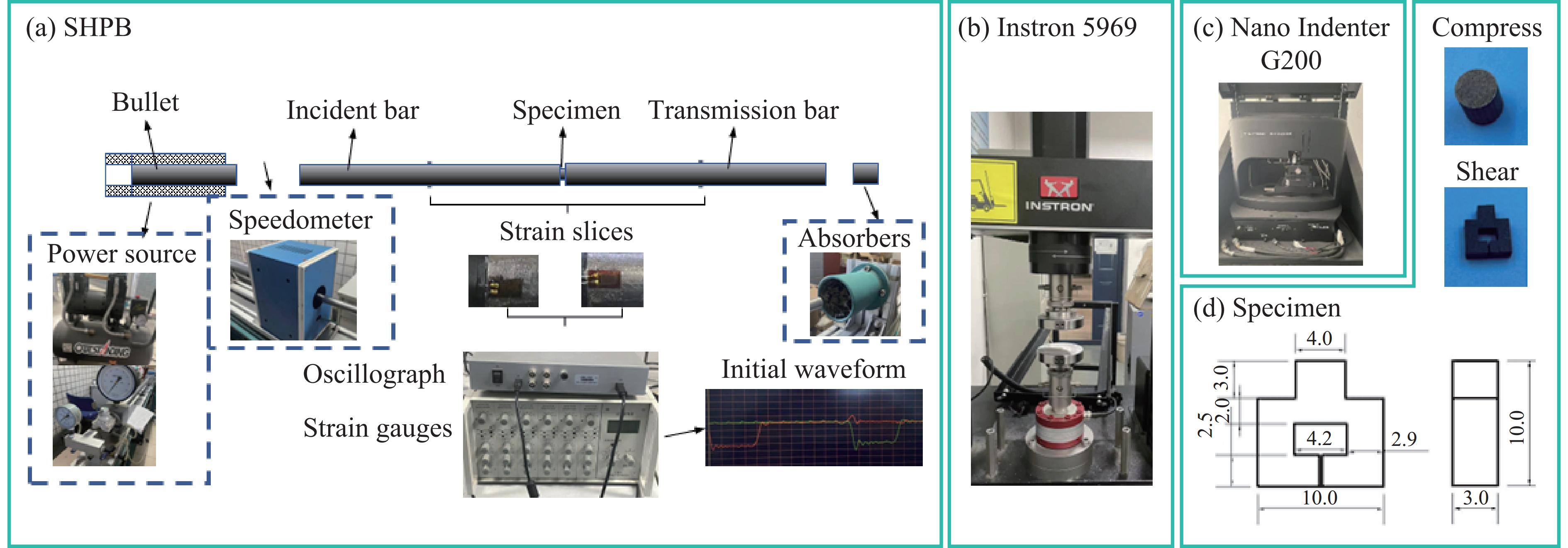
Type c A/MPa ${\varepsilon _{\text{s}}}$ n Quasi-static −0.14 304.67 1.46300 0.18394 Dynamic −0.27 413.16 0.09025 0.06015 
下载: 导出CSV
表 2 入射杆、透射杆和试件的材料及几何参数
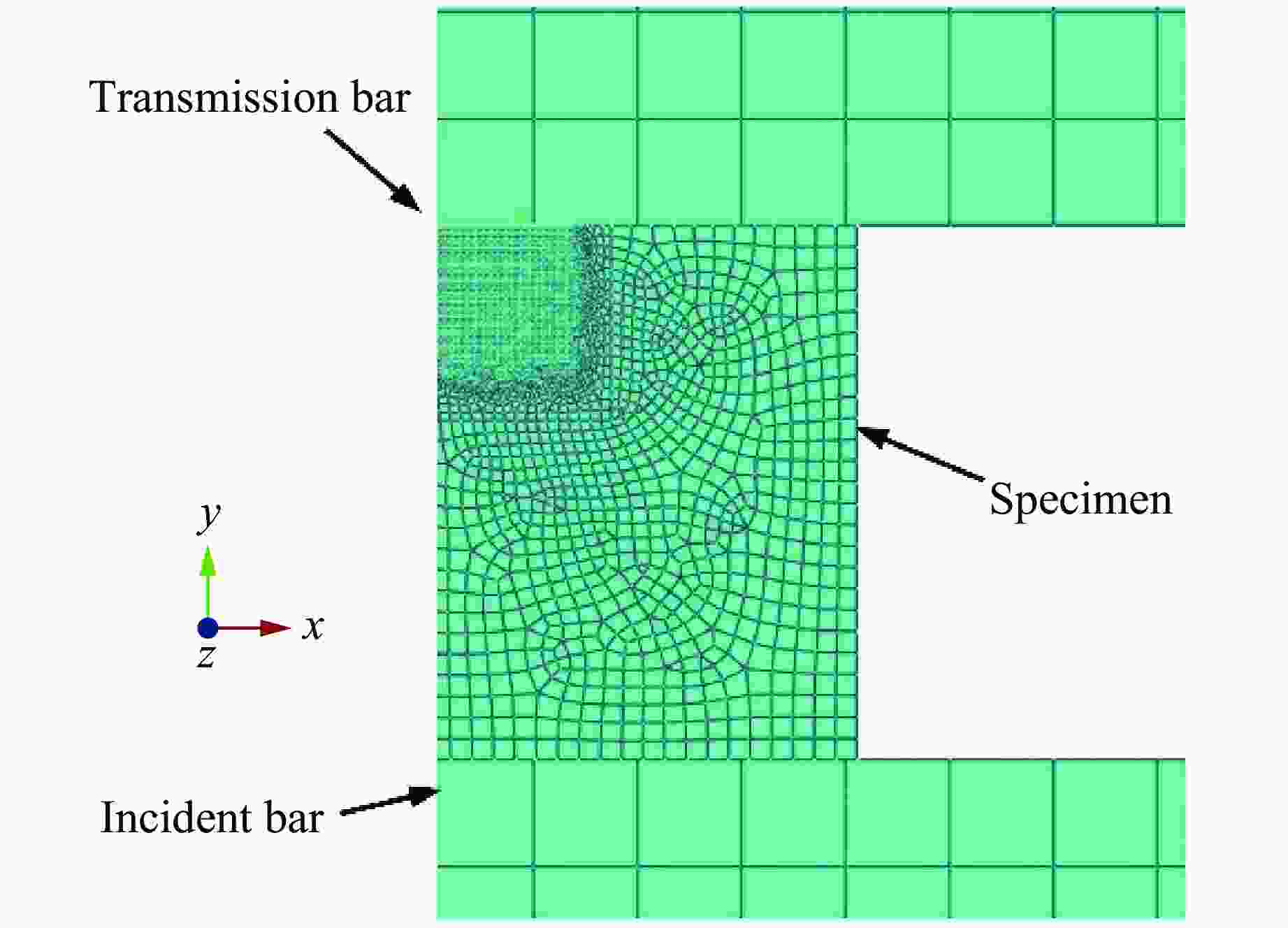
Table 2. Material and geometric parameters of incident bar, transmission bar and the specimen
Component Density/(g·cm−3) E/GPa ν Diameter/mm Length/mm Incident/transmission bar 7.9 210 0.30 37 2000 Specimen 8.0 183 0.25 8 5
下载: 导出CSV
表 3 二次多项式拟合参数
Table 3. Quadratic polynomial fitting parameters
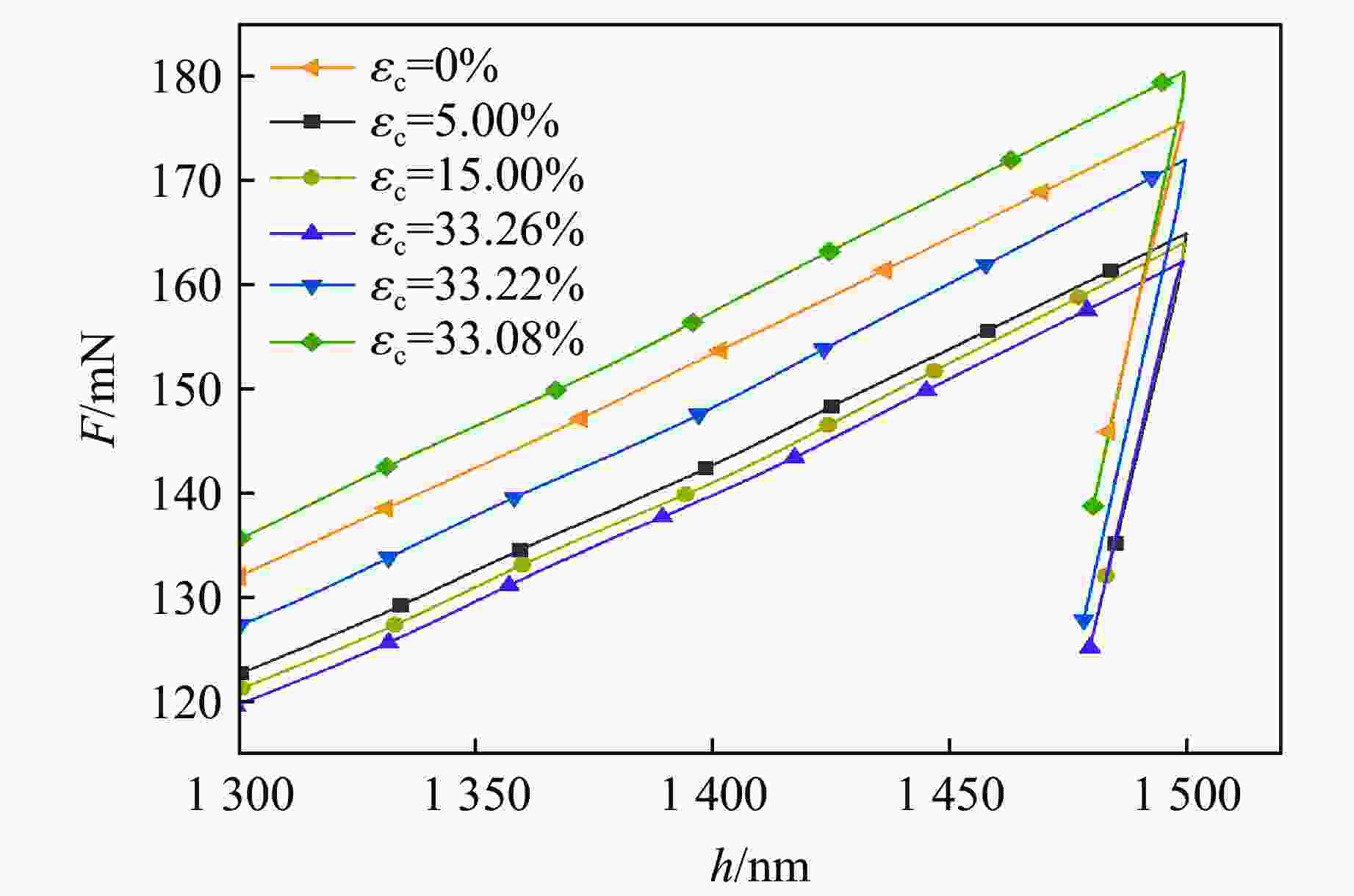
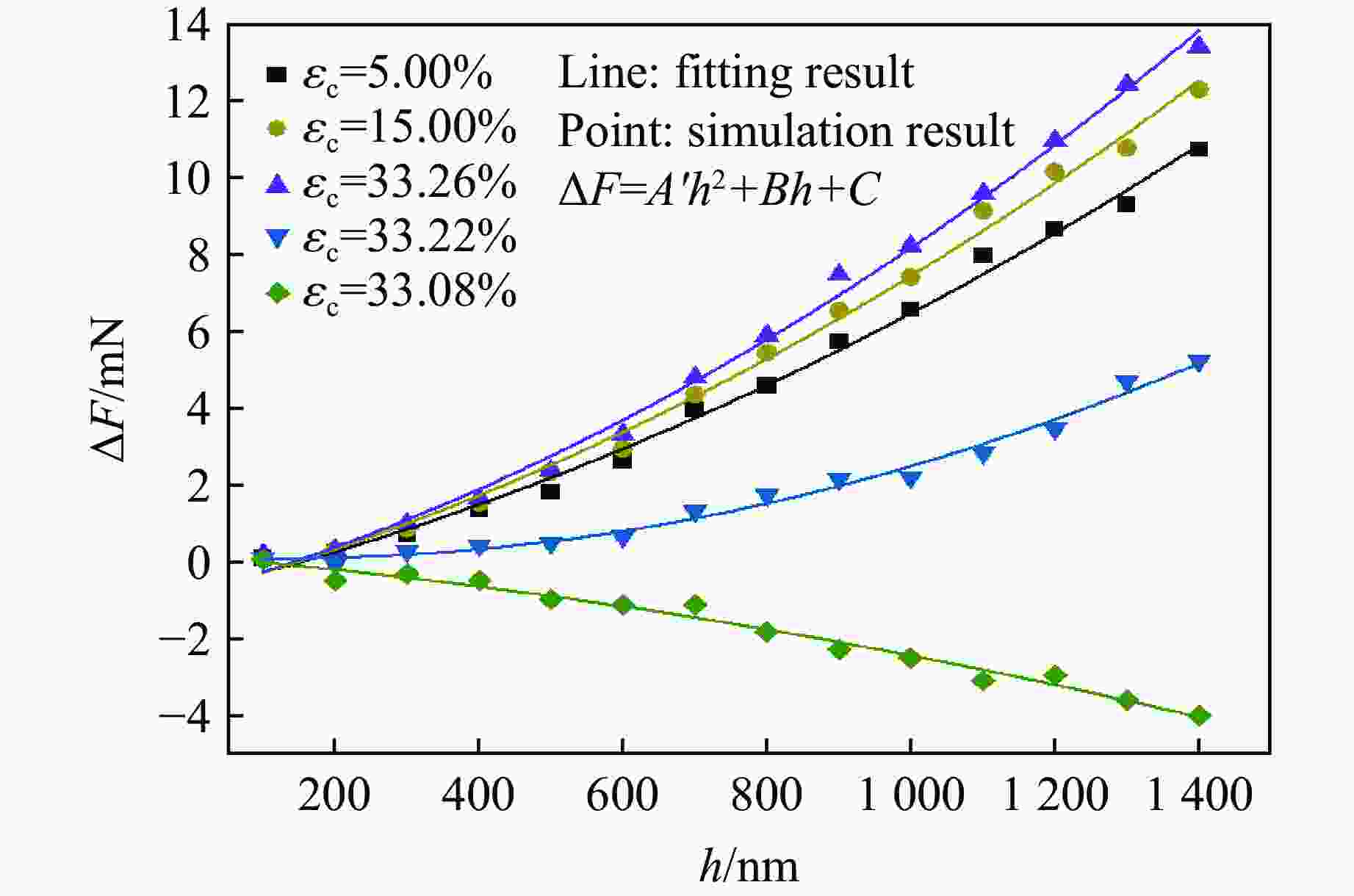
εc/% A'/(mN·nm−2) B/(mN·nm−1) C/mN R2 ${\bar \sigma _{\max }}$/MPa 5.00 2.656×10−6 0.0046 − 0.7647 0.9946 318.4 15.00 3.159×10−6 0.0051 − 0.8223 0.9954 333.2 33.26 3.654×10−6 0.0054 − 0.8409 0.9961 345.6 33.22 3.103×10−6 − 0.0008 0.1249 0.9874 212.5 33.08 −1.003×10−6 − 0.0016 0.1498 0.9813 18.6
下载: 导出CSV
-
[1] 朱浩霖, 张天辉, 刘志芳. 重复冲击载荷下泡沫铝夹芯壳的动态响应 [J]. 高压物理学报, 2024, 38(5): 054205. doi: 10.11858/gywlxb.20240721ZHU H L, ZHANG T H, LIU Z F. Dynamic responses of aluminum foam sandwich shells under repeated impact loadings [J]. Chinese Journal of High Pressure Physics, 2024, 38(5): 054205. doi: 10.11858/gywlxb.20240721 [2] 鲁渴伟, 敬霖. 道砟冲击下高速列车设备舱底板的动态响应 [J]. 高压物理学报, 2023, 37(4): 044203. doi: 10.11858/gywlxb.20230642LU K W, JING L. Dynamic response of equipment cabin bottom plate of high-speed train subjected to ballast impact [J]. Chinese Journal of High Pressure Physics, 2023, 37(4): 044203. doi: 10.11858/gywlxb.20230642 [3] 李巧歌, 梁增友, 王春光, 等. 碳纤维复合靶板抗破片冲击性能研究 [J]. 高压物理学报, 2024, 38(4): 044103. doi: 10.11858/gywlxb.20240720LI Q G, LIANG Z Y, WANG C G, et al. Study on anti-fragment impact performance of carbon fiber reinforced plastics [J]. Chinese Journal of High Pressure Physics, 2024, 38(4): 044103. doi: 10.11858/gywlxb.20240720 [4] ROSSINI N S, DASSISTI M, BENYOUNIS K Y, et al. Methods of measuring residual stresses in components [J]. Materials & Design, 2012, 35: 572–588. doi: 10.1016/j.matdes.2011.08.022 [5] ANAWA E M, OLABI A G. Control of welding residual stress for dissimilar laser welded materials [J]. Journal of Materials Processing Technology, 2008, 204(1/2/3): 22–33. doi: 10.1016/j.jmatprotec.2008.03.047 [6] 李龙丰, 郭威, 赵觅, 等. 低活化中/高熵合金的研究进展与展望 [J/OL]. 中国有色金属学报 (2025-01-06)[2025-01-17]. http://kns.cnki.net/kcms/detail/43.1238.TG.20250106.1411.002.html.LI L F, GUO W, ZHAO M, et al. Research progress and prospect of low activation medium/high entropy alloys [J/OL]. The Chinese Journal of Nonferrous Metals (2025-01-06) [2025-01-17]. http://kns.cnki.net/kcms/detail/43.1238.TG.20250106.1411.002.html. [7] 李天昕, 王书道, 卢一平, 等. 高熵合金材料研究进展与展望 [J]. 中国工程科学, 2023, 25(3): 170–181. doi: 10.15302/J-SSCAE-2023.03.016LI T X, WANG S D, LU Y P, et al. Research progress and prospect of high-entropy alloy materials [J]. Strategic Study of CAE, 2023, 25(3): 170–181. doi: 10.15302/J-SSCAE-2023.03.016 [8] POULIA A, GEORGATIS E, LEKATOU A, et al. Microstructure and wear behavior of a refractory high entropy alloy [J]. International Journal of Refractory Metals and Hard Materials, 2016, 57: 50–63. doi: 10.1016/j.ijrmhm.2016.02.006 [9] HUANG X F, LIU Z W, XIE H M. Recent progress in residual stress measurement techniques [J]. Acta Mechanica Solida Sinica, 2013, 26(6): 570–583. doi: 10.1016/S0894-9166(14)60002-1 [10] GUO J, FU H Y, PAN B, et al. Recent progress of residual stress measurement methods: a review [J]. Chinese Journal of Aeronautics, 2021, 34(2): 54–78. doi: 10.1016/j.cja.2019.10.010 [11] LEE S H, LEE J, KIM Y, et al. Surface residual stress in H-section steel beams processed by quenching and self-tempering using instrumented indentation testing [J]. Journal of Materials Research and Technology, 2024, 32: 177–184. doi: 10.1016/j.jmrt.2024.07.156 [12] SANGUEDOLCE M, SAFFIOTI M R, ROTELLA G, et al. Numerical simulation of nanoindentation process on pre-stressed Ti6Al4V alloy for residual stresses evaluation [J]. Procedia CIRP, 2021, 102: 121–125. doi: 10.1016/j.procir.2021.09.021 [13] 许海涛, 邱吉, 肖革胜, 等. 动态预压缩对CoCrFeNiMn高熵合金微尺度压入硬度的影响 [J]. 高压物理学报, 2021, 35(6): 064101. doi: 10.11858/gywlxb.20210773XU H T, QIU J, XIAO G S, et al. Effect of dynamic pre-compression on micro-scale indentation hardness of CoCrFeNiMn high-entropy alloy [J]. Chinese Journal of High Pressure Physics, 2021, 35(6): 064101. doi: 10.11858/gywlxb.20210773 [14] ANDRADE U, MEYERS M A, VECCHIO K S, et al. Dynamic recrystallization in high-strain, high-strain-rate plastic deformation of copper [J]. Acta Metallurgica et Materialia, 1994, 42(9): 3183–3195. doi: 10.1016/0956-7151(94)90417-0 [15] DAI L J, LIU Y, YANG S Z, et al. Strain dependence of adiabatic shearing behaviors of CoCrFeNi high-entropy alloy fabricated via laser powder bed fusion under impact loads [J]. Journal of Materials Research and Technology, 2024, 31: 1151–1163. doi: 10.1016/j.jmrt.2024.06.159 [16] ZHU F, ZHANG Q, CHEN J H, et al. Effect of crystallographic orientation on the deformation and mechanical behavior of CoCrFeNi in Berkovich nanoindentation [J]. Materials Science and Engineering: A, 2024, 914: 147106. doi: 10.1016/j.msea.2024.147106 [17] DING H X, ZHU T, WANG X R, et al. A yield function based on stress invariants and its extensions: modeling and validation [J]. Mechanics of Materials, 2025, 200: 105205. doi: 10.1016/j.mechmat.2024.105205 [18] GAO X S, ZHANG T T, ZHOU J, et al. On stress-state dependent plasticity modeling: significance of the hydrostatic stress, the third invariant of stress deviator and the non-associated flow rule [J]. International Journal of Plasticity, 2011, 27(2): 217–231. doi: 10.1016/j.ijplas.2010.05.004 [19] CAZACU O. A criterion for description of anisotropy and yield differential effects in pressure-insensitive metals [J]. International Journal of Plasticity, 2004, 20(11): 2027–2045. doi: 10.1016/j.ijplas.2003.11.021 [20] WU X D, ZHANG Z, ZHANG W K. A study on anisotropic hardening of 7075 aluminum alloy based on non-associated flow rules [J]. Journal of Materials Research and Technology, 2024, 33: 612–619. doi: 10.1016/J.JMRT.2024.09.084 [21] BARLAT F, HA J J, GRáCIO J J, et al. Extension of homogeneous anisotropic hardening model to cross-loading with latent effects [J]. International Journal of Plasticity, 2013, 46: 130–142. doi: 10.1016/j.ijplas.2012.07.002 [22] ZHOU A N, WU S S, LI J. A constitutive model for unsaturated soils using degree of capillary saturation and effective interparticle stress as constitutive variables [C]//Proceedings of GeoShanghai 2018 International Conference: Multi-physics Processes in Soil Mechanics and Advances in Geotechnical Testing. Singapore: Springer, 2018: 79–86. [23] WANG H, LI L, LI J P, et al. A simple stress correction method for explicit integration algorithm of elastoplastic constitutive models and its application to advanced anisotropic S-CLAY1 model [J]. Computers and Geotechnics, 2022, 148: 104817. doi: 10.1016/j.compgeo.2022.104817 [24] TÓTH G, DE ZEEUW D L, GOMBOSI T I, et al. A parallel explicit/implicit time stepping scheme on block-adaptive grids [J]. Journal of Computational Physics, 2006, 217(2): 722–758. doi: 10.1016/j.jcp.2006.01.029 [25] PÉREZ-DÍAZ S, BENEDICTO R M, DE SEVILLA M F. An effective algorithm for computing the asymptotes of an implicit curve [J]. Journal of Computational and Applied Mathematics, 2024, 437: 115468. doi: 10.1016/j.cam.2023.115468 [26] ZHANG H W, ZHOU L. Implicit integration of a chemo-plastic constitutive model for partially saturated soils [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 32(14): 1715–1735. doi: 10.1002/nag.690 [27] GENG D J, DAI N, GUO P J, et al. Implicit numerical integration of highly nonlinear plasticity models [J]. Computers and Geotechnics, 2021, 132: 103961. doi: 10.1016/j.compgeo.2020.103961 [28] KAMBLE A, TANDAIYA P. Modeling and simulation of dynamic compression of bulk metallic glasses at room and elevated temperatures using split Hopkinson pressure bar setup [J]. International Journal of Plasticity, 2024, 174: 103915. doi: 10.1016/j.ijplas.2024.103915 [29] MA Y, ZHANG Y, YU H F, et al. Plastic characterization of metals by combining nanoindentation test and finite element simulation [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(8): 2368–2373. doi: 10.1016/S1003-6326(13)62743-0 [30] WU M, GAO X R, LIN H. Simulation analysis of the deformation behavior of nanoindentation based on elasto-plastic constitutive model [J]. Polymer Bulletin, 2023, 80(5): 4879–4889. doi: 10.1007/s00289-022-04292-1 -
下载:
点击查看大图
图(11) / 表(3)
计量
- 文章访问数: 131
- HTML全文浏览量: 46
- PDF下载量: 22
