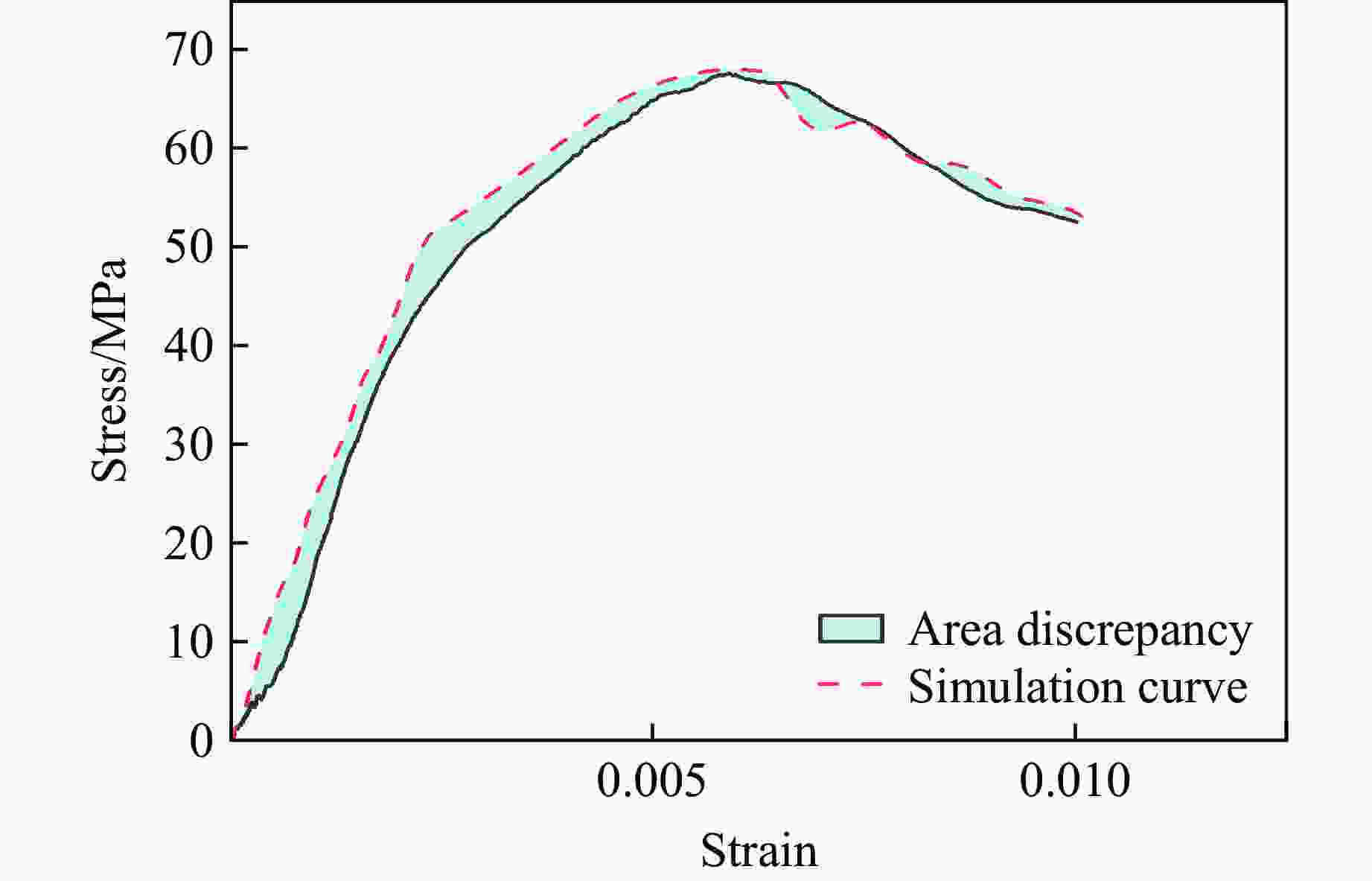
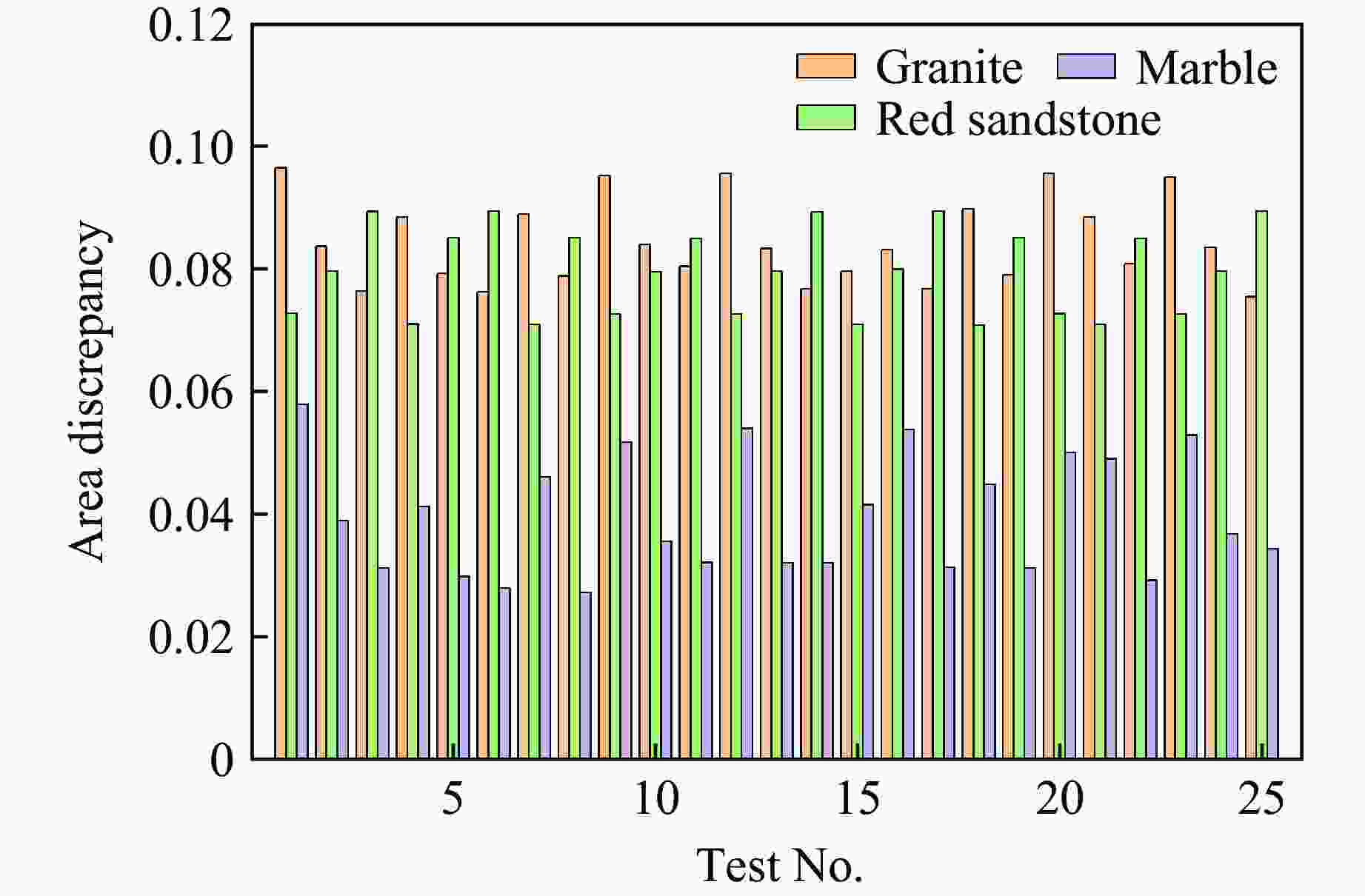
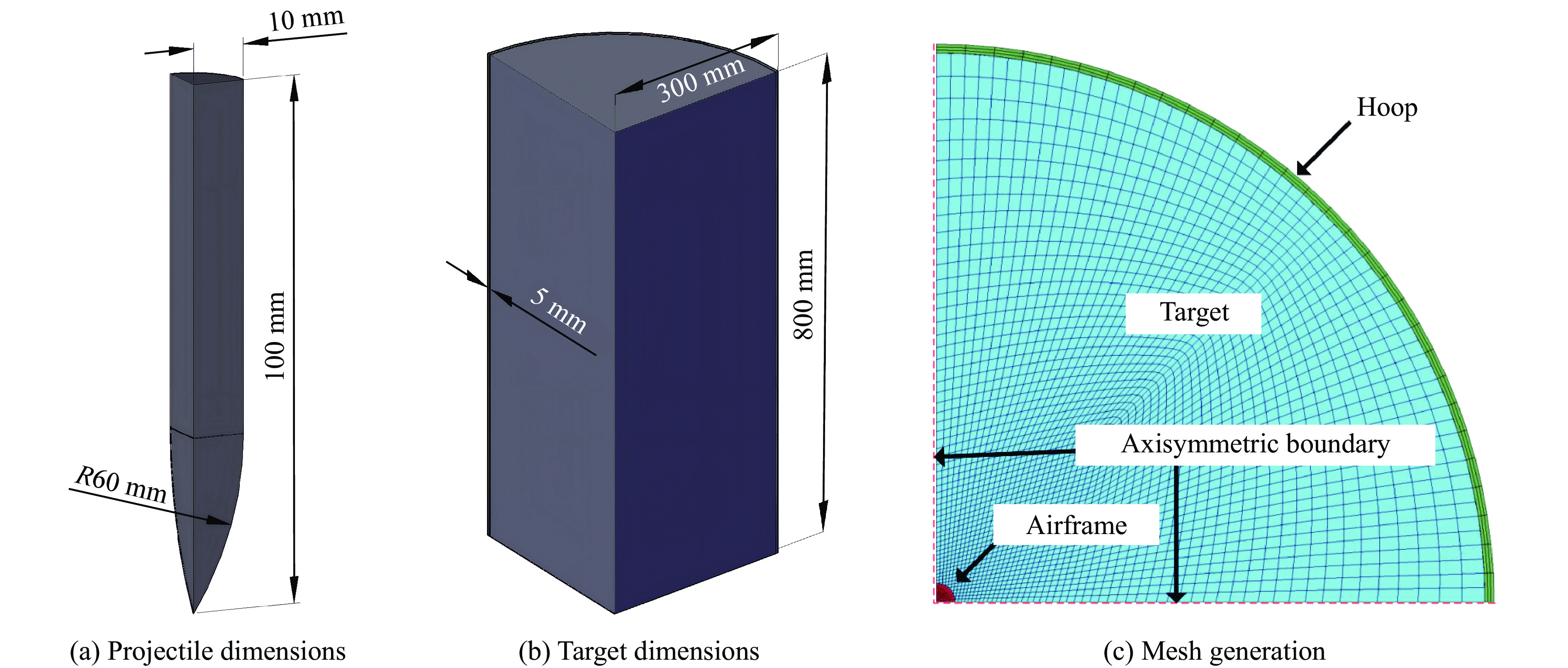
Sensitivity Analysis and Determination of Some Parameters of the Rock RHT Model
-
摘要: Riedel-Hiermaier-Thoma(RHT)本构模型被广泛应用于爆炸冲击、侵彻等问题的数值模拟和分析,而模拟结果的准确性在很大程度上取决于模型参数取值。为完成不同岩石RHT模型参数的敏感性分析及参数确定,利用LS-DYNA软件开展单一因素变化下弹体侵彻靶体及分离式霍普金森压杆(split Hopkinson pressure bar,SHPB)冲击模拟试验,分析参数取值变化对模拟结果的影响,进而通过正交试验分析,确定参数的交互效应。结果表明:不同工况条件下,模型参数的敏感性排序存在差异,确定了Lode角相关系数、拉伸屈服面参数、参考压缩应变率、参考拉伸应变率、失效压缩应变率及失效拉伸应变率对SHPB冲击曲线弹性阶段、线性强化阶段及损伤软化阶段的影响。利用SHPB冲击正交试验验证了6个参数间无显著交互作用,单因素敏感性分析结果有效,通过量化分析得到了花岗岩、红砂岩及大理岩RHT模型中6个参数的最优取值。研究结果可为岩石类RHT模型参数的敏感性分析及确定提供参考。Abstract: The Riedel-Hiermaier-Thoma (RHT) model is extensively used in the numerical simulation and analysis of phenomena such as explosive impacts and penetration. The accuracy of the simulation results is primarily dependent on the constitutive model and the parameter values used within it. To perform sensitivity analysis and parameter determination for Lode angle correlation coefficient, the tensile yield surface parameter, the reference compressive strain rate, the reference tensile strain rate, the failure compressive strain rate and the failure tensile strain rate in the RHT model for various rock types, LS-DYNA was employed to simulate the projectile penetration into a target and split Hopkinson pressure bar (SHPB) impact tests under single-factor variations. The effects of changes in parameter values on the simulation results were analyzed, followed by an orthogonal test to assess the interaction effects between parameters and determine the optimal parameter values. The results indicate that the sensitivity ranking of the six parameters varies under different operational conditions, and the effects of these parameters on the elastic, linear strengthening, and damage-softening stages of the SHPB impact stress-strain curve were identified. Further orthogonal SHPB impact simulation tests confirm the absence of interaction between these parameters, validating that the single-factor sensitivity analysis results are effective. The optimal values for these parameters in the RHT models of granite, red sandstone, and marble are determined. This finding provides valuable insights for the sensitivity analysis and parameter determination in rock-type RHT models.
-
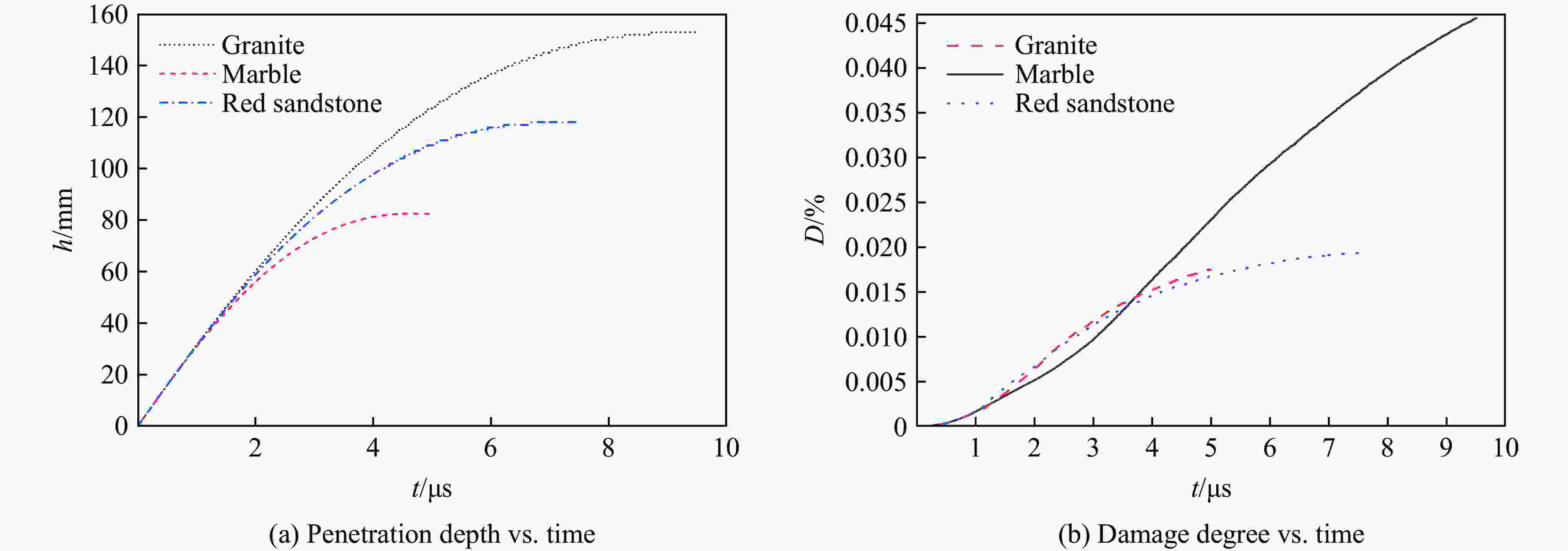
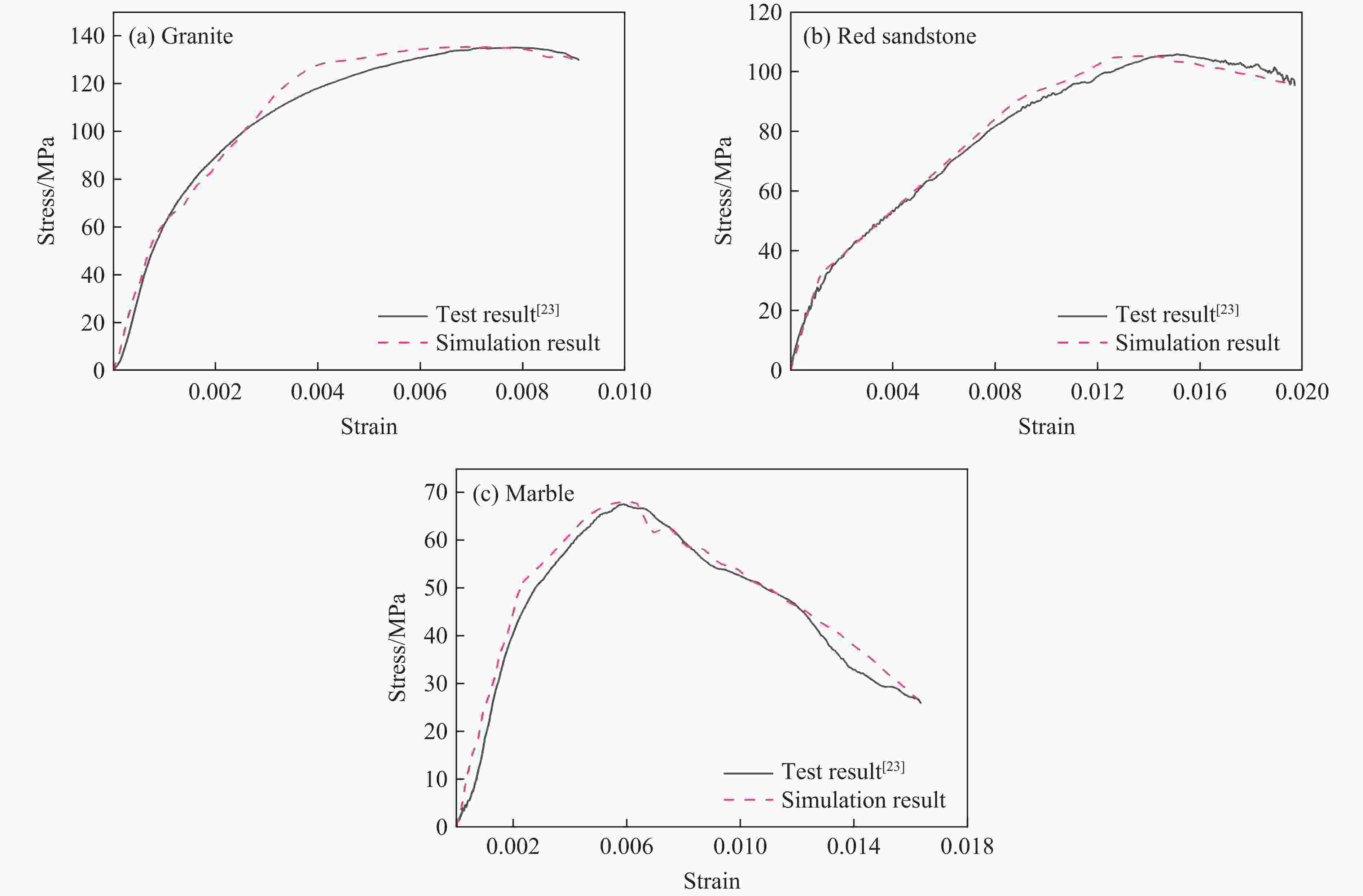
Rock type Target material properties Penetration depth ρ0/(g·cm−3) E/GPa fc/MPa ft/MPa Exp./cm Sim./cm Error/% Red sandstone 2.445 24.826 101.913 5.836 12.134 11.784 −2.884 Marble 2.690 61.212 73.679 5.077 15.059 15.353 −1.952 Granite 2.686 39.874 130.967 7.705 8.410 8.151 −3.080 表 2 参数取值
Table 2. Parameter selection
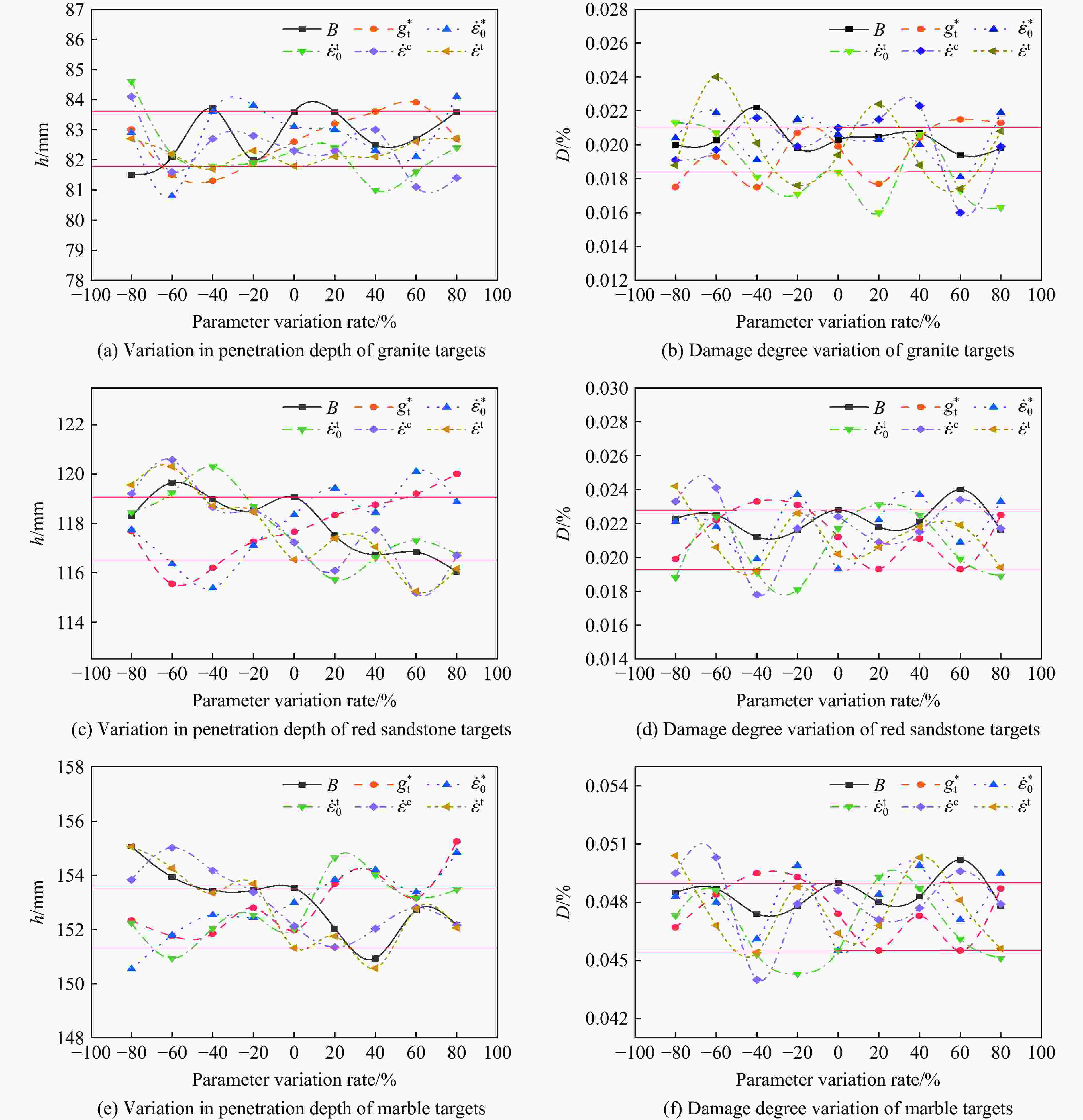
Variation rate/% B $ {g}_{\rm t}^{\mathrm{*}} $ $ {\dot{\varepsilon }}_{0}^{\mathrm{c}} $/s−1 $ {\dot{\varepsilon }}_{0}^{\mathrm{t}} $/s−1 $ {\dot{\varepsilon }}^{\mathrm{c}} $/s−1 $ {\dot{\varepsilon }}^{\mathrm{t}} $/s−1 Red sandstone Marble Granite −80 0.0021 0.1228 0.1344 0.1202 6.00×10−6 6.00×10−7 6.00×1024 6.00×1024 −60 0.0042 0.2456 0.2688 0.2404 1.20×10−5 1.20×10−6 1.20×1025 1.20×1025 −40 0.0063 0.3684 0.4032 0.3606 1.80×10−5 1.80×10−6 1.80×1025 1.80×1025 −20 0.0084 0.4912 0.5376 0.4808 2.40×10−5 2.40×10−6 2.40×1025 2.40×1025 0 0.0105 0.6140 0.6720 0.6010 3.00×10−5 3.00×10−6 3.00×1025 3.00×1025 20 0.0126 0.7368 0.8064 0.7212 3.60×10−5 3.60×10−6 3.60×1025 3.60×1025 40 0.0147 0.8596 0.9408 0.8414 4.20×10−5 4.20×10−6 4.20×1025 4.20×1025 60 0.0168 0.9824 1.0752 0.9616 4.80×10−5 4.80×10−6 4.80×1025 4.80×1025 80 0.0189 1.1052 1.2096 1.0818 5.40×10−5 5.40×10−6 5.40×1025 5.40×1025 表 3 不同参数的平均敏感度系数
Table 3. Average sensitivity analysis factor of different parameters
Parameter Average SAF Granite Red sandstone Marble B 5.13×10−4 5.35×10−4 3.87×10−4 $ {g}_{\rm t}^{\mathrm{*}} $ 1.09×10−3 1.07×10−3 5.23×10−4 $ {\dot{\varepsilon }}_{0}^{\rm c} $ 1.34×10−3 1.07×10−3 5.72×10−4 $ {\dot{\varepsilon }}_{0}^{\rm t} $ 1.75×10−3 1.44×10−3 6.30×10−4 $ {\dot{\varepsilon }}^{\rm c} $ 9.04×10−4 8.66×10−4 4.56×10−4 $ {\dot{\varepsilon }}^{\rm t} $ 7.98×10−4 8.43×10−4 5.03×10−4 表 4 SHPB冲击试验参数
Table 4. SHPB impact test parameters
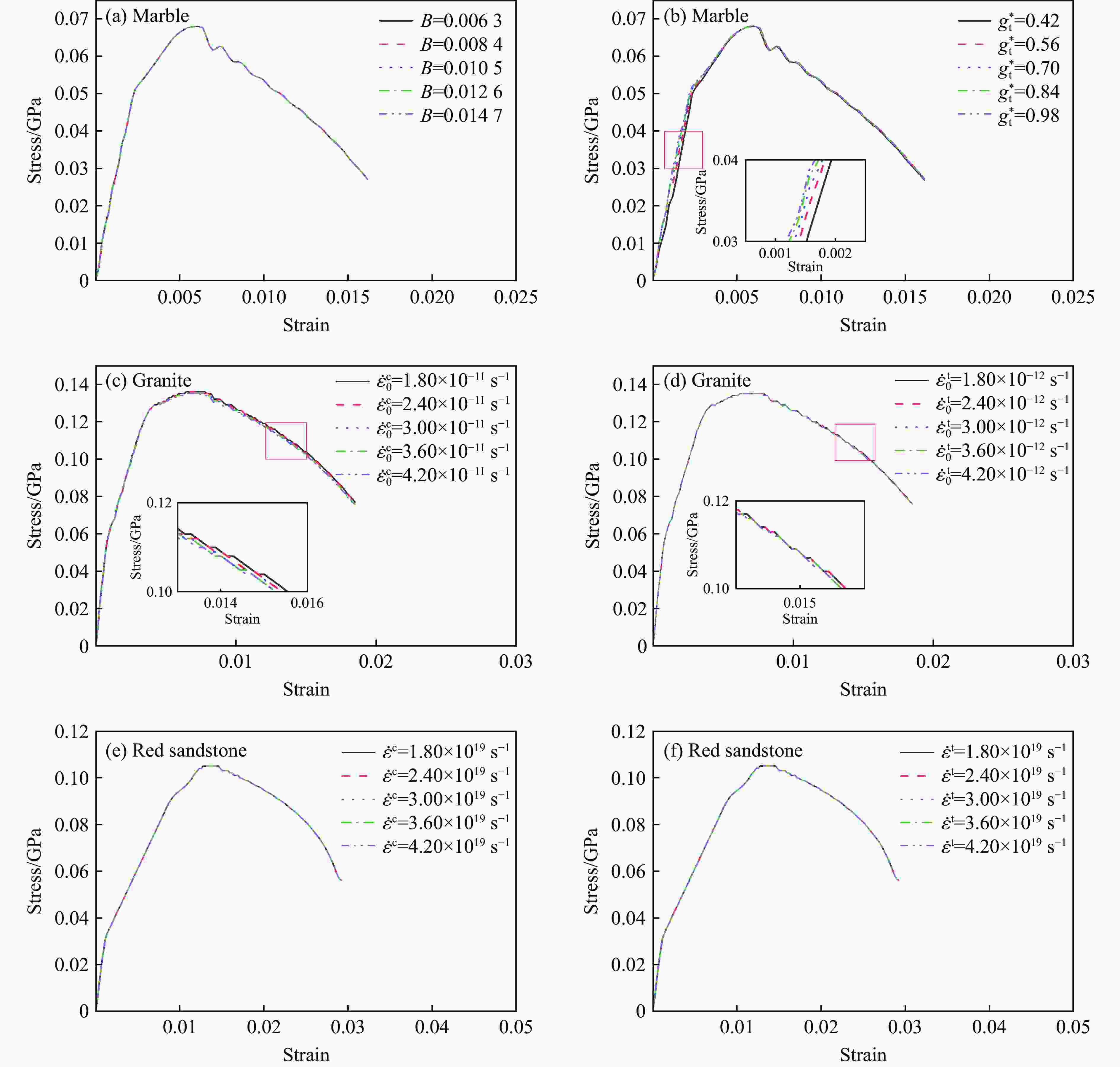
Variation rate/% B $ {g}_{\rm t}^{\mathrm{*}} $ $ {\dot{\varepsilon }}_{0}^{\mathrm{c}} $/s−1 $ {\dot{\varepsilon }}_{0}^{\mathrm{t}} $/s−1 $ {\dot{\varepsilon }}^{\mathrm{c}} $/s−1 $ {\dot{\varepsilon }}^{\mathrm{t}} $/s−1 −40 0.0063 0.42 1.80×10−11 1.80×10−12 1.80×1019 1.80×1019 −20 0.0084 0.56 2.40×10−11 2.40×10−12 2.40×1019 2.40×1019 0 0.0105 0.70 3.00×10−11 3.00×10−12 3.00×1019 3.00×1019 20 0.0126 0.84 3.60×10−11 3.60×10−12 3.60×1019 3.60×1019 40 0.0147 0.98 4.20×10−11 4.20×10−12 4.20×1019 4.20×1019 表 5 VIF计算结果
Table 5. Results of VIF calculation
Argument VIF Granite Red sandstone Marble B 1.0004 1.0005 1.0002 $ {g}_{\rm t}^{\mathrm{*}} $ 1.0001 1.0002 1.0005 $ {\dot{\varepsilon }}_{0}^{\mathrm{c}} $ 1.0005 1.0004 1.0004 $ {\dot{\varepsilon }}_{0}^{\mathrm{t}} $ 1.0001 1.0003 1.0003 $ {\dot{\varepsilon }}^{\mathrm{c}} $ 1.0003 1.0001 1.0001 $ {\dot{\varepsilon }}^{\mathrm{t}} $ 1.0002 1.0003 1.0002 -
[1] RIEDEL W, THOMA K, HIERMAIER S. Penetration of reinforced concrete by BETA-B-500 numerical analysis using a new macroscopic concrete model for hydrocodes [C]//Proceedings of the 9th International Symposium on the Effects of Munitions with Structures, 1999. [2] 张雄, 廉艳平, 刘岩, 等. 物质点法[M]. 北京: 清华大学出版社, 2013.ZHANG X, LIAN Y P, LIU Y, et al. Material point method [M]. Beijing: Tsinghua University Press, 2013. [3] 李忠献, 刘泽锋. 混凝土动态本构模型综述 [J]. 天津大学学报(自然科学与工程技术版), 2015, 48(10): 853–863. doi: 10.11784/tdxbz201412081LI Z X, LIU Z F. Review of concrete dynamic constitutive model [J]. Journal of Tianjin University (Science and Technology), 2015, 48(10): 853–863. doi: 10.11784/tdxbz201412081 [4] 黄永辉, 孙博, 张智宇, 等. 岩石RHT本构的爆破碎裂判定方法优化及验证 [J]. 北京理工大学学报, 2023, 43(6): 565–574. doi: 10.15918/j.tbit1001-0645.2022.157HUANG Y H, SUN B, ZHANG Z Y, et al. Optimization and verification of blasting fragmentation judgment method for RHT constitutive model of rock [J]. Transactions of Beijing Institute of Technology, 2023, 43(6): 565–574. doi: 10.15918/j.tbit1001-0645.2022.157 [5] 李洪超, 刘殿书, 赵磊, 等. 大理岩RHT模型参数确定研究 [J]. 北京理工大学学报, 2017, 37(8): 801–806. doi: 10.15918/j.tbit1001-0645.2017.08.006LI H C, LIU D S, ZHAO L, et al. Study on parameters determination of marble RHT model [J]. Transactions of Beijing Institute of Technology, 2017, 37(8): 801–806. doi: 10.15918/j.tbit1001-0645.2017.08.006 [6] LI H C, LIU D S, ZHAO L, et al. Experimental study on the time-dependent dynamic mechanical behaviour of C60 concrete under high-temperatures [J]. Journal of Beijing Institute of Technology, 2015, 24(3): 313–320. doi: 10.15918/j.jbit1004-0579.201524.0305 [7] TANG Z Q, YANG S L, ZHANG R, et al. An RHT-model-based equivalent parameter scheme for blast response simulation of RC frames [J]. International Journal of Structural Stability and Dynamics, 2022, 22(1): 2250010. doi: 10.1142/S0219455422500109 [8] TU Z G, LU Y. Modifications of RHT material model for improved numerical simulation of dynamic response of concrete [J]. International Journal of Impact Engineering, 2010, 37(10): 1072–1082. doi: 10.1016/j.ijimpeng.2010.04.004 [9] ABDEL-KADER M. Modified settings of concrete parameters in RHT model for predicting the response of concrete panels to impact [J]. International Journal of Impact Engineering, 2019, 132: 103312. doi: 10.1016/j.ijimpeng.2019.06.001 [10] 凌天龙, 王宇涛, 刘殿书, 等. 修正RHT模型在岩体爆破响应数值模拟中的应用 [J]. 煤炭学报, 2018, 43(Suppl 2): 434–442. doi: 10.13225/j.cnki.jccs.2017.1698LING T L, WANG Y T, LIU D S, et al. Modified RHT model for numerical simulation of dynamic response of rock mass under blasting load [J]. Journal of China Coal Society, 2018, 43(Suppl 2): 434–442. doi: 10.13225/j.cnki.jccs.2017.1698 [11] 王卫华, 刘洋, 张理维, 等. 基于RHT模型双孔同时爆破均质岩体损伤的数值模拟 [J]. 黄金科学技术, 2022, 30(3): 414–426. doi: 10.11872/j.issn.1005-2518.2022.03.130WANG W H, LIU Y, ZHANG L W, et al. Numerical simulation of homogeneous rock mass damage caused by two-hole simultaneous blasting based on RHT model [J]. Gold Science and Technology, 2022, 30(3): 414–426. doi: 10.11872/j.issn.1005-2518.2022.03.130 [12] 张若棋, 丁育青, 汤文辉, 等. 混凝土HJC、RHT本构模型的失效强度参数 [J]. 高压物理学报, 2011, 25(1): 15–22. doi: 10.11858/gywlxb.2011.01.003ZHANG R Q, DING Y Q, TANG W H, et al. The failure strength parameters of HJC and RHT concrete constitutive models [J]. Chinese Journal of High Pressure Physics, 2011, 25(1): 15–22. doi: 10.11858/gywlxb.2011.01.003 [13] 饶军应, 薛炀皓, 沈阳, 等. 基于RHT模型的层理分布与爆破损伤关联耦合性分析 [J]. 中南大学学报(自然科学版), 2023, 54(3): 1204–1218.RAO J Y, XUE Y H, SHEN Y, et al. Analysis of correlation coupling between bedding distribution and blasting damage based on RHT model [J]. Journal of Central South University (Science and Technology), 2023, 54(3): 1204–1218. [14] 王宇涛. 基于RHT本构的岩体爆破破碎模型研究 [D]. 北京: 中国矿业大学(北京), 2015.WANG Y T. The study of the broken model for rock mass blasting based on RHT constitutive equations [D]. Beijing: China University of Mining and Technology (Beijing), 2015. [15] 李洪超, 陈勇, 刘殿书, 等. 岩石RHT模型主要参数敏感性及确定方法研究 [J]. 北京理工大学学报, 2018, 38(8): 779–785. doi: 10.15918/j.tbit1001-0645.2018.08.002LI H C, CHEN Y, LIU D S, et al. Sensitivity analysis determination and optimization of rock RHT parameters [J]. Transactions of Beijing Institute of Technology, 2018, 38(8): 779–785. doi: 10.15918/j.tbit1001-0645.2018.08.002 [16] 刘殿柱, 刘娜, 高天赐, 等. 应用正交试验法的RHT模型参数敏感性研究 [J]. 北京理工大学学报, 2019, 39(6): 558–564. doi: 10.15918/j.tbit1001-0645.2019.06.002LIU D Z, LIU N, GAO T C, et al. Study on the parameter sensitivity of RHT concrete model by orthogonal test technique [J]. Transactions of Beijing Institute of Technology, 2019, 39(6): 558–564. doi: 10.15918/j.tbit1001-0645.2019.06.002 [17] 辛健. 爆炸作用下RHT模型参数敏感性分析 [J]. 舰船电子工程, 2019, 39(4): 111–113, 122. doi: 10.3969/j.issn.1672-9730.2019.04.024XIN J. Sensitivity analysis of RHT model parameters under explosive attack [J]. Ship Electronic Engineering, 2019, 39(4): 111–113, 122. doi: 10.3969/j.issn.1672-9730.2019.04.024 [18] 聂铮玥, 彭永, 陈荣, 等. 侵彻条件下岩石类材料RHT模型参数敏感性分析 [J]. 振动与冲击, 2021, 40(14): 108–116. doi: 10.13465/j.cnki.jvs.2021.14.015NIE Z Y, PENG Y, CHEN R, et al. Sensitivity analysis of RHT model parameters for rock materials under penetrating condition [J]. Journal of Vibration and Shock, 2021, 40(14): 108–116. doi: 10.13465/j.cnki.jvs.2021.14.015 [19] 马凯, 任高峰, 葛永翔, 等. 硬石膏矿RHT动力学模型参数研究 [J]. 爆破, 2024, 41(4): 35–44. doi: 10.3963/j.issn.1001-487X.2024.04.005MA K, REN G F, GE Y X, et al. Study on parameters of anhydrite RHT dynamic model [J]. Blasting, 2024, 41(4): 35–44. doi: 10.3963/j.issn.1001-487X.2024.04.005 [20] 张伟, 王建国, 王勉, 等. 基于RHT本构模型的连续装药预裂爆破孔距优化研究 [J]. 高压物理学报, 2025, 39(1): 015201. doi: 10.11858/gywlxb.20240834ZHANG W, WANG J G, WANG M, et al. Optimization study of pre-splitting hole spacing for continuous charging based on RHT constitutive model [J]. Chinese Journal of High Pressure Physics, 2025, 39(1): 015201. doi: 10.11858/gywlxb.20240834 [21] YOU Y Y, YANG R S, ZUO J J, et al. Research on the fragmentation characteristics of ironore based on RHT constitutive model calibration and charge structure optimization [J]. Mining, Metallurgy & Exploration, 2024, 41(4): 1819–1834. [22] 聂铮玥. 三种典型岩石材料的RHT模型参数研究[D]. 长沙: 国防科技大学, 2021.NIE Z Y. Experimental study on RHT model parameters of three typical rock materials [D]. Changsha: National University of Defense Technology, 2021. [23] 李洪超. 岩石RHT模型理论及主要参数确定方法研究 [D]. 北京: 中国矿业大学(北京), 2016.LI H C. The study of the rock RHT model and to determine the values of main parameters [D]. Beijing: China University of Mining & Technology (Beijing), 2016. [24] 胡春亚. 基于方差膨胀因子的衰老矿井通风系统优化指标体系的研究与应用 [D]. 徐州: 中国矿业大学, 2016.HU C Y. Research and application of index system optimizition of aging mine ventilation based on variance inflation factor [D]. Xuzhou: China University of Mining and Technology, 2016. -






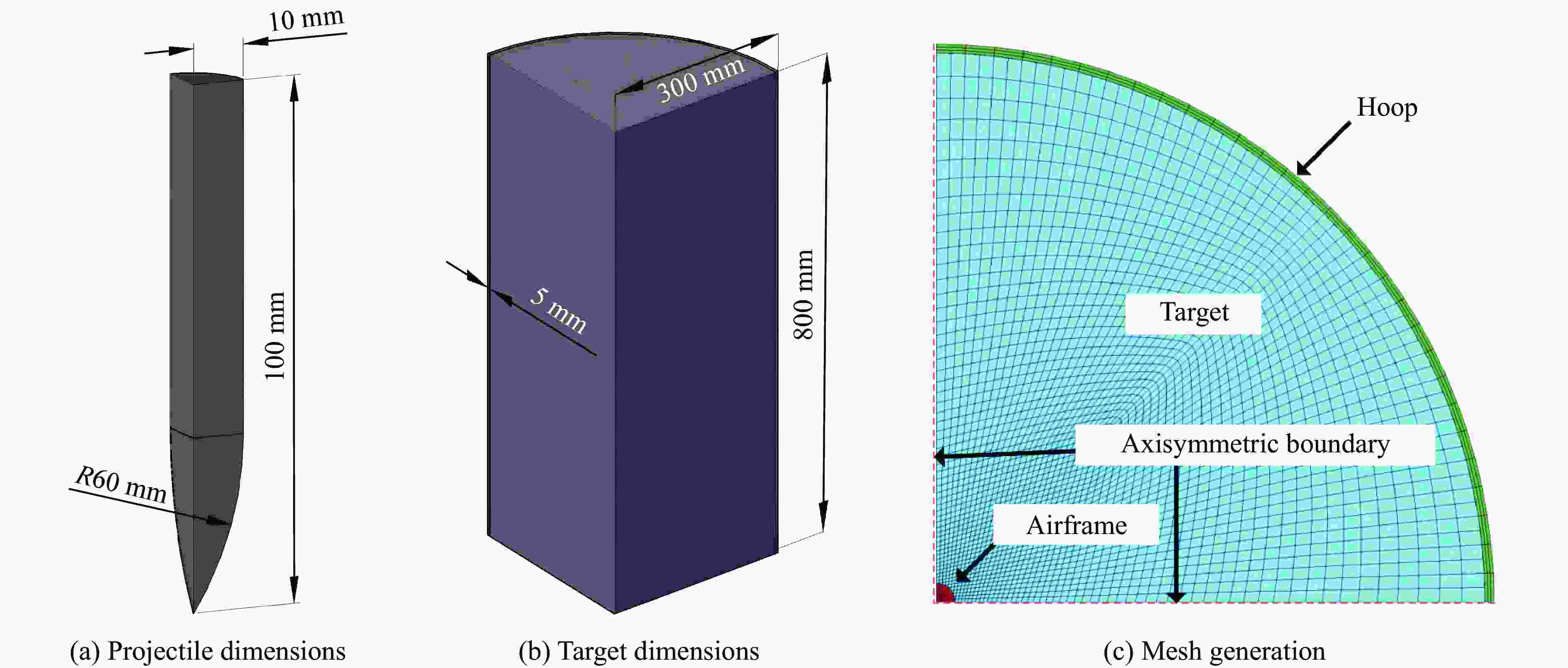
 下载:
下载: