露井联采台阶爆破对井下巷道振动的影响

徐杰; 李祥龙; 王建国; 胡涛; 张彪; 刘金保

doi:10.11858/gywlxb.20240942

露井联采台阶爆破对井下巷道振动的影响

doi: 10.11858/gywlxb.20240942

徐杰^{1, 2,},
李祥龙^{1, 2,*, ,},
王建国^{1, 2},
胡涛^{1, 2},
张彪³,
刘金保^{1, 2}

1.
昆明理工大学国土资源工程学院, 云南昆明　650093
2.
云南省教育厅爆破新技术工程研究中心, 云南昆明　650093
3.
凉山矿业股份有限公司, 四川会理　615146

基金项目: 国家自然科学基金（52274083）；云南省基础研究计划面上项目（202201AT070178）；云南省重大科技专项计划项目（202102AG050024）

详细信息

作者简介:
徐　杰（1998－），男，硕士研究生，主要从事爆破振动研究. E-mail：xujie202407@163.com

通讯作者:
李祥龙（1981－），男，博士，教授，主要从事工程爆破及岩石破碎研究. E-mail：lxl00014002@163.com

中图分类号: O383; TD235; O521.9
计量
- 文章访问数: 27
- HTML全文浏览量: 19
- PDF下载量: 1
出版历程
- 收稿日期: 2024-11-19
- 修回日期: 2024-12-24
- 网络出版日期: 2025-04-09

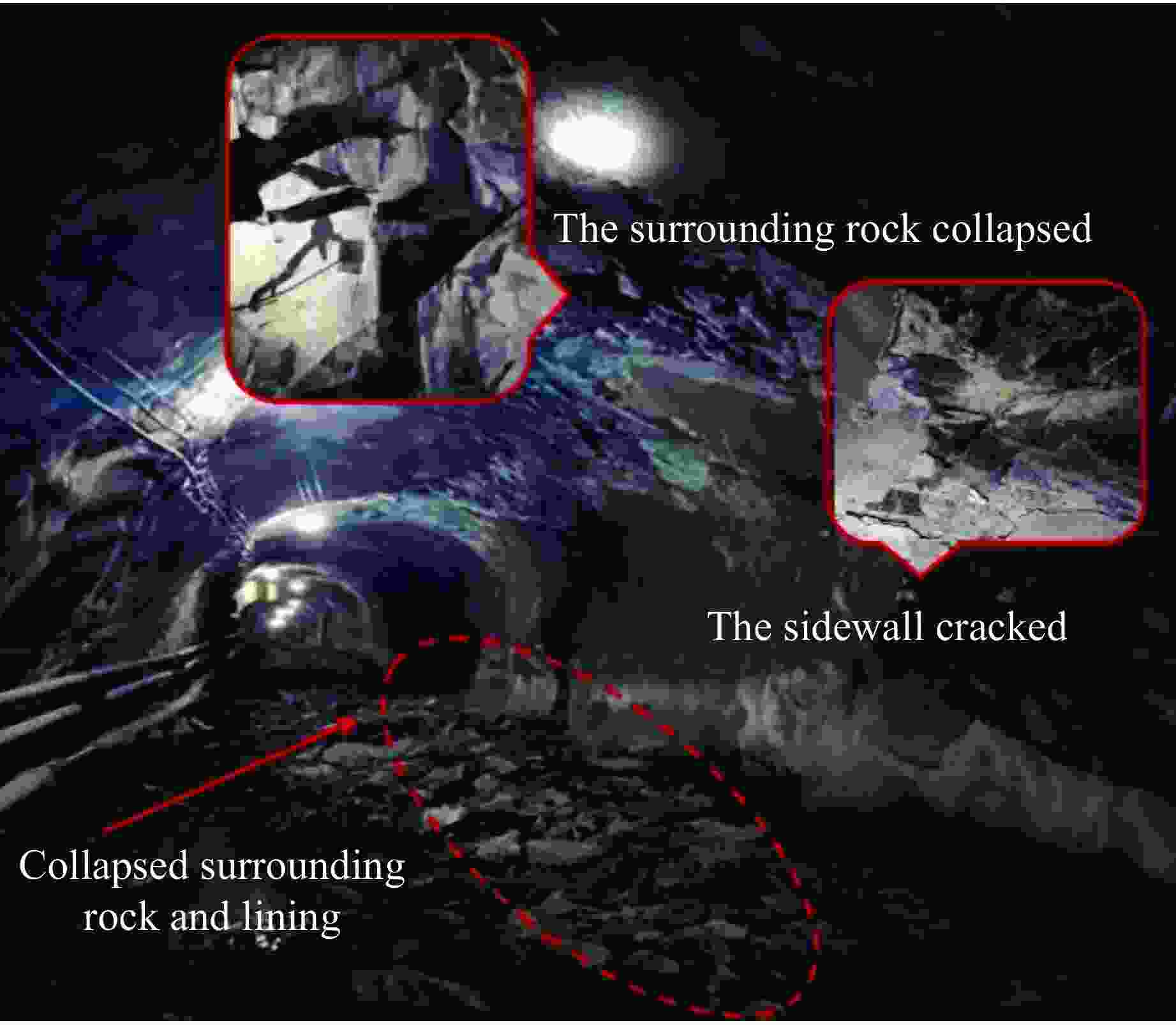
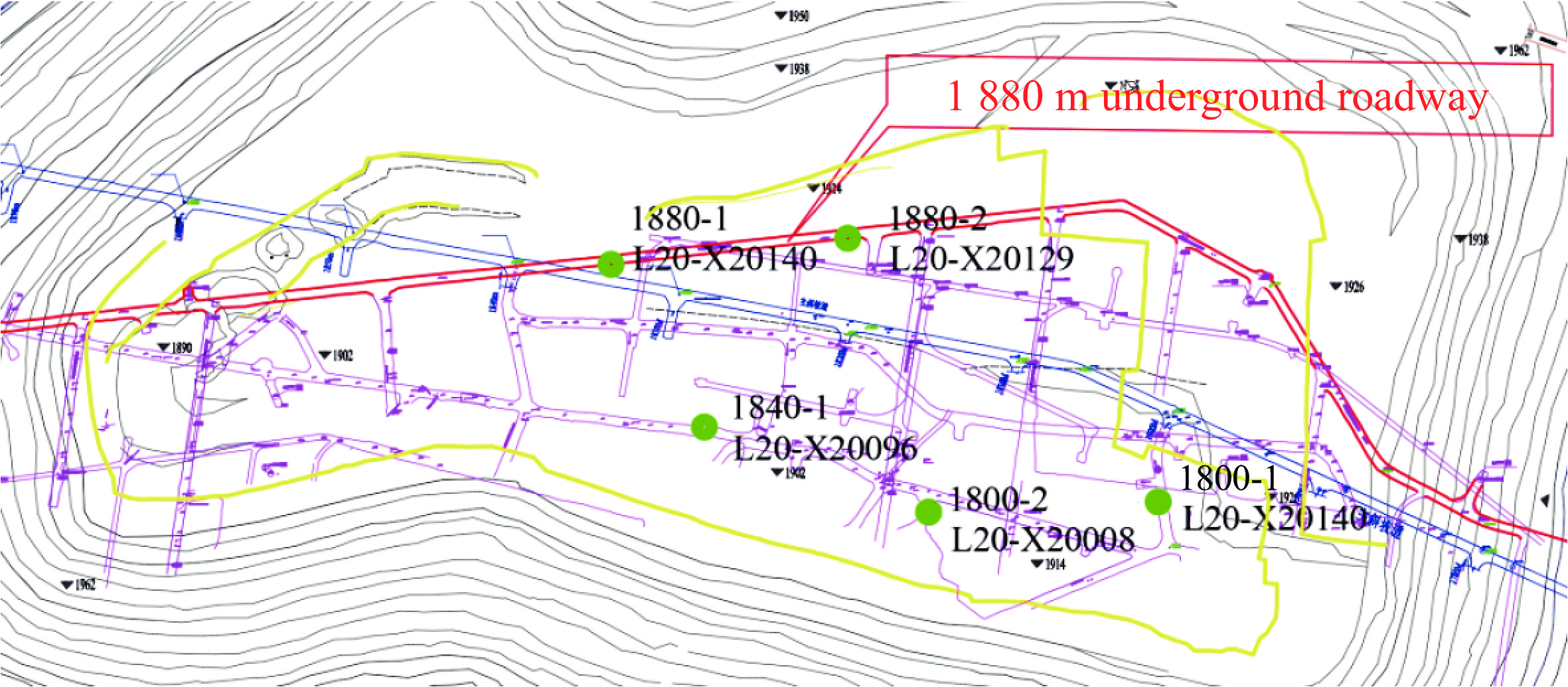
Effect of Bench Blasting on Vibration in Underground Roadways during Open Pit-Underground Combined Mining

XU Jie^{1, 2
,},
LI Xianglong^{1, 2,*
, ,},
WANG Jianguo^{1, 2},
HU Tao^{1, 2},
ZHANG Biao³,
LIU Jinbao^{1, 2}

1.
Faculty of Land Resource Engineering, Kunming University of Science and Technology, Kunming 650093, Yunnan, China
2.
Advanced Blasting Technology Engineering Research Center of Yunnan Province Education Department, Kunming 650093, Yunnan, China
3.
Liangshan Mining Co., Ltd., Huili 615146, Sichuan, China

摘要

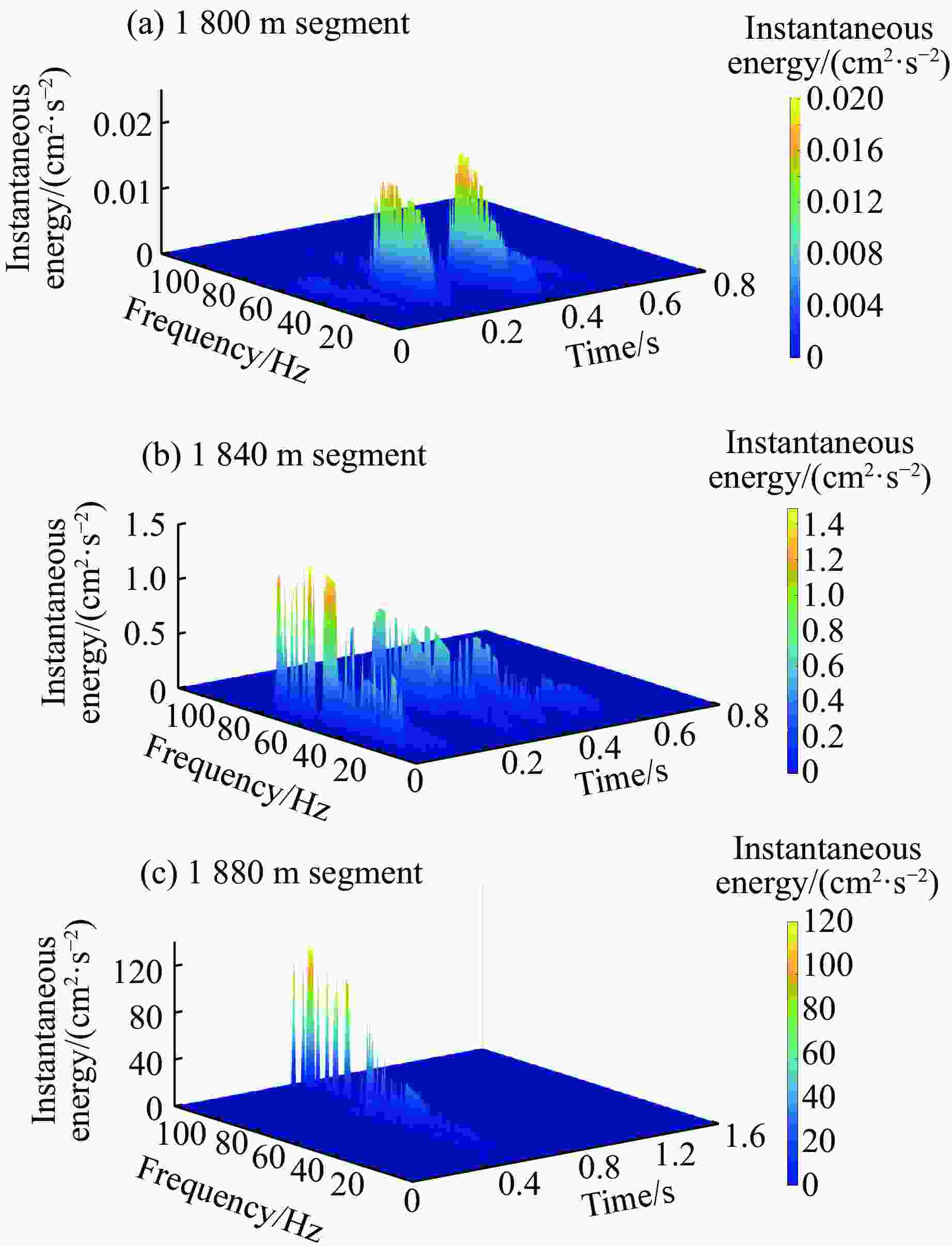
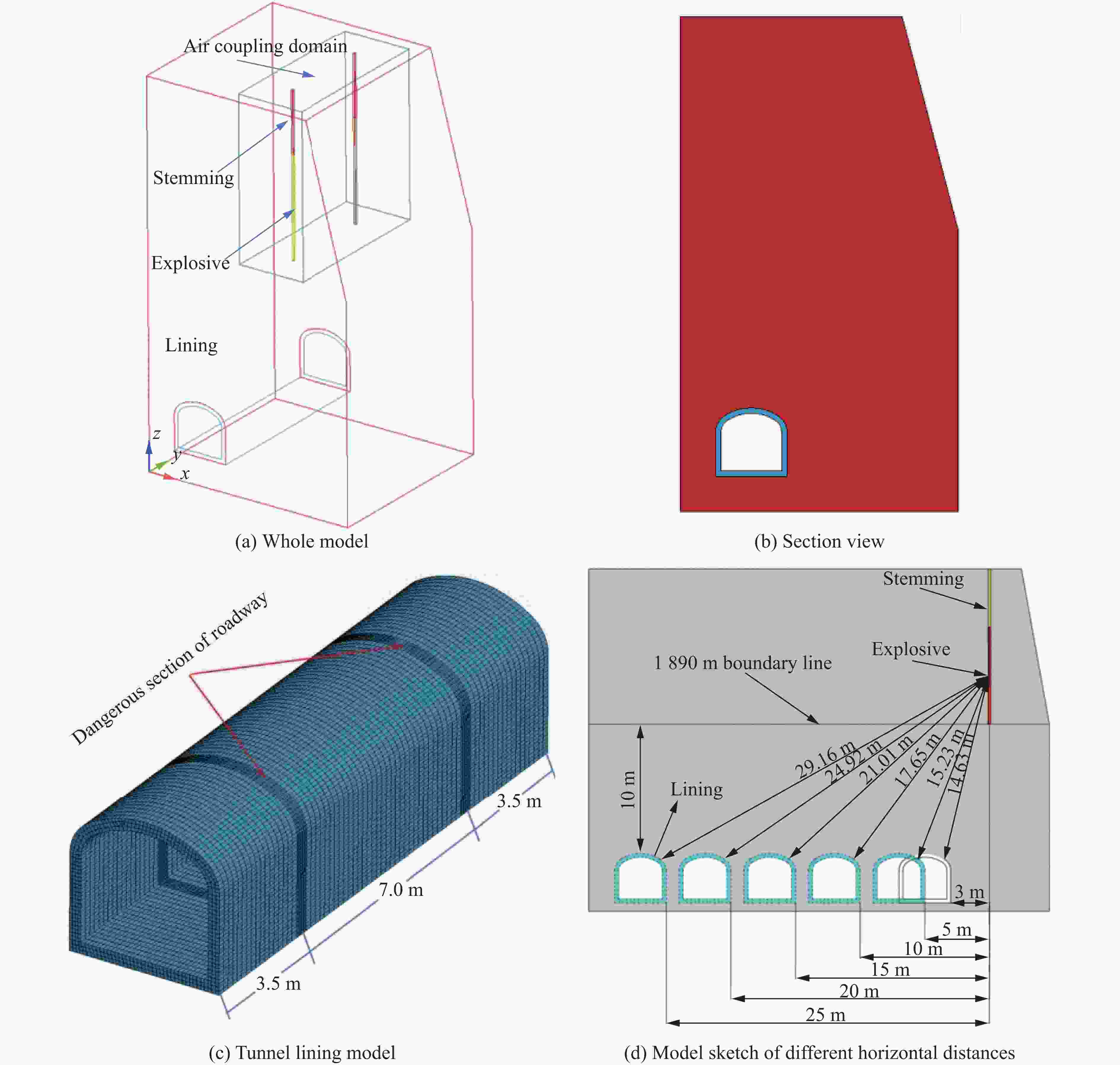
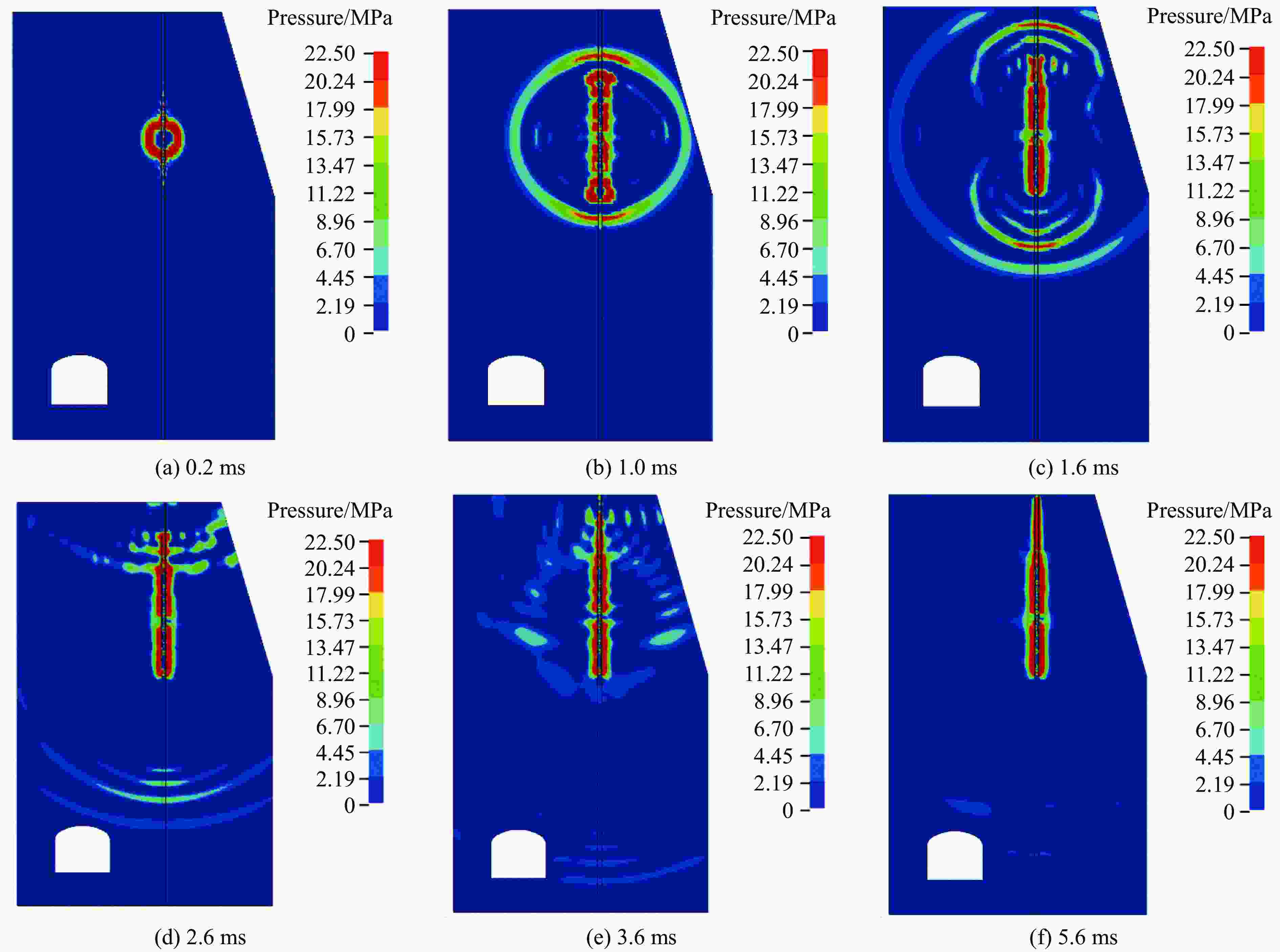
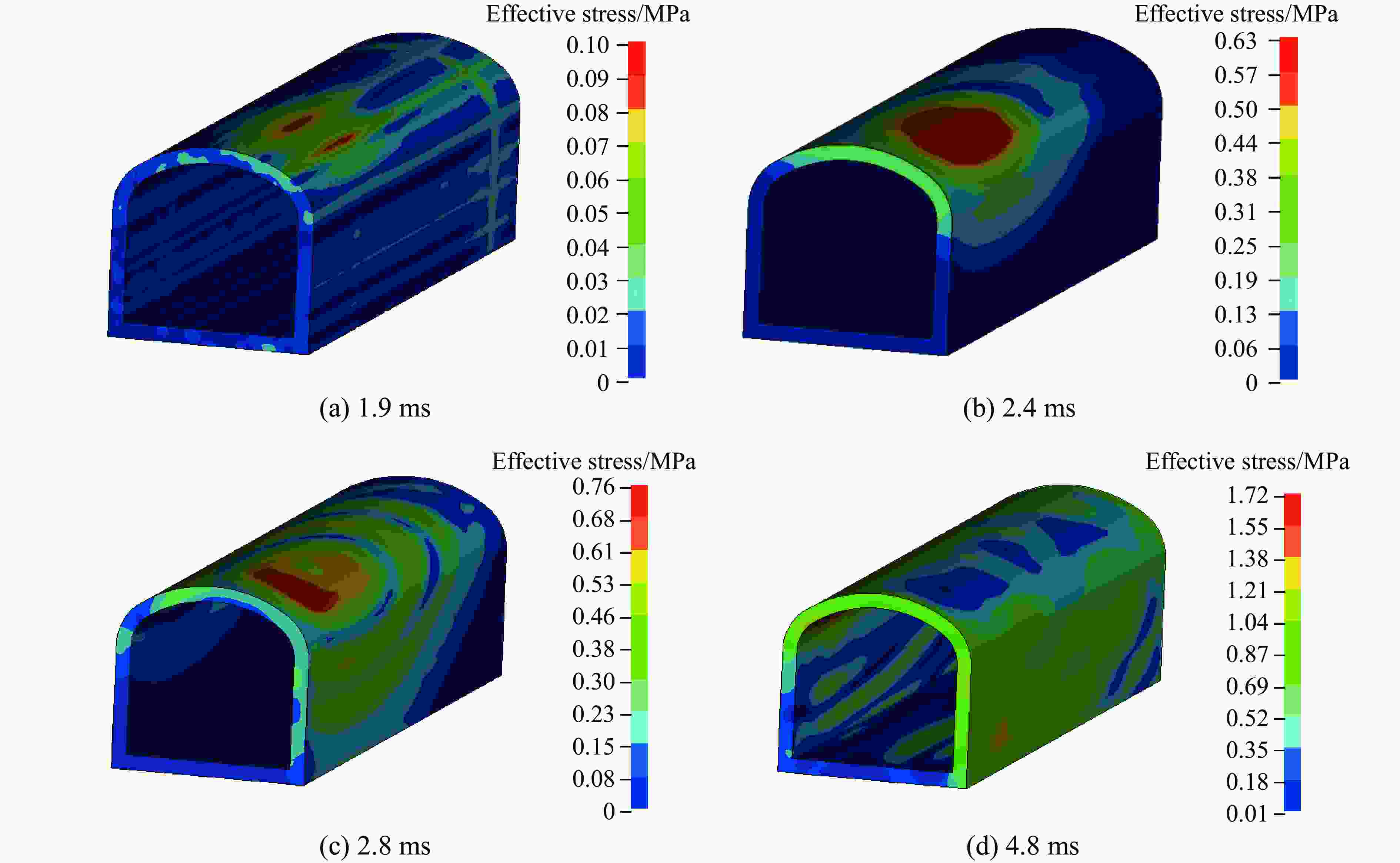
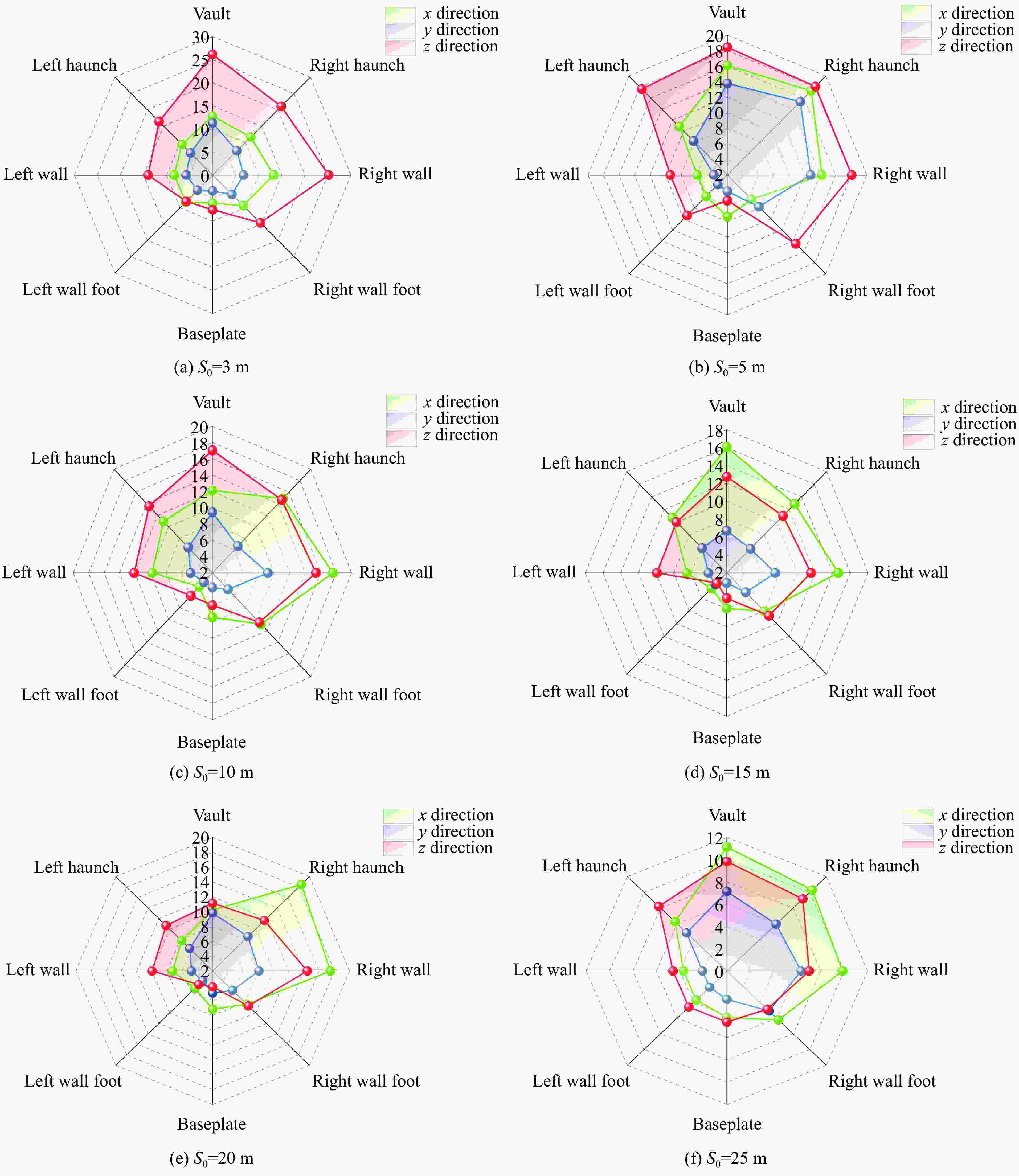
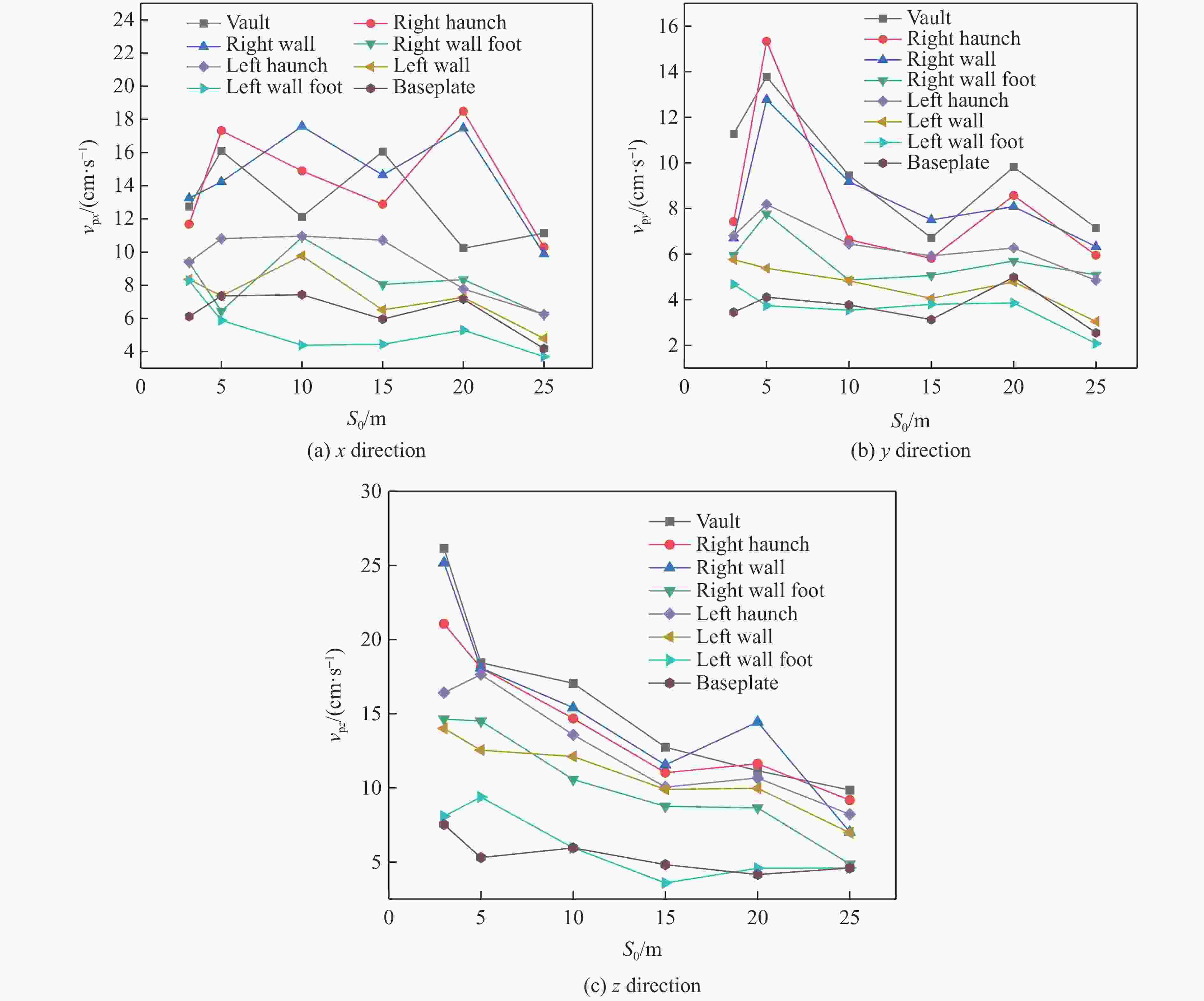
摘要: 在露井联采过程中，为了控制露天台阶爆破振动对井下邻近既有巷道衬砌的破坏，以拉拉铜矿露天转井下过渡开采阶段为背景，采用现场振动监测、理论计算、数值模拟方法，研究既有邻近巷道的动力响应规律。通过对监测数据进行回归分析，得出井下振动衰减规律，并对振动主频及瞬时能量进行了分析。采用LS-DYNA数值模拟软件，对露天台阶和井下巷道建立6种不同相对空间位置的模型，进而建立双孔延期爆炸模型，研究了爆破荷载作用下邻近井下既有巷道的动态响应规律。结果表明：露天台阶爆破过程中，爆源下方邻近既有巷道产生的最大振速主要出现在拱部和迎爆侧的边墙部；巷道与爆源的相对空间位置不同，峰值振速所在的方向和位置也不同；在巷道拱顶与炮孔底部竖直方向距离固定为10 m的情况下，巷道边墙与炮孔水平距离在15 m以内时，炸药起爆后巷道结构竖直方向振速较大，超过15 m后，巷道结构水平径向振速较大。通过拟合应力与振速之间的关系，利用巷道极限动态抗拉强度推导出振速阈值为19 cm/s。基于安全阈值调整爆破参数后，可以保证邻近既有巷道的安全。
- 露井联采 /
- 露天台阶爆破 /
- 既有邻近巷道 /
- 振动响应 /
- 安全阈值
Abstract: In order to control the lining damage of underground roadways induced by the vibration effect of bench blasting in an open-pit quarry, the dynamic response of the existing adjacent roadway at the transition mining stage from open pit to underground in Lara Copper Mine were studied by means of field vibration monitoring, theoretical calculation and numerical simulation. Through regression analysis of the monitoring data, the vibration attenuation law was obtained, and the dominant frequency and instantaneous energy of the vibration were analyzed. Six models with different relative spatial positions between the open-pit bench and underground roadway were established using the LS-DYNA software. Subsequently, double-hole delayed blasting models were developed to investigate the dynamic response of adjacent existing roadways under blasting loads. The results show that for the existing roadway located below the explosion source of the open pit bench, its maximum vibration velocity mainly appears in the arch and the side wall on the explosion-facing side. The direction and position of the peak vibration velocity change with the different relative spatial position of the roadway and the explosion source. When the vertical distance between the roadway vault and the bottom of the blast hole is fixed at 10 m, and the horizontal distance between the roadway sidewall and the blast hole is less than 15 m, the vibration velocity in the vertical direction of the tunnel structure is greater after explosion. Beyond this 15 m horizontal distance, the vibration velocity in the horizontal and radial directions of the tunnel structure is larger. By fitting the relationship between peak effective stress and peak particle velocity and utilizing the ultimate dynamic tensile strength of the roadway, a vibration velocity threshold of 19 cm/s was derived. After adjusting blasting parameters according to the safety threshold, the safety of adjacent existing roadway can be ensured.
- open-underground combined mining /
- open-pit bench blasting /
- adjacent existing underground roadway /
- vibration response /
- security threshold

HTML全文

图 1 井下巷道及振动监测点位置

Figure 1. Underground roadway and the location of vibration monitoring points

下载: 全尺寸图片幻灯片

图 2 1880 m分段巷道衬砌垮落

Figure 2. Collapse of 1880 m segment roadway lining

下载: 全尺寸图片幻灯片

图 3 测振仪安装

Figure 3. Installation of vibrometer

下载: 全尺寸图片幻灯片

图 4 振动衰减规律

Figure 4. Law of the vibration attenuation

下载: 全尺寸图片幻灯片

图 5 主振频率分布

Figure 5. Distribution of the vibration main frequency

下载: 全尺寸图片幻灯片

图 6 振速时程曲线

Figure 6. Time-history curves of vibration velocity

下载: 全尺寸图片幻灯片

图 7 各监测点的三维能量谱

Figure 7. Three-dimensional energy spectra of each monitoring point

下载: 全尺寸图片幻灯片

图 8 模型示意图

Figure 8. Schematic diagram of the model

下载: 全尺寸图片幻灯片

图 9 实测波形与模拟波形

Figure 9. Measured and simulated waveform

下载: 全尺寸图片幻灯片

图 10 不同时刻岩体的压力等值线

Figure 10. Isoline of rock pressure at different time

下载: 全尺寸图片幻灯片

图 11 邻近既有巷道的有效应力云图

Figure 11. Effective stress nephogram of adjacent existing roadway

下载: 全尺寸图片幻灯片

图 12 监测点位置

Figure 12. Locations of monitoring points

下载: 全尺寸图片幻灯片

图 13 不同水平距离下巷道结构的峰值振速（单位：cm/s）

Figure 13. PPVs of tunnel structure at different horizontal distances (Unit: cm/s)

下载: 全尺寸图片幻灯片

图 14 不同水平距离下各方向的峰值振速变化

Figure 14. PPVs in each direction at different horizontal distances

下载: 全尺寸图片幻灯片

图 15 不同水平距离下峰值有效应力的变化

Figure 15. Variations of peak effective stress at different horizontal distances

下载: 全尺寸图片幻灯片

图 16 巷道关键部位的峰值振速-峰值有效应力拟合曲线

Figure 16. Fitting curves of peak vibration velocity-peak effective stress in key positions of roadway

下载: 全尺寸图片幻灯片

图 17 爆区与巷道的位置关系

Figure 17. Relation of blasting area and roadway position

下载: 全尺寸图片幻灯片

图 18 2个监测点测得的振速时程曲线

Figure 18. Time-history curves of vibration velocity obtained by two measuring points

下载: 全尺寸图片幻灯片

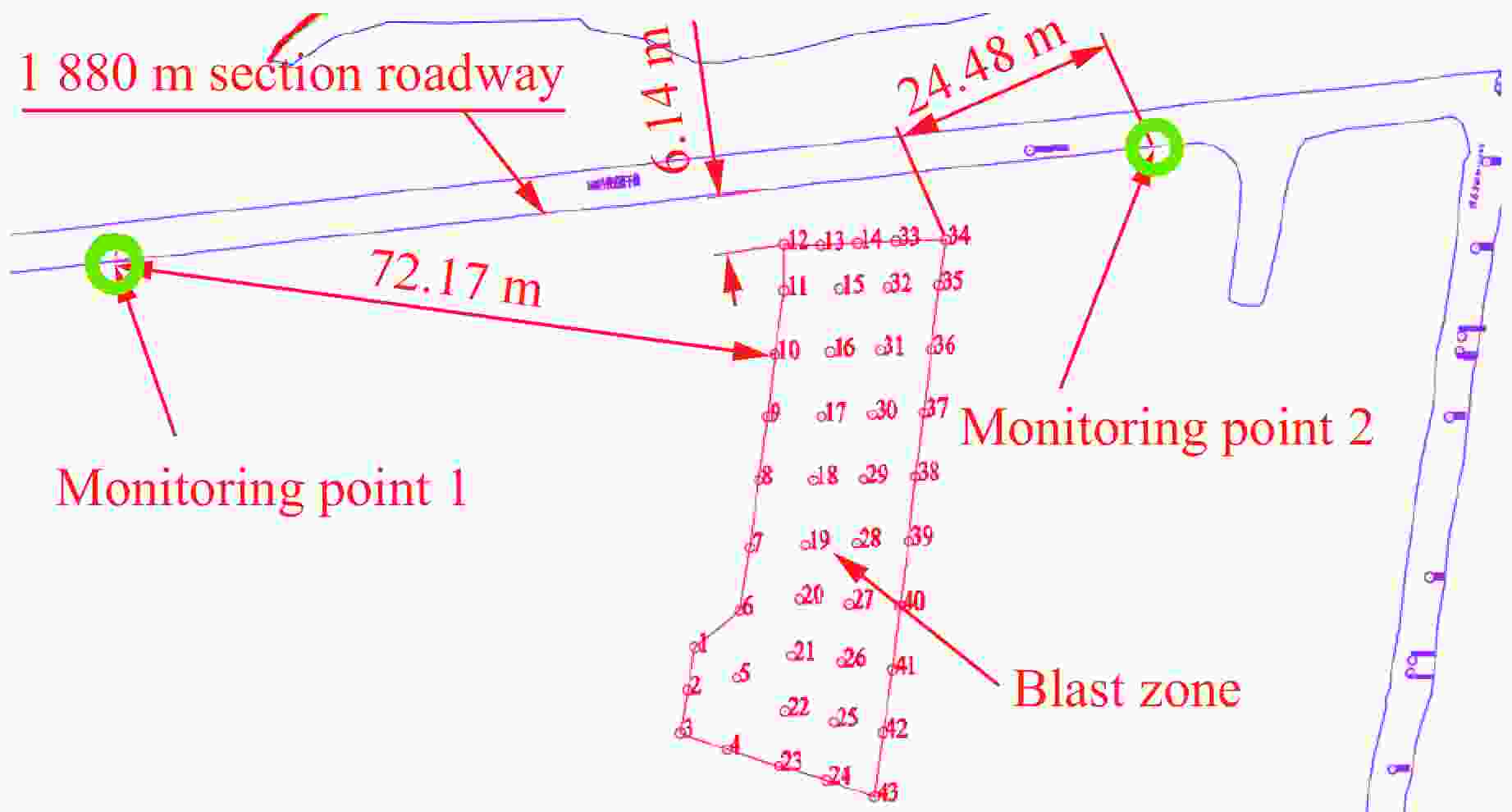
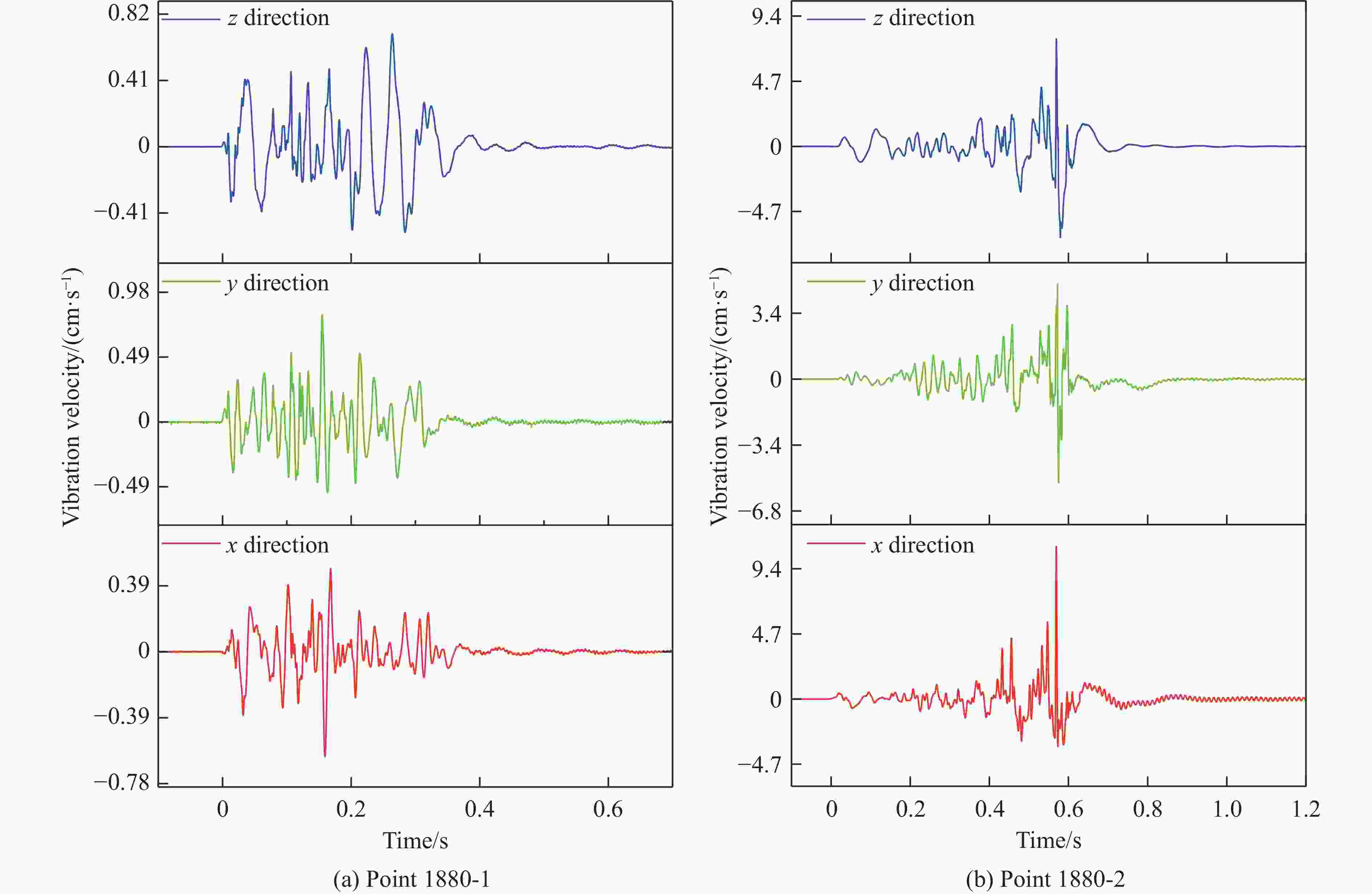
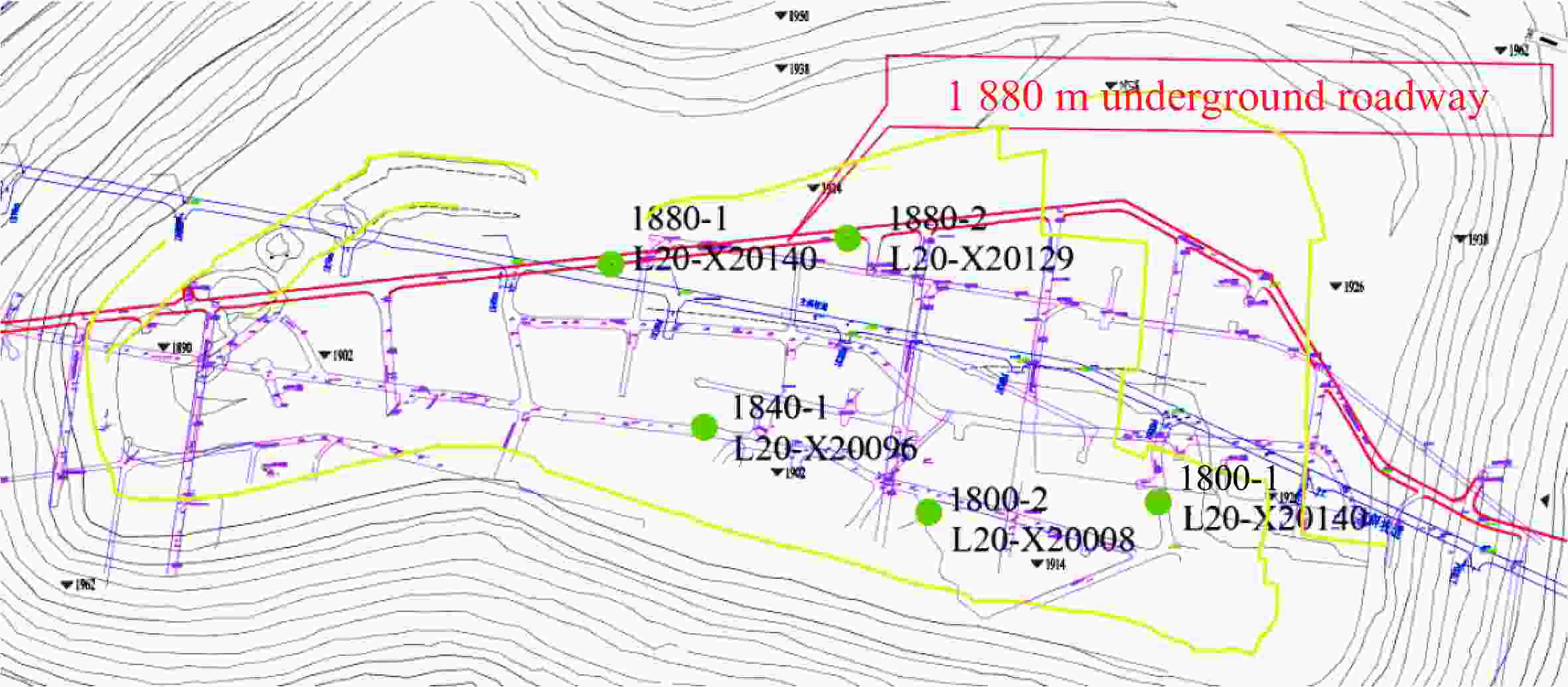
表 1 现场实测振动数据

Table 1. On-site measured vibration data

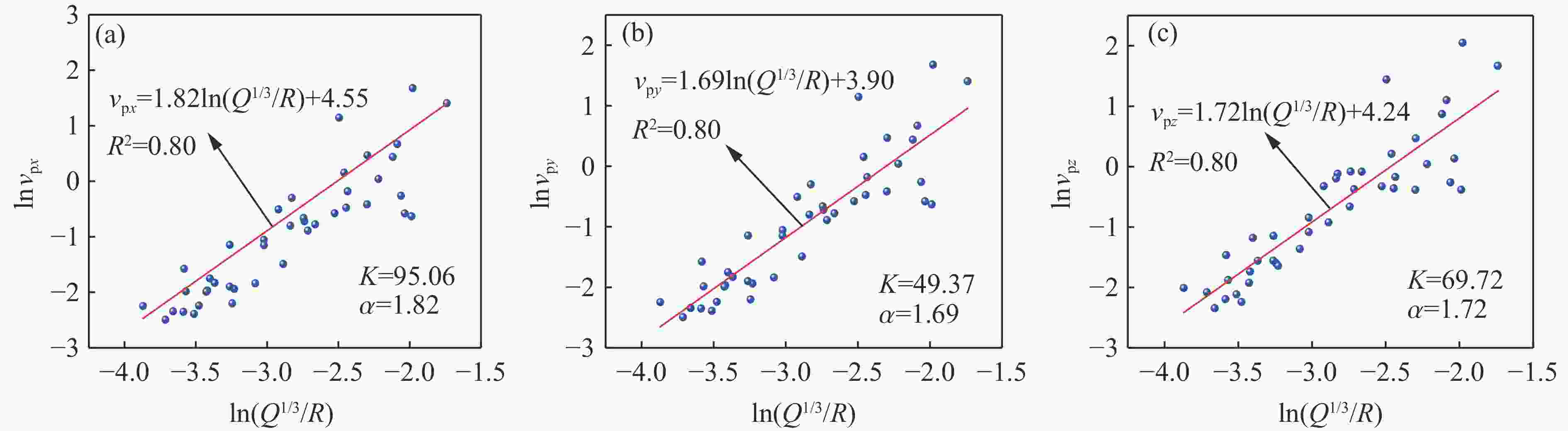
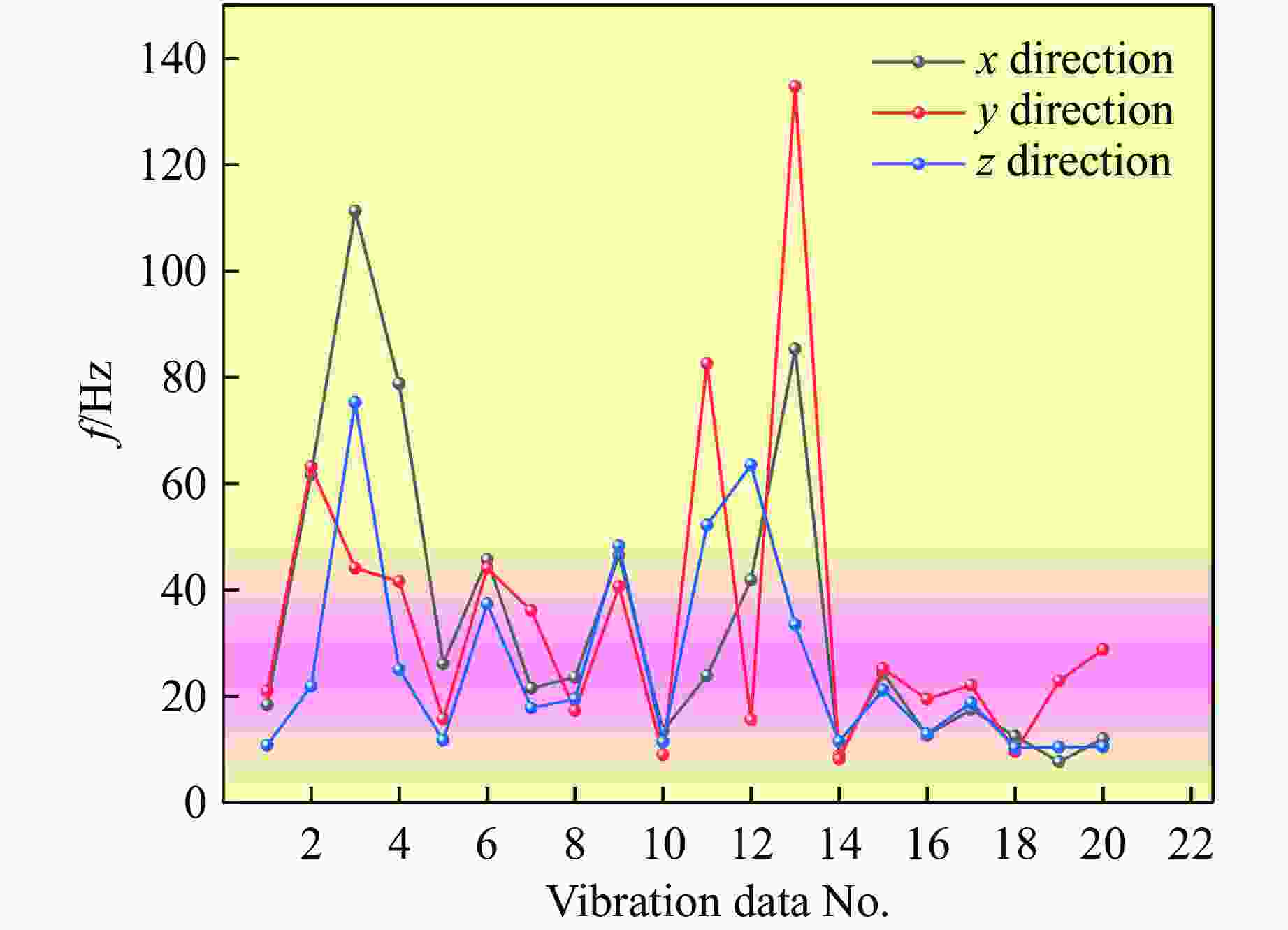
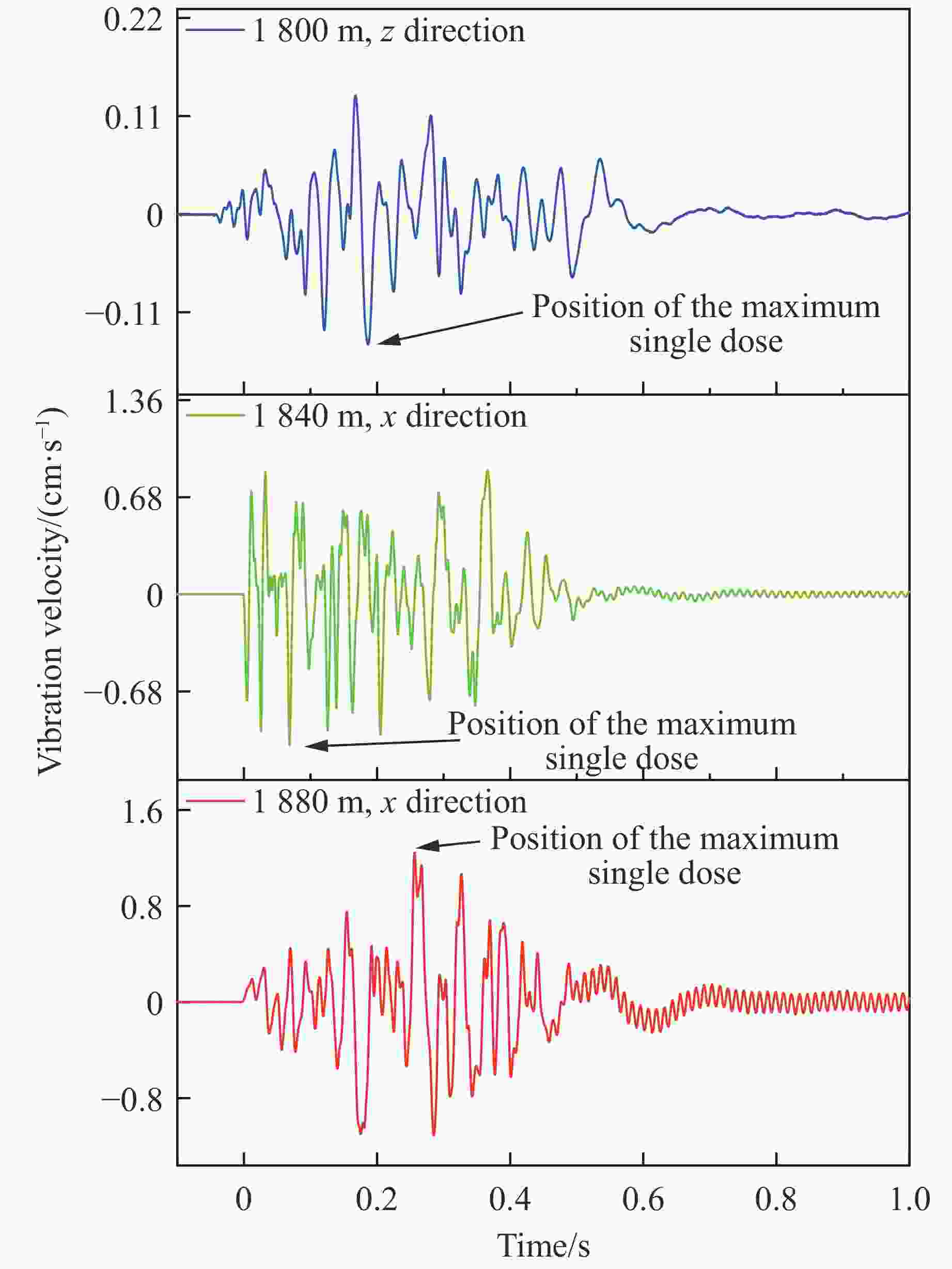
Test No.	Measuring point	L/m	H/m	R/m	m_m/kg	v_p/(cm·s⁻¹)			f/Hz
Test No.	Measuring point	L/m	H/m	R/m	m_m/kg	x direction	y direction	z direction	x direction	y direction	z direction
1	1880-1	128.06	14	128.82	370	0.23	0.54	0.40	18.4	21.0	10.8
2	1880-1	82.37	14	83.55	380	0.62	0.81	0.70	61.7	63.2	21.9
2	1880-2	50.48	14	52.39	380	11.00	5.35	7.77	111.3	44.1	75.3
3	1880-1	108.42	14	109.32	380	0.41	0.69	0.69	78.8	41.6	25.0
3	1880-2	111.01	14	111.89	380	0.68	0.49	0.92	26.1	15.7	11.7
4	1880-1	56.36	14	56.37	400	0.56	0.96	1.14	45.7	44.1	37.4
4	1880-2	67.80	14	67.81	400	1.24	1.34	1.04	21.5	36.1	17.8
5	1880-1	298.34	26	299.47	390	0.08	0.11	0.12	23.6	17.3	19.5
6	1880-1	88.98	14	90.07	410	3.15	3.34	4.24	46.5	40.6	48.3
7	1880-1	208.52	26	210.13	380	0.16	0.23	0.21	13.5	9.0	11.4
8	1880-1	39.54	14	41.95	400	4.08	8.07	5.31	23.9	82.6	52.2
9	1880-1	45.74	14	47.83	300	10.12	5.57	5.71	41.9	15.6	63.5
10	1880-1	85.10	14	86.24	400	1.17	1.62	1.24	85.3	134.7	33.5
10	1880-2	135.91	14	136.63	400	0.60	0.63	0.72	8.8	8.2	11.5
11	1880-1	337.01	14	338.01	350	0.14	0.11	0.13	24.3	25.2	21.2
11	1880-2	252.08	14	253.42	350	0.27	0.21	0.23	12.7	19.5	12.9
12	1880-1	235.25	26	236.68	390	0.13	0.20	0.11	17.5	22.1	18.8
12	1880-2	147.76	26	150.03	390	0.32	0.38	0.34	12.5	9.6	10.3
13	1880-1	183.98	26	185.81	360	0.16	0.15	0.21	7.7	22.9	10.4
13	1880-2	85.07	26	88.95	360	0.56	0.69	0.72	12.0	28.8	10.5

下载: 导出CSV

表 2 不同距离下最大单段药量

Table 2. Maximum charge per delay at different distances

R/m	Q/kg
R/m	Horizontal radial	Horizontal tangential	Vertical
10	64.37	166.78	94.24
13	141.42	366.42	207.06
16	263.67	683.14	386.04
19	441.53	1143.95	646.44
22	685.43	1775.89	1003.55
25	1005.81	2605.95	1472.62

下载: 导出CSV

表 3 岩石材料模型参数

Table 3. Parameters of the rock material model

ρ₀/(kg·m⁻³)	E/GPa	ν	σ_c/MPa	E_t/GPa	β
2700	71.25	0.24	75.5	0.4	0.5

下载: 导出CSV

表 4 衬砌材料参数

Table 4. Parameters of the lining material

ρ₁/(g·cm⁻³)	G/GPa	A	B	S_max	c	n	μ₁	μ_c	p_l/GPa
2.40	10.63	0.23	1.84	7	0.005	0.88	0.12	0.005	0.8

p_c/MPa	f_c/MPa	T/MPa	$ {\dot \varepsilon _0} $/s⁻¹	ε_fmin	D₁	D₂	K₁/GPa	K₂/GPa	K₃/GPa
10	20	2.8	1×10⁻⁶	0.01	0.04	1	85	−171	208

下载: 导出CSV

表 5 MAT_SOIL_AND_FOAM材料参数^[16]

Table 5. MAT_SOIL_AND_FOAM material parameters^[16]

γ_sat/(kN·m⁻³)	G_s/MPa	K_s/MPa	A₀/MPa	A₁/MPa	A₂/MPa	p_tc/MPa
17	2.524	4673	0.0010	0.0049	0.0079	−0.005

下载: 导出CSV

表 6 不同压力下土的应变^[16]

Table 6. Strain values of soil at different pressures^[16]

Pressure/MPa	Volumetric strain	Pressure/MPa	Volumetric strain
0	0	800	−0.1878
100	−0.0216	1000	−0.2408
200	−0.0437	2000	−0.5586
400	−0.0895	3000	−1.0272
600	−0.1374	4000	−1.9380

下载: 导出CSV

表 7 测点峰值振速对比

Table 7. Comparison of peak particle velocities of measured points

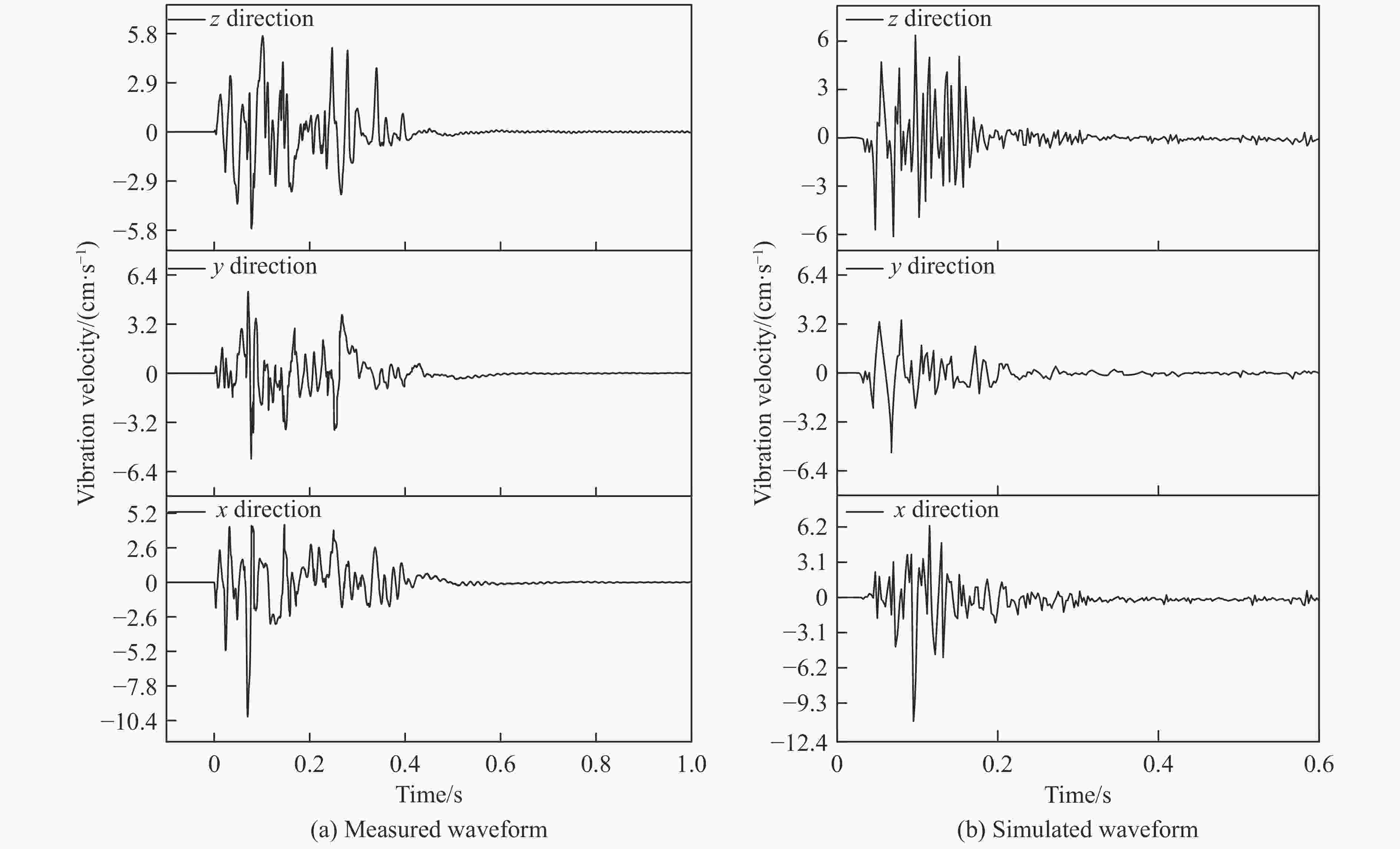
Direction	v_max/(cm·s⁻¹)		Error/%
Direction	Simulation	Test	Error/%
x	10.89	10.12	7.6
y	5.11	5.57	8.3
z	6.13	5.71	7.4

下载: 导出CSV

表 8 巷道关键部位峰值有效应力-峰值振速拟合方程

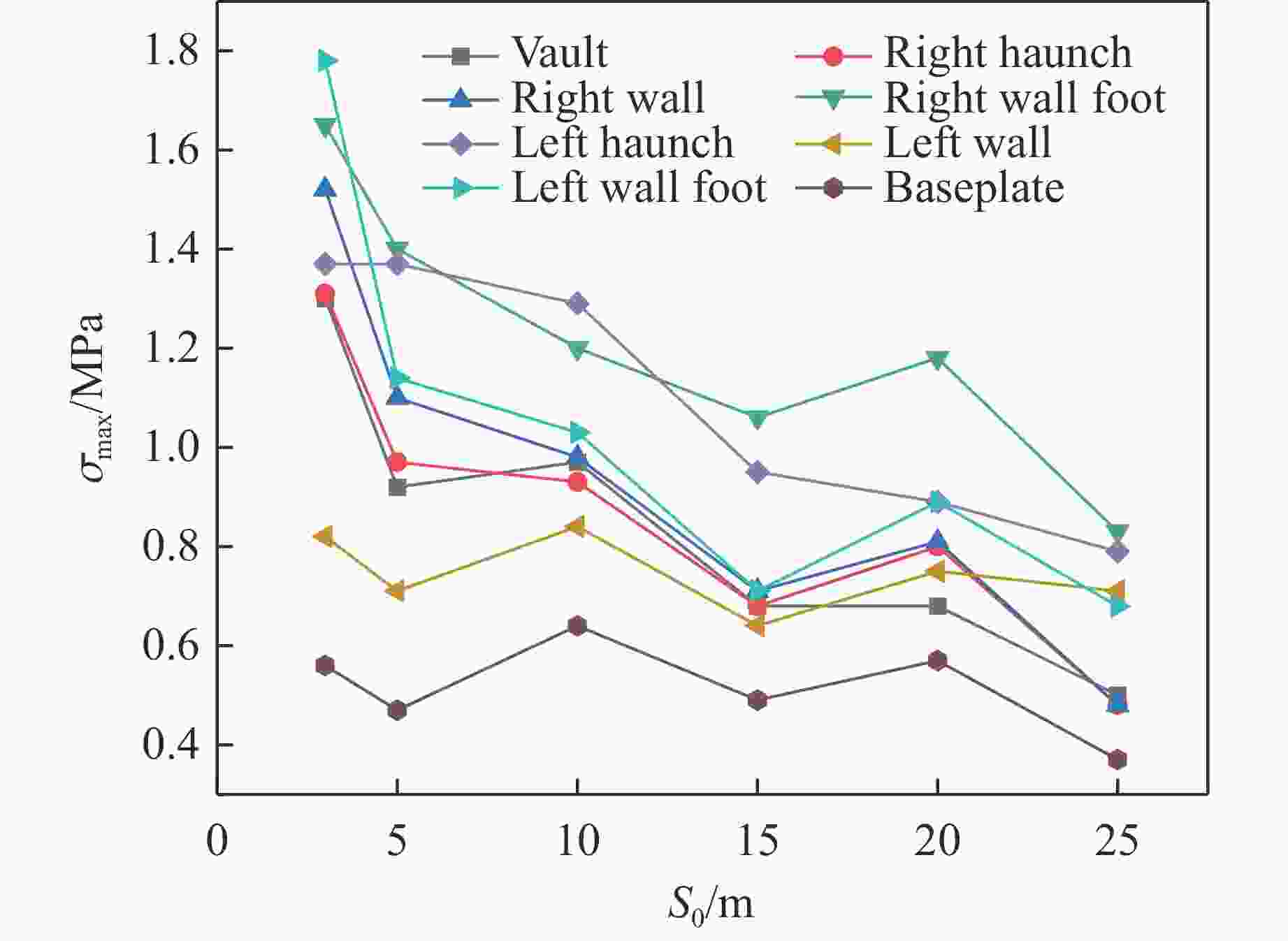
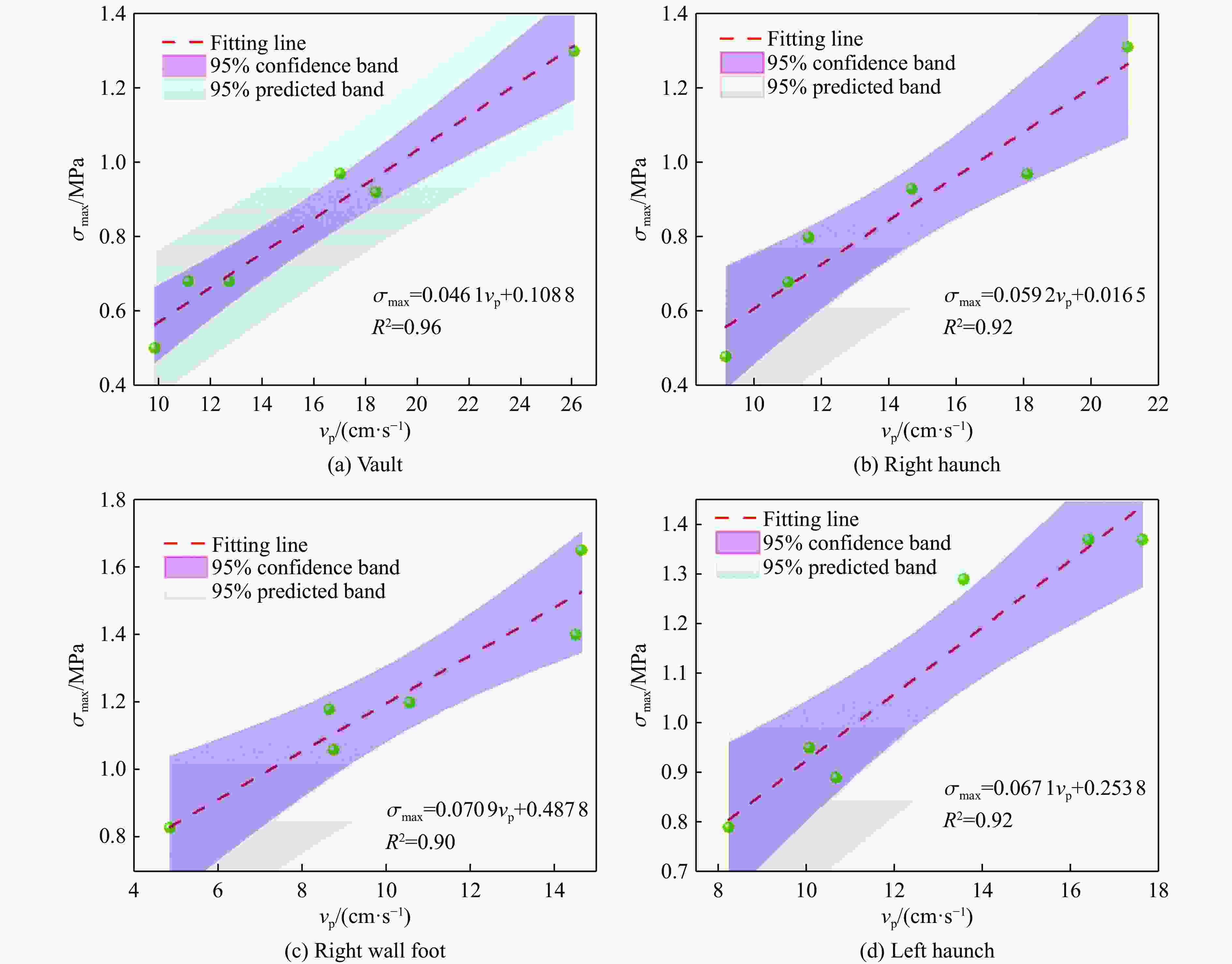
Table 8. Fitting equations of peak effective stress-peak vibration velocity in key positions of roadway

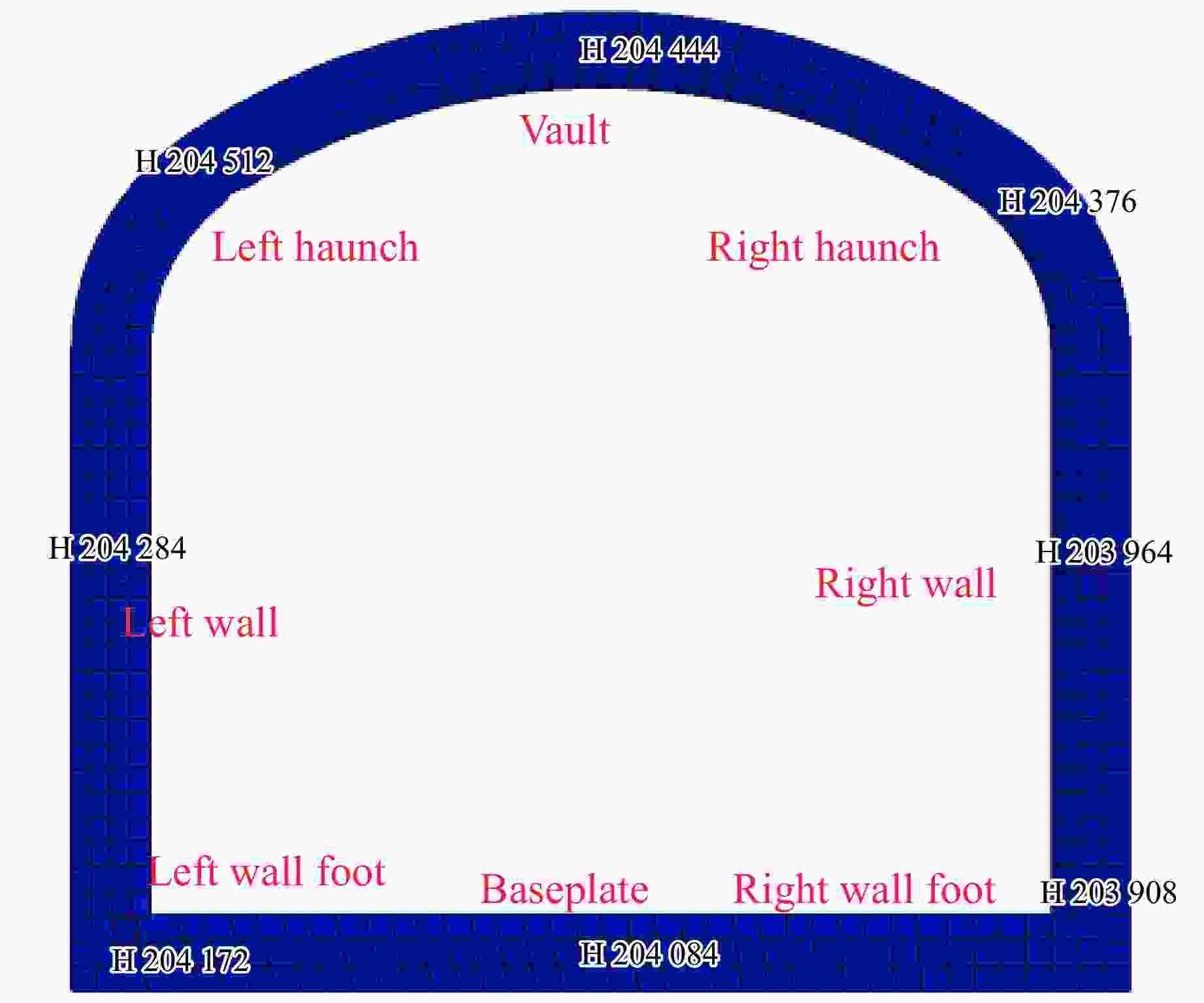
Part of the roadway	Fitting equation
Vault	$ {\sigma _{\max }} = 0.046\,1{v_{\text{p}}}+0.108\,8 $
Right haunch	$ {\sigma _{\max }} = 0.059\,2{v_{\text{p}}}+0.016\,5 $
Right wall foot	$ {\sigma _{\max }} = 0.070\,9{v_{\text{p}}}+0.487\,8 $
Left haunch	$ {\sigma _{\max }} = 0.067\,1{v_{\text{p}}}+0.253\,8 $

下载: 导出CSV

表 9 调整前后参数

Table 9. Parameters before and after adjustment

Adjustment	Blast hole diameter/mm	Hole spacing/m	Array pitch/m	Interval length/m	Length of charge/m	Charge per hole/kg
Before	200	7.0	5.5	0	8.5	360
After	200	4.0	4.0	2.5	6.0	250

下载: 导出CSV

参考文献(21)

[1]	DOWDING C H. Suggested method for blast vibration monitoring [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1992, 29(2): 145–156. doi: 10.1016/0148-9062(92)92124-U
[2]	JIANG N, ZHOU C B. Blasting vibration safety criterion for a tunnel liner structure [J]. Tunnelling and Underground Space Technology, 2012, 32: 52–57. doi: 10.1016/j.tust.2012.04.016
[3]	XU T. Blasting vibration safety criterion of surrounding rock of a circular tunnel [J]. Geotechnical and Geological Engineering, 2019, 37(4): 3077–3084. doi: 10.1007/s10706-019-00826-z
[4]	LI Y X, WANG Z B, LUO Q Q, et al. Stability analysis of civil air defense tunnel under blasting vibration [J]. Journal of Vibroengineering, 2024, 26(4): 892–903. doi: 10.21595/jve.2024.23892
[5]	XUE F, XIA C C, LI G L, et al. Safety threshold determination for blasting vibration of the lining in existing tunnels under adjacent tunnel blasting [J]. Advances in Civil Engineering, 2019(1): 8303420. doi: 10.1155/2019/8303420
[6]	HOU S J, XIE F, TIAN S K, et al. Effects of blasting vibrations on an arch in the Jiaohuayu tunnel described by energy response spectrum analysis [J]. Applied Sciences, 2022, 12(22): 11395. doi: 10.3390/app122211395
[7]	凌同华. 爆破震动效应及其灾害的主动控制 [D]. 长沙: 中南大学, 2004. LING T H. Blast vibration effect and initiative control of vibrational damage [D]. Changsha: Central South University, 2004.
[8]	张在晨, 林从谋, 黄志波, 等. 隧道爆破近区振动的预测方法 [J]. 爆炸与冲击, 2014, 34(3): 367–372. doi: 10.11883/1001-1455(2014)03-0367-0 ZHANG Z C, LIN C M, HUANG Z B, et al. Prediction of blasting vibration of area near tunnel blasting source [J]. Explosion and Shock Waves, 2014, 34(3): 367–372. doi: 10.11883/1001-1455(2014)03-0367-0
[9]	杨润强, 严鹏, 王高辉, 等. 地应力水平对深埋隧洞爆破振动频谱结构的影响 [J]. 爆炸与冲击, 2019, 39(5): 055201. YANG R Q, YAN P, WANG G H, et al. Effect of in-situ stress level on frequency spectrum of blasting vibration in a deep-buried tunnel [J]. Explosion and Shock Waves, 2019, 39(5): 055201.
[10]	刘家明, 张俊儒, 王智勇, 等. 硬质地层下近接隧道爆破振动影响分区及动力响应研究 [J]. 现代隧道技术, 2023, 60(2): 125–137. doi: 10.13807/j.cnki.mtt.2023.02.014 LIU J M, ZHANG J R, WANG Z Y, et al. Impact zoning and dynamic response to blasting vibration in adjacent tunnel under hard rock strata [J]. Modern Tunnelling Technology, 2023, 60(2): 125–137. doi: 10.13807/j.cnki.mtt.2023.02.014
[11]	薛方方, 胡广柱, 张建伟, 等. 深埋倾斜式压力钢管壁厚与间隙参数的敏感性分析 [J]. 华北水利水电大学学报(自然科学版), 2021, 42(6): 8–13. doi: 10.19760/j.ncwu.zk.2021074 XUE F F, HU G Z, ZHANG J W, et al. Sensitivity analysis of wall thickness and clearance parameters of deep buried inclined penstock [J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2021, 42(6): 8–13. doi: 10.19760/j.ncwu.zk.2021074
[12]	苏凯, 杨逢杰, 年夫喜, 等. 超深埋隧洞防渗排水措施与衬砌外水压力分布规律 [J]. 中南大学学报(自然科学版), 2024, 55(6): 2222–2235. doi: 10.11817/j.issn.1672-7207.2024.06.015 SU K, YANG F J, NIAN F X, et al. Anti-seepage and drainage measures of ultra-deep buried tunnel and distribution law of external water pressure of lining [J]. Journal of Central South University (Science and Technology), 2024, 55(6): 2222–2235. doi: 10.11817/j.issn.1672-7207.2024.06.015
[13]	费鸿禄, 郭玉新. 基于LS-DYNA的交错扇形深孔崩落法排间间隔时间优化研究 [J]. 中国安全生产科学技术, 2022, 18(4): 127–134. doi: 10.11731/j.issn.1673-193x.2022.04.018 FEI H L, GUO Y X. Study on optimized selection for row interval time of staggered sector deep-hole caving method based on LS-DYNA [J]. Journal of Safety Science and Technology, 2022, 18(4): 127–134. doi: 10.11731/j.issn.1673-193x.2022.04.018
[14]	金键, 侯海量, 陈鹏宇, 等. PMT水下内爆冲击波强度与传播特性研究 [J]. 振动与冲击, 2018, 37(13): 100–104, 122. doi: 10.13465/j.cnki.jvs.2018.13.015 JIN J, HOU H L, CHEN P Y, et al. Shock wave intensity and propagation features of a PMT’s underwater implosion [J]. Journal of Vibration and Shock, 2018, 37(13): 100–104, 122. doi: 10.13465/j.cnki.jvs.2018.13.015
[15]	刘江超, 高文学, 张声辉, 等. 水间隔装药孔壁爆炸应力分布规律 [J]. 兵工学报, 2021, 42(12): 2646–2654. doi: 10.3969/j.issn.1000-1093.2021.12.012 LIU J C, GAO W X, ZHANG S H, et al. Distribution law of explosion stress on hole wall of water interval charge [J]. Acta Armamentarii, 2021, 42(12): 2646–2654. doi: 10.3969/j.issn.1000-1093.2021.12.012
[16]	XIE L X, LU W B, ZHANG Q B, et al. Damage evolution mechanisms of rock in deep tunnels induced by cut blasting [J]. Tunnelling and Underground Space Technology, 2016, 58: 257–270. doi: 10.1016/j.tust.2016.06.004
[17]	LIU K, LI Q Y, WU C Q, et al. A study of cut blasting for one-step raise excavation based on numerical simulation and field blast tests [J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 109: 91–104. doi: 10.1016/j.ijrmms.2018.06.019
[18]	管晓明, 傅洪贤, 王梦恕, 等. 隧道爆破振动下砌体结构局部动力反应研究 [J]. 现代隧道技术, 2017, 54(3): 135–141. doi: 10.13807/j.cnki.mtt.2017.03.019 GUAN X M, FU H X, WANG M S, et al. Local dynamic response of a masonry structure to the vibrations of tunnel blasting [J]. Modern Tunnelling Technology, 2017, 54(3): 135–141. doi: 10.13807/j.cnki.mtt.2017.03.019
[19]	左壮壮. 露天矿爆破作用下邻近巷道围岩的振动控制及损伤规律研究 [D]. 阜新: 辽宁工程技术大学, 2023: 13–14. ZUO Z Z. Study on vibration control and damage law of surrounding rock of adjacent roadway under open-pit blasting [D]. Fuxin: Liaoning Technical University, 2023: 13–14.
[20]	曹明星, 严松宏, 郑永强, 等. 邻近隧道爆破振动响应分析 [J/OL]. 工程爆破(2023-10-25)[2024-10-29]. https://doi.org/10.19931/j.EB.20230100. CAO M X, YAN S H, ZHENG Y Q, et al. Analysis of blasting vibration response of adjacent tunnel [J/OL]. Engineering Blasting (2023-10-25)[2024-10-29]. https://doi.org/10.19931/j.EB.20230100.
[21]	CAO H Q, WANG D Y, GUO J F, et al. Blasting safety criterion of existing high speed railway tunnel over tunnel [J]. Journal of Vibroengineering, 2024, 26(7): 1670–1685. doi: 10.21595/jve.2024.24186