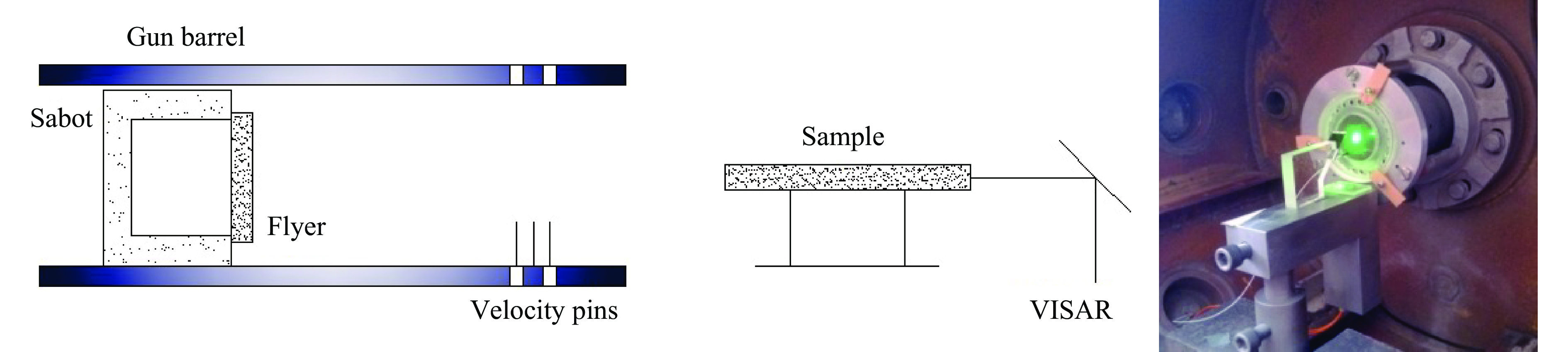
Dynamic Mechanical Behaviors of High Strength Steel Based on Taylor Rod
-
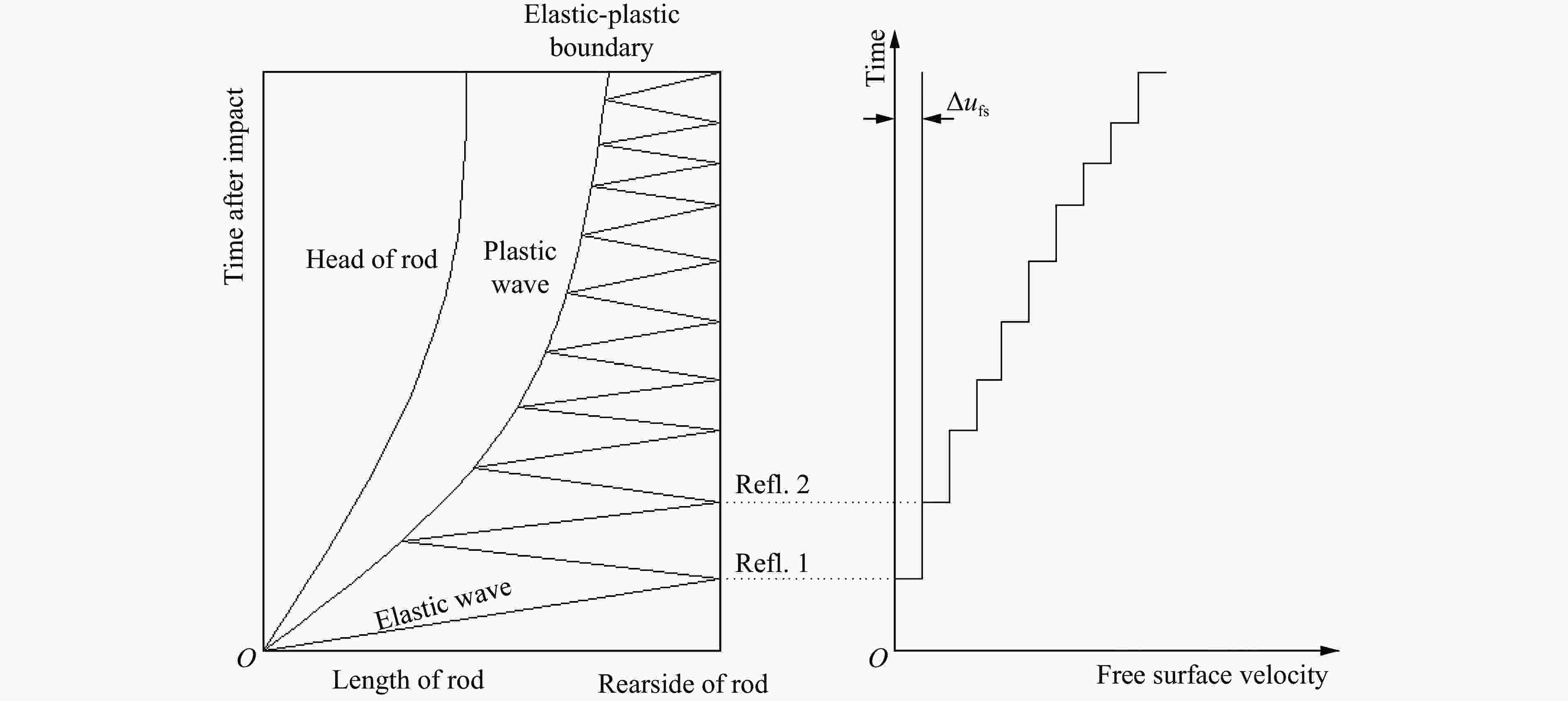
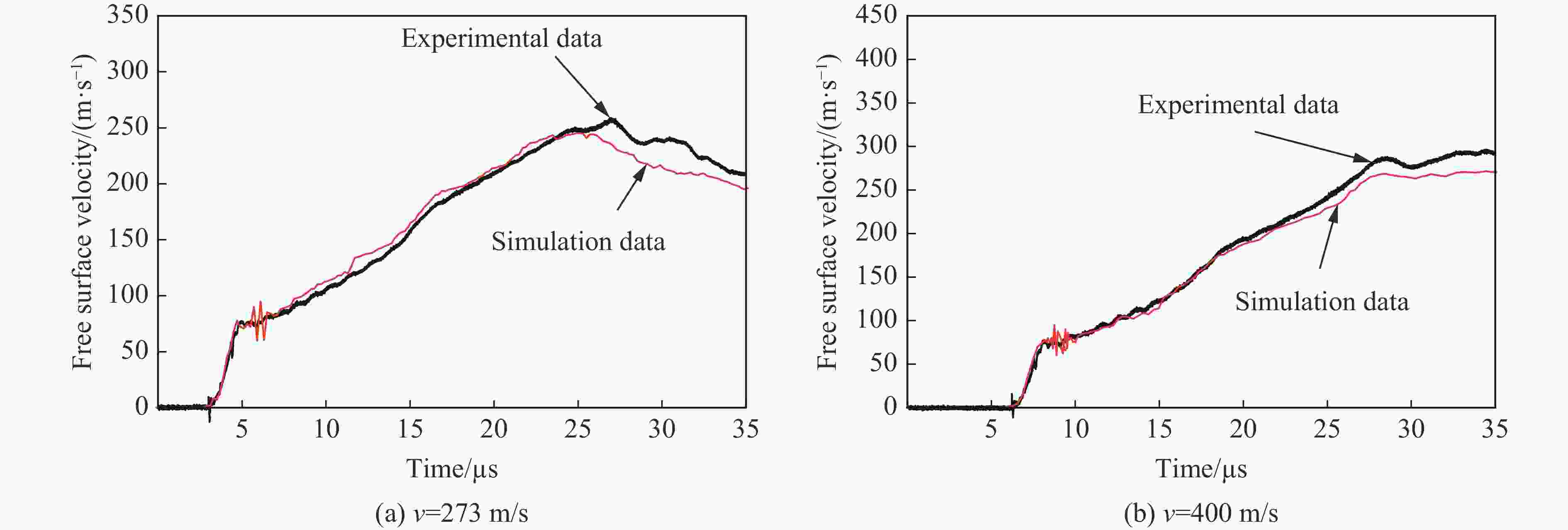
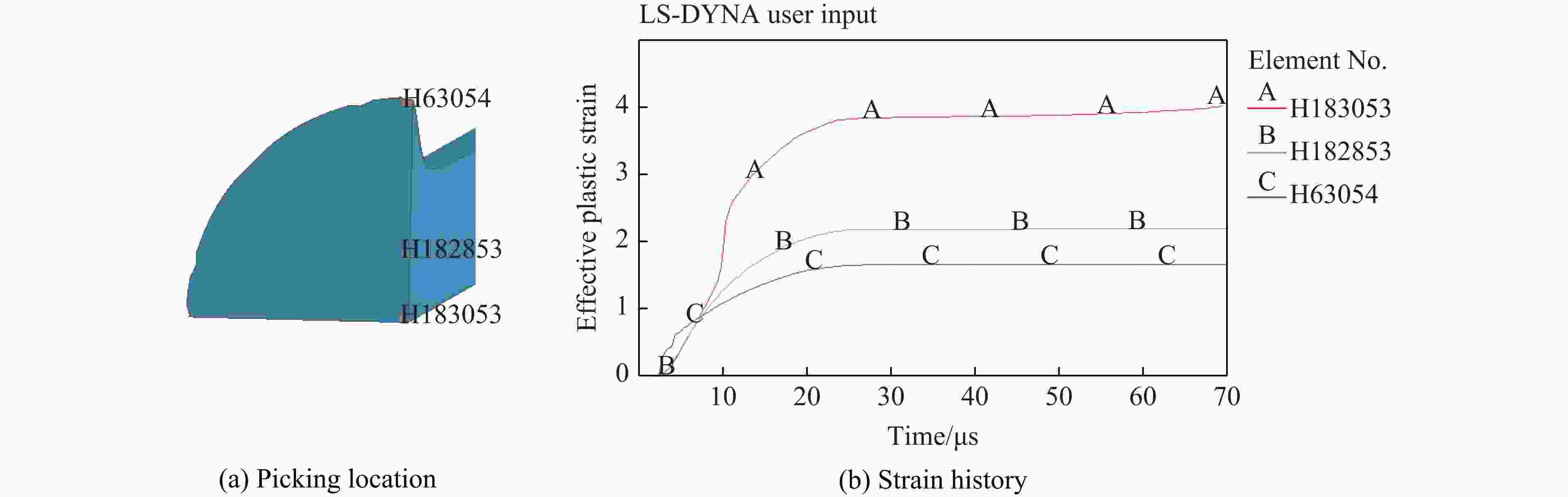
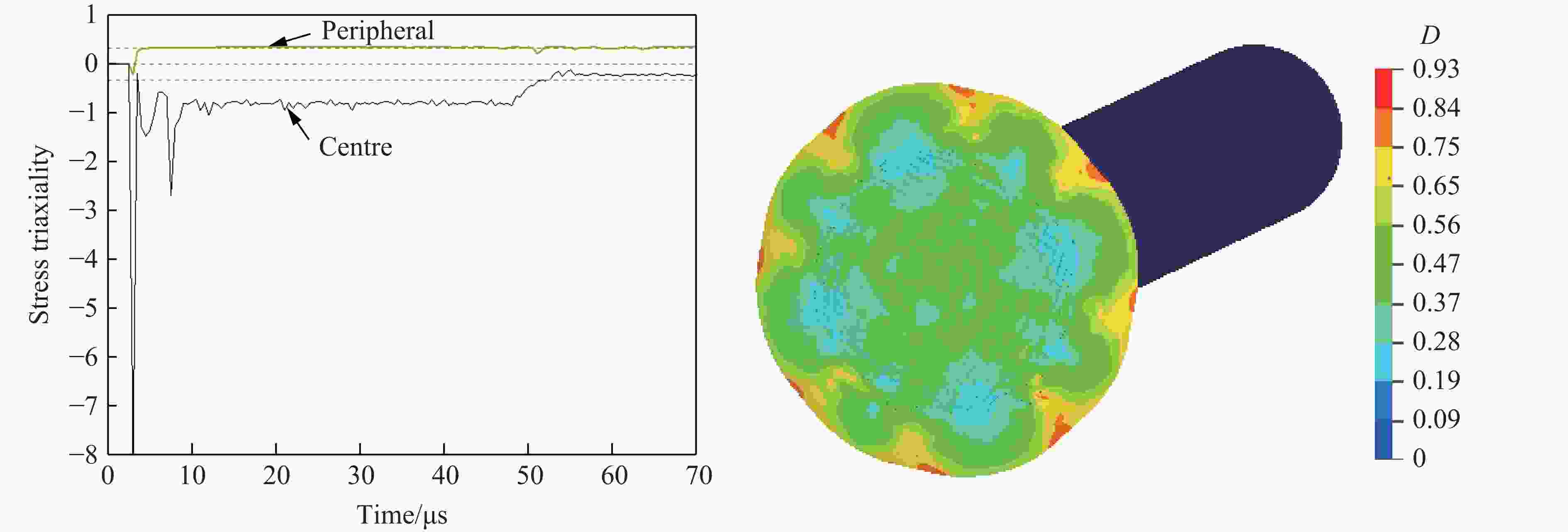
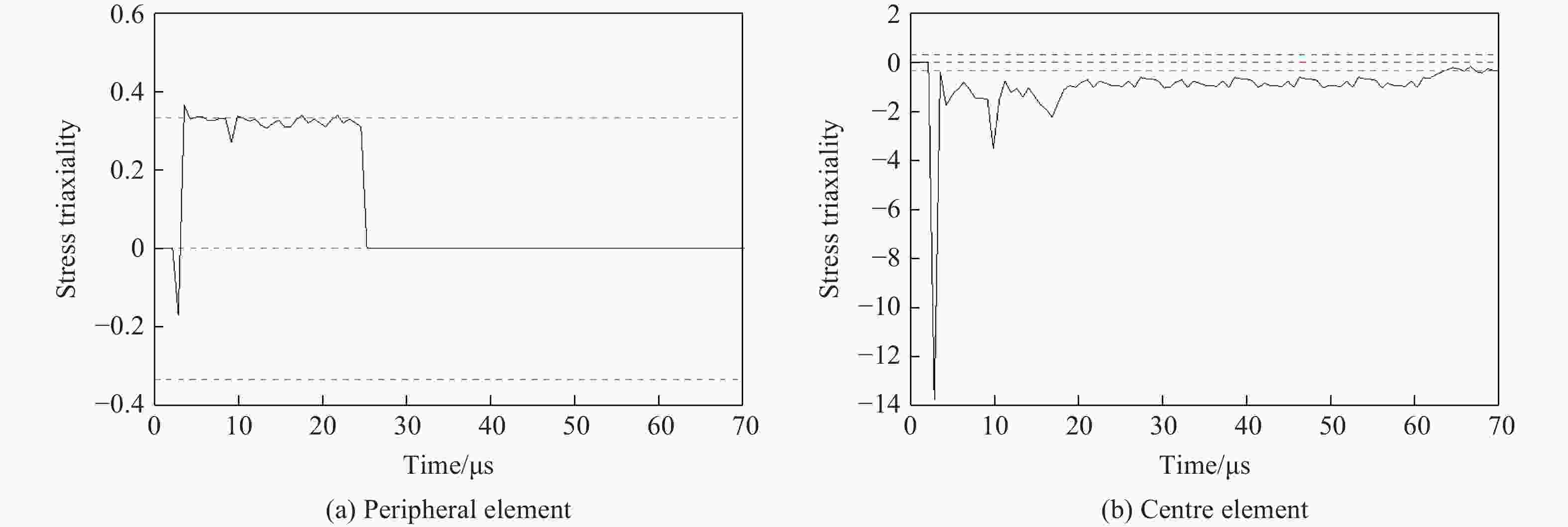
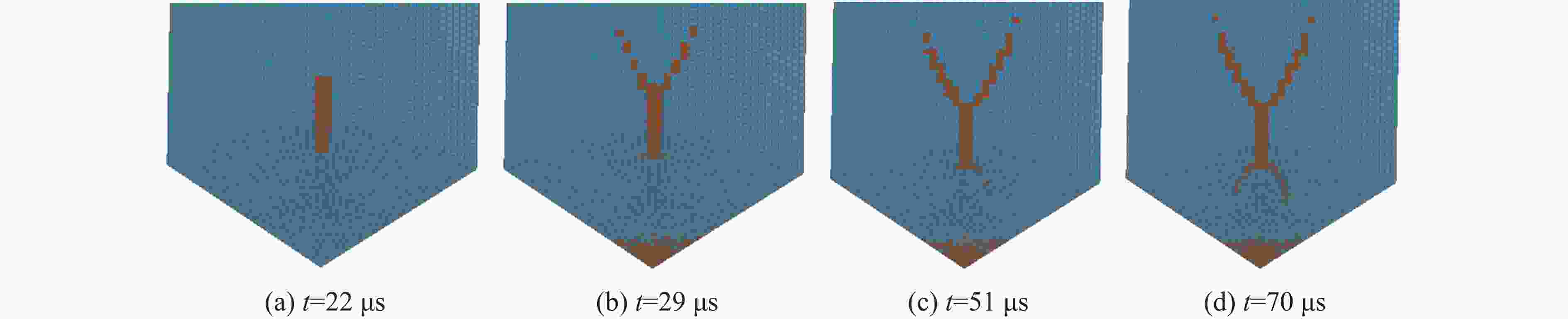
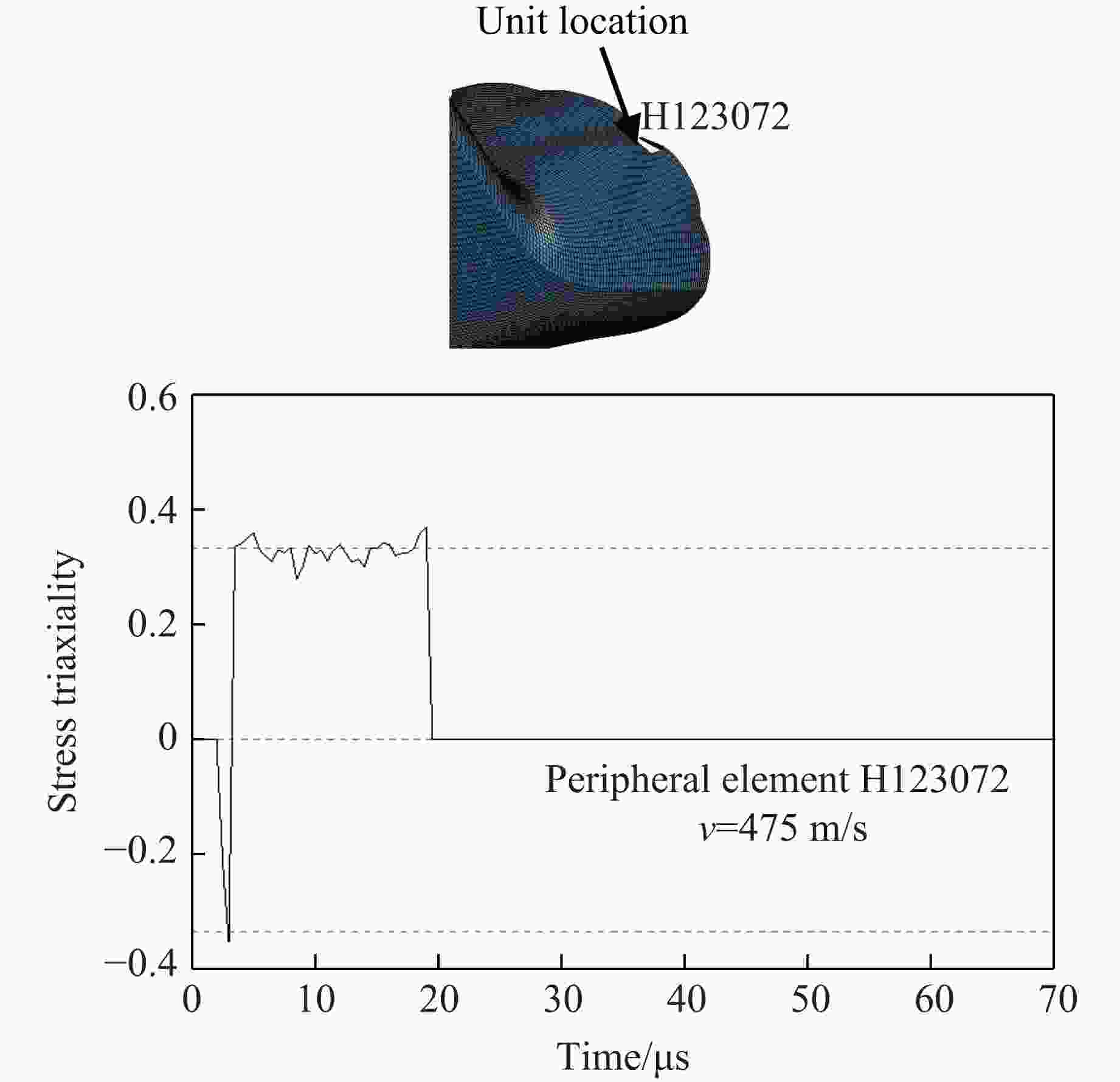
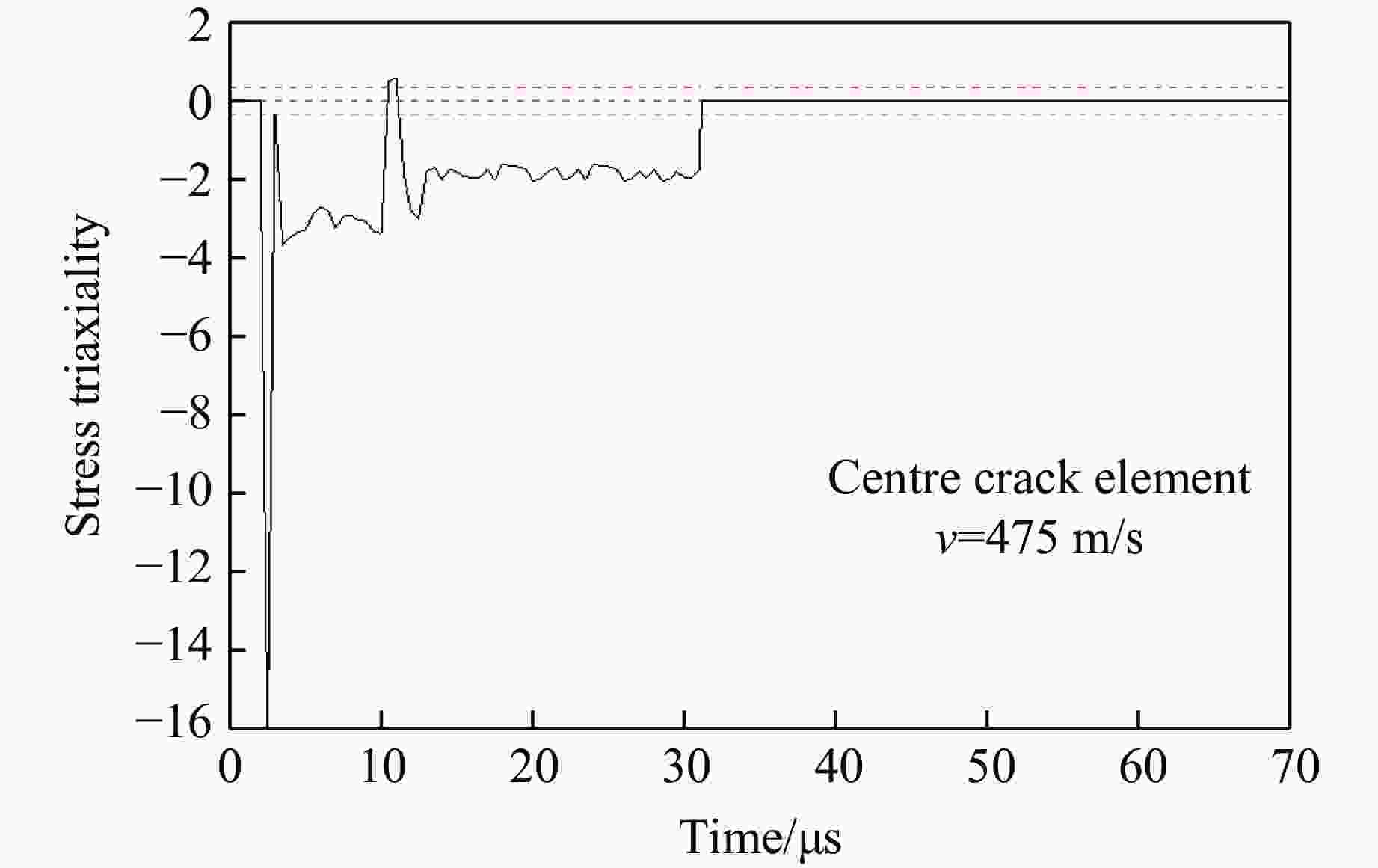
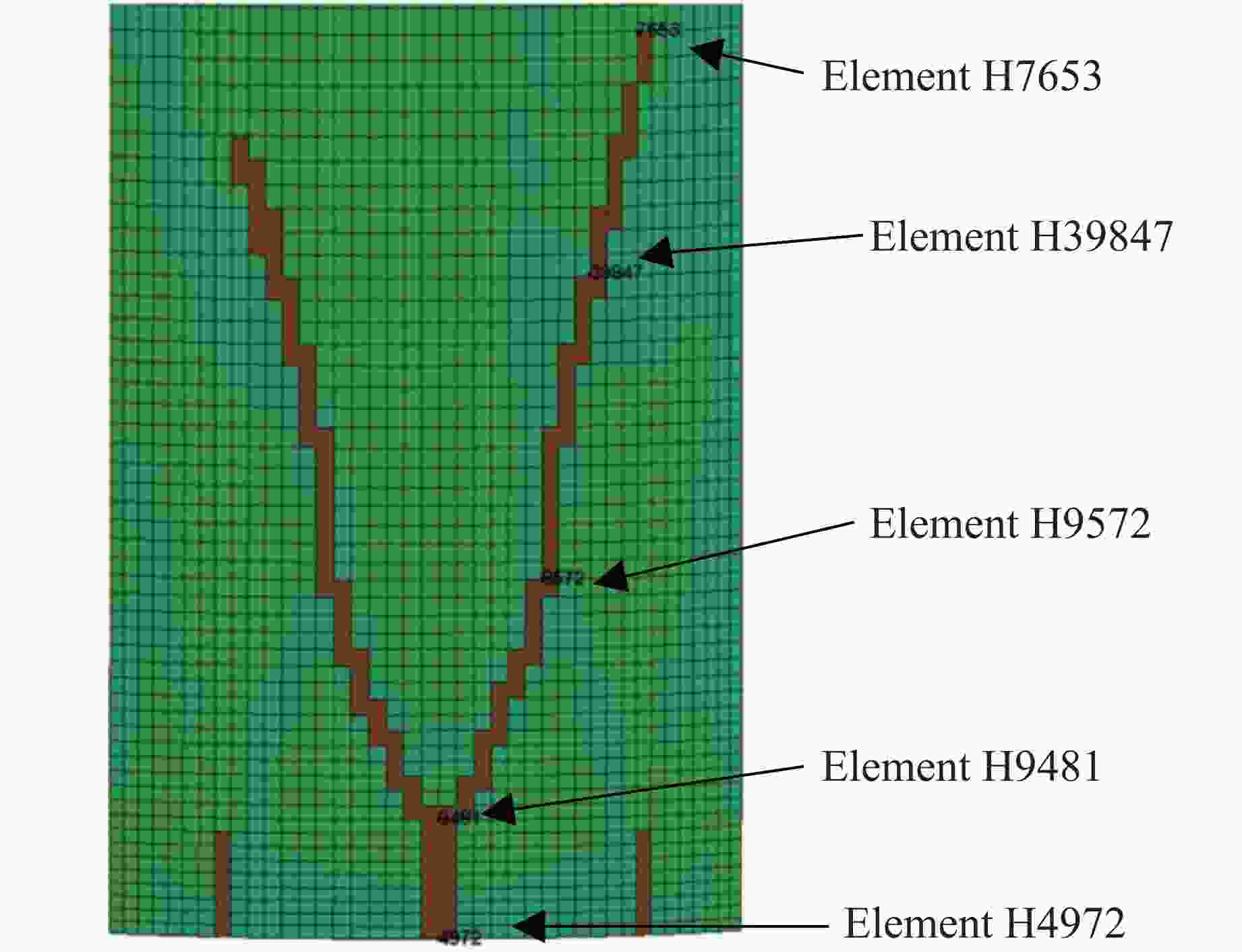
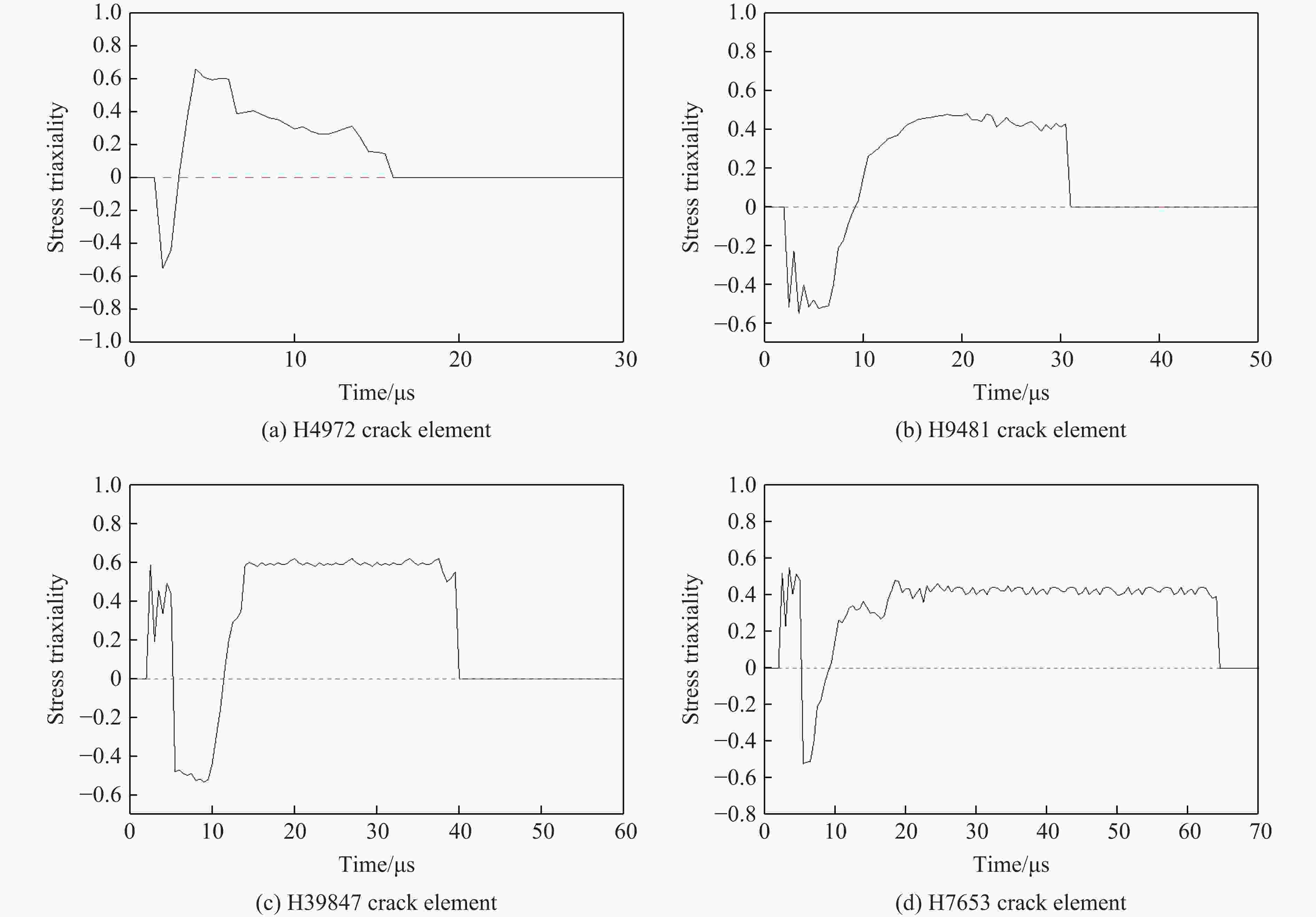
摘要: 利用反向Taylor杆撞击实验和数值模拟方法研究了30CrMnSiNi2A钢在高应变率冲击下的动态特性。首先，在Taylor杆冲击实验的基础上，采用Johnson-Cook本构模型和失效模型，对30CrMnSiNi2A钢的反向Taylor杆撞击进行了数值模拟，并将数值模拟结果与实验得到的杆件自由面速度曲线进行对比验证，两者吻合良好。然后，研究了不同长径比的30CrMnSiNi2A钢杆件对反向Taylor杆撞击实验中任意反射面激光干涉测速技术（velocity interferometer system for any reflector，VISAR）测试结果的影响，得到了适用于VISAR测试的Taylor杆长径比范围。最后，运用应力三轴度及损伤度分析了Taylor杆的断裂破坏机理和变形模式，得到了镦粗、蘑菇状变形、花瓣状开裂3种变形模式，并分析了杆件断裂破坏的原因。结果表明：Taylor杆撞击端中心破坏是由于材料受压引起，而撞击端边缘开裂是由于材料处于拉伸状态造成的，且断裂先从边缘开始。
-
关键词:
- 反向Taylor杆 /
- Johnson-Cook本构模型 /
- 应力三轴度 /
- 断裂破坏机理
Abstract: The dynamic mechanical properties of 30CrMnSiNi2A steel under high strain rate impact were studied using both Taylor rod impact experiment and numerical simulation. Based on the result of Taylor rod impact experiment, the Johnson-Cook constitutive model and failure model were utilized to simulate the free surface velocity of 30CrMnSiNi2A steel under Taylor rod impact. The numerical simulation results were then compared with the experimental free surface velocity profiles obtained, demonstrating a high degree of congruence. Subsequently, the influence of Taylor rod specimens with varying length-to-diameter ratios (l/d) on the outcome of velocity interferometer system for any reflector (VISAR) test within the reverse Taylor rod impact test was examined. The study identified the optimal l/d range for Taylor rod that are suitable for VISAR testing. Employing the concepts of stress traxiality and damage number, the fracture failure mechanism and deformation mode of the Taylor rod were analyzed. Three distinct deformation modes were identified: rough deformation, mushroom deformation, and petal cracking. The analysis of the Taylor rod’s fracture failure mechanism has elucidated that the failure occurring at the central region of the sample is predominantly a result of compressive forces. Conversely, the cracking observed at the periphery of the sample is primarily attributed to the influence of tensile forces. It was also observed that fractures of the Taylor rod initiate preferentially at the edge. -
图 1 采用VISAR测试技术的反向Taylor撞击实验装置及示意图
Figure 1. Reverse Taylor impact experimental setup and schematic diagram using VISAR testing technology
图 3 反向Taylor杆自由面速度时程曲线
Figure 3. Reverse Taylor rod free surface velocity-time history curves
图 4 Taylor杆自由面速度时程曲线对比
Figure 4. Comparison of free surface velocity-time history curves for Taylor rods
图 5 撞击速度为400 m/s的Taylor杆的等效塑性应变分布和结构变形
Figure 5. Equivalent plastic strain distribution and structural deformation of Taylor rod with impact velocity of 400 m/s
图 6 Taylor杆撞击中2个阶段的几何变形
Figure 6. Geometric deformation in two stages of Taylor impact
图 7 不同长径比杆件的自由表面速度
Figure 7. Free surface velocity of rods with different aspect ratios
图 8 不同长径比杆件屈服点处的自由表面速度
Figure 8. Free surface velocity at the yield point of rods with different aspect ratios
图 9 横向应力测试点所取单元位置(1/4模型)
Figure 9. Element positions taken for lateral stress testing points (1/4 model)
图 10 不同长径比条件下自由面附近内部单元横向应力曲线
Figure 10. Lateral stress curves of internal elements near free surfaces with different aspect ratios
图 12 不同撞击速度下Taylor杆的变形
Figure 12. Deformation of Taylor rod at different impact velocities
图 13 Taylor杆撞击断面的三点塑性应变历程（380 m/s）
Figure 13. Three point plastic strain history of Taylor rod impact section (380 m/s)
图 14 Taylor杆两点的应力三轴度历程与损伤云图（380 m/s）
Figure 14. Stress triaxiality history and damage cloud map of Taylor rod at two points (380 m/s)
图 15 Taylor杆撞击端边缘点和中心点的应力三轴度历程（400 m/s）
Figure 15. Stress triaxiality history of Taylor rod impact end edge point and centre point (400 m/s)
图 16 2种撞击速度下的Taylor杆蘑菇状变形
Figure 16. Mushroom shaped deformation of Taylor rod at two different impact velocities
图 22 4个典型失效单元的应力三轴度历程及应力状态对裂纹损伤的贡献
Figure 22. Stress triaxiality history and damage contribution of stress states of four typical failure elements in cracks
表 1 反向Taylor实验参数
Table 1. Reverse Taylor experiment parameters
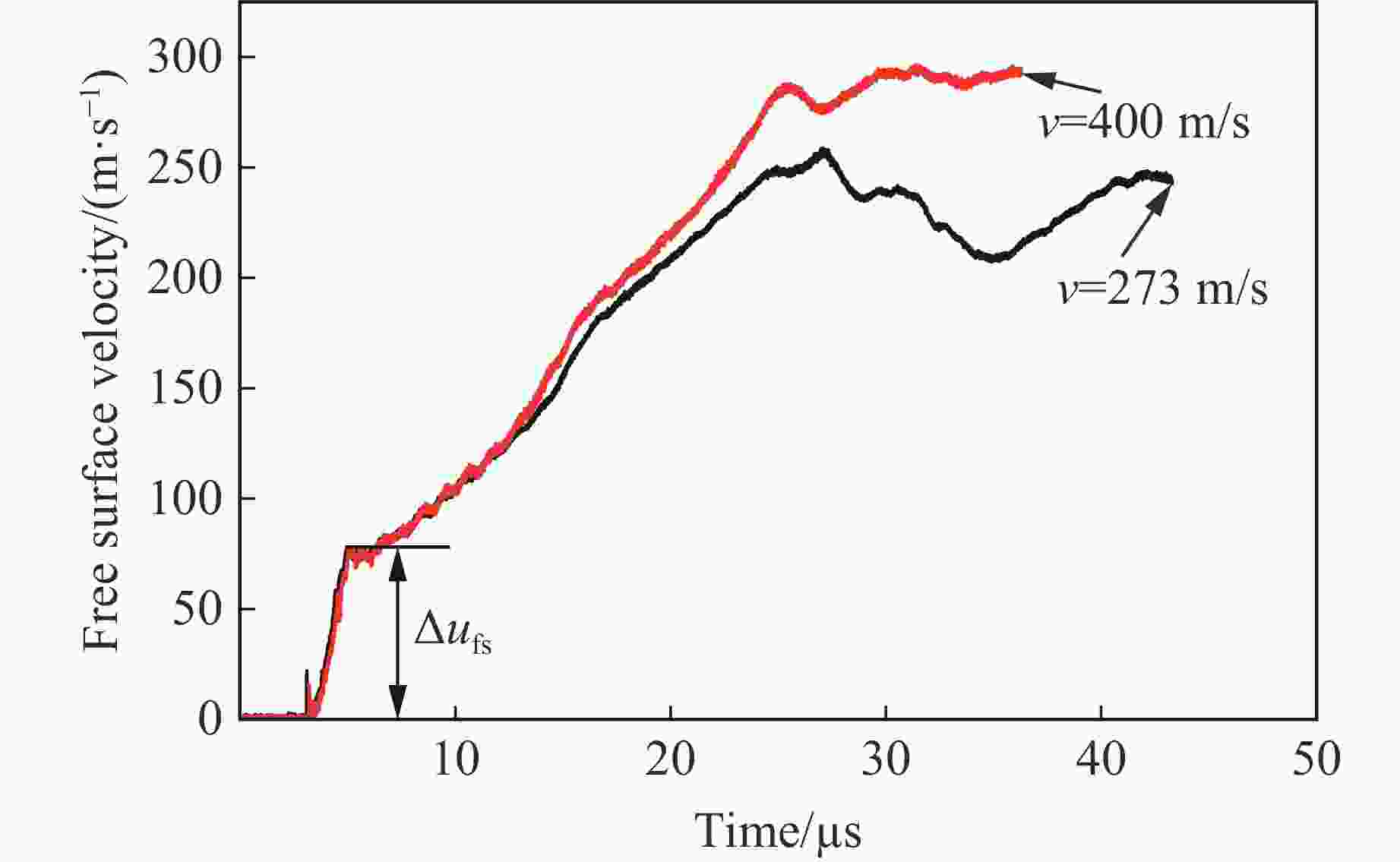
v/(m·s−1) Flyer size/(mm×mm) Taylor rod size/(mm×mm) Length-diameter ratio of Taylor rod 273 $\varnothing $24×12 $\varnothing $5×40.0 8.0 400 $\varnothing $24×12 $\varnothing $5×40.0 8.0 
下载: 导出CSV
表 2 30CrMnSiNi2A钢反向Taylor实验参数
Table 2. Reverse Taylor experimental parameters of 30CrMnSiNi2A steel
v/(m·s−1) ufs/(m·s−1) up/(m·s−1) $ {\sigma _{\rm{Y}}} $/MPa $ \varepsilon $/10−3 $ \dot \varepsilon $/s−1 273 77.10 38.55 1 560 8.34 4 109 400 77.85 38.93 1 600 8.42 4 617
下载: 导出CSV
表 3 30CrMnSiNi2A钢[15]和304不锈钢的材料参数
Table 3. Material parameters of 30CrMnSiNi2A steel[15] and 304 stainless steel
Material ρ/(g·cm−3) E/GPa A/GPa B/GPa C n m 30CrMnSiNi2A steel[15] 7.8 217 1.58 0.38 0.020 0.245 1.06 304 stainless steel 7.8 207 0.34 0.25 0.014 0.210 1.03
下载: 导出CSV
表 4 Taylor杆尺寸
Table 4. Taylor rod size
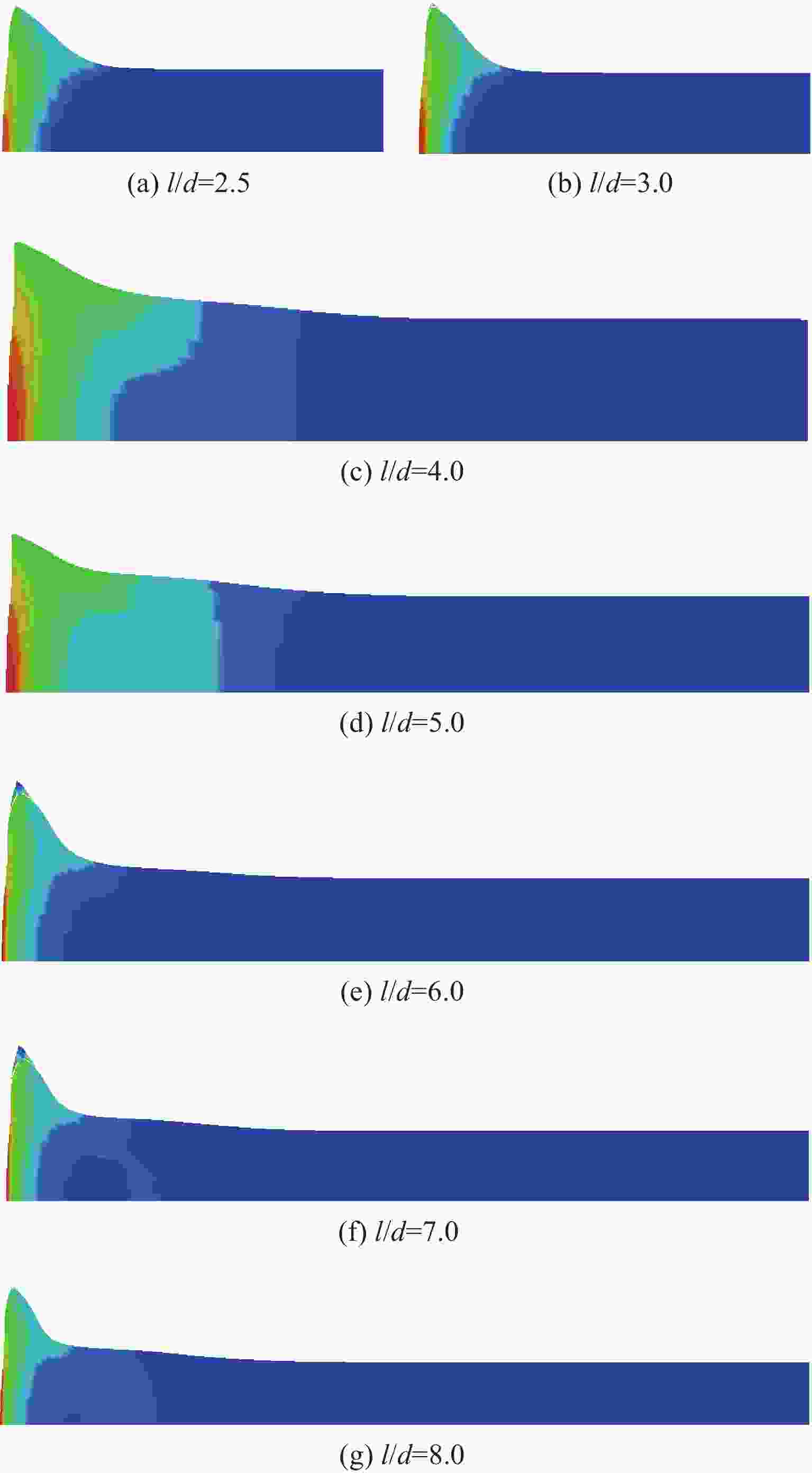
Flyer size/(mm×mm) l/d Taylor rod size/(mm×mm) Flyer size/(mm×mm) l/d Taylor rod size/(mm×mm) $\varnothing $24×12 2.5 $\varnothing $5×12.5 $\varnothing $24×12 6.0 $\varnothing $5×30.0 3.0 $\varnothing $5×15.0 7.0 $\varnothing $5×35.0 4.0 $\varnothing $5×20.0 8.0 $\varnothing $5×40.0 5.0 $\varnothing $5×25.0
下载: 导出CSV
表 5 不同长径比Taylor杆的数值模拟结果
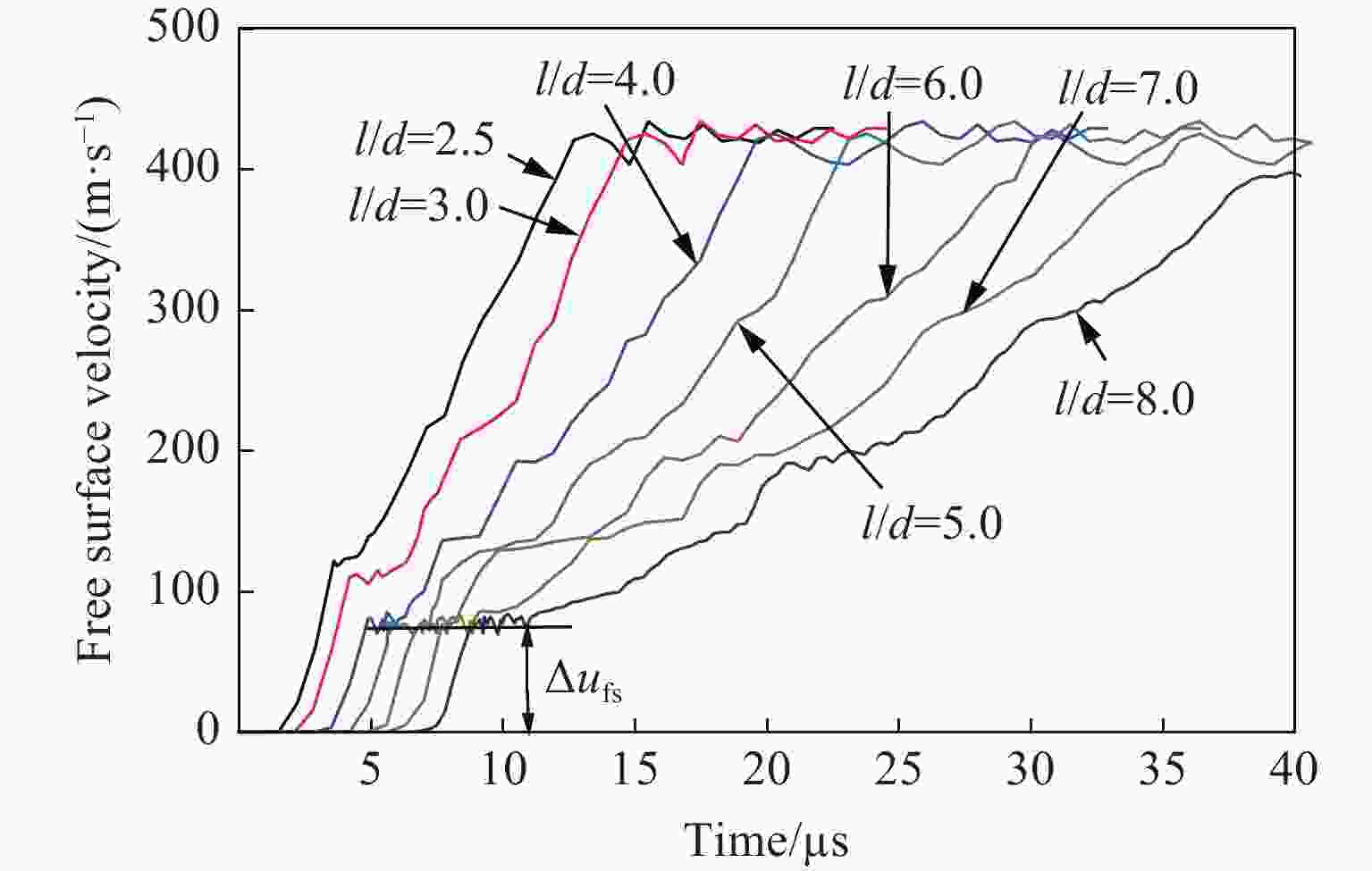
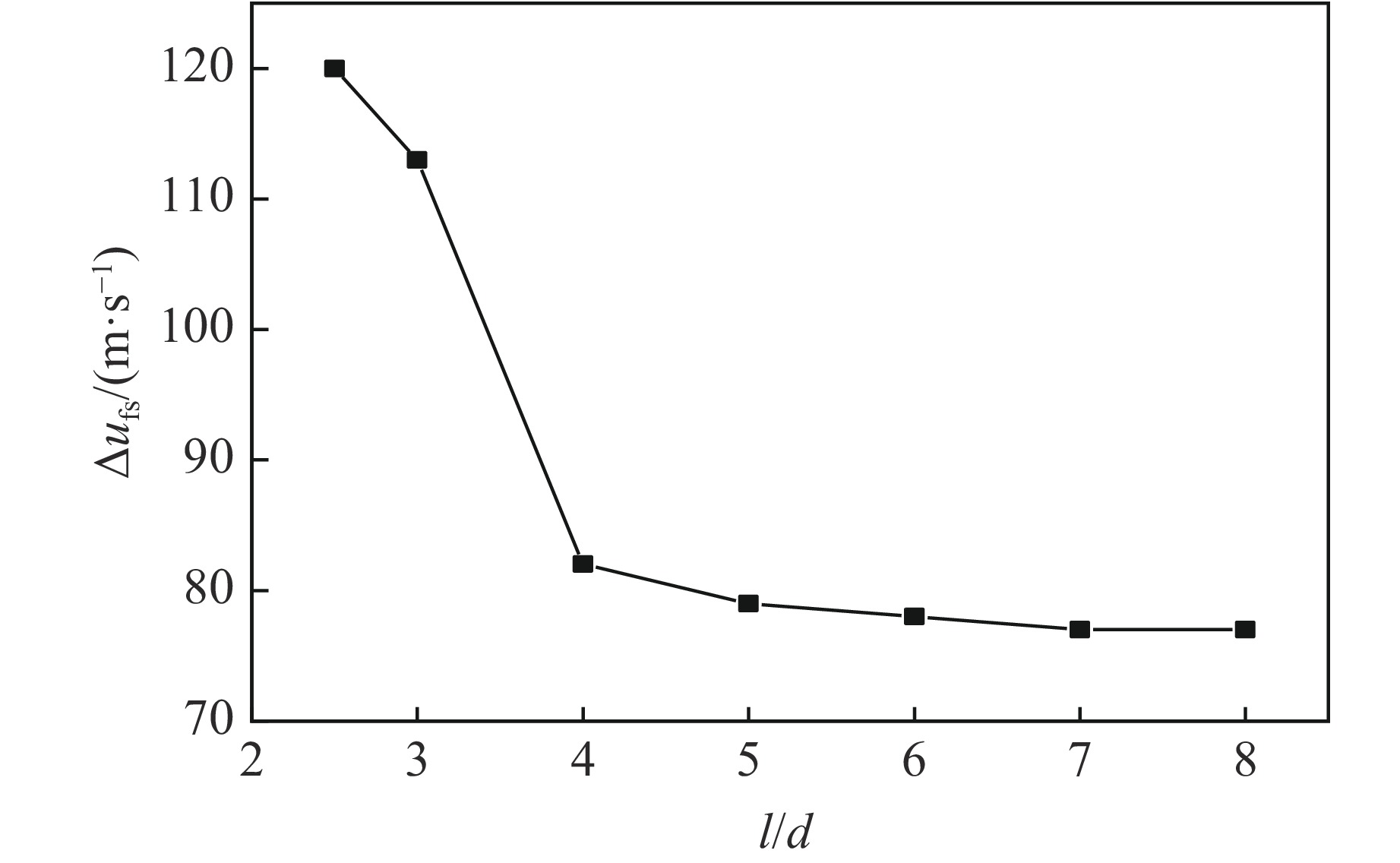
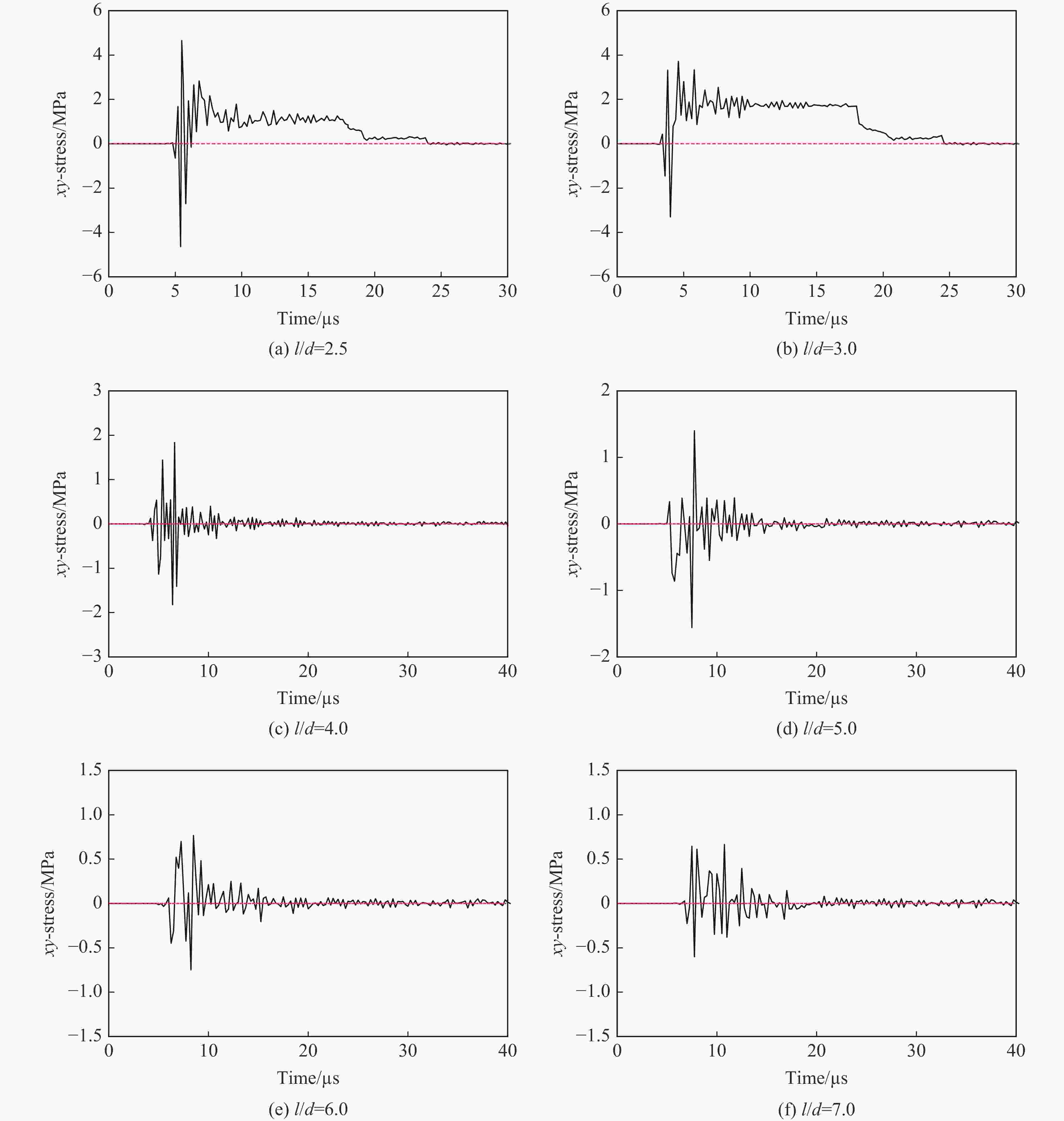
Table 5. Statistical analysis of numerical simulation of Taylor rods with different aspect ratios
l/d $\Delta {u_{\rm{fs}}} $/(m·s−1) Expansion area Lateral stress tend to zero Stress state 2.5 120 No No Three-dimensional 3.0 113 No No Three-dimensional 4.0 82 Yes Yes One-dimensional 5.0 79 Yes Yes One-dimensional 6.0 78 Yes Yes One-dimensional 7.0 77 Yes Yes One-dimensional 8.0 77 Yes Yes One-dimensional
下载: 导出CSV
表 6 不同应力场下的应力状态参数
Table 6. Stress state parameter values under different stress fields
Loading method Principal stress component σ* σ1 σ2 σ3 Three directions equal pull σ σ σ Positive infinity Three directions unequal pull σ σ 0.5σ 1.67 Two way equal pull σ σ 0 0.67 Uniaxial tension σ 0 0 0.33 Torsion σ 0 –σ 0 Uniaxial compression 0 0 –σ –0.33 Two-direction equal pressure 0 –σ –σ –0.67 Three-direction unequal pressure –0.5σ –σ –σ –1.67 Three-direction uniform pressure –σ –σ –σ Negative infinity
下载: 导出CSV
表 7 不同撞击速度下超高强度钢Taylor杆的变形及断裂情况
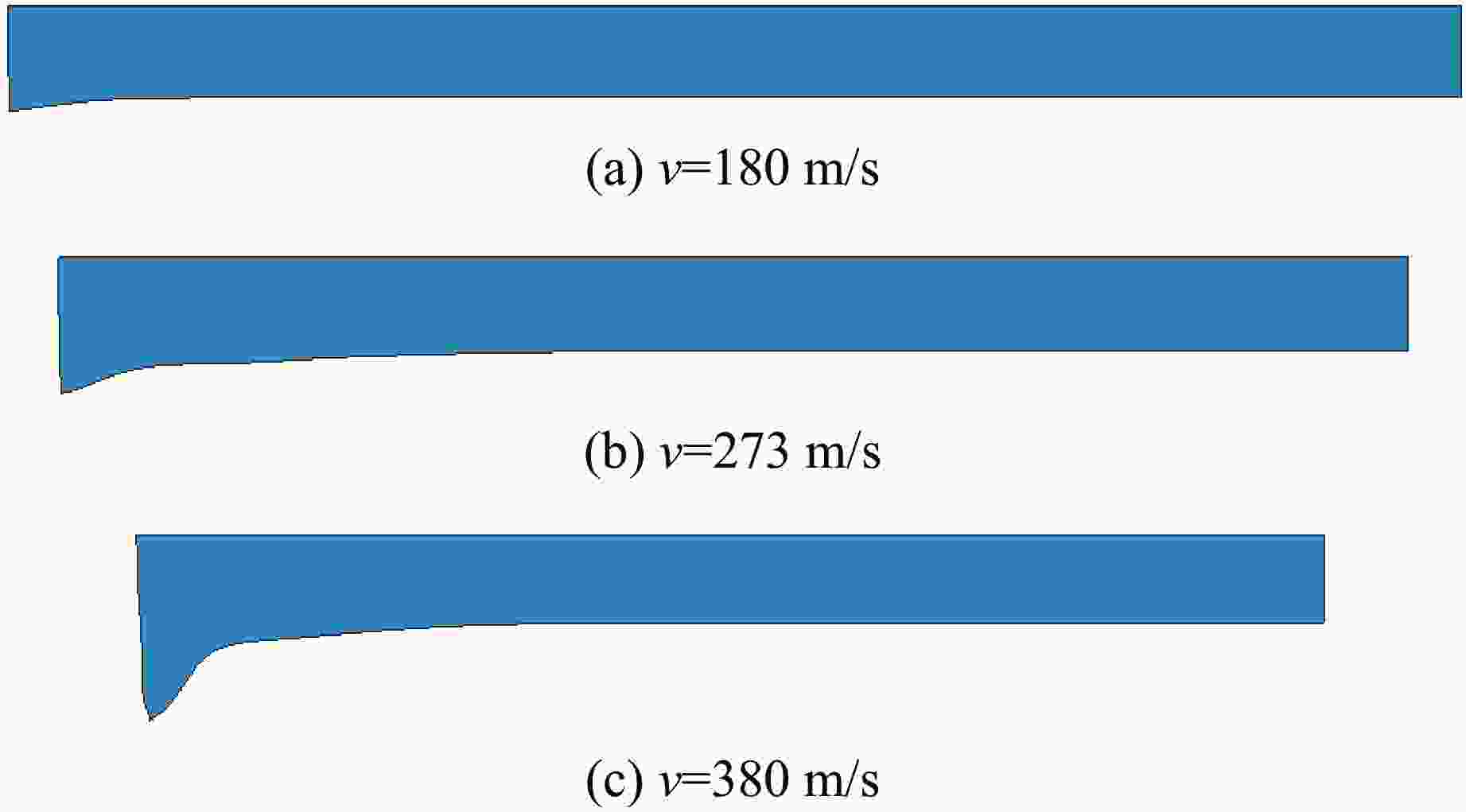
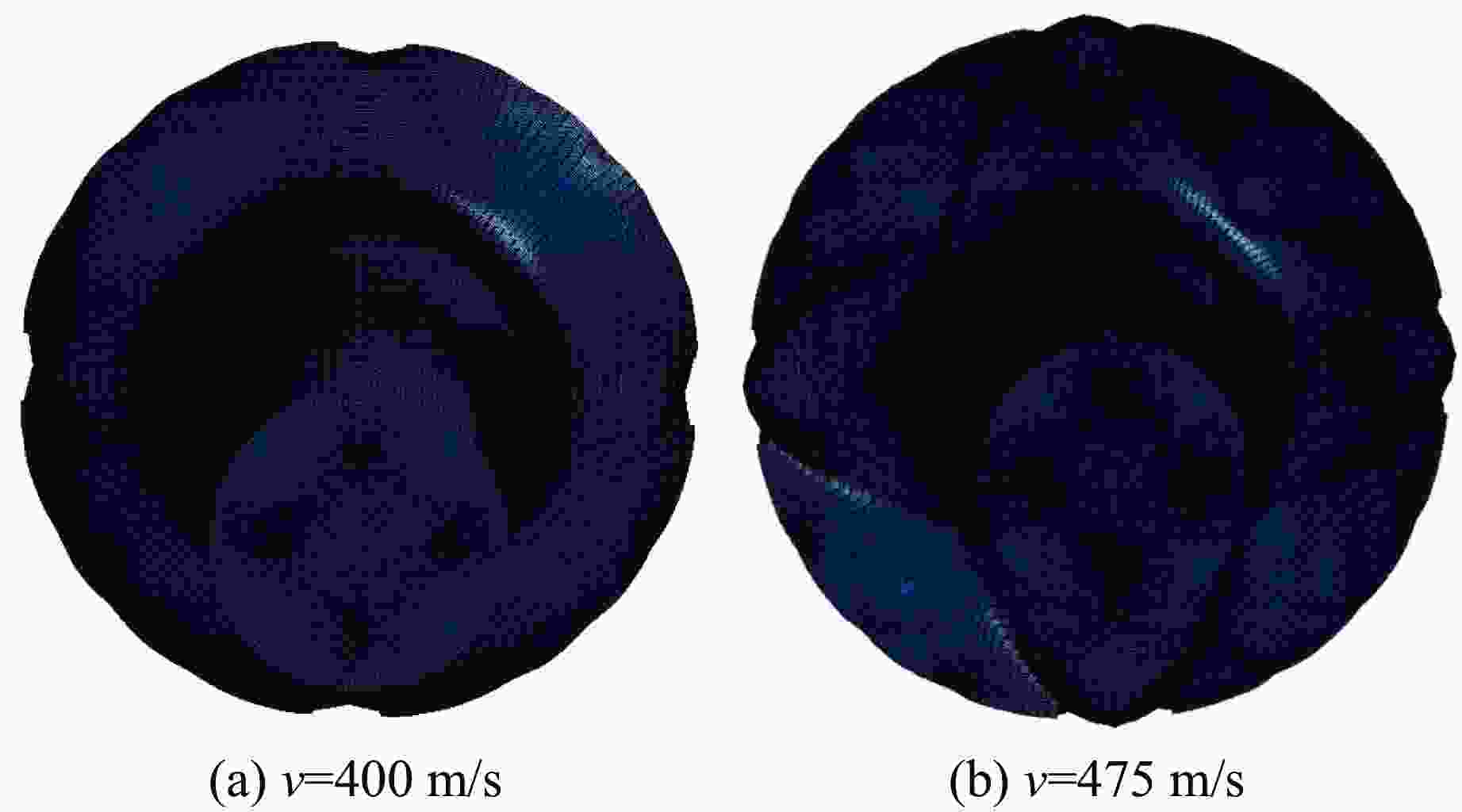
Table 7. Deformation and fracture modes of Taylor rod with ultra-high strength steel under different impact velocities
v/(m·s−1) d0/mm l0/mm df/mm lf/mm Deformation and fracture modes 180 5 40.0 6.20 37.80 Slight deformation 230 5 40.0 7.20 36.60 Upsetting 273 5 40.0 7.70 36.30 Upsetting 350 5 40.0 9.60 33.95 Upsetting 380 5 40.0 10.63 33.00 Upsetting 400 5 40.0 11.30 32.35 Mushroom shaped deformation 450 5 40.0 12.92 30.58 Mushroom shaped deformation 475 5 40.0 13.84 29.81 Mushroom shaped deformation 500 5 40.0 14.01 28.95 Petal shaped cracking 550 5 40.0 27.08 Petal shaped cracking 610 5 40.0 21.03 Petal shaped cracking
下载: 导出CSV
-
[1] 余万千, 郁锐, 崔世堂. 考虑应力三轴度影响的30CrMnSiNi2A钢韧性断裂研究 [J]. 爆炸与冲击, 2021, 41(3): 031404. doi: 10.11883/bzycj-2020-0334YU W Q, YU R, CUI S T, et al. On ductile fracture of 30CrMnSiNi2A steel considering effects of stress triaxiality [J]. Explosion and Shock Waves, 2021, 41(3): 031404. doi: 10.11883/bzycj-2020-0334 [2] 李磊, 张先锋, 吴雪, 等. 不同硬度30CrMnSiNi2A钢的动态本构与损伤参数 [J]. 高压物理学报, 2017, 31(3): 239–248. doi: 10.11858/gywlxb.2017.03.005LI L, ZHANG X F, WU X, et al. Dynamic constitutive and damage parameters of 30CrMnSiNi2A steel with different hardnesses [J]. Chinese Journal of High Pressure Physics, 2017, 31(3): 239–248. doi: 10.11858/gywlxb.2017.03.005 [3] 陈刚, 陈忠富, 陶俊林, 等. 45钢动态塑性本构参量与验证 [J]. 爆炸与冲击, 2005, 25(5): 451–456. doi: 10.3321/j.issn:1001-1455.2005.05.010CHEN G, CHEN Z F, TAO J L, et al. Investigation and validation on plastic constitutive parameters of 45 steel [J]. Explosion and Shock Waves, 2005, 25(5): 451–456. doi: 10.3321/j.issn:1001-1455.2005.05.010 [4] 陈刚, 陈忠富, 徐伟芳, 等. 45钢的J-C损伤失效参量研究 [J]. 爆炸与冲击, 2007, 27(2): 131–135. doi: 10.3321/j.issn:1001-1455.2007.02.007CHEN G, CHEN Z F, XU W F, et al. Investigation on the J-C ductile fracture parameters of 45 steel [J]. Explosion and Shock Waves, 2007, 27(2): 131–135. doi: 10.3321/j.issn:1001-1455.2007.02.007 [5] JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates, and high temperatures [C]//Proceedings of the Seventh International Symposium on Ballistics. The Hague, Netherlands, 1983: 541−547. [6] JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures [J]. Engineering Fracture Mechanics, 1985, 21(1): 31–48. doi: 10.1016/0013-7944(85)90052-9 [7] CHEN X W, CHEN G, ZHANG F J. Deformation and failure modes of soft steel projectiles impacting harder steel targets at increasing velocity [J]. Experimental Mechanics, 2008, 48(3): 335–354. doi: 10.1007/s11340-007-9110-4 [8] 黄魏银, 陈刚, 李俊承, 等. 半球头和平头试件的泰勒撞击 [J]. 高压物理学报, 2021, 35(3): 034204. doi: 10.11858/gywlxb.20200643HUANG W Y, CHEN G, LI J C, et al. Hemispherical and flat head cylindrical specimen Taylor impact [J]. Chinese Journal of High Pressure Physics, 2021, 35(3): 034204. doi: 10.11858/gywlxb.20200643 [9] 沈子楷, 戴湘晖, 王可慧, 等. Taylor撞击塑性变形的尺寸效应研究 [J]. 振动与冲击, 2023, 42(17): 86–95.SHEN Z K, DAI X H, WANG K H, et al. Size effect of Taylor impact plastic deformation [J]. Journal of Vibration and Shock, 2023, 42(17): 86–95. [10] TENG X, WIERZBICKI T, HIERMAIER S, et al. Numerical prediction of fracture in the Taylor test [J]. International Journal of Solids and Structures, 2005, 42(9/10): 2929–2948. [11] TENG X Q, WIERZBICKI T. Effect of fracture criteria on high velocity perforation of thin beams [J]. International Journal of Computational Methods, 2004, 1(1): 171–200. doi: 10.1142/S0219876204000058 [12] GAUTAM S S, BABU R, DIXIT P M. Ductile fracture simulation in the Taylor rod impact test using continuum damage mechanics [J]. International Journal of Damage Mechanics, 2011, 20(3): 347–369. doi: 10.1177/1056789509357119 [13] VON KARMAN T, DUWEZ P. The propagation of plastic deformation in solids [J]. Journal of Applied Physics, 1950, 21(10): 987–994. [14] ROHR I, NAHME H, THOMA K. Material characterization and constitutive modelling of ductile high strength steel for a wide range of strain rates [J]. International Journal of Impact Engineering, 2005, 31(4): 401–433. [15] 武海军, 姚伟, 黄风雷, 等. 超高强度钢30CrMnSiNi2A动态力学性能实验研究 [J]. 北京理工大学学报, 2010, 30(3): 258–262.WU H J, YAO W, HUANG F L, et al. Experimental study on dynamic mechanical properties of ultrahigh strength 30CrMnSiNi2A steel [J]. Transactions of Beijing Institute of Technology, 2010, 30(3): 258–262. [16] TAYLOR G I. The use of flat-ended projectiles for determining dynamic yield stress Ⅰ. theoretical considerations [J]. Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences, 1948, 194(1038): 289–299. [17] JOHNSON G R, HOLMQUIST T J. Evaluation of cylinder-impact test data for constitutive model constants [J]. Journal of Applied Physics, 1988, 64(8): 3901–3910. [18] ALLEN D J, RULE W K, JONES S E. Optimizing material strength constants numerically extracted from Taylor impact data [J]. Experimental Mechanics, 1997, 37(3): 333–338. doi: 10.1007/BF02317427 [19] JONES S E, GILLIS P P, FOSTER JR J C, et al. A one-dimensional, two-phase flow model for Taylor impact specimens [J]. Journal of Engineering Materials and Technology, 1991, 113(2): 228–235. [20] 王习术. 材料力学行为试验与分析 [M]. 北京: 清华大学出版社, 2010.WANG X S. Test and analysis on mechanical behavior of materials [M]. Beijing: Tsinghua University Press, 2010. [21] 李庆芬. 断裂力学及其工程应用 [M]. 哈尔滨: 哈尔滨工程大学出版社, 2005: 17−29.LI Q F. Fracture mechanics and its engineering applications [M]. Harbin: Harbin Engineering University Press, 2005: 17−29. [22] 郑长卿. 金属韧性破坏的细观力学及其应用研究 [M]. 北京: 国防工业出版社, 1995.ZHENG C Q. Study on the micromechanics and application of metal toughness failure [M]. Beijing: National Defense Industry Press, 1995. [23] 马向宇. 基于应力状态的金属材料变形行为研究 [D]. 太原: 太原科技大学, 2013.MA X Y. Research on deformation behavior of metal materials based on stress state [D]. Taiyuan: Taiyuan University of Science and Technology, 2013. -
下载:
点击查看大图
计量
- 文章访问数: 85
- HTML全文浏览量: 29
- PDF下载量: 13
