Adiabatic Shear Failure Behavior of 30CrMnMo Steel under Pulse Stress Impact
-
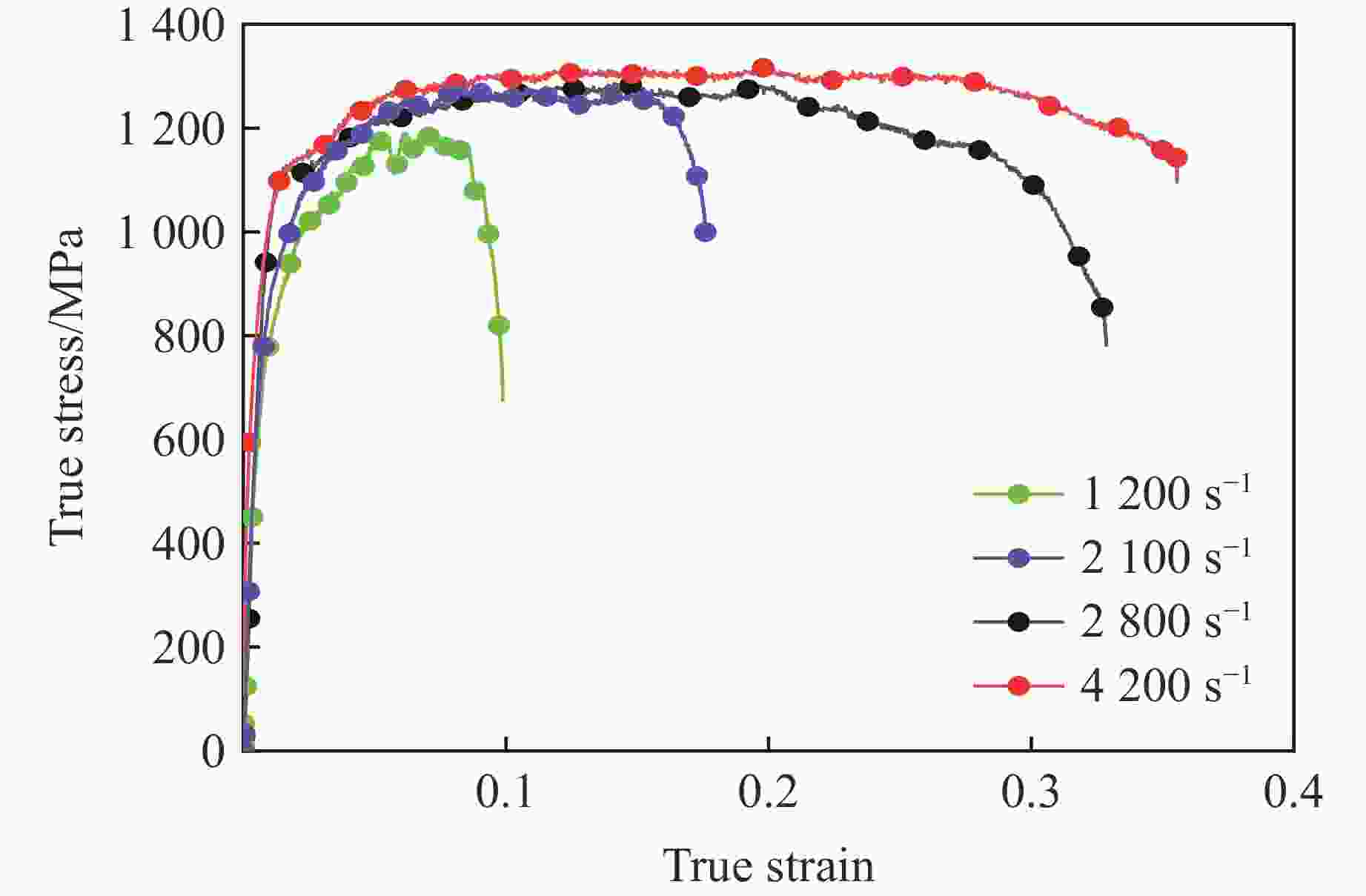
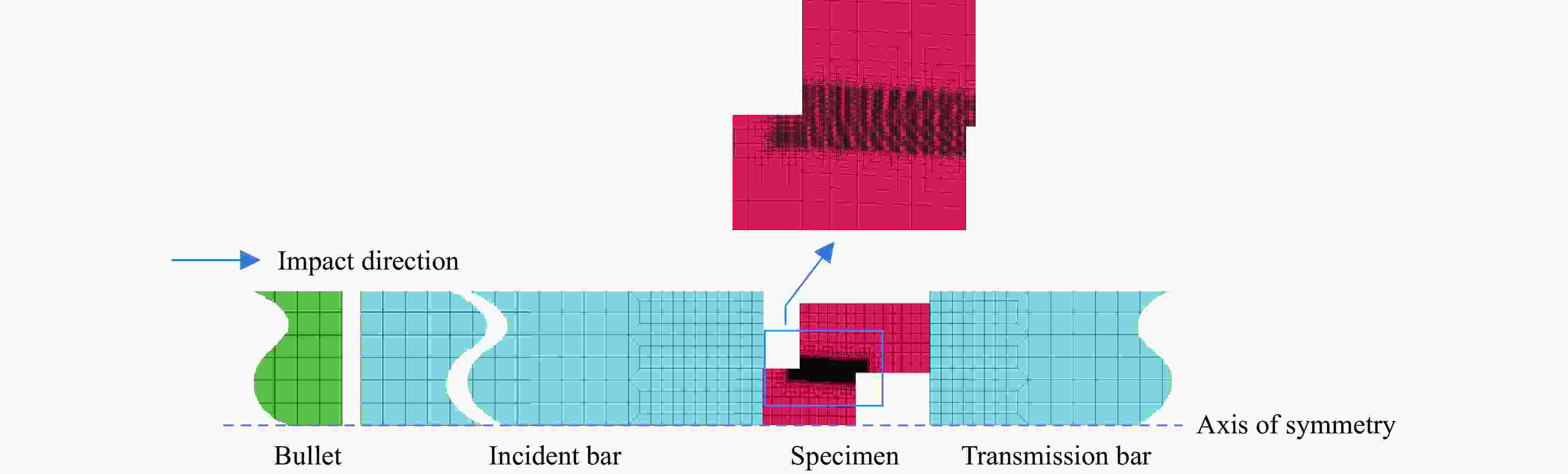
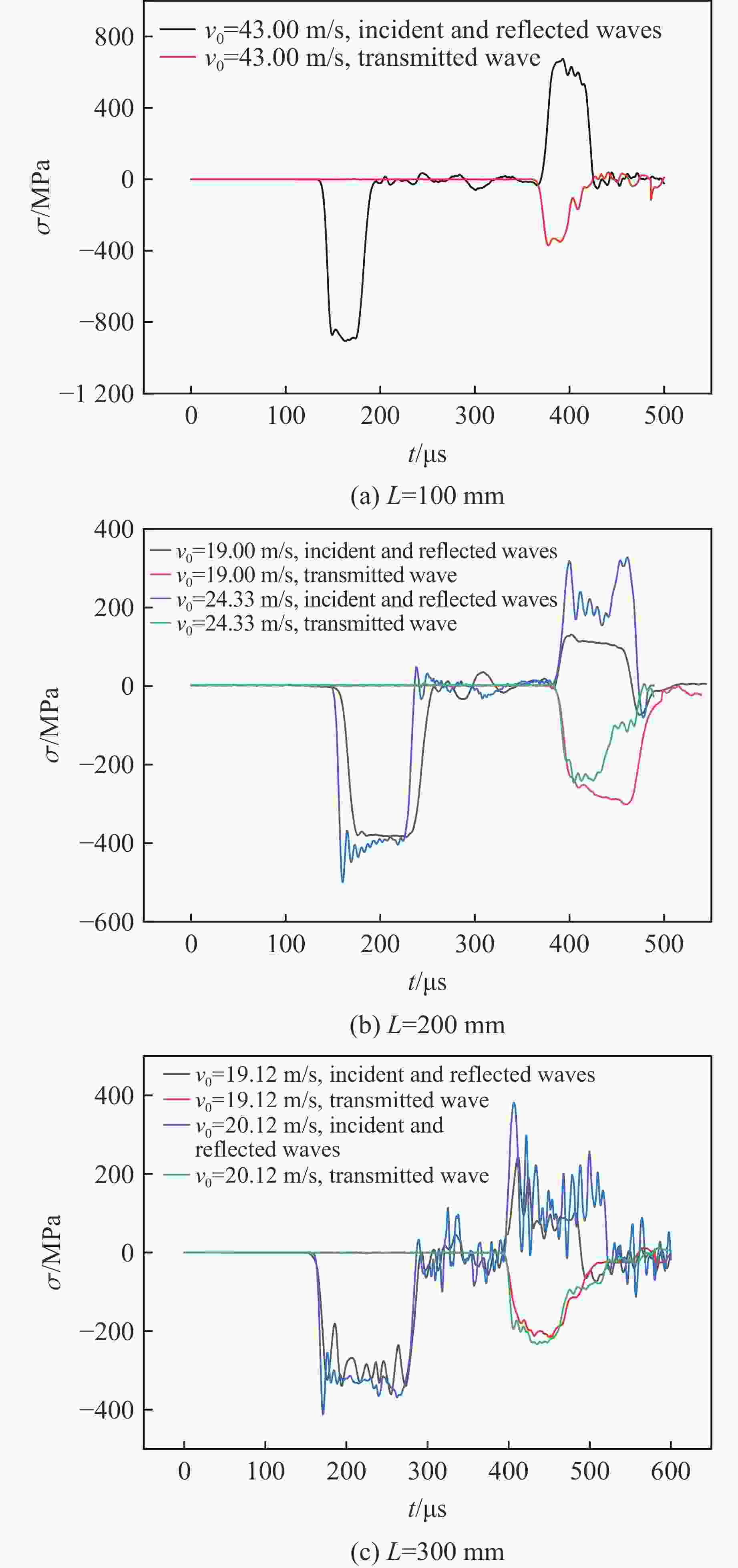
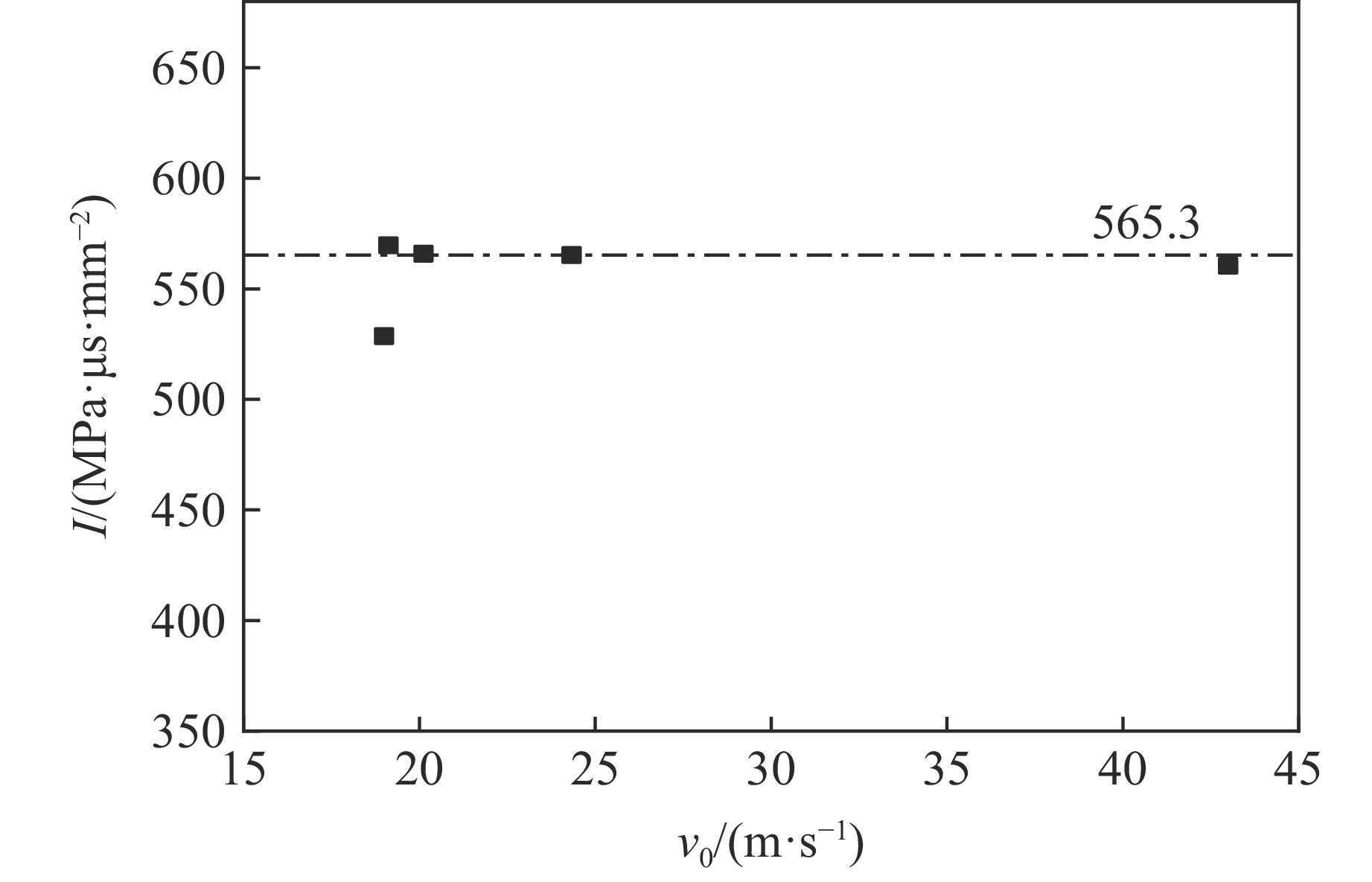
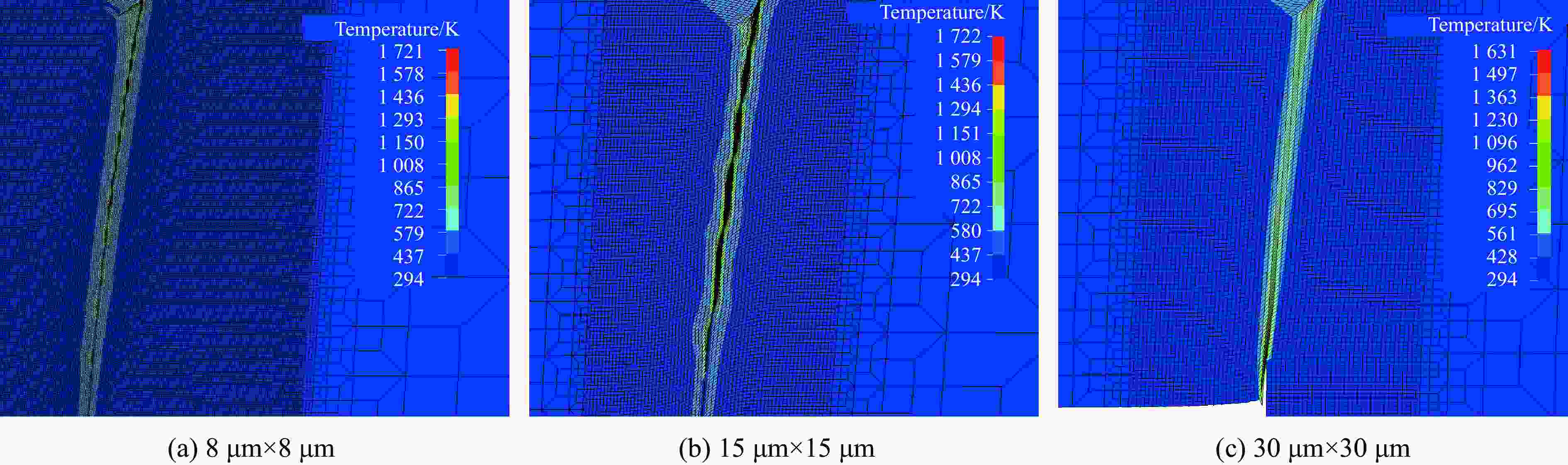
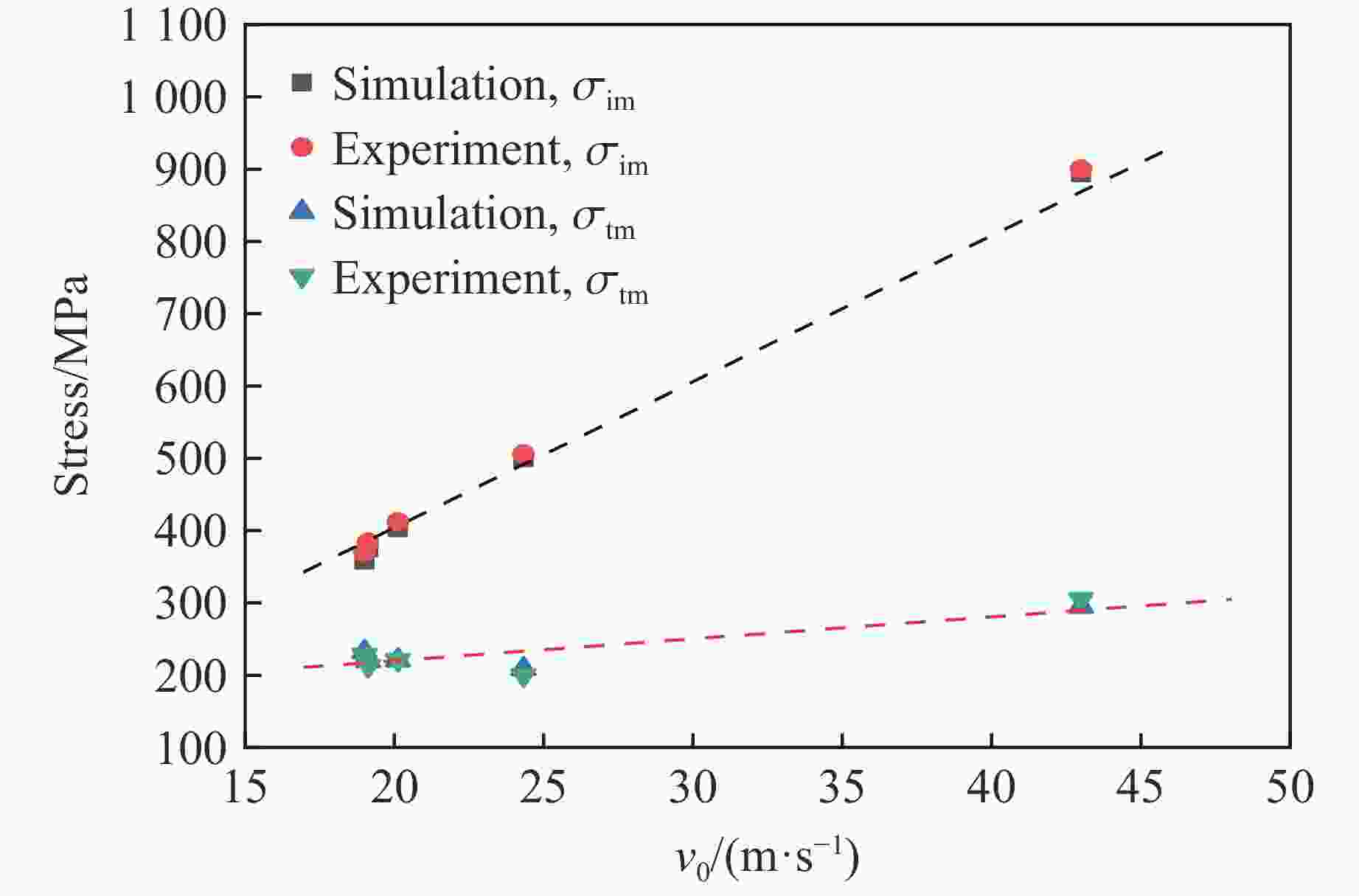
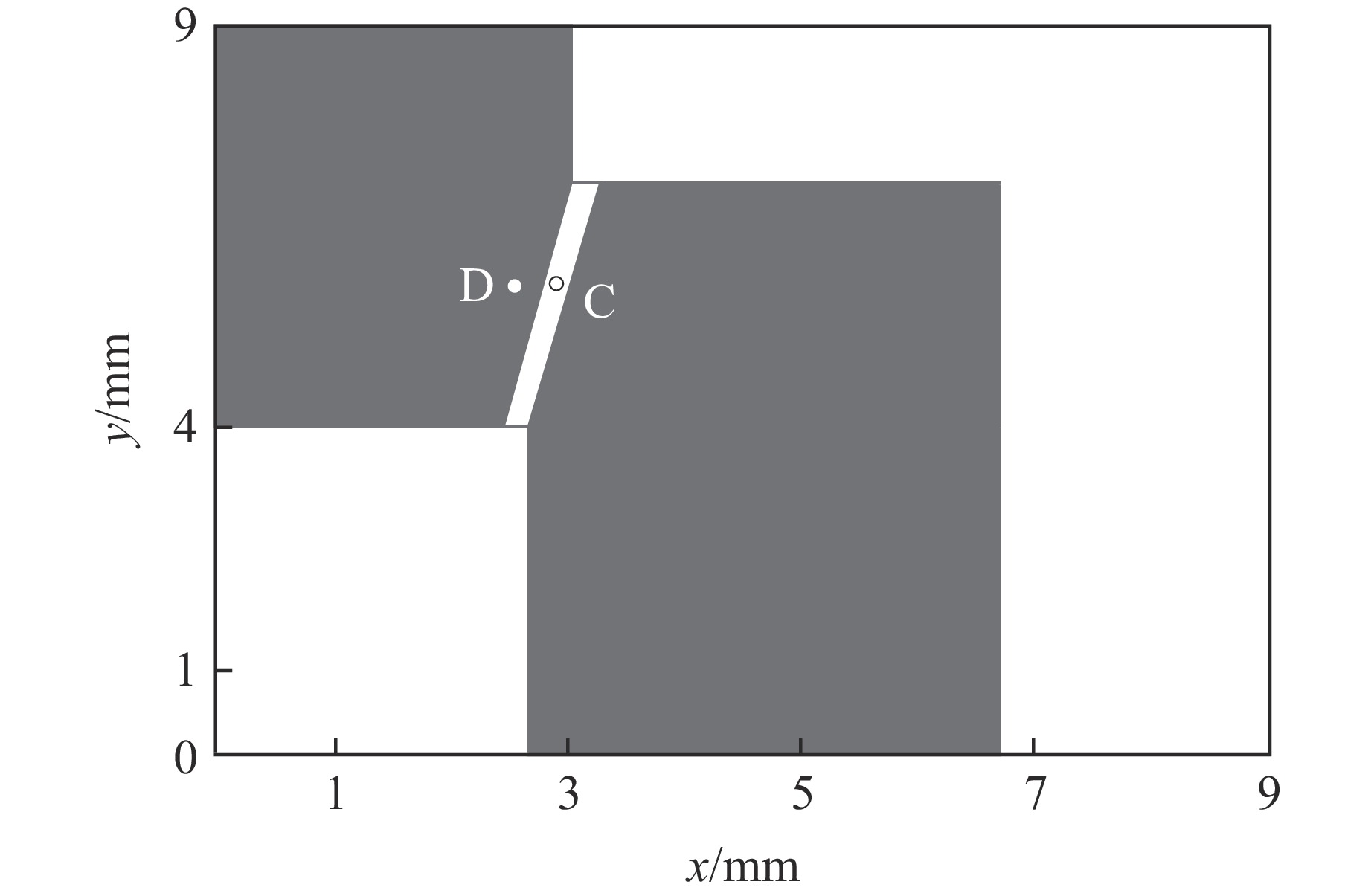
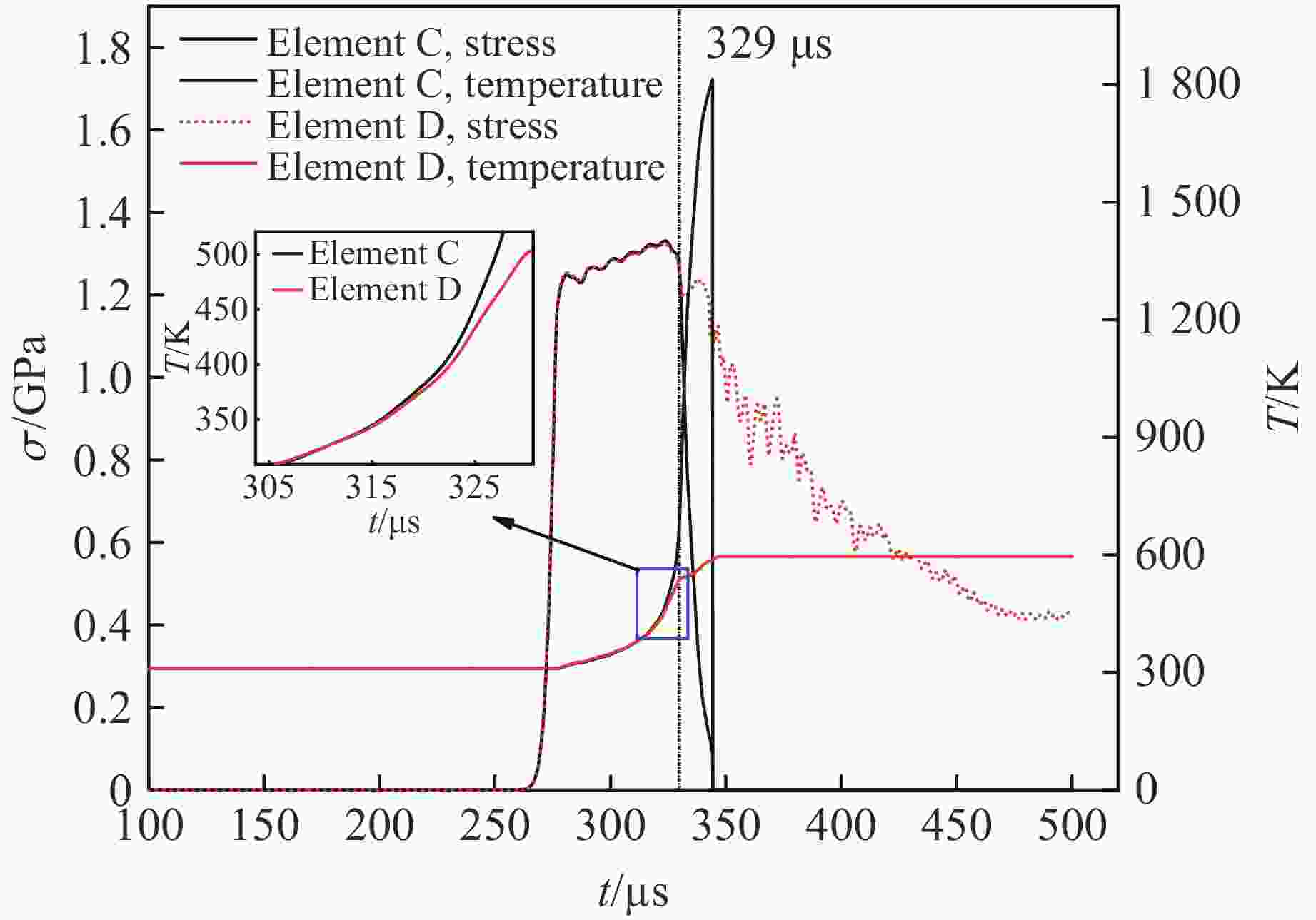
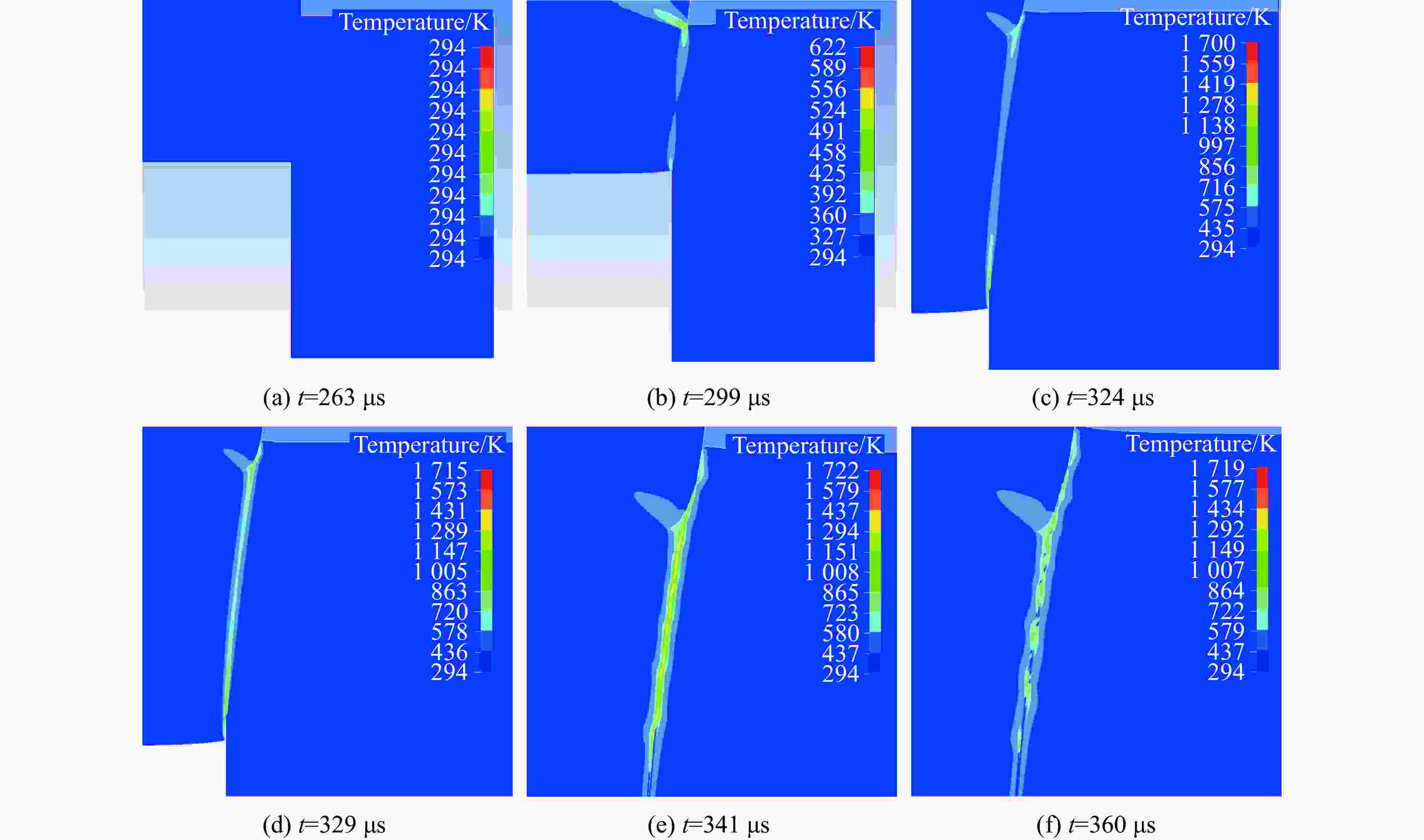
摘要: 为研究30CrMnMo钢在脉冲应力冲击载荷下的绝热剪切失效及演化特性，利用分离式霍普金森压杆对一种轴对称帽型试件进行冲击剪切实验，并运用LS-DYNA动力学有限元软件对不同入射脉冲应力载荷下的剪切失效演化及剪切区温度分布进行数值模拟。结果表明，帽型试件的绝热剪切失效与脉冲应力比冲量相关，对于30CrMnMo钢帽型试件，其绝热剪切失效对应的脉冲应力比冲量近似为常量。数值模拟中，当网格尺寸小于剪切带宽度时，能够有效模拟剪切带内的局部温升热点特性。绝热剪切演化表现为失稳由帽型试件剪切区拐角处启动并同时向中心传播，剪切带内外材料主要经历均匀剪切变形和失稳快速扩展2个阶段。Abstract: In order to study the adiabatic shear failure behavior and evolution characteristics of 30CrMnMo steel under pulse stress impact, a split Hopkinson pressure bar was used to conduct an axisymmetric cap shaped specimen for impact shear experiments. The shear failure evolution and temperature distribution in the shear zone under different incident pulse stress loads were numerically simulated using LS-DYNA dynamic finite element software. The results indicate that the adiabatic shear failure of the cap shaped specimen is related to the specific impulse of the pulse stress. For cap shaped specimen of 30CrMnMo steel, the specific impulse of pulse stress corresponding to the adiabatic shear failure is approximately constant. In numerical simulation, when the grid size is smaller than the width of the shear band, the local temperature rise of hot spot within the shear band can be effectively simulated. The evolution of adiabatic shear instability is characterized by simultaneous propagation from the corner of the shear zone to the center, and the materials inside and outside the shear zone mainly undergo two stages: uniform shear deformation and rapid expansion of instability.
-
图 2 30CrMnMo钢的动态真应力-真应变曲线
Figure 2. Dynamic true stress-strain curves of 30CrMnMo steel
图 3 帽型试件SHPB冲击剪切夹持端状态
Figure 3. State of the SHPB impact shear clamping end of the cap shaped specimen
图 4 不同长度子弹撞击产生的脉冲应力波形
Figure 4. Pulse stress waveforms generated by bullet impacts of different lengths
图 5 不同速度冲击时帽型试件的脉冲应力比冲量
Figure 5. Pulse stress specific impulse of hat shaped specimens under different impact velocities
图 6 采用不同网格尺寸模拟的绝热剪切带的温度云图
Figure 6. Temperature nephogram of simulated adiabatic shear bands with different grid sizes
图 7 脉冲应力幅值-撞击速度曲线的模拟结果与实验结果的对比
Figure 7. Comparison of simulation and experimental results of pulse stress amplitude-impact velocity curves
图 9 典型单元的等效应力及温度随时间变化曲线
Figure 9. Variations of equivalent stress and temperature of typical elements with time
图 11 绝热剪切带形成过程中典型时刻的温度云图
Figure 11. Temperature nephogram at typical moments during the formation of adiabatic shear bands
表 1 帽型试件的冲击剪切实验
Table 1. Impact shear experiment on cap shaped specimens
Case L/mm v0/(m·s−1) σim/MPa Δt/μs ts/μs As/mm2 I/(MPa·μs·mm−2) 1 100 43.00 900 39 34 54.6 560.4 2 200 19.00 370 77 54.6 528.6 3 200 24.33 506 77 61 54.6 565.3 4 300 19.12 384 115 81 54.6 569.7 5 300 20.12 412 115 75 54.6 565.9 
下载: 导出CSV
表 2 采用3种网格尺寸模拟得到的剪切区
Table 2. Results of shear zone simulated with three grid sizes
Mesh size/(μm×μm) Calculation time/h Data file/GB CPU number ASB formation 8×8 90.00 180 8 Yes 15×15 1.36 54 8 Yes 30×30 0.24 30 8 Yes
下载: 导出CSV
-
[1] KURIYAMA S, MEYERS M A. Numerical modeling of the propagation of an adiabatic shear band [J]. Metallurgical Transactions A, 1986, 17(3): 443–450. doi: 10.1007/BF02643951 [2] BONNET-LEBOUVIER A S, MOLINARI A, LIPINSKI P, et al. Analysis of the dynamic propagation of adiabatic shear bands [J]. International Journal of Solids and Structures, 2002, 39(16): 4249–4269. doi: 10.1016/S0020-7683(02)00244-5 [3] MEDYANIK S N, LIU W K, LI S F. On criteria for dynamic adiabatic shear band propagation [J]. Journal of the Mechanics and Physics of Solids, 2007, 55(7): 1439–1461. doi: 10.1016/j.jmps.2006.12.006 [4] TENG X, WIERZBICKI T, COUQUE H. On the transition from adiabatic shear banding to fracture [J]. Mechanics of Materials, 2007, 39(2): 107–125. doi: 10.1016/j.mechmat.2006.03.001 [5] 付应乾, 董新龙. 帽型试样动态绝热剪切破坏演化分析 [J]. 固体力学学报, 2015, 36(5): 392–400. doi: 10.19636/j.cnki.cjsm42-1250/o3.2015.05.004FU Y Q, DONG X L. Study of evolution of adiabatic shear failure in hat-shaped specimen under dynamic loading [J]. Chinese Journal of Solid Mechanics, 2015, 36(5): 392–400. doi: 10.19636/j.cnki.cjsm42-1250/o3.2015.05.004 [6] GUO Y Z, RUAN Q C, ZHU S X, et al. Dynamic failure of titanium: temperature rise and adiabatic shear band formation [J]. Journal of the Mechanics and Physics of Solids, 2020, 135: 103811. doi: 10.1016/j.jmps.2019.103811 [7] ZHU S X, GUO Y Z, CHEN H S, et al. Formation of adiabatic shear band within Ti-6Al-4V: effects of stress state [J]. Mechanics of Materials, 2019, 137: 103102. doi: 10.1016/j.mechmat.2019.103102 [8] 王财源, 余丰. 复杂应力状态下GCr15轴承钢的动态剪切及熔融特性研究 [J]. 力学季刊, 2022, 43(1): 84–92. doi: 10.15959/j.cnki.0254-0053.2022.01.009WANG C Y, YU F. Research on dynamic shearing and melting characteristics of GCr15 bearing steel under complex stress state [J]. Chinese Quarterly of Mechanics, 2022, 43(1): 84–92. doi: 10.15959/j.cnki.0254-0053.2022.01.009 [9] MEYER L W, MANWARING S. Critical adiabatic shear strength of low alloyed steel under compressive loading [M]//MURR L E, STAUDHAMMER K P, MEYERS M A. Metallurgical Applications of Shock Wave and High-Strain-Rate Phenomena. New York: Marcel Dekker Inc., 1985: 657–674. [10] 王礼立. 应力波基础 [M]. 2版. 北京: 国防工业出版社, 2005.WANG L L. Foundation of stress waves [M]. 2nd ed. Beijing: National Defense Industry Press, 2005. [11] 杨扬, 程信林. 绝热剪切的研究现状及发展趋势 [J]. 中国有色金属学报, 2002, 12(3): 401–408. doi: 10.3321/j.issn:1004-0609.2002.03.001YANG Y, CHENG X L. Current status and trends in researches on adiabatic shearing [J]. The Chinese Journal of Nonferrous Metals, 2002, 12(3): 401–408. doi: 10.3321/j.issn:1004-0609.2002.03.001 [12] TRESCA M H. On further applications of the flow of solids [J]. Proceedings of the Institution of Mechanical Engineers, 1878, 29(1): 301–345. doi: 10.1243/PIME_PROC_1878_029_017_02 [13] RULE W K, JONES S E. A revised form for the Johnson-Cook strength model [J]. International Journal of Impact Engineering, 1998, 21(8): 609–624. doi: 10.1016/S0734-743X(97)00081-X [14] BØRVIK T, DEY S, CLAUSEN A H. Perforation resistance of five different high-strength steel plates subjected to small-arms projectiles [J]. International Journal of Impact Engineering, 2009, 36(7): 948–964. doi: 10.1016/j.ijimpeng.2008.12.003 [15] 周刚毅. TA2钛合金绝热剪切破坏特性及应力状态、晶粒度影响 [D]. 宁波: 宁波大学, 2018.ZHOU G Y. Adiabatic shearing behavior of TA2 titanium alloy and its influence of stress state, grain size [D]. Ningbo: Ningbo University, 2018. [16] LI J R, YU J L, WEI Z G. Influence of specimen geometry on adiabatic shear instability of tungsten heavy alloys [J]. International Journal of Impact Engineering, 2003, 28(3): 303–314. doi: 10.1016/S0734-743X(02)00022-2 [17] WEI Z G, YU J L, LI J, et al. Influence of stress condition on adiabatic shear localization of tungsten heavy alloys [J]. International Journal of Impact Engineering, 2001, 26(1): 843–852. [18] RANC N, TARAVELLA L, PINA V, et al. Temperature field measurement in titanium alloy during high strain rate loading-adiabatic shear bands phenomenon [J]. Mechanics of Materials, 2008, 40(4/5): 255–270. doi: 10.1016/j.mechmat.2007.08.002 [19] WRIGHT T W, OCKENDON H. A model for fully formed shear bands [J]. Journal of the Mechanics and Physics of Solids, 1992, 40(6): 1217–1226. doi: 10.1016/0022-5096(92)90013-R [20] BRONKHORST C A, CERRETA E K, XUE Q, et al. An experimental and numerical study of the localization behavior of tantalum and stainless steel [J]. International Journal of Plasticity, 2006, 22(7): 1304–1335. doi: 10.1016/j.ijplas.2005.10.002 -
下载:
点击查看大图
计量
- 文章访问数: 62
- HTML全文浏览量: 23
- PDF下载量: 21
