基于数值模拟的SHPB实验数据处理方法

张军徽; 尚兵

doi:10.11858/gywlxb.2016.03.006

Numerical Study of the Data Processing Methods in SHPB Experiments

doi: 10.11858/gywlxb.2016.03.006

ZHANG Jun-Hui^1
,,
SHANG Bing^{2,*
, ,}

1.
School of Civil Engineering, North China University of Technology, Beijing 100144, China
2.
Department of Harbor Engineering, Guangzhou Maritime Institute, Guangzhou 510725, China

Funds:

National Natural Science Foundation of China 11572001

More Information

Author Bio:
ZHANG Jun-Hui(1978—), male, Doctor, lecturer, major in solid mechanics.E-mail:jasonstina@gmail.com

Corresponding author: SHANG Bing(1979—), male, Doctor, lecturer, major in impact mechanics.E-mail:shang@mail.ustc.edu.cn

摘要

摘要: 在分离式霍普金森压杆(SHPB)实验中,可以精确测得加载试件边界上的应力和速度。然而,基于这些测量结果得到一条精确的应力应变曲线有一定难度。根据SHPB实验技术的原理,有3组公式可以处理实验数据,并且3组公式都对波头的选择敏感。由于波动效应的影响以及选择波头的误差,3种方法得到的应力-应变曲线缺乏一致性。为了解决正确对齐波头的问题,编写了三波耦合法的数据处理程序。该方法基于动量守恒,可以得到更可靠的应力-应变曲线。为了证明该方法的正确性,进行SHPB的数值模拟实验。结果显示,利用这种方法可以得到唯一的应力-应变曲线。这种方法可以避免对齐波头时的误差,而传统的两波法或三波法则不能。
- 有限单元法 /
- 分离式霍普金森压杆 /
- 三波耦合法 /
- 数据处理
Abstract: Accurate measurement of the stresses and velocities at the boundaries of a dynamically loaded specimen may be obtained using split Hopkinson pressure bars (SHPB).However, the determination of a representative stress-strain curve based on these measurements can be challenging.According to the principle of SHPB technique, there are three groups of formulae to process the experimental data, and all the formulas are sensitive to time shifting.Due to transient effects and the error of time shifting, the stress-strain curves lack consistency.In order to solve the problem of time shifting, we introduce the three-wave mutual-checking method based on the conservation of momentum and the corresponding data processing program.It is shown that a more reliable stress-strain curve could be obtained using this method.In order to prove the correctness of this curve, numerical simulations of the SHPB experiments were performed.The results show that by using this program, the same result can be obtained by either the three-wave method or the two-wave method, and what matters more is that this method can avoid the error of time shifting which the traditional method cannot.
- finite elements /
- SHPB /
- three-wave mutual-checking method /
- data processing

HTML全文

Figure 1. The schematic diagram of a SHPB setup

下载: 全尺寸图片幻灯片

Figure 2. Loading pressure pulse

下载: 全尺寸图片幻灯片

Figure 3. Strain histories of points B and E in a numerical SHPB test

下载: 全尺寸图片幻灯片

4a. The waves and their relative positions

下载: 全尺寸图片幻灯片

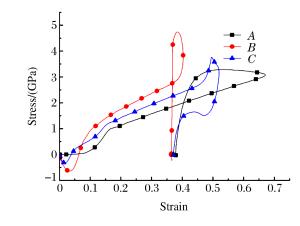
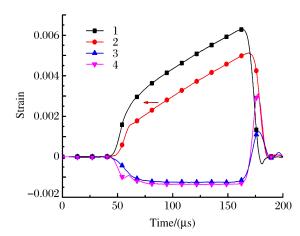
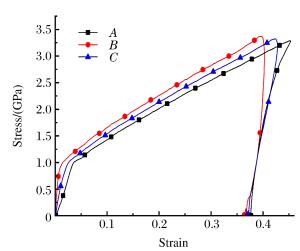
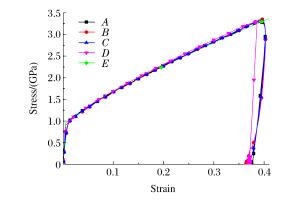
4b. The stress-strain curves obtained from Fig. 4(a)

下载: 全尺寸图片幻灯片

5a. The waves and their relative positions

下载: 全尺寸图片幻灯片

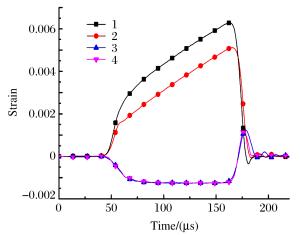
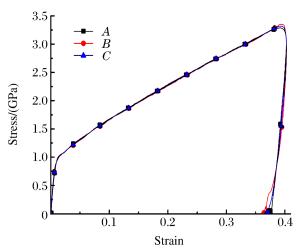
5b. The stress-strain curves obtained from Fig. 5(a)

下载: 全尺寸图片幻灯片

6a. The waves and their relative positions

下载: 全尺寸图片幻灯片

6b. The stress-strain curves obtained from Fig. 6(a)

下载: 全尺寸图片幻灯片

Figure 7. Comparison of stress-strain curves

下载: 全尺寸图片幻灯片

参考文献(15)

[1]	TAI Y S.Uniaxial compression tests at various loading rates for reactive powder concrete[J].Theor Appl Fract Mech, 2009.52(1):14-21. doi: 10.1016/j.tafmec.2009.06.001
[2]	SONG B, CHEN W N, LUK V.Impact compressive response of dry sand[J].Mech Mater, 2009, 41(6):777-785. doi: 10.1016/j.mechmat.2009.01.003
[3]	SHI B, ATTIA M H.Evaluation criteria of the constitutive law formulation for the metal-cutting process[J].J Eng Manufact, 2010, 224(B9):1313-1328. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=6b66a24d0728817b8d988a1843fe5f86
[4]	LEE O S, HWANG S W, CHOI H B, et al.Dynamic deformation of aluminum alloys at high temperature by using SHPB techniques[C]//9th International Conference on the Mechanical and Physical Behaviour of Materials under Dynamic Loading.Brussels, Belgium, 2009: 26-32.
[5]	LEE O S, LEE J Y, KIM G H, et al.High strain-rate deformation of composite materials using a split Hopkinson bar technique[J].Key Eng Mater, 2000, 183:307-312. http://www.scientific.net/KEM.183-187.307
[6]	TRAUTMANN A, SIVIOUR C R, WALLEY S M, et al.Lubrication of polycarbonate at cryogenic temperatures in the split Hopkinson pressure bar[J].Int J Impact Eng, 2005, 31(5):523-544. doi: 10.1016/j.ijimpeng.2004.02.007
[7]	SHAZLY M, PRAKASH V, LERCH B A.High strain-rate behavior of ice under uniaxial compression[J].Int J Solids Struct, 2009, 46(6):1499-1515. doi: 10.1016/j.ijsolstr.2008.11.020
[8]	GRAY G T Ⅲ.Classic split-Hopkinson pressure bar technique.Mechanical testing and evaluation[M].Novelty, OH:ASM, 2000:8-14.
[9]	WANG L L, ZHU J, HU S S.An analysis of stress uniformity for concrete-like specimens during SHPB tests[J].Int J Impact Eng, 2009, 36(1):61-72. doi: 10.1016/j.ijimpeng.2008.04.007
[10]	尚兵, 胡时胜, 姜锡权.金属材料SHPB实验数据处理的三波校核法[J].爆炸与冲击, 2010(4):429-432. http://d.old.wanfangdata.com.cn/Periodical/bzycj201004016 SHANG B, HU S S, JIANG X Q.A three-wave coupling method for data treatment in SHPB experiments with metal samples[J].Explosion and Shock Waves, 2010, 30(4):429-432. http://d.old.wanfangdata.com.cn/Periodical/bzycj201004016
[11]	FREW D J, FORRESTAL M J, CHEN W.Pulse shaping techniques for testing brittle materials with a split Hopkinson pressure bar[J].Exp Mech, 2002, 42(1):93-106. doi: 10.1007/BF02411056
[12]	FREW D J, FORRESTAL M J, CHEN W.A split Hopkinson pressure bar technique to determine compressive stress-strain data for rock materials[J].Exp Mech, 2001, 41(1):40-46. doi: 10.1007/BF02323102
[13]	LI Q M, MENG H.About the dynamic strength enhancement of concrete-like materials in a split Hopkinson pressure bar test[J].Int J Solids Struct, 2003, 40(2):343-360. doi: 10.1016/S0020-7683(02)00526-7
[14]	HUA Z, ZHU W H, WANG G D.The study of numerical character for femtosecond pulse shaping[J].Chinese Physics, 2007, 16(11):3429-3433. doi: 10.1088/1009-1963/16/11/047
[15]	CHEN W, SONG B.Split Hopkinson (Kolsky) bar:Desing, testing and applications[M].New York:Springer, 2011:22-36.