Interaction Effect of Two Ellipse Richtmyer-Meshkov Flows
-
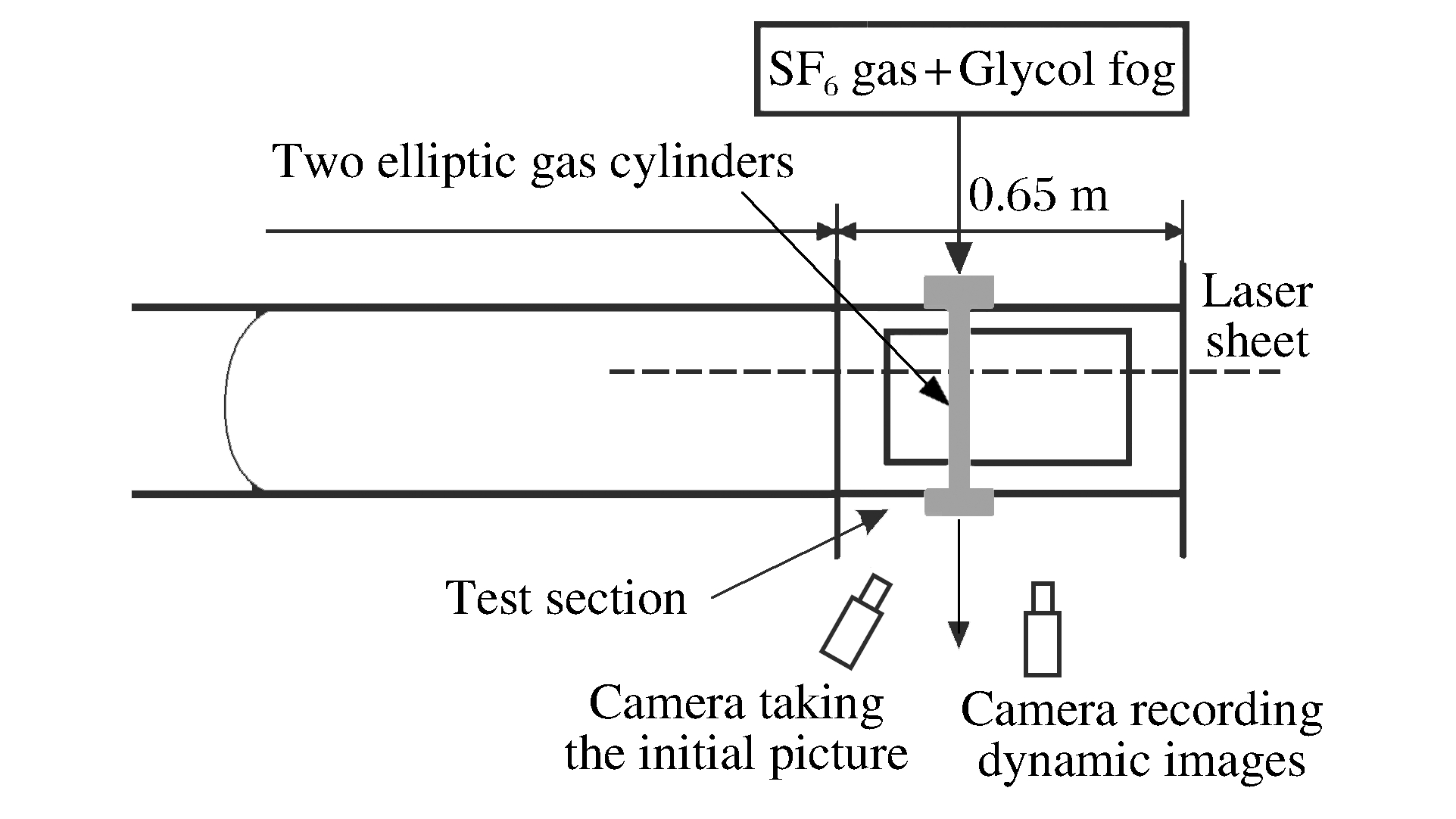
摘要: 实验研究了在马赫数为1.18的平面激波冲击作用下，双椭圆界面Richtmyer-Meshkov不稳定性演化的动力学过程。椭圆短轴b与入射激波方向垂直，通过改变双椭圆的中心间距d，采用片光高速摄影和PIV(粒子图像测速)技术，观测了4种不同情形的演化模态，获得了界面演化多幅像和700 μs时刻的速度场，分析了双椭圆气柱之间的相互干扰效应。当d/b为4.0或3.0时，相互干扰效应较弱，双椭圆气柱演化为两个反向旋转的对涡，速度极大值接近30 m/s，出现在2个位置，速度最小值几乎为零，出现在4个位置。当d/b为2.0或1.2时，相互干扰效应很强，两个内涡完全消失，双椭圆气柱演化为一个反向旋转的涡对结构, 速度极大值出现在4个位置，速度极小值出现在两个位置。d/b =2.0时，界面演化图像与圆形气柱演化过程类似。相比d/b =2.0的情形，d/b =1.2时产生更大的斜压涡量，界面演化发展更快，后期出现二次涡现象和分叉结构，整体结构类似于单椭圆气柱演化过程。当d/b在2.0~3.0之间变化时，存在一个是否形成两个内涡的非线性临界值。针对双气柱界面演化明显的内涡弱化现象，分析了4种可能的机制。
-
关键词:
- 双椭圆界面 /
- Richtmyer-Meshkov不稳定性 /
- 高速摄影 /
- 粒子图像测速技术
Abstract: The dynamic evolution process and velocity field of two elliptic heavy-gas (SF6) cylinders accelerated by a planar shock wave are studied by laser-sheet high-speed photograph and PIV (particle image velocimetry) diagnostics techniques, respectively.The minor axes (b) of the elliptic cross-sections are aligned perpendicular to the shock direction.While the cylinder dimensions are fixed, we adjust the center-to-center separation (d) between the cylinders.The flow morphologies are visualized and the interaction effect between cylinders is analyzed.When d/b equals 4.0 or 3.0, the two elliptical cylinders roll up into 2 counter-rotating vortex pairs and the interaction is weak.The maximal velocity appears at 2 positions and its magnitude is close to 30 m/s, while the minimal velocity is close to zero and arises at 4 positions.Whend/b decreases to 2.0 or 1.2, due to the strong interaction of the two inner vortices, the inner structure completely disappears and the flow morphology evolves into a counter-vortex pair.The maximal velocity occurs at 4 locations, while the minimal velocity only appears at 2 positions.For the d/b =2.0 case, the evolving images assemble those of the single circular cylinder except for the small gap in the middle.Compared with the d/b =2.0 case, larger amount of baroclinic vorticity is produced in the d/b =1.2 case, and the morphology is similar to the single elliptic cylinder case, with a second vortex phenomenon and bifurcation structure occurring at later times.Actually, we observe a nonlinear, threshold-type behavior of inner vortex formation when d/b varies from 2.0 to 3.0.Finally, we outline and discuss 4 possible mechanisms which may lead to the obvious weakening phenomenon of inner vortices. -
图 1 激波管装置、光测系统和初始气柱示意图
Figure 1. Schematic of the shock tube, optical diagnostic system and initial elliptic cylinders
图 2 激波管波系图(横轴0处为破膜位置，虚线表示观测窗位置，箭头所指为采集数据的时-空区域)
Figure 2. Wave diagram of the shock tube (Position 0 is the location of the diaphram, and the dotted line represents the viewing window, the arrow shows the region in space-time domain where data are taken)
图 3 双椭圆气柱示意图(Ma=1.18)
Figure 3. Schematic of two elliptic cylinders and the incident shock (Ma=1.18)
图 4 双椭圆气柱界面的涡量分布示意图
Figure 4. Vorticity distributions due to the interaction of a shock wave with two elliptic gas cylinders
图 5 弱干扰情形双椭圆气柱演化图像(从左到右依次为t=0, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0 ms)
Figure 5. Weak interaction image sequences at t=0 (initial) and t=0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 and 1.0 ms (dynamic) after shock passage
图 6 强干扰情形双椭圆气柱演化图像(从左到右依次为t=0, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0 ms)
Figure 6. Strong interaction image sequences at t=0 (initial) and t=0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0 ms (dynamic) after shock passage
图 7(a) 情形2中，700 μs时刻PIV图像(左)及速度场(右)
Figure 7(a). PIV image (left) and velocity field (right) at 700 μs for case 2 (d/b =3.0)
图 7(b) 情形3中，700 μs时刻PIV图像(左)及速度场(右)
Figure 7(b). PIV image (left) and velocity field (right) at 700 μs for case 3 (d/b =2.0)
表 1 双椭圆气柱的初始尺寸
Table 1. Initial gas cylinder geometry sizes
Case a/
(mm)b/
(mm)d/
(mm)d/b 1 10.0 2.5 10.0 4.0 2 10.0 2.5 7.5 3.0 3 10.0 2.5 5.0 2.0 4 10.0 2.5 3.0 1.2 
下载: 导出CSV
-
[1] Richtmyer R D. Taylor instability in shock acceleration of compressible fluids[J]. Commun Pure Appl Math, 1960, 13(2): 297-319. doi: 10.1002/cpa.3160130207 [2] Meshkov E E. Instability of the interface of two gases accelerated by a shock wave[J]. Fluid Dyn, 1969, 4(5): 101-104. doi: 10.1007/BF01015969 [3] Arnett W D, Bahcall J N, Kirshner R P, et al. Supernova 1987A[J]. Annu Rev Astron Astrophys, 1989, 27: 629-700. doi: 10.1146/annurev.aa.27.090189.003213 [4] Lindl D L, McCrory R L, Campbell E M. Progress toward ignition and burn propagation in inertial confinement fusion[J]. Phys Today, 1992, 45(9): 32-40. doi: 10.1063/1.881318 [5] Brouillette M. The Richtmyer-Meshkov instability[J]. Annu Rev Fluid Mech, 2002, 34: 445-468. doi: 10.1146/annurev.fluid.34.090101.162238 [6] Dimotakis P. Turbulent mixing[J]. Ann Rev Fluid Mech, 2005, 37: 329-356. doi: 10.1146/annurev.fluid.36.050802.122015 [7] Ranjan D, Oakley J, Bonazza R. Shock-bubble interactions[J]. Annu Rev Fluid Mech, 2011, 43: 117-140. doi: 10.1146/annurev-fluid-122109-160744 [8] Prestridge K, Orlicz G, Balasubramanian S, et al. Experiments of the Richtmyer-Meshkov instability[J]. Phil Trans R Soc A, 2013, 371: 20120165. doi: 10.1098/rsta.2012.0165 [9] Samtaney R, Zabusky N. Circulation deposition on shock-accelerated planar and curved density-stratified interfaces: Models and scaling laws[J]. J Fluid Mech, 1994, 269: 45-78. doi: 10.1017/S0022112094001485 [10] Picone J M, Boris J P. Vorticity generation by shock propagation through bubbles in a gas[J]. J Fluid Mech, 1988, 189: 23-51. doi: 10.1017/S0022112088000904 [11] Yang J, Kubota T, Zukoski E E. Application of shock-induced mixing to supersonic combustion[J]. AIAA J, 1993, 31(5): 854-862. doi: 10.2514/3.11696 [12] Quirk J J, Karni S. On the dynamics of a shock-bubble interaction[J]. J Fluid Mech, 1996, 318: 129-163. doi: 10.1017/S0022112096007069 [13] Haas J F, Sturtevant B. Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities[J]. J Fluid Mech, 1987, 181: 41-76. doi: 10.1017/S0022112087002003 [14] Jacobs J W. Shock-induced mixing of a light-gas cylinder[J]. J Fluid Mech, 1992, 234: 629-649. doi: 10.1017/S0022112092000946 [15] Jacobs J W. The dynamics of shock-accelerated light and heavy gas cylinders[J]. Phys Fluids A, 1993, 5: 2239-2247. doi: 10.1063/1.858562 [16] Zoldi C A. A numerical and experimental study of a shock-accelerated heavy gas cylinder[D]. New York: State University of New York at Stony Brook, 2002. [17] Prestridge K, Vorobieff P, Rightley P M, et al. Validation of an instability growth model using particle image velocimetry measurements[J]. Phys Rev Lett, 2000, 84(19): 4353-4356. doi: 10.1103/PhysRevLett.84.4353 [18] Prestridge K, Rightley P M, Vorobieff P, et al. Simultaneous density-field visualization and PIV of a shock-accelerated gas curtain[J]. Exp Fluids, 2000, 29(4): 339-346. doi: 10.1007/s003489900091 [19] Rightley P M, Vorobieff P, Benjamin R F. Evolution of a shock-accelerated thin fluid layer[J]. Phys Fluids, 1997, 9: 1770-1782. doi: 10.1063/1.869299 [20] Rightley P M, Vorobieff P, Martin R, et al. Experimental observations of the mixing transition in a shock-accelerated gas curtain[J]. Phys Fluids, 1999, 11: 186-200. doi: 10.1063/1.869911 [21] Schilling O. Proceedings of the 8th IWPCTM, UCRL-ID-146350[R]. Califorlia: Pasadena, 2001. [22] Tomkins C, Kumar S, Vorobieff P, et al. Visualizing the onset and growth of secondary instabilities in Richtmyer-Meshkov-unstable flows[C]//Proceedings of the 9th IWPCTM. UK: Cambridge, 2004. [23] Tomkins C, Prestridge K, Rightley P, et al. Flow morphologies of two shock-accelerated unstable gas cylinders[J]. J Vis, 2002, 5(3): 273-283. doi: 10.1007/BF03182335 [24] Tomkins C, Prestridge K, Rightley P, et al. A quantitative study of the interaction of two Richtmyer-Meshkov-unstable gas cylinders[J]. Phys Fluids, 2005, 15(4): 986-1004. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=b771736daa30ceb89ca974670189aa78 [25] Goodenough C, Kumar S, Marr-Lyon M, et al. Planar velocity and scalar concentration measurements in shock-accelerated, unstable fluid interfaces[C]//26th International Conference on High-Speed Photography and Photonics. USA: Proc SPIE 5580, 2005: 186-192. [26] Kumar S, Orlicz G, Tomkins C, et al. Stretching of material lines in shock-accelerated gaseous flows[J]. Phys Fluids, 2005, 17: 082107. doi: 10.1063/1.2031347 [27] Kumar S, Vorobieff P, Orlicz G, et al. Complex flow morphologies in shock-accelerated gaseous flows[J]. Physica D, 2007, 235(1): 21-28. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=bdbcdf0e0282f4b502c2c68e5b86d83b [28] Balakumar B J, Orlicz G C, Ristorcelli J R, et al. Turbulent mixing in a Richtmyer-Meshkov fluid layer after reshock: Velocity and density statistics[J]. J Fluid Mech, 2012, 696: 67-93. doi: 10.1017/jfm.2012.8 [29] Tomkins C D, Balakumar B J, Orlicz G, et al. Evolution of the density self-correlation in developing Richtmyer-Meshkov turbulence[J]. J Fluid Mech, 2013, 735: 288-306. doi: 10.1017/jfm.2013.430 [30] Balasubramanian S, Orlicz G C, Prestridge K P. Experimental study of initial condition dependence on turbulent mixing in shock-accelerated Richtmyer-Meshkov fluid layers[J]. J Turbulence, 2013, 14(3): 170-196. doi: 10.1080/14685248.2013.792932 [31] Si T, Zhai Z G, Luo X S. Experimental study of Richtmyer-Meshkov instability in a cylindrical converging shock tube[J]. Laser Part Beams, 2014, 32(3): 343-351. doi: 10.1017/S0263034614000202 [32] 何惠琴, 翟志刚, 司廷, 等.反射激波作用下两种重气柱界面不稳定性实验研究[J].实验流体力学, 2014, 28(6): 56-60. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ltlxsyycl201406008He H Q, Zhai Z G, Si T, et al. Experimental study on the shocked RM instability of two kinds of heavy gas cylinder[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(6): 56-60. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ltlxsyycl201406008 [33] 沙莎, 陈志华, 薛大文.激波冲击R22重气柱所导致的射流和混合研究[J].物理学报, 2013, 62(14): 144701. http://qikan.cqvip.com/Qikan/Article/Detail?id=46504159Sha S, Chen Z H, Xue D W. The generation of jet and mixing induced by the interaction of shock wave with R22 cylinder[J]. Acta Physica Sinica, 2013, 62(14): 144701. (in Chinese) http://qikan.cqvip.com/Qikan/Article/Detail?id=46504159 [34] 邹立勇, 刘金宏, 谭多望, 等.弱激波冲击无膜重气柱和气帘界面的实验研究[J].高压物理学报, 2010, 24(4): 241-247. http://www.cqvip.com/QK/96553X/201004/34963986.htmlZou L Y, Liu J H, Tan D W, et al. Experimental study on the membraneless heavy gas cylinder and gas curtain interfaces impacted by a weak shock wave[J]. Chinese Journal of High Pressure Physics, 2010, 24(4): 241-247. (in Chinese) http://www.cqvip.com/QK/96553X/201004/34963986.html [35] Zou L Y, Liu C L, Tan D W, et al. On interaction of shock wave with elliptic gas cylinder[J]. J Visual, 2010, 13(4): 347-353. doi: 10.1007/s12650-010-0053-y [36] Bai J S, Zou L Y, Wang T, et al. Experimental and numerical study of shock-accelerated elliptic heavy gas cylinders[J]. Phys Rev E, 2010, 82: 056318. doi: 10.1103/PhysRevE.82.056318 [37] Zou L Y, Huang W B, Liu C L, et al. On the evolution of double shock-accelerated elliptic gas cylinders[J]. J Fluid Eng(Trans ASME), 2014, 136: 031204. doi: 10.1115/1.4026196 -
下载:
图(8) / 表(1)
计量
- 文章访问数: 6415
- HTML全文浏览量: 1953
- PDF下载量: 216
