Out-of-Plane Compression Performance of Gradient Honeycomb Inspired by Royal Water Lily
-
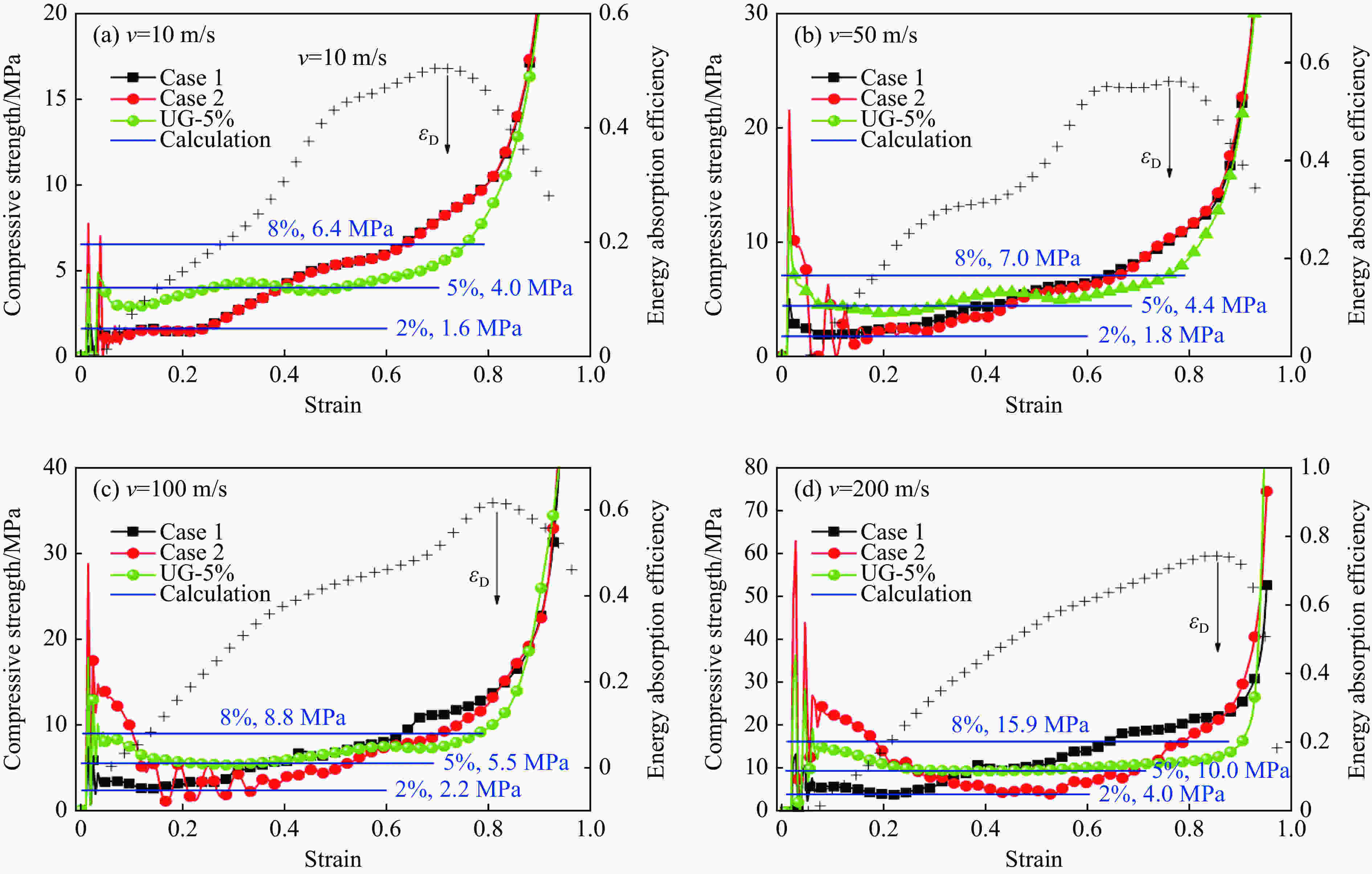
摘要: 利用ABAQUS有限元软件对仿王莲脉络分层梯度蜂窝进行准静态与动态压缩数值模拟,分析了其准静态压缩平台应力与相对密度,以及动态压缩强度与相对密度、冲击速度之间的关系。结果表明:当冲击速度较低时(10 m/s),芯层呈现渐进压溃模式;在高速冲击下(200 m/s),芯层压溃模式与梯度分布方式密切相关,初始为渐进压溃模式,当冲击波传播至远端时,各层的压溃和密实化取决于其静态压缩强度,密实化依次出现在压缩强度较低的芯层。Abstract: Inspired by the venation of Royal Water Lily leaves, we conducted numerical simulations on the quasi-static and dynamic compression of layered-gradient honeycomb using the finite element software ABAQUS. Then the relationship of the quasi-static compression plateau stress with the relative density, as well as the relationship of the dynamic compressive strength with the relative density and the impact velocity was analyzed. The results show that: the progressive collapse mode appears at a low impact velocity (10 m/s); the collapse mode presents closely related to the gradient distribution at the impact velocity of 200 m/s, and the initial collapse mode just turns to be progressive. When the shock wave propagates to the far end (fixed end), the layer’s collapse and compaction depend on its static compressive strength, and the compaction occurs in the layer with lower compressive strength in turn.
-
Key words:
- bionic honeycomb /
- gradient core /
- compressive strength /
- deformation mode
-
表 1 6060T4铝合金材料参数
Table 1. Material parameters of 6060T4 aluminum alloy
$\,\rho $/(kg·m−3) E/GPa $\,\mu $ $\,\sigma $cY/GPa Etan/GPa 2 700 70 0.3 0.08 0.07 表 2 模型类型与相关参数
Table 2. Model and related parameters
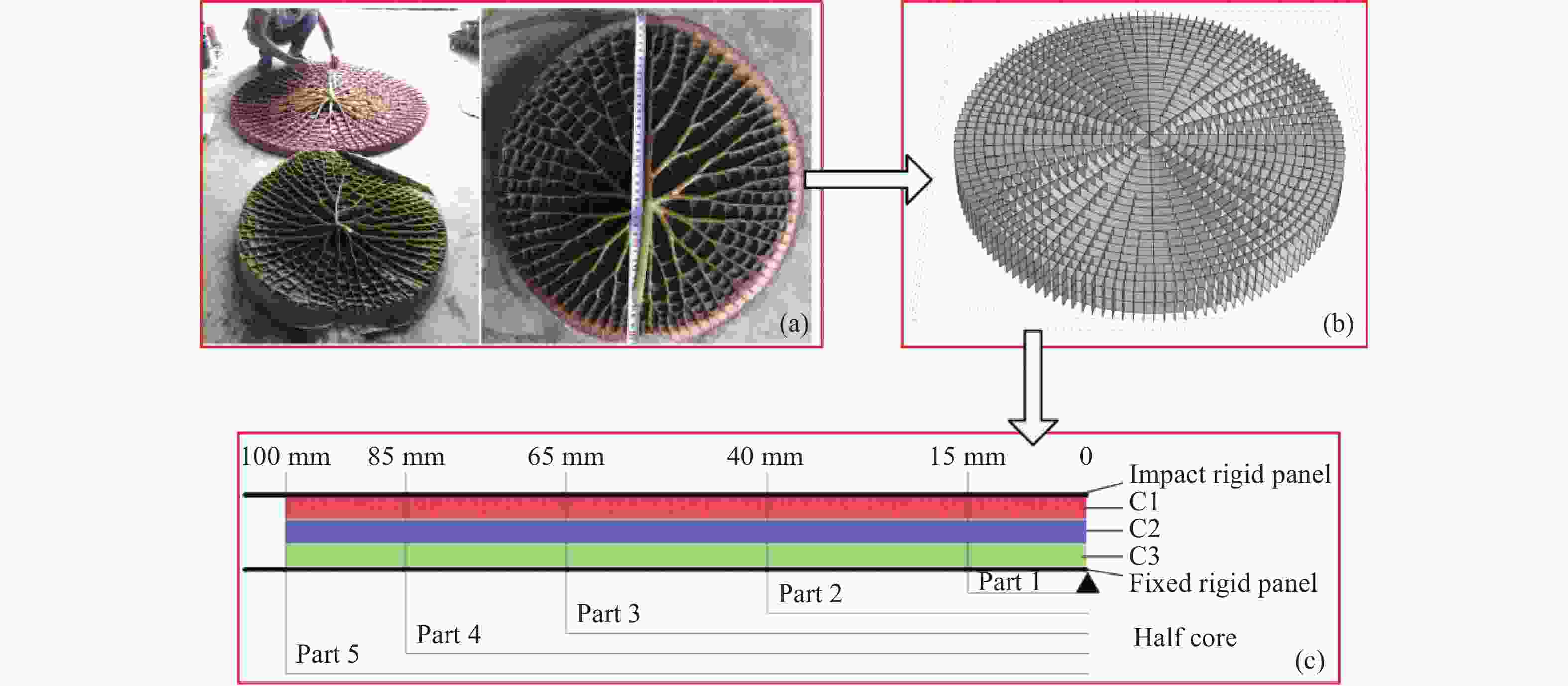
Model Wall thicknesses of C2 layer/mm Relative density of out-of-plane/% Part 1 Part 2 Part 3 Part 4 Part 5 C1 C2 C3 Case 1 0.190 0.180 0.175 0.150 0.120 2 5 8 Case 2 0.190 0.180 0.175 0.150 0.120 8 5 2 UG-5% 0.190 0.180 0.175 0.150 0.120 5 5 5 -
[1] LIU Z Q, MEYERS M A, ZHANG Z F, et al. Functional gradients and heterogeneities in biological materials: design principles, functions, and bioinspired applications [J]. Progress in Materials Science, 2017, 88: 467–498. doi: 10.1016/j.pmatsci.2017.04.013 [2] ZHANG Q C, YANG X H, LI P, et al. Bioinspired engineering of honeycomb structure—using nature to inspire human innovation [J]. Progress in Materials Science, 2015, 74(1): 332–400. [3] WU E, JIANG W S. Axial crush of metallic honeycombs [J]. International Journal of Impact Engineering, 1997, 19(5/6): 439–456. [4] MAHMOUDABADI M Z, SADIGHI M. A theoretical and experimental study on metal hexagonal honeycomb crushing under quasi-static and low velocity impact loading [J]. Materials Science and Engineering A, 2011, 528(15): 4958–4966. doi: 10.1016/j.msea.2011.03.009 [5] 王中钢, 鲁寨军. 铝蜂窝异面压缩吸能特性实验评估 [J]. 中南大学学报(自然科学版), 2013, 44(3): 1246–1251.WANG Z G, LU Z J. Experimental assessment on energy absorption property of aluminum honeycomb under out-of-plane compression [J]. Journal of Central South University (Science and Technology), 2013, 44(3): 1246–1251. [6] TANG S, DENG Y L, JIANG K D, et al. A study on dynamic compressive mechanical behaviors of aluminum honeycombs [J]. Material Sciences, 2014, 4(3): 96–102. doi: 10.12677/MS.2014.43015 [7] WANG Z G, LIU J F, LIU Z J, et al. Mechanical behavior of composited structure filled with tandem honeycombs [J]. Composites Part B: Engineering, 2017, 114: 128–138. doi: 10.1016/j.compositesb.2017.01.018 [8] 甄建伟, 安振涛, 陈玉成, 等. 蜂窝增强泡沫塑料的静动态力学性能 [J]. 复合材料学报, 2011, 28(3): 223–228.ZHEN J W, AN Z T, CHEN Y C, et al. Quasi-static and dynamic mechanical properties of honeycomb reinforced plastic foam [J]. Acta Materiae Compositae Sinica, 2011, 28(3): 223–228. [9] 赵雪, 闫雷雷, 卢天健, 等. 多层金属多孔复合结构面外压缩吸能特性实验 [J]. 空军工程大学学报(自然科学版), 2017, 18(4): 28–33.ZHAO X, YAN L L, LU T J, et al. An experiment investigation on energy absorption of multi-layer sandwich structures with metallic corrugated cores under out-of-plane compressive load [J]. Journal of Air Force Engineering University (Natural Science Edition), 2017, 18(4): 28–33. [10] 张新春, 刘颖. 密度梯度蜂窝材料动力学性能研究 [J]. 工程力学, 2012, 29(8): 372–377. doi: 10.6052/j.issn.1000-4750.2010.12.0872ZHANG X C, LIU Y. Research on the dynamic crushing of honeycombs with density gradient [J]. Engineering Mechanics, 2012, 29(8): 372–377. doi: 10.6052/j.issn.1000-4750.2010.12.0872 [11] 吴鹤翔, 刘颖. 梯度变化对密度梯度蜂窝材料力学性能的影响 [J]. 爆炸与冲击, 2013, 33(2): 163–168. doi: 10.3969/j.issn.1001-1455.2013.02.008WU H X, LIU Y. Influences of density gradient variation on mechanical performances of density-graded honeycomb materials [J]. Explosion and Shock Waves, 2013, 33(2): 163–168. doi: 10.3969/j.issn.1001-1455.2013.02.008 [12] 谭思博, 侯兵, 李玉龙, 等. 基体材料对铝蜂窝动态强化特性的影响 [J]. 爆炸与冲击, 2015, 35(1): 16–21. doi: 10.11883/1001-1455(2015)01-0016-06TAN S B, HOU B, LI Y L, et al. Effect of base materials on the dynamic enhancement of aluminium honeycombs [J]. Explosion and Shock Waves, 2015, 35(1): 16–21. doi: 10.11883/1001-1455(2015)01-0016-06 [13] XIAO D B, DONG Z C, Li Y, et al. Compression behavior of the graded metallic auxetic reentrant honeycomb: experiment and finite element analysis [J]. Materials Science and Engineering A, 2019, 758(1): 163–171. [14] 樊喜刚, 尹西岳, 陶勇, 等. 梯度蜂窝面外动态压缩力学行为与吸能特性研究 [J]. 固体力学学报, 2015, 36(2): 114–122.FAN X G, YIN X Y, TAO Y, et al. Mechanical behavior and energy absorption of graded honeycomb materials under out-of-plane dynamic compression [J]. Chinese Journal of Solid Mechanics, 2015, 36(2): 114–122. [15] WANG X K, ZHENG Z J, YU J L. Crashworthiness design of density-graded cellular metals [J]. Theoretical & Applied Mechanics Letters, 2013, 3(3): 031001. [16] REID S R, PENG C. Dynamic uniaxial crushing of wood [J]. International Journal of Impact Engineering, 1997, 19(5/6): 531–570. [17] RUAN D, LU G, WANG B, et al. In-plane dynamic crushing of honeycombs—a finite element study [J]. International Journal of Impact Engineering, 2003, 28(2): 161–182. doi: 10.1016/S0734-743X(02)00056-8 [18] QIAO J X, CHEN C Q. Impact resistance of uniform and functionally graded auxetic double arrowhead honeycombs [J]. International Journal of Impact Engineering, 2015, 83(1): 47–58. [19] 陶义, 王宗彦, 王珂, 等. 基于王莲叶脉分布的塔式起重机臂架结构仿生设计 [J]. 机械设计与制造, 2017(3): 36–39. doi: 10.3969/j.issn.1001-3997.2017.03.010TAO Y, WANG Z Y, WANG K, et al. Structural bionic design for tower cranes boom based on King Lotus leaf vein branched structure [J]. Machinery Design & Manufacture, 2017(3): 36–39. doi: 10.3969/j.issn.1001-3997.2017.03.010 [20] LIU Z F, HAO W Q, XIE J M, et al. Axial-impact buckling modes and energy absorption properties of thin-walled corrugated tubes with sinusoidal patterns [J]. Thin-Walled Structures, 2015, 94(1): 410–423. [21] 朱跃峰. 基于ABAQUS的显式动力学分析方法研究 [J]. 机械设计与制造, 2015(3): 107–109. doi: 10.3969/j.issn.1001-3997.2015.03.029ZHU Y F. Research on analysis methods of explicit dynamics based on ABAQUS [J]. Machinery Design & Manufacture, 2015(3): 107–109. doi: 10.3969/j.issn.1001-3997.2015.03.029 [22] FAN J H, ZHANG J J, WANG Z H, et al. Dynamic crushing behavior of random and functionally graded metal hollow sphere foams [J]. Materials Science and Engineering A, 2013, 561: 352–361. [23] FLECK N A, DESHPANDE V S. The resistance of clamped sandwich beams to shock loading [J]. Journal of Applied Mechanics, 2004, 71(3): 386–401. doi: 10.1115/1.1629109 [24] ZHU F, WANG Z H, LU G X, et al. Some theoretical considerations on the dynamic response of sandwich structures under impulsive loading [J]. International Journal of Impact Engineering, 2010, 37(6): 625–637. doi: 10.1016/j.ijimpeng.2009.11.003 -






 下载:
下载: