Dynamic Responses of Nare-Like Voronoi Structure under Impact Loading
-
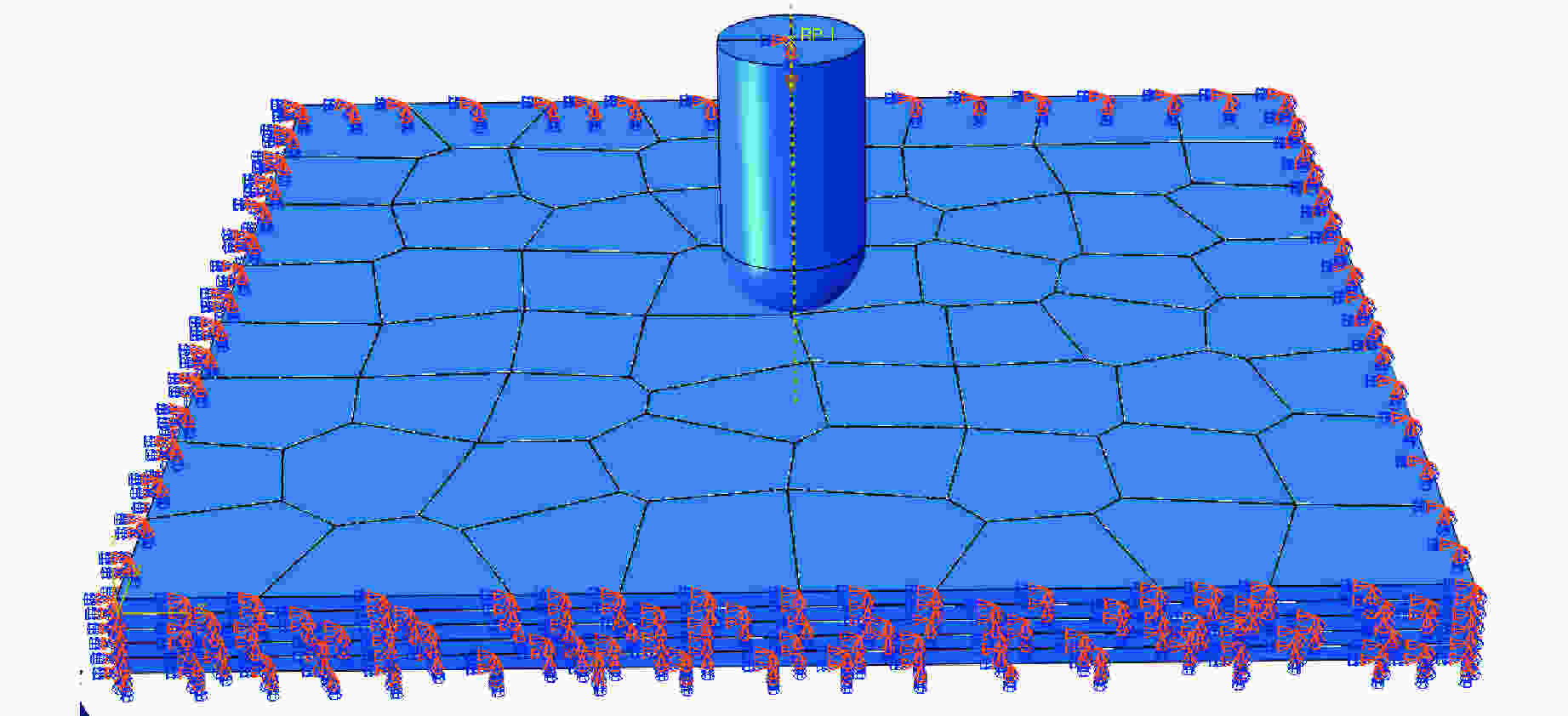
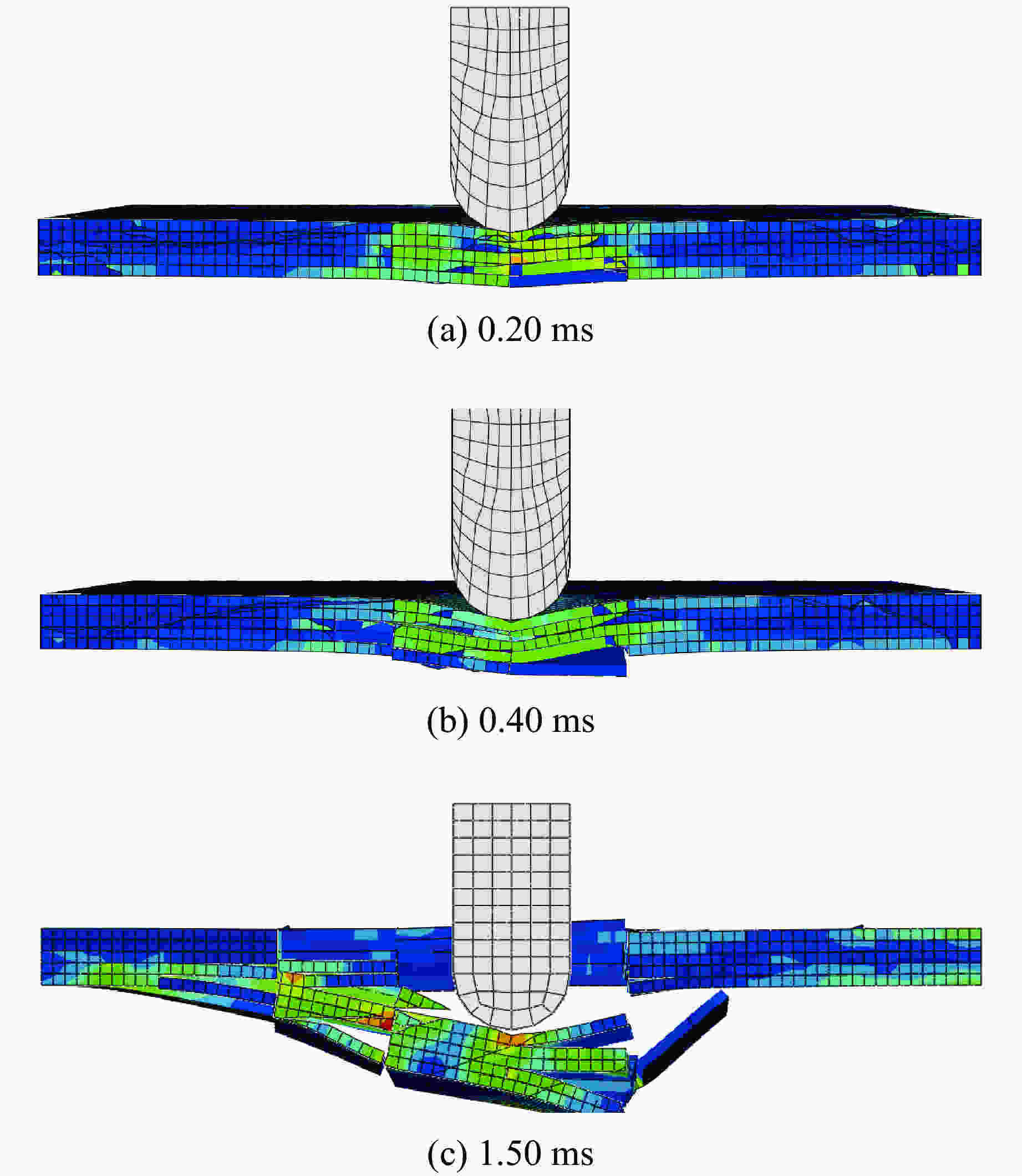
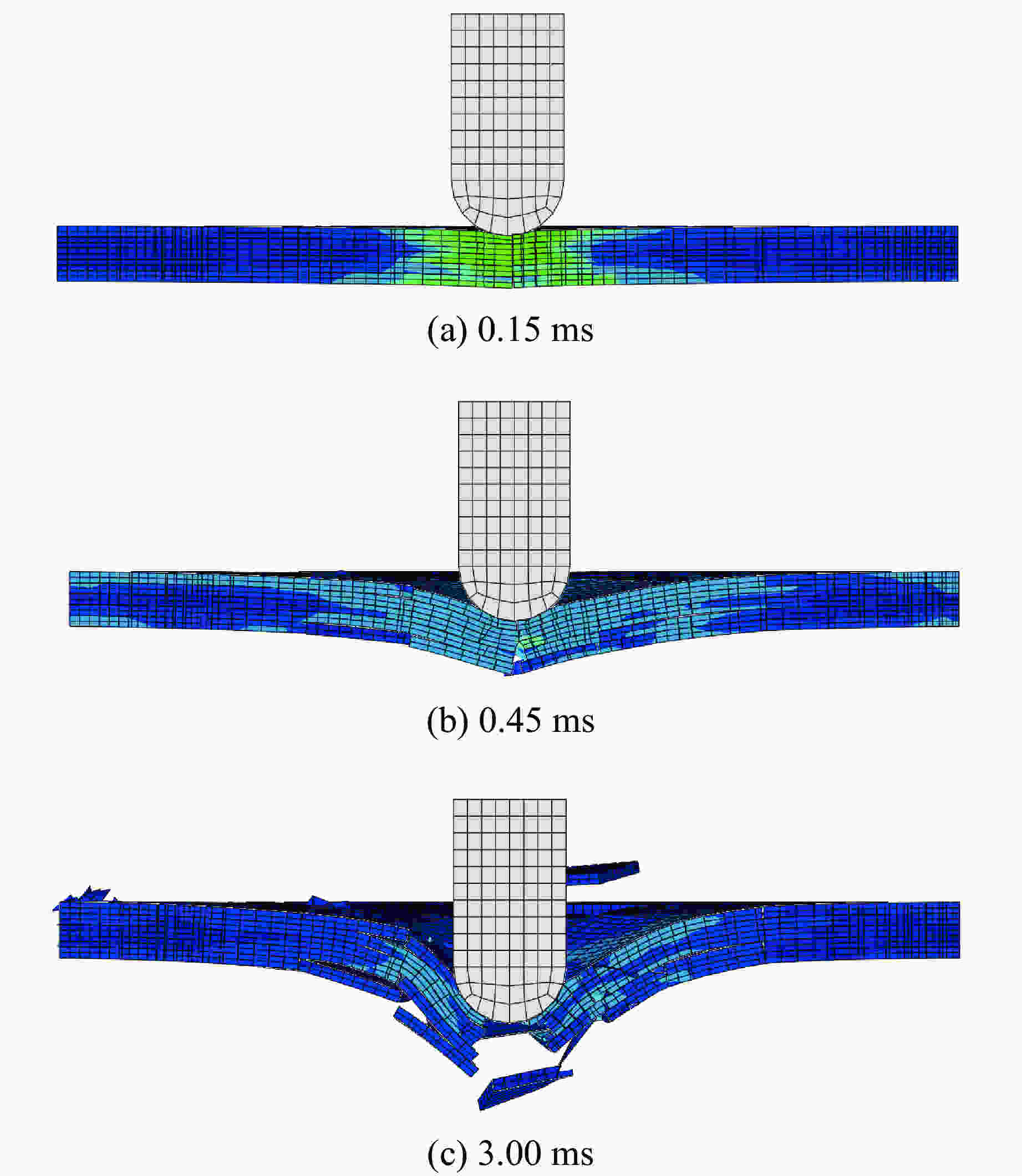
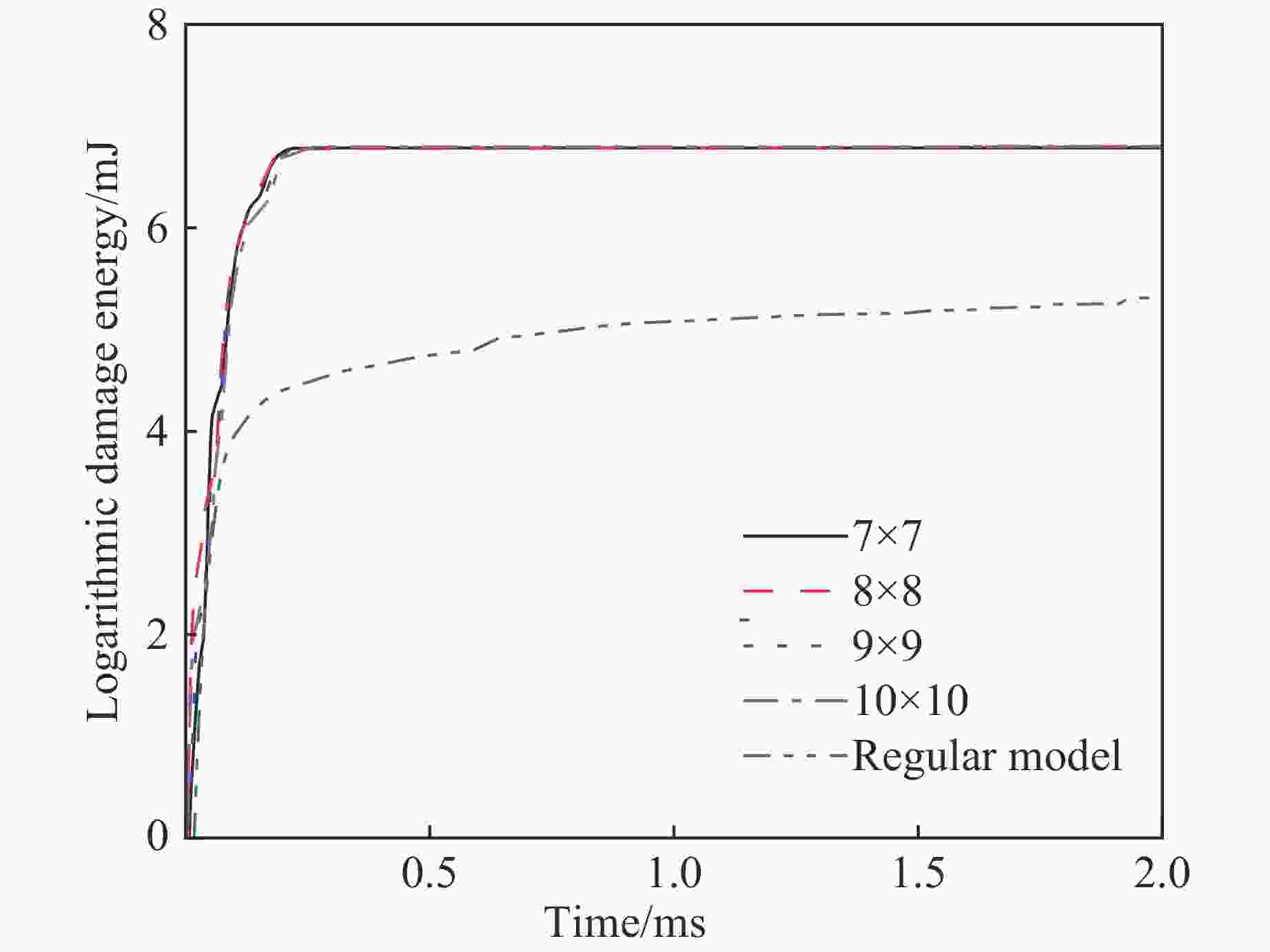
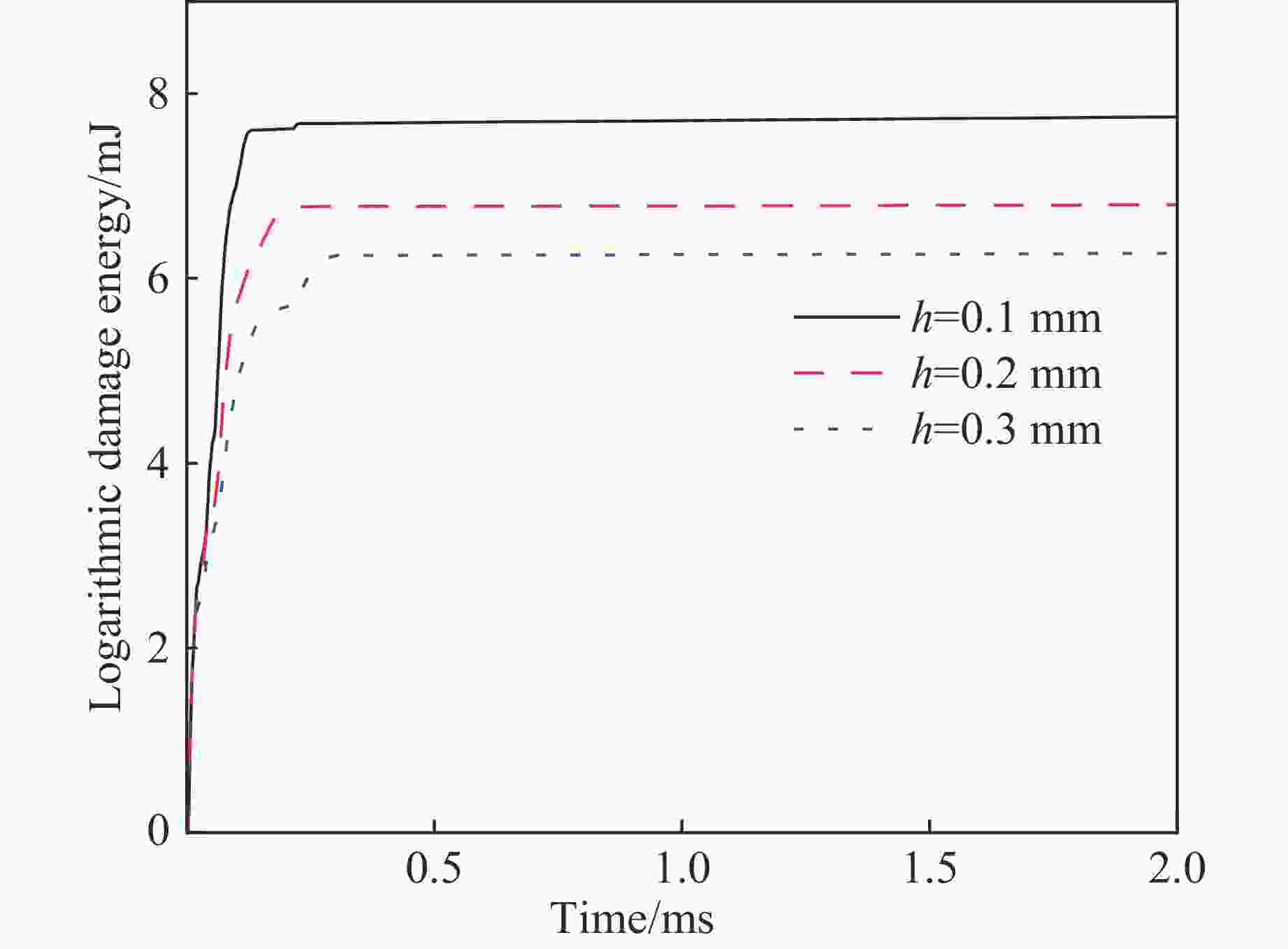
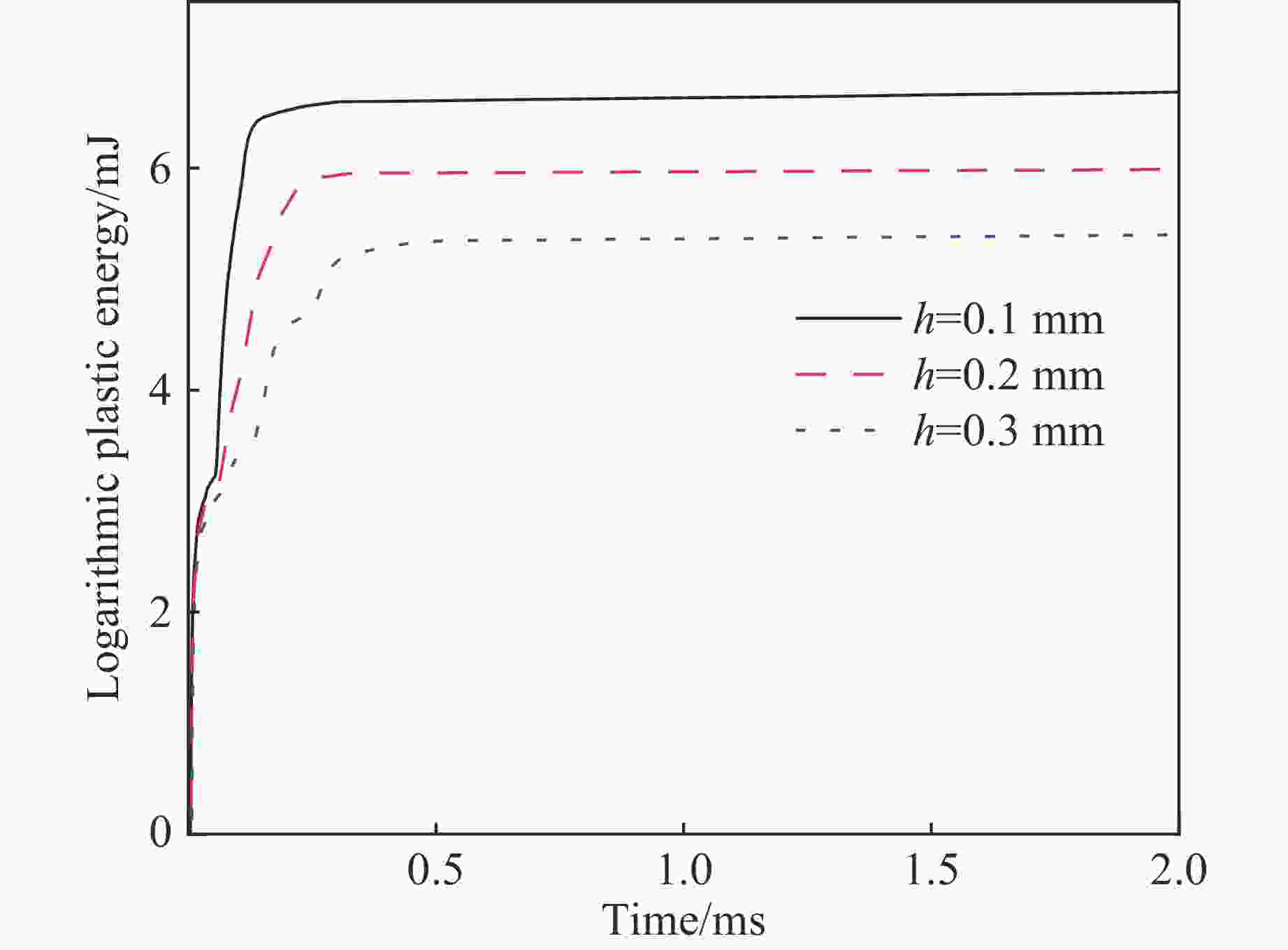
摘要: 贝壳珍珠层复合结构是一种有效的抗压结构系统，微观上具有Voronoi随机结构，具有良好的力学特性。为了研究仿贝壳珍珠层Voronoi结构在冲击载荷下的动态力学响应，建立了一种铝/乙烯基复合材料的三维Voronoi模型。首先，应用随机Voronoi技术建立仿贝壳珍珠层Voronoi随机模型，然后在随机多边形铝片之间引入黏结层，模拟黏结和分层过程，从最大变形、损伤分布和耗散能量等方面探讨Voronoi片板模型在弹丸冲击荷载作用下的力学性能，并与规则片板模型进行对比分析。结果显示：Voronoi结构更有利于冲击能量的扩散与吸收，减小应力集中，更好地发挥能量共享机制；而规则模型的冲击损伤主要集中在弹丸冲击点附近区域。最后讨论了黏结层厚度和分块尺寸对Voronoi模型力学性能的影响，结果表明：分块尺寸对Voronoi模型抗冲击性能的影响很小；黏结层对损伤耗散能和塑性能的影响很明显，黏结层越薄，模型的抗冲击性能越好。Abstract: As an effective structure system for resisting the compression, the nacre composite structure has random Voronoi structure at a microscopic level and good mechanical performance. In this study, a three-dimensional Voronoi model consisting of aluminum/vinyl composite structure was presented to investigate the dynamic responses of nare-like Voronoi model under impact loading. Firstly the stochastic Voronoi model was built using the Voronoi technology, and then the adhesive layers were introduced between random polygonal aluminium sheets to simulate the bonding and delaminating processes. Via the maximum deformation, damage distribution and dissipation energy, the mechanical performances of Voronoi plate model were evaluated and compared with those of the regular plate model. The results showed that the Voronoi model is in favor of energy spreading and absorbing, reducing the stress concentration and making the energy sharing mechanism work better. But the impact damage of the regular plate model is concentrated near the impacting point of the bullet. Finally the influences of adhesive thickness and block size on mechanical performances were discussed. It was indicated that the block size has little effect on the impact resistance of the Voronoi model while the adhesive thickness exerts significant influence on the damage dissipation energy and plastic energy. It was found that the thinner is the adhesive thickness, the better is the impact resistance performance of the model.
-
Key words:
- nacre /
- Voronoi structure /
- dynamic response /
- impact loading /
- finite element analysis
-
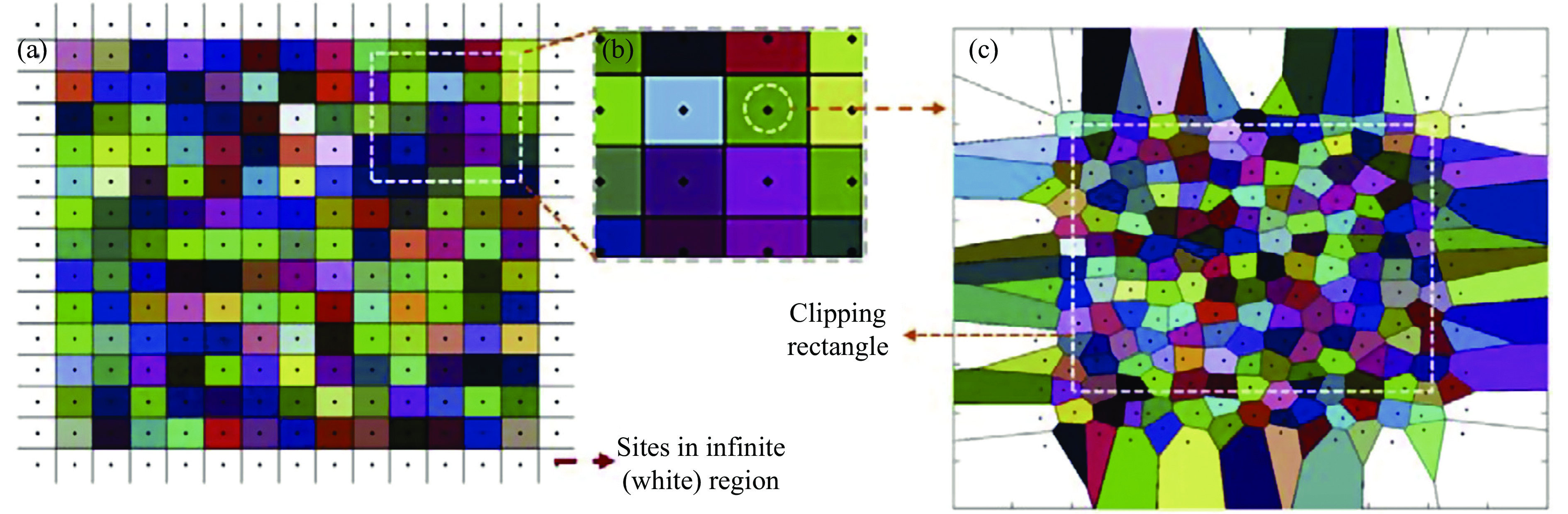
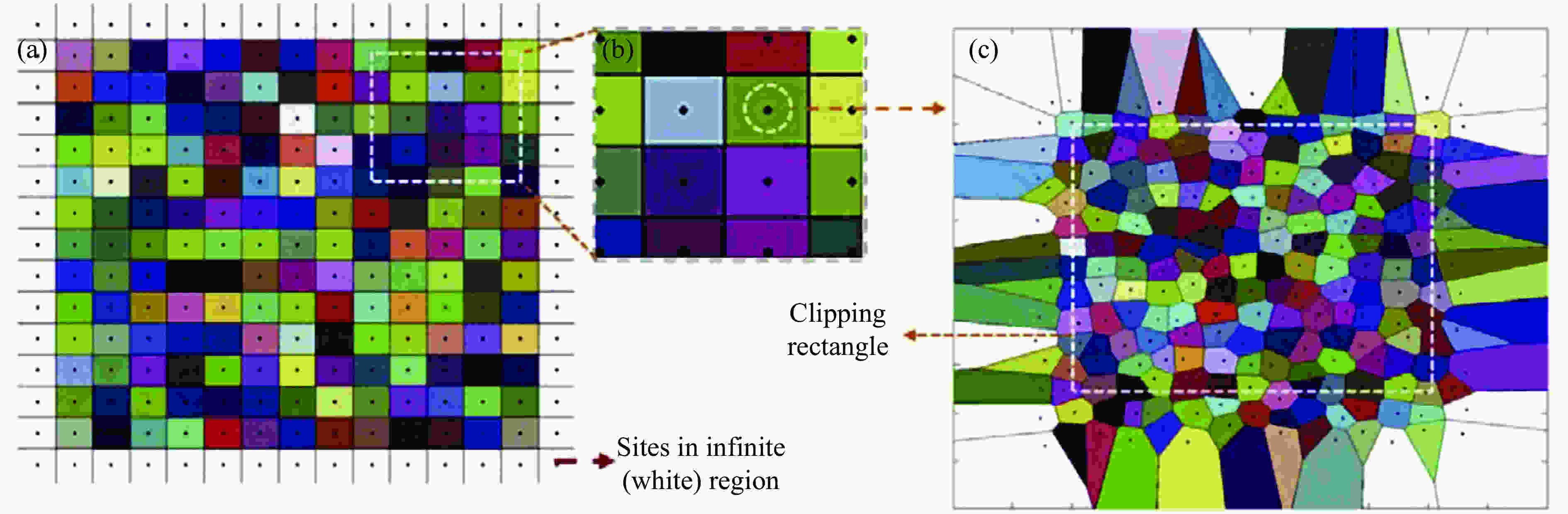
图 1 (a) Voronoi图的初始网格构型；（b）每个站点都在一个圆圈区域内随机移动；（c）新的Voronoi图是从新的站点系统中生成，通过矩形裁剪，形成有限区域的随机Voronoi图[25]
Figure 1. (a) Initial grid formation of Voronoi diagram; (b) each site moves randomly within a circle region; (c) a new Voronoi diagram is generated from the new site system, and by a rectangle cut, a finite Voronoi diagram is generated[25]
图 2 规则8 × 8模型和随机Voronoi模型的示意图
Figure 2. Schematic of regular 8 × 8 model and random Voronoi models
图 4 不同时刻规则片板模型的von Mises应力云图剖视图
Figure 4. Cutaway views of von Mises stress contours of regular plate model at different times
图 5 不同时刻Voronoi片板模型的von Mises应力云图剖视图
Figure 5. Cutaway views of von Mises stress contours of Voronoi plate model at different times
图 6 3.00 ms时规则片板模型的von Mises应力云图俯视图
Figure 6. Top view of von Mises stress contours of regular plate model at 3.00 ms
图 7 3.00 ms时Voronoi片板模型的von Mises应力云图俯视图
Figure 7. Top view of von Mises stress contours of Voronoi plate model at 3.00 ms
图 8 规则模型和不同分块尺寸Voronoi模型的损伤耗能
Figure 8. Damage energy of regular model and Voronoi models with different block sizes
图 9 规则模型和不同分块尺寸Voronoi模型的塑性能
Figure 9. Plastic energy of regular model and Voronoi models with different block sizes
图 10 具有不同黏性层厚度的Voronoi模型的损伤耗能
Figure 10. Damage energy of Voronoi models with different adhesive thicknesses
图 11 具有不同黏性层厚度的Voronoi模型的塑性能
Figure 11. Plastic energy of Voronoi model with different adhesive thicknesses
表 1 铝片的材料参数
Table 1. Parameters of aluminum plate
Material $\;\rho $/（kg·m−3） $\nu $ E/GPa Aluminum 2750 0.3 72 
下载: 导出CSV
表 2 Cohesive模型的材料参数
Table 2. Parameters of Cohesive model
$t_{\rm{n} }^{{0} }$/MPa $t_{\rm{s} }^{{0} }$/MPa $t_{\rm{t} }^{{0} }$/MPa $G_{\rm{n} }^{{0} }$/(kJ·m−2) $G_{\rm{s} }^{{0} }$/(kJ·m−2) $G_{\rm{t} }^{{0} }$/(kJ·m−2) $\;\rho $/(kg·m−3) Es/GPa Et/GPa 80 80 80 1 1 1 1 850 4 1.5
下载: 导出CSV
-
[1] CURREY J D. Mechanical properties of mother of pearl in tension [J]. Proceedings of the Royal Society B: Biological Sciences, 1977, 196(1125): 443–463. doi: 10.1098/rspb.1977.0050 [2] BARTHELAT F, TANG H, ZAVATTIERI P D, et al. On the mechanics of mother-of-pearl: a key feature in the material hierarchical structure [J]. Journal of the Mechanics and Physics of Solids, 2007, 55(2): 306–337. doi: 10.1016/j.jmps.2006.07.007 [3] IMBALZANO G, TRAN P, NGO T D, et al. A numerical study of auxetic composite panels under blast loadings [J]. Composite Structures, 2016, 135: 339–352. doi: 10.1016/j.compstruct.2015.09.038 [4] NGUYEN Q T, NGO T D, TRAN P, et al. Influences of clay and manufacturing on fire resistance of organoclay/thermoset nanocomposites [J]. Composites Part A: Applied Science and Manufacturing, 2015, 74: 26–37. doi: 10.1016/j.compositesa.2015.03.014 [5] PRO J W, LIM R K, PETZOLD L R, et al. GPU-based simulations of fracture in idealized brick and mortar composites [J]. Journal of the Mechanics and Physics of Solids, 2015, 80: 68–85. doi: 10.1016/j.jmps.2015.03.011 [6] ZHANG N, YANG S F, XIONG L M, et al. Nanoscale toughening mechanism of nacre tablet [J]. Journal of the Mechanical Behavior of Biomedical Materials, 2016, 53: 200–209. doi: 10.1016/j.jmbbm.2015.08.020 [7] SARIKAYA M. An introduction to biomimetics: a structural viewpoint [J]. Microscopy Research and Technique, 1994, 27(5): 360–375. doi: 10.1002/jemt.1070270503 [8] GAO H J, JI B H, JÄGER I L, et al. Materials become insensitive to flaws at nanoscale: lessons from nature [J]. Proceedings of the National Academy of Sciences of the United States of America, 2003, 100(10): 5597–5600. doi: 10.1073/pnas.0631609100 [9] SONG F, SOH A K, BAI Y L. Structural and mechanical properties of the organic matrix layers of nacre [J]. Biomaterials, 2003, 24(20): 3623–3631. doi: 10.1016/S0142-9612(03)00215-1 [10] BARTHELAT F. Nacre from mollusk shells: a model for high-performance structural materials [J]. Bioinspiration & Biomimetics, 2010, 5(3): 035001. doi: 10.1088/1748-3182/5/3/035001 [11] TRAN P, NGO T D, MENDIS P. Bio-inspired composite structures subjected to underwater impulsive loading [J]. Computational Materials Science, 2014, 82: 134–139. doi: 10.1016/j.commatsci.2013.09.033 [12] FLORES-JOHNSON E A, SHEN L M, GUIAMATSIA I, et al. A numerical study of bioinspired nacre-like composite plates under blast loading [J]. Composite Structures, 2015, 126: 329–336. doi: 10.1016/j.compstruct.2015.02.083 [13] DUTTA A, TEKALUR S A. Crack tortuousity in the nacreous layer-topological dependence and biomimetic design guideline [J]. International Journal of Solids and Structures, 2014, 51(2): 325–335. doi: 10.1016/j.ijsolstr.2013.10.006 [14] KOTHA S P, LI Y, GUZELSU N. Micromechanical model of nacre tested in tension [J]. Journal of Materials Science, 2001, 36(8): 2001–2007. doi: 10.1023/A:1017526830874 [15] BARTHELAT F, RABIEI R. Toughness amplification in natural composites [J]. Journal of the Mechanics and Physics of Solids, 2011, 59(4): 829–840. doi: 10.1016/j.jmps.2011.01.001 [16] SONG F, BAI Y L. Effects of nanostructures on the fracture strength of the interfaces in nacre [J]. Journal of Materials Research, 2003, 18(8): 1741–1744. doi: 10.1557/JMR.2003.0239 [17] RABIEI R, BEKAH S, BARTHELAT F. Failure mode transition in nacre and bone-like materials [J]. Acta Biomaterialia, 2010, 6(10): 4081–4089. doi: 10.1016/j.actbio.2010.04.008 [18] SHAO Y, ZHAO H P, FENG X Q, et al. Discontinuous crack-bridging model for fracture toughness analysis of nacre [J]. Journal of the Mechanics and Physics of Solids, 2012, 60(8): 1400–1419. doi: 10.1016/j.jmps.2012.04.011 [19] GHAZLAN A, NGO T, VAN LE T, et al. Blast performance of a bio-mimetic panel based on the structure of nacre: a numerical study [J]. Composite Structures, 2020, 234: 111691. doi: 10.1016/j.compstruct.2019.111691 [20] KO K, JIN S, LEE S E, et al. Impact resistance of nacre-like composites diversely patterned by 3D printing [J]. Composite Structures, 2020, 238: 111951. doi: 10.1016/j.compstruct.2020.111951 [21] WU K J, ZHENG Z J, ZHANG S S, et al. Interfacial strength-controlled energy dissipation mechanism and optimization in impact-resistant nacreous structure [J]. Materials & Design, 2019, 163: 107532. doi: 10.1016/j.matdes.2018.12.004 [22] 刘金义, 刘爽. Voronoi图应用综述 [J]. 工程图学学报, 2004, 25(2): 125–132. doi: 10.3969/j.issn.1003-0158.2004.02.023LIU J Y, LIU S. A survey on applications of Voronoi diagrams [J]. Journal of Engineering Graphics, 2004, 25(2): 125–132. doi: 10.3969/j.issn.1003-0158.2004.02.023 [23] BARGMANN S, KLUSEMANN B, MARKMANN J, et al. Generation of 3D representative volume elements for heterogeneous materials: a review [J]. Progress in Materials Science, 2018, 96: 322–384. doi: 10.1016/j.pmatsci.2018.02.003 [24] BAHMANI A, LI G, WILLETT T L, et al. Generating realistic representative microstructure of biomimetic composite materials for computational assessment of mechanical properties [J]. Materials Today: Proceedings, 2019, 7: 373–381. doi: 10.1016/j.matpr.2018.11.098 [25] GHAZLAN A, NGO T D, TRAN P. Three-dimensional Voronoi model of a nacre-mimetic composite structure under impulsive loading [J]. Composite Structures, 2016, 153: 278–296. doi: 10.1016/j.compstruct.2016.06.020 -
下载:
点击查看大图
计量
- 文章访问数: 8352
- HTML全文浏览量: 3760
- PDF下载量: 57
