Anti-Blast Performance of Ultra-High Performance Concrete-Filled Double Steel Tubes under Close-in Blast Loading
-
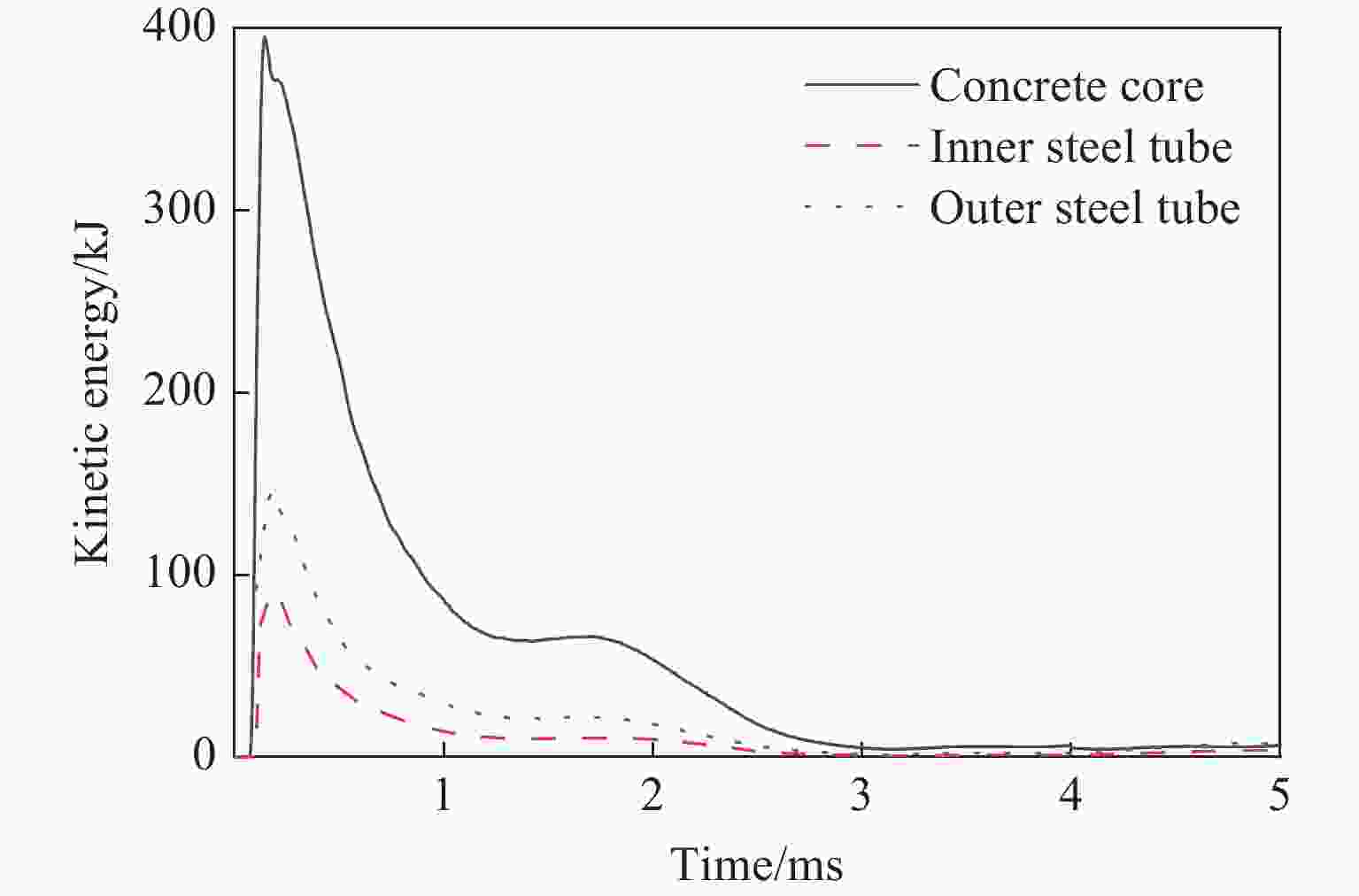
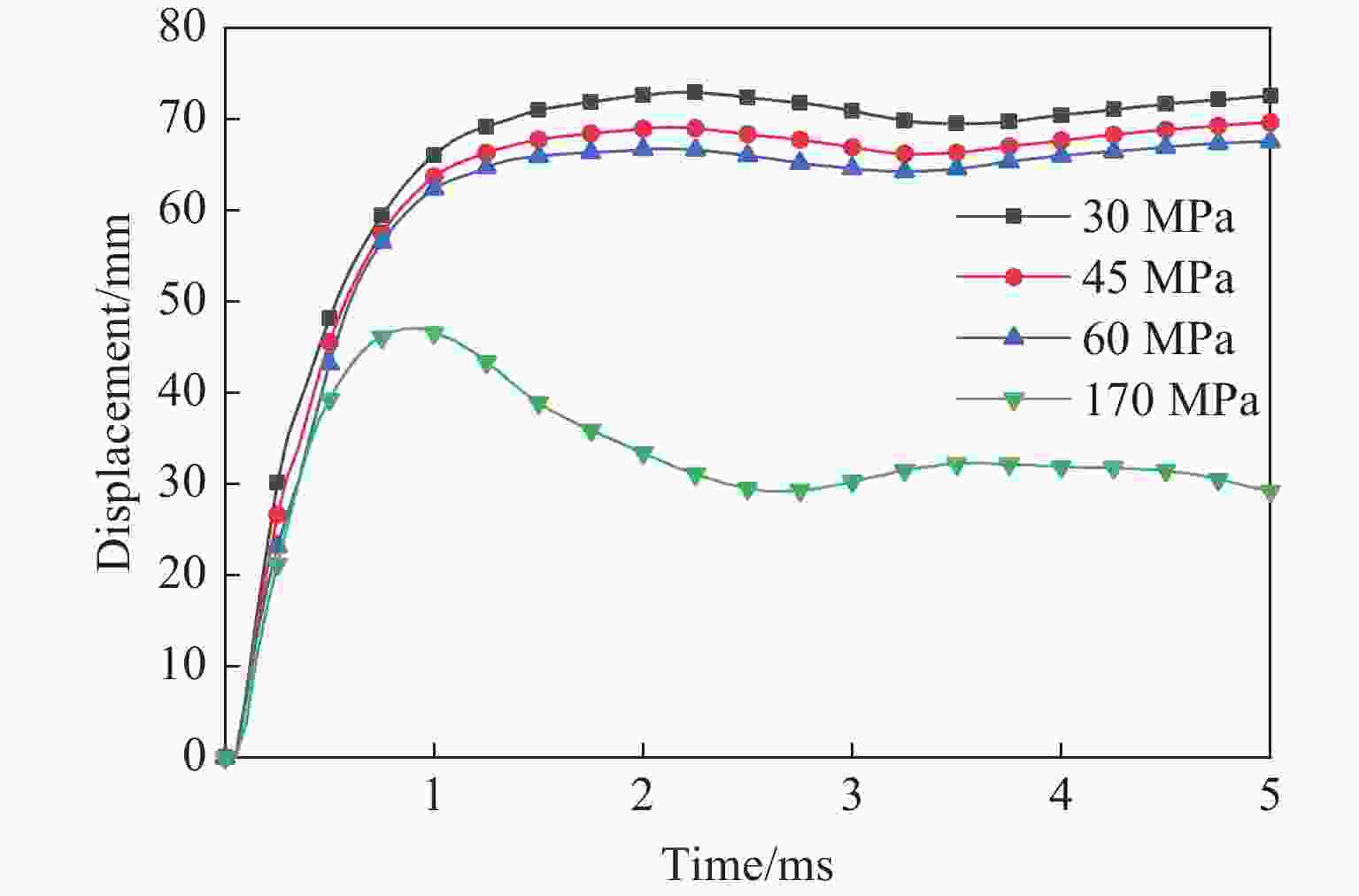
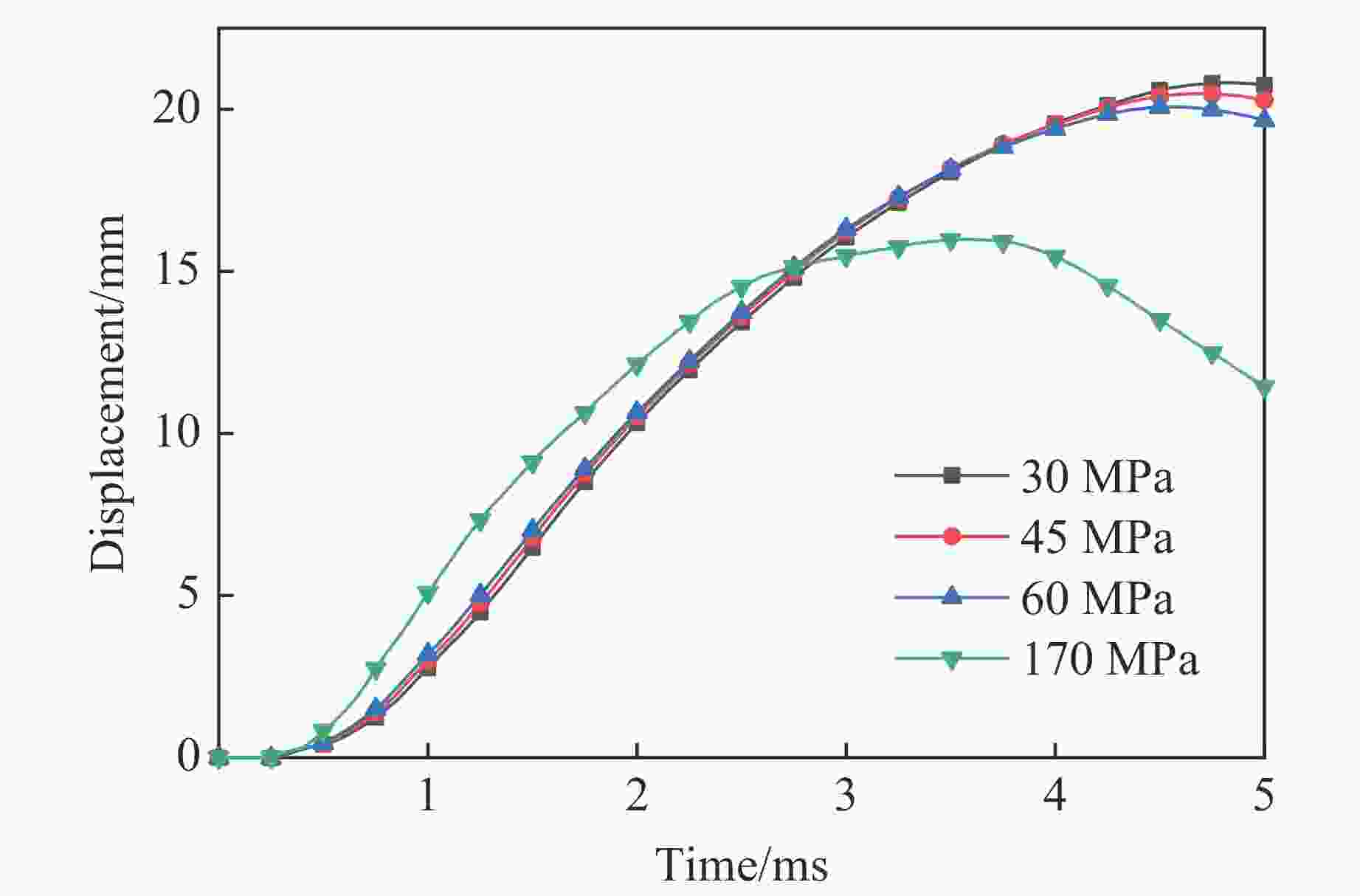
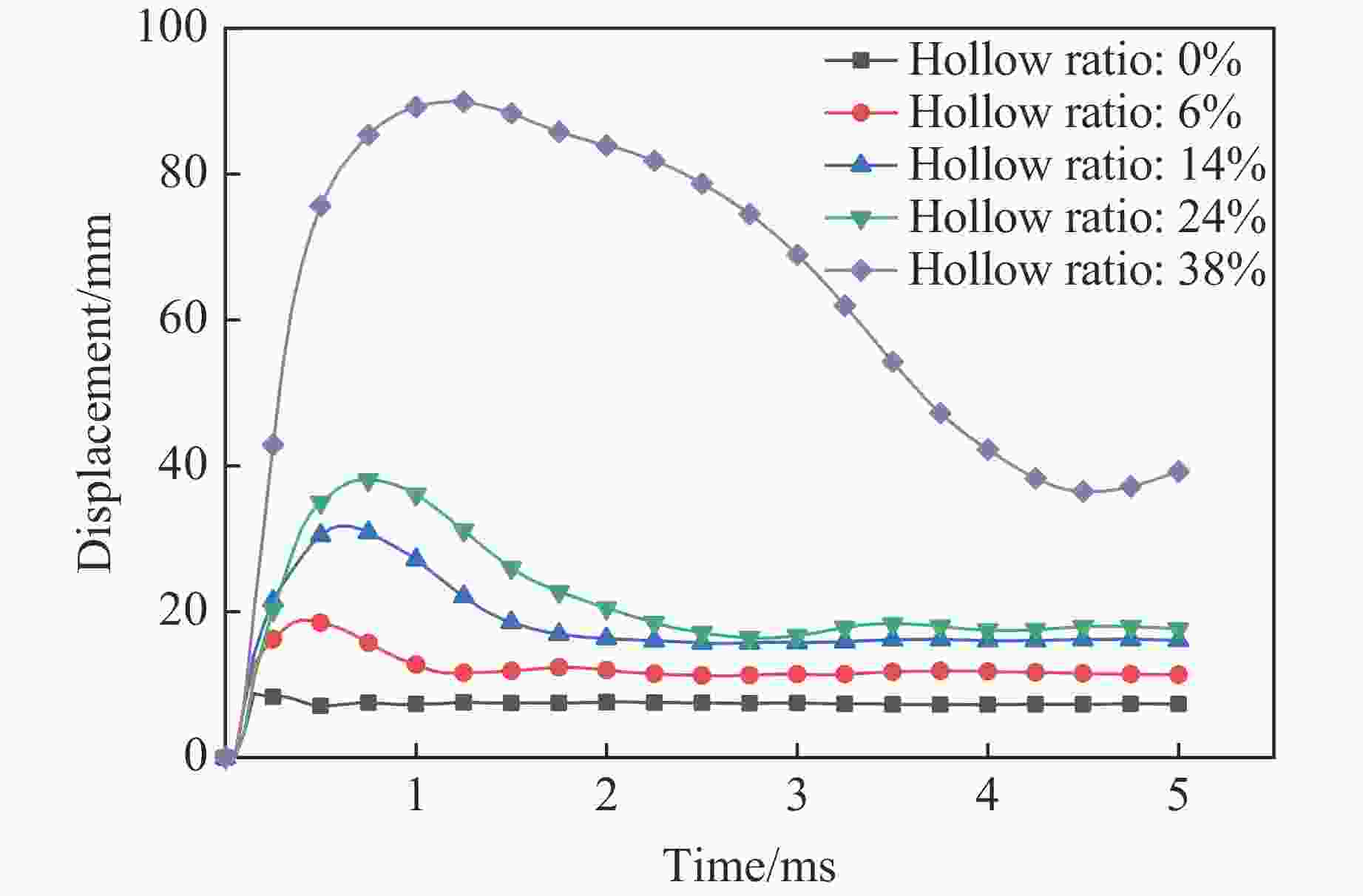
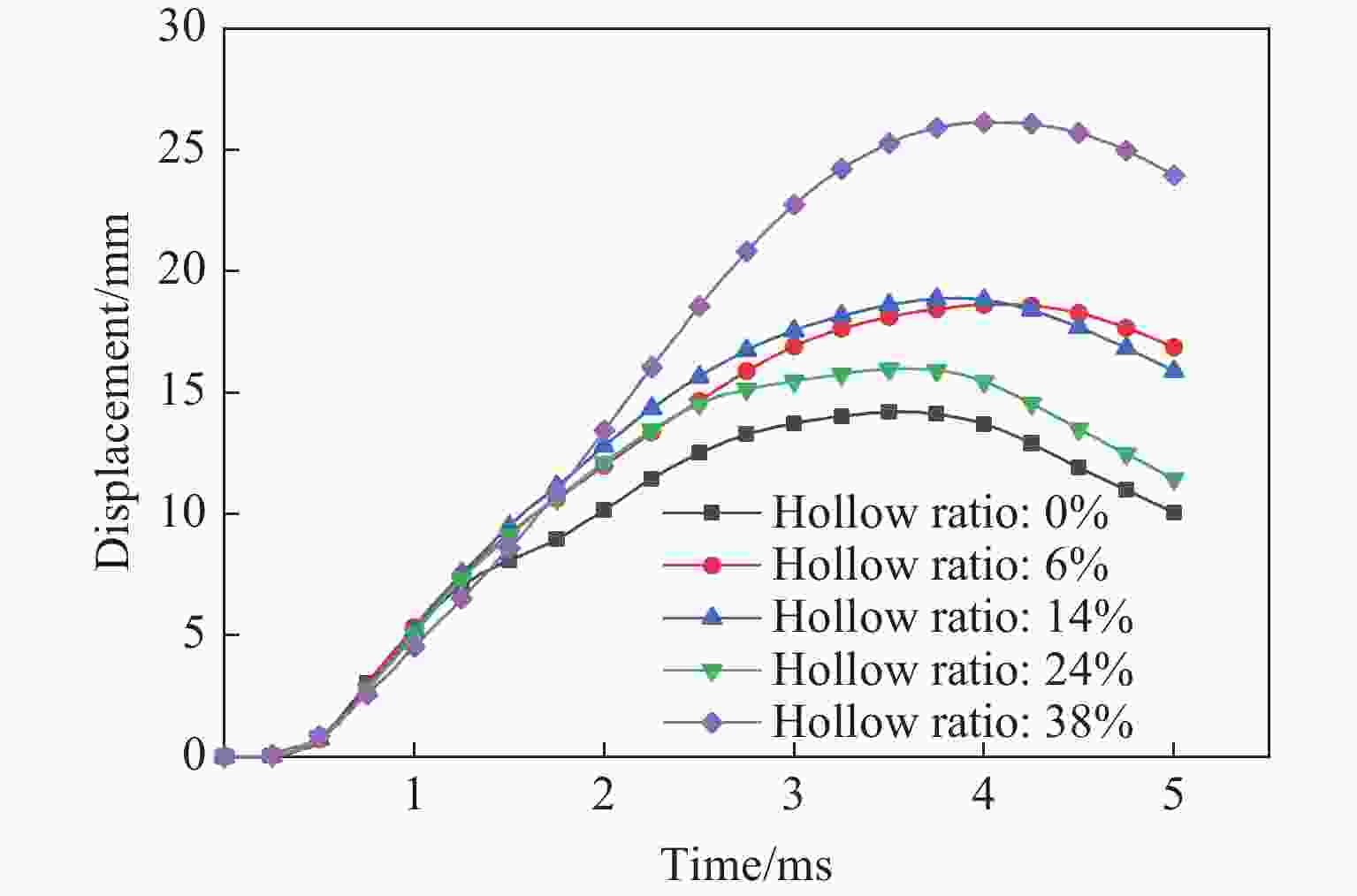
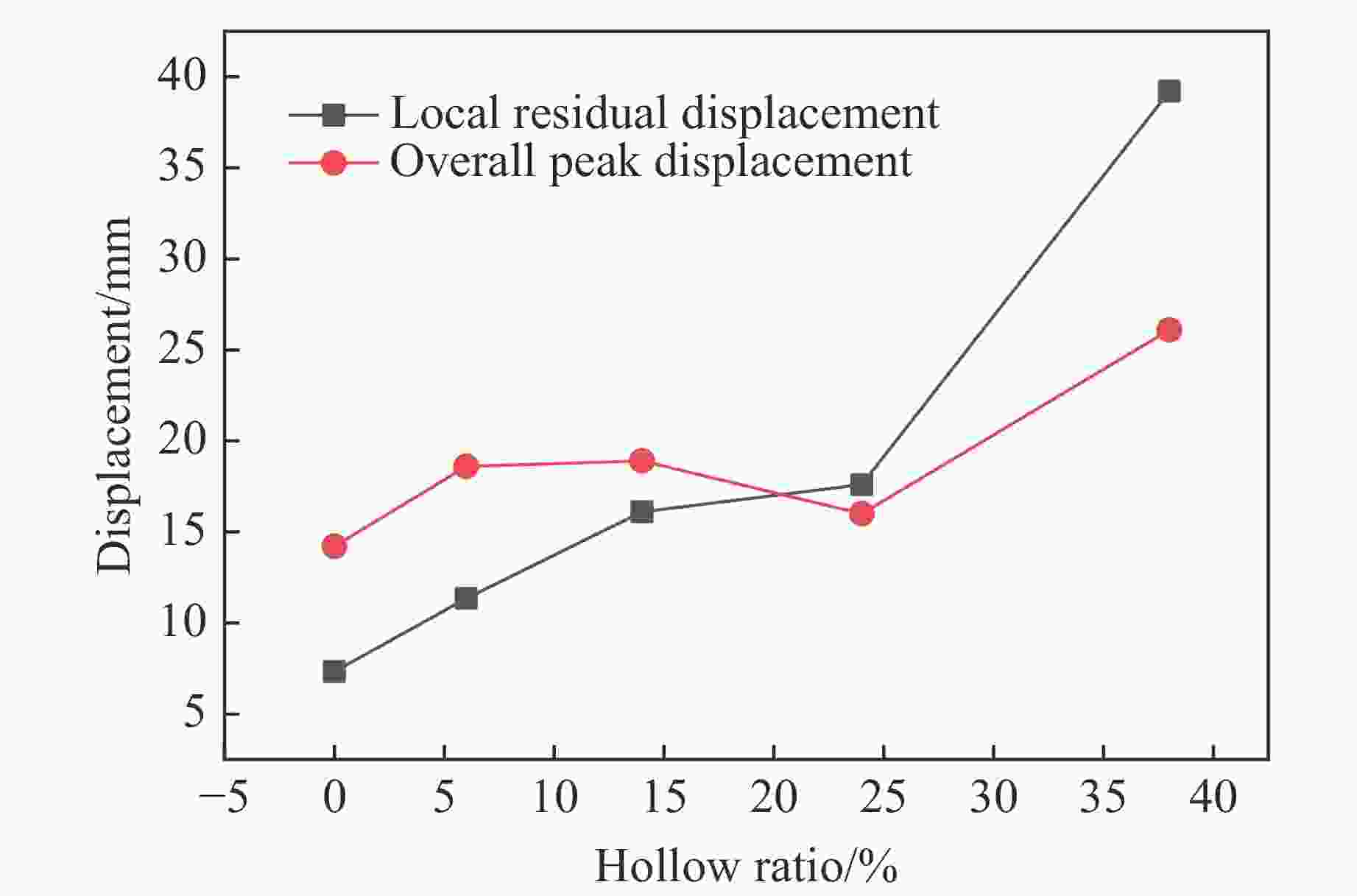
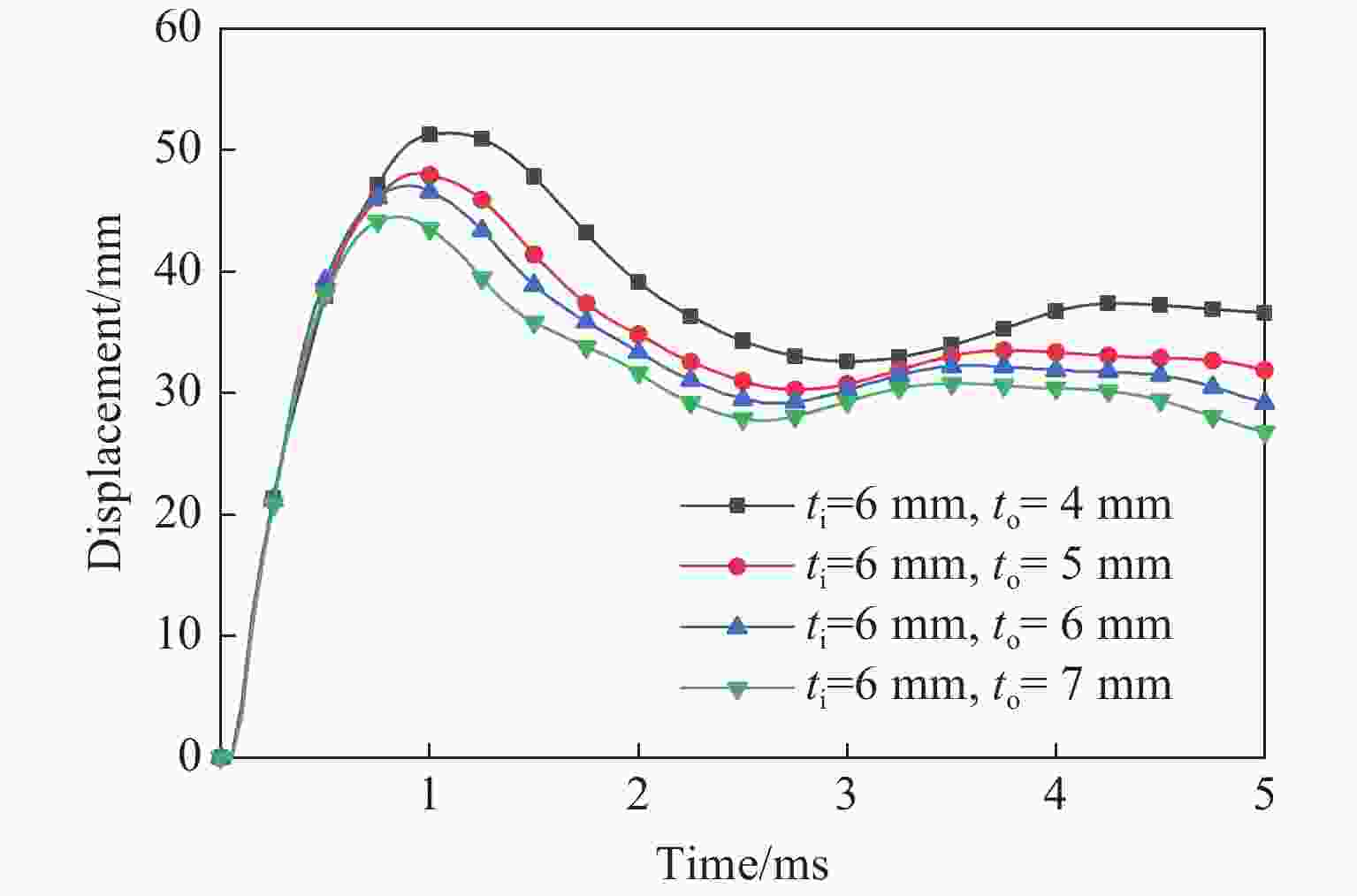
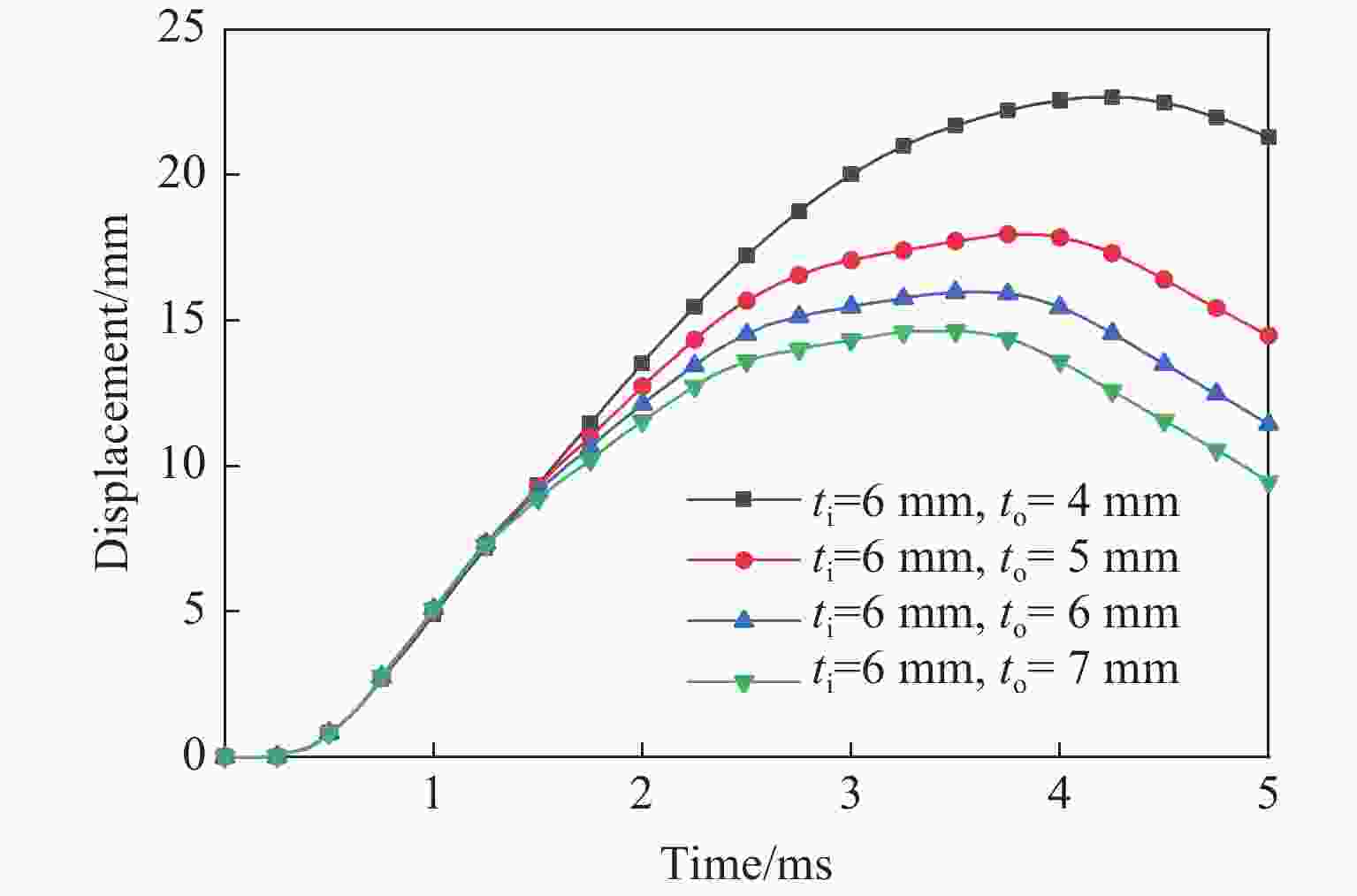
摘要: 为研究中空夹层超高性能钢管混凝土(Ultra-high performance concrete-filled double skin steel tubes, UHPCFDST)柱在近爆载荷作用下的抗爆性能,建立了TNT炸药-UHPCFDST柱-空气三维有限元模型,采用ALE多物质流固耦合算法分析了UHPCFDST柱在近爆作用下的损伤机理、能量吸收特性和影响参数,计算结果表明:UHPCFDST柱在近爆作用下的典型破坏模式为钢管的塑性变形和混凝土芯柱的凹陷破坏,且混凝土芯柱的损伤过程可以分为3个阶段;与填充普通混凝土柱相比,UHPCFDST柱具有优异的抗爆性能;在一定范围内,减小截面空心率可以有效提升UHPCFDST柱的抗爆性能;增加内外钢管厚度均可提升UHPCFDST柱的抗爆性能,但增加外层钢管厚度时提升效果更显著;有无轴压对UHPCFDST柱的变形有较大影响,在一定范围内增加轴压比有利于抵抗整体变形,但同时局部变形增大,当轴压比较大时,UHPCFDST柱在近爆载荷和轴向载荷作用下失去承载能力。
-
关键词:
- 中空夹层超高性能钢管混凝土柱 /
- 近爆 /
- 损伤机理 /
- 能量吸收特性
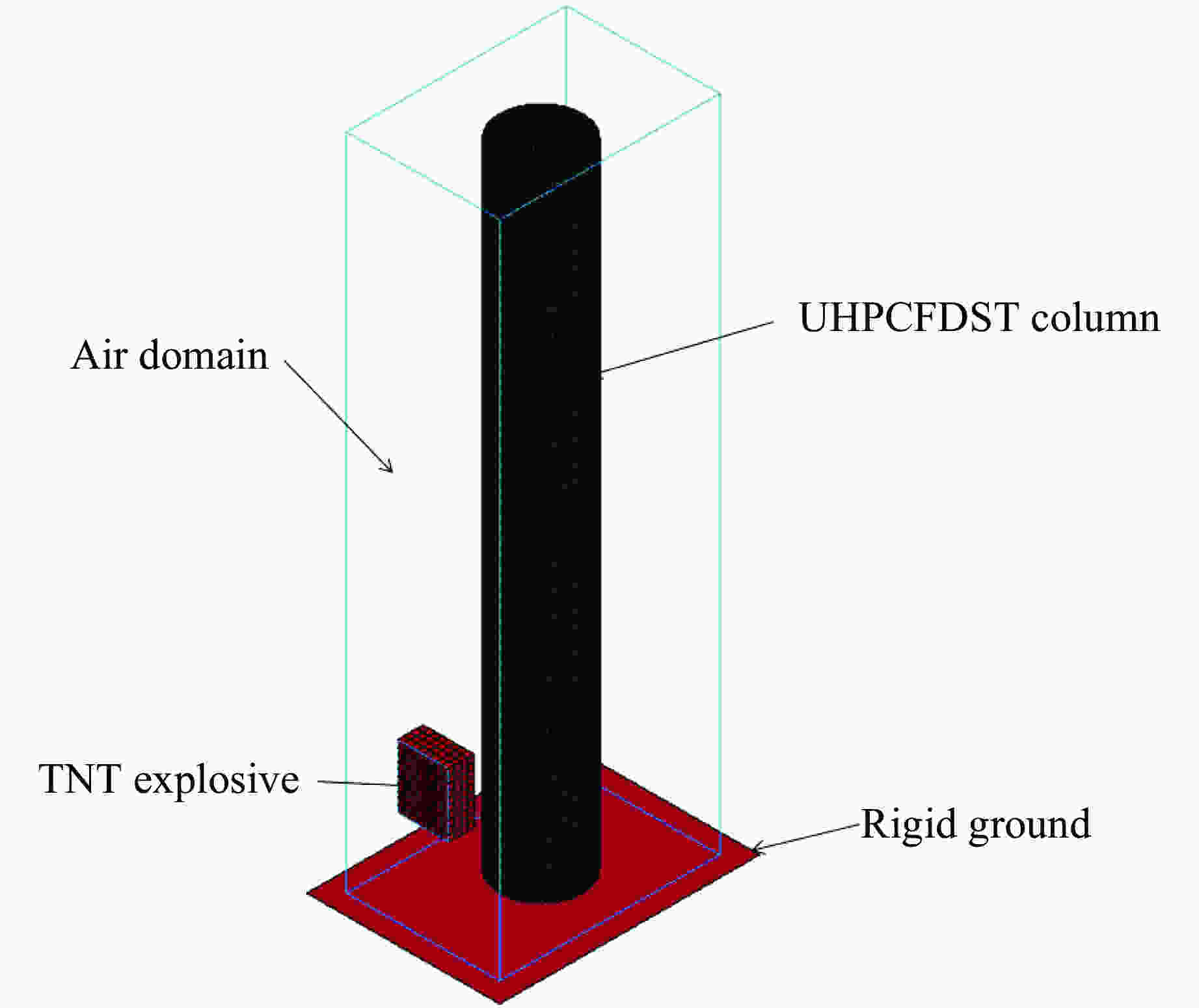
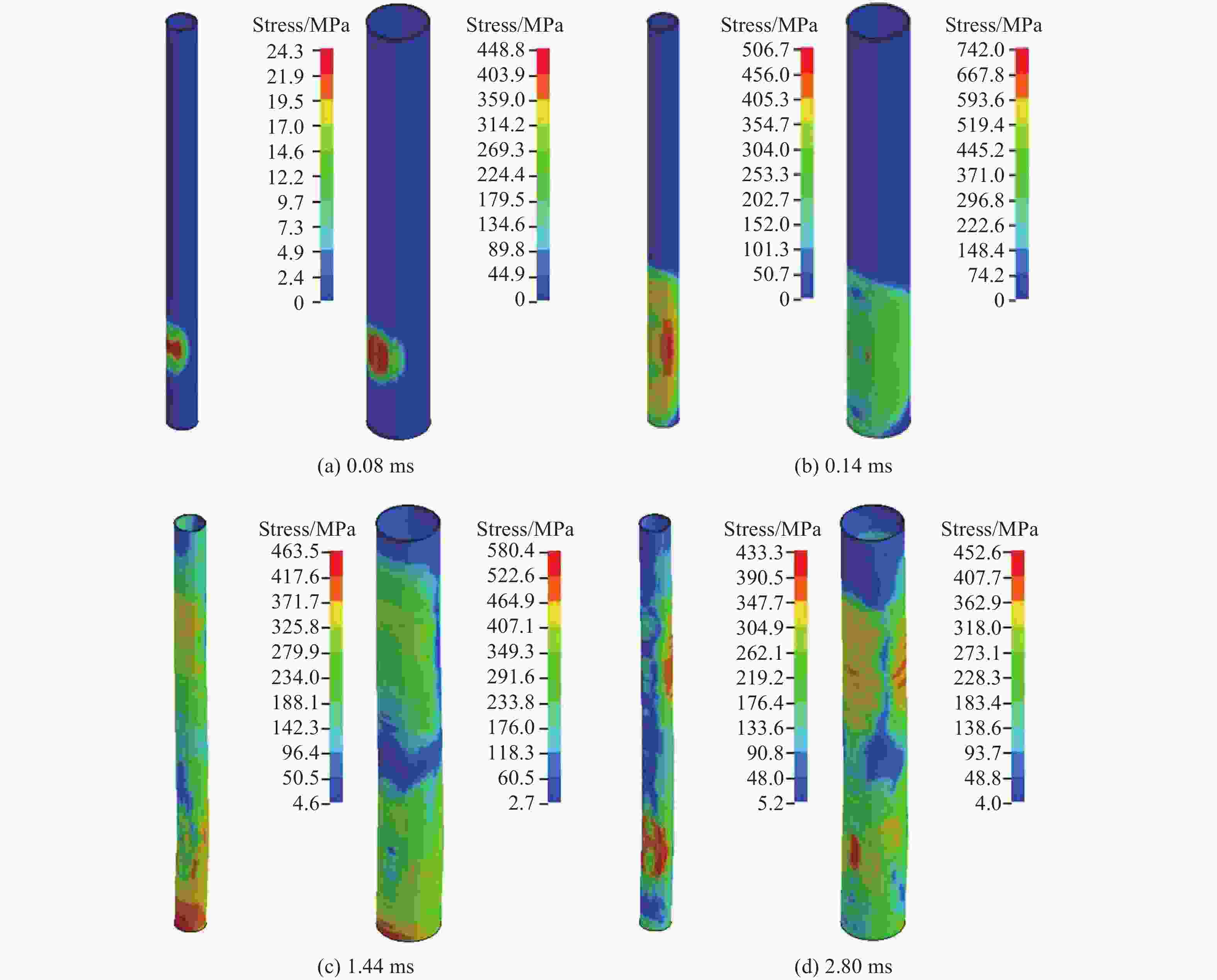
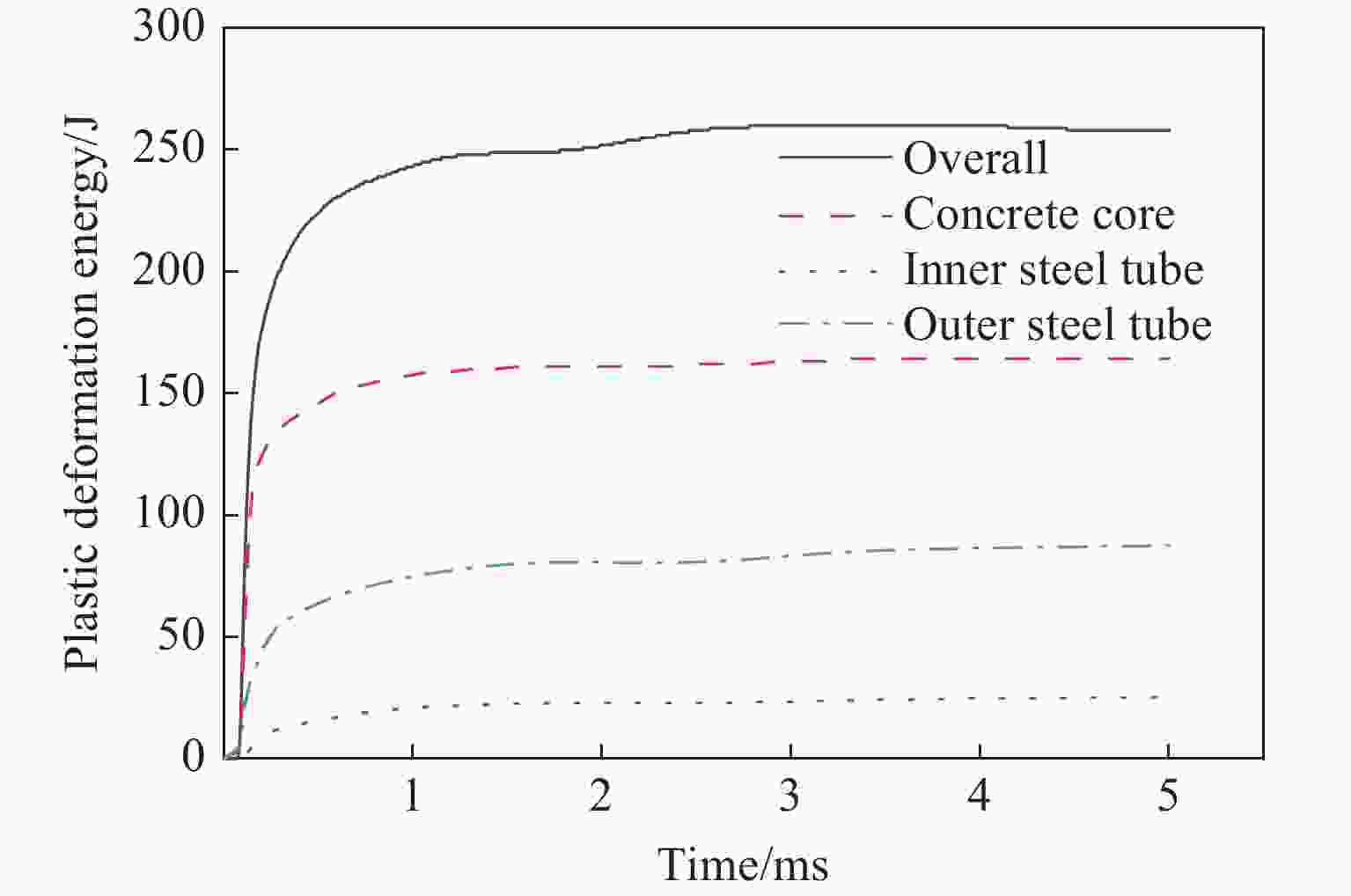
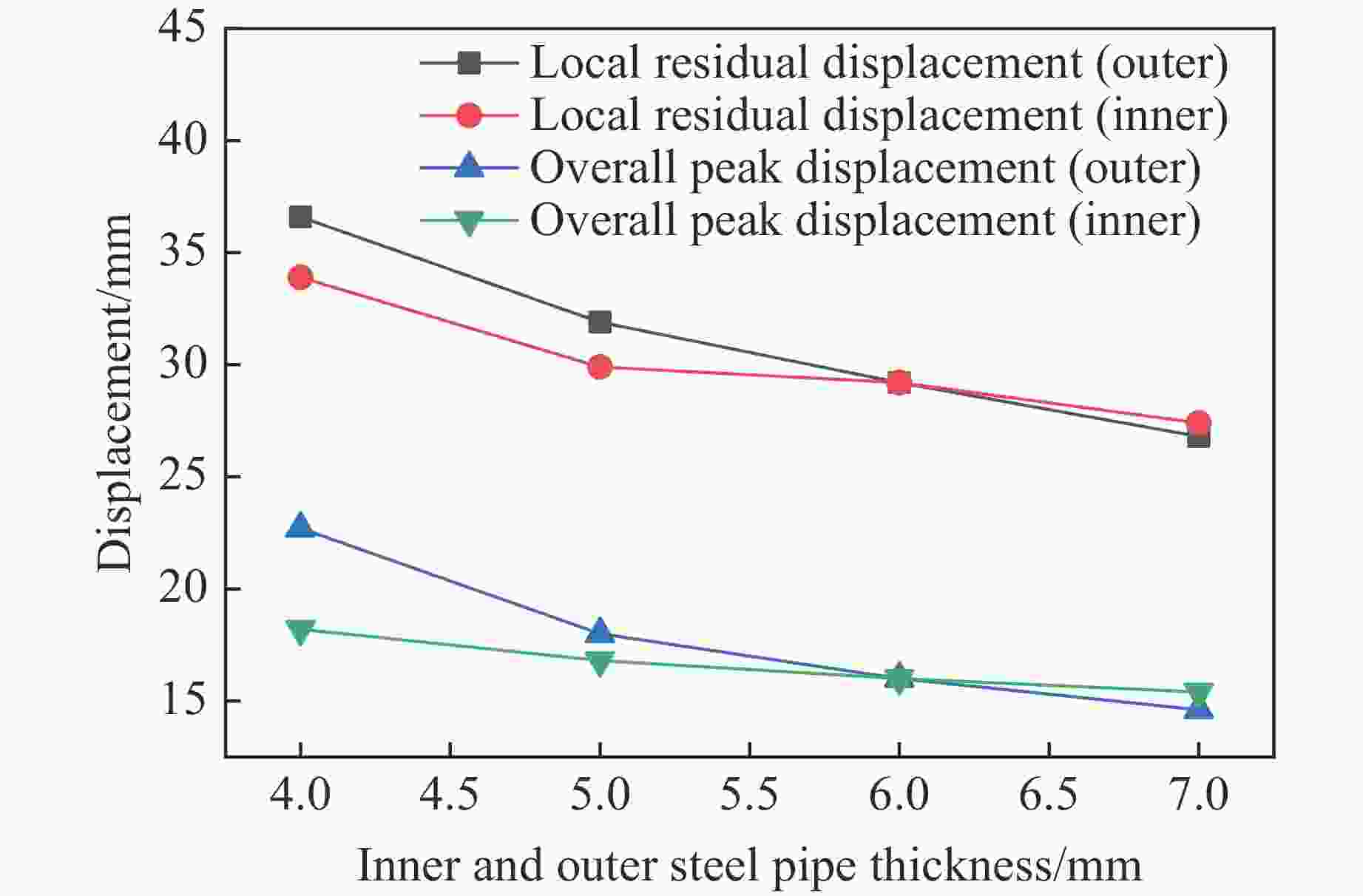
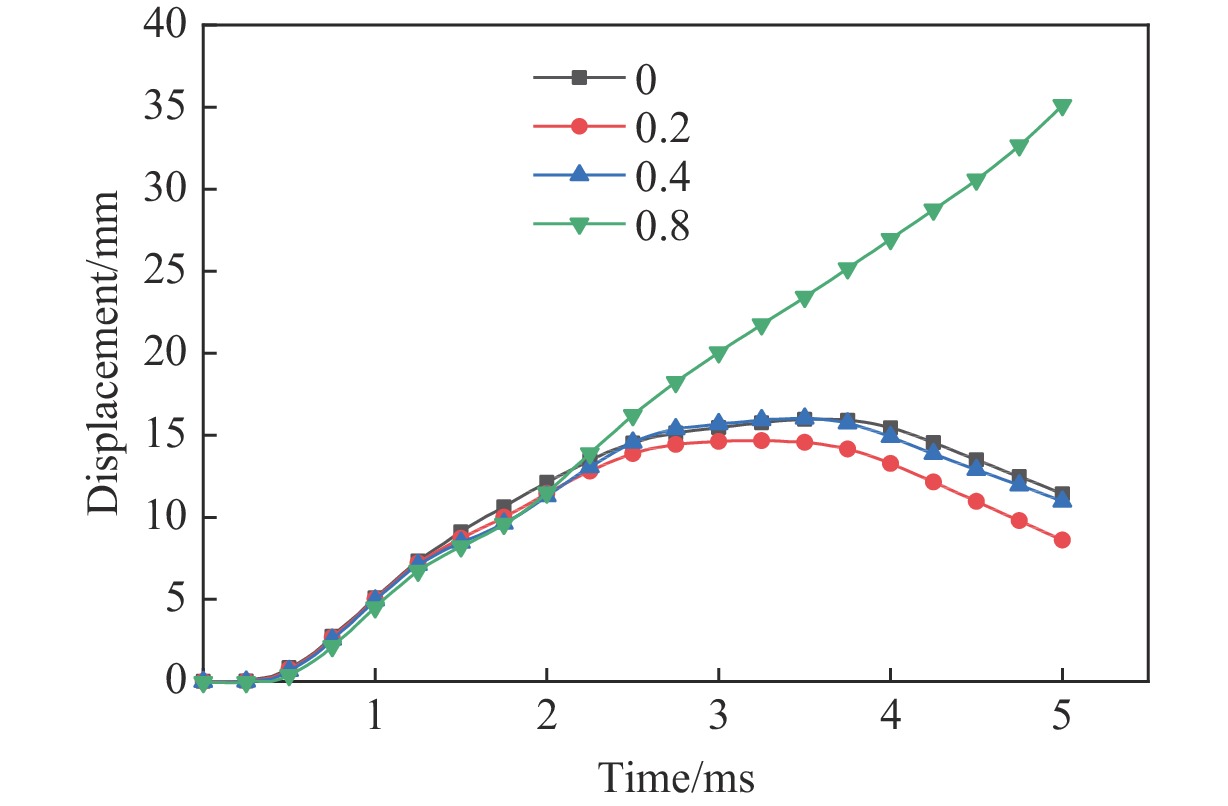
Abstract: In order to study the explosion resistance of ultra-high performance concrete-filled double skin steel tubes (UHPCFDST) under near-explosive loads, a three-dimensional finite element model of TNT explosives-UHPCFDST columns-air was established. The ALE multi-material fluid-solid coupling algorithm is used to analyze the damage mechanism, energy absorption characteristics and influence parameters of UHPCFDST columns under near-explosion. The calculation results show that the typical failure modes of UHPCFDST columns under near-explosion are plastic deformation and the collapse of the concrete core pillar. The damage process of the concrete core pillar can be divided into three stages. Compared with the ordinary concrete column, the UHPCFDST column has superior anti-blast performance; within a certain range, reducing the cross-section hollow ratio can effectively improve the explosion resistance of UHPCFDST columns; increasing the thickness of inner and outer steel pipes, particularly for the inner pipe, can increase the explosion resistance of UHPCFDST columns. The presence of axial pressure has a great influence on the deformation of the UHPCFDST column. The increase of axial pressure ratio, within a certain range is beneficial to resisting the overall deformation. As the axial pressure continues to increase, local deformation increases and the UHPCFDST column would lose its strength under the combined effects of the near-blast and the axial loads. -
A/GPa B/GPa R1 R2 $\omega $ $\;\rho $e/(kg·m−3) D/(m·s−1) p/GPa E/(MJ·kg−1) 373.8 3.75 4.5 0.9 0.35 1 640 5730 19 6.93 表 2 空气的主要参数
Table 2. Main parameters of air
C0 C1 C2 C3 C4 C5 C6 $\;\rho $a/(kg·m−3) E0/(J·m−3) V0 0 0 0 0 0.4 0.4 0 1.29 2.5 × 105 1.0 Material $\;\rho $s/(kg·m−3) Es/GPa $\nu $ Y/MPa $\tau $/GPa C/s−1 P Steel 7 850 206 0.3 348.5 2.1 6 844 3.91 表 4 UHPC关键参数
Table 4. Key parameters of UHPC
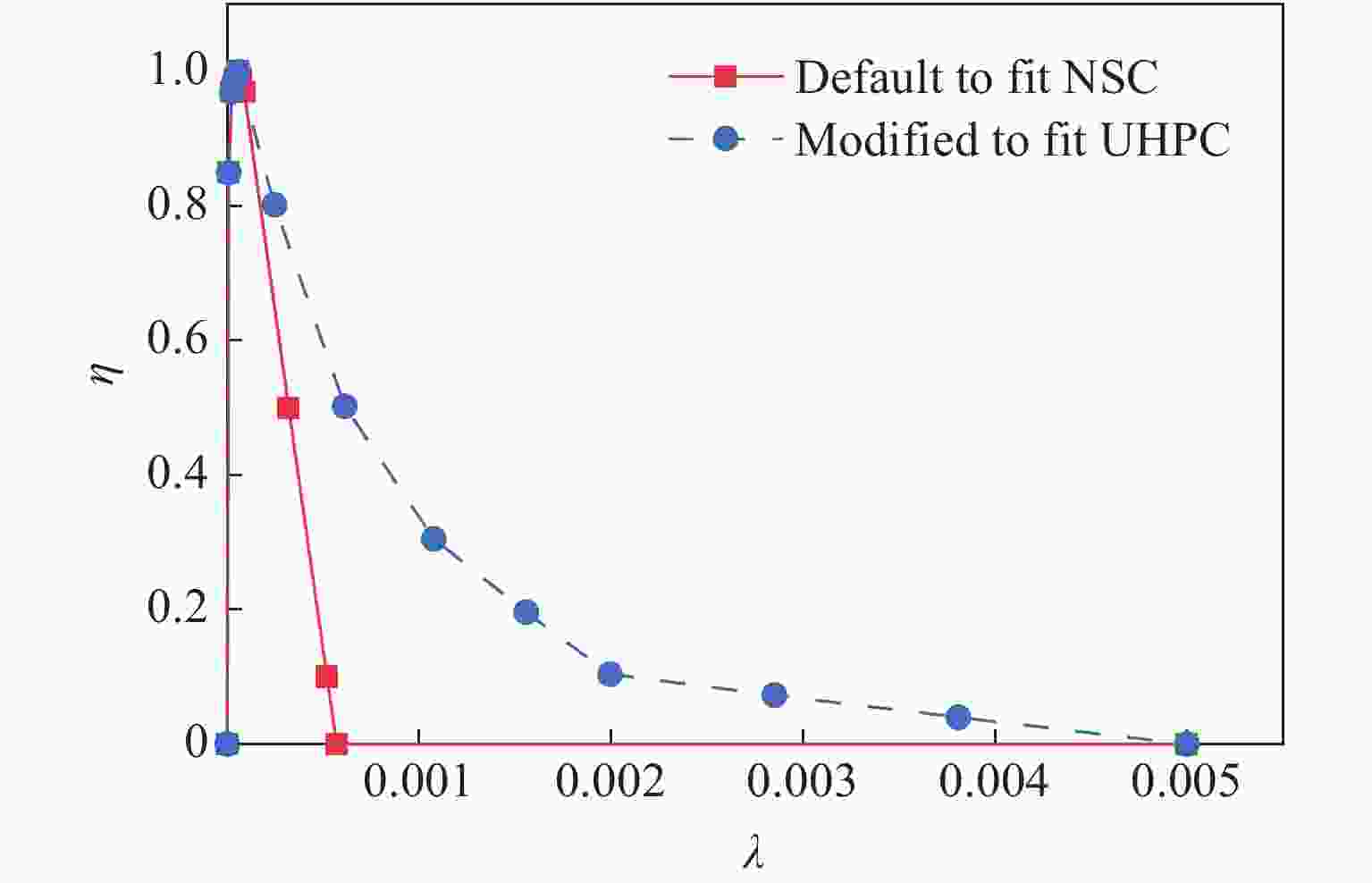
Material $\;\rho $0/(kg·m-3) Fc/MPa Ft/MPa $\nu $ B1 WLZ/mm $\omega $ UHPC 2 400 170 18 0.19 0.80 6 0.10 表 5 网格划分细节和结果
Table 5. Meshing details and results
Mesh No. Meshing details Denting depth/mm Along the radial Along the circumference Along the height 1 1 + 8 + 1 40 100 66.5 2 2 + 15 + 2 80 200 72.6 3 3 + 15 + 3 120 300 73.2 表 6 CFDST凹陷位移试验值[10]与数值模拟值对比
Table 6. Comparison of the CFDST depression displacement between experiments[10] and numerical simulations
Explosive mass/kg CFDST depression displacement/mm Error/% Experiment Simulation 5 29.3 28.6 2.4 8 77.7 72.6 6.6 表 7 不同工况数值模型参数
Table 7. Model parameters in different working conditions
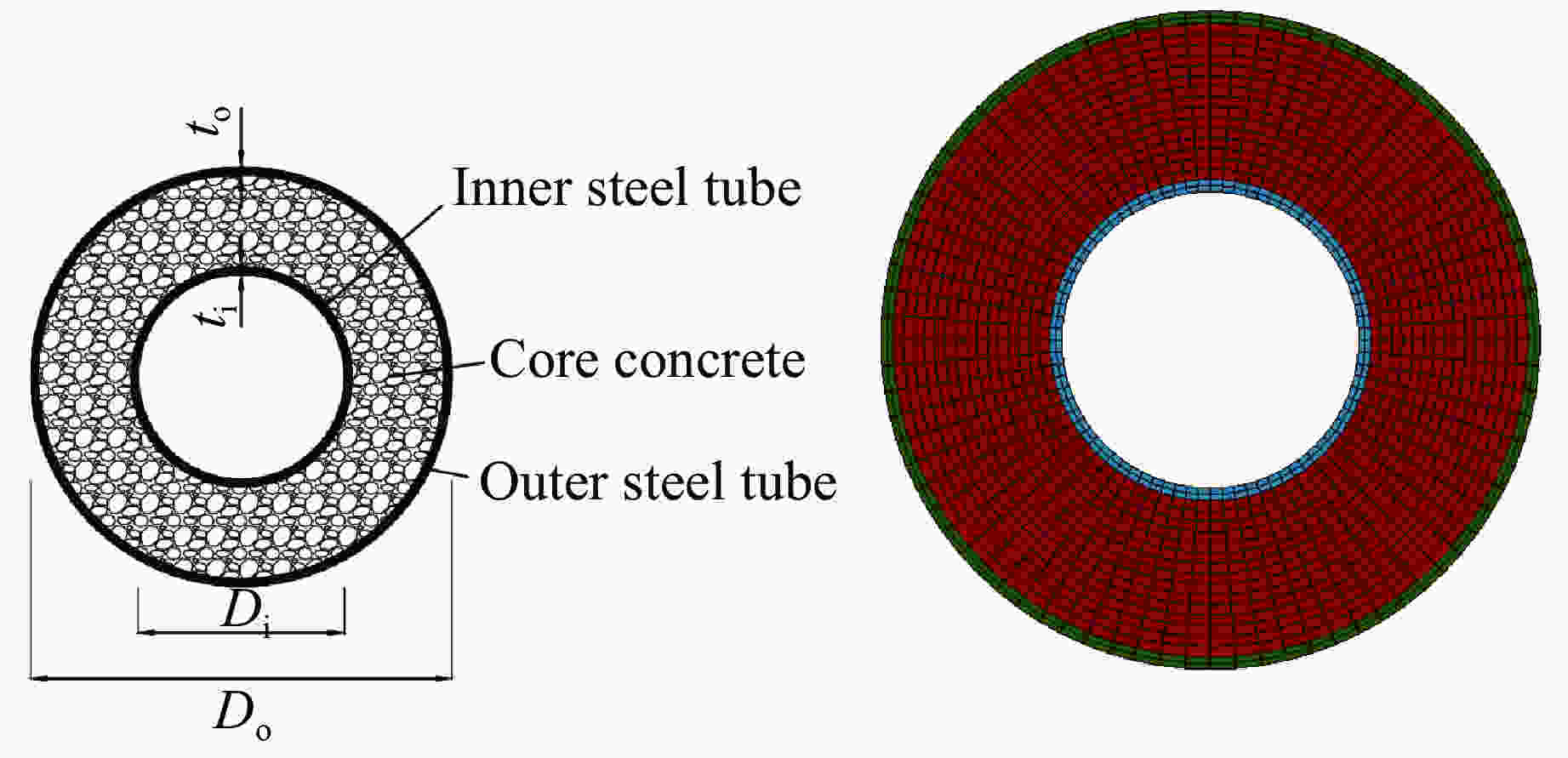
Group No. Di/mm ti/mm Do/mm to/mm Outer steel pipe thickness change 1 159 6 325 4 2 159 6 325 5 3 159 6 325 6 4 159 6 325 7 Inner steel pipe thickness change 5 159 4 325 6 6 159 5 325 6 7 159 6 325 6 8 159 7 325 6 -
[1] XU J C, WU C Q, XIANG H B, et al. Behaviour of ultra high performance fibre reinforced concrete columns subjected to blast loading [J]. Engineering Structures, 2016, 118(1): 97–107. [2] AOUDE H, BELGHITI M, COOK W D, et al. Response of steel fiber-reinforced concrete beams with and without stirrups [J]. ACI Structural Journal, 2012, 109(3): 359–367. [3] 金何伟, 刘中宪, 刘申永, 等. 钢管超高强钢纤维混凝土柱抗爆性能试验研究 [J]. 建筑结构, 2016, 46(4): 45–49.JIN H W, LIU Z X, LIU S Y, et al. Experimental study of ultra-high performance fiber reinforced concrete filled steel tube columns under blast loading [J]. Building Structure, 2016, 46(4): 45–49. [4] ZHANG F R, WU C Q, ZHAO X L, et al. Experimental and numerical study of blast resistance of square CFDST columns with steel-fibre reinforced concrete [J]. Engineering Structures, 2017, 149: 50–63. doi: 10.1016/j.engstruct.2016.06.022 [5] 徐慎春, 刘中宪, 吴成清. 方形中空夹层钢管超高性能钢纤维混凝土柱抗爆性能数值模拟与实验验证 [J]. 振动与冲击, 2017, 36(1): 45–54.XU S C, LIU Z X, WU C Q. Numerical simulation and test validation for ultra-high performance steel fiber reinforced concrete-tilled double skin steel tube column under blast loading [J]. Journal of Vibration and Shock, 2017, 36(1): 45–54. [6] 徐慎春, 刘中宪, 吴成清. 圆形中空夹层钢管超高性能钢纤维混凝土柱抗爆性能野外实验与数值模拟 [J]. 爆炸与冲击, 2017, 37(4): 649–660.XU S C, LIU Z X, WU C Q. Field blast test and numerical simulation of ultra-high performance steel fiber reinforced concrete-filled double skin steel tube column under blast loading [J]. Explosion and Shock Waves, 2017, 37(4): 649–660. [7] 赵海鸥. LS-DYNA动力分析指南 [M]. 北京: 兵器工业出版社, 2003: 82–86.ZHAO H O. LS-DYNA dynamic analysis guide [M]. Beijing: Ordnance Industry Press, 2003: 82–86. [8] 于川, 李良忠, 黄毅民. 含铝炸药爆轰产物JWL状态方程研究 [J]. 爆炸与冲击, 1999, 19(3): 274–279.YU C, LI L Z, HUANG Y M. Studies on JWL equation of state of detonation product for aluminized explosives [J]. Explosion and Shock Waves, 1999, 19(3): 274–279. [9] 李翼祺, 马素贞. 爆炸力学 [M]. 北京: 科学出版社, 1992: 60–67.LI Y Q, MA S Z. Explosion mechanics[M]. Beijing: Science Press, 1992: 60–67. [10] LI M H, ZONG Z H, HAO H, et al. Experimental and numerical study on the behaviour of CFDST columns subjected to close-in blast loading [J]. Engineering Structures, 2019, 185(1): 203–220. [11] WANG R, HAN L H, ZHAO X L, et al. Analytical behavior of concrete filled double steel tubular (CFDST) members under lateral impact [J]. Thin-Walled Structures, 2016, 101(1): 129–140. [12] WANG R, HAN L H, HOU C C. Behavior of concrete filled steel tubular (CFST) members under lateral impact: experiment and FEA model [J]. Journal of Constructional Steel Research, 2013, 80: 188–201. doi: 10.1016/j.jcsr.2012.09.003 [13] MAO L, BARNETT S, BEGG D, et al. Numerical simulation of ultra high performance fibre reinforced concrete panel subjected to blast loading [J]. International Journal of Impact Engineering, 2014, 64: 91–100. doi: 10.1016/j.ijimpeng.2013.10.003 [14] ISAACS J, MAGALLANES J, REBENTROST M, et al. Exploratory dynamic material characterizing tests on ultra-high performance fibre reinforced concrete [C]//Proceedings of 8th International Conference on Shock and Impact Loads on Structures. Adelaide, Australia, 2009, 1(4): 337–344. [15] JAYASOORIYA R, THAMBIRATNAM D P, PERERA N J. Blast response and safety evaluation of a composite column for use as key element in structural systems [J]. Engineering Structures, 2014, 61: 31–43. doi: 10.1016/j.engstruct.2014.01.007 [16] WU K C, LI B, TSAI K C. The effects of explosive mass ratio on residual compressive capacity of contact blast damaged composite columns [J]. Journal of Constructional Steel Research, 2011, 67(4): 602–612. doi: 10.1016/j.jcsr.2010.12.001 [17] MALVAR L J, CRAWFORD J E, WESEVICH J W, et al. A plasticity concrete material model for DYNA3D [J]. International Journal of Impact Engineering, 1997, 19(9/10): 847–873. [18] MALVAR L J, CRAWFORD J E, MORRILL K B, et al. K&C concrete material model release Ⅲ: automated generation of material model input: TR-99-24 -B1 [R]. K&C Technical Report, 2009: 154–163. [19] WANG F W Y, CHONG Q Y K, LIM C H. Reinforced concrete slab subjected to close-in explosion [C]//The Second International Workshop on Performance Procection and Strengthening of Structure under Extreme Loading, 2009: 43–48. -










 下载:
下载: