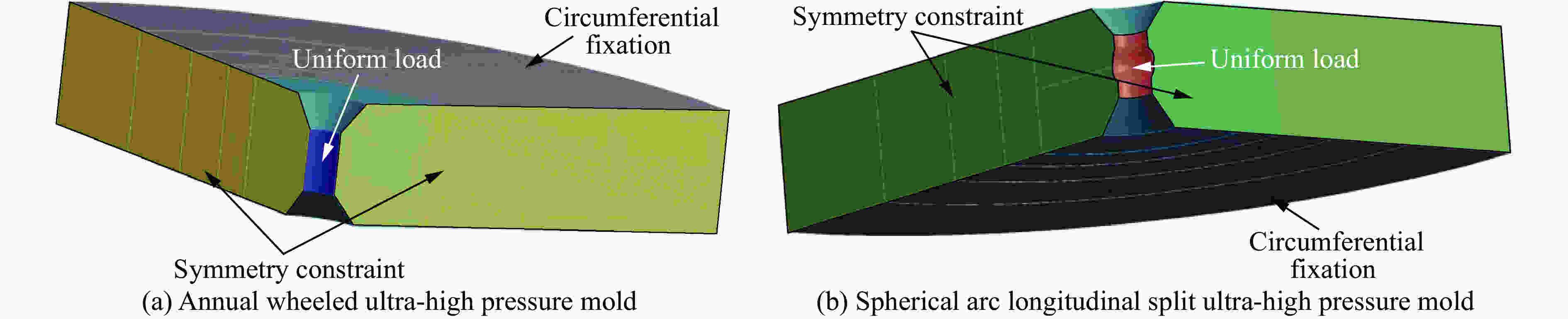
Spherical Arc Longitudinal Split Ultra-High Pressure Mold
-
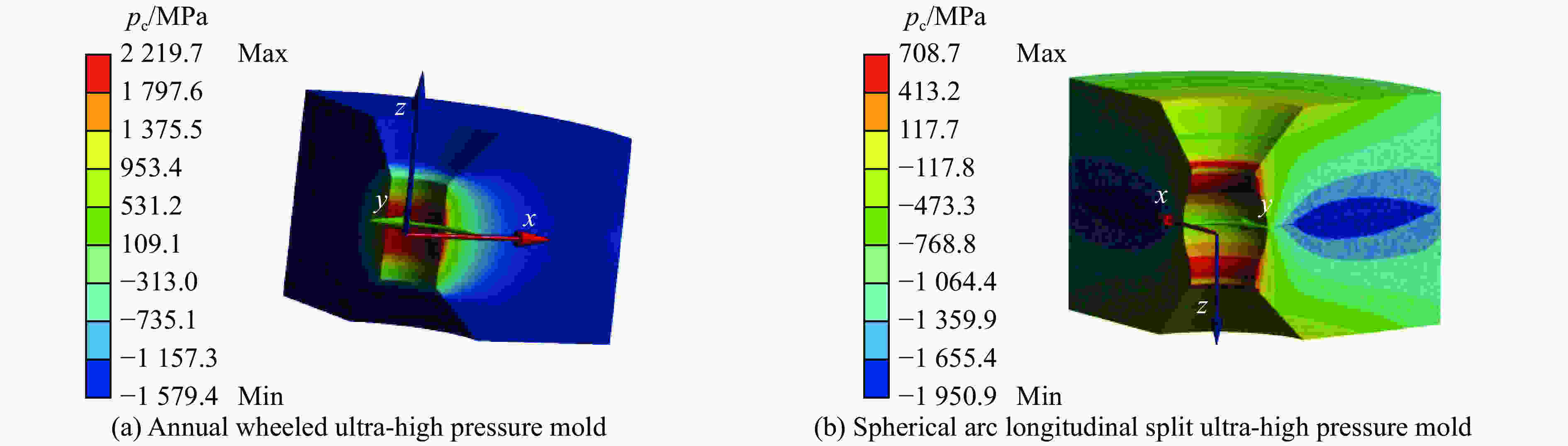
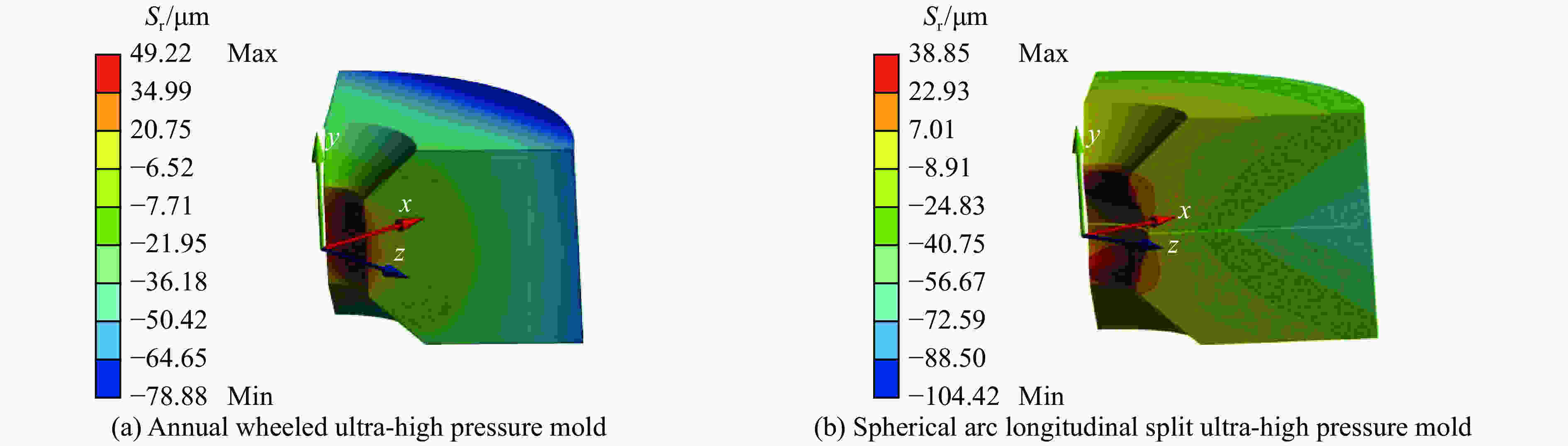
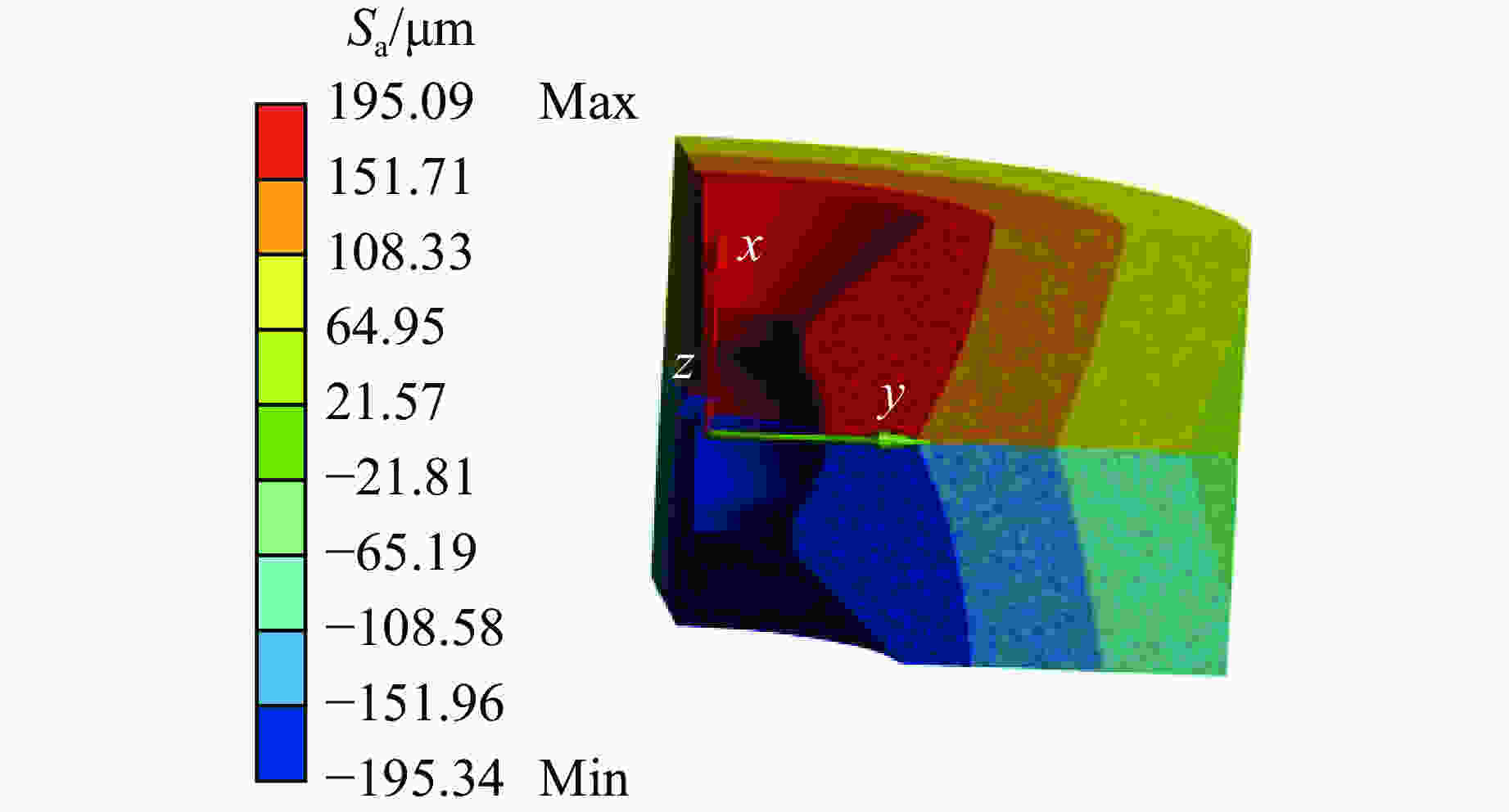
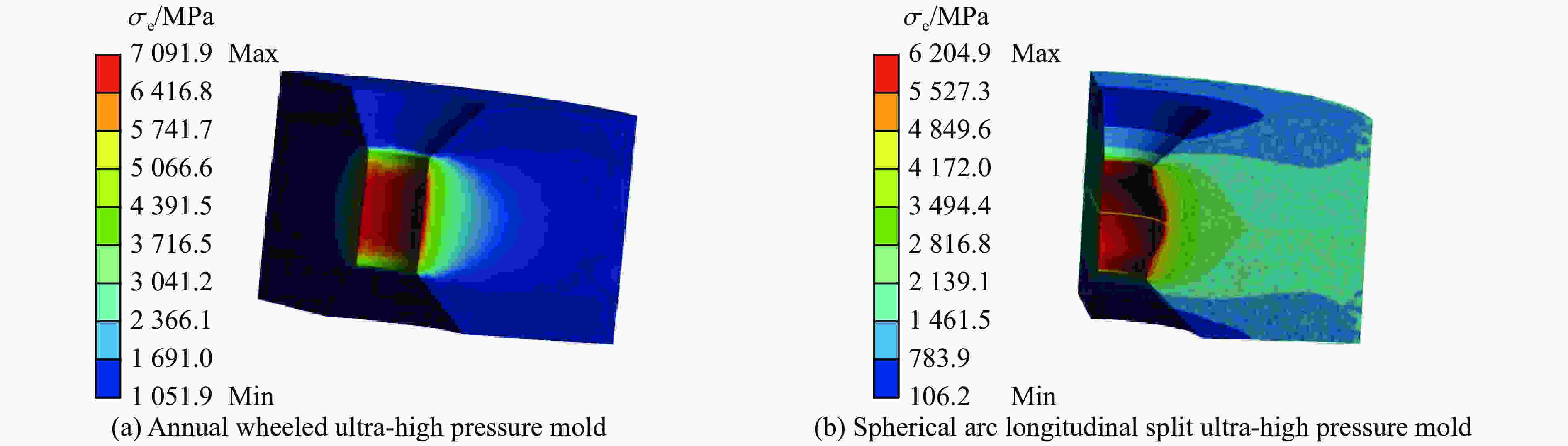
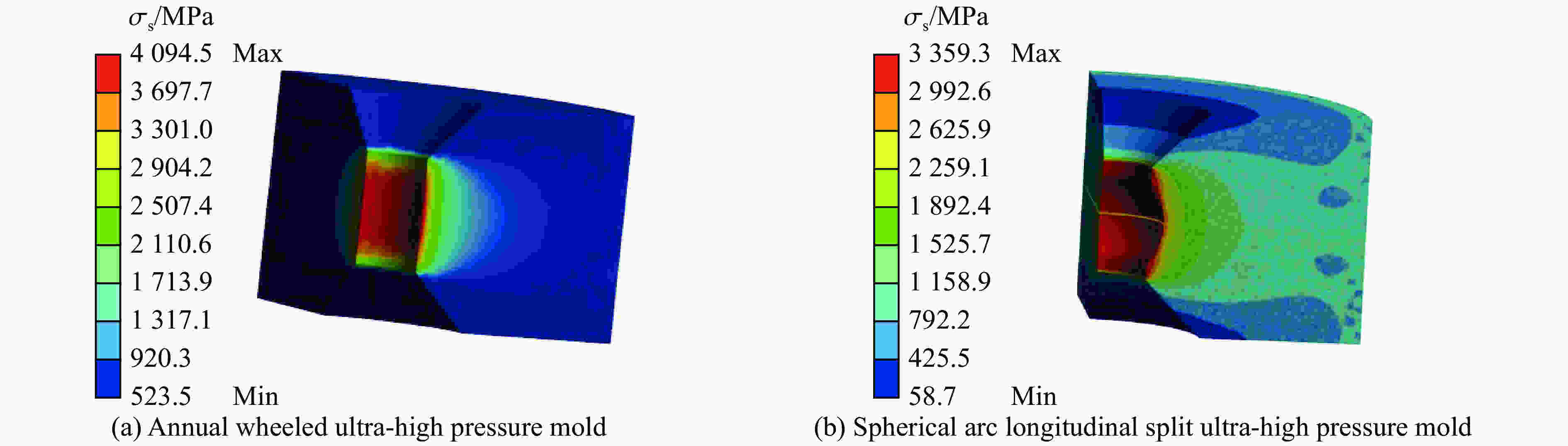
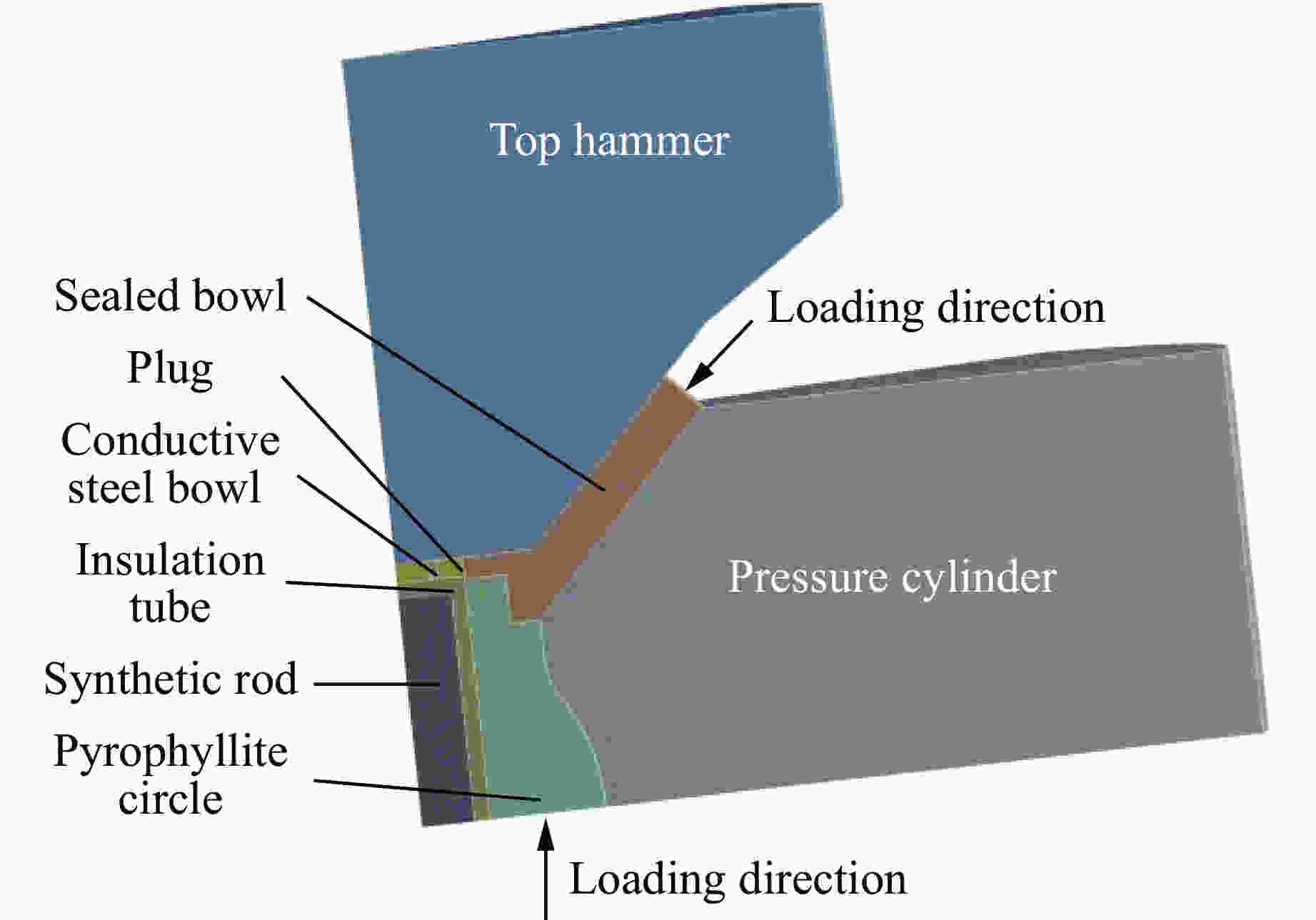
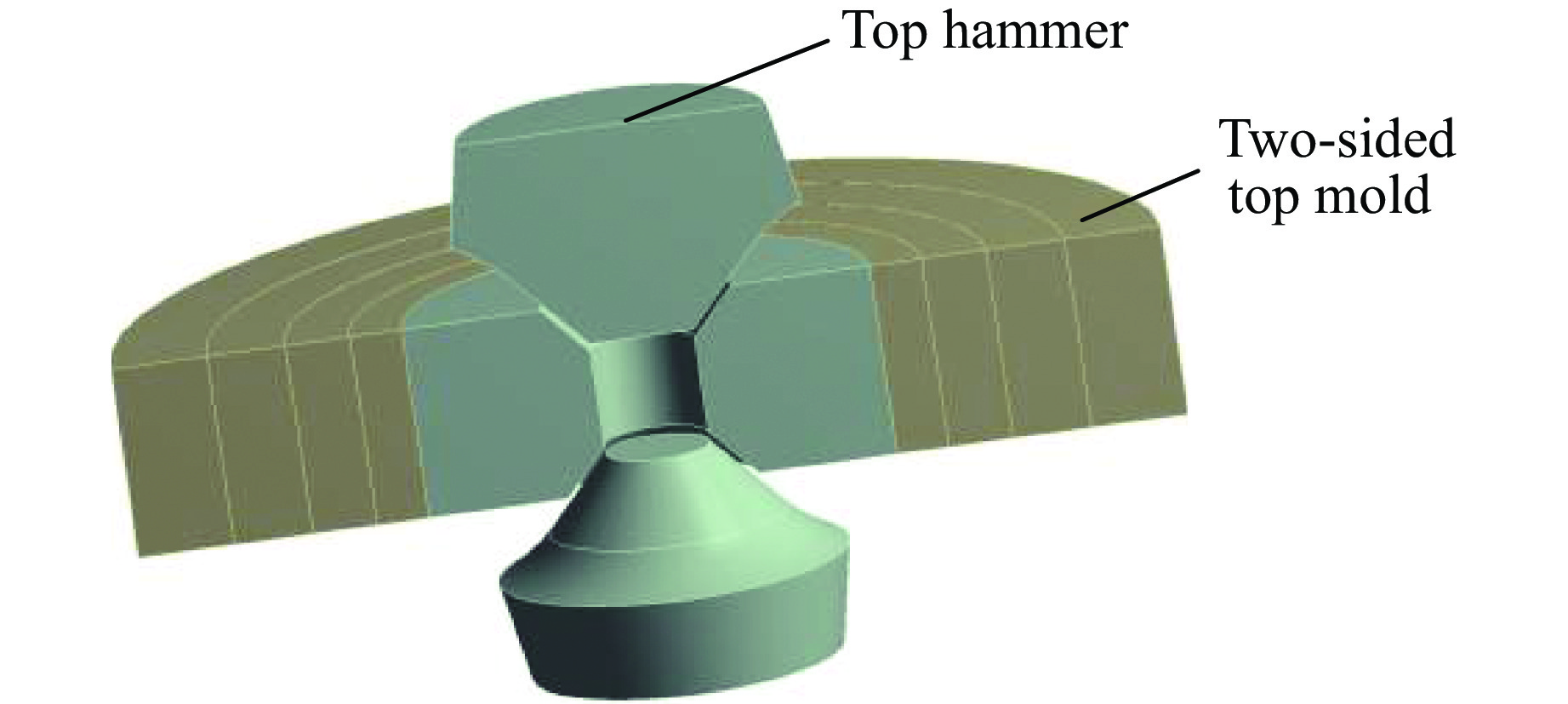
摘要: 为了提高普通年轮式超高压模具的最大承载能力,提出了一种新型球弧式纵向剖分超高压模具结构。该模具的球弧式结构将对超高压模具损害最大的周向拉应力转变为轴向应力,并通过纵向剖分方式降低了轴向应力,提高了超高压模具压缸的极限承载能力。球弧式纵向剖分超高压模具不仅可以降低超高压模具的最大等效应力和最大切向应力,而且模具的腔体容积也相应增大。数值模拟结果表明:在相同载荷条件下,球弧式纵向剖分超高压模具的周向拉应力、等效应力和最大切向应力分别比普通年轮式超高压模具减小了68.1%、12.5%和18.0%。球弧式纵向剖分超高压模具的径向位移也有利于提高压缸的保压能力,同时球弧式纵向剖分超高压模具的腔体容积也比普通年轮式模具提高了约43%。分析表明,球弧式纵向剖分结构有利于提高生产效率,增加模具的使用寿命。Abstract: In order to improve the maximum bearing capacity of ordinary annual wheeled ultra-high pressure molds, a new spherical arc longitudinally split ultra-high pressure mold structure is proposed. Due to the spherical-arc structure, the circumferential tensile stress of the ultra-high pressure mold that has suffered the most damage is converted into axial stress. Then, the axial stress is reduced by the longitudinal division method, thus improving the ultimate bearing capacity of the ultra-high pressure mold cylinder. Spherical-arc longitudinal splitting of the ultra-high pressure mold can not only reduce the equivalent stress and the maximum tangential stress of the ultra-high pressure mold, but also greatly increase the cavity volume of the mold. The numerical analysis results show that: under the same load condition, the circumferential tensile stress, equivalent stress and maximum tangential stress of the spherical-type longitudinally split ultra-high pressure mold are lower than ordinary annual wheel-type ultra-high pressure molds by 68%, 12.5% and 18.0%, respectively. The radial displacement of the spherical-arc longitudinally split ultra-high pressure mold is also conducive to improving the pressure-holding capacity of the cylinder, and the cavity volume of the spherical-arc longitudinally split ultra-high pressure mold is also increased by about 43% compared to that of the ordinary annual wheel mold. The analysis shows that the spherical-arc longitudinal split structure helps to improve the production efficiency and mold life.
-
Key words:
- ultra-high pressure mould /
- ball-arc /
- longitudinal division /
- numerical analysis
-
Material Density/(g·cm−3) Elastic modulus/GPa Poisson’s ratio Failure strength/MPa Shear strength/MPa YG8 14.60 578 0.22 6 200 3 250 45CrNiMoVA 7.83 210 0.29 1 600 800 表 2 两种模具压缸相关应力和腔体容积
Table 2. Various stresses and cavity volumes of the two mold cylinders
Mold type Circumferential
tensile stress/MPaRadial expansion
displacement/μmMaximum
equivalent stress/MPaMaximum
shear stress/MPaCavity
volume/mm3Annual wheeled
mold2219.7 49.22 7091.9 4094.5 859.35 Spherical arc
longitudinally split mold708.7 38.85 6204.9 3359.3 1228.30 -
[1] 王伯龙, 李明哲, 刘志卫, 等. 新型切向分块式两面顶超高压模具 [J]. 高压物理学报, 2019, 33(1): 013102. doi: 10.11858/gywlxb.20180595WANG B L, LI M Z, LIU Z W, et al. A novel tangential split-belt ultrahigh pressure apparatus [J]. Chinese Journal of High Pressure Physics, 2019, 33(1): 013102. doi: 10.11858/gywlxb.20180595 [2] 姚裕成. Belt型超高压模具若干问题研究和降低金刚石生产成本的途径 [J]. 人工晶体学报, 1995, 24(2): 166–171. doi: 10.16553/j.cnki.issn1000-985x.1995.02.018YAO Y C. Research on some problems with Belt-type tools and the ways of reducing the production costs of diamond [J]. Journal of Synthetic Crystals, 1995, 24(2): 166–171. doi: 10.16553/j.cnki.issn1000-985x.1995.02.018 [3] 赵亮. 剖分式超高压模具的设计与研究[D]. 长春: 吉林大学, 2018.ZHAO L. Design and research of split-type ultra-high pressure die [D]. Changchun: Jilin University, 2018. [4] 郭泽荣, 袁梦琦. 机械与压力容器安全[M]. 北京: 北京理工大学出版社, 2017: 120−121.GUO Z R, YUAN M Q. Safety of mechanical and pressure vessels [M]. Beijing: Beijing Institute of Technology Press, 2017: 120−121. [5] 杨云飞. 压缸切向剖分式超高压模具的研究[D]. 长春: 吉林大学, 2016.YANG Y F. Research on tangential split cylinder of ultrahigh pressure die [D]. Changchun: Jilin University, 2016. [6] 刘志国, 千正男. 高压技术[M]. 哈尔滨: 哈尔滨工业大学出版社, 2012: 48−51.LIU Z G, QIAN Z N. High pressure technology [M]. Harbin: Harbin Institute of Technology Press, 2012: 48−51. [7] 颜永年, 俞新陆. 机械设计中的预应力结构[M]. 北京: 机械工业出版社, 1989: 55−56.YAN Y N, YU X L. Prestressed structure in mechanical design [M]. Beijing: Machinery Industry Press, 1989: 55−56. [8] 依卓. 双层剖分式超高压模具结构设计与有限元分析[D]. 长春: 吉林大学, 2019.YI Z. Structural design and finite element analysis of double-layer split ultrahigh pressure die [D]. Changchun: Jilin University, 2019. [9] 刘志卫. 多层交错剖分式超高压模具设计及其数值模拟[D]. 长春: 吉林大学, 2014.LIU Z W. Design and simulation of multilayer stagger-split type ultrahigh pressure die [D]. Changchun: Jilin University, 2014. [10] 王伯龙. 预紧式多层交错剖分超高压模具研究[D]. 长春: 吉林大学, 2016.WANG B L. Research on prestressed multilayer stagger-split ultrahigh pressure die [D]. Changchun: Jilin University, 2016. [11] 依卓, 付文智, 李明哲. 双层剖分式超高压模具数值模拟及实验 [J]. 吉林大学学报(工学版), 2019, 49(5): 1593–1599. doi: 10.13229/j.cnki.jdxbgxb20180556YI Z, FU W Z, LI M Z. Numerical simulation and experiment on double-layered split ultrahigh pressure die [J]. Journal of Jilin University (Engineering and Technology Edition), 2019, 49(5): 1593–1599. doi: 10.13229/j.cnki.jdxbgxb20180556 [12] 来小丽, 周春梅, 王强. 预应力结构模具设计理论的研究 [J]. 科技信息, 2009(8): 7–8. doi: 10.3969/j.issn.1001-9960.2009.08.005LAI X L, ZHOU C M, WANG Q. Research on die design theory of prestressed structure [J]. Science & Technology Information, 2009(8): 7–8. doi: 10.3969/j.issn.1001-9960.2009.08.005 [13] 王鹏, 王强, 蔡冬梅, 等. Marc有限元在Belt型两面顶模具应力分析中的应用 [J]. 人工晶体学报, 2008, 37(1): 162–166. doi: 10.16553/j.cnki.issn1000-985x.2008.01.019WANG P, WANG Q, CAI D M, et al. Application of marc software in stress analysis of Belt-type apparatus [J]. Journal of Synthetic Crystals, 2008, 37(1): 162–166. doi: 10.16553/j.cnki.issn1000-985x.2008.01.019 -







 下载:
下载: