-
石榴子石的分子式为X3Y2Z3φ12，X、Y、Z分别表示十二面体、八面体和四面体位置，φ表示阴离子位。通常来说，X和Y位分别被2价阳离子（Ca2+、Mg2+、Fe2+、Mn2+）和3价阳离子（Al3+、Fe3+、Cr3+）占据；Z位被Si4+占据，φ表示的阴离子位被O2−、OH−和F−占据[1]。由于十二面体和八面体位置可广泛发生离子替代，因此天然石榴子石往往以复杂的固溶体形式存在。离子替代会改变石榴子石结构，进而影响体弹模量[2-4]、微量元素分配[5-6]、宏观热力学性质[7-11]等物理及化学性质。
振动光谱可以用于固溶体结构研究，如键长、键角、离子有序度和晶格畸变等[12-15]。前人研究主要侧重2价阳离子替代[12, 14, 16]，其中，由于Mg2+、Ca2+的离子半径差较大，镁铝榴石-钙铝榴石（Pyr-Gro）固溶体被重点关注[12-14]。研究表明，较大的离子半径差使得低频峰位发生明显偏移，随成分变化线性程度差，亦可产生双模式振动[17]。
现阶段针对3价阳离子替代的研究较少。考虑到八面体位置上Fe3+、Al3+的质量和半径（0.654和0.535 Å[18]）均有较大差别，钙铝榴石-钙铁榴石（Gro-And）固溶体的混合行为值得关注。已有的X射线衍射研究表明，Gro-And固溶体晶胞大小并非理想变化，且在近钙铝榴石端元处有负超额体积[19-20]。McAloon等[15]和Boffa Ballaran等[19]的红外（IR）光谱研究结果表明，多数固溶体样品峰位随成分呈线性变化，低频峰位线性较差。Fe3+平动峰强度大于Al3+，同时观测到大离子半径差造成双模式振动。目前，Gro-And固溶体的拉曼（Raman）光谱研究仍然缺乏。
本研究首先合成10组不同成分的Gro-And固溶体样品（3 GPa，1 100～1 200 ℃），通过Raman光谱分析Al3+-Fe3+替代对结构的影响；然后讨论高、中、低频峰变化特点及其与结构的关系，并解释额外峰和峰宽化现象的产生原因；最后通过建立半峰宽与热力学性质的关系，预测Gro-And固溶体混合焓特征。
-
钙铝榴石-钙铁榴石固溶体（Ca3(AlxFe1-x)2Si3O12, 0 ≤ x ≤ 1.0）合成实验在北京大学高温高压实验室的六面顶压机[21]中完成，合成压力为3 GPa，合成温度为1200 ℃，合成时间为24～28 h。实验细节参考文献[20]。实验所有样品均产出石榴子石相和熔体相。电子探针数据结果显示，石榴子石成分均匀，3价铁比例（Fe3+/(Fe2++Fe3+)）大于95%，样品描述参考文献[20]。
常温常压下非偏正拉曼光谱测试在北京大学地球与空间科学学院完成，测试仪器为雷尼绍公司In Via Reflex激光显微拉曼光谱仪，波数采集范围为100～1 200 cm−1。实验使用50 × 长焦距物镜，激光波长532 nm，发射功率50 mW。仪器光斑直径约1 µm，光谱分辨率1 cm−1，使用硅片校准精确度。由于含Fe石榴子石具有高热传导率，钙铝榴石端元又有荧光效应，因此，整个固溶体系列拉曼光谱采集的激光强度无法统一。每个实验样品记录10组以上光谱数据，采集于随机的矿物颗粒（本研究中的Raman峰位均为多组光谱拟合平均值）。收集到的光谱被分隔出多个区域，分别扣除光滑基线，通过Peakfit v4.12软件进行数据拟合。采用Gauss + Lorentz峰形拟合Raman峰位和半峰宽，在拟合钙铝榴石、钙铁榴石的Raman峰[14, 17, 22]的同时，也拟合“额外峰”以获得更加精确的数据。
-
石榴子石空间群为Ia
$ \bar{3} $ d，由四面体、八面体和十二面体构成。四面体和八面体通过角相连组成石榴子石的基本框架。四面体与十二面体由2个共享边和4个共享角相连，八面体与周围十二面体由6个共享边相连。群论分析结果表明，石榴子石结构共产生25个具有活性的拉曼峰[23]$ \varGamma = 3{A_{1{\rm{g}}}} + 8{E_{\rm{g}}} + 14{T_{2{\rm{g}}}} $ 由于3价阳离子振动极化率不变，可以预测，离子振动不会产生活性拉曼峰。本研究采用Hofmeister等[17]和Kolesov等[14]对石榴子石Raman光谱振动峰的指认方式：高频区域由硅氧四面体（SiO4）中Si-O伸缩振动产生，即(Si-O)str.；中频区域由SiO4中Si-O弯曲振动产生，即(Si-O)bend；低频区域由晶格振动（也称外振动）产生，包括SiO4整体转动（R(SiO4)）、平动（T(SiO4)）和2价阳离子平动（Ca2+；T(Ca)）。
图1显示了不同成分石榴子石的非偏正拉曼峰。拟合结果表明，钙铝榴石、钙铁榴石端元的Raman峰位与文献[14, 17, 22]中较为一致。由于峰位重叠及强度较低，群论预测的25个Raman峰未能全部观察到。对于钙铝榴石端元，共观测到20个Raman峰：P904（前人研究[17]中峰位为904 cm−1的Raman峰）与P577强度过弱，无法准确拟合；P852与C峰（848 cm−1）峰位重叠；P178与U峰（182 cm−1）重叠；P383与M强峰（376 cm−1）接近，在本次研究中未被观察到。对于钙铁榴石端元，共观测到19个Raman峰，其他6组峰包括：P874与B峰（874 m−1）重叠，P843与C峰（842 cm−1）重叠，P494与J峰（493 cm−1）重叠，P370与M峰（371 cm−1）重叠，P174与U峰（174 cm−1）重叠，P593峰强较弱。
图 1 钙铝榴石-钙铁榴石固溶体的拉曼光谱（光谱分为5个区域[14, 17]，数字表示钙铁榴石含量，标注星号的峰未在钙铁榴石端元中发现，灰色区域为额外峰出现位置）
Figure 1. Raman spectra of grossular-andradite solid solutions （The spectra are divided into 5 regions[14, 17]. The number represents the mole fraction of andradite component. The peaks with asterisk can’t be observed for andradite end-member. Grey areas mark the zones where extra peaks are observed.）
石榴子石固溶体Raman峰位与成分变化关系如图2所示。随着Fe3+含量XFe的增加，所有峰位向低波数偏移。多数峰呈近线性变化，C、G和J峰的线性程度较差。其中，C峰位于B和D强峰之间，拟合过程中存在较大的不确定性。G和J峰的非线性变化可能与离子替代及耦合振动相关。多数峰在整个固溶体系列中可追踪，E、G和I峰在系列中出现不连续。E和G峰分别在钙铁榴石和钙铝榴石端元处消失，I峰只出现在近钙铝榴石端元处，消失于15%And（钙铁榴石成分为15%的样品）。I峰不连续可能受到额外峰的干扰（中间组分），与强H峰的影响（钙铁榴石端元）有关。
图 2 钙铝榴石-钙铁榴石固溶体的拉曼峰频率-成分变化关系：（a）高频振动模式(Si-O)str.，（b）中频振动模式(Si-O)bend，（c）低频（晶格）振动模式（部分振动模式在固溶体系列中表现不连续性。倒三角为(Si-O)str.，右三角为(Si-O)bend，菱形为R(SiO4)，正三角为T(Ca)，正方形为T(SiO4)。黑色表示T2g，红色表示Eg，蓝色表示A1g。所有峰均采用最小二乘法拟合。y轴采用相同比例尺，以便对比不同振动模式受离子替代的影响程度。）
Figure 2. Raman frequencies of grossular-andradite solid solution as a function of composition: (a) high frequency (Si-O)str. modes, (b) medium frequency (Si-O)bend modes, (c) low frequency lattice modes.（Several modes show discontinuity along solid solutions. Symbols: downward pointing triangle = (Si-O)str., rightward pointing triangle = (Si-O)bend, diamonds = R(SiO4), upward pointing triangles = T(Ca), squares = T(SiO4). Colors: black = T2g, red = Eg, blue = A1g. A linear regression by least-squares analyses was applied to all the peak frequencies. Note that the y axes have the same scales and the steepness of the slopes can be compared between the three plots.）
所有峰位与成分的关系均使用最小二乘法拟合（结果见表1），斜率表示Al3+-Fe3+替代的影响程度。(Si-O)str.的变化率为−7.28 cm−1/mol %，表明Fe3+-Al3+替代对Si-O伸缩振动的影响较小。低频峰受到的影响更大：T(SiO4)的变化率为−9.13 cm−1/mol%；T(Ca)的变化率为−16.33 cm−1/mol%；R(SiO4)的变化率为−17.08 cm−1/mol%；(Si-O)bend变化率最大，为−25.52 cm−1/mol%。
Peak No. ν0/cm−1 Slope/(cm−1·mol−1% ) Error Assign AVG/(cm−1·Å−1) R2 A 1007 −10.96 0.42 (Si-O)str. −34.67 0.99 B 880 −4.44 0.35 0.95 C 848 −4.49 0.89 0.73 D 825 −9.22 0.51 0.97 E 629 −25.49 0.85 (Si-O)bend −121.52 0.99 F 591 −14.95 0.22 1.00 G −25.11 2.12 0.95 H 550 −35.54 0.40 1.00 I 527 −23.42 J 510 −18.60 0.79 0.98 K 479 −27.02 0.41 1.00 L 418 −34.02 0.26 1.00 M 376 −6.64 0.77 R(SiO4) −81.33 0.89 N 370 −17.81 0.47 0.99 O 350 −24.42 0.48 1.00 P 332 −19.43 0.30 1.00 Q 318 −22.07 0.99 T(Ca) −77.76 0.99 R 279 −14.72 0.25 1.00 S 248 −12.20 0.55 0.98 T 240 −10.14 0.17 T(SiO4) −43.48 1.00 U 182 −8.13 0.54 0.96 Note: (1) The Raman modes of Gro and And are assigned according to Kolesov, et al[14].
(2) AVG：average value of slopes in each assignment. Unit cell parameters of grossular and andradite are 11.84 Å and 12.05 Å respectively according to our single crystal XRD data.表 1 钙铝榴石-钙铁榴石固溶体拉曼频率的最小二乘法拟合结果
Table 1. Linear regression results of Raman frequencies of Gro-And solid solution versus composition
图3显示了不同Raman峰半峰宽（FWHM）与成分的关系。所有Raman峰均在中间组分表现出宽化现象。此外，光谱中观察到不属于石榴子石的额外峰，峰形差且明显较宽，主要集中于4个区域（图1中灰色区域）：R峰右侧，K、J、E、A峰左侧和940 cm−1处的新峰。根据额外峰的特点，940 cm−1处的新峰可能为低频强峰的倍频峰或和频峰，如钙铝榴石H峰（550 cm−1）与M峰（376 cm−1）以及926 cm−1和频峰，其余峰可能与结构对称性降低有关。
图 3 钙铝榴石-钙铁榴石固溶体的半峰宽-成分变化，5个拉曼峰分别归属于[14]：(a) Si-O伸缩振动，(b) Si-O弯曲振动，(c) SiO4转动，(d) Ca平动，(e) SiO4平动
Figure 3. Peak widths of selected Raman modes change with composition along grossular-andradite solid solution. The vibrations these peaks can be assigned to Kolesov, et al.[14] are: Si-O stretching (a), Si-O bending (b), SiO4 rotation (c), Ca translation (d) and SiO4 translation (e)
-
振动频率与键长、离子质量、离子键类型相关，而固溶体系列中键强受键长控制[15]。如图2所示，与Al3+相比，由于Fe3+的质量和半径更大，在八面体中当Fe3+替代了Al3+，高、中、低频峰向低波数方向偏移。
高频区的(Si-O)str.不受其他振动干扰，被用于表征四面体畸变程度[12]。Gro-And固溶体高频峰偏移小且线性程度较好，与Si-O键长变化特征对应[20]。
低频区的T(Ca2+)随成分变化的线性程度较好，与McAloon等[15]的IR研究结果一致。根据Wang等[20]的研究结果，Gro-And固溶体中的Ca-O键长在30%～40%And处出现负偏差，该现象在振动光谱中没有明显表现。Hofmeister等[17]的研究表明，T(Ca)与X-O键长的关系并不大，主要与X2+离子质量相关。此外，低频区易发生耦合振动，也难以准确表现某单一振动的特点[14, 24-25]。
中频区(Si-O)bend受Al3+-Fe3+替代影响最大。该现象与其他石榴子石固溶体相差较多[12-14, 17]，亦与Gro-And固溶体较小的Si-O键长、O-Si-O夹角变化不符[20]。本研究中，(Si-O)str.变化率为34.67 cm−1/Å，(Si-O)bend变化率为121.52 cm−1/Å，分别对应镁铝榴石-钙铝榴石（Pyr-Gro）固溶体的变化率为130 cm−1/Å和63 cm−1/Å[13]。已有研究[13, 17]多将(Si-O)bend更大的变化率归结为弯曲振动较小的力常数，该解释与本研究中
$\Delta $ ν(Si-O)bend >$\Delta $ ν(Si-O)str.现象不符。石榴子石结构紧密，四面体与八面体角相连，Al3+-Fe3+替代会影响四面体并产生畸变[9, 20, 26-27]。Gro-And及Alm-Ski（铁铁榴石，Fe2+3Fe3+2Si3O12）固溶体Raman、IR中频峰均发生较明显的偏移[19]。对于Gro-And固溶体，Fe3+替代Al3+并不仅仅使晶格膨胀，也会造成四面体转角α显著增加（Alm-Ski固溶体四面体转角亦有较大变化[27]）。J和K峰在30%～50%And处的负偏差可能与四面体转角α非线性变化对应。
中频峰较大变化率也可能是耦合振动的结果。Hofmeister等[17]研究结果表明，中频峰频率主要与阳离子质量相关。Fe的相对原子质量为Al的两倍，离子替代会对Raman峰产生明显影响。虽然群论预测认为3价阳离子不产生Raman活性峰，但群论预测未考虑耦合振动的影响[17]。Kolesov等[14]和Pascale等[24-25]的研究结果表明，除高频区域外，Raman和IR峰均包含多种振动参与。Al-O键与Si-O键的强度相当，T(Al)在IR光谱中已经影响到中频区，出现在423和472 cm−1[15]。因此，Al3+通过耦合振动的方式影响Raman光谱中频区也是原因之一。
如图3所示，本研究中的5个振动峰均出现了峰宽化现象。中间组分峰宽化现象较为常见，可能与离子无序度增加、晶格畸变相关[12, 17]，也可能由折合质量及力常数改变导致[28]。
在其他石榴子石固溶体的振动光谱中也发现类似的额外峰现象[13, 17, 29]。离子替代会造成有序度降低，引起晶格畸变[20]，结构对称性降低，使振动光谱更复杂[29]。有研究认为，离子替代可能使石榴子石空间群降为I213或Im
$ \bar{3} $ m[17, 30]，矽卡岩矿床中Gro-And固溶体异常消光现象说明确实发生了对称性降低[31-33]。具有异常消光特点的石榴子石成分在30%～70%之间，与结构畸变较一致[20]。IR光谱研究中未观察到类似额外峰，可能与IR光谱对有序度不敏感有关[15]，亦可能因为天然石榴子石的离子更加无序[17]。 -
晶格畸变、离子有序度变化是造成IR、Raman峰宽化的重要原因，峰宽化程度可以反映结构中的应力大小，预测混合焓的弹性能贡献[12, 19]。Boffa Ballaran等[12]通过研究Pyr-Gro固溶体IR光谱，利用峰宽参数预测热力学混合性质，并提出经验公式。本研究尝试使用Raman光谱半峰宽（FWHM）预测Gro-And固溶体的热力学混合性质。
Al3+-Fe3+离子替换对中频区域峰位影响最大，且Pascale等[24-25]的研究表明中频区可同时受到Fe3+和Al3+离子振动的影响，为此建立中频H峰半峰宽与混合焓的关系。由于H峰的超额半峰宽
$\Delta {h^{{\rm{ex}}}}$ 分布较为对称，选用单参数Margule方程描述$\Delta {h^{{\rm{ex}}}}$ 和$\Delta {H^{{\rm{ex}}}}$ 的变化$\Delta {h^{{\rm{ex}}}}{\rm{}} = {\rm{}}{X_{{\rm{Gro}}}}{X_{{\rm{And}}}}{W_1}$ $\Delta {H^{{\rm{ex}}}} = {X_{{\rm{Gro}}}}{X_{{\rm{And}}}}{W_2}$ 式中：
$\Delta {h^{{\rm{ex}}}}$ 表示Gro-And固溶体的超额半峰宽；$\Delta {H^{{\rm{ex}}}}$ 表示超额混合焓；${X_{{\rm{Gro}}}}$ 和$ {X_{{\rm{And}}}}$ 分别表示钙铝榴石和钙铁榴石的摩尔分数，${X_{{\rm{Gro}}}} + {X_{{\rm{And}}}} = 1$ ；$ {W}_{1} $ 、$ {W}_{2} $ 为Margules参数。$\Delta {H^{{\rm{ex}}}}$ 与$\Delta {h^{{\rm{ex}}}}$ 的比例$\frac{{\Delta {H^{{\rm{ex}}}}}}{{\Delta {h^{{\rm{ex}}}}}} = {\rm{}}\frac{{{X_{{\rm{Gro}}}}{X_{{\rm{And}}}}{W_2}}}{{{X_{{\rm{Gro}}}}{X_{{\rm{And}}}}{W_1}}} = {\rm{}}\frac{{{W_2}}}{{{W_1}}} = {C_1}$ 结果表明，
$\Delta {H^{{\rm{ex}}}}$ 和$\Delta {h^{{\rm{ex}}}}$ 的比为常数C1。通过式（2）拟合H峰的半峰宽，可得$ {W}_{1}=(22.13 $ ± 1.84) cm−1，拟合曲线如图4所示。根据Becker等[34]的计算结果，50%And处的超额混合焓为0.75 kJ/mol，对应$ {W}_{2} $ = 3 kJ/mol，C1 = 0.14。Gro-And固溶体的预测混合焓（$\Delta H_{{\rm{FWHM}}}^{{\rm{ex}}}$ ）如图4所示。
图 4 钙铝榴石-钙铁榴石固溶体H峰的超额半峰宽（
$\Delta {h^{{\rm{ex}}}}$ ）和预测混合焓（$\Delta {H^{{\rm{ex}}}}$ ）拟合曲线Figure 4. Fitting curve of
$\Delta {h^{{\rm{ex}}}}$ of peak H and the predicted$\Delta {H^{{\rm{ex}}}}$ for grossular-andradite solid solutionPyr-Gro固溶体的Raman光谱[13]和测热混合焓[10]被用于验证该方法的准确性。根据Pascale等[24-25]的研究结果，受到Mg2+和Ca2+离子共同影响的L峰[13]可用于混合焓预测。考虑到L峰的
$\Delta {h^{{\rm{ex}}}}$ 非对称性特点，采用双参数Margules方程描述$\Delta {h^{{\rm{ex}}}}$ 和${\rm{\Delta }}{H^{{\rm{ex}}}}$ $\Delta {h^{{\rm{ex}}}} = {X_{{\rm{Gro}}}}{X_{{\rm{And}}}}\left( {{X_{{\rm{Gro}}}}{W_3} + {X_{{\rm{And}}}}{W_4}} \right)$ $\Delta {H^{{\rm{ex}}}} = {X_{{\rm{Gro}}}}{X_{{\rm{And}}}}\left( {{X_{{\rm{Gro}}}}{W_5} + {X_{{\rm{And}}}}{W_6}} \right)$ $\Delta {h^{{\rm{ex}}}}$ 的拟合曲线及相关参数（$ {W}_{3} $ 和$ {W}_{4} $ ）见图5。$\Delta {H^{{\rm{ex}}}}$ 与$\Delta {h^{{\rm{ex}}}}$ 的比值
图 5 镁铝榴石-钙铝榴石固溶体的超额半峰宽（
$\Delta {h^{{\rm{ex}}}}$ ）拟合曲线（黑色虚线为Du等[13]的L峰数据，红色点线为预测超额混合焓（$\Delta H_{{\rm{FWHM}}}^{{\rm{ex}}}$ ）曲线，红色实线为超额混合焓测热数据（$\Delta H_{{\rm{Cal}}}^{{\rm{ex}}}$ ）拟合曲线[10]）Figure 5. Fitting curve of
$\Delta {h^{{\rm{ex}}}}$ for pyrope-grossular solid solution (Black dashed line: peak L of Du, et al.[13] Red dotted line: the predicted excess enthalpy of mixing curve. Red solid line: the fitting curve for calorimetric excess enthalpy of mixing data from Newton, et al.[10])$\frac{{\Delta {H^{{\rm{ex}}}}}}{{\Delta {h^{{\rm{ex}}}}}} = {\rm{}}\frac{{{W_5} - {W_6}}}{{{W_3} - {W_4}}} + \dfrac{{{W_6} - \dfrac{{{W_4}\left( {{W_5} - {W_6}} \right)}}{{{W_3} - {W_4}}}}}{{\left( {{W_3} - {W_4}} \right){X_{{\rm{Gro}}}} + {W_4}}}$ 由于回归值
$ {W}_{3} $ 和$ {W}_{4} $ 较为接近（图5），与$ {W}_{4} $ 相比，$\left( {{W_3} - {W_4}} \right){X_{{\rm{Gro}}}}$ 可以忽略。因此，$\Delta {H^{{\rm{ex}}}}$ 与$\Delta {h^{{\rm{ex}}}}$ 的比值近似为$\frac{{\Delta {H^{{\rm{ex}}}}}}{{{\rm{\Delta }}{h^{{\rm{ex}}}}}} \approx \frac{{{W_6}}}{{{W_4}}} = {C_2}$ 通过式（6）拟合
$\Delta H_{{\rm{Cal}}}^{{\rm{ex}}}$ [10]，得到$ {W}_{5} $ 和$ {W}_{6} $ （图5），同时C2 = 1.46、$\Delta H_{{\rm{FWHM}}}^{{\rm{ex}}}$ =$\Delta {h^{{\rm{ex}}}}$ × C2。$\Delta H_{{\rm{FWHM}}}^{{\rm{ex}}}$ 与$\Delta H_{{\rm{Cal}}}^{{\rm{ex}}}$ 的对比如图5所示，误差可能来自于$\left( {{W_3} - {W_4}} \right){X_{{\rm{Gro}}}}$ 的近似处理，或有限数据点拟合。 -
在钙铝榴石、钙铁榴石端元的拉曼光谱实验中分别观测到20和19个拉曼峰，由于峰位重叠和峰强较弱，部分峰未观测到。多数峰位随成分线性、连续变化，中频区峰位变化较大且线性程度差，可能因为：（1）Al3+-Fe3+替代造成四面体转角增加，对Si-O弯曲振动产生影响；（2）Al3+通过耦合振动的方式影响中频峰。额外峰的出现与和（倍）频峰及结构对称性降低有关。由于有序度降低及局部晶格扭曲，中间组分出现峰宽化现象。采用峰宽程度表征混合焓中的弹性能贡献，使用半峰宽预测了固溶体的混合焓特征。
感谢北京大学地球与空间科学学院丁竑瑞在拉曼光谱测试中提供的帮助，感谢北京大学地球与空间科学学院刘曦老师、孙樯老师和李慧娟的重要帮助。
钙铝榴石-钙铁榴石固溶体的拉曼光谱
Raman Scattering of Grossular-Andradite Solid Solution
-
摘要: 为了研究Al3+-Fe3+离子替代对固溶体结构的影响，进行了钙铝榴石-钙铁榴石固溶体的拉曼光谱研究。结果表明：钙铝榴石、钙铁榴石端元分别观测到20和19个拉曼峰，多数峰位随成分呈连续、线性变化，光谱中未发现双模式振动；中频峰峰位变化较大，可能与结构联动或耦合振动有关；由于结构对称性降低，振动光谱中发现了额外峰；拉曼峰宽化现象与有序度降低及结构的畸变有关。通过单参数的Margules方程拟合半峰宽，预测了固溶体的混合焓特征。Abstract: The effects of Al3+-Fe3+ substitution on 10 synthesized garnet samples along the grossular-andradite binary were investigated using Raman spectroscopy. Twenty and nineteen peaks were observed in non-polarized Raman spectra for grossular and andradite end-members, respectively. The frequencies of most peaks were changed almost linearly with the composition. Two-mode behavior was not observed in this study. Differing from previous reports on other garnet solid solutions, the medium frequency modes, which are assigned to internal bending vibrations, have the largest average rate of change with the composition, which may be related to structural connectivity and coupled vibrations. Due to the reduction of symmetry, extra peaks appear in the Raman spectra of garnets with intermediate compositions. Peak broadening in intermediate compositions was also observed, which is related to disordering and distortion. One-parameter Margules equation was used to describe the full width at half maximum of peaks, and a relationship with enthalpy of mixing was proposed.
-
Key words:
- grossular-andradite /
- Raman spectroscopy /
- bending vibration /
- extra peak /
- enthalpy of mixing
-
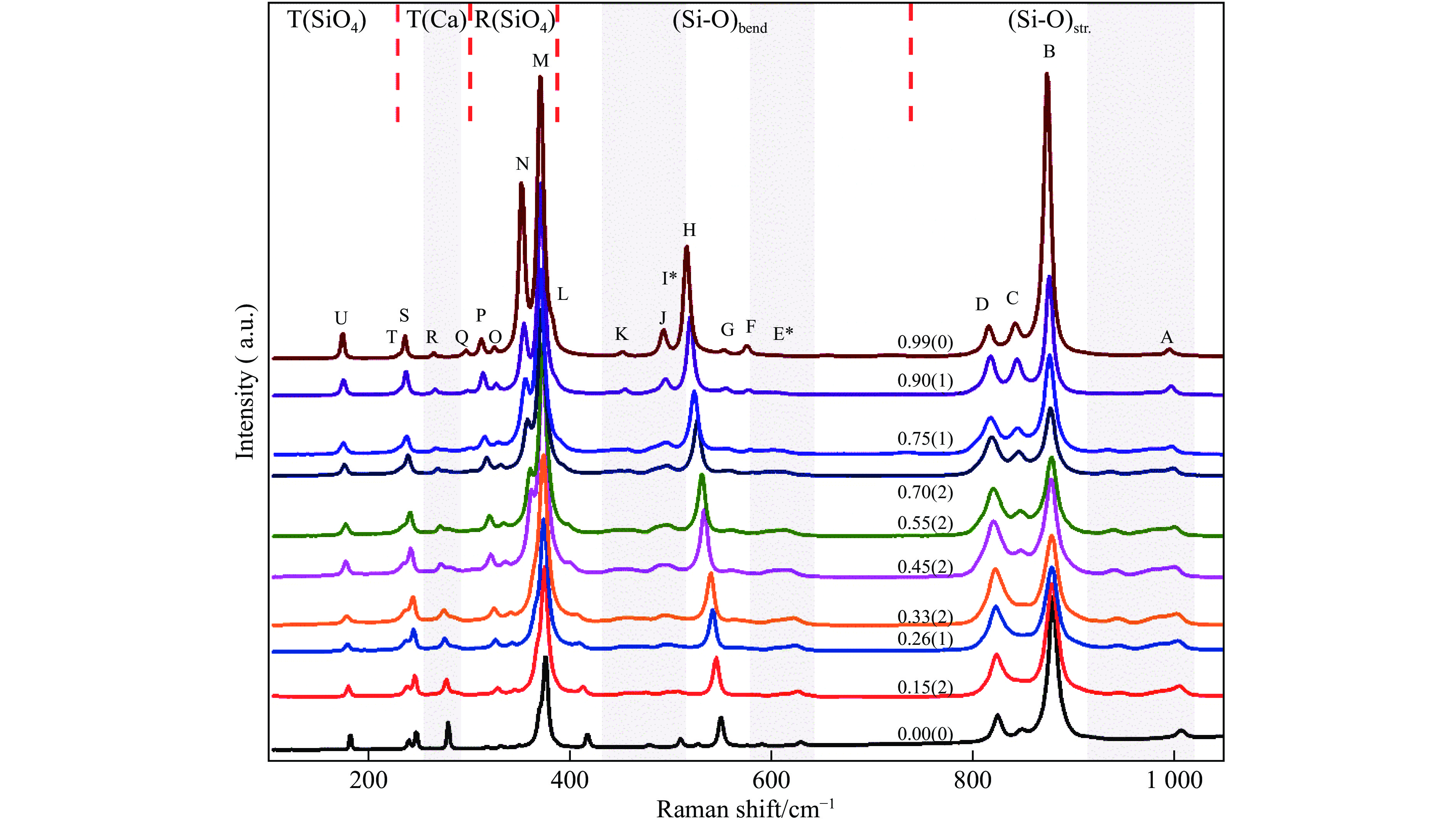
图 1 钙铝榴石-钙铁榴石固溶体的拉曼光谱（光谱分为5个区域[14, 17]，数字表示钙铁榴石含量，标注星号的峰未在钙铁榴石端元中发现，灰色区域为额外峰出现位置）
Figure 1. Raman spectra of grossular-andradite solid solutions （The spectra are divided into 5 regions[14, 17]. The number represents the mole fraction of andradite component. The peaks with asterisk can’t be observed for andradite end-member. Grey areas mark the zones where extra peaks are observed.）
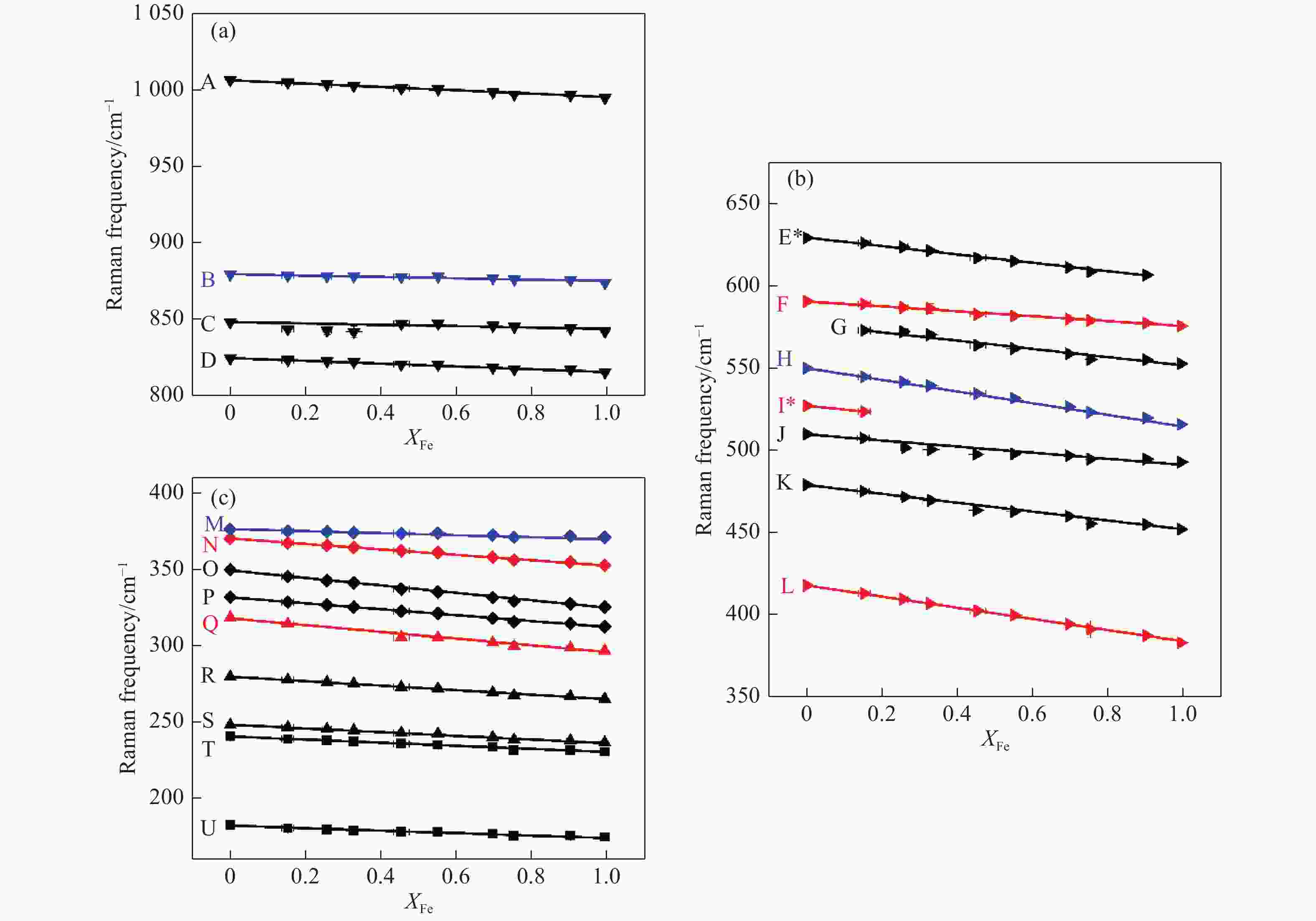
图 2 钙铝榴石-钙铁榴石固溶体的拉曼峰频率-成分变化关系：（a）高频振动模式(Si-O)str.，（b）中频振动模式(Si-O)bend，（c）低频（晶格）振动模式（部分振动模式在固溶体系列中表现不连续性。倒三角为(Si-O)str.，右三角为(Si-O)bend，菱形为R(SiO4)，正三角为T(Ca)，正方形为T(SiO4)。黑色表示T2g，红色表示Eg，蓝色表示A1g。所有峰均采用最小二乘法拟合。y轴采用相同比例尺，以便对比不同振动模式受离子替代的影响程度。）
Figure 2. Raman frequencies of grossular-andradite solid solution as a function of composition: (a) high frequency (Si-O)str. modes, (b) medium frequency (Si-O)bend modes, (c) low frequency lattice modes.（Several modes show discontinuity along solid solutions. Symbols: downward pointing triangle = (Si-O)str., rightward pointing triangle = (Si-O)bend, diamonds = R(SiO4), upward pointing triangles = T(Ca), squares = T(SiO4). Colors: black = T2g, red = Eg, blue = A1g. A linear regression by least-squares analyses was applied to all the peak frequencies. Note that the y axes have the same scales and the steepness of the slopes can be compared between the three plots.）
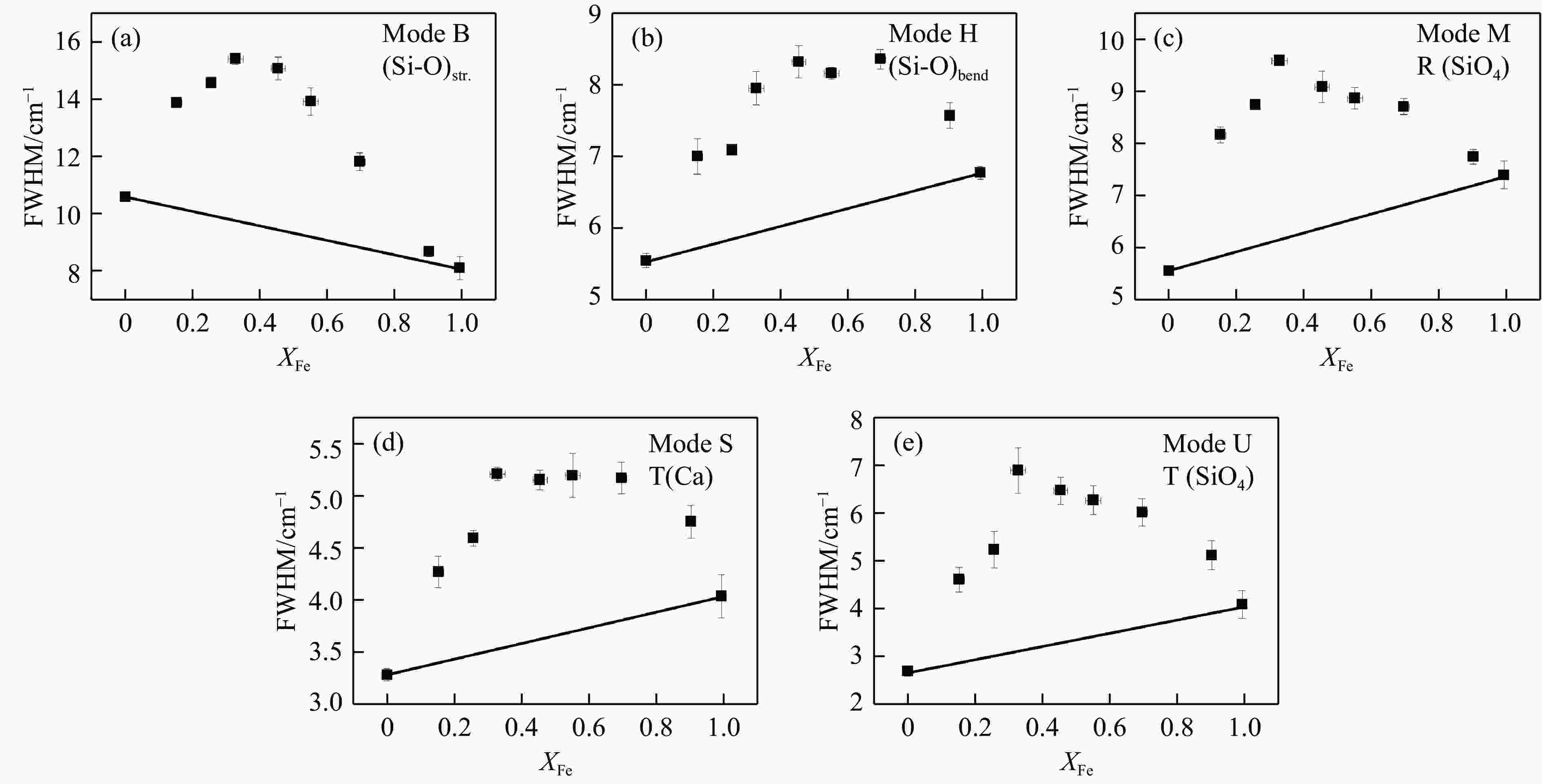
图 3 钙铝榴石-钙铁榴石固溶体的半峰宽-成分变化，5个拉曼峰分别归属于[14]：(a) Si-O伸缩振动，(b) Si-O弯曲振动，(c) SiO4转动，(d) Ca平动，(e) SiO4平动
Figure 3. Peak widths of selected Raman modes change with composition along grossular-andradite solid solution. The vibrations these peaks can be assigned to Kolesov, et al.[14] are: Si-O stretching (a), Si-O bending (b), SiO4 rotation (c), Ca translation (d) and SiO4 translation (e)
图 4 钙铝榴石-钙铁榴石固溶体H峰的超额半峰宽（
$\Delta {h^{{\rm{ex}}}}$ ）和预测混合焓（$\Delta {H^{{\rm{ex}}}}$ ）拟合曲线Figure 4. Fitting curve of
$\Delta {h^{{\rm{ex}}}}$ of peak H and the predicted$\Delta {H^{{\rm{ex}}}}$ for grossular-andradite solid solution
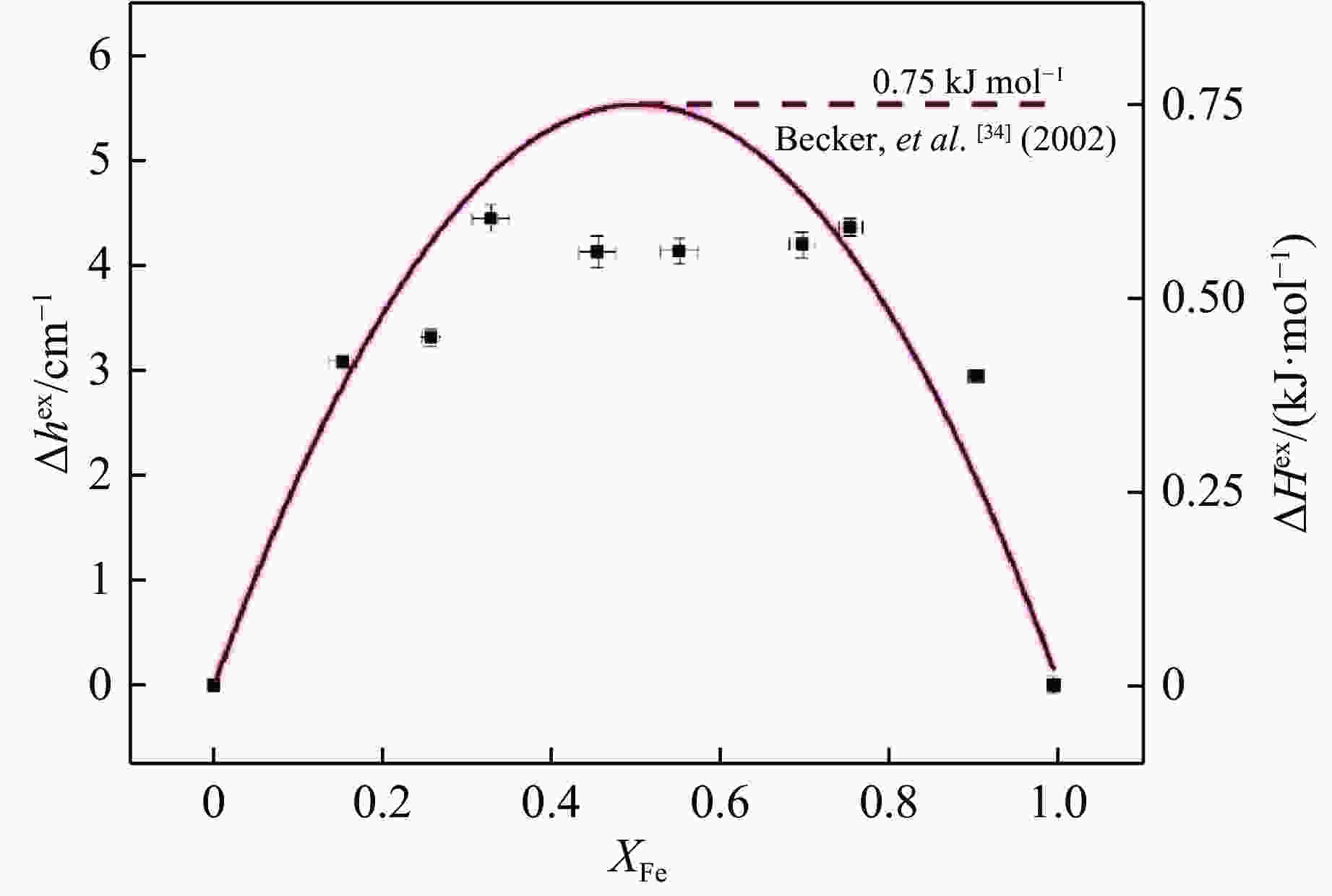
图 5 镁铝榴石-钙铝榴石固溶体的超额半峰宽（
$\Delta {h^{{\rm{ex}}}}$ ）拟合曲线（黑色虚线为Du等[13]的L峰数据，红色点线为预测超额混合焓（$\Delta H_{{\rm{FWHM}}}^{{\rm{ex}}}$ ）曲线，红色实线为超额混合焓测热数据（$\Delta H_{{\rm{Cal}}}^{{\rm{ex}}}$ ）拟合曲线[10]）Figure 5. Fitting curve of
$\Delta {h^{{\rm{ex}}}}$ for pyrope-grossular solid solution (Black dashed line: peak L of Du, et al.[13] Red dotted line: the predicted excess enthalpy of mixing curve. Red solid line: the fitting curve for calorimetric excess enthalpy of mixing data from Newton, et al.[10])表 1 钙铝榴石-钙铁榴石固溶体拉曼频率的最小二乘法拟合结果
Table 1. Linear regression results of Raman frequencies of Gro-And solid solution versus composition
Peak No. ν0/cm−1 Slope/(cm−1·mol−1% ) Error Assign AVG/(cm−1·Å−1) R2 A 1007 −10.96 0.42 (Si-O)str. −34.67 0.99 B 880 −4.44 0.35 0.95 C 848 −4.49 0.89 0.73 D 825 −9.22 0.51 0.97 E 629 −25.49 0.85 (Si-O)bend −121.52 0.99 F 591 −14.95 0.22 1.00 G −25.11 2.12 0.95 H 550 −35.54 0.40 1.00 I 527 −23.42 J 510 −18.60 0.79 0.98 K 479 −27.02 0.41 1.00 L 418 −34.02 0.26 1.00 M 376 −6.64 0.77 R(SiO4) −81.33 0.89 N 370 −17.81 0.47 0.99 O 350 −24.42 0.48 1.00 P 332 −19.43 0.30 1.00 Q 318 −22.07 0.99 T(Ca) −77.76 0.99 R 279 −14.72 0.25 1.00 S 248 −12.20 0.55 0.98 T 240 −10.14 0.17 T(SiO4) −43.48 1.00 U 182 −8.13 0.54 0.96 Note: (1) The Raman modes of Gro and And are assigned according to Kolesov, et al[14].
(2) AVG：average value of slopes in each assignment. Unit cell parameters of grossular and andradite are 11.84 Å and 12.05 Å respectively according to our single crystal XRD data.
下载: 导出CSV
-
[1] GREW E S, LOCOCK A J, MILLS S J, et al. Nomenclature of the garnet supergroup [J]. American Mineralogist, 2013, 98(4): 785–810. doi: 10.2138/am.2013.4201 [2] HAZEN R M, DOWNS R T, CONRAD P G, et al. Comparative compressibilities of majorite-type garnets [J]. Physics and Chemistry of Minerals, 1994, 21(5): 344–349. doi: 10.1007/BF00202099 [3] CONRAD P G, ZHA C S, MAO H K, et al. The high-pressure, single-crystal elasticity of pyrope, grossular, and andradite [J]. American Mineralogist, 1999, 84(3): 374–383. doi: 10.2138/am-1999-0321 [4] DU W, CLARK S M, WALKER D. Thermo-compression of pyrope-grossular garnet solid solutions: non-linear compositional dependence [J]. American Mineralogist, 2015, 100(1): 215–222. doi: 10.2138/am-2015-4752 [5] BLUNDY J, WOOD B. Prediction of crystal-melt partition coefficients from elastic moduli [J]. Nature, 1994, 372(6505): 452–454. doi: 10.1038/372452a0 [6] SUN C G, LIANG Y. The importance of crystal chemistry on REE partitioning between mantle minerals (garnet, clinopyroxene, orthopyroxene, and olivine) and basaltic melts [J]. Chemical Geology, 2013, 358: 23–36. doi: 10.1016/j.chemgeo.2013.08.045 [7] GANGULY J, CHENG W J, O’NEILL H S C. Syntheses, volume, and structural changes of garnets in the pyrope-grossular join: implications for stability and mixing properties [J]. American Mineralogist, 1993, 78(5/6): 583–593. [8] GEIGER C A. Silicate garnet: a micro to macroscopic (re)view [J]. American Mineralogist, 2008, 93(2/3): 360–372. doi: 10.2138/am.2008.2588 [9] GEIGER C A, FEENSTRA A. Molar volumes of mixing of almandine-pyrope and almandine-spessartine garnets and the crystal chemistry and thermodynamic-mixing properties of the aluminosilicate garnets [J]. American Mineralogist, 1997, 82(5/6): 571–581. doi: 10.2138/am-1997-5-617 [10] NEWTON R C, CHARLU T V, KLEPPA O J. Thermochemistry of high pressure garnets and clinopyroxenes in the system CaO-MgO-Al2O3-SiO2 [J]. Geochimica et Cosmochimica Acta, 1977, 41(3): 369–377. doi: 10.1016/0016-7037(77)90264-2 [11] UNGARETTI L, LEONA M, MERLI M, et al. Non-ideal solid-solution in garnet: crystal-structure evidence and modelling [J]. European Journal of Mineralogy, 1995, 7(6): 1299–1312. doi: 10.1127/ejm/7/6/1299 [12] BOFFA BALLARAN T, CARPENTER M A, GEIGER C A, et al. Local structural heterogeneity in garnet solid solutions [J]. Physics and Chemistry of Minerals, 1999, 26(7): 554–569. doi: 10.1007/s002690050219 [13] DU W, HAN B F, CLARK S M, et al. Raman spectroscopic study of synthetic pyrope-grossular garnets: structural implications [J]. Physics and Chemistry of Minerals, 2018, 45(2): 197–209. doi: 10.1007/s00269-017-0908-z [14] KOLESOV B A, GEIGER C A. Raman spectra of silicate garnets [J]. Physics and Chemistry of Minerals, 1998, 25(2): 142–151. doi: 10.1007/s002690050097 [15] MCALOON B P, HOFMEISTER A M. Single-crystal IR spectroscopy of grossular-andradite garnets [J]. American Mineralogist, 1995, 80(11/12): 1145–1156. doi: 10.2138/am-1995-11-1205 [16] HOFMEISTER A M, FAGAN T J, CAMPBELL K M, et al. Single-crystal IR spectroscopy of pyrope-almandine garnets with minor amounts of Mn and Ca [J]. American Mineralogist, 1996, 81(3/4): 418–428. doi: 10.2138/am-1996-3-416 [17] HOFMEISTER A M, CHOPELAS A. Vibrational spectroscopy of end-member silicate garnets [J]. Physics and Chemistry of Minerals, 1991, 17(6): 503–526. doi: 10.1007/BF00202230 [18] SHANNON R D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides [J]. Acta Crystallographica Section A, 1976, 32(5): 751–767. doi: 10.1107/S0567739476001551 [19] BOFFA BALLARAN T, WOODLAND A B. Local structure of ferric iron-bearing garnets deduced by IR-spectroscopy [J]. Chemical Geology, 2006, 225(3/4): 360–372. doi: 10.1016/j.chemgeo.2005.08.028 [20] WANG Y C, SUN Q, DUAN D F, et al. The study of crystal structure on grossular-andradite solid solution [J]. Minerals, 2019, 9(11): 691. doi: 10.3390/min9110691 [21] LIU X, CHEN J L, TANG J J, et al. A large volume cubic press with a pressure-generating capability up to about 10 GPa [J]. High Pressure Research, 2012, 32(2): 239–254. doi: 10.1080/08957959.2012.657634 [22] GILLET P, FIQUET G, MALEZIEUX J M, et al. High-pressure and high-temperature Raman spectroscopy of end-member garnets: pyrope, grossular and andradite [J]. European Journal of Mineralogy, 1992, 4(4): 651–664. doi: 10.1127/ejm/4/4/0651 [23] MOORE R K, WHITE W B, LONG T V. Vibrational spectra of the common silicates: I. the garnets [J]. American Mineralogist, 1971, 56(1/2): 54–71. [24] PASCALE F, CATTI M, DAMIN A, et al. Vibration frequencies of Ca3Fe2Si3O12 andradite: an ab initio study with the CRYSTAL code [J]. Journal of Physical Chemistry B, 2005, 109(39): 18522–18527. doi: 10.1021/jp052991e [25] PASCALE F, ZICOVICH-WILSON C M, ORLANDO R, et al. Vibration frequencies of Mg3Al2Si3O12 pyrope. an ab initio study with the CRYSTAL code [J]. The Journal of Physical Chemistry B, 2005, 109(13): 6446–6152. doi: 10.1021/jp050316z [26] BORN L, ZEMANN J. Abstandsberechnungen und gitterenergetische Berechnungenan Granaten [J]. Beiträgezur Mineralogie und Petrographie, 1964, 10(1): 2–23. doi: 10.1007/BF01192531 [27] WOODLAND A B, ROSS II C R. A crystallographic and mössbauer spectroscopy study of ${ {\rm{Fe}}_3^{2 + } }$ ${{\rm{Fe}}_3^{2 + }{\rm{Fe}}_2^{3 + }}$ ${{\rm{Fe}}_3^{2 + }}$ ${{\rm{Fe}}_3^{2 + }{\rm{Fe}}_2^{3 + }}$ [28] ZIMAN J M. Models of disorder: the theoretical physics of homogeneously disordered systems [M]. Cambridge: Cambridge University Press, 1979. [29] DE LA PIERRE M, NOEL Y, MUSTAPHA S, et al. The infrared vibrational spectrum of andradite-grossular solid solutions: a quantum mechanical simulation [J]. American Mineralogist, 2013, 98(5/6): 966–976. doi: 10.2138/am.2013.4156 [30] DEMPSEY M J. Evidence for structural changes in garnet caused by calcium substitution [J]. Contributions to Mineralogy and Petrology, 1980, 71(3): 281–282. doi: 10.1007/BF00371669 [31] FEI X H, ZHANG Z C, CHENG Z G, et al. Factors controlling the crystal morphology and chemistry of garnet in skarn deposits: a case study from the Cuihongshan polymetallic deposit, Lesser Xing’an Range, NE China [J]. American Mineralogist, 2019, 104(10): 1455–1468. doi: 10.2138/am-2019-6968 [32] GASPAR M, KNAACK C, MEINERT L D, et al. REE in skarn systems: a LA-ICP-MS study of garnets from the Crown Jewel gold deposit [J]. Geochimica et Cosmochimica Acta, 2008, 72(1): 185–205. doi: 10.1016/j.gca.2007.09.033 [33] XU J, CIOBANU C L, COOK N J, et al. Skarn formation and trace elements in garnet and associated minerals from Zhibula copper deposit, Gangdese Belt, southern Tibet [J]. Lithos, 2016, 262: 213–231. doi: 10.1016/j.lithos.2016.07.010 [34] BECKER U, POLLOK K. Molecular simulations of interfacial and thermodynamic mixing properties of grossular-andradite garnets [J]. Physics and Chemistry of Minerals, 2002, 29(1): 52–64. doi: 10.1007/s002690100211 -
点击查看大图
计量
- 文章访问数: 285
- 阅读全文浏览量: 245
- PDF下载量: 5
