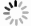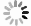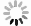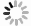A Macroscopic Dynamic Constitutive Model for Ceramic Materials
doi: 10.11858/gywlxb.20190863
-
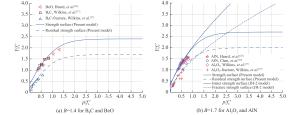
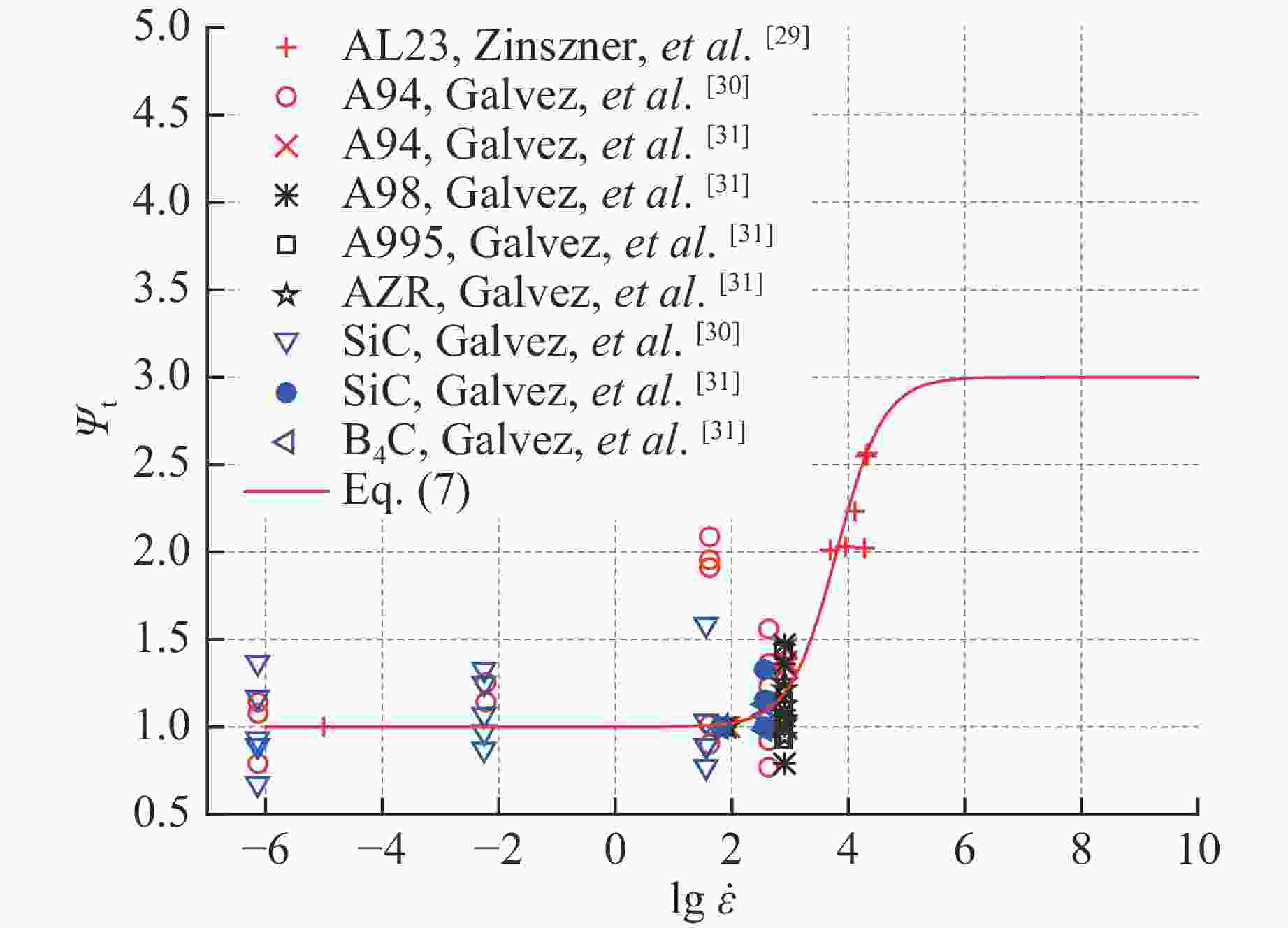
摘要: 基于已有混凝土材料的相关研究,建立了陶瓷材料在动态载荷作用下的宏观本构模型。模型中状态方程采用多项式描述,强度面模型中考虑了压力相关性、Lode角效应、应变率效应、剪切损伤及拉伸软化等的影响。采用一个新的函数来描述陶瓷材料的强度面,其在较高压力下趋于一个平台值;并采用动态增强因子(DIF)考察剥除惯性效应后陶瓷材料的真实应变率效应。通过将模型预测的压力-体应变响应、准静态强度面以及应变率效应与相关实验数据进行对比,验证了该模型。单个单元测试模拟得到的结果与三轴实验数据以及侵彻实验数据高度吻合,进一步验证了此模型。为显示模型的优越性,还与JH-2模型的预测结果进行了比较。结果表明:所提出的本构模型能够很好地预测陶瓷材料在不同加载条件下的力学行为,且优于现有的模型。Abstract: A macroscopic constitutive model is presented herein for ceramic materials subjected to dynamic loadings by closely following a previous study on concrete. The equation of state is described by a polynomial equation and the strength model takes into account various effects such as pressure hardening, Lode angle, strain rate, shear damage and tensile softening. In particular, the strength surface of ceramic materials is characterized by a new function which levels out at very high pressures and strain rate effect is taken into account by dynamic increase factor (DIF) which excludes inertial effect. The present model is verified against some available experimental data for ceramic materials in terms of pressure-volumetric response, quasi-static strength surface and strain rate effect. The model is further verified against the data for triaxial test by single element simulation approach and the test data for depth of penetration in AD99.5/RHA struck by tungsten alloy penetrators. Furthermore, comparisons are also made between numerical results of the present model and the JH-2 model. It is demonstrated that the present model can be employed to describe the mechanical behavior of ceramic materials under different loading conditions with reasonable confidence and is advantageous over the existing model.
-
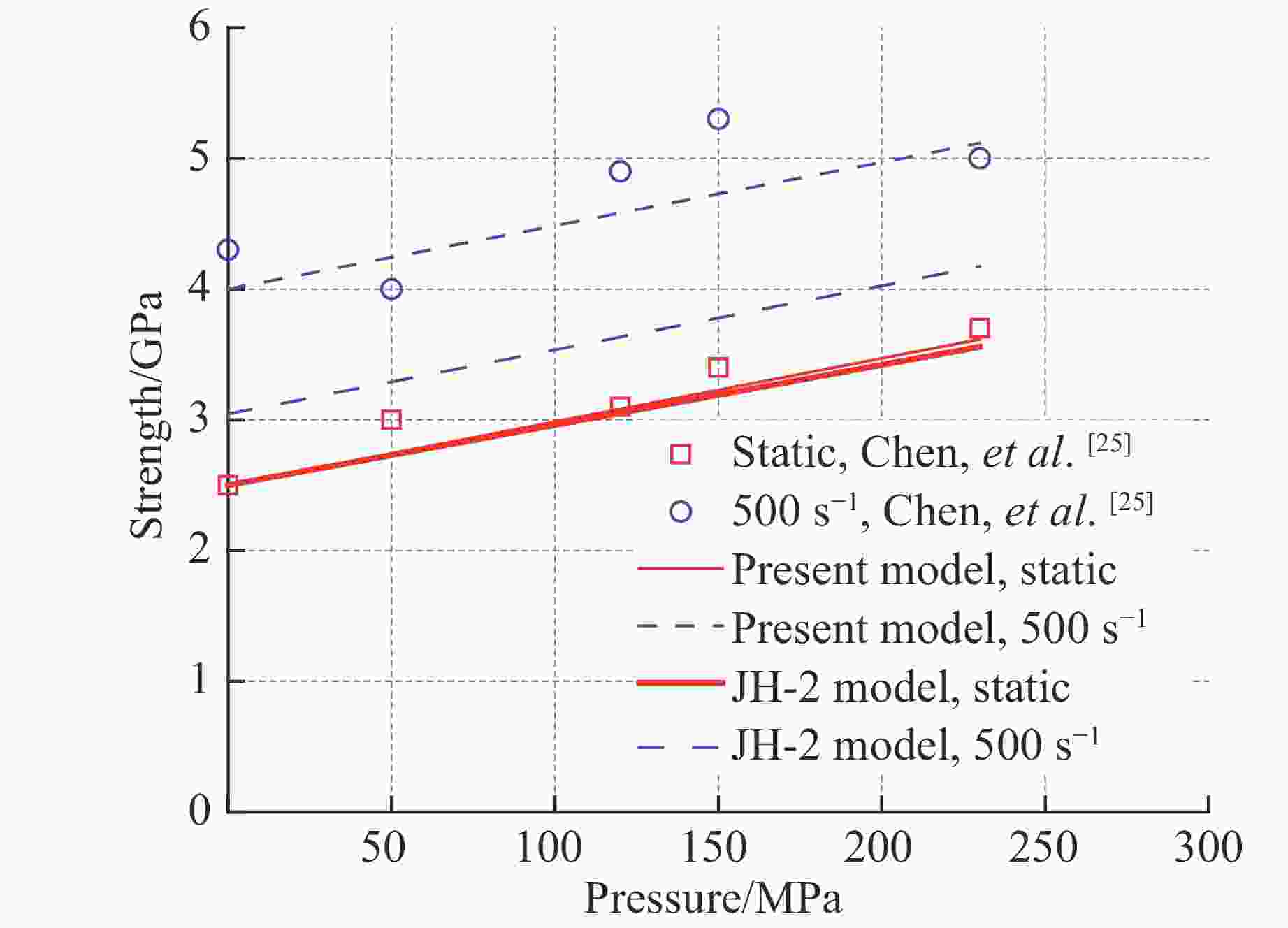
Figure 5. Comparison between the experimental data[25] and the predictions by the present model of strength varies with pressure at different strain rates of AlN
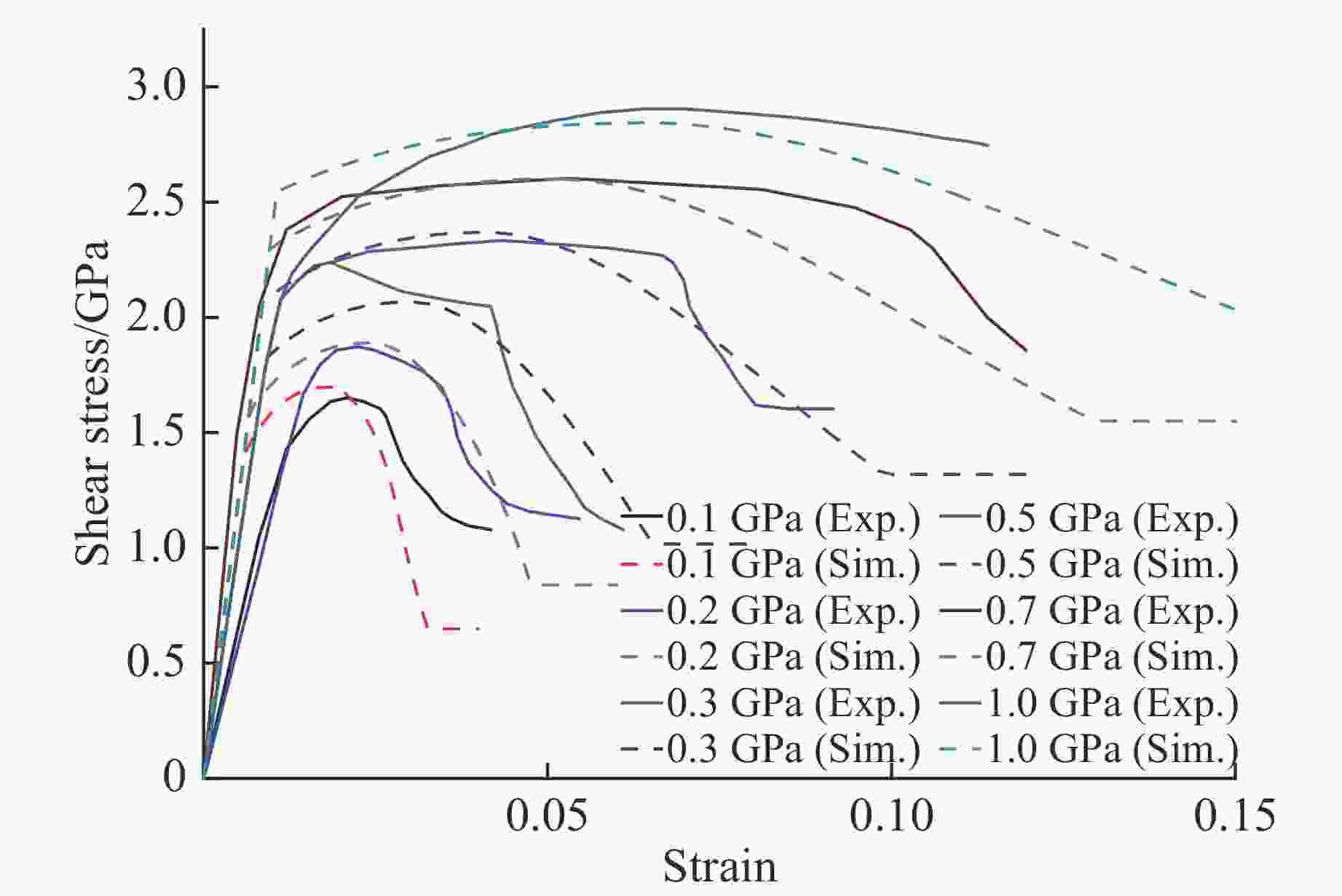
Figure 6. Comparison of stress-strain curves for BeO under triaxial compression between the present model and experimental data[22]
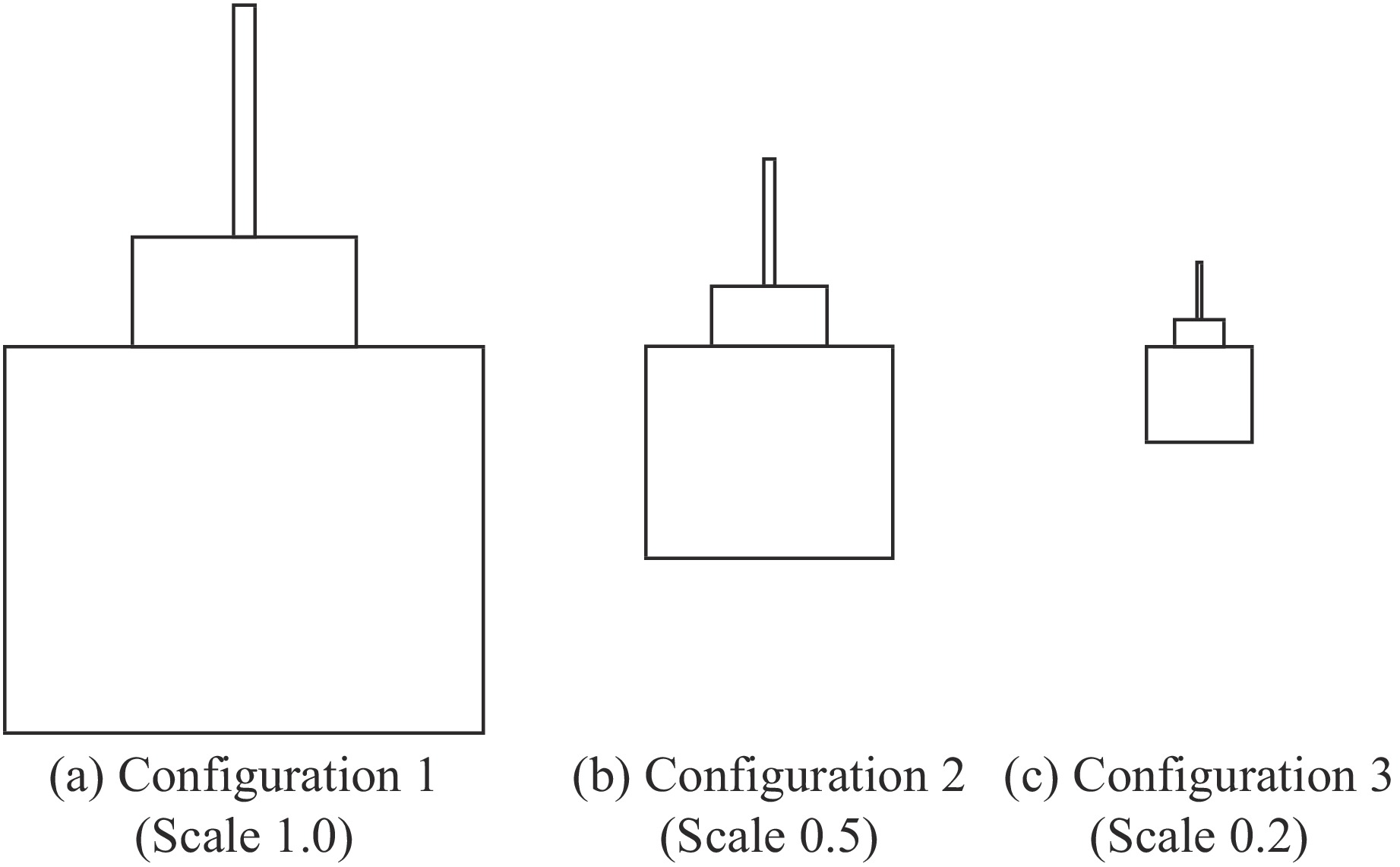
Figure 11. Comparison between the numerical results and the test data for the depth of penetration in AD99.7/RHA targets by flat-nosed tungsten alloy penetrators[35]
Table 1. Values of parameters for BeO in the present model
Equation of state parameters Constitutive model parameters K1/GPa K2/GPa K3/GPa ρc/(kg·m−3) Fm Wx Wy S 181.5 1 207.9 −2 991 3 030 3 3.8 2 1.25 Constitutive model parameters ${f_{{\rm{c}}}'}$/GPa ft/GPa B G/GPa λm λs l r 1.5 0.15 1.2 125 0.3 7.5 0.8 0.3 Table 2. Values of parameters for AlN in the present model
Equation of state parameters Constitutive model parameters ρc/(kg·m−3) K1/GPa K2/GPa K3/GPa K4/GPa K5/GPa K6/GPa Fm Wx Wy 3 229 181.5 1 207.9 −2 991 181.9 335.6 −283 3 3.8 2 Constitutive model parameters ${f_{{\rm{c}}}'}$/GPa ft/GPa B G/GPa S λm λs l r 3 0.3 1.7 127 1.25 0.3 7.5 0.8 0.3 Table 3. Values of various parameters for AlN ceramic (JH-2 model)
Equation of state parameters Constitutive model parameters ρc/(kg·m−3) K1/GPa K2/GPa K3/GPa a b C n m 3 229 201 260 0 1.36 1.0 0.013 0.75 0.65 Constitutive model parameters HEL/GPa pHEL/GPa σHEL/GPa μHEL T/GPa β d1 d2 9.0 5.0 6.0 0.024 2 0.32 1.0 0.02 1.85 Table 4. Values of various parameters for AD99.7 ceramic[35] (The present model)
Equation of state parameters Constitutive model parameters ρc/(kg·m−3) K1/GPa K1/GPa K3/GPa Fm Wx Wy S 3 809 181.5 1 207.9 −2 991 3 3.8 2 1.25 Constitutive model parameters ${f_{{\rm{c}}}'}$/GPa ft/GPa B G/GPa λm λs l r 3 0.3 1.4 135 0.3 7.5 0.8 0.3 Table 5. Values of various parameters for tungsten alloy[35] (JC model)
Constitutive model parameters ρc/(kg·m−3) G/GPa A1/GPa B1/GPa N1 C1 M1 ${\dot \varepsilon_{_0}}$/s−1 17 600 122 1.506 0.177 0.12 0.016 1.0 1.0 Constitutive model parameters cp/(J·kg−1·K−1) Tm/K Tr/K D1 D2 D3 D4 D5 134 1 723 300 2.0 0 0 0 0 Equation of state parameters Cs/(m·s−1) S1 S2 S3 γ0 A0 4 029 1.23 0 0 1.54 0.4 Table 6. Values of various parameters for RHA[35] (JC model)
Constitutive model parameters ρc/(kg·m−3) G/GPa A1/GPa B1/GPa N1 C1 M1 ${\dot \varepsilon _{_{0}}}$/s−1 7 800 77 0.792 0.51 0.26 0.014 1.03 1.0 Constitutive model parameters cp/(J·kg−1·K−1) Tm/K Tr/K D1 D2 D3 D4 D5 477 1 793 294 0.05 3.44 −2.12 0.002 0.61 Equation of state parameters Cs/(m·s−1) S1 S2 S3 γ0 A0 4 569 1.49 0 0 2.17 0.460 -
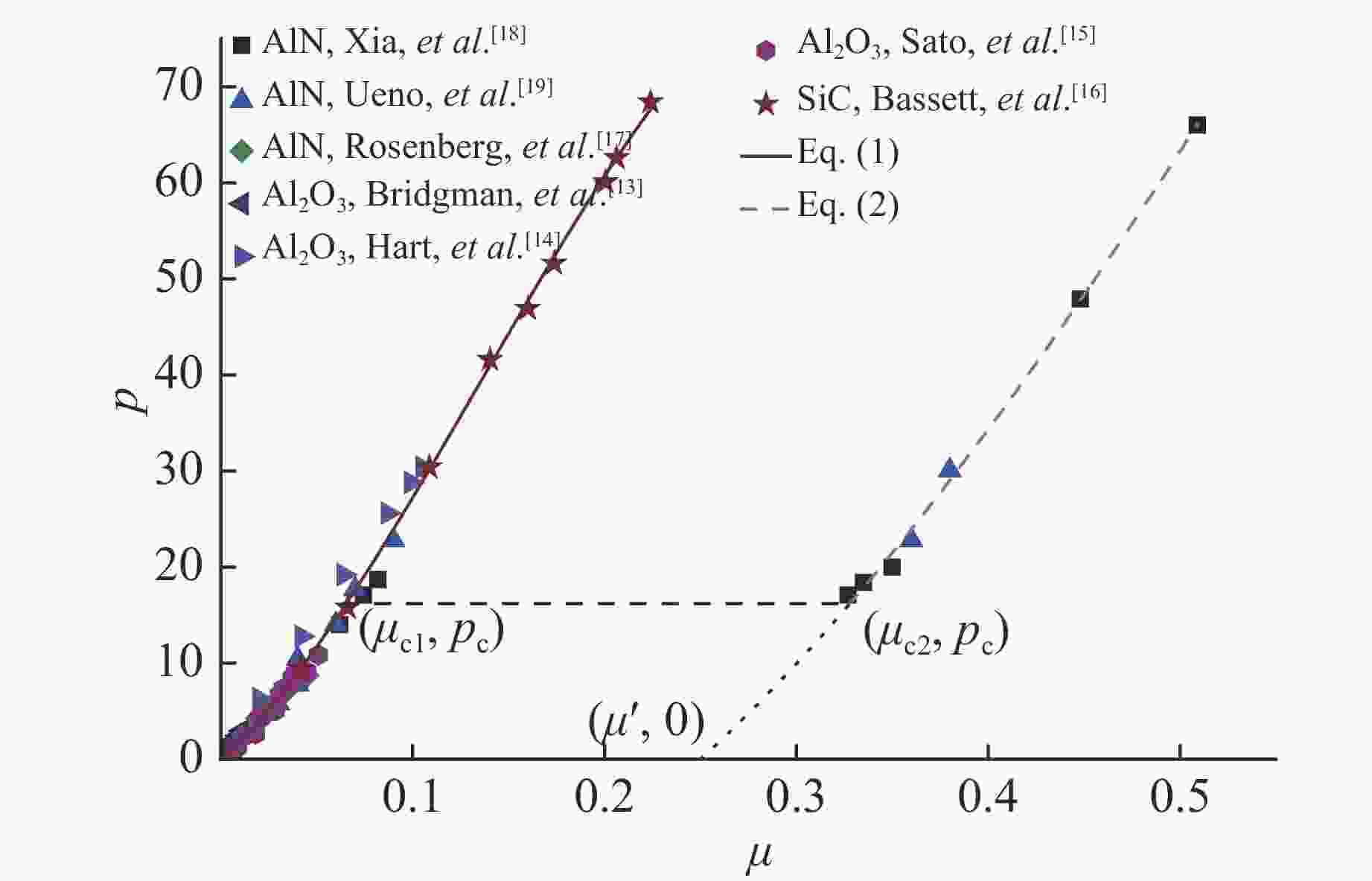
[1] FAHRENTHOLD E P. A continuum damage model for fracture of brittle solids under dynamic loading [J]. Journal of Applied Mechanics, 1991, 58(4): 904–909. doi: 10.1115/1.2897704 [2] RAJENDRAN A M. Modeling the impact behavior of AD85 ceramic under multiaxial loading [J]. International Journal of Impact Engineering, 1994, 15(6): 749–768. doi: 10.1016/0734-743X(94)90033-H [3] JOHNSON G R, HOLMQUIST T J. An improved computational constitutive model for brittle materials [J]. High Pressure Science and Technology, 2008, 309(1): 981–984. [4] SIMHA C H, BLESS S, BEDFORD A, et al. Computational modeling of the penetration response of a high-purity ceramic [J]. International Journal of Impact Engineering, 2002, 27(1): 65–86. doi: 10.1016/S0734-743X(01)00036-7 [5] RAVICHANDRAN G, SUBHASH G. A micromechanical model for high strain rate behavior of ceramics [J]. International Journal of Solids and Structures, 1995: 2627–2646. [6] ESPINOSA H D. On the dynamic shear resistance of ceramic composites and its dependence on applied multiaxial deformation [J]. International Journal of Solids and Structures, 1995, 32(21): 3105–3128. doi: 10.1016/0020-7683(94)00300-L [7] ESPINOSA H D, XU Y, BRAR N S. Micromechanics of failure waves in glass: Ⅱ, modeling [J]. Journal of the American Ceramic Society, 1997, 80(8): 2074–2085. [8] STEINBERG D J. Computer studies of the dynamic strength of ceramics [M]//Shock Waves. Berlin: Springer, 1992: 415–422. [9] XU H, WEN H M. A computational constitutive model for concrete subjected to dynamic loadings [J]. International Journal of Impact Engineering, 2016, 91: 116–125. doi: 10.1016/j.ijimpeng.2016.01.003 [10] XU H, WEN H M. Semi-empirical equations for the dynamic strength enhancement of concrete-like materials [J]. International Journal of Impact Engineering, 2013, 60: 76–81. doi: 10.1016/j.ijimpeng.2013.04.005 [11] ZHAO F Q, WEN H M. A comment on the maximum dynamic tensile strength of a concrete-like material [J]. International Journal of Impact Engineering, 2018, 115: 32–35. doi: 10.1016/j.ijimpeng.2018.01.009 [12] ZHAO F Q, WEN H M. Effect of free water content on the penetration of concrete [J]. International Journal of Impact Engineering, 2018, 121: 180–190. doi: 10.1016/j.ijimpeng.2018.06.007 [13] BRIDGMAN P W. Linear compressions to 30 000 kg/cm2, including relatively incompressible substances [J]. Proceedings of the American Academy of Arts and Sciences, 1949, 77(6): 189–234. doi: 10.2307/20023541 [14] HART H V, DRICKAMER H G. Effect of high pressure on the lattice parameters of Al2O3 [J]. Journal of Chemical Physics, 1965, 43(7): 2265–2266. doi: 10.1063/1.1697121 [15] SATO Y, AKIMOTO S. Hydrostatic compression of four corundum-type compounds: α-Al2O3, V2O3, Cr2O3, and α-Fe2O [J]. Journal of Applied Physics, 1979, 50(8): 5285–5291. doi: 10.1063/1.326625 [16] BASSETT W A, WEATHERS M S, WU T C, et al. Compressibility of SiC up to 68.4 GPa [J]. Journal of Applied Physics, 1993, 74(6): 3824–3826. doi: 10.1063/1.354476 [17] ROSENBERG Z, BRAR N S, BLESS S J. Dynamic high-pressure properties of AlN ceramic as determined by flyer plate impact [J]. Journal of Applied Physics, 1991, 70(1): 167–171. doi: 10.1063/1.350337 [18] XIA Q, XIA H, RUOFF A L. Pressure induced rocksalt phase of aluminum nitride: a metastable structure at ambient condition [J]. Journal of Applied Physics, 1993, 73(12): 8198–8200. doi: 10.1063/1.353435 [19] UENO M, ONODERA A, SHIMOMURA O, et al. X-ray observation of the structural phase transition of aluminum nitride under high pressure [J]. Physical Review B, 1992, 45(17): 10123. doi: 10.1103/PhysRevB.45.10123 [20] ROSENBERG Z, YAZIV D, YESHURUN Y, et al. Shear strength of shock-loaded alumina as determined with longitudinal and transverse manganin gauges [J]. Journal of Applied Physics, 1987, 62(3): 1120–1122. doi: 10.1063/1.339721 [21] BOURNE N K, MILLETT J, PICKUP I, et al. Delayed failure in shocked silicon carbide [J]. Journal of Applied Physics, 1997, 81(9): 6019–6023. doi: 10.1063/1.364450 [22] FENG R, RAISER G F, GUPTA Y M, et al. Material strength and inelastic deformation of silicon carbide under shock wave compression [J]. Journal of Applied Physics, 1998, 83(1): 79–86. doi: 10.1063/1.366704 [23] PICKUP I M, BARKER A K. Deviatoric strength of silicon carbide subject to shock [J]. AIP Conference Proceedings, 2000, 505(1): 573–576. [24] LEE M, BRANNON R M, BRONOWSKI D R. Uniaxial and triaxial compression tests of silicon carbide ceramics under quasi-static loading condition [R]. Albuquerque, New Mexico: Sandia National Laboratories, 2005. [25] CHEN W, RAVICHANDRAN G. Static and dynamic compressive behavior of aluminum nitride under moderate confinement [J]. Journal of the American Ceramic Society, 1996, 79(3): 579–584. [26] HEARD H C, CLINE C F. Mechanical behaviour of polycrystalline BeO, Al2O3 and AlN at high pressure [J]. Journal of Materials Science, 1980, 15(8): 1889–1897. doi: 10.1007/BF00550614 [27] WILKINS M L, CLINE C F, HONODEL C A. Fourth progress report of light armor program [R]. Livermore: Lawrence Radiation Laboratories, 1969. [28] HOLMQUIST T J, TEMPLETON D W, BISHNOI K D. Constitutive modeling of aluminum nitride for large strain, high-strain rate, and high-pressure applications [J]. International Journal of Impact Engineering, 2001, 25(3): 211–231. doi: 10.1016/S0734-743X(00)00046-4 [29] ZINSZNER J L, ERZAR B, FORQUIN P, et al. Dynamic fragmentation of an alumina ceramic subjected to shockless spalling: an experimental and numerical study [J]. Journal of the Mechanics and Physics of Solid, 2015, 85: 112–127. doi: 10.1016/j.jmps.2015.08.014 [30] GALVEZ F, RODRIGUEZ J, SANCHEZ V. Tensile strength measurements of ceramic materials at high rates of strain [J]. Le Journal de Physique IV, 1997, 7(C3): 151. [31] GALVEZ F, RODRIGUEZ J, SANCHEZ V. The spalling of long bars as a reliable method of measuring the dynamic tensile strength of ceramics [J]. International Journal of Impact Engineering, 2002, 27(2): 161–177. doi: 10.1016/S0734-743X(01)00039-2 [32] BOURNE N K. Shock-induced brittle failure of boron carbide [J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 2002, 458: 1999–2006. doi: 10.1098/rspa.2002.0968 [33] VOGLER T J, REINHART W D, CHHABILDAS L C. Dynamic behavior of boron carbide [J]. Journal of Applied Physics, 2004, 95: 4173–4183. doi: 10.1063/1.1686902 [34] HAYUN S, PARIS V, DARIEL M P, et al. Static and dynamic mechanical properties of boron carbide processed by spark plasma sintering [J]. Journal of the European Ceramic Society, 2009, 29(16): 3395–3400. doi: 10.1016/j.jeurceramsoc.2009.07.007 [35] LUNDBERG P, WESTERLING L, LUNDBERG B. Influence of scale on the penetration of tungsten rods into steel-backed alumina targets [J]. International Journal of Impact Engineering, 1996, 18(4): 403–416. doi: 10.1016/0734-743X(95)00049-G -





 下载:
下载: