Effect of Spin Transition of Iron on Thermodynamic Properties of Magnesiosiderite
-
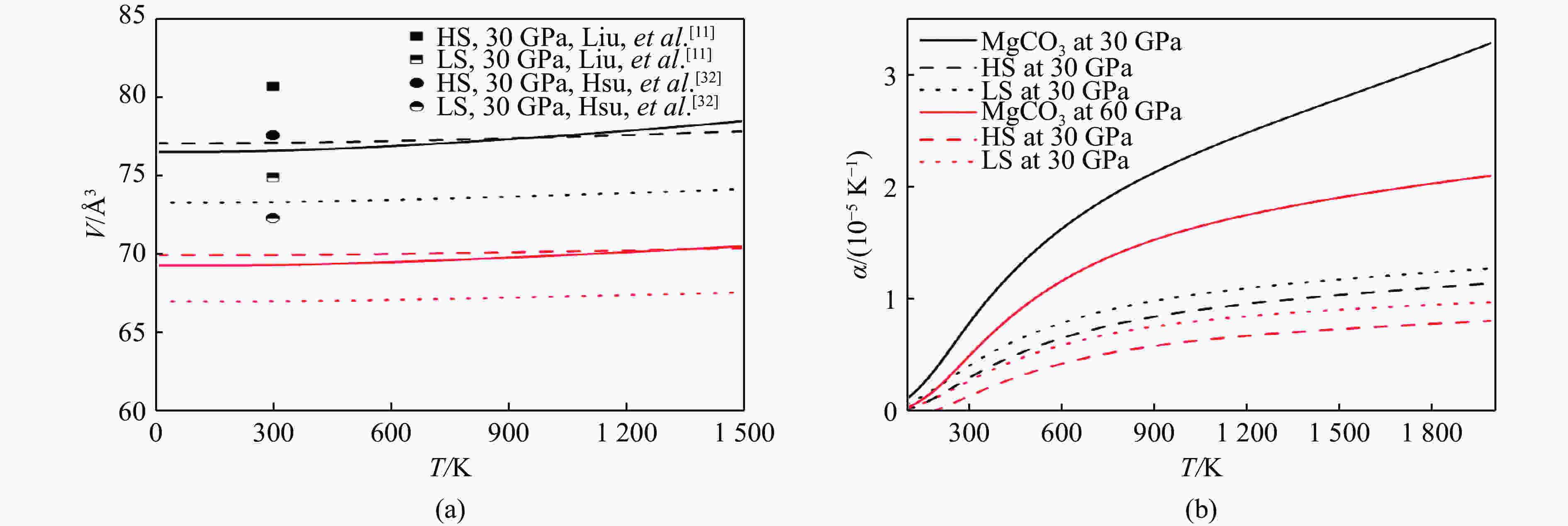
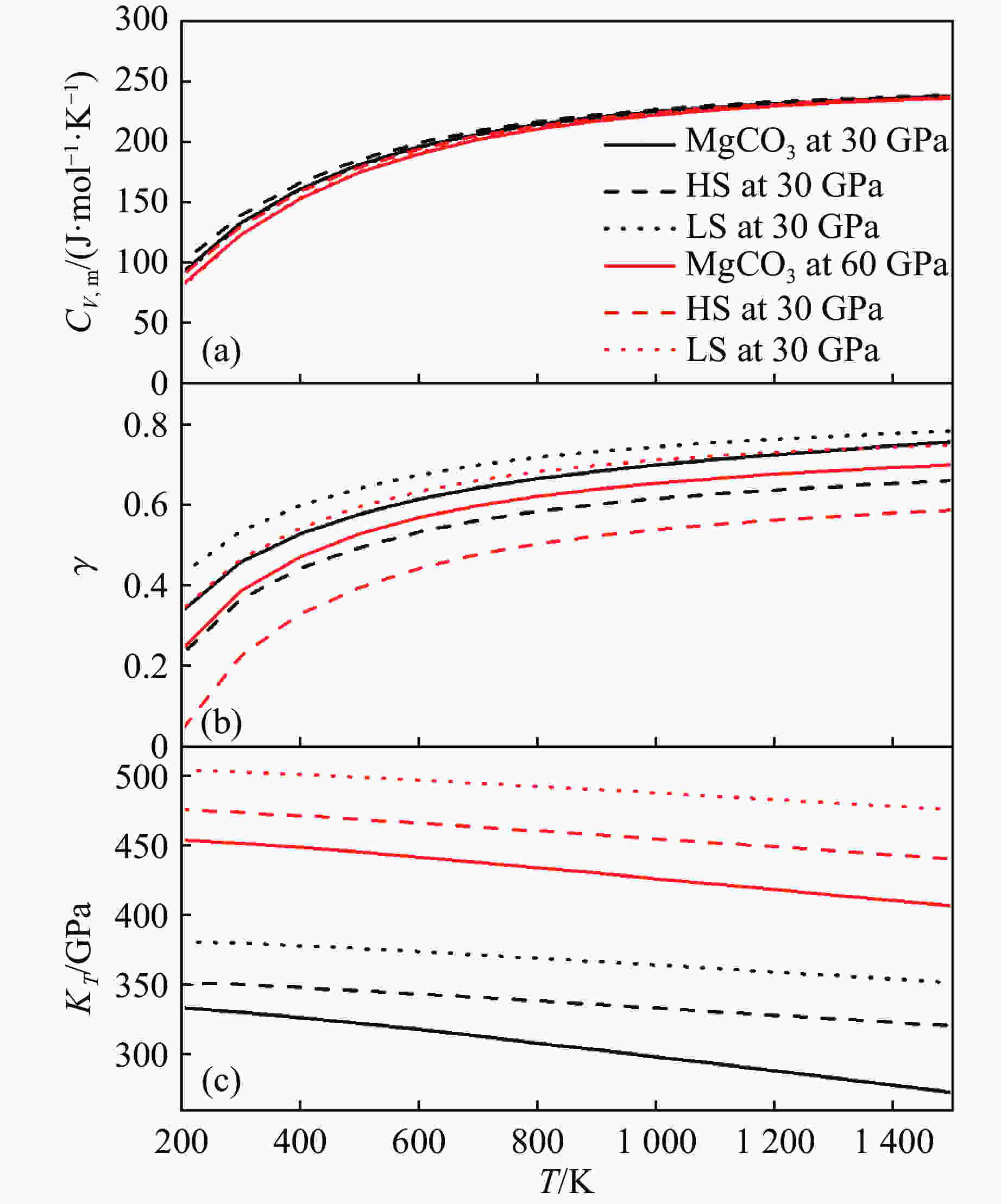
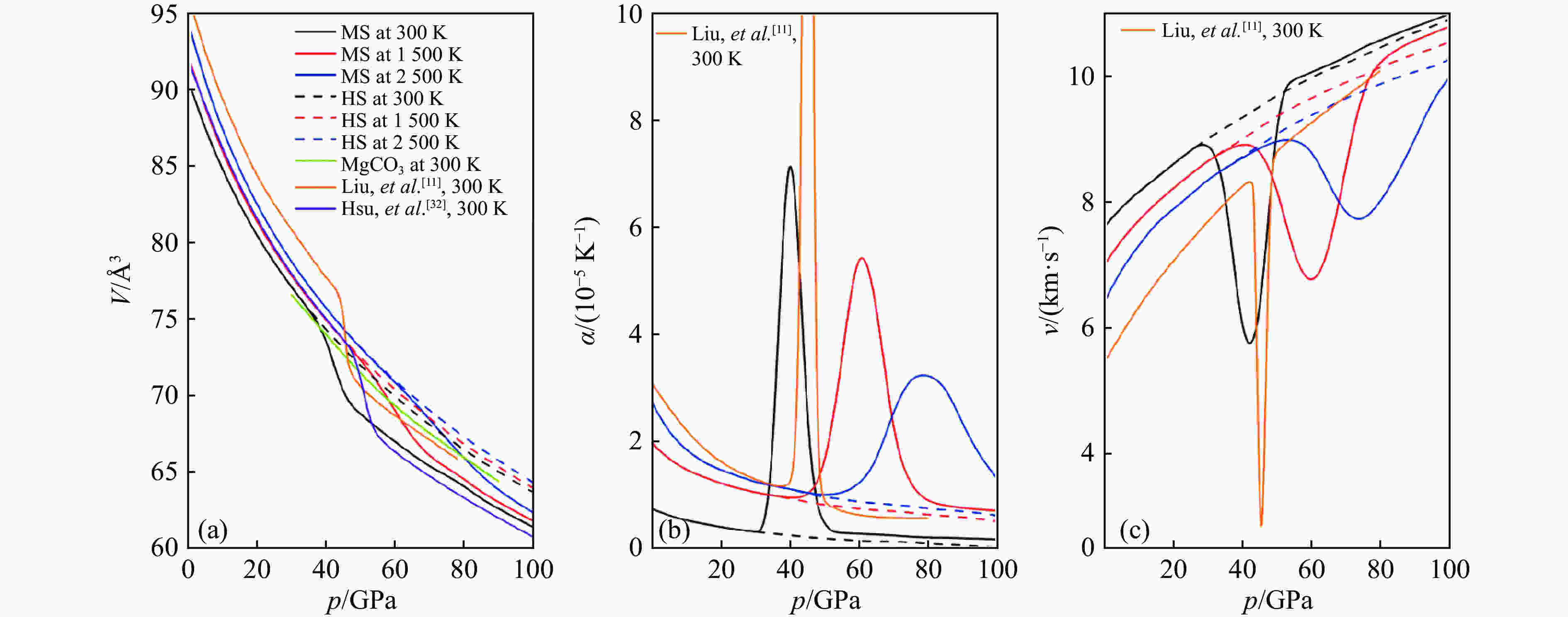
摘要: 含铁菱镁矿(Mg,Fe)CO3是碳进入地球深部的主要载体之一,铁的进入会引起矿物物理性质的变化。采用第一性原理计算方法,研究了菱镁矿含铁及铁的自旋转变对菱镁矿热力学性质的影响。含铁菱镁矿的低自旋态体积比不含铁菱镁矿小;高自旋态在低温端的体积比不含铁菱镁矿略微增大,在高温端却减小;在所研究的温压范围内,低自旋态的体积始终比高自旋态的体积小。含铁菱镁矿高自旋态的热膨胀系数减小,而自旋转变会导致热膨胀系数增加。考虑高低两种自旋态共存时的热力学性质时,计算结果表明:自旋态共存时的热膨胀系数、速度在自旋共存区间内分别呈现异常增大峰和异常减小峰,并且这些异常变化峰随着温度的升高向高压方向移动。
-
关键词:
- 菱镁矿[(Mg,Fe)CO3] /
- 自旋转变 /
- 热力学性质 /
- 混合自旋态 /
- 第一性原理
Abstract: Magnesiosiderite [(Mg,Fe)CO3] is one of the main carriers for carbon to enter the deep Earth, and the presence of iron will cause great change of mineral physical properties. The effects of ferrous iron’s spin transition on the thermodynamic properties of magnesiosiderite have been studied by first principle calculations. The volume of (Mg,Fe)CO3 low spin state (LS) decreases, while the volume of (Mg,Fe)CO3 high spin state (HS) decreases slightly at lower temperature and increases at higher temperature, as compared with that of MgCO3. In the whole range of temperature and pressure studied in this work, the volume of LS state is smaller than that of HS state. The thermal expansions of HS and LS magnesiosiderite reduce with respect to that of MgCO3, respectively. The effects of coexistence of HS and LS have been considered, in which the calculations show that the thermal expansion and velocity present abnormal increase and decrease, respectively. Meanwhile, the abnormal change peaks could move to high pressure as the increasing of temperature. -
图 5
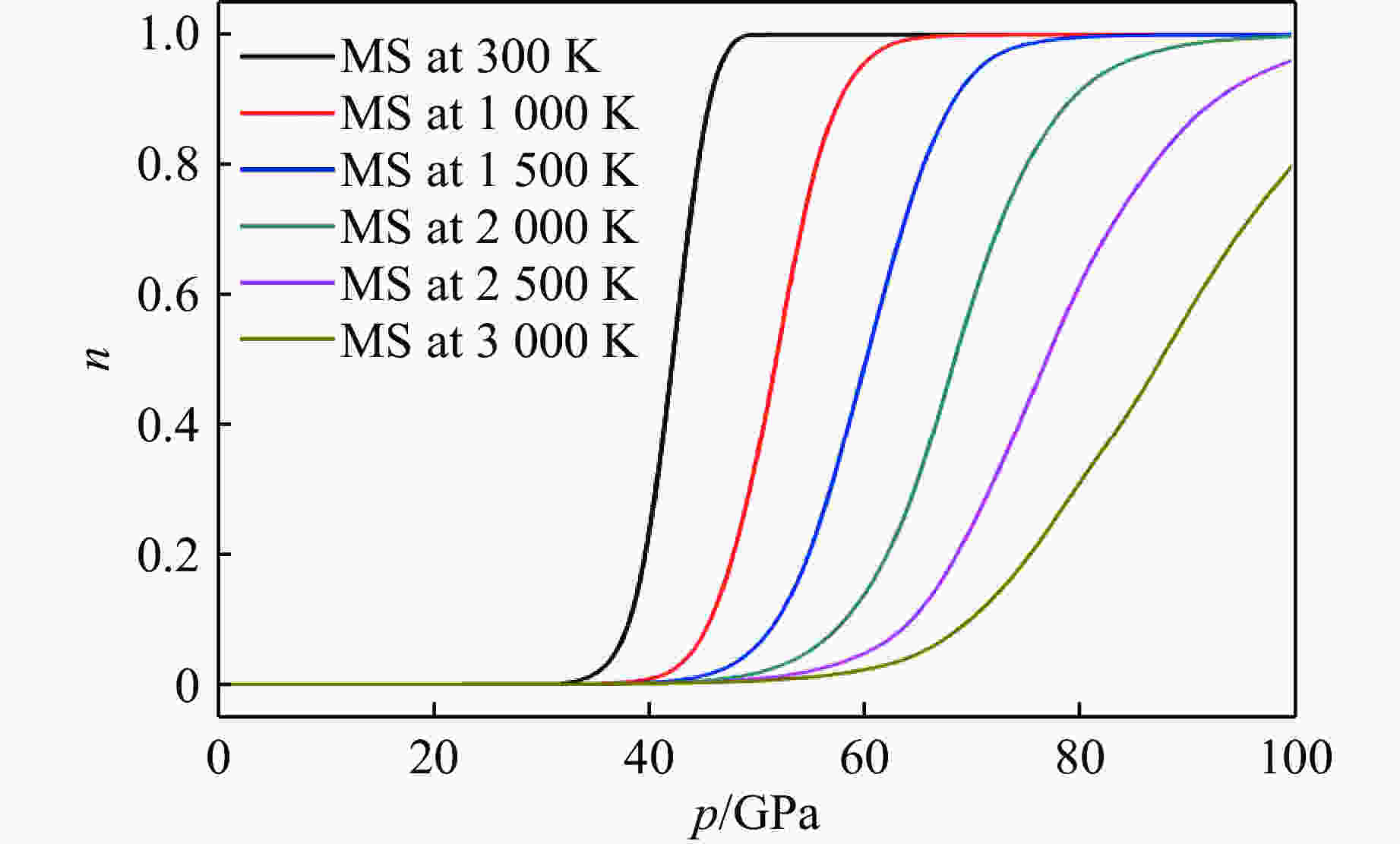
${\left. {\dfrac{{\partial n}}{{\partial T}}} \right|_p}$ 随温度的变化关系(a) 及${\left. {\dfrac{{\partial n}}{{\partial p}}} \right|_T}$ 随压力的变化关系(b)Figure 5.
${\left. {\dfrac{{\partial n}}{{\partial T}}} \right|_p}$ as the function of temperature (a) and${\left. {\dfrac{{\partial n}}{{\partial p}}} \right|_T}$ as the function of pressure (b) -
[1] MANNING C E, SHOCK E L, SVERJENSKY D A. The chemistry of carbon in aqueous fluids at crustal and upper-mantle conditions: experimental and theoretical constraints [J]. Reviews in Mineralogy and Geochemistry, 2013, 75(1): 109–148. doi: 10.2138/rmg.2013.75.5 [2] DASGUPTA R, HIRSCHMANN M M. Melting in the Earth’s deep upper mantle caused by carbon dioxide [J]. Nature, 2006, 440(7084): 659–662. doi: 10.1038/nature04612 [3] ROHRBACH A, SCHMIDT M W. Redox freezing and melting in the Earth’s deep mantle resulting from carbon-iron redox coupling [J]. Nature, 2011, 472(7342): 209–212. doi: 10.1038/nature09899 [4] WALTER M J, KOHN S C, ARAUJO D, et al. Deep mantle cycling of oceanic crust: evidence from diamonds and their mineral inclusions [J]. Science, 2011, 334(6052): 54–57. doi: 10.1126/science.1209300 [5] LAVINA B, DERA P, DOWNS R T, et al. Siderite at lower mantle conditions and the effects of the pressure-induced spin-pairing transition [J]. Geophysical Research Letters, 2009, 36(23): 23306. doi: 10.1029/2009GL039652 [6] LAVINA B, DERA P, DOWNS R T, et al. Effect of dilution on the spin pairing transition in rhombohedral carbonates [J]. High Pressure Research, 2010, 30(2): 224–229. doi: 10.1080/08957959.2010.485391 [7] LAVINA B, DERA P, DOWNS R T, et al. Structure of siderite FeCO3 to 56 GPa and hysteresis of its spin-pairing transition [J]. Physical Review B, 2010, 82(6): 064110. doi: 10.1103/PhysRevB.82.064110 [8] NAGAI T, ISHIDO T, SETO Y, et al. Pressure-induced spin transition in FeCO3-siderite studied by X-ray diffraction measurements [J]. Journal of Physics: Conference Series, 2010, 215(1): 012002. [9] FARFAN G, WANG S B, MA H W, et al. Bonding and structural changes in siderite at high pressure [J]. American Mineralogist, 2012, 97(8/9): 1421–1426. [10] LIN J F, LIU J, JACOBS C, et al. Vibrational and elastic properties of ferromagnesite across the electronic spin-pairing transition of iron [J]. American Mineralogist, 2012, 97(4): 583–591. doi: 10.2138/am.2012.3961 [11] LIU J, LIN J F, MAO Z, et al. Thermal equation of state and spin transition of magnesiosiderite at high pressure and temperature [J]. American Mineralogist, 2014, 99(1): 84–93. doi: 10.2138/am.2014.4553 [12] LIU J, LIN J F, PRAKAPENKA V B. High-pressure orthorhombic ferromagnesite as a potential deep-mantle carbon carrier [J]. Scientific Reports, 2015, 5(1): 07640. doi: 10.1038/srep07640 [13] HAZEN R M, JONES A P, BAROSS J A. Carbon in Earth [J]. Reviews in Mineralogy and Geochemistry, 2013, 75(1). [14] ISSHIKI M, IRIFUNE T, HIROSE K, et al. Stability of magnesite and its high-pressure form in the lowermost mantle [J]. Nature, 2004, 427(6969): 60–63. doi: 10.1038/nature02181 [15] OGANOV A R, ONO S, MA Y M, et al. Novel high-pressure structures of MgCO3, CaCO3 and CO2 and their role in Earth’s lower mantle [J]. Earth and Planetary Science Letters, 2008, 273(1/2): 38–47. [16] LIN J F, SPEZIALE S, MAO Z, et al. Effects of the electronic spin transitions of iron in lower mantle minerals: implications for deep mantle geophysics and geochemistry [J]. Reviews of Geophysics, 2013, 51(2): 244–275. doi: 10.1002/rog.20010 [17] SPEZIALE S, MILNER A, LEE V E, et al. Iron spin transition in Earth’s mantle [J]. Proceedings of the National Academy of Sciences of the United States of America, 2005, 102(50): 17918–17922. doi: 10.1073/pnas.0508919102 [18] TSUCHIYA T, WENTZCOVITCH R M, DA SILVAC R S, et al. Spin transition in magnesiowüstite in Earth’s lower mantle [J]. Physical Review Letters, 2006, 96(19): 198501. doi: 10.1103/PhysRevLett.96.198501 [19] GONCHAROV A F, STRUZHKIN V V, JACOBSEN S D. Reduced radiative conductivity of low-spin (Mg, Fe)O in the lower mantle [J]. Science, 2006, 312(5777): 1205–1208. doi: 10.1126/science.1125622 [20] LIN J F, VANKÓ G, JACOBSEN S D, et al. Spin transition zone in Earth’s lower mantle [J]. Science, 2007, 317(5845): 1740–1743. doi: 10.1126/science.1144997 [21] CROWHURST J C, BROWN J M, GONCHAROV A F, et al. Elasticity of (Mg, Fe)O through the spin transition of iron in the lower mantle [J]. Science, 2008, 319(5862): 451–453. doi: 10.1126/science.1149606 [22] WENTZCOVITCH R M, JUSSTO J F, WU Z, et al. Anomalous compressibility of ferropericlase throughout the iron spin cross-over [J]. Proceedings of the National Academy of Sciences of the United States of America, 2009, 106(21): 8447–8452. doi: 10.1073/pnas.0812150106 [23] MARQUARDT H, SPEZIALE S, REICHMANN H J, et al. Elastic shear anisotropy of ferropericlase in Earth’s lower mantle [J]. Science, 2009, 324(5924): 224–226. doi: 10.1126/science.1169365 [24] HSU H, UMEMOTO K, WU Z Q, et al. Spin-state crossover of iron in lower-mantle minerals: results of DFT+U investigations [J]. Reviews in Mineralogy and Geochemistry, 2010, 71(1): 169–199. doi: 10.2138/rmg.2010.71.09 [25] ANTONANGELI D, SIEBERT J, ARACNE C M, et al. Spin crossover in ferropericlase at high pressure: aseismologically transparent transition? [J]. Science, 2011, 331(6013): 64–67. doi: 10.1126/science.1198429 [26] WU Z Q, JUSTO J F, WENTZCOVITCH R M. Elastic anomalies in a spin-crossover system: ferropericlase at lower mantle conditions [J]. Physical Review Letters, 2013, 110(22): 228501. doi: 10.1103/PhysRevLett.110.228501 [27] HOLMSTRÖM E, STIXRUDE L. Spin crossover in ferropericlase from first-principles molecular dynamics [J]. Physical Review Letters, 2015, 114(11): 117202. doi: 10.1103/PhysRevLett.114.117202 [28] SONG Y L, HE K H, SUN J, et al. Effects of iron spin transition on the electronic structure, thermal expansivity and lattice thermal conductivity of ferropericlase: a first principles study [J]. Scientific Reports, 2019, 9(1): 4172. doi: 10.1038/s41598-019-40454-4 [29] CERANTOLA V, MCCAMMON C, KUPENKO I, et al. High-pressure spectroscopic study of siderite (FeCO3) with a focus on spin crossover [J]. American Mineralogist, 2015, 100(11/12): 2670–2681. [30] MATTILA A, PYLKKÄNEN T, RUEFF J-P, et al. Pressure induced magnetic transition in siderite FeCO3 studied by X-ray emission spectroscopy [J]. Journal of Physics: Condensed Matter, 2007, 19(38): 386206. doi: 10.1088/0953-8984/19/38/386206 [31] SHI H, LUO W L, JOHANSSON B, et al. First-principles calculations of the electronic structure and pressure-induced magnetic transition in siderite FeCO3 [J]. Physical Review B, 2008, 78(15): 155119. doi: 10.1103/PhysRevB.78.155119 [32] HSU H, HUANG S C. Spin crossover and hyperfine interactions of iron in (Mg, Fe)CO3 ferromagnesite [J]. Physical Review B, 2016, 94(6): 060404. doi: 10.1103/PhysRevB.94.060404 [33] FU S, YANG J, LIN J F. Abnormal elasticity of single-crystal magnesiosiderite across the spin transition in Earth’s lower mantle [J]. Physical Review Letters, 2017, 118(3): 036402. doi: 10.1103/PhysRevLett.118.036402 [34] KRESSE G, FUTHMÜLLER J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set [J]. Physical Review B, 1996, 54(16): 11169–11186. doi: 10.1103/PhysRevB.54.11169 [35] KRUKAU A V, VYDROV O A, IZMAYLOV A F, et al. Influence of the exchange screening parameter on the performance of screened hybrid functional [J]. The Journal of Chemical Physics, 2006, 125(22): 224106. doi: 10.1063/1.2404663 [36] MONKHORST H J, PACK J D. Special points for Brillouin-zone integrations [J]. Physical Review B, 1976, 13(12): 5188–5192. doi: 10.1103/PhysRevB.13.5188 [37] TOGO A, OBA F, TANAKA I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures [J]. Physical Review B, 2008, 78(13): 4106. [38] WU Z, JUSTO J F, DA SILVAC R S, et al. Anomalous thermodynamic properties in ferropericlase throughout its spin crossover [J]. Physical Review B, 2009, 80(1): 014409. doi: 10.1103/PhysRevB.80.014409 [39] KOMABAYASHI T, HIROSE K, NAGAYA Y, et al. High-temperature compression of ferropericlase and the effect of temperature on iron spin transition [J]. Earth and Planetary Science Letters, 2010, 297(3/4): 691–699. [40] MAO Z, LIN J F, LIU J, et al. Thermal equation of state of lower-mantle ferropericlase across the spin crossover [J]. Geophysical Research Letters, 2011, 38(23): 23308. -






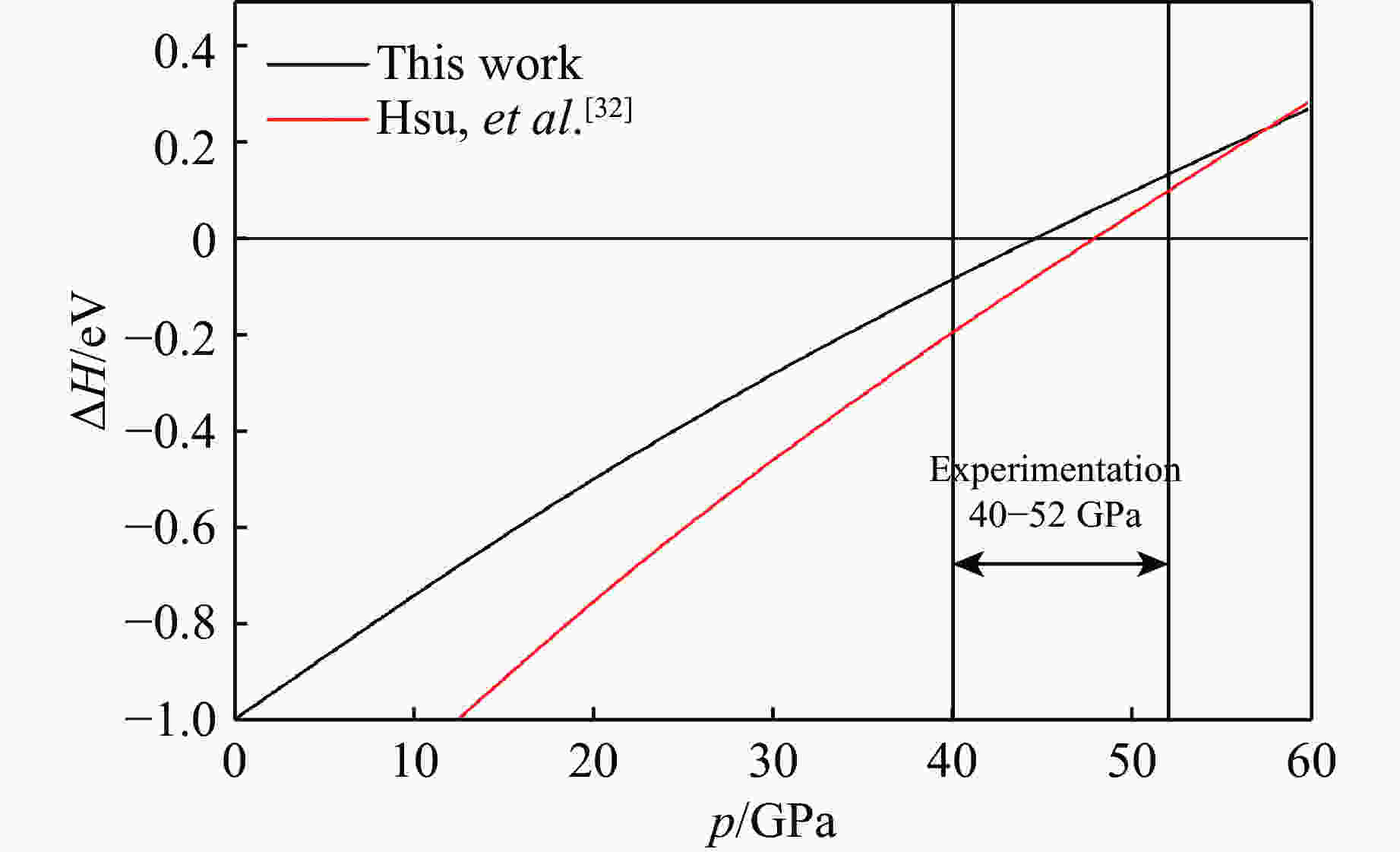
 下载:
下载: