Comparative Study on Dynamic Tensile and Compressive Strength of the Saturated Fine Sandstone
-
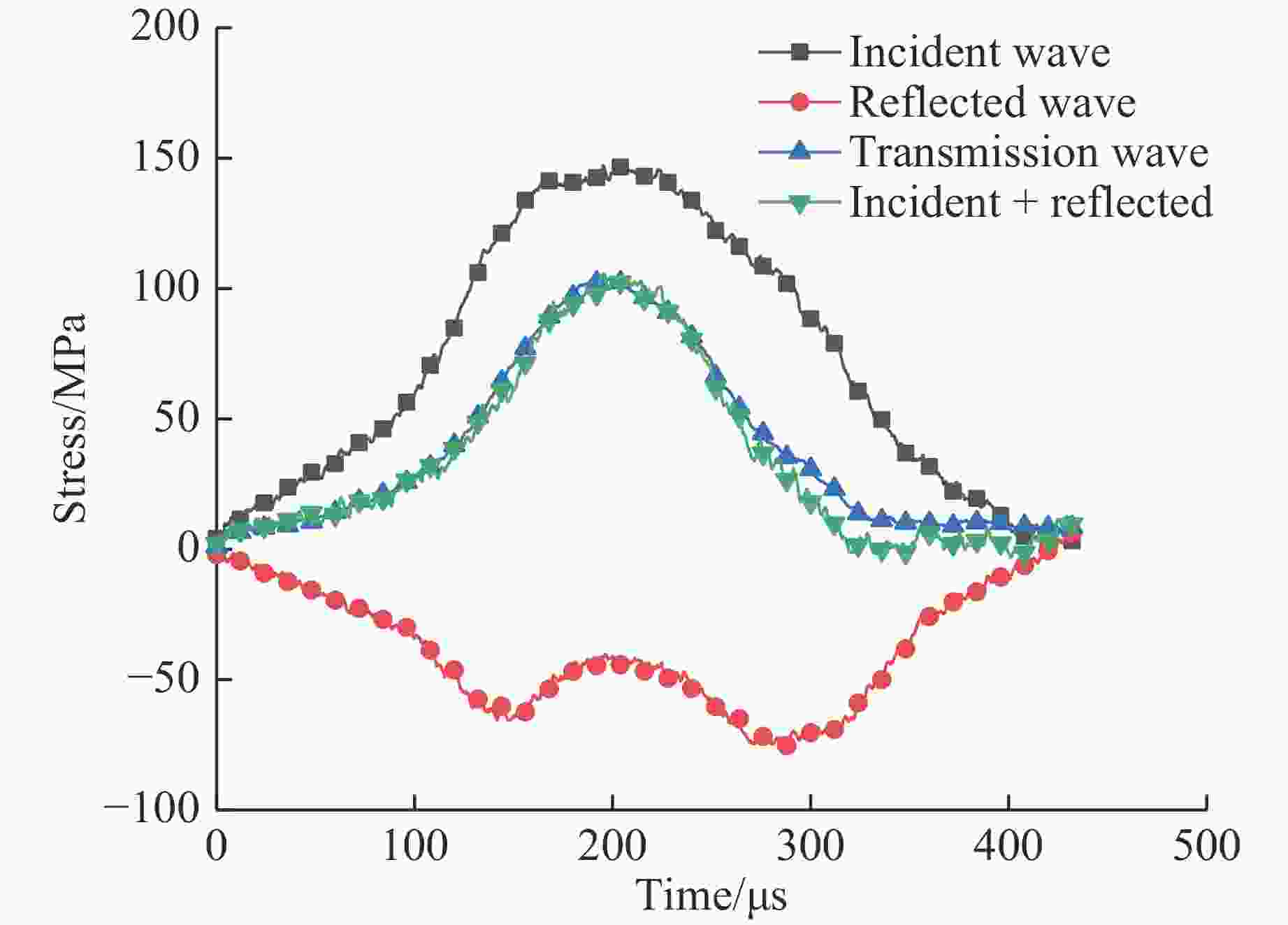
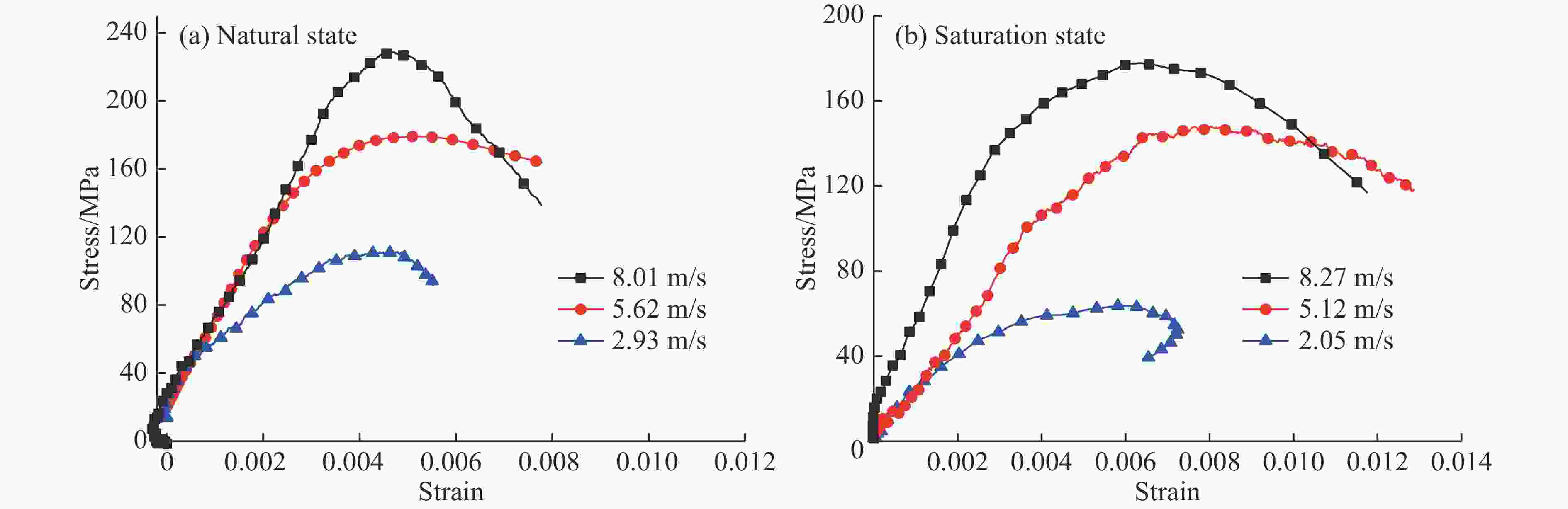
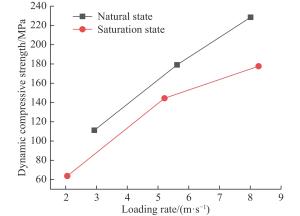
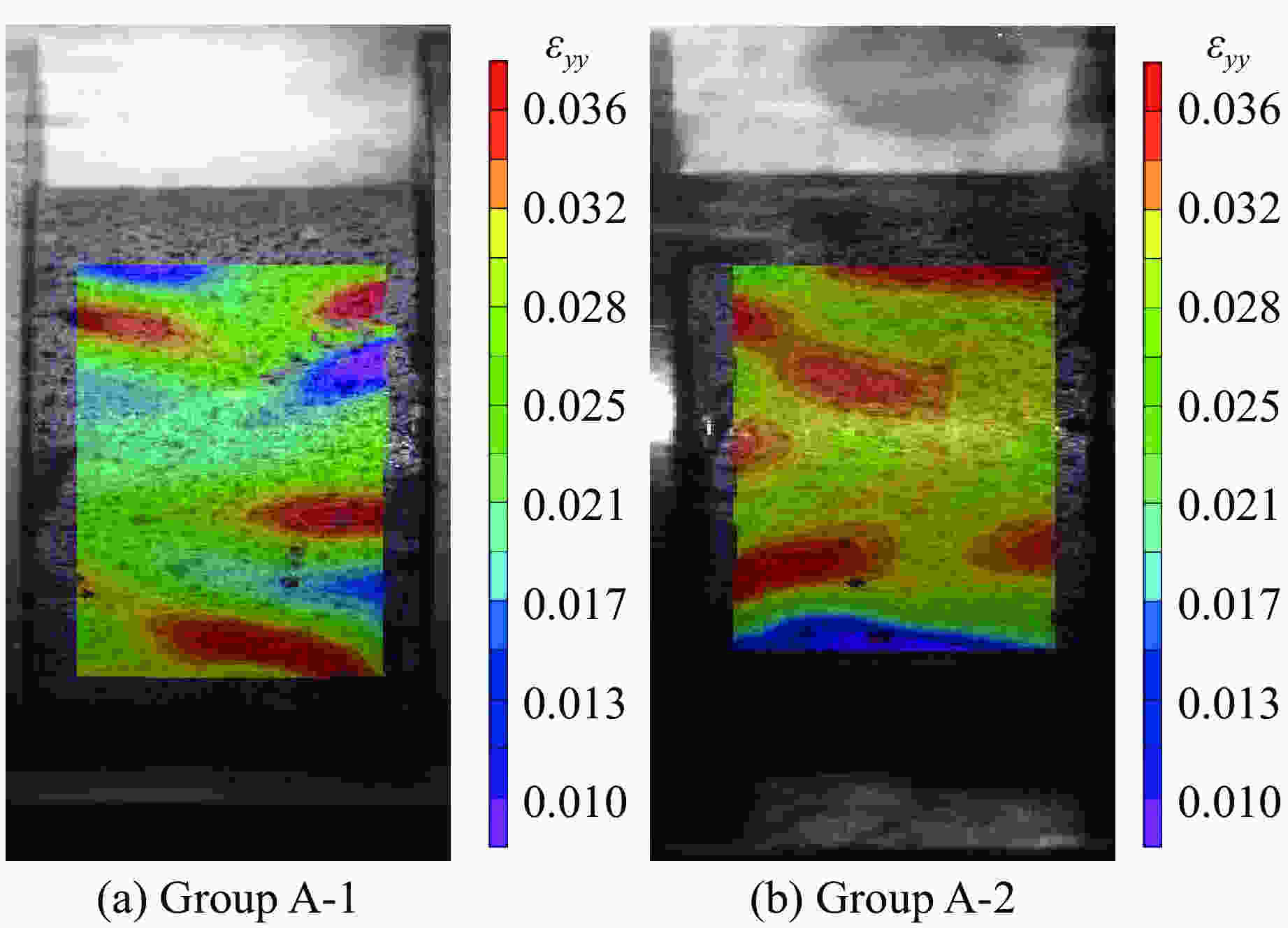
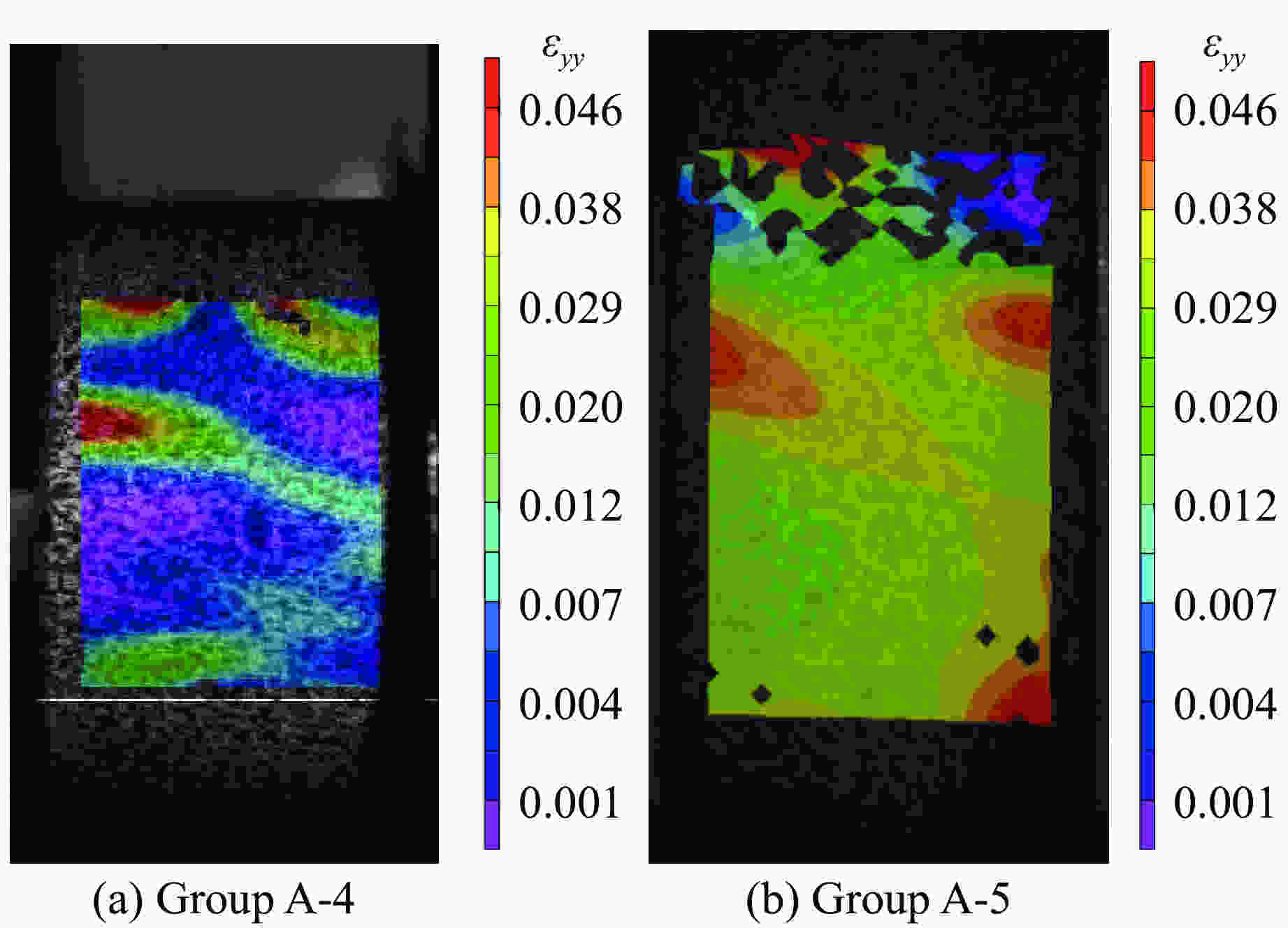
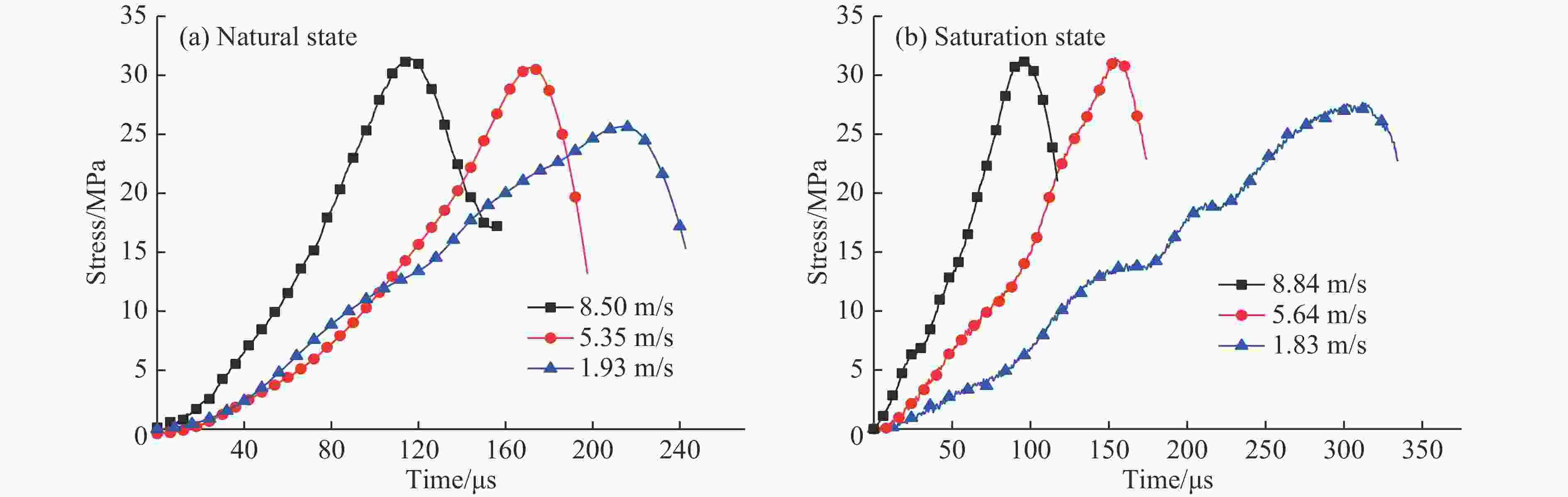
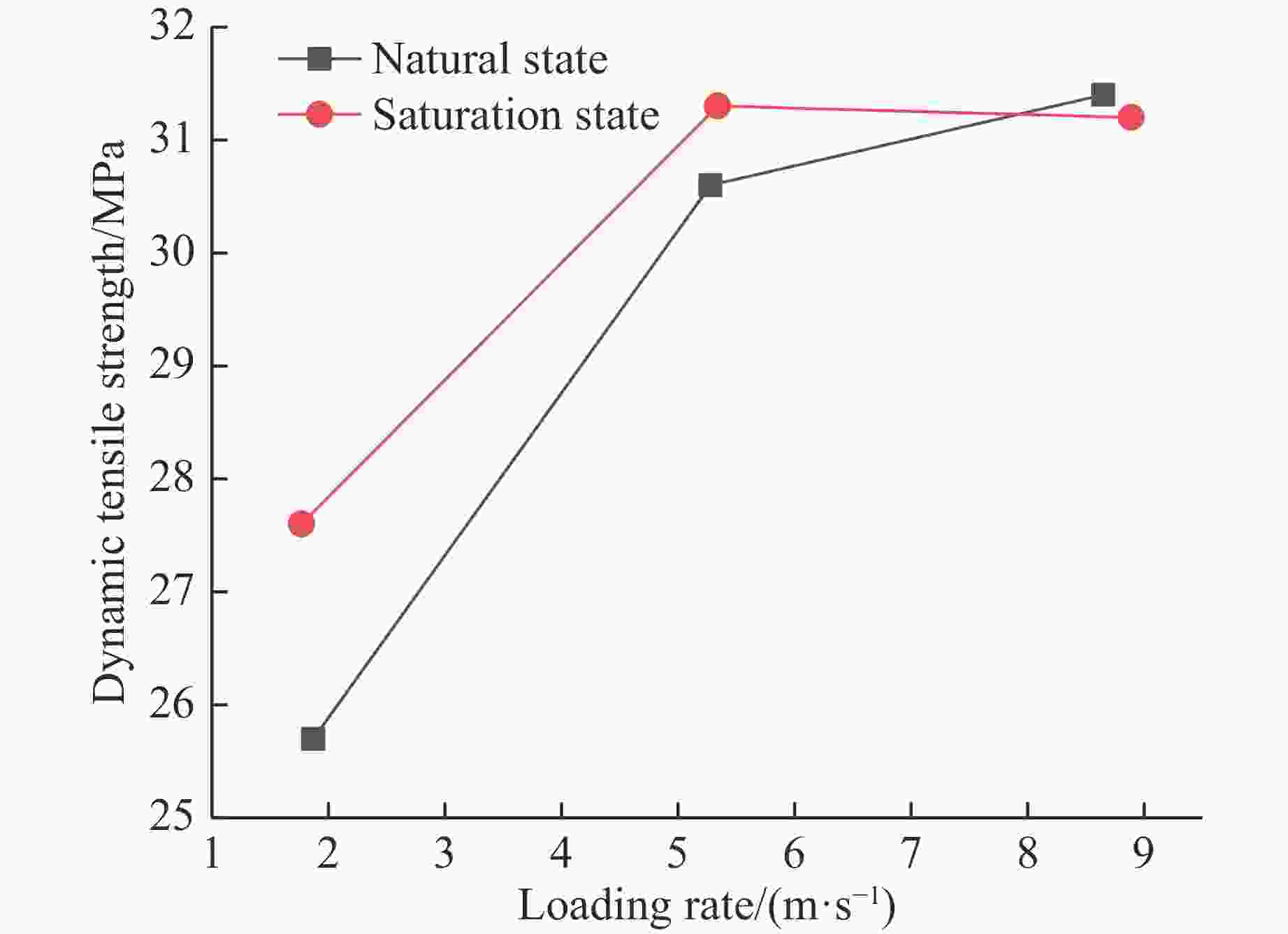
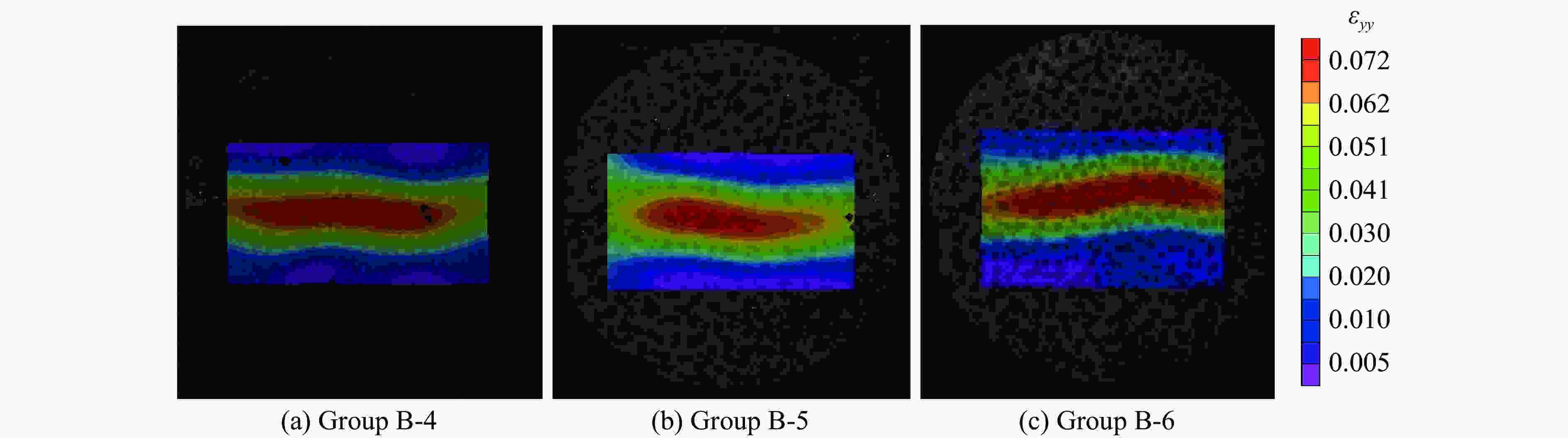
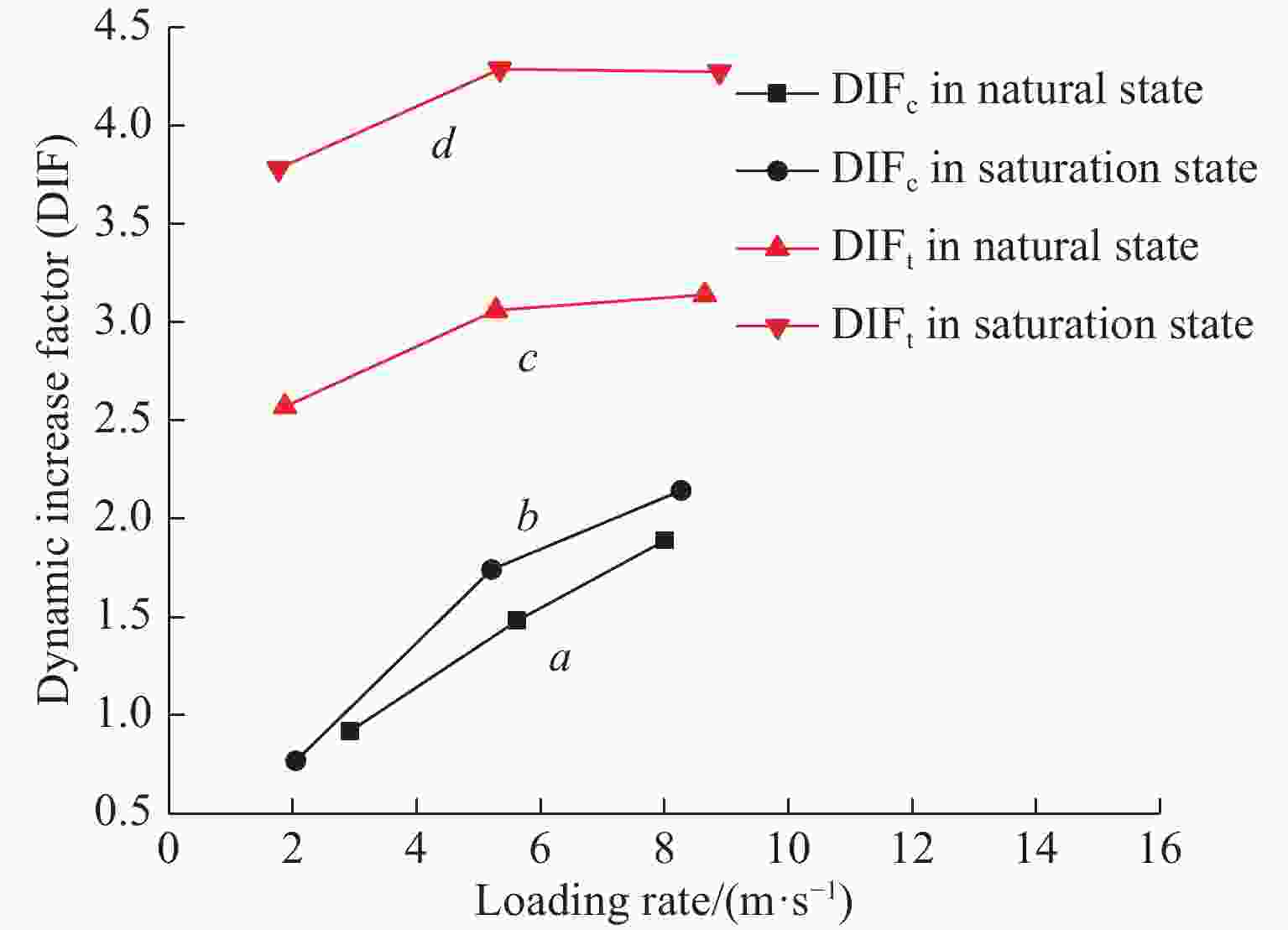
摘要: 使用霍普金森压杆(SHPB)装置对天然状态和饱水状态下的细砂岩进行单轴动态压缩试验和动态劈裂试验,研究水和加载速率对细砂岩动态抗拉、抗压强度的影响及其差异性,并且结合数字图像相关(DIC)技术,分析细砂岩动态抗拉、抗压时的破坏机制。试验结果表明:两种状态下的细砂岩动态抗拉、抗压强度有明显的率效应,随着加载速率的增大而增大,且相同加载速率下,细砂岩在饱水状态下比天然状态下的动态抗压强度小,而抗拉强度比天然状态下的大;水的存在对细砂岩动态抗压强度和抗拉强度的应变率效应影响不大,但水能提高细砂岩动态抗压和抗拉强度增强因子,并且对细砂岩动态抗拉强度增强因子的提高更显著;在动态受压过程中饱水状态岩样表面的应变集中处较天然状态下明显更少,应变梯度更显著,在动态受拉过程中拉剪效果被削弱。Abstract: Using split Hopkinson compression bar (SHPB) device, uniaxial dynamic compression tests and dynamic split tests on fine sandstone in natural state and saturated state were carried out. The influence and difference of water and loading rate on dynamic tensile and compressive strength of fine sandstone were studied, and the failure mechanism of the fine sandstone in dynamic tension and compression was analyzed with digital image correlation (DIC) technology. The test results show that the dynamic compressive strength and tensile strength of the fine sandstone under the two states have obvious strain rate dependent effect, and they increase with the increase of loading rate. Under the same loading rate, the dynamic compressive strength of fine sandstone in saturated state is smaller than that in natural state, while the tensile strength in saturated state is larger. Water has little effect on the strain rate effect of dynamic compressive strength and tensile strength for the fine sandstone. However, water can improve the dynamic compressive strength and tensile strength enhancement factor of the fine sandstone, and has a more significant effect on the dynamic tensile strength enhancement factor. In the process of dynamic compression, the surface strain concentration of the rock specimen in saturated state is significantly less than that in natural state, the strain gradient is more significant, and the tensile-shear effect is weakened during the dynamic tensile process.
-
表 1 试验分组
Table 1. Test group
Type of test State of rock samples Group Loading rate/(m·s–1) Temperature/℃ Compression test Natural state A-1 8.01 20 A-2 5.62 20 A-3 2.93 20 Saturation state A-4 8.27 20 A-5 5.12 20 A-6 2.05 20 Splitting test Natural state B-1 8.65 20 B-2 5.28 20 B-3 1.87 20 Saturation state B-4 8.89 20 B-5 5.34 20 B-6 1.44 20 -
[1] 王宇, 常德龙, 李建林, 等. 复杂应力路径下饱水砂岩宏细观力学特性研究 [J]. 岩土力学, 2016, 37(11): 3105–3114.WANG Y, CHANG D L, LI J L, et al. Research on macro- and meso-mechanical properties of water-saturated sandstone under complex stress path [J]. Rock and Soil Mechanics, 2016, 37(11): 3105–3114. [2] 吴疆宇, 冯梅梅, 张文力, 等. 围压及孔隙水压对饱水砂岩能耗特征的影响 [J]. 应用基础与工程科学学报, 2019(1): 180–193.WU J Y, FENG M M, ZHANG W L, et al. Confining pressure and pore pressure effect on the energy dissipation of water-saturated sandstone [J]. Journal of Basic Science and Engineering, 2019(1): 180–193. [3] HAWKINS A B, MCCONNELL B J. Sensitivity of sandstone strength and deformability to changes in moisture content [J]. Quarterly Journal of Engineering Geology and Hydrogeology, 1992, 25(2): 115–130. doi: 10.1144/GSL.QJEG.1992.025.02.05 [4] DYKE C G, DOBEREINER L. Evaluating the strength and deformability of sandstones [J]. Quarterly Journal of Engineering Geology and Hydrogeology, 1991, 24(1): 123. doi: 10.1144/GSL.QJEG.1991.024.01.13 [5] 高峰, 熊信, 周科平, 等. 冻融循环作用下饱水砂岩的强度劣化模型 [J]. 岩土力学, 2019, 40(3): 926–932.GAO F, XIONG X, ZHOU K P, et al. Strength deterioration model of saturated sandstone under freeze-thaw cycles [J]. Rock and Soil Mechanics, 2019, 40(3): 926–932. [6] ZHANG Z, GAO F. Experimental investigation on the energy evolution of dry and water-saturated red sandstones [J]. International Journal of Mining Science and Technology, 2015, 25(3): 383–388. doi: 10.1016/j.ijmst.2015.03.009 [7] WU J, FENG M, YU B, et al. Experimental investigation on dilatancy behavior of water-saturated sandstone [J]. International Journal of Mining Science and Technology, 2018, 28(2): 323–329. doi: 10.1016/j.ijmst.2017.09.003 [8] 王斌, 李夕兵. 单轴荷载下饱水岩石静态和动态抗压强度的细观力学分析 [J]. 爆炸与冲击, 2012, 32(4): 423–431. doi: 10.3969/j.issn.1001-1455.2012.04.013WANG B, LI X B. Mesomechanics analysis of static compressive strength and dynamic compressive strength of water-saturated rock under uniaxial load [J]. Explosion and Shock Waves, 2012, 32(4): 423–431. doi: 10.3969/j.issn.1001-1455.2012.04.013 [9] 王斌, 李夕兵, 尹土兵, 等. 饱水砂岩动态强度的SHPB试验研究 [J]. 岩石力学与工程学报, 2010, 29(5): 1003–1009.WANG B, LI X B, YIN T B, et al. Split Hopkinson pressure bar (SHPB) experiments on dynamic strength of water-saturated sandstone [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(5): 1003–1009. [10] ZHOU Z L, CAI X, ZHAO Y, et al. Strength characteristics of dry and saturated rock at different strain rates [J]. Transactions of Nonferrous Metals Society of China, 2016, 26(7): 1919–1925. doi: 10.1016/S1003-6326(16)64314-5 [11] SELYUTINA N S, PETROV Y V. The water-saturation effect for concretes and rocks subjected to high strain rates [J]. Procedia Structural Integrity, 2018, 13: 705–709. doi: 10.1016/j.prostr.2018.12.117 [12] 褚夫蛟, 刘敦文, 陶明, 等. 基于SHPB的不同含水状态砂岩动态响应 [J]. 工程科学学报, 2017, 39(12): 1783–1790.CHU F J, LIU D W, TAO M, et al. Dynamic response of sandstones with different water contents based on SHPB [J]. Chinese Journal of Engineering, 2017, 39(12): 1783–1790. [13] 高富强, 张军, 何朋立. 不同围压荷载和含水状态下砂岩SHPB试验研究 [J]. 矿业研究与开发, 2018, 38(6): 65–68.GAO F Q, ZHANG J, HE P L. SHPB test of sandstone with different confining loads and moisture contents [J]. Mining Research and Development, 2018, 38(6): 65–68. [14] 郑广辉, 许金余, 王鹏, 等. 不同饱水度红砂岩静态本构关系及动态力学性能研究 [J]. 振动与冲击, 2018, 37(16): 31–37.ZHENG G H, XU J Y, WANG P, et al. Static constitutive relation and dynamic mechanical properties of red sandstone with different water saturation [J]. Journal of Vibration and Shock, 2018, 37(16): 31–37. [15] WENG L, WU Z, LIU Q, et al. Energy dissipation and dynamic fragmentation of dry and water-saturated siltstones under sub-zero temperatures [J]. Engineering Fracture Mechanics, 2019, 220: 106659. doi: 10.1016/j.engfracmech.2019.106659 [16] KIM E, STINE M A, DE OLIVEIRA D B M, et al. Correlations between the physical and mechanical properties of sandstones with changes of water content and loading rates [J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 100: 255–262. doi: 10.1016/j.ijrmms.2017.11.005 [17] ZHOU Z, CAI X, MA D, et al. Water saturation effects on dynamic fracture behavior of sandstone [J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 114: 46–61. doi: 10.1016/j.ijrmms.2018.12.014 [18] 王茹, 唐春安, 王述红. 岩石点荷载试验若干问题的研究 [J]. 东北大学学报(自然科学版), 2008(1): 130–132, 140.WANG R, TANG C A, WANG S H. Study on several problems about point load test of rock [J]. Journal of Northeastern University (Natural Science), 2008(1): 130–132, 140. [19] 中国水电顾问集团成都勘测设计研究院. 工程岩体试验方法标准: GB/T 50266—2013 [S]. 北京: 中国计划出版社, 2013. [20] 王海龙, 李庆斌. 饱和混凝土静动力抗压强度变化的细观力学机理 [J]. 水利学报, 2006, 37(8): 958–962. doi: 10.3321/j.issn:0559-9350.2006.08.010WANG H L, LI Q B. Micro-mechanism of static and dynamic strengths for saturated concrete [J]. Journal of Hydraulic Engineering, 2006, 37(8): 958–962. doi: 10.3321/j.issn:0559-9350.2006.08.010 [21] ZHENG D, LI Q. An explanation for rate effect of concrete strength based on fracture toughness including free water viscosity [J]. Engineering Fracture Mechanics, 2004, 71(16/17): 2319–2327. -







 下载:
下载: