Damage of 3D Random Aggregate Concrete under Ultrasonic Dynamic Load
-
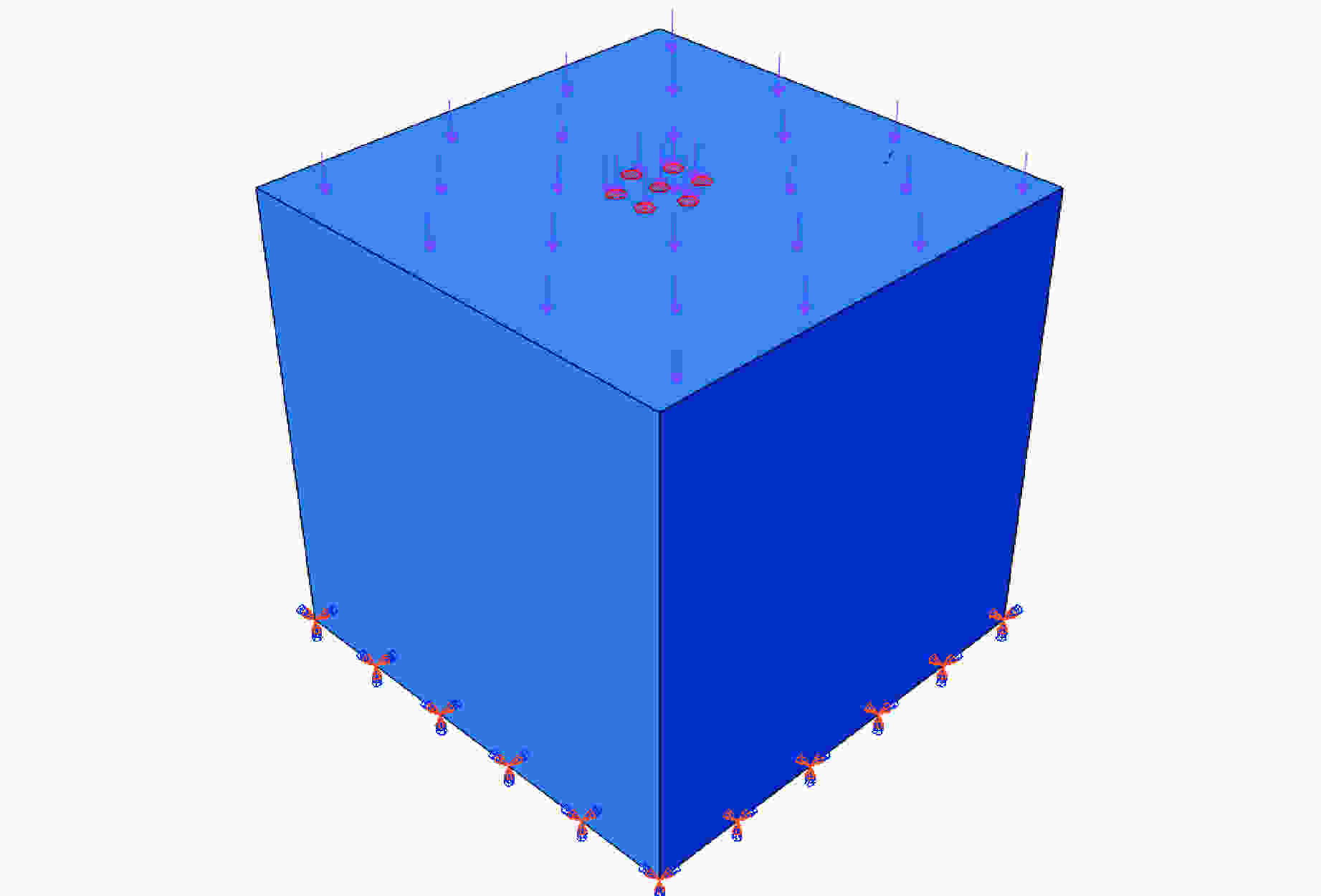
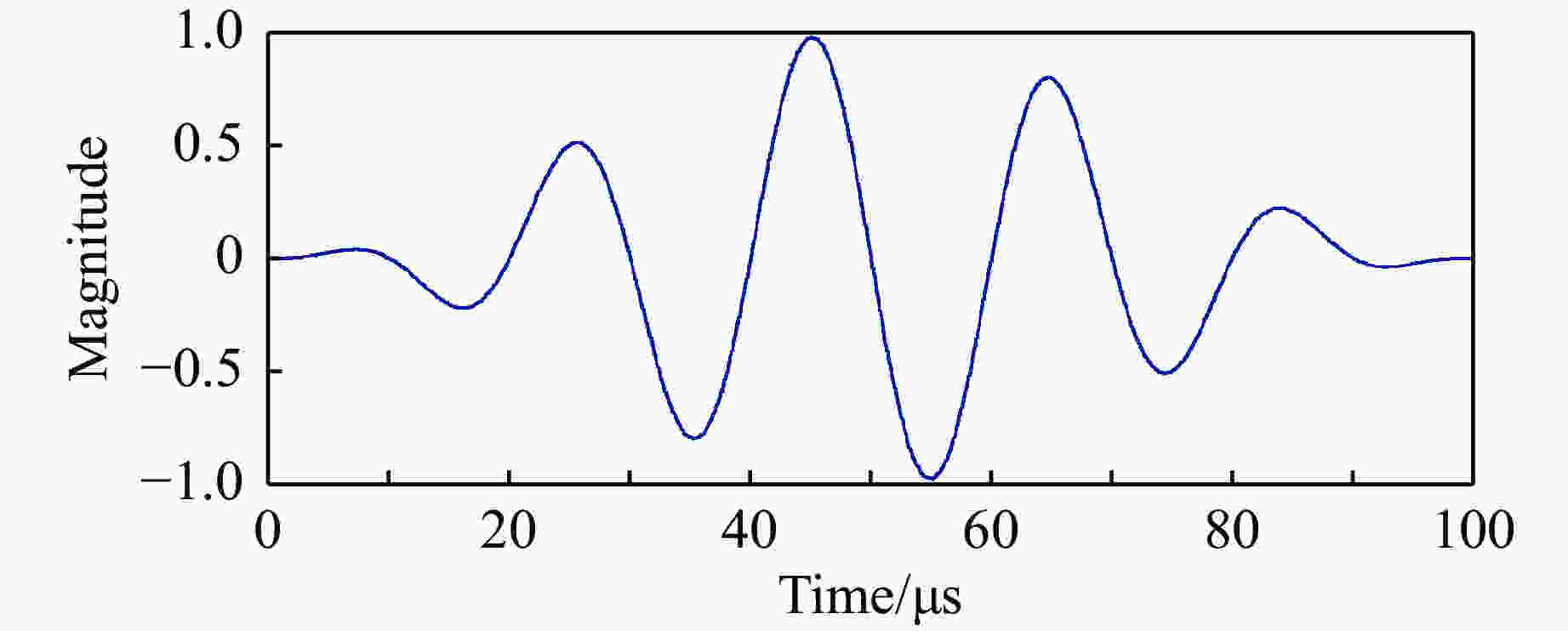
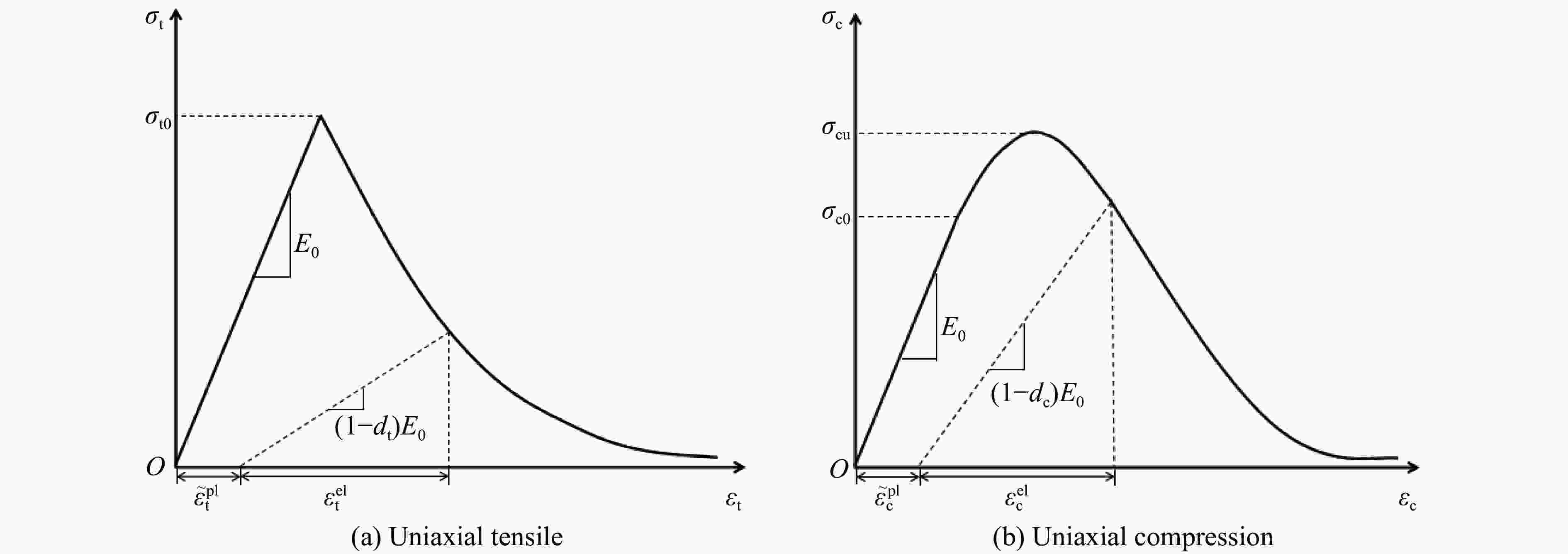
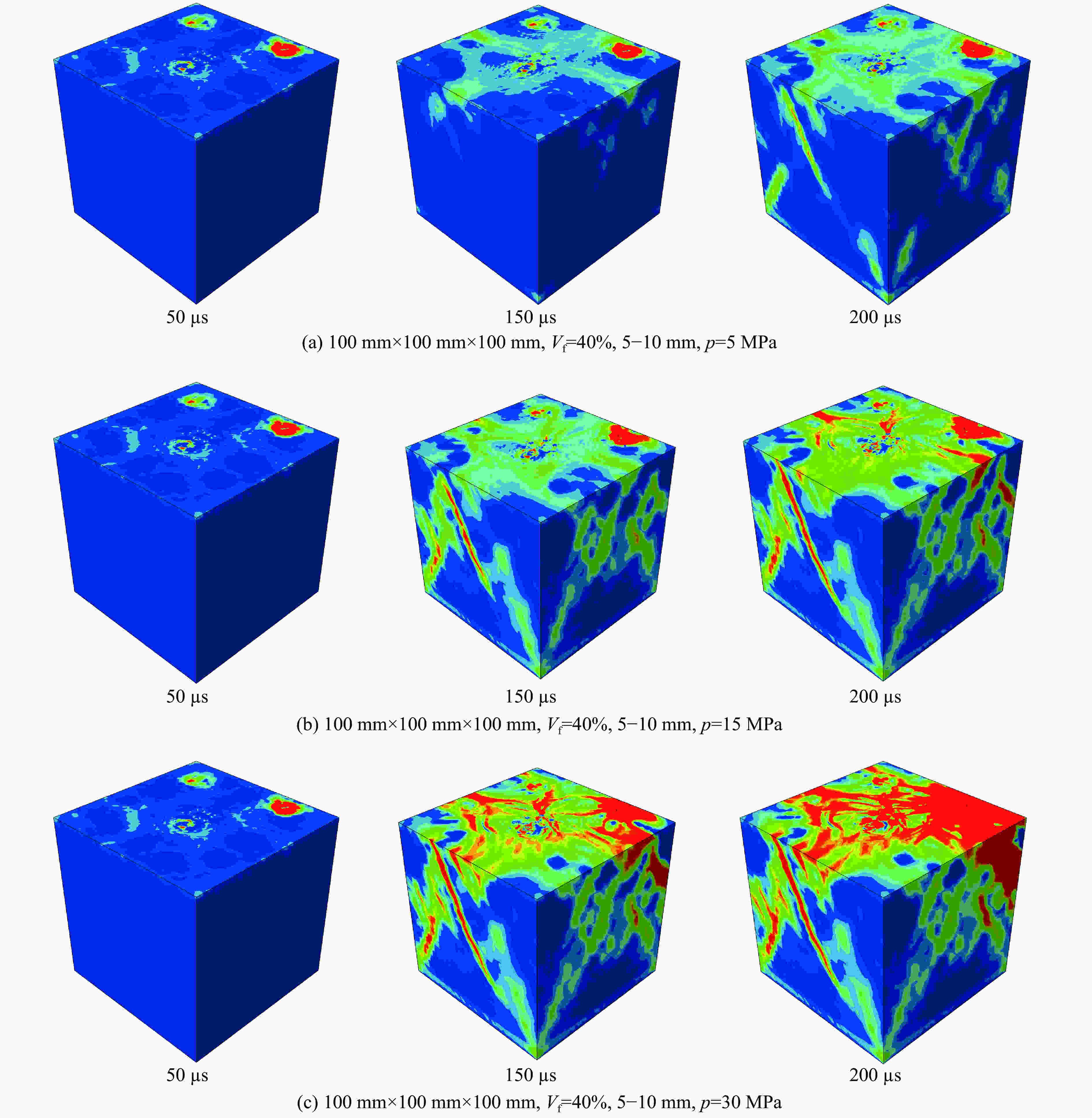
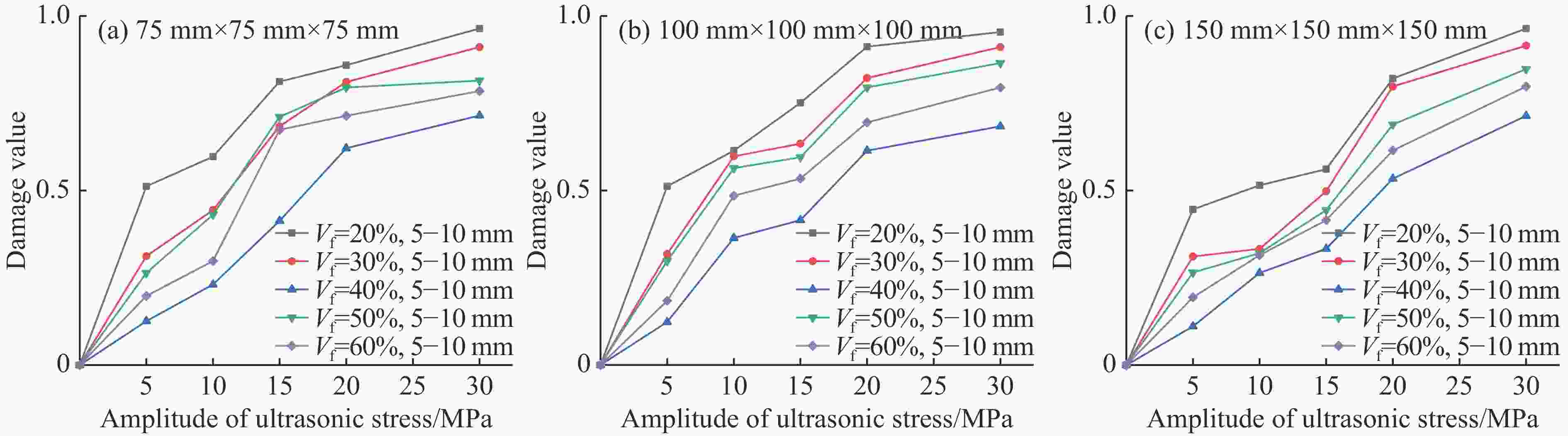
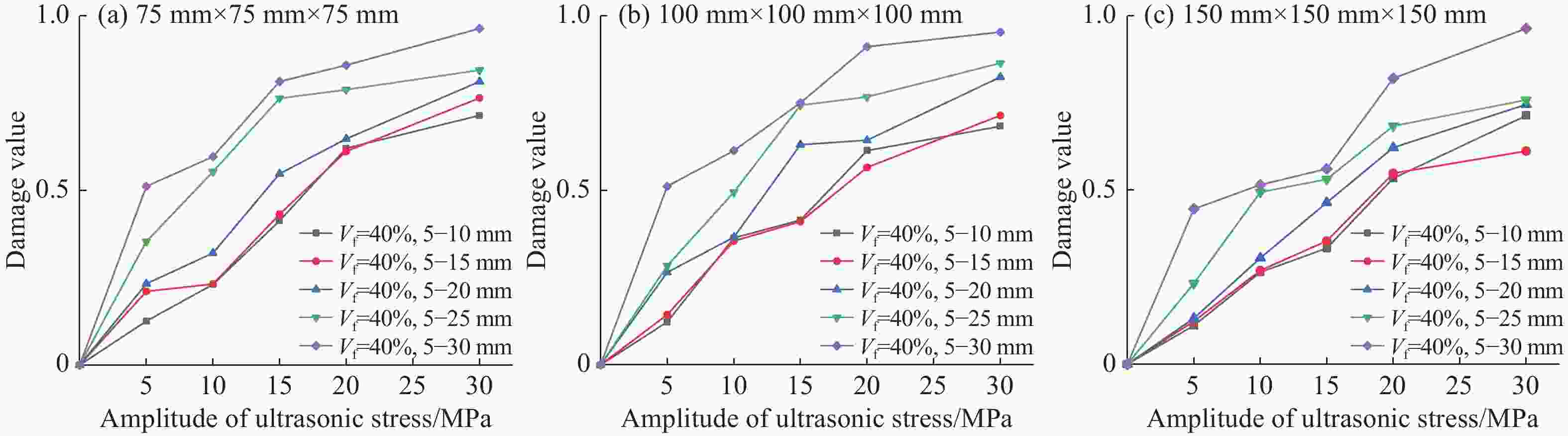
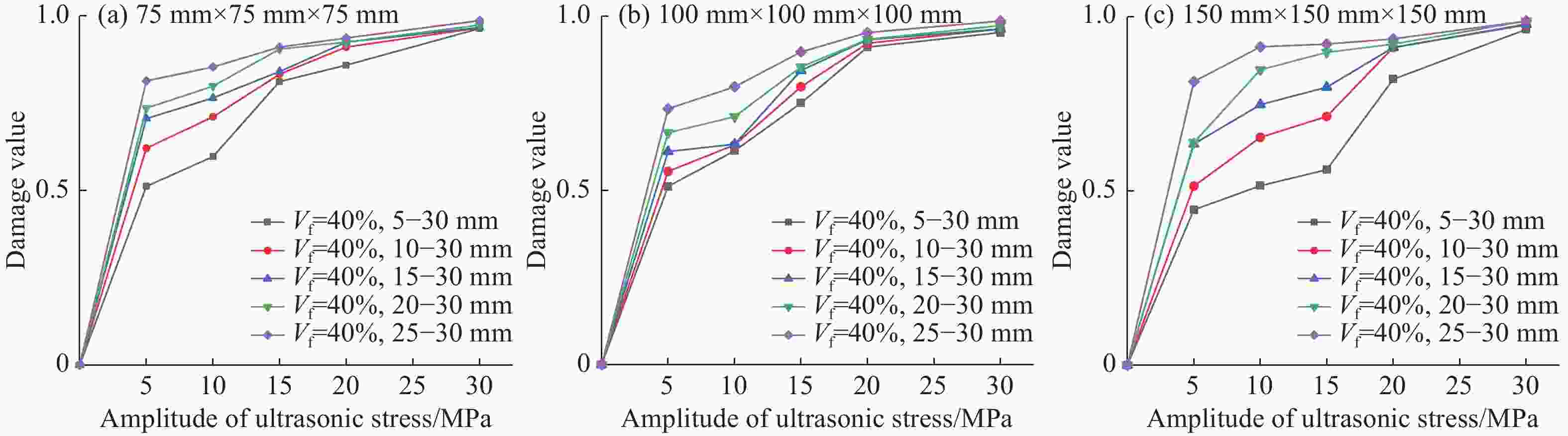
摘要: 混凝土是一种由粗骨料与水泥砂浆组成的非均质复合材料。本研究利用APDL语言程序编写三维水泥混凝土骨料随机投放程序并导入ABAQUS中,同时赋予各相材料塑性损伤本构关系来研究混凝土动态加载下的破坏规律,运用超声波在混凝土破碎中的作用机理对混凝土动态损伤破坏过程进行模拟研究。结果表明:随着超声动态载荷的增大,粗骨料体积分数为40%的混凝土始终能够承受最大应力载荷;随着超声应力波幅值增大,混凝土在动载荷下的损伤值逐渐增大,且粗骨料体积分数为40%时,其抗损伤能力最优;当粗骨料最大粒径逐渐增大,或者当粗骨料最小粒径增大,混凝土级配不合理导致性能不稳定,更易损伤破坏。Abstract: Concrete is a heterogeneous that is composed of coarse aggregate and cement mortar. The dynamic damage process of concrete was numerically simulated by the action mechanism of ultrasonic in concrete crushing in this paper. The random placement procedure of 3D concrete aggregate was prepared by APDL and introduced into ABAQUS, and the plastic damage constitutive relationship of each phase material was applied to study concrete damage law for dynamic loading. The numerical simulation results show that with the increase of ultrasonic dynamic load, the concrete with 40% coarse aggregate can always withstand the maximum stress load. As the amplitude of ultrasonic stress wave increases, the damage value of concrete under dynamic load increases gradually, and the damage resistance is optimal when the volume fraction is 40%. When the maximum particle size of the coarse aggregate gradually increases, or the minimum particle size of the coarse aggregate increases, the concrete grading is unreasonable, resulting in unstable performance and more vulnerable to damage.
-
Key words:
- concrete /
- ultrasonic /
- random aggregate model /
- plastic damage
-
表 1 模型参数
Table 1. Model parameters
Material E/GPa ν γ/(N·m–3) ψ/(°) ε Kc αf Aggregate 23 0.167 2.6 Mortar 10.66 0.2 2.1 35 0.1 0.667 1.16 -
[1] OLIVEIRA DIAS A R, AMANCIO F A, CARVALHO RAFAEL M F, et al. Study of propagation of ultrasonic pulses in concrete exposed at high temperatures [J]. Procedia Structural Integrity, 2018, 11(1): 84–90. [2] WITTMANN F H, ROELFSTRA P E, KAMP C L. Drying of concrete: an application of the 3L-approach [J]. Nuclear Engineering and Design, 1988, 105(2): 185–198. doi: 10.1016/0029-5493(88)90339-1 [3] BAZANT Z P, TABBARA M R, KAZEMI M T, et al. Random particle models for fracture of aggregate or fiber composites [J]. Journal of Engineering Mechanics, 1990, 116(8): 1686–1705. doi: 10.1061/(ASCE)0733-9399(1990)116:8(1686) [4] PEDERSEN R R, SIMONE A, SLUYS L J. Mesoscopic modeling and simulation of the dynamic tensile behaviour of concrete [J]. Cement Concrete Research, 2013, 50(1): 74–87. [5] PARK S W, XIA Q, ZHOU M. Dynamic behaviour of concrete at high strain rates and pressure: Ⅱ. numerical simulation [J]. International Journal of Impact Engineering, 2001, 25(9): 887–910. doi: 10.1016/S0734-743X(01)00021-5 [6] 李杰, 卢朝辉, 张其云. 混凝土随机损伤本构关系——单轴受压分析 [J]. 同济大学学报, 2003, 31(5): 505–509.LI J, LU Z H, ZHANG Q Y. Study on stochastic damage constitutive law for concrete material subjected to uniaxial compressive stress [J]. Journal of Tongji University, 2003, 31(5): 505–509. [7] 刘海峰, 韩莉. 二维骨料随机分布混凝土的动态力学性能数值模拟 [J]. 高压物理学报, 2016, 30(3): 191–199. doi: 10.11858/gywlxb.2016.03.003LIU H F, HAN L. Numerical simulation of dynamic mechanical behavior of concrete with two-dimensional random distribution of coarse aggregate [J]. Chinese Journal of High Pressure Physics, 2016, 30(3): 191–199. doi: 10.11858/gywlxb.2016.03.003 [8] 刘光廷, 王宗敏. 用随机骨料模型数值模拟混凝土材料的断裂 [J]. 清华大学学报(自然科学版), 1996, 36(1): 84–89. doi: 10.3321/j.issn:1000-0054.1996.01.007LIU G T, WANG Z M. Numerical simulation study of fracture of concrete materials using random aggregate model [J]. Journal of Tsinghua University (Science & Technology), 1996, 36(1): 84–89. doi: 10.3321/j.issn:1000-0054.1996.01.007 [9] 程书怀, 任志刚, 李培鹏, 等. 基于LS-DYNA的混凝土三维随机凹凸型骨料数值建模 [J]. 武汉理工大学学报, 2014, 36(12): 89–94, 121.CHENG S H, REN Z G, LI P P, et al. Numerical simulation of concrete aggregates with arbitrary shapes based on ANSYS/LS-DYNA [J]. Journal of Wuhan University of Technology, 2014, 36(12): 89–94, 121. [10] 李建波, 林皋, 陈建云. 随机凹凸型骨料在混凝土细观数值模型中配置算法研究 [J]. 大连理工大学学报, 2008, 48(6): 869–874. doi: 10.7511/dllgxb200806016LI J B, LIN G, CHEN J Y. Numerical generation and efficient distribution for random shape aggregates in mesoscopic concrete model [J]. Journal of Dalian University of Technology, 2008, 48(6): 869–874. doi: 10.7511/dllgxb200806016 [11] LIU H F, NING J G. Constitutive model for concrete subjected to impact loading [J]. Journal of Southeast University: English Edition, 2012, 28(1): 79–84. [12] 蒋橙炜, 陈启东, 顾泽堃. 超声破碎混凝土的力学模型与仿真分析 [J]. 机械制造与自动化, 2019, 48(2): 84–88.JIANG C W, CHEN Q D, GU Z K. Mechanical model and simulation analysis of ultrasonic crushed concrete [J]. Machine Building & Automation, 2019, 48(2): 84–88. [13] MATZENMILLER A, LUBLINER J, TAYLOR R L. A constitutive model for anisotropic damage in fiber-composites [J]. Mechanics of Materials, 1995, 20(2): 125–152. doi: 10.1016/0167-6636(94)00053-0 [14] 徐礼华, 李长宁, 李彪, 等. 循环受压状态下钢纤维混凝土一维弹塑性损伤本构模型研究 [J]. 土木工程学报, 2018, 51(11): 77–87.XU L H, LI C N, LI B, et al. Investigation on 1D elasto-plastic constitutive model of steel fiber reinforced concrete under uniaxial cyclic compression [J]. China Civil Engineering Journal, 2018, 51(11): 77–87. [15] 韩宇栋, 张君, 高原. 粗骨料体积含量对混凝土断裂参数的影响 [J]. 工程力学, 2013, 30(3): 191–197.HAN Y D, ZHANG J, GAO Y. Effect of coarse aggregate content on fracture parameters of concrete [J]. Engineering Mechanics, 2013, 30(3): 191–197. -






 下载:
下载: