Impact Initiation Characteristics of TATB Based Insensitive Explosives Mixed with HMX by Electromagnetic Velocity Gauges
-
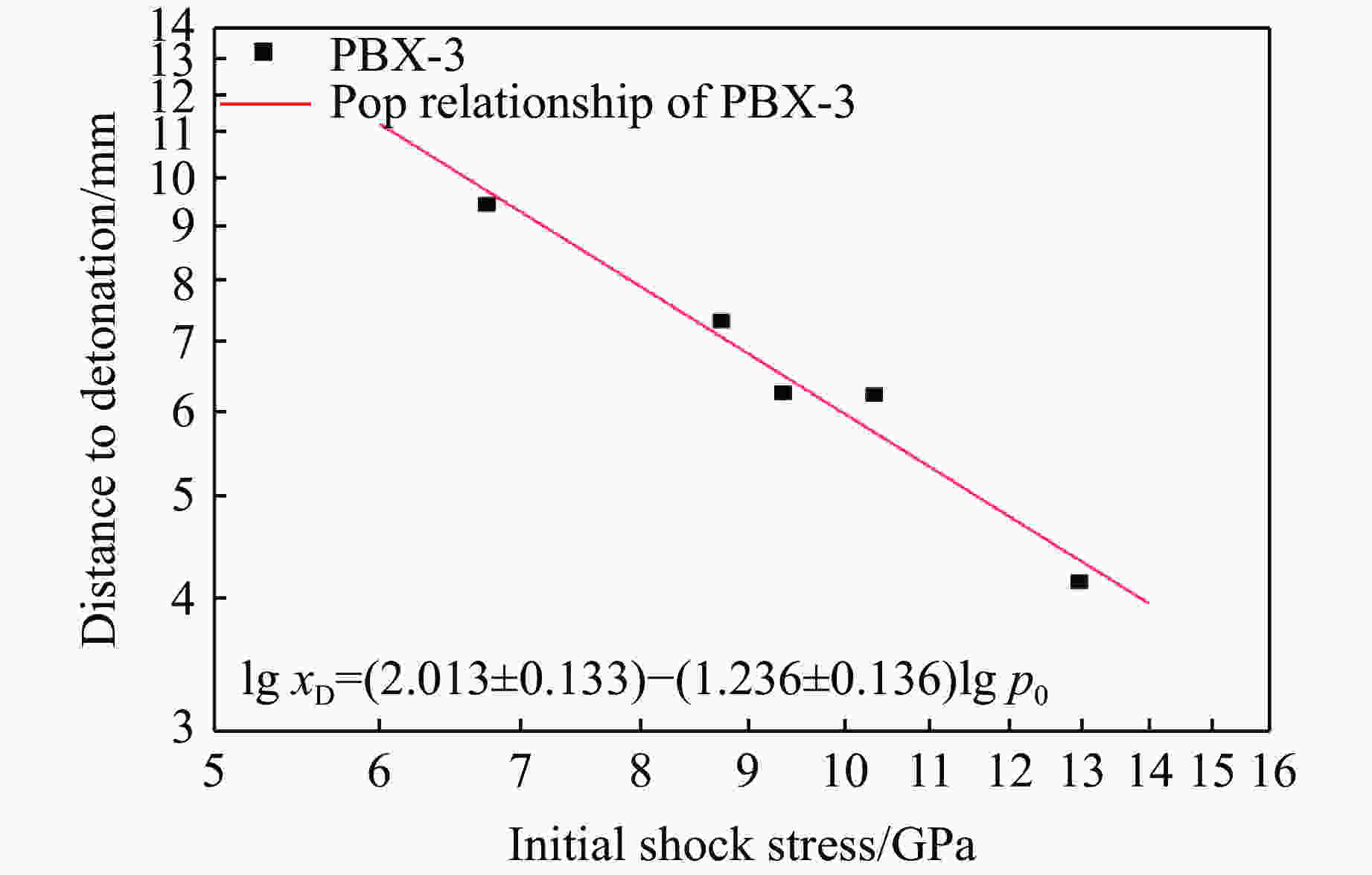
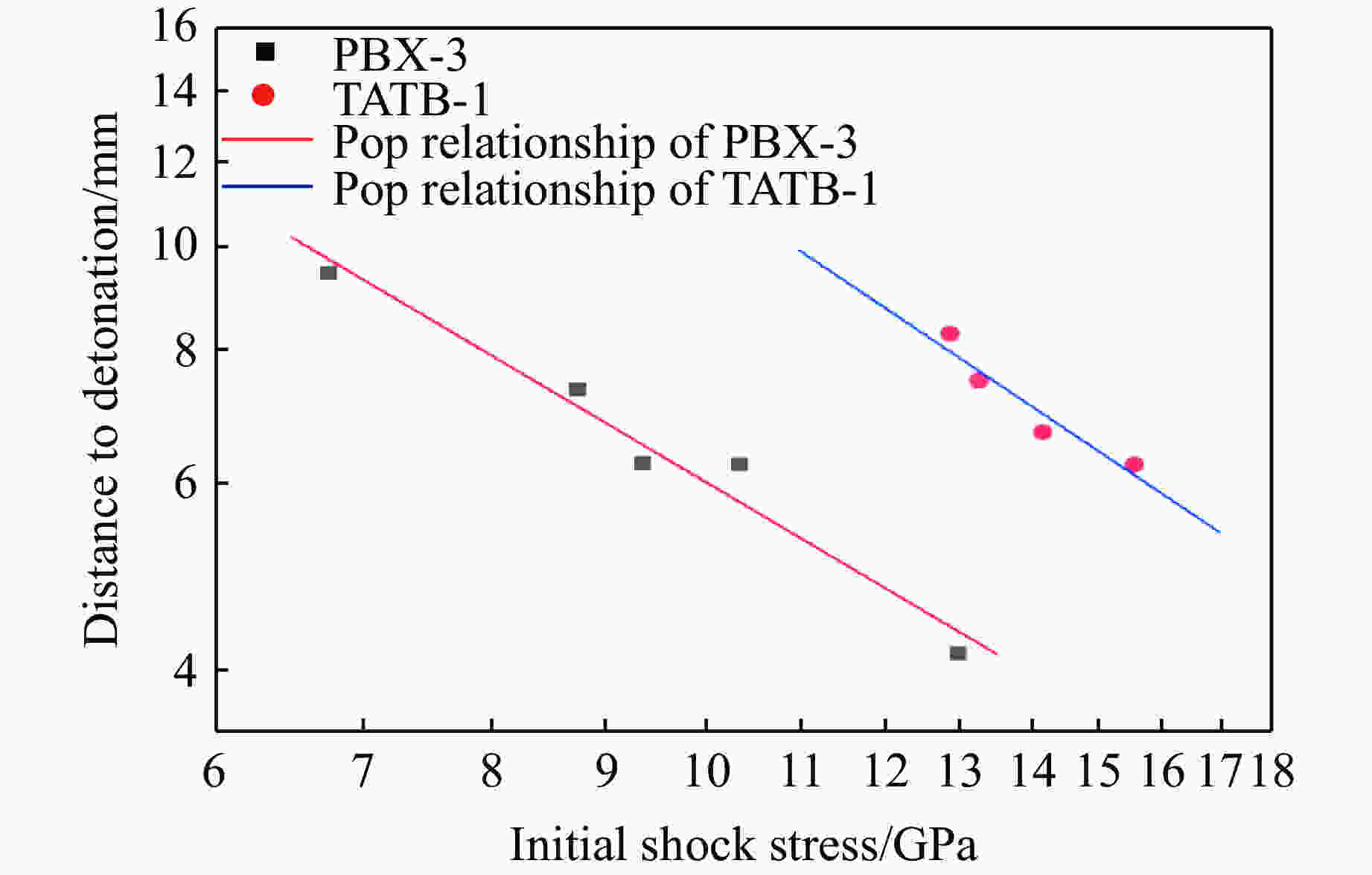
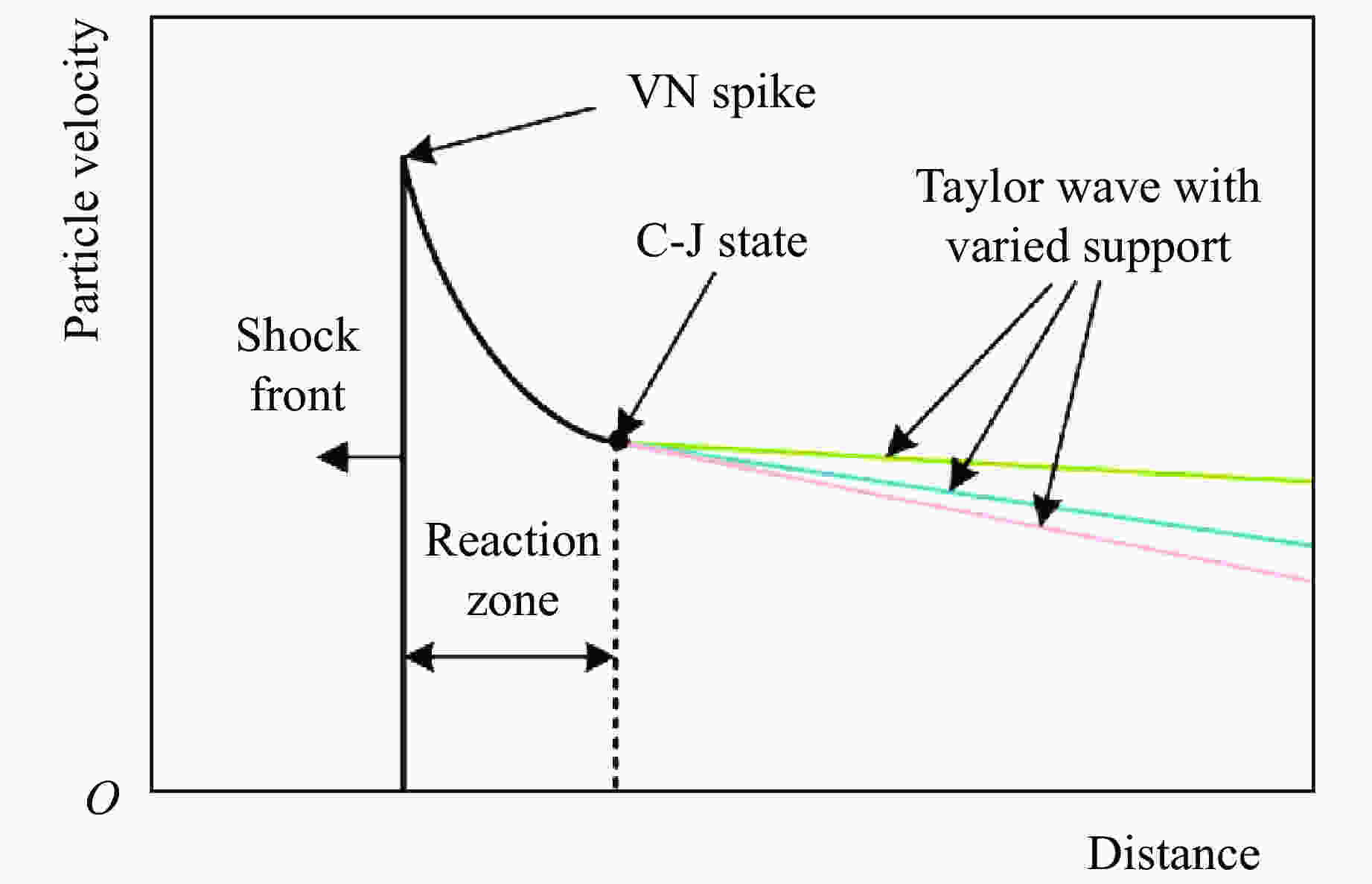
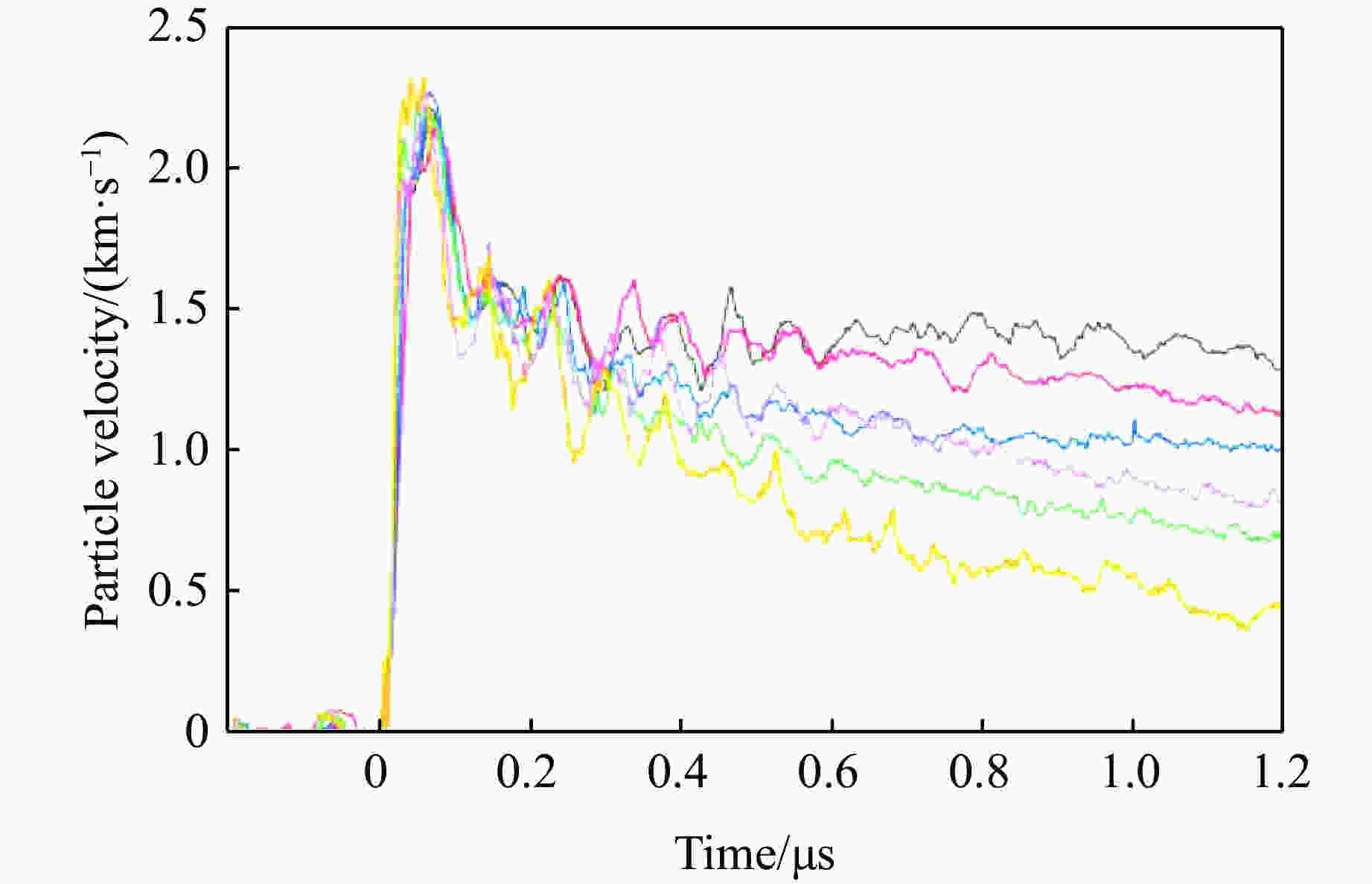
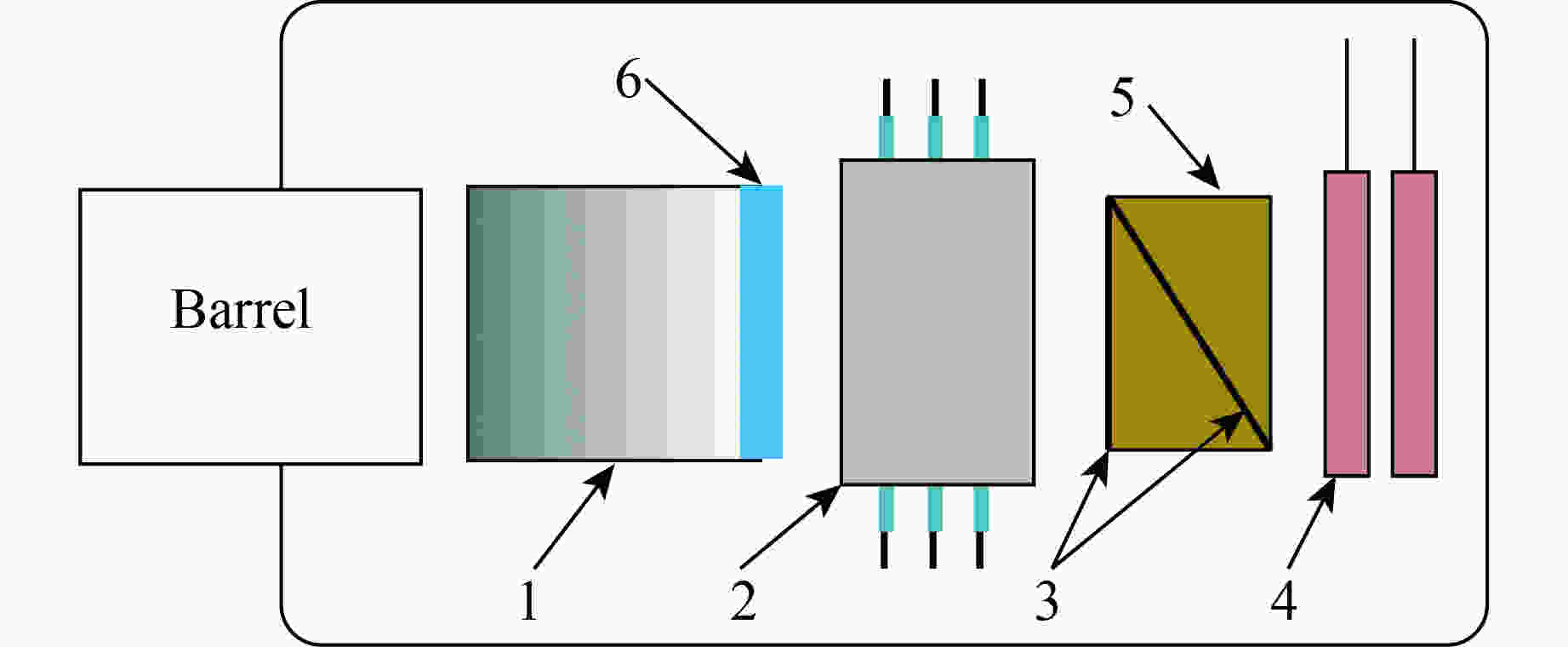
摘要: 为研究含有少量奥克托金(HMX)且以三氨基三硝基苯(TATB)为基的高能钝感炸药PBX-3的冲击起爆反应增长规律,采用火炮驱动蓝宝石飞片的方法和铝基组合式电磁粒子速度计技术进行了一维平面冲击实验。通过实验测量撞击表面及内部不同深度处的冲击波后粒子速度,得到PBX-3炸药的Hugoniot关系。根据冲击波示踪器所测数据绘制了炸药到爆轰的时间-距离(x-t)图,获得了反映炸药冲击起爆性能的Pop关系。将入射压力为12.964 GPa时达到爆轰的6条速度曲线修整成相同零点,通过读取6条曲线的分离点即反应区末端的C-J点,计算出化学反应区时间和宽度。
-
关键词:
- 奥克托金(HMX) /
- 组合式电磁粒子速度计 /
- Hugoniot关系 /
- Pop关系 /
- 化学反应区
Abstract: In order to study the growth law of the impact initiation reaction of high energy insensitive PBX-3explosive based on tri-amino-tri-nitro-benzene (TATB), containing a small amount of Oktokin (HMX), a one-dimensional plane impact test was carried out by the artillery-driven sapphire flyer method and the aluminum-based embedded multiple electromagnetic particle velocity gauge technique. The Hugoniot relationship of the unreacted PBX-3 explosive was obtained by measuring the velocity of the explosive on the surface and different depths inside. The x-t of the explosive to the detonation time versus distance was established by the data measured by the shock wave tracer, and the Pop-plot reflecting the explosive initiation performance of the explosive was obtained. Six speed-to-detonation speed curves with an incident pressure of 12.964 GPa were trimmed to the same zero point. The time and width of the chemical reaction zone were obtained by reading the separation point of the six curves (the C-J point at the end of the reaction zone). -
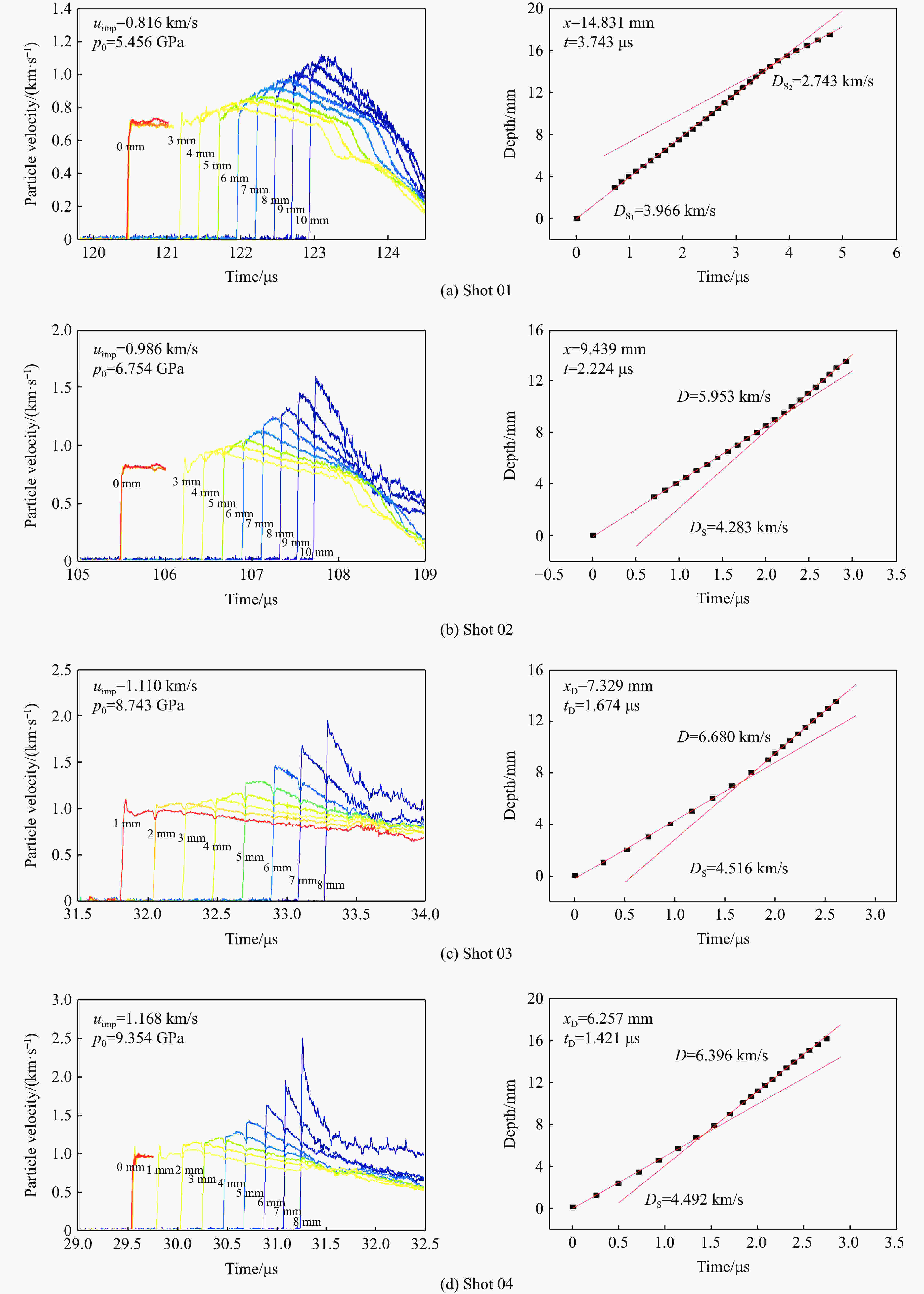
表 1 PBX-3炸药平面冲击实验参数
Table 1. Parameters of plane impact experiments on PBX-3 explosive
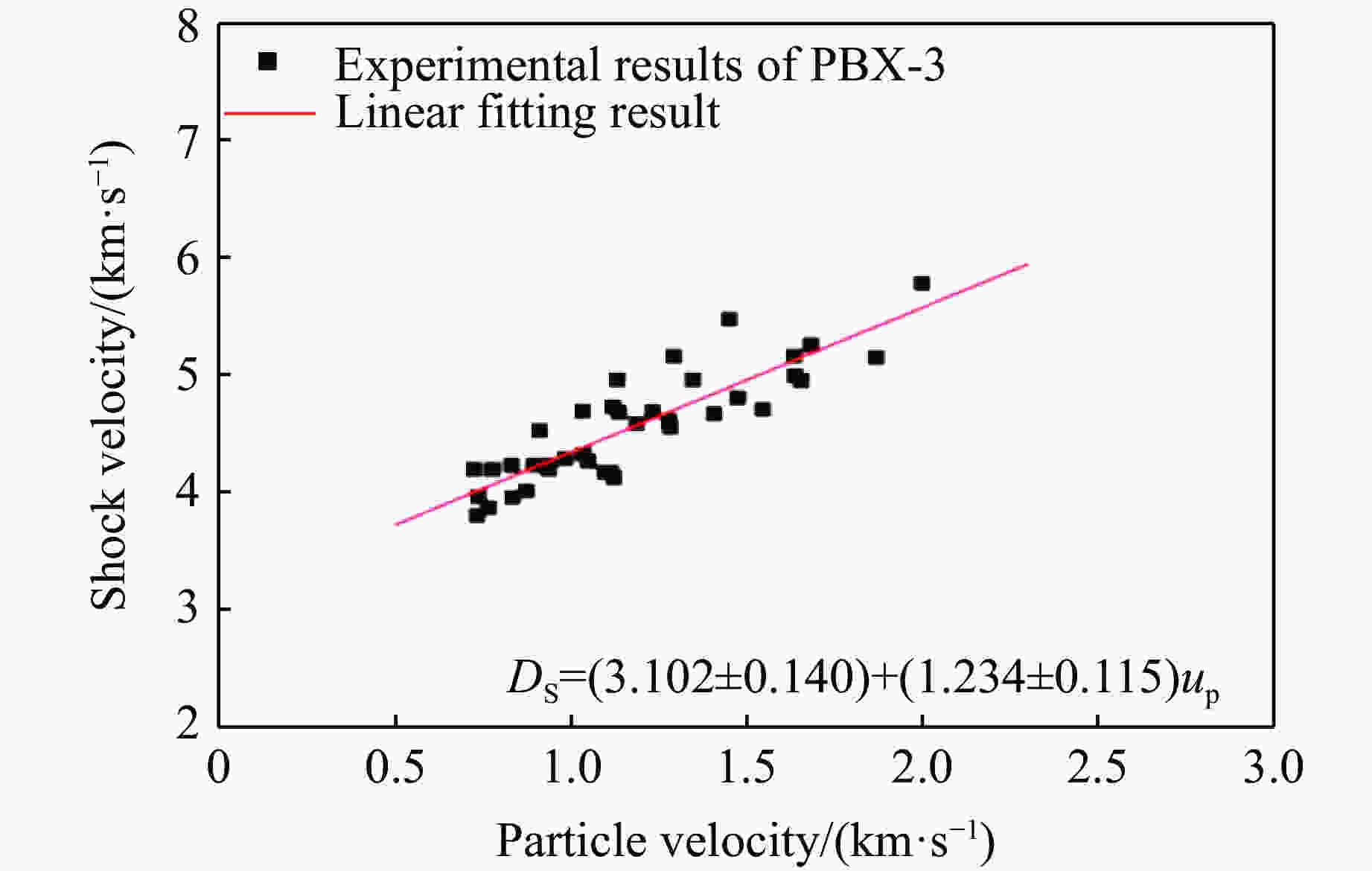
Shot No. m/g ρ0/(g·cm–3) DS/(km·s–1) up/(km·s–1) p0/GPa 01 500 1.900 3.966 0.724 5.456 02 600 1.900 4.283 0.830 6.754 03 700 1.900 4.516 1.019 8.743 04 800 1.900 4.492 1.096 9.354 05 900 1.900 4.808 1.132 10.341 06 1 100 1.900 5.281 1.292 12.964 表 2 PBX-3炸药的 DS
-up实验数据 Table 2. Experimental results of DS-up for PBX-3 explosive
Depth/mm Shot 01 Shot 02 Shot 03 up/(km·s–1) DS/(km·s–1) up/(km·s–1) DS/(km·s–1) up/(km·s–1) DS/(km·s–1) 0 0.724 4.189 0.830 4.224 1.019 3.489 1 1.104 3.489 2 1.049 4.259 3 0.776 4.189 0.894 4.224 1.033 4.686 4 0.737 3.956 0.911 4.521 1.118 4.726 5 0.732 3.796 0.938 4.229 1.282 4.546 6 0.766 3.864 1.034 4.318 1.474 4.799 7 0.833 3.950 1.187 4.579 1.682 5.252 8 0.873 4.007 1.279 4.604 1.957 5.165 9 0.937 4.190 1.450 5.470 10 0.983 4.280 1.598 4.960 Depth/mm Shot 04 Shot 05 Shot 06 up/(km·s–1) DS/(km·s–1) up/(km·s–1) DS /(km·s–1) up/(km·s–1) DS/(km·s–1) 0 1.096 4.164 1.131 4.955 1.292 5.152 1 1.113 4.164 2 1.122 4.119 3 1.137 4.680 1.347 4.955 1.634 5.152 4 1.232 4.682 1.545 4.699 1.998 5.774 5 1.407 4.664 1.654 4.947 2.230 6.187 6 1.637 4.990 1.867 5.144 2.066 7.353 7 1.962 5.213 2.104 5.656 2.282 7.082 8 2.510 5.868 2.137 7.083 2.120 7.043 9 2.308 6.746 10 2.318 6.699 2.283 7.374 表 3 PBX-3炸药Pop关系相关参数
Table 3. Related parameters of PBX-3 explosive’s Pop-plot
Shot No. ρ0/(g·cm–3) p0/GPa xD/mm tD/μs 01 1.900 5.456 02 1.900 6.754 9.439 2.224 03 1.900 8.743 7.329 1.674 04 1.900 9.354 6.257 1.421 05 1.900 10.341 6.234 1.292 06 1.900 12.964 4.143 0.785 表 4 PBX-3炸药化学反应区实验参数
Table 4. Parameters of chemical reaction zone of PBX-3 explosive
Depth/mm up/(km·s–1) t/μs x/mm Depth/mm up/(km·s–1) t/μs x/mm 5 1.539 0.226 1.429 8 1.425 0.226 1.454 6 1.540 0.226 1.428 9 1.370 0.226 1.467 7 1.436 0.226 1.452 10 1.386 0.226 1.463 -
[1] 张琪敏, 张旭, 赵康, 等. TATB基钝感炸药JB-9014的冲击起爆反应增长规律 [J]. 爆炸与冲击, 2019, 39(4): 041405.ZHANG Q M, ZHANG X, ZHAO K, et al. Law of reaction growth of shock initiation on the TATB based insensitive explosive JB-9014 [J]. Explosion and Shock Waves, 2019, 39(4): 041405. [2] HILL L G, GUSTAVSEN R L, ALCON R R, et al. Shock initiation of new and aged PBX 9501 measured with embedded electromagnetic particle velocity gauges: LA-13634-MS [R]. New Mexico, US: Los Alamos National Laboratory, 1999. [3] ZHANG X, WANG Y F, HUANG W B, et al. Reaction buildup of PBX explosives JOB-9003 under different initiation pressures [J]. Journal of Energetic Materials, 2017, 35(2): 197–212. doi: 10.1080/07370652.2016.1250841 [4] GUSTAVSEN R L, GEHR R J, BUCHOLTZ S M, et al. Shock initiation of the tri-amino-tri-nitro-benzene explosive PBX9502 cooled to -55 ℃ [J]. Journal of Applied Physics, 2012, 112(7): 074909. doi: 10.1063/1.4757599 [5] 张涛, 赵继波, 伍星, 等. 未反应JBO-9021炸药冲击雨贡纽曲线的研究 [J]. 高压物理学报, 2016, 30(6): 457–462. doi: 10.11858/gywlxb.2016.06.004ZHANG T, ZHAO J B, WU X, et al. Hugoniot curve of unreacted JBO-9021 explosive [J]. Chinese Journal of High Pressure Physics, 2016, 30(6): 457–462. doi: 10.11858/gywlxb.2016.06.004 [6] GUSTAVSEN R L, SHEFFIELD S A, ALCON R R. Measurements of shock initiation in the tri-amino-tri-nitro-benzene based explosive PBX 9502: wave forms from embedded gauges and comparison of four different material lots [J]. Journal of Applied Physics, 2006, 99(11): 114907. doi: 10.1063/1.2195191 [7] 张涛, 谷岩, 赵继波, 等. JBO-9021炸药的化学反应区宽度 [J]. 爆炸与冲击, 2017, 37(3): 415–421. doi: 10.11883/1001-1455(2017)03-0415-07ZHANG T, GU Y, ZHAO J B, et al. Chemical reaction zone length of JBO-9021 [J]. Explosion and Shock Waves, 2017, 37(3): 415–421. doi: 10.11883/1001-1455(2017)03-0415-07 [8] SHEFFIELD S A, BLOOMQUIST D D, TARVER C M. Subnanosecond measurements of detonation fronts in solid high explosives [J]. The Journal of Chemical Physics, 1984, 80(8): 3831–3844. doi: 10.1063/1.447164 [9] 裴红波, 黄文斌, 覃锦程, 等. 基于多普勒测速技术的JB-9014炸药反应区结构研究 [J]. 爆炸与冲击, 2018, 38(3): 485–490.PEI H B, HUANG W B, QIN J C, et al. Reaction zone structure of JB-9014 explosive measured by PDV [J]. Explosion and Shock Waves, 2018, 38(3): 485–490. [10] 赵同虎, 张新彦, 李斌, 等. 用光电法研究钝感炸药JB-9014反应区结构 [J]. 高压物理学报, 2002, 16(2): 111–119. doi: 10.3969/j.issn.1000-5773.2002.02.005ZHAO T H, ZHANG X Y, LI B, et al. Detonation reaction zones tructure of JB-9014 [J]. Chinese Journal of High Pressure Physics, 2002, 16(2): 111–119. doi: 10.3969/j.issn.1000-5773.2002.02.005 [11] LOBOIKO B G, LUBYATINSKY S N. Reaction zones of detonating solid explosives [J]. Combustion, Explosion, and Shock Waves, 2000, 36(6): 716–733. doi: 10.1023/A:1002898505288 -






 下载:
下载: