Raman Scattering Investigations of Adamantane under High Pressure
-
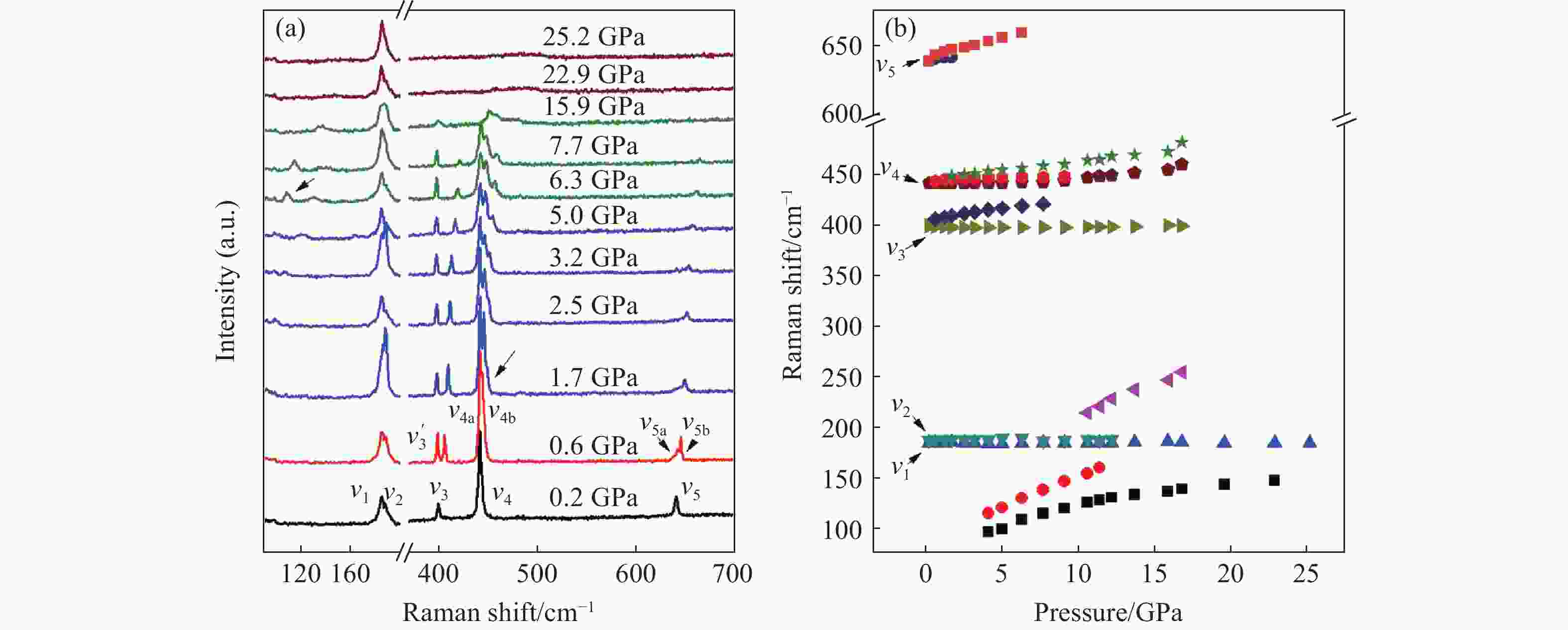
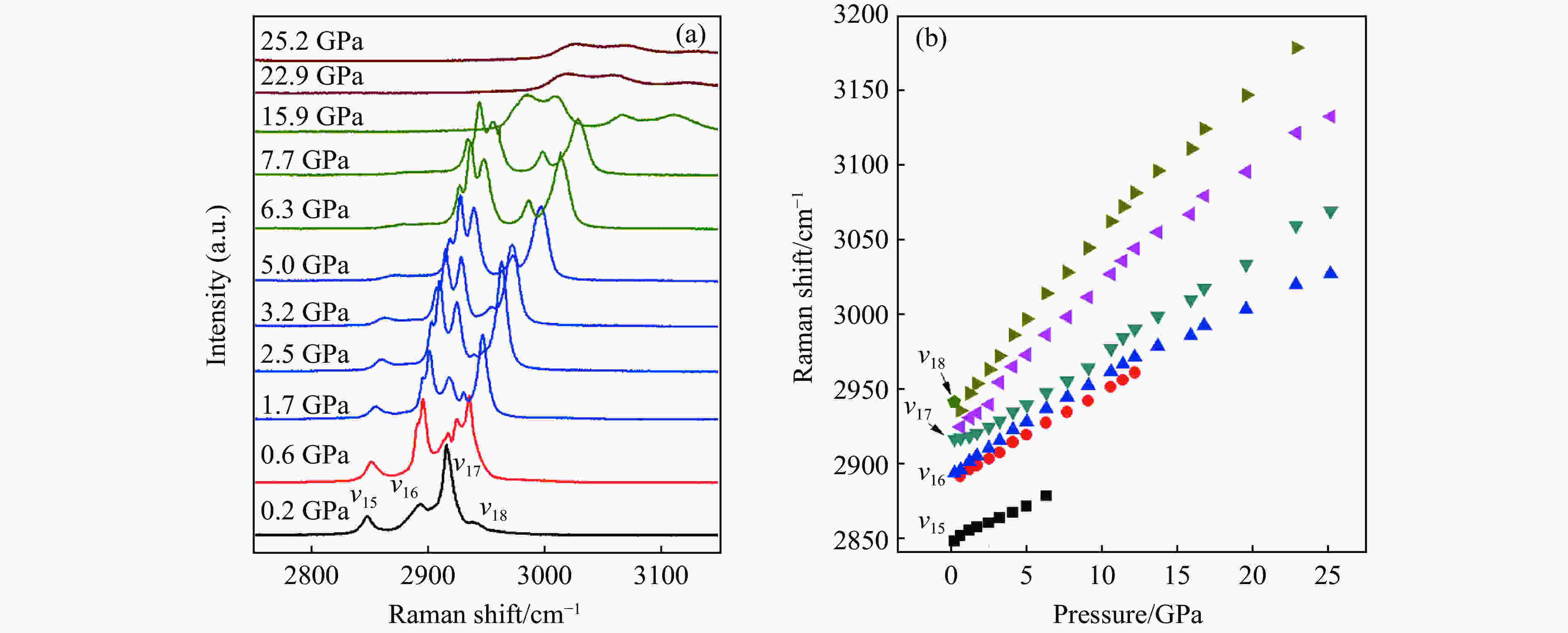
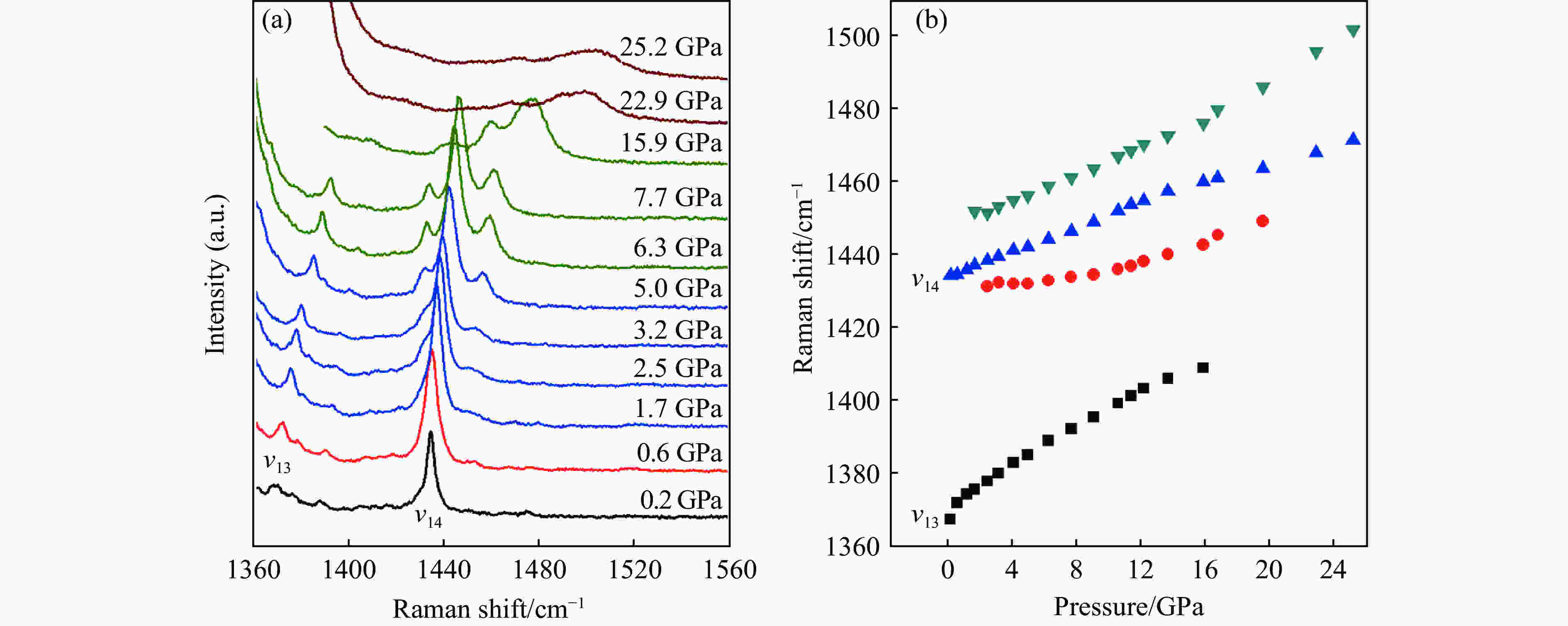
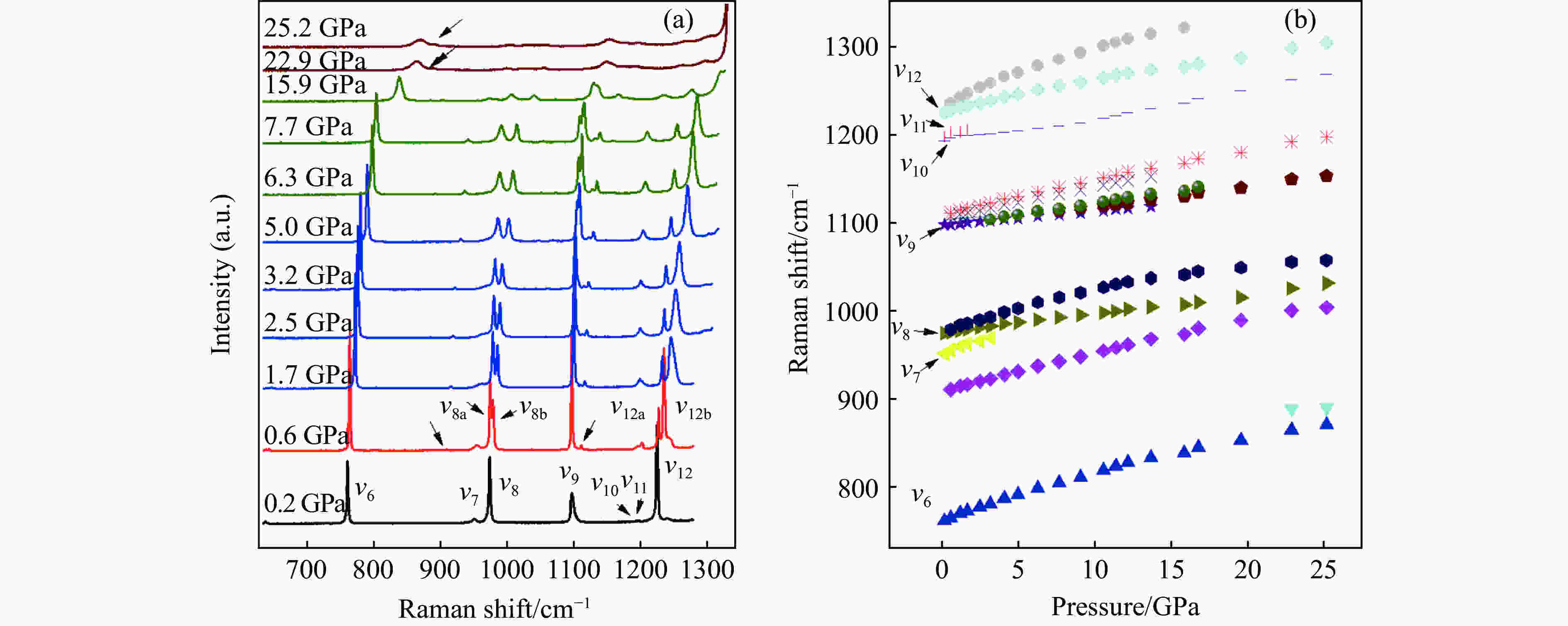
摘要: 对金刚烷(C10H16)进行了常温原位高压拉曼光谱研究,最高压力为25 GPa。通过分析高压拉曼光谱,结合拉曼频移随压力的变化情况,得出在实验压力范围内C10H16发生了多次相变。0.6 GPa时,C10H16由常温常压下的无序相(
$\alpha$ 相)转变为有序相($\beta $ 相);继续加压至1.7 GPa时,第2次结构相变开始,直至3.2 GPa,第2次相变完全结束;第3次相变开始于6.3 GPa,结束于7.7 GPa;22.9 GPa时发生了第4次结构相变。另外,首次在拉曼光谱上探测到第3次相变过程中晶格振动峰的变化,说明第3次相变并非前人报道的等结构相变。Abstract: Results of Raman scattering measurements under pressure up to 25 GPa on adamantane (C10H16) carried out at room temperature are reported. The analysis of Raman data indicated four phase transitions. The ambient pressure disordered Fm3m structure ($\alpha$ -C10H16) transformed to a high pressure ordered phase at 0.6 GPa. Continue to pressurize to 1.7 GPa, the second structure phase transition began, and completely accomplished until 3.2 GPa. The third transition began at 6.3 GPa, ended at 7.7 GPa. C10H16 transformed to a new phase at 22.9 GPa. Because of the new lattice peak occurred during the third transition, it was defined to a first-order transition.-
Key words:
- adamantane /
- high pressure /
- Raman scattering /
- phase transition
-
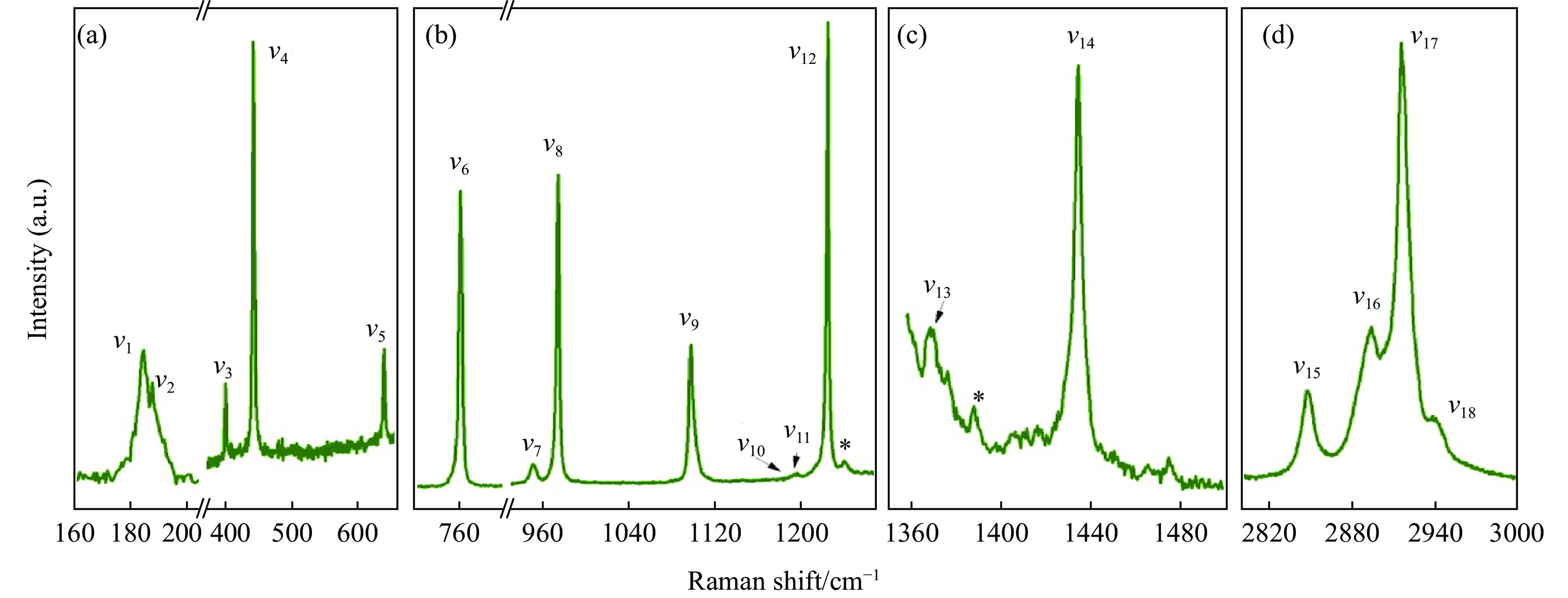
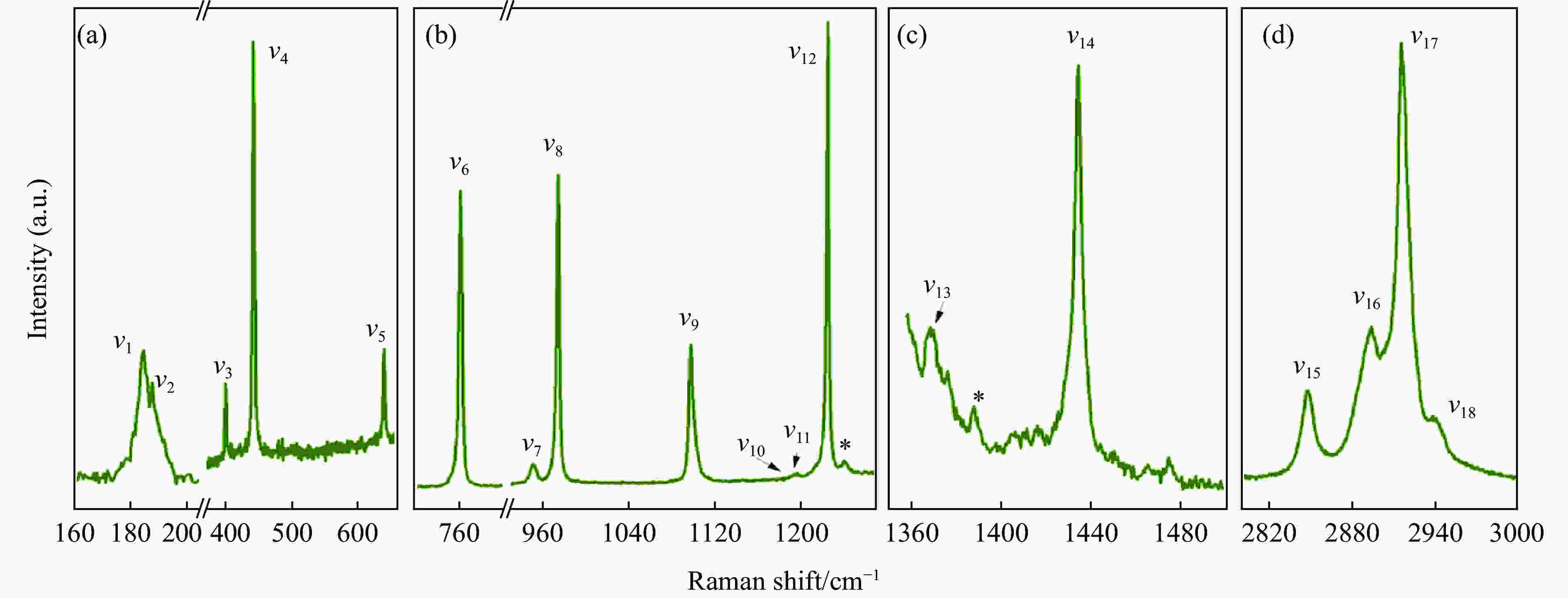
表 1 常温常压下金刚烷拉曼振动峰的指认以及与文献的对比
Table 1. Assignments and vibrational frequencies (cm–1) of observed Raman modes of C10H16 at ambient condition
Frequency/cm–1 Mode This work Ref.[20] Ref.[17] Ref.[16] Assignment 2941 2944 2943 2940 $\nu _{18}$ C–H stretching mode 2916 2917 2913 2915 $\nu _{17}$ C–H stretching mode 2893 2895 2983 2894 $\nu _{16}$ C–H stretching mode 2847 2845 2847 $\nu _{15}$ C–H stretching mode 1474 1450 1434 1437 1440 1435 $\nu _{14}$ CH2 scissor mode 1367 1371 $\nu _{13}$ CH bending mode 1315 1225 1223 1225 1221 $\nu _{12}$ CH bending mode 1197 $\nu _{11}$ 1193 $\nu _{10}$ 1097 1102 1097 $\nu _{9}$ C–H rock mode 974 972 976 971 $\nu _{8}$ C–C stretching mode 950 951 $\nu _{7}$ C–C stretching mode 761 760 759 759 $\nu _{6}$ C–C stretching mode 640 $\nu _{5}$ Lattice mode 441 443 440 442 $\nu _{4}$ C–C–C deformation mode 399 $\nu _{3}$ Lattice mode 187 $\nu _{2}$ Lattice mode 184 $\nu _{1}$ Lattice mode -
[1] DUCLOS S J, BRISTER K, HADDON R C, et al. Effects of pressure and stress on C60 fullerite to 20 GPa [J]. Nature, 1991, 351(6325): 380–382. doi: 10.1038/351380a0 [2] VAUGHAN G B M, HEIEY P A, LUZZI D E, et al. Orientational disorder in solvent-free solid C70 [J]. Science, 1991, 254(5036): 1350–1353. doi: 10.1126/science.254.5036.1350 [3] KITAIGORODSKI A I. Organic chemical crystallography [M]. New York: Consultants Bureau Enterprises, 1961: 113. [4] AMOUREUX J P, BEE M, DAMIEN J C. Structure of adamantane, C10H16, in the disordered phase [J]. Acta Crystallographica Section B: Structural Crystallography and Crystal Chemistry, 1980, 36(11): 2633–2636. doi: 10.1107/S0567740880009570 [5] AMOUREUX J P, BEE M. A cubic harmonic analysis of the plastic crystal structures of adamantane, C10H16, and adamantanone, C10H14O, at room temperature [J]. Acta Crystallographica Section B: Structural Crystallography and Crystal Chemistry, 1980, 36(11): 2636–2642. doi: 10.1107/S0567740880009582 [6] NORDMAN C E, SCHMITKONS D L. Phase transition and crystal structures of adamantane [J]. Acta Crystallographica, 1965, 18(4): 764–767. doi: 10.1107/S0365110X65001755 [7] MUJICA A, RUBIO A, MUNOZ A, et al. High-pressure phases of group-IV, III-V, and II-VI compounds [J]. Reviews of Modern Physics, 2003, 75(3): 863. doi: 10.1103/RevModPhys.75.863 [8] HEMLEY R J, ASHCROFT N W. The revealing role of pressure in the condensed matter sciences [J]. Physics Today, 1998, 51(8): 26–32. doi: 10.1063/1.882374 [9] JAYARAMAN A. Ultrahigh pressures [J]. Review of Scientific Instruments, 1986, 57(6): 1013–1031. doi: 10.1063/1.1138654 [10] PARISE J B. High pressure studies [J]. Reviews in Mineralogy and Geochemistry, 2006, 63(1): 205–231. doi: 10.2138/rmg.2006.63.9 [11] STÖFFLER D. Minerals in the deep Earth: a message from the asteroid belt [J]. Science, 1997, 278(5343): 1576–1577. doi: 10.1126/science.278.5343.1576 [12] WILLIAMS Q, HEMLEY R J. Hydrogen in the deep Earth [J]. Annual Review of Earth and Planetary Sciences, 2001, 29(1): 365–418. doi: 10.1146/annurev.earth.29.1.365 [13] ITO T. Pressure-induced phase transition in adamantane [J]. Acta Crystallographica Section B: Structural Crystallography and Crystal Chemistry, 1973, 29(2): 364–365. doi: 10.1107/S0567740873002517 [14] MURUGAN N A, RAO R S, YASHONATH S, et al. High-pressure study of adamantane: variable shape simulations up to 26 GPa [J]. The Journal of Physical Chemistry B, 2005, 109(36): 17296–17303. doi: 10.1021/jp053542h [15] MURUGAN N A, YASHONATH S. Pressure-induced ordering in adamantane: a Monte Carlo simulation study [J]. The Journal of Physical Chemistry B, 2005, 109(5): 2014–2020. doi: 10.1021/jp047178i [16] BURNS G, DACOL F H, WELBER B. Lattice vibrational study of the phase transition in the plastic crystal adamantane (C10H16) [J]. Solid State Communications, 1979, 32(2): 151–155. doi: 10.1016/0038-1098(79)91077-9 [17] RAO R, SAKUNTALA T, DEB S K, et al. High pressure Raman scattering studies on adamantane [J]. The Journal of Chemical Physics, 2000, 112(15): 6739–6744. doi: 10.1063/1.481227 [18] VIJAYAKUMAR V, GARG A B, GODWAL B K, et al. High-pressure phase transitions in adamantane [J]. Chemical Physics Letters, 2000, 330(3/4): 275–280. [19] BISTRIČIĆ L, BARANOVIĆ G, ILIJIĆ S. Raman study of structural relaxation and boson peak in amorphous films of adamantane [J]. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 2005, 61(7): 1537–1546. doi: 10.1016/j.saa.2004.11.015 [20] 刘卅, 郭建维. 金刚烷的结构、溶解性及热力学性质 [J]. 含能材料, 2006, 14(6): 485–490. doi: 10.3969/j.issn.1006-9941.2006.06.019LIU S, GUO J W. Structure analysis, solubility and thermodynamics properties of adamantine [J]. Chinese Journal of Energetic Materials, 2006, 14(6): 485–490. doi: 10.3969/j.issn.1006-9941.2006.06.019 [21] AOKI K, BAER B J, CYNN H C, et al. Raman study of molecular rearrangement in HCN under pressure [M]//PUCCI R, PICCITTO G. Molecular Systems under High Pressure. North-Holland: Elsevier Science, 1991: 283. -









 下载:
下载: