Theoretical Simulation and Physical Properties of MgN8 Crystal Structure under High Pressure
-
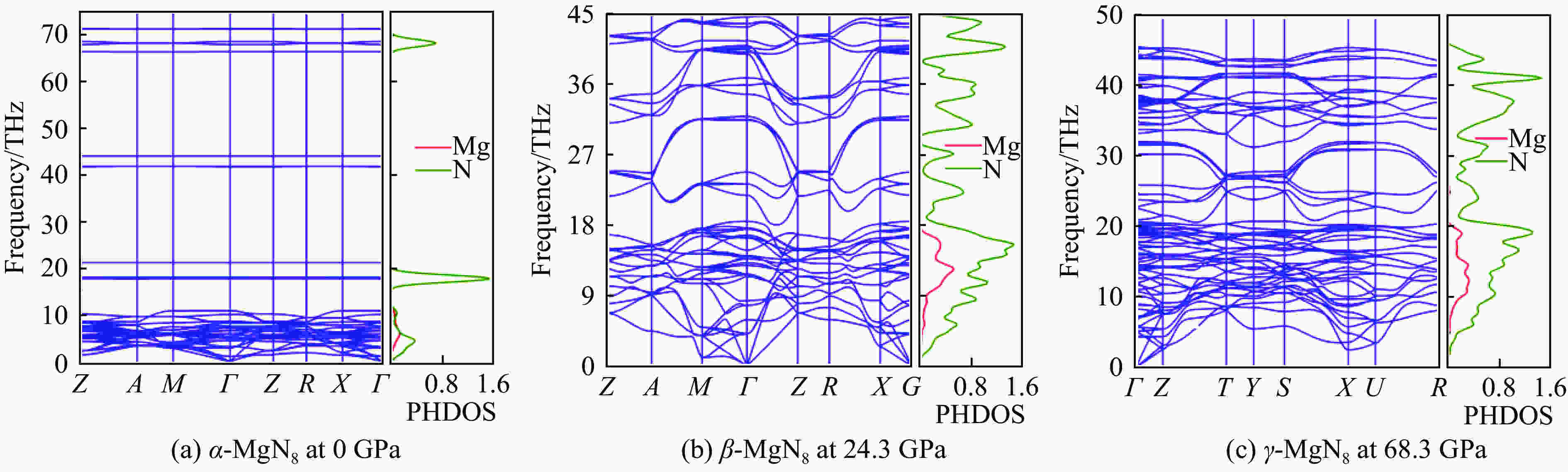
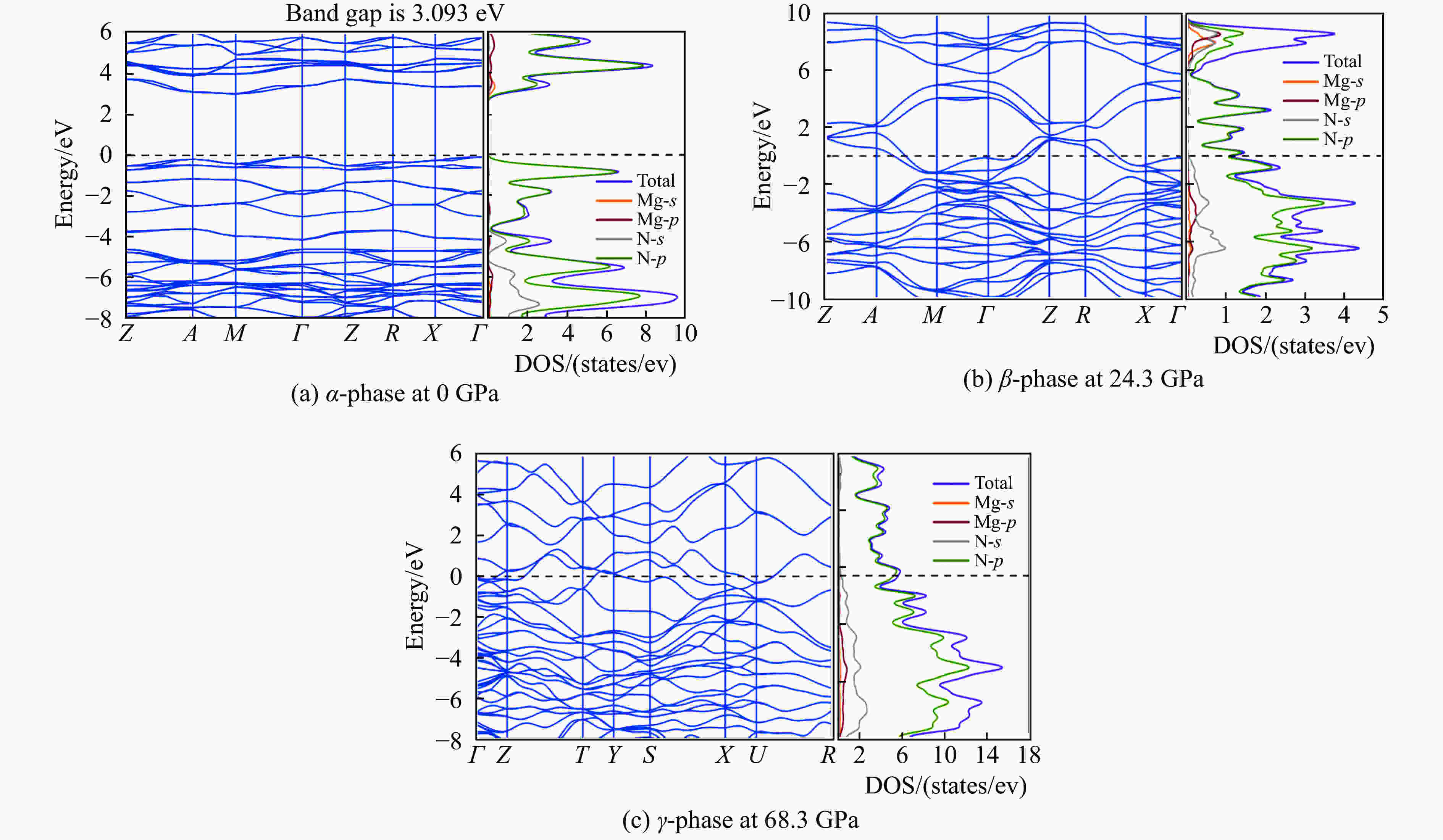
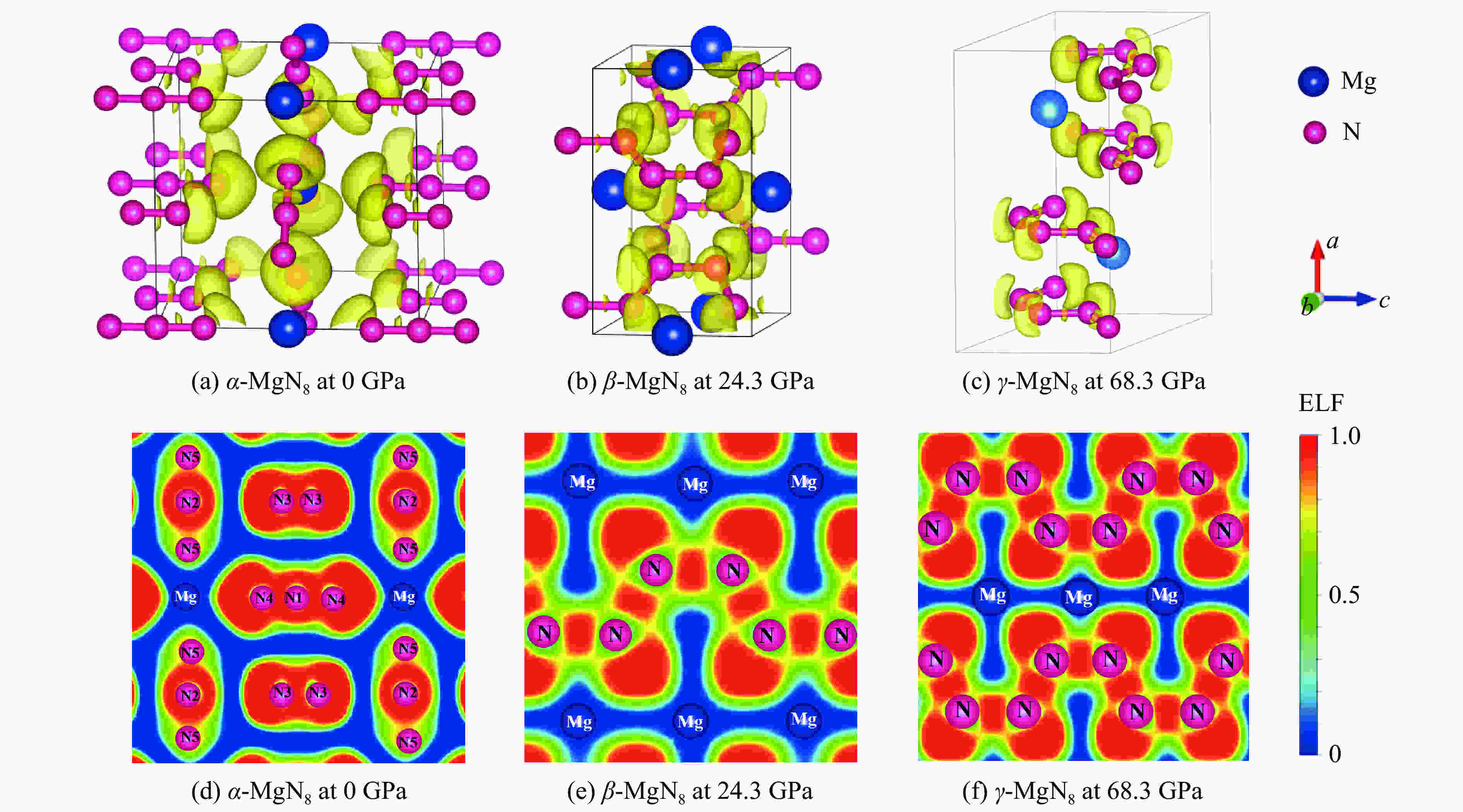
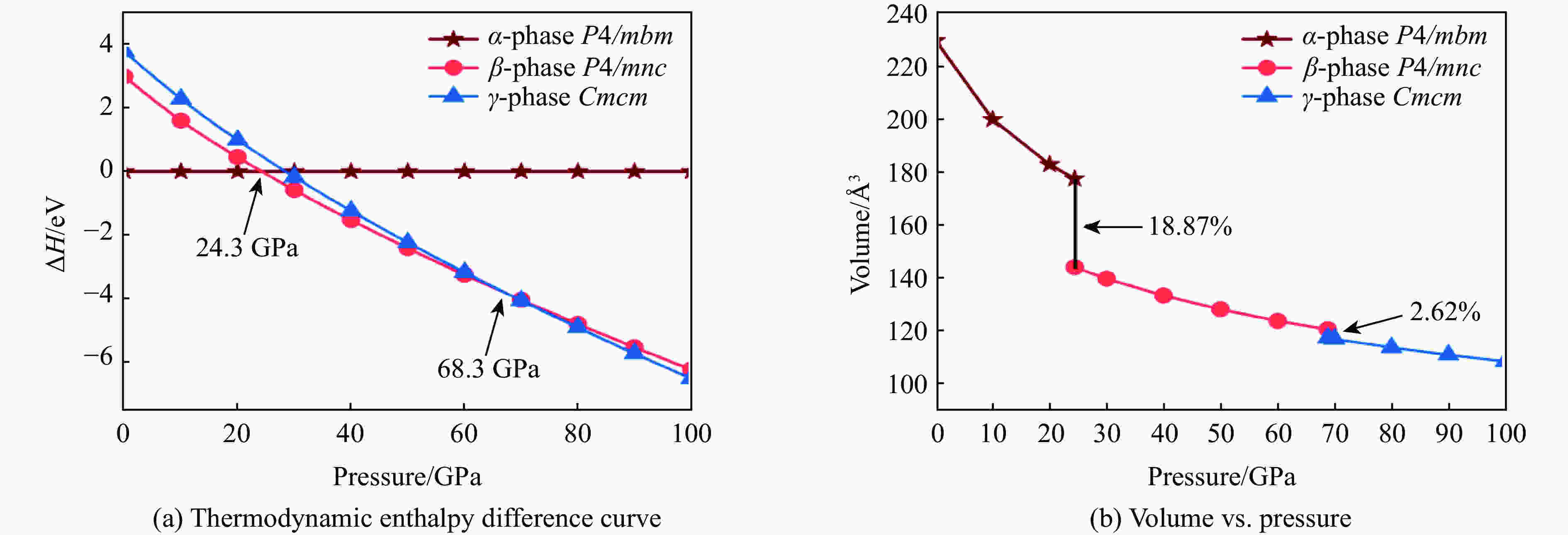
摘要: 基于密度泛函理论第一性原理的方法,使用CALYPSO结构搜索技术结合VASP软件,在0~100 GPa压强范围内对MgN8的晶体结构进行预测,并对预测的结构进行系统研究。结果表明:在常压下,空间群为P4/mbm的α-MgN8晶体结构的焓值最低;当压强达到24.3 GPa和68.3 GPa时发生相变,分别相变成空间群为P4/mnc的β-MgN8相和空间群为Cmcm的γ-MgN8相,两次相变均为对应体积坍塌的一级相变。电子性质计算结果表明,α-MgN8相的导带与价带之间具有3.09 eV的带隙,表明该结构具有非金属性;β相和γ相具有明显的金属特征。Bader电荷转移计算表明,随着压力的增加,Mg原子向N原子转移的电荷逐渐增多。Abstract: Based on the first principle of density functional theory, the crystal structure of MgN8 was predicted in the pressure range of 0–100 GPa by using CALYPSO structure search technique and VASP software. After systematically studying the predicted structure, it was found that the enthalpy of α-MgN8 crystal with space group P4/mbm was the lowest at ambient pressure. The phase was changed to β-MgN8 phase of P4/mnc and γ-MgN8 phase of Cmcm when the pressure reached 24.3 GPa and 68.3 GPa, respectively. And both of the phase transitions were the first order phase transition of corresponding volume collapse. The calculated results of electronic properties suggested that the existence of a band gap of 3.09 eV between the conduction band and valence band of α-MgN8 phase revealed the non-gold properties of the structure, whereas the obvious metal characteristics appeared in the β-MgN8 phase and γ-MgN8 phase. Bader charge transfer calculation showed that the charge which transferred from Mg atom to N atom, increased gradually with the increase of pressure.
-
Key words:
- high pressure /
- first-principles /
- crystal structure prediction /
- MgN8 /
- charge transfer /
- phase transition
-
表 1 α-MgN8、β-MgN8和γ-MgN8相的平衡态晶格常数
Table 1. Lattice parameters of α-MgN8, β-MgN8 and γ-MgN8 in the equilibrium state
Phase Pressure/GPa a/Å b/Å c/Å α/(°) β/(°) γ/(°) α-MgN8 (P4/mbm) 0 5.913 5.913 6.572 90.0 90.0 90.0 β-MgN8 (P4/mnc) 24.3 6.219 6.219 3.724 90.0 90.0 90.0 γ-MgN8 (Cmcm) 68.3 4.167 4.167 8.680 90.0 90.0 51.1 表 2 α-MgN8、β-MgN8和γ-MgN8相的平衡态晶格常数和原子位置
Table 2. Lattice parameters and atomic coordinate of α-MgN8, β-MgN8 and γ-MgN8 in the equilibrium state
Phase Pressure/GPa Atoms Wyckoff position x y z α-MgN8 (P4/mbm) 0 Mg 2b 0.000 0.000 0.500 N1 2a 0.000 0.000 0.000 N2 2c 0.000 0.500 0.500 N3 4e 0.000 0.000 0.821 N4 4f 0.000 0.500 0.915 N5 4h 0.859 0.359 0.500 β-MgN8 (P4/mnc) 24.3 Mg 2a 0.000 0.000 1.000 N 16i 0.416 0.219 0.823 γ-MgN8 (Cmcm) 68.3 Mg 8g 0.624 –0.376 1.250 N1 16h 0.226 –0.135 0.617 N2 16h 1.115 0.471 1.386 表 3 α-MgN8、β-MgN8、γ-MgN8相电荷转移
Table 3. Calculated Bader charges of α-MgN8, β-MgN8 and γ-MgN8
Phase Pressure/GPa Atoms Number Charge value/e Charge transfer/e α-MgN8 (P4/mbm) 0 Mg 1 6.26 1.74 N1 1 4.84 0.16 N2 1 4.86 0.13 N3 2 5.04 –0.04 N4 2 5.46 –0.46 N5 2 5.52 –0.52 β-MgN8 (P4/mnc) 24.3 Mg 1 6.06 1.94 N 8 5.24 –0.24 γ-MgN8 (Cmcm) 68.3 Mg 1 5.80 2.20 N1 4 5.28 –0.28 N2 4 5.27 –0.27 -
[1] GROCHALA W, HOFFMANN R, FENG J, et al. The chemical imagination at work in very tight places [J]. Angewandte Chemie International Edition, 2007, 46(20): 3620–3642. doi: 10.1002/anie.200602485 [2] HEMLEY R J. Effects of high pressure on molecules [J]. Annual Review of Physical Chemistry, 2000, 51(1): 763–800. doi: 10.1146/annurev.physchem.51.1.763 [3] SCHETTINO V, BINI R. Molecules under extreme conditions: chemical reactions at high pressure [J]. Physical Chemistry Chemical Physics, 2003, 5(10): 1951–1965. doi: 10.1039/b301381b [4] 李鑫, 马雪姣, 高文泉, 等. 高压下Ir2P晶体结构预测与物理性质 [J]. 高压物理学报, 2019, 33(1): 011103. doi: 10.11858/gywlxb.20180645LI X, MA X J, GAO W Q, et al. Evolution of crystal structures and electronic properties for Ir2P under high pressure [J]. Chinese Journal of High Pressure Physics, 2019, 33(1): 011103. doi: 10.11858/gywlxb.20180645 [5] MA X J, LI X, ZHOU D, et al. Phase diagram and bonding states of Ir-P binary compounds at high pressures [J]. Journal of Alloys and Compounds, 2019, 791: 1257–1262. doi: 10.1016/j.jallcom.2019.03.051 [6] BRULS R J, HINTZEN H T, METSELAAR R. Preparation and characterisation of MgSiN2 powders [J]. Journal of Materials Science, 1999, 34(18): 4519–4531. doi: 10.1023/A:1004645407523 [7] PARKIN I P, NARTOWSKI A M. Solid state metathesis routes to Group IIIa nitrides: comparison of Li3N, NaN3, Ca3N2 and Mg3N2 as nitriding agents [J]. Polyhedron, 1998, 17(16): 2617–2622. doi: 10.1016/S0277-5387(97)00454-3 [8] KOBASHI M, OKAYAMA N, CHOH T. Synthesis of AlN/Al alloy composites by in situ reaction between Mg3N2 and aluminum [J]. Materials Transactions, JIM, 1997, 38(3): 260–265. doi: 10.2320/matertrans1989.38.260 [9] EREMETS M I, GAVRILIUK A G, TROJAN I A, et al. Single-bonded cubic form of nitrogen [J]. Nature Materials, 2004, 3(8): 558–563. doi: 10.1038/nmat1146 [10] LORENZ H, KÜHNE U, HOHLFELD C, et al. Influence of MgO on the growth of cubic boron nitride using the catalyst Mg3N2 [J]. Journal of Materials Science Letters, 1988, 7(1): 23–24. doi: 10.1007/BF01729904 [11] PAPACONSTANTOPOULOS D A, PICKETT W E, KLEIN B M, et al. Electronic properties of transition-metal nitrides: the group-V and group-VI nitrides VN, NbN, TaN, CrN, MoN, and WN [J]. Physical Review B, 1985, 31(2): 752–761. doi: 10.1103/PhysRevB.31.752 [12] MENG Y, MAO H K, ENG P J, et al. The formation of sp3 bonding in compressed BN [J]. Nature Materials, 2004, 3(2): 111–114. doi: 10.1038/nmat1060 [13] RAZA Z, PICKARD C J, PINILLA C, et al. High energy density mixed polymeric phase from carbon monoxide and nitrogen [J]. Physical Review Letters, 2013, 111(23): 235501. doi: 10.1103/PhysRevLett.111.235501 [14] KNITTLE E, WENTZCOVITCH R M, JEANLOZ R, et al. Experimental and theoretical equation of state of cubic boron nitride [J]. Nature, 1989, 337(6205): 349–352. doi: 10.1038/337349a0 [15] XIA Y, LI Q, MA Y M. Novel superhard polymorphs of Be3N2 predicted by first-principles [J]. Computational Materials Science, 2010, 49(1): S76–S79. doi: 10.1016/j.commatsci.2010.01.045 [16] ZHU S S, PENG F, LIU H Y, et al. Stable calcium nitrides at ambient and high pressures [J]. Inorganic Chemistry, 2016, 55(15): 7550–7555. doi: 10.1021/acs.inorgchem.6b00948 [17] JI D P, CHONG X Y, FENG J. Electronic, mechanical and hydrogen storage properties of novel Mg3N2 [J]. Journal of Alloys and Compounds, 2019, 800: 8–15. doi: 10.1016/j.jallcom.2019.06.021 [18] WANG Y C, LV J, ZHU L, et al. Crystal structure prediction via particle-swarm optimization [J]. Physical Review B, 2010, 82(9): 094116. doi: 10.1103/PhysRevB.82.094116 [19] MONKHORST H J, PACK J D. Special points for Brillouin-zone integrations [J]. Physical Review B, 1976, 13(12): 5188. doi: 10.1103/PhysRevB.13.5188 [20] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Physical Review Letters, 1996, 77(18): 3865–3868. doi: 10.1103/PhysRevLett.77.3865 [21] BORN M, HUANG K. Dynamical theory of crystal lattices [J]. American Journal of Physics, 1954, 39(2): 113–127. [22] BECKE A D, EDGECOMBE K E. A simple measure of electron localization in atomic and molecular systems [J]. The Journal of Chemical Physics, 1990, 92(9): 5397–5403. doi: 10.1063/1.458517 [23] BADER R F W. Atoms in molecules [J]. Accounts of Chemical Research, 1985, 18(1): 9–15. doi: 10.1021/ar00109a003 [24] OGANOV A R, CHEN J H, GATTI C, et al. Ionic high-pressure form of elemental boron [J]. Nature, 2009, 457(7231): 863–867. doi: 10.1038/nature07736 -






 下载:
下载: