-
石榴子石是一族岛状结构硅酸盐矿物的总称，是上地幔和地幔转换带最重要的组成矿物之一[1-2]。石榴子石的化学组成较为复杂，不同元素构成不同组合，其化学通式为X3Y2(SiO4)3，其中：当Y位置为铝时，称为铝系列榴石，主要有3种，即铁铝榴石（Fe3Al2(SiO4)3，Almandine，以下简称Al）、镁铝榴石（Mg3Al2(SiO4)3，Pyrope，以下简称Py）和锰铝榴石（Mn3Al2(SiO4)3，Spessartine，以下简称Sp）；当X位置为钙时，称为钙系列榴石，主要有3种，即钙铁榴石（Ca3Fe2(SiO4)3，Andradite，以下简称An）、钙铝榴石（Ca3Al2(SiO4)3，Grossular，以下简称Gr）和钙铬榴石（Ca3Cr2(SiO4)3，Uvarovite，以下简称Uv）。根据Pyrolite和Piclogite模型，上地幔中石榴石的含量为15%～30%，过渡带可以达到40%～80%[3-4]；而在洋中脊玄武岩（MORB）中，石榴石的含量可达25%～90%[5]。因此研究高温高压下石榴石的物性演化特征对了解地幔物质组成、结构及动力学过程有重要意义，一直是人们关注的重点。Wang和Ji[6]研究了在0～3 GPa下6种石榴子石（铁铝榴石、钙铁榴石、钙铝榴石、镁铝榴石、钙铬榴石、Py25Al56Sp19）的密度、弹性模量和地震波速，发现钙系列和铝系列榴石的晶胞密度与体弹模量的比值不同，铝系列榴石的泊松比与密度为负相关，而钙系列榴石则相反，两个系列榴石的体弹模量一阶导数差别不大。Conrad等[7]发现0～10 GPa压力下3种天然石榴子石（镁铝榴石、钙铝榴石、钙铁榴石）的弹性常数和地震波速随着压力的增加而线性增加。Babuška等[8]利用矩形平行六面体共振法（RPR）确定常温常压下5种天然石榴子石（铁铝榴石、镁铝榴石、锰铝榴石、钙铝榴石、钙铁榴石）的密度、弹性模量和波速，发现铁铝榴石和镁铝榴石不满足摩尔体积定律（即晶体的体弹模量与摩尔体积的乘积为定值[9-10]），而钙铝榴石和钙铁榴石在使用摩尔体积定律时也有一定偏差。Hazen[11]通过对6 GPa下镁铝榴石和钙铝榴石在压缩过程中键长和键角变化的统计研究，得出具有较低电荷阳离子的较大多面体比具有较高电荷阳离子的较小多面体更易压缩，且扭曲的多面体在高压下变得更加规则。Leger等[12]利用X射线衍射技术研究0～25 GPa下合成镁铝榴石、锰铝榴石、钙铬榴石的状态方程发现，各向异性应力分量对石榴石的体积测定有很大影响。Zhang等[13]测量了0～15 GPa压力下5种合成石榴子石（镁铝榴石、铁铝榴石、锰铝榴石、钙铝榴石、钙铁榴石）的晶体结构变化特征，发现高压下镁十二面体存在异常压缩行为，且石榴石不遵循摩尔体积定律。
研究发现，镁铝-铁铝榴石二端元固溶体系列的体弹模量（K）随着铁铝榴石含量的增加而减小[14-16]。Fan等[17]发现锰铝-铁铝榴石固溶体系列的体弹模量随着铁铝榴石含量的增加而增加。声速测量表明，少量铁（质量分数小于5%）掺入镁铁榴石中并不显著影响其弹性模量和声速梯度[18]。对于钙铝-钙铁榴石固溶体，其体弹模量随着钙铝榴石组分的增加而增加[19-20]，而镁铝-钙铝榴石二元固溶体系列的体弹模量并未随着镁铝榴石或钙铝榴石组分呈规律性变化[21]。显然，不同石榴子石弹性模量随组分的变化规律还需进一步研究确定，然而目前关于两个系列不同石榴子石之间差别的系统研究仍较少[6, 8, 13, 19-20]。
随着计算机技术的发展，基于密度泛函理论的计算已成功地应用于矿物性质的模拟研究中，取得了丰硕的成果，且计算结果的精度不断提高[22-30]。本工作拟采用第一性原理研究高压下铝系列榴石（镁铝榴石、铁铝榴石、锰铝榴石）和钙系列榴石（钙铬榴石、钙铝榴石、钙铁榴石）6种常见石榴子石的晶胞参数、弹性模量、地震波速等性质，系统地比较不同系列石榴子石的物性差异，为了解高压下石榴子石物性演化及其在地球深部赋存特征提供数据支持。
-
利用平面波赝势法结合广义梯度近似（GGA）的密度泛函理论（DFT），采用CA-PZ参数描述交换关联势[23, 31]，价电子与核的相互作用由超软赝势描述，Kohn-Sham轨道用平面波展开，平面波的截止能量为500 eV，倒空间k点积分在2×2×2的Monhhorst-Pack网格上进行。在平面波赝势框架中，晶体晶胞上的应力张量可以借助应力定理直接计算[32-33]。在给定的压力下，通过最小化原子上的Hellmann-Feynman力和单位晶胞上的应力分量，同时优化晶体常数和晶体内部坐标的压力[32, 34]。石榴子石属于立方晶系（Ia3d），单位晶胞内含有160个原子，其中孤立的[SiO4]四面体在晶体内部呈岛状分布，形成结构骨架，以三价阳离子为中心的[YO6]（Y一般为Al3+、Fe3+、Cr3+等）八面体连接 [SiO4]四面体，[SiO4]四面体与[YO6]八面体间形成[XO8]（X一般为Ca2+、Mg2+、Fe2+、Mn2+等）十二面体空隙，二价阳离子占据其中。
-
立方晶系石榴子石单位晶胞内含有160个原子，对其物性模拟所需的计算量十分巨大，为此计算了0～16 GPa压力下铝系列榴石和钙系列榴石中6种常见石榴子石的晶胞参数、弹性模量和地震波速。为了测试本研究所用计算方法的可靠性，将模拟得到的结果与前人结果进行了比较（见表1和表2），结果显示模拟计算所得6种石榴子石的晶胞边长、密度、弹性模量和地震波速等参数都与前人差别不大。整体来看，晶胞边长比平均值整体偏高，而弹性模量整体较平均值小，原因是计算时使用的GGA近似低估了原子间的内聚力。计算结果与实验值之间的一致性证明了本研究方案的有效性。
Garnet Lattice parameter/Å Density/（g·cm–3） Method Bulk modulus/GPa Shear modulus/GPa Pyrope 11.559 Exp.[35] 199.0 11.466 3.582 Exp.[7] 172.7 92.0 Exp.[36] 173.6 94.9 3.610 Exp.[6] 170.1 90.2 11.447 3.569 Exp.[37] 167.0 11.472 Exp.[38] 173.7 11.486 3.587 Average 176.0 92.4 11.581 3.448 This study 154.5 83.1 Almandine 11.532 4.312 Exp.[14] 168.0 4.289 Exp.[6] 175.1 92.1 11.519 Exp.[13] 185.0 11.507 3.916 Exp.[8] 173.7 95.4 11.535 3.930 Exp.[8] 174.9 95.5 11.523 4.110 Average 175.3 94.3 11.591 4.250 This study 166.6 79.4 Uvarovite 11.99 3.850 Exp.[39] 162.0 92.0 3.841 Exp.[6] 164.8 89.9 11.990 3.846 Average 163.4 91.0 12.070 3.780 This study 139.1 79.8 Spessartine 11.617 4.195 Exp.[40] 178.8 96.3 11.611 4.172 Exp.[8] 176.4 96.5 11.608 4.185 Exp.[8] 171.8 93.3 11.612 4.184 Average 175.7 95.4 11.744 4.060 This study 165.6 89.8 Grossular 11.849 3.600 Exp.[7] 166.8 108.9 11.848 3.602 Exp.[40] 168.4 109.0 11.870 3.659 Exp.[8] 161.2 102.6 11.910 3.667 Exp.[8] 162.4 102.9 11.869 3.632 Average 164.7 105.9 11.991 3.471 This study 143.4 87.4 Andradite 12.048 3.840 Exp.[7] 159.4 90.0 12.054 3.836 Exp.[39] 157.0 90.0 12.009 3.775 Exp.[8] 147.3 92.7 3.938 Exp.[6] 162.5 86.0 12.037 3.847 Average 156.6 89.7 11.977 3.930 This study 151.9 89.3 表 1 常压下石榴子石晶胞参数和弹性模量
Table 1. Lattice parameters and elastic modulus of garnet under normal pressure
Garnet C11/GPa C12/GPa C44/GPa vP/（m·s–1） vS/（m·s–1） Ref. Pyrope 297.6 109.8 92.7 9.08 5.07 [7] 301.0 110.0 94.3 [36] 8.94 5.02 [6] 90.7 8.92 4.99 [8] 91.7 8.92 5.00 [8] 263.1 100.1 84.2 8.78 4.91 This study Almandine 309.0 111.0 96.0 [41] 8.33 4.64 [6] 95.0 8.77 4.94 [8] 94.9 8.77 4.93 [8] 270.9 114.4 80.1 8.01 4.32 This study Uvarovite 304 91 84 8.85 4.64 [39] 8.60 4.83 [6] 259.7 78.7 73.4 8.34 4.75 This study Spessartine 309.5 113.5 95.2 [41] 96.2 8.55 4.81 [8] 92.0 8.41 4.72 [8] 283.1 114.4 90.9 8.38 4.70 This study Grossular 321.7 104.6 91.4 9.49 5.54 [7] 321.7 104.6 91.4 [40] 98.8 9.02 5.30 [8] 9.04 5.30 [8] 274.7 80.7 77.7 8.65 5.02 This study Andradite 8.49 4.73 [6] 87.9 8.47 4.96 [8] 289 92 85 9.05 5.09 [7] 289 92 85 8.38 4.95 [39] 285.5 85.1 82.7 8.30 4.77 This study 表 2 石榴子石的弹性常数（C11、C12、C44）和波速
Table 2. Elastic constants (C11, C12, C44) and wave velocity of garnet
-
0～16 GPa压力下6种石榴子石的晶胞边长见图1，晶胞边长随压力的增加而线性减小[12, 13, 35, 42]。除了钙铁榴石之外，其他5种石榴子石的晶胞边长都略高于前人结果，可能是由于本计算所使用的GGA近似低估了原子间的内聚力，造成计算所得晶胞边长偏大。至于钙铁榴石晶胞边长低于Zhang等[13]结果的原因可能是实验使用的合成钙铁榴石不纯，受到了其他组分的影响。因为六配位的Al3+离子半径小于钙系列中Fe3+、Cr3+离子半径，且处在镁铝榴石、铁铝榴石和锰铝榴石中十二面体处的Mg2+、Fe2+、Mn2+离子半径均小于Ca2+，因此铝系列榴石的晶胞边长小于钙系列榴石，即石榴子石晶胞边长的增大过程是由铝系列榴石向钙系列榴石变化的过程（如图1所示）。对于铝系列榴石，其晶胞边长由小到大依次为镁铝榴石、铁铝榴石、锰铝榴石，晶胞边长的变化特征与晶格中X位置上二价阳离子半径的变化特征一致。对于钙系列榴石，低压条件下（压力p<8 GPa），晶胞边长由小到大依次为钙铁榴石、钙铝榴石、钙铬榴石，与离子半径变化规律(即r(Fe3+)<r(Al3+)<r(Cr3+))一致；但是当p>8 GPa，晶胞边长由小到大依次为钙铝榴石、钙铁榴石、钙铬榴石。这可能是由于高压使原子轨道部分重叠，引起Fe3+自旋相变进而影响离子半径[43]，导致Fe3+半径小于Al3+半径。因此石榴子石晶胞边长的变化特征与阳离子半径的变化规律一致。
图 1 石榴子石的晶胞边长随压力的变化
Figure 1. Variation of the lattice parameter of garnet with pressure
石榴子石的晶胞密度随着压力的增加而线性增加（见图2）。其中，镁铝榴石、钙铝榴石和钙铬榴石三者的密度相近，且低于钙铁榴石、锰铝榴石和铁铝榴石，这与石榴子石的晶胞质量和晶胞体积有关。在拥有相同原子数目组成的前提下，可用相对分子质量近似代替石榴子石质量，镁铝榴石、铁铝榴石、锰铝榴石、钙铝榴石、钙铁榴石和钙铬榴石6种石榴子石的相对分子质量分别为402、498、495、450、508和500 g/mol，其中铁铝榴石、锰铝榴石、钙铁榴石的相对分子质量在500 g/mol左右。由于物质密度与晶胞体积呈反比，因此钙铁榴石、锰铝榴石和铁铝榴石的密度依次增大；而镁铝榴石、钙铝榴石和钙铬榴石的相对分子质量依次增大，其密度也按照相对分子质量的增大顺序依次增大。
图 2 石榴子石晶体密度随深度的变化
Figure 2. Variation of density of garnets with depth
在地球浅部，石榴子石的密度高于典型的密度结构剖面（见图2），镁铝榴石、钙铝榴石、钙铬榴石的密度在410 km附近与PREM和AK135模型相交，然后转变为低于密度模型计算值；而铁铝榴石、锰铝榴石和钙铁榴石的密度在所研究的整个深度范围内都高于地球密度模型计算值。因此，不同组成的石榴子石及固溶体的存在可能对地球地幔的密度结构产生重要影响。
-
为了解石榴子石的压缩机制，计算了在0～16 GPa压力下石榴子石中的多面体体积随压力的变化特征。压缩过程中石榴子石中的[SiO4]四面体、[YO6]八面体和[XO8]十二面体体积随压力的增加而线性减小，如图3所示。无论是本研究结果还是Hazen[11]的结果都可以看出，钙系列榴石中的四面体、八面体、十二面体3种多面体的体积（图3中淡绿色区域所示）均大于铝系列榴石。其中，钙系列榴石和铝系列榴石的[SiO4]四面体体积在零压下的差别较大，但是在压力从0 GPa增加到16 GPa的过程中，变化量差别不大。除锰铝榴石外，铝系列榴石的八面体体积压缩量小于钙系列榴石，而十二面体体积压缩量的大小顺序则相反。对于锰铝榴石而言，3种多面体体积的压缩量都较小，锰铝榴石明显更难压缩。
图 3 石榴子石中四面体、八面体和十二面体体积随压力的变化
Figure 3. Volume changes of tetrahedron, octahedron and dodecahedron of garnets with pressure
铝系列榴石和钙系列榴石晶体结构中[SiO4]四面体、[YO6]八面体和[XO8]十二面体在压缩过程中的体积变化率占各自总变化率的百分比如图4所示。在6种石榴子石的压缩过程中，多面体体积变化率从大到小依次是[XO8]十二面体、[YO6]八面体、[SiO4]四面体，而且这3种多面体体积变化率之比接近3∶2∶1，因此，在压缩过程中十二面体体积变化率最大。高压下铝系列榴石中十二面体体积变化率略大于钙系列榴石，而四面体的体积变化率则小于钙系列榴石，这可能会引起两系列榴石之间弹性等力学性质的不同。
图 4 四面体、八面体和十二面体的体积变化率所占比例关系
Figure 4. Proportion of volumetric change rates for tetrahedron, octahedron, and dodecahedron
-
在石榴子石的压缩过程中，键长变短，部分键角出现偏离多面体标准值的现象。键角方差可用于描述键角的整体变化情况：键角方差越大，说明键角偏离标准值越大，多面体畸变程度越大；键角方差越小，则说明多面体的畸变程度越小。四面体和八面体的键角方差公式如下
$ {\sigma_\theta }{\left( {\rm {oct}}\right)^2} = \sum\nolimits_{i = 1}^{12} {{{\left( {{\theta _i} - {{90}^ \circ }} \right)}^2}/11} $ $ {\sigma_\theta }{\left( {\rm {tet}}\right)^2} = \sum\nolimits_{i = 1}^6 {{{\left( {{\theta _i} - {{109.47}^ \circ }} \right)}^2}/5} $ 式中：
${\sigma _\theta }{\left( {{\rm{oct}}} \right)^2}$ 和${\sigma_\theta }{\left( {{\rm{tet}}} \right)^2}$ 分别表示八面体和四面体中化学键键角方差，${\theta _i}$ 代表O–Si–O和O–Y–O（Y为Al3+、Fe3+、Cr3+等）的键角大小。压缩过程中，两个系列榴石的O–Si–O键、O–Y–O键（Y为Al3+、Fe3+、Cr3+等）的键角方差随压力的变化情况如图5所示。除锰铝榴石的O–Si–O键，铝系列榴石的键角方差整体大于钙系列榴石，表明在压缩过程中铝系列榴石的键角偏离标准值的程度大于钙系列榴石。
图 5 石榴子石的O–Y–O键、O–Si–O键的键角方差
Figure 5. Bond angle variances of the O–Y–O bond and the O–Si–O bond of two series of garnets
在钙系列榴石的压缩过程中，O–Si–O键、O–Y–O键（Y为Al3+、Fe3+、Cr3+等）的键角方差均随着压力的增加而线性减小，表明高压使钙系列榴石的四面体和八面体变得更加规则，如图5所示。而对于铝系列榴石，O–Al–O键的键角方差随着压力线性减小，八面体结构趋于更加规则，但是O–Si–O键的键角方差随着压力的增加而增加，表明高压下硅氧四面体发生了畸变，使铝系列榴石的四面体变得不规则，这可能是造成铝系列榴石的剪切模量小于钙系列榴石的原因。
-
石榴子石的弹性性质是约束上地幔矿物组成模型的重要参数。6种石榴子石的体弹模量和剪切模量随压力的变化分别如图6（a）和图6（b）所示。可见，体弹模量和剪切模量随着压力的增加近似呈线性增加。6种石榴子石的体弹模量及剪切模量与前人的实验结果相近，但整体偏低[6, 13]，这是由于采用GGA近似模拟低估了原子间的内聚力。Li等[44]利用第一性原理计算的镁铝榴石体弹模量（K=158 GPa）及剪切模量（G=84 GPa）与本研究结果（K=154.8 GPa，G=83.1 GPa）非常相近。对于压力的影响，3种钙系列榴石的体弹模量关于压力的一阶导数
$K'_p $ 相近；而3种铝系列榴石的体弹性模量关于压力的一阶导数$K'_p $ 不一样，铁铝榴石和镁铝榴石的$K'_p $ 相近，而锰铝榴石的$K'_p $ 较小，表明其受压力的影响存在差异。Leger[12]通过超声波实验，得到钙铬榴石和镁铝榴石的$K'_p $ 分别为4.7和3.4，与本研究获得的4.7和4.2相近，而锰铝榴石的$K'_p $ （7.3）与本研究得到的值（3.2）差别较大，可能是锰铝榴石在5～7 GPa压力条件下对有机硅润滑脂产生的各向异性应力分量不太敏感所致[12]。
图 6 6种石榴子石的弹性模量随压力的变化
Figure 6. Elastic modulus of six garnets varies with pressure
从图6（a）中可以发现，钙铝榴石与钙铬榴石的体弹模量相近，且在6种石榴子石中最小，而铁铝榴石最大。Wang和Ji[6]发现，铁铝榴石等5种石榴子石的体弹性模量从大到小依次为：铁铝榴石、镁铝榴石、钙铝榴石、钙铬榴石、钙铁榴石。因此，在多元石榴子石固溶体中，体弹模量往往随着铁铝榴石含量的增加而增加，随着钙铬榴石和钙铝榴石含量的增加而减少[6, 13]，与图6（a）中显示的铝系列榴石的体弹性模量总体低于钙系列榴石结果一致。
由图6（b）可知，铁铝榴石与钙铬榴石的剪切模量相近，而且在6种石榴子石中最小，两者相比铁铝榴石更小一点，而6种榴石中钙铝榴石的剪切模量最大。本研究计算得到的石榴子石剪切模量之间的相对大小与前人结果[6, 13]一致，而Zhang等[13]得到的钙铁榴石剪切模量对压力的一阶导数值明显偏大，可能与Fe3+的自旋有关。整体上剪切模量会随着钙铬榴石和钙铝榴石含量的增加而增加，随着铁铝榴石和钙铁榴石含量的增加而减少，这种趋势与体弹性模量的变化正好相反。
-
作为上地幔、地幔转换带的重要组成矿物，高压下石榴子石的地震波速对了解地球深部的结构和物质组成具有重要意义。根据不同压力下石榴子石的晶胞密度和弹性模量计算的6种石榴子石的压缩波速（VP）和剪切波速（VS）如图7所示。铁铝榴石的波速在6种石榴子石中最低，而钙铝榴石和镁铝榴石的波速较高。两种系列的石榴子石由于在各自内部有类质同象现象而导致波速出现微小波动，但是在两大系列之间却有规律可循，即铝系列榴石的波速整体小于钙系列榴石；同时如果排除镁铝榴石，其余5种榴石的P波和S波波速之间的相对大小完全一致。
图 7 6种石榴子石的地震波速随深度的变化
Figure 7. Variations of seismic velocity of six garnets with depth
Wang和Ji[6]利用超声波干涉仪相位比较法在0～3 GPa压力条件下得到镁铝榴石等5种石榴子石的P波和S波波速，其中VS由大到小依次为：钙铝榴石、镁铝榴石、钙铬榴石、钙铁榴石、铁铝榴石，与本研究获得的S波波速大小顺序相同。但是对于P波，Wang和Ji[6]获得的铁铝榴石的波速在5种榴石中最大，而本计算得到的铁铝榴石波速在6种榴石中最小，可能是因为本计算中未考虑Fe的自旋影响以及超声波测试实验条件的差异所共同导致的。
在铝系列榴石中，按照波速从大到小依次为镁铝榴石、锰铝榴石、铁铝榴石，表明在铝系列榴石中的十二面体上，Fe2+、Mn2+替换镁铝榴石上的Mg2+会导致P波和S波波速减小。在钙系列榴石中，按照波速由大到小依次为钙铝榴石、钙铬榴石、钙铁榴石，表明Cr3+、Al3+替换钙铁榴石八面体上的Fe3+会导致P波和S波波速增加。
图7中Wang和Ji[6]获得的实验结果在整个地球地幔深度范围内与地球波速结构模型没有交点，均高于波速模型。本研究获得的镁铝榴石和钙铝榴石的波速在整个计算深度范围内均高于地球典型波速模型；而铁铝榴石的S波波速低于波速模型，P波波速在约250 km处与波速模型相交而后随着深度增加转为低于波速模型。同时通过计算发现，在约410 km处，钙铬榴石、钙铁榴石、锰铝榴石的P波和S波波速与PREM和AK135模型相交。铁铝榴石、镁铝榴石、钙铝榴石是自然界常见的石榴子石固溶体，如果根据计算结果拟合此固溶体的波速，可以发现此固溶体的波速在410 km附近也与地球典型波速模型有交点。因此本结果也证明石榴子石是地幔中的重要组分，且不同组成的石榴子石及固溶体的存在可能对地球地幔的波速结构产生重要影响。
-
为了系统比较钙系列和铝系列榴石之间的物性差异、探索其在地幔深部赋存特征，利用第一性原理方法计算了0～16 GPa压力下镁铝榴石、铁铝榴石、锰铝榴石、钙铬榴石、钙铝榴石和钙铁榴石6种常见石榴子石的晶体结构和弹性性质的变化特征。研究发现：铝系列榴石的晶胞体积小于钙系列榴石；除镁铝榴石外，铝系列榴石的密度高于钙系列榴石，镁铝榴石的低密度可能是由于其相对分子质量较小。在石榴子石的压缩过程中，多面体体积变化率从大到小依次为[XO8]十二面体、[YO6]八面体、[SiO4]四面体，变化率之比接近3∶2∶1，表明石榴子石的压缩机制主要受其结构中十二面体的控制。键角方差的变化表明，高压可以使钙系列榴石的四面体和八面体变得更加规则；铝系列则与其不同，高压下铝系列榴石的四面体变得更加不规则。
计算发现：钙铝榴石与钙铬榴石的体弹模量相近，且在6种石榴子石中最小，而铁铝榴石最大；对于剪切模量，铁铝榴石与钙铬榴石的剪切模量相近，在6种石榴子石中最小，且比铁铝榴石更小，6种榴石中钙铝榴石的剪切模量最大。因此，石榴子石的体弹模量随着铁铝榴石含量的增加而增大，随着钙铬榴石和钙铝榴石含量的增加而减小；而剪切模量则随着钙铝榴石含量的增加而增大，随着铁铝榴石和钙铬榴石含量的增加而减小。
研究发现：在铝系列榴石中，按照波速从大到小依次为镁铝榴石、锰铝榴石、铁铝榴石，表明在铝系列榴石中的十二面体上，Fe2+、Mn2+替换Mg2+导致P波和S波波速减小；在钙系列榴石中，按照波速从大到小依次为钙铝榴石、钙铬榴石、钙铁榴石，表明由Cr3+、Al3+替换钙铁榴石八面体上的Fe3+会导致P波和S波波速的增加。除了镁铝榴石外，其余5种榴石的P波和S波波速的相对大小顺序一致。计算结果显示，石榴子石及其固溶体的波速在410 km附近与地球典型波速模型有交点，证明石榴子石是地幔中的重要组分，且不同组成的石榴子石及其固溶体的存在可能对地球地幔的波速结构产生重要影响。本研究弥补了石榴子石压缩过程中多面体体积变化率及键角扭转过程研究的不足，为研究石榴子石类质同象现象特征提供了新的数据支持，同时关于高温高压下两个系列石榴子石及其不同组分固溶体的性质差别还需要开展进一步的研究工作，以探索其在地幔深部的赋存及对地幔物质组成和结构的影响。
高压下石榴子石结构和弹性的第一性原理研究
Structure and Elasticity of Garnet under High Pressure by First-Principles Simulation
-
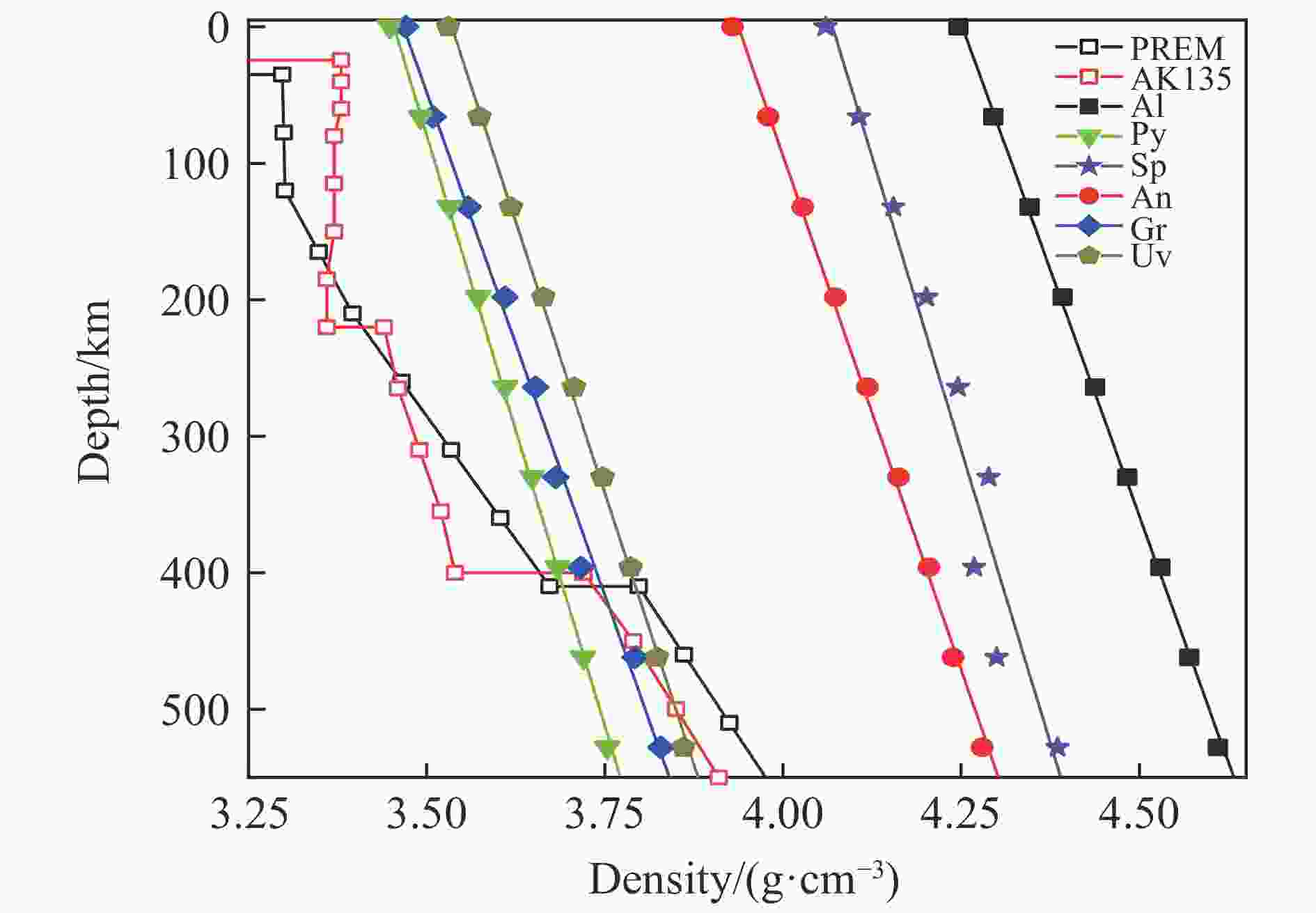
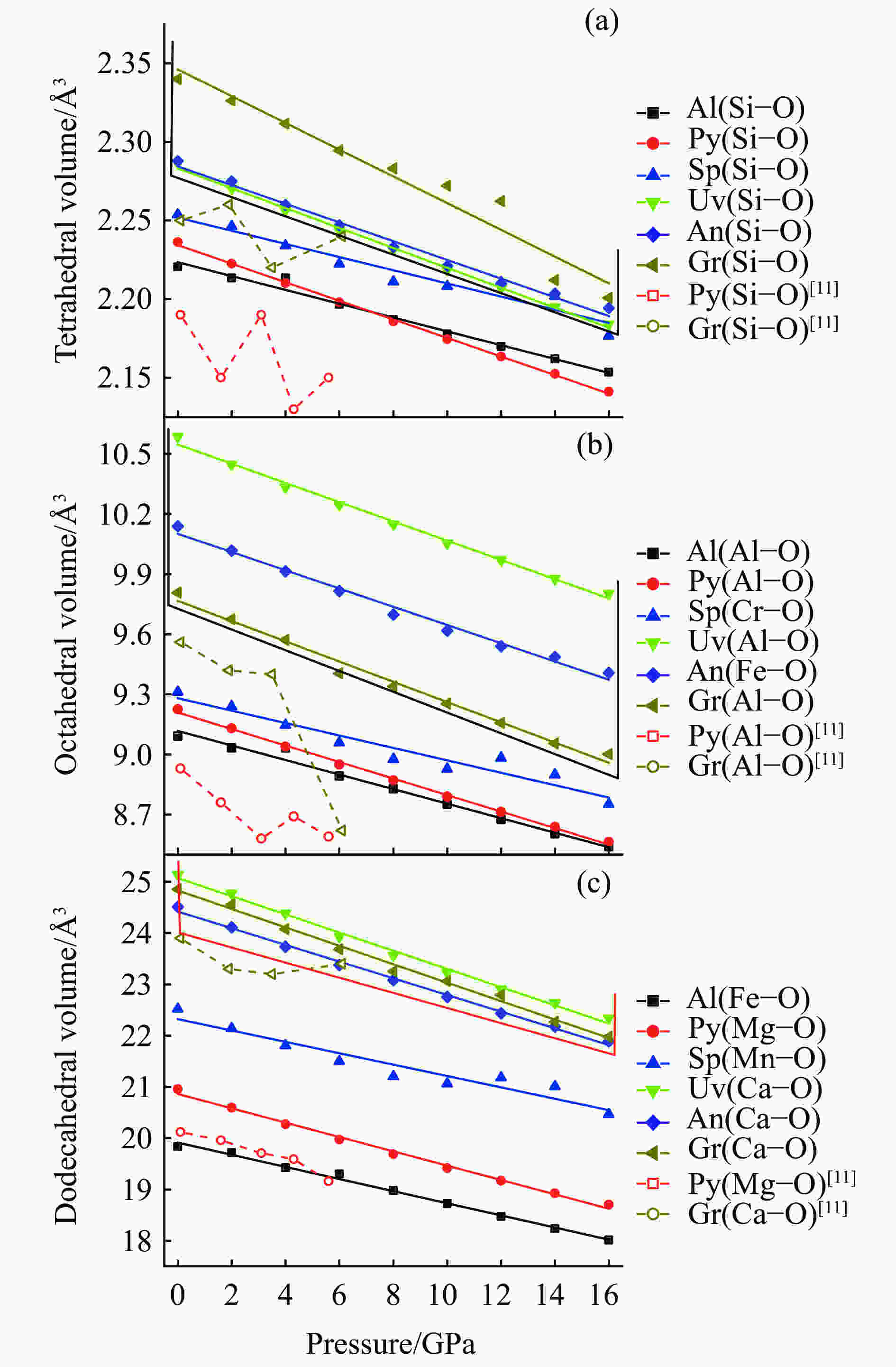
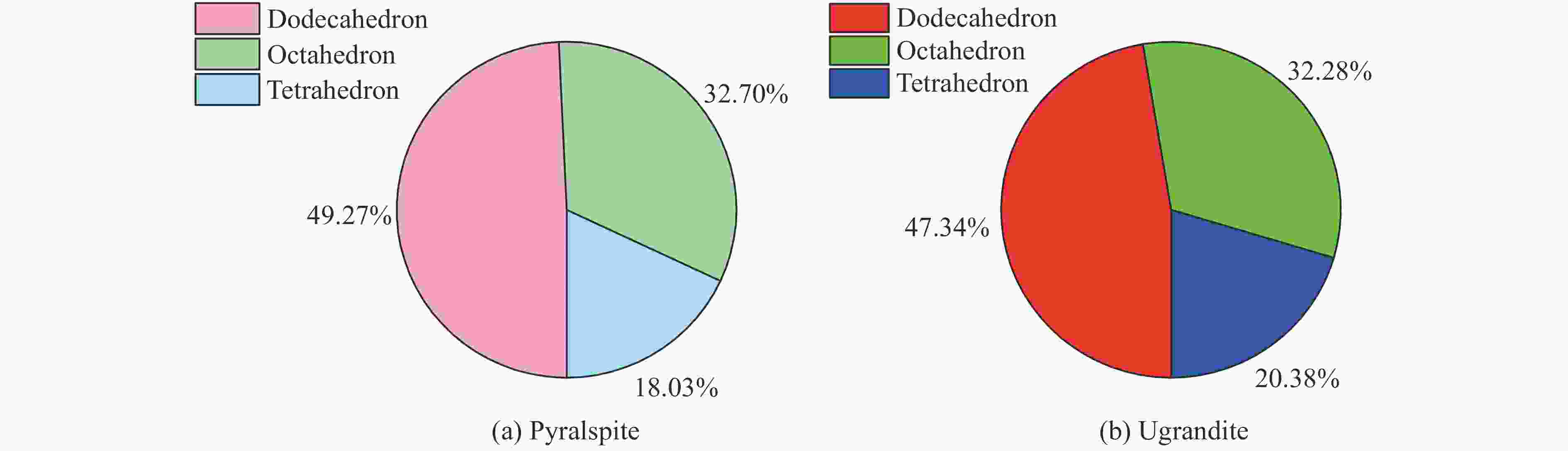
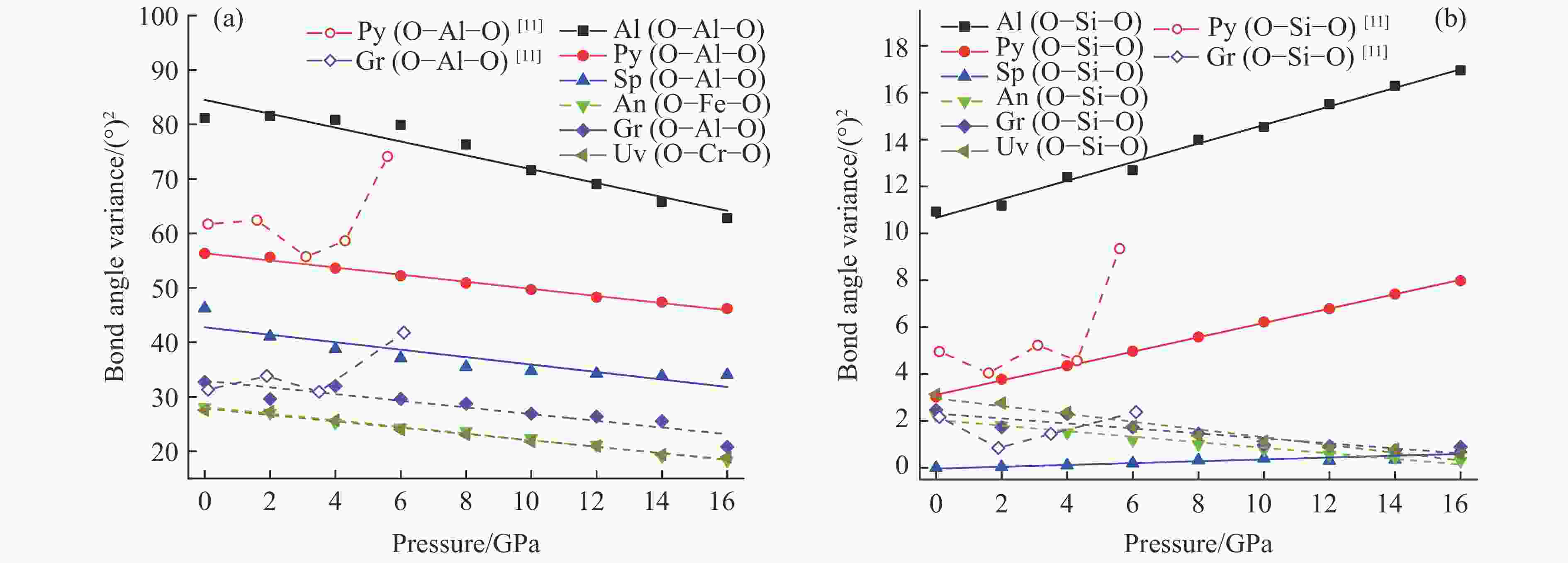
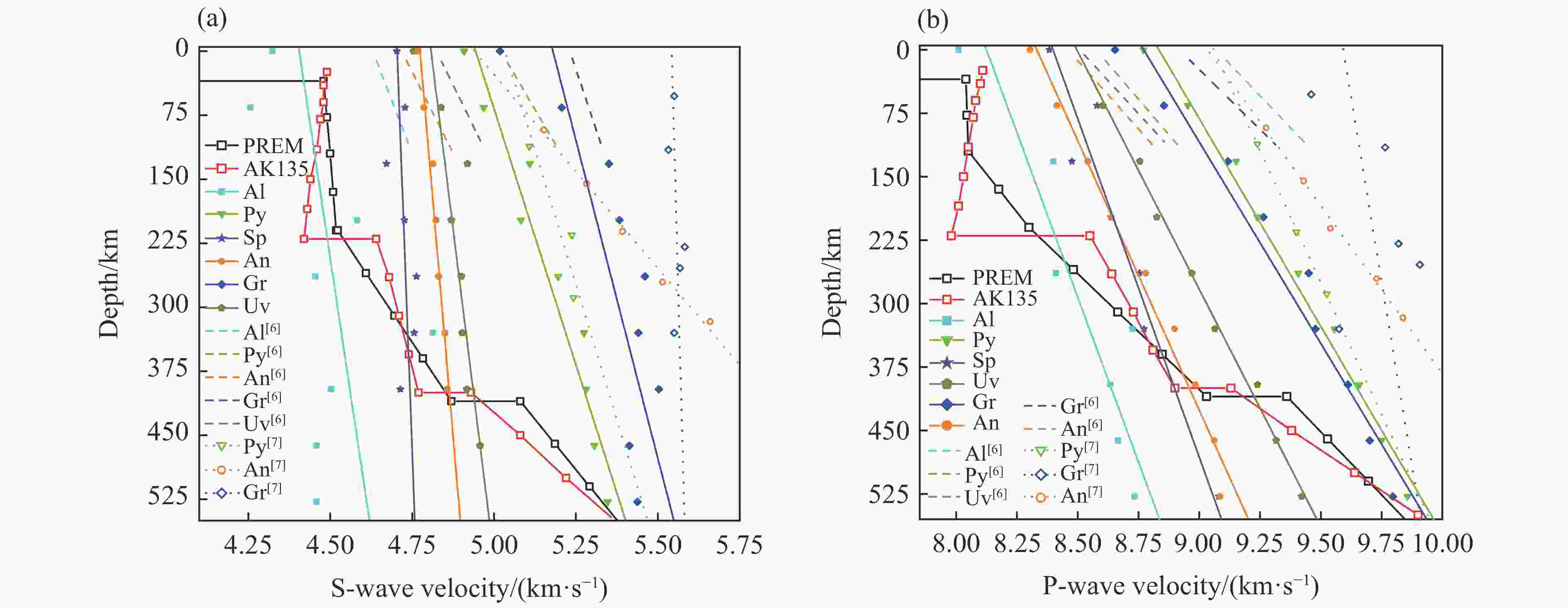
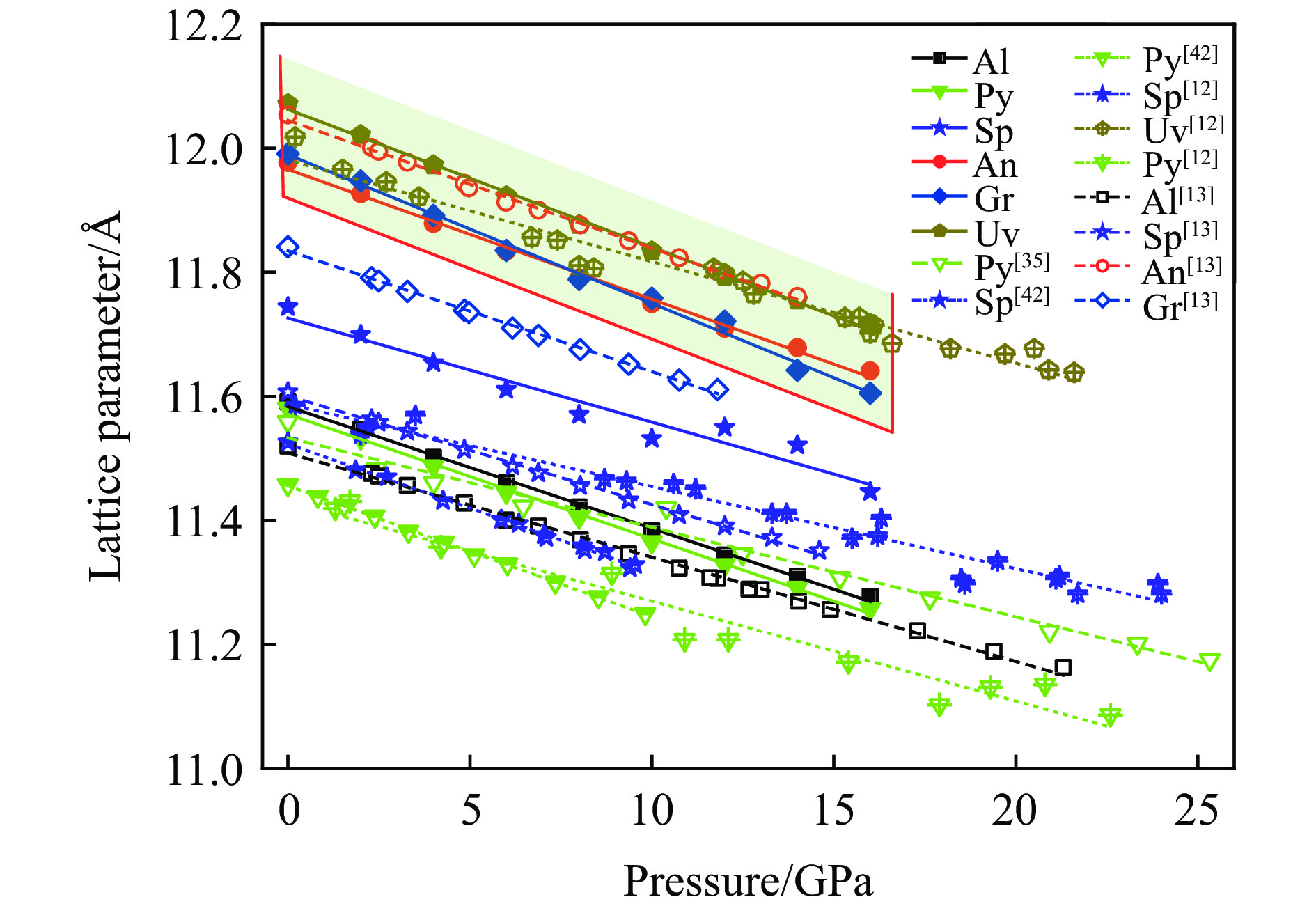
摘要: 石榴子石是上地幔和地幔转换带的重要成分，掌握其高温高压下的物性演化特征对了解地幔物质组成、结构以及动力学过程具有重要意义。为此，利用第一性原理计算了0～16 GPa压力下铝系列和钙系列常见的6种榴石（镁铝榴石、铁铝榴石、锰铝榴石、钙铬榴石、钙铝榴石和钙铁榴石）的晶体结构和弹性性质。结果表明：铝系列榴石的晶胞体积小于钙系列榴石；除镁铝榴石外，铝系列榴石的密度高于钙系列榴石。在石榴子石压缩过程中，多面体体积变化率由大到小依次为[XO8]十二面体、[YO6]八面体、[SiO4]四面体，且变化率之比接近3∶2∶1，表明石榴子石的压缩机制主要受其结构中的十二面体控制。键角方差的变化表明：高压可以使钙系列榴石的四面体和八面体变得更加规则；而铝系列榴石则与其不同，高压下铝系列榴石的四面体变得更加不规则。研究发现：石榴子石的体弹模量随着铁铝榴石含量的增加而增大，随着钙铬榴石和钙铝榴石含量的增加而减小；而剪切模量则随着钙铝榴石含量的增加而增大，随着铁铝榴石和钙铬榴石含量的增加而减小。除镁铝榴石外，铝系列榴石的波速整体小于钙系列榴石。通过计算结果发现，石榴子石及其固溶体的波速在410 km附近与地球典型波速模型有交点，证明了石榴子石是地幔中的重要组分，且不同组成的石榴子石及固溶体的存在可能对地球地幔的波速结构产生重要影响。Abstract: Garnet is an important component of the upper mantle and mantle transition zone, and its properties under high temperature and pressure are of great significance to understand the composition, structure and dynamic process of mantle. Therefore, the crystal structure and elastic properties of pyrope, almandine, spessartite, uvarovite, grossular and andradite under 0–16 GPa, the six most common garnet in the Earth, were calculated by first principle method. The results show the unit cell volume of pyralaspite (pyrope, almandine, spessartite) is smaller than that of ugrandite (uvarovite, grossular and andradite), and the density of pyralaspite is higher than that of ugrandite except for pyrope. During structural compression, the volume change of polyhedron is from large to small as [XO8] dodecahedron, [YO6] octahedron and [SiO4] tetrahedron, and their ratio is close to 3∶2∶1, indicating that the compression mechanism of garnet is mainly controlled by the dodecahedron. The variation of bond angle shows that tetrahedron and octahedron of the ugrandite would be more regular under high pressure; while the tetrahedron of pyralaspite becomes more irregular under high pressure. The bulk modulus of garnet increases with the increase of almandine, and decreases with the increase of uvarovite and grossular; while the shear modulus of garnet increases with the increase of grossular, and decreases with the increase of almandine and uvarovite. The wave velocity of pyralaspite is smaller than that of ugrandite except for pyrope. Calculation results show that the wave velocities of garnet intersect with the typical wave velocity model of the Earth near 410 km, proving that garnet is an important component of the mantle, and the existence of garnet and its solid solution with different compositions may have an important influence on the wave velocity structure of the Earth’s mantle.
-
Key words:
- garnet /
- crystal structure /
- elasticity /
- high pressure /
- first principle simulation
-
图 1 石榴子石的晶胞边长随压力的变化
Figure 1. Variation of the lattice parameter of garnet with pressure
图 3 石榴子石中四面体、八面体和十二面体体积随压力的变化
Figure 3. Volume changes of tetrahedron, octahedron and dodecahedron of garnets with pressure
图 4 四面体、八面体和十二面体的体积变化率所占比例关系
Figure 4. Proportion of volumetric change rates for tetrahedron, octahedron, and dodecahedron
图 5 石榴子石的O–Y–O键、O–Si–O键的键角方差
Figure 5. Bond angle variances of the O–Y–O bond and the O–Si–O bond of two series of garnets
图 7 6种石榴子石的地震波速随深度的变化
Figure 7. Variations of seismic velocity of six garnets with depth
表 1 常压下石榴子石晶胞参数和弹性模量
Table 1. Lattice parameters and elastic modulus of garnet under normal pressure
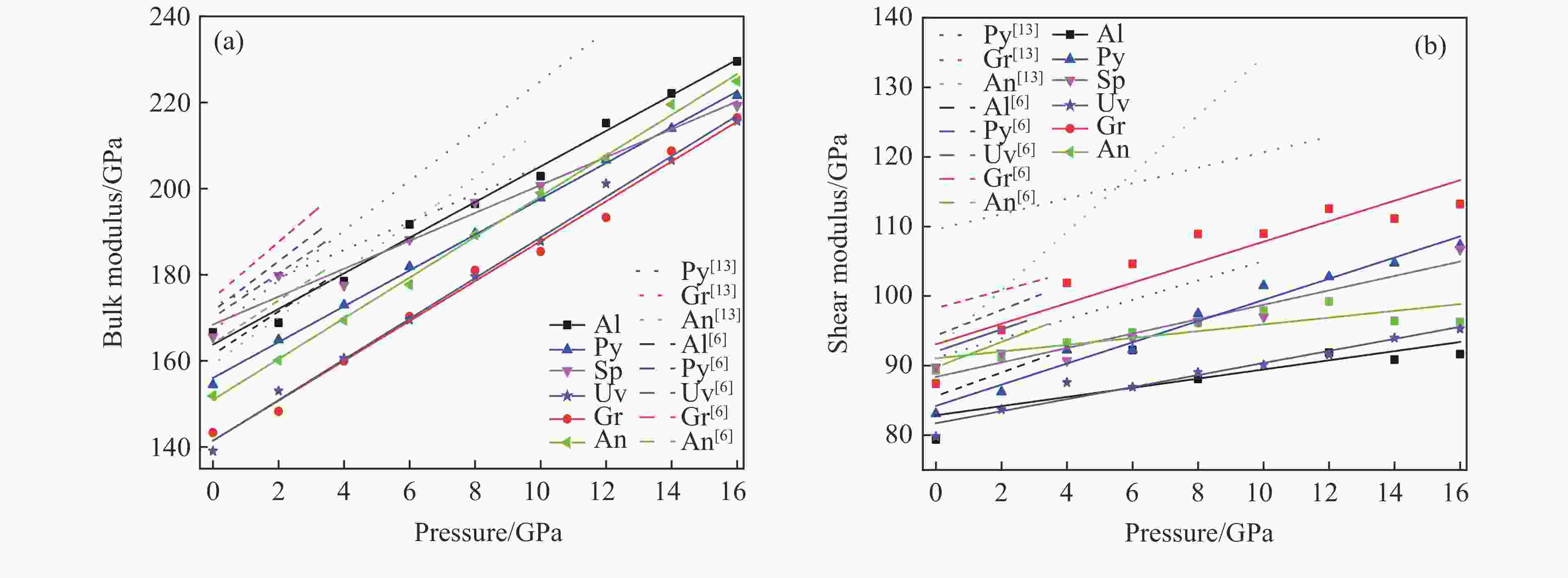
Garnet Lattice parameter/Å Density/（g·cm–3） Method Bulk modulus/GPa Shear modulus/GPa Pyrope 11.559 Exp.[35] 199.0 11.466 3.582 Exp.[7] 172.7 92.0 Exp.[36] 173.6 94.9 3.610 Exp.[6] 170.1 90.2 11.447 3.569 Exp.[37] 167.0 11.472 Exp.[38] 173.7 11.486 3.587 Average 176.0 92.4 11.581 3.448 This study 154.5 83.1 Almandine 11.532 4.312 Exp.[14] 168.0 4.289 Exp.[6] 175.1 92.1 11.519 Exp.[13] 185.0 11.507 3.916 Exp.[8] 173.7 95.4 11.535 3.930 Exp.[8] 174.9 95.5 11.523 4.110 Average 175.3 94.3 11.591 4.250 This study 166.6 79.4 Uvarovite 11.99 3.850 Exp.[39] 162.0 92.0 3.841 Exp.[6] 164.8 89.9 11.990 3.846 Average 163.4 91.0 12.070 3.780 This study 139.1 79.8 Spessartine 11.617 4.195 Exp.[40] 178.8 96.3 11.611 4.172 Exp.[8] 176.4 96.5 11.608 4.185 Exp.[8] 171.8 93.3 11.612 4.184 Average 175.7 95.4 11.744 4.060 This study 165.6 89.8 Grossular 11.849 3.600 Exp.[7] 166.8 108.9 11.848 3.602 Exp.[40] 168.4 109.0 11.870 3.659 Exp.[8] 161.2 102.6 11.910 3.667 Exp.[8] 162.4 102.9 11.869 3.632 Average 164.7 105.9 11.991 3.471 This study 143.4 87.4 Andradite 12.048 3.840 Exp.[7] 159.4 90.0 12.054 3.836 Exp.[39] 157.0 90.0 12.009 3.775 Exp.[8] 147.3 92.7 3.938 Exp.[6] 162.5 86.0 12.037 3.847 Average 156.6 89.7 11.977 3.930 This study 151.9 89.3 
下载: 导出CSV
表 2 石榴子石的弹性常数（C11、C12、C44）和波速
Table 2. Elastic constants (C11, C12, C44) and wave velocity of garnet
Garnet C11/GPa C12/GPa C44/GPa vP/（m·s–1） vS/（m·s–1） Ref. Pyrope 297.6 109.8 92.7 9.08 5.07 [7] 301.0 110.0 94.3 [36] 8.94 5.02 [6] 90.7 8.92 4.99 [8] 91.7 8.92 5.00 [8] 263.1 100.1 84.2 8.78 4.91 This study Almandine 309.0 111.0 96.0 [41] 8.33 4.64 [6] 95.0 8.77 4.94 [8] 94.9 8.77 4.93 [8] 270.9 114.4 80.1 8.01 4.32 This study Uvarovite 304 91 84 8.85 4.64 [39] 8.60 4.83 [6] 259.7 78.7 73.4 8.34 4.75 This study Spessartine 309.5 113.5 95.2 [41] 96.2 8.55 4.81 [8] 92.0 8.41 4.72 [8] 283.1 114.4 90.9 8.38 4.70 This study Grossular 321.7 104.6 91.4 9.49 5.54 [7] 321.7 104.6 91.4 [40] 98.8 9.02 5.30 [8] 9.04 5.30 [8] 274.7 80.7 77.7 8.65 5.02 This study Andradite 8.49 4.73 [6] 87.9 8.47 4.96 [8] 289 92 85 9.05 5.09 [7] 289 92 85 8.38 4.95 [39] 285.5 85.1 82.7 8.30 4.77 This study
下载: 导出CSV
-
[1] PALKE A C, STEBBINS J F, GEIGER C A, et al. Cation order-disorder in Fe-bearing pyrope and grossular garnets: a 27Al and 29Si MAS NMR and 57Fe Mossbauer spectroscopy study [J]. American Mineralogist, 2015, 100(2/3): 536–547. [2] 范大伟, 李博, 陈伟, 等. 石榴子石族矿物状态方程研究进展 [J]. 高压物理学报, 2018, 32(1): 010101. doi: 10.11858/gywlxb.20170597
FAN D W, LI B, CHEN W, et al. Research progress of the equation of state for garnet minerals [J]. Chinese Journal of High Pressure Physics, 2018, 32(1): 010101. doi: 10.11858/gywlxb.20170597[3] FEI Y, BERTKA C M. Phase transitions in the Earth’s mantle and mantle mineralogy [J]. Mantle Petrology: Field Observations and High Pressure Experimentation, 1999, 6: 189–207. [4] RINGWOOD A E. Phase transformations and their bearing on the constitution and dynamics of the mantle [J]. Geochimica et Cosmochimica Acta, 1991, 55(8): 2083–2110. doi: 10.1016/0016-7037(91)90090-R [5] IRIFUNE T, RINGWOOD A E. Phase transformations in subducted oceanic crust and buoyancy relationships at depths of 600–800 km in the mantle [J]. Earth and Planetary Science Letters, 1993, 117(1/2): 101–110. [6] WANG Z, JI S. Elasticity of six polycrystalline silicate garnets at pressure up to 3.0 GPa [J]. American Mineralogist, 2001, 86(10): 1209–1218. doi: 10.2138/am-2001-1009 [7] CONRAD P G, ZHA C S, MAO H K, et al. The high-pressure, single-crystal elasticity of pyrope, grossular, and andradite [J]. American Mineralogist, 1999, 84(3): 374–383. doi: 10.2138/am-1999-0321 [8] BABUŠKA V, FIALA J, KUMAZAWA M, et al. Elastic properties of garnet solid-solution series [J]. Physics of the Earth and Planetary Interiors, 1978, 16(2): 157–176. doi: 10.1016/0031-9201(78)90086-9 [9] ANDERSON O L, NAFE J E. The bulk modulus-volume relationship for oxide compounds and related geophysical problems [J]. Journal of Geophysical Research, 1965, 70(16): 3951–3963. doi: 10.1029/JZ070i016p03951 [10] ANDERSON D L, ANDERSON O L. The bulk modulus-volume relationship for oxides [J]. Journal of Geophysical Research, 1970, 75(26): 3494–3500. [11] HAZEN R M. Crystal structures and compressibilities of pyrope and grossular to 60 kbar [J]. American Mineralogist, 1978, 63(3/4): 297–303. [12] LEGER J M, REDON A M, CHATEAU C. Compressions of synthetic pyrope, spessartine and uvarovite garnets up to 25 GPa [J]. Physics and Chemistry of Minerals, 1990, 17(2): 161–167. [13] ZHANG L, AHSBAHS H, KUTOGLU A, et al. Single-crystal hydrostatic compression of synthetic pyrope, almandine, spessartine, grossular and andradite garnets at high pressures [J]. Physics and Chemistry of Minerals, 1999, 27(1): 52–58. doi: 10.1007/s002690050240 [14] TAKAHASHI T, LIU L G. Compression of ferromagnesian garnets and the effect of solid solutions on the bulk modulus [J]. Journal of Geophysical Research, 1970, 75(29): 5757–5766. doi: 10.1029/JB075i029p05757 [15] HUANG S, CHEN J. Equation of state of pyrope–almandine solid solution measured using a diamond anvil cell and in situ synchrotron X-ray diffraction [J]. Physics of the Earth and Planetary Interiors, 2014, 228: 88–91. doi: 10.1016/j.pepi.2014.01.014 [16] MILANI S, NESTOLA F, ALVARO M, et al. Diamond-garnet geobarometry: the role of garnet compressibility and expansivity [J]. Lithos, 2015, 227: 140–147. doi: 10.1016/j.lithos.2015.03.017 [17] FAN D, XU J, MA M, et al. P-V-T equation of state of spessartine-almandine solid solution measured using a diamond anvil cell and in situ synchrotron X-ray diffraction [J]. Physics and Chemistry of Minerals, 2015, 42(1): 63–72. doi: 10.1007/s00269-014-0700-2 [18] MURAKAMI M, SINOGEIKIN S V, LITASOV K, et al. Single-crystal elasticity of iron-bearing majorite to 26 GPa: implications for seismic velocity structure of the mantle transition zone [J]. Earth and Planetary Science Letters, 2008, 274(3/4): 339–345. [19] FAN D W, WEI S Y, LIU J, et al. High pressure X-ray diffraction study of a grossular-andradite solid solution and the bulk modulus variation along this solid solution [J]. Chinese Physics Letters, 2011, 28(7): 076101. doi: 10.1088/0256-307X/28/7/076101 [20] FAN D W, KUANG Y, XU J, et al. Thermoelastic properties of grossular-andradite solid solution at high pressures and temperatures [J]. Physics and Chemistry of Minerals, 2017, 44(2): 137–147. doi: 10.1007/s00269-016-0843-4 [21] DU W, CLARK S M, WALKER D. Thermo-compression of pyrope-grossular garnet solid solutions: non-linear compositional dependence [J]. American Mineralogist, 2014, 100(1): 215–222. [22] GILLAN M J, ALFÈD, BRODHOLT J, et al. First-principles modelling of Earth and planetary materials at high pressures and temperatures [J]. Reports on Progress in Physics, 2006, 69(8): 2365–2441. doi: 10.1088/0034-4885/69/8/R03 [23] PERDEW J P, ZUNGER A. Self-interaction correction to density-functional approximations for many-body systems [J]. Physical Review B, 1981, 23(10): 5048–5079. doi: 10.1103/PhysRevB.23.5048 [24] WENTZCOVITCH R M, MARTINS J L, PRICE G D. Ab initio molecular dynamics with variable cell shape: application to MgSiO3 [J]. Physical Review Letters, 1993, 70(25): 3947–3950. doi: 10.1103/PhysRevLett.70.3947 [25] DA SILVA C, STIXRUDE L, WENTZCOVITCH R M. Elastic constants and anisotropy of forsterite at high pressure [J]. Geophysical Research Letters, 1997, 24(15): 1963–1966. doi: 10.1029/97GL01756 [26] KARKI B B, STIXRUDE L, WENTZCOVITCH R M. High-pressure elastic properties of major materials of Earth’s mantle from first principles [J]. Reviews of Geophysics, 2015, 39(4): 507–534. [27] LIU L, DU J G, ZHAO J, et al. Elastic properties of hydrous forsterites under high pressure: first-principle calculations [J]. Physics of the Earth and Planetary Interiors, 2009, 176(1): 89–97. [28] LIU L, DU J, LIU W, et al. Elastic behavior of (Mg xFe1- x)2SiO4 olivine at high pressure from first-principles simulations [J]. Journal of Physics and Chemistry of Solids, 2010, 71(8): 1094–1097. doi: 10.1016/j.jpcs.2010.03.013 [29] LIU L, DU J G, LIU H, et al. Differential stress effect on the structural and elastic properties of forsterite by first-principles simulation [J]. Physics of the Earth and Planetary Interiors, 2014, 233: 95–102. doi: 10.1016/j.pepi.2014.06.010 [30] LIU L, LV C J, ZHUANG C Q, et al. Effects of differential stress on the structure and Raman spectra of calcite from first-principles calculations [J]. American Mineralogist, 2016, 101(8): 1892–1897. doi: 10.2138/am-2016-5558 [31] CEPERLEY D M, ALDER B J. Ground state of the electron gas by a stochastic method [J]. Physical Review Letters, 1980, 45(7): 566–569. doi: 10.1103/PhysRevLett.45.566 [32] NIELSEN O H, MARTIN, RICHARD M. First-principles calculation of stress [J]. Physical Review Letters, 1983, 50(9): 697–700. doi: 10.1103/PhysRevLett.50.697 [33] VANDERBILT D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism [J]. Physical Review B, 1990, 41(11): 7892–7895. doi: 10.1103/PhysRevB.41.7892 [34] NIELSEN O H, MARTIN R M. Quantum-mechanical theory of stress and force [J]. Physical Review B, 1985, 32(6): 3780–3791. doi: 10.1103/PhysRevB.32.3780 [35] 马艳梅, 彭刚, 李敏. 镁铝石榴子石的高压X射线衍射研究 [J]. 高压物理学报, 2008, 22(3): 305–308. doi: 10.3969/j.issn.1000-5773.2008.03.014
MA Y M, PENG G, LI M. X-ray diffraction investigation of pyrope under pressure [J]. Chinese Journal of High Pressure Physics, 2008, 22(3): 305–308. doi: 10.3969/j.issn.1000-5773.2008.03.014[36] WEBB S L. The elasticity of the upper mantle orthosilicates olivine and garnet to 3 GPa [J]. Physics and Chemistry of Minerals, 1989, 16(7): 684–692. [37] ZOU Y, GRÉAUX S, IRIFUNE T, et al. Thermal equation of state of Mg3Al2Si3O12 pyrope garnet up to 19 GPa and 1700 K [J]. Physics and Chemistry of Minerals, 2012, 39(7): 589–598. doi: 10.1007/s00269-012-0514-z [38] HAZEN R M, DOWNS R T, CONRAD P G, et al. Comparative compressibilities of majorite-type garnets [J]. Physics and Chemistry of Minerals, 1994, 21(5): 344–349. [39] BASS J D. Elasticity of uvarovite and andradite garnets [J]. Journal of Geophysical Research: Solid Earth, 1986, 91(B7): 7505–7516. doi: 10.1029/JB091iB07p07505 [40] BASS J D. Elasticity of grossular and spessartite garnets by Brillouin spectroscopy [J]. Journal of Geophysical Research, 1989, 94(B6): 7621–7628. doi: 10.1029/JB094iB06p07621 [41] O’NEILL B, BASS J, R. SMYTH J, et al Elasticity of a grossular-pyrope-almandine garnet [J]. Journal of Geophysical Research Solid Earth, 1989, 94(B12): 17819–17824. doi: 10.1029/JB094iB12p17819 [42] SATO Y, AKAOGI M, AKIMOTO S I. Hydrostatic compression of the synthetic garnets pyrope and almandine [J]. Journal of Geophysical Research, 1978, 83(B1): 335–338. doi: 10.1029/JB083iB01p00335 [43] 徐光宪, 王祥云. 物质结构[M]. 2版. 北京: 高等教育出版社, 1987: 621–622.
XU G X, WANG X Y. Material structure [M]. 2nd ed. Beijing: Higher Education Press, 1987: 621–622.[44] LI L, WEIDNER D J, BRODHOLT J, et al. Ab initio molecular dynamic simulation on the elasticity of Mg3Al2Si3O12 pyrope [J]. Journal of Earth Science, 2011, 22(2): 169–175. doi: 10.1007/s12583-011-0169-6 -
点击查看大图
图(7)表(2)
计量
- 文章访问数: 239
- 阅读全文浏览量: 239
- PDF下载量: 6
