p-$\alpha $ and p-$\lambda $ Model for Describing Shock Compressive Behavior of W-Cu Powder Mixture
-
摘要: 研究了3种p-
$\alpha $ 模型和p-$\lambda $ 模型在预测非均质W-Cu混合粉末冲击压实响应的适用性。利用Mie-Grüneisen方法和Barry等压混合法,基于单质W、Cu粉末的Hugoniot关系预测了同孔隙度的W-Cu混合粉末的Hugoniot线,在高压段与实验结果符合较好,但在低压段与实验偏差较大。分别应用3种p-$\alpha $ 模型和p-$\lambda $ 模型对实验结果进行拟合,发现除p-$\alpha $ PL模型外,其他模型均较好地描述W-Cu混合粉末的冲击压缩响应,受经验参数选择的影响,所有模型的压溃强度和压缩路径各不相同,预测功能较差。-
关键词:
- W-Cu混合粉末 /
- 冲击压缩 /
- p-$\alpha $模型 /
- Hugoniot测量
Abstract: This study investigated the applicability of three p-$\alpha $ models and p-$\lambda $ model for predicting shock compaction response of heterogeneous W-Cu powder mixture. Mie-Grüneisen method and Barry isobaric mixing method were employed to predict the Hugoniot of W-Cu powder mixture with the same porosity based on the Hugoniot relationships. At high pressure section, the results were in good agreement with the experimental results, but it deviated greatly at the low pressure section. The p-$\alpha $ models and p-$\lambda $ model were applied to fit the experimental results, and it was found that all the other models were able to describe the shock compression response of W-Cu powder mixture except p-$\alpha $ PL model. The crush strength and compression path of all models are different due to selection of empirical parameters, and they are with poor prediction function.-
Key words:
- W-Cu powder mixture /
- shock compressive /
- p-$\alpha $ model /
- Hugoniot measurement
-
图 4 典型的入射波(a)和传播波(b)的DISAR轮廓曲线(显示了结构化波形,以及50%的均衡到达时间和10%、90%的不确定到达时间,用于计算冲击波速度)
Figure 4. Typical extracted profile for input (a) and propagated waves (b) that illustrating structured waveforms (Locations of 50% equilibrium time of arrival and 10% and 90% uncertainty arrival times used for calculation of shock velocity are also marked.)
表 1 实验相关参数计算结果及误差范围
Table 1. Calculated results and errors of the related experimental parameters
No. ${\rho _{00}}$/(g·cm–3) vI/ (km·s–1) uS/(km·s–1) uP/(km·s–1) p/GPa $\rho $/(g·cm–3) 1 10.696±0.910 0.622±0.003 1.254±0.041 0.457±0.019 6.126±0.434 16.826±1.122 2 10.484±0.731 0.270±0.001 0.913±0.055 0.213±0.013 2.038±0.223 13.668±0.536 3 10.707±1.229 0.784±0.004 1.549±0.089 0.546±0.028 9.056±0.913 16.639±1.324 4 10.237±1.370 0.508±0.003 1.107±0.030 0.388±0.016 4.392±0.211 15.752±1.370 表 2 组分和混合物的相关冲击和材料特性
Table 2. Relevant shock and material properties of constituents and mixtures
Material ${\rho _0}$/(g·cm–3) C0/(km·s–1) S ${\gamma _0}$ V0/(cm3·g–1) Y/GPa W 19.35 4.064 1.204 1.78 0.052 0 1.700 Cu 8.93 3.910 1.510 1.97 0.112 1 0.065 W-Cu 15.117 4.027 1.277 1.83 0.066 4 1.030 表 3 模型拟合参数
Table 3. Model fitting parameters
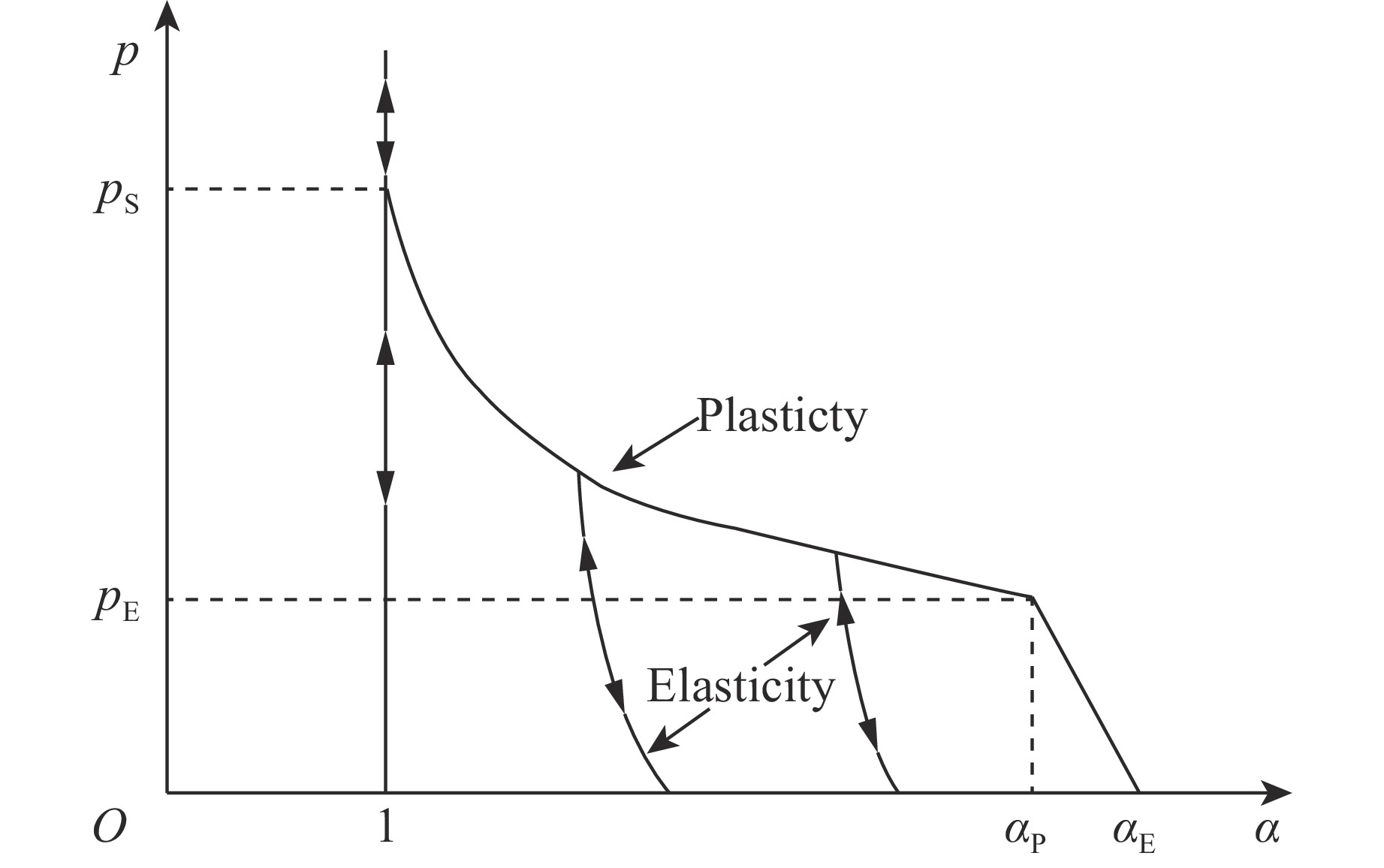
Model Parameters pS/GPa pE/GPa ${ \alpha _{\rm{E} } }$ N p-${\alpha} $(MQ) 4.60 0.057 7 1.359 1.952 p-${\alpha} $(PL) pS/GPa n 4.60 7.80 p-${\alpha} $(SS) Y/GPa 1.273 4 p-$\lambda $ n 1.51 -
[1] ALTSHULER L V, KRUPNIKOV K K, LEDENEV B N, et al. Dynamic compressibility and equation of state for iron under high pressure [J]. Soviet Physics-JETP, 1958: 34. [2] MCQUEEN R G, MARSH S P, TAYLOR J W, et al. The equation of state of solids from shock wave studies [M]. Los Alamos, New Mexico: University of California, 1970: 293–417. [3] FREDENBURG D A. Shock compaction and impact response of thermit powder mixtures [D]. Georgia: Georgia Institute of Technology, 2010. [4] HERRMANN W. Constitutive equation for the dynamic compaction of ductile porous materials [J]. Journal of Applied Physics, 1969, 40(6): 2490–2499. doi: 10.1063/1.1658021 [5] DAI C D, EAKINS D E, THADHANI N N. Dynamic densification behavior of nanoiron powders under shock compression [J]. Journal of Applied Physics, 2008, 103(9): 093503. doi: 10.1063/1.2908209 [6] BUTCHER B M, KARNES C H. Dynamic compaction of porous iron [J]. Journal of Applied Physics, 1969, 40(7): 2967–2976. doi: 10.1063/1.1658109 [7] CARROLL M M, HOLT A C. Static and dynamic pore‐collapse relations for ductile porous materials [J]. Journal of Applied Physics, 1972, 43(4): 1626–1636. doi: 10.1063/1.1661372 [8] GRADY D, KERLEY E G I, KUHNS L D, et al. Computational modeling and wave propagation in media with inelastic deforming microstructure [J]. Journal de Physique, IV: Proceedings of International Conference, 2000, 10(9): 15–20. [9] MEYERS M A. Shock waves: equations of state [M]. John Wiley & Sons, Inc., 2007. [10] MCQUEEN R G, MARSH S P. Equation of state for nineteen metallic elements from shock‐wave measurements to two megabars [J]. Journal of Applied Physics, 1960, 31(7): 1253–1269. doi: 10.1063/1.1735815 [11] ALEKSEEV Y F, AL’TSHULER L V, KRUPNIKOVA V P. Shock compression of two-component paraffin-tungsten mixtures [J]. Journal of Applied Mechanics Technical Physics, 1971, 12(4): 624–627. [12] BATSANOV S S. Effects of explosions on materials [M]. New York: Springer, 1994. [13] MEYERS M A. Dynamic Behavior of Materials [M]. San Diego: University of California, 1994. [14] KRUEGER B R, MUTZ A H, VREELAND T. Correlation of shock initiated and thermally initiated chemical reactions in a 1∶1 atomic ratio nickel‐silicon mixture [J]. Journal of Applied Physics, 1991, 70(10): 5362–5368. doi: 10.1063/1.350217 [15] WENG J, TAN H, WANG X, et al. Optical-fiber interferometer for velocity measurements with picosecond resolution [J]. Applied Physics Letters, 2006, 89(11): 111101. doi: 10.1063/1.2335948 [16] FREDENBURG D A, KOLLER D D, RIGG P A, et al. High-fidelity Hugoniot analysis of porous materials [J]. Review of Scientific Instruments, 2013, 84(1): 013903. doi: 10.1063/1.4774394 [17] MITCHELL A C, NELLIS W J. Shock compression of aluminum, copper, and tantalum [J]. Journal of Applied Physics, 1981, 52(5): 3363–3374. doi: 10.1063/1.329160 [18] FREDENBURG D A, THADHANI N N. On the applicability of the P- $\alpha $ and P-$\lambda $ models to describe the dynamic compaction response of highly heterogeneous powder mixtures [J]. Journal of Applied Physics, 2013, 113(4): 043507. doi: 10.1063/1.4788700[19] BROWN J L, VOGLER T J, GRADY D E, et al. Dynamic compaction of sand [C]//Shock Compression of Condensed Matter-2007, 2007: 1363–1366. [20] NEEL C H. Shock compression of a heterogeneous, porous polymer composite [J]. Dissertations & Theses-Gradworks, 2010. -












 下载:
下载: