Numerical Study of the Interaction between High-Speed Gas and Elliptical Column Cloud
-
摘要: 高速颗粒流在天文、自然灾害、工业安全、医疗工业和国防等领域有着重要应用。采用基于分层流模型的直接数值模拟方法,对平面激波与椭圆柱云的相互作用进行数值研究,重点关注椭圆柱横截面的不同长短轴之比和椭圆柱横截面长轴与来流方向所成角度对流场的影响,从气体来流方向上的速度、x轴和y轴方向上的均方根速度、动能、内能和湍动能的分布上进行分析,对能量在计算域的上游区域、椭圆柱云区域和下游区域进行定量分析。同时针对椭圆柱改进了一维体积平均模型,利用该模型拟合了由直接数值模拟得到的反射激波和透射激波位置,获得了最适配的一维体积平均模型中的人工有效阻力系数,并探讨此系数的分布规律。Abstract: High-speed particle-laden flow has important applications in astronomy, natural disasters, industrial safety, medical industry, and national defense. In this work, a direct numerical simulation method based on the stratified flow model is used to study the interaction between a planar shock wave and an elliptical column cloud. The influence of the aspect ratio and the tilt angle, the distributions of the flow velocity, RMS velocities along x axis, kinetic energy, internal energy, and turbulent kinetic energy are analyzed; energy values in the upstream region, the elliptical column cloud region and the downstream region of the computational domain are quantitatively analyzed. The 1-D volume-average model is improved for elliptical columns. Based on this model, the appropriate artificial effective drag coefficients are decided by fitting the positions of the reflected shock and the transmitted shock from the direct numerical simulation results, and the distribution of the optimal artificial effective drag coefficients is also discussed.
-
Key words:
- shock wave /
- elliptical column /
- direct numerical simulation /
- 1-D volume-averaged model
-
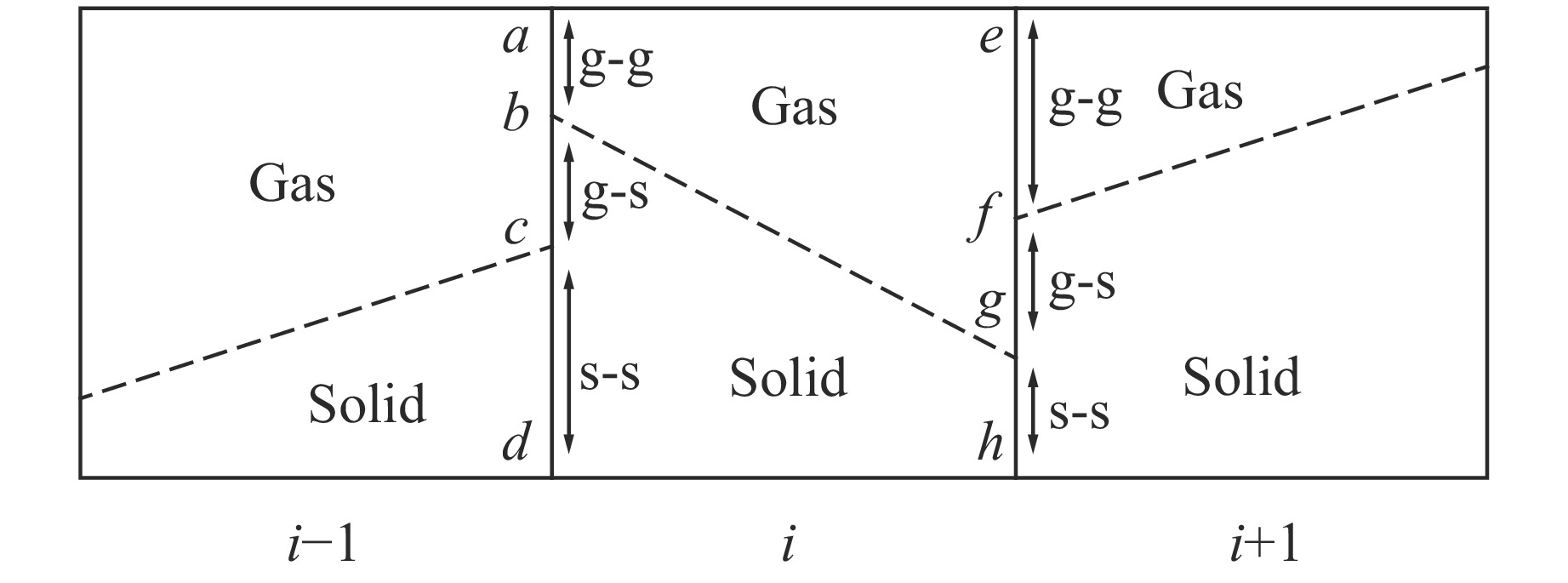
图 2 分层流模型示意图[25](i–1、i和i + 1表示网格索引号,界面
$\overline {ab} $ 和$\overline {ef} $ 为气-气界面,$\overline {bc} $ 和$\overline {fg} $ 为气-固界面,$\overline {cd} $ 和$\overline {gh} $ 为固-固界面)Figure 2. Illustration of the stratified flow model[25] (Where i –1, i and i + 1 are the indexes of the cell.
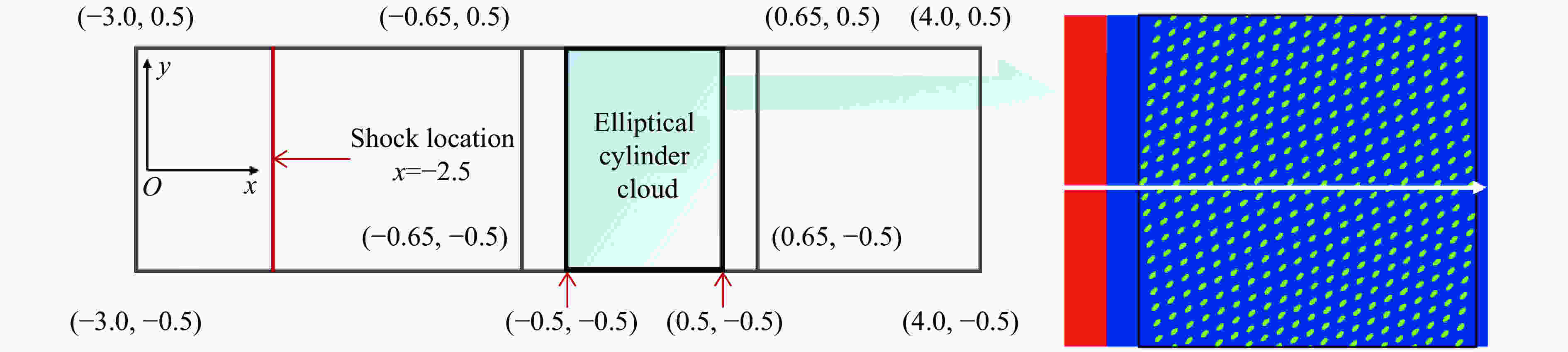
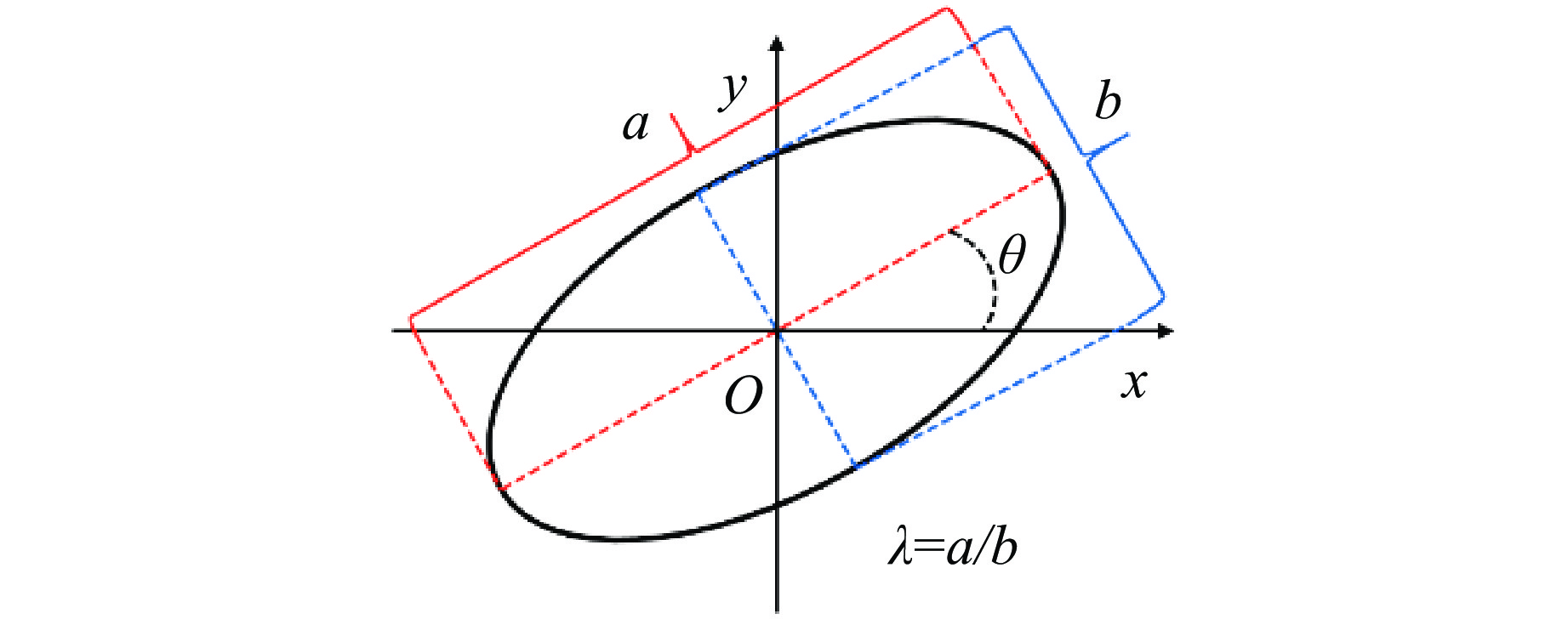
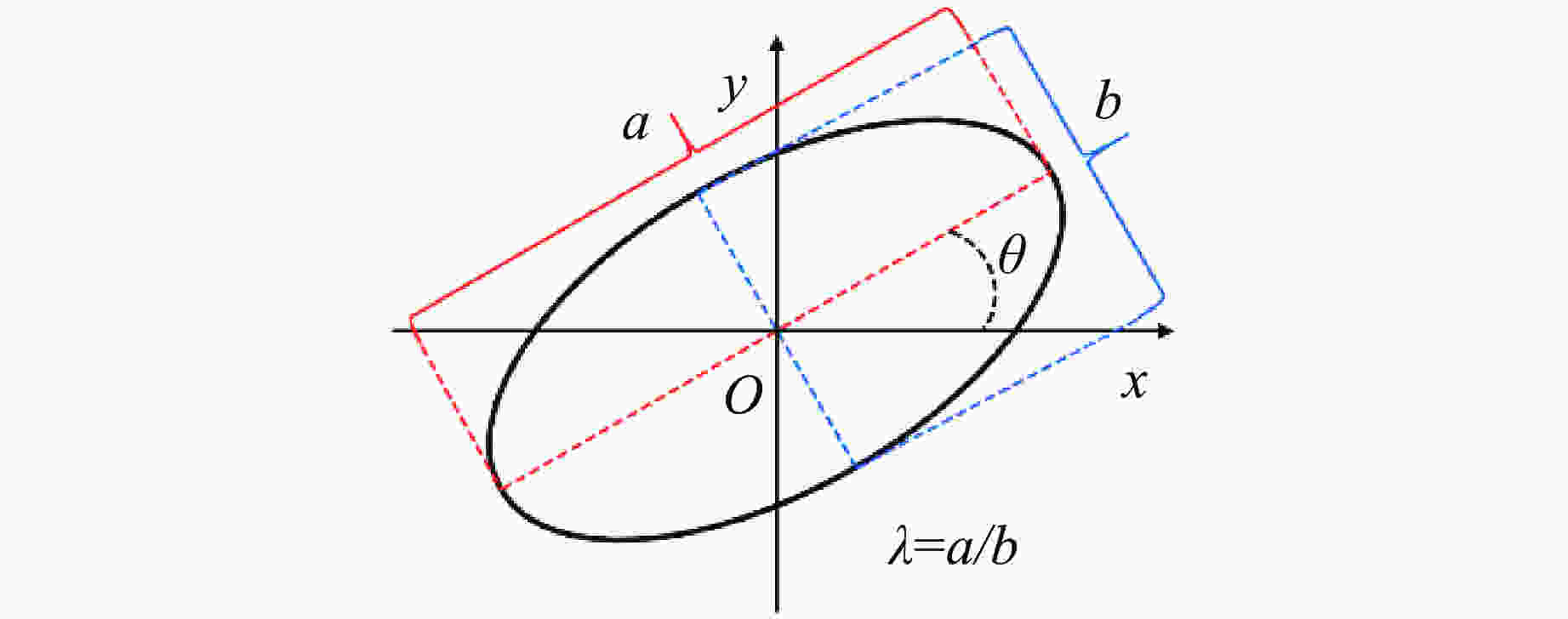
$\overline {ab} $ and$\overline {ef} $ are the interfaces between the gas phases,$\overline {bc} $ and$\overline {fg} $ are the interfaces between the gas phase and solid phase,$\overline {cd} $ and$\overline {gh} $ are the interfaces between the solid phases.)图 4 x-y平面计算区域设置示意图(右图为初始椭圆柱云分布图,蓝色表示低压区域,红色表示高压区域)
Figure 4. Illustration of the computational domain setting in the x-y plane (The right plot shows the initial distribution of the elliptical cylinder cloud. The red and blue regions represent the high-pressure and low-pressure regions, respectively.)
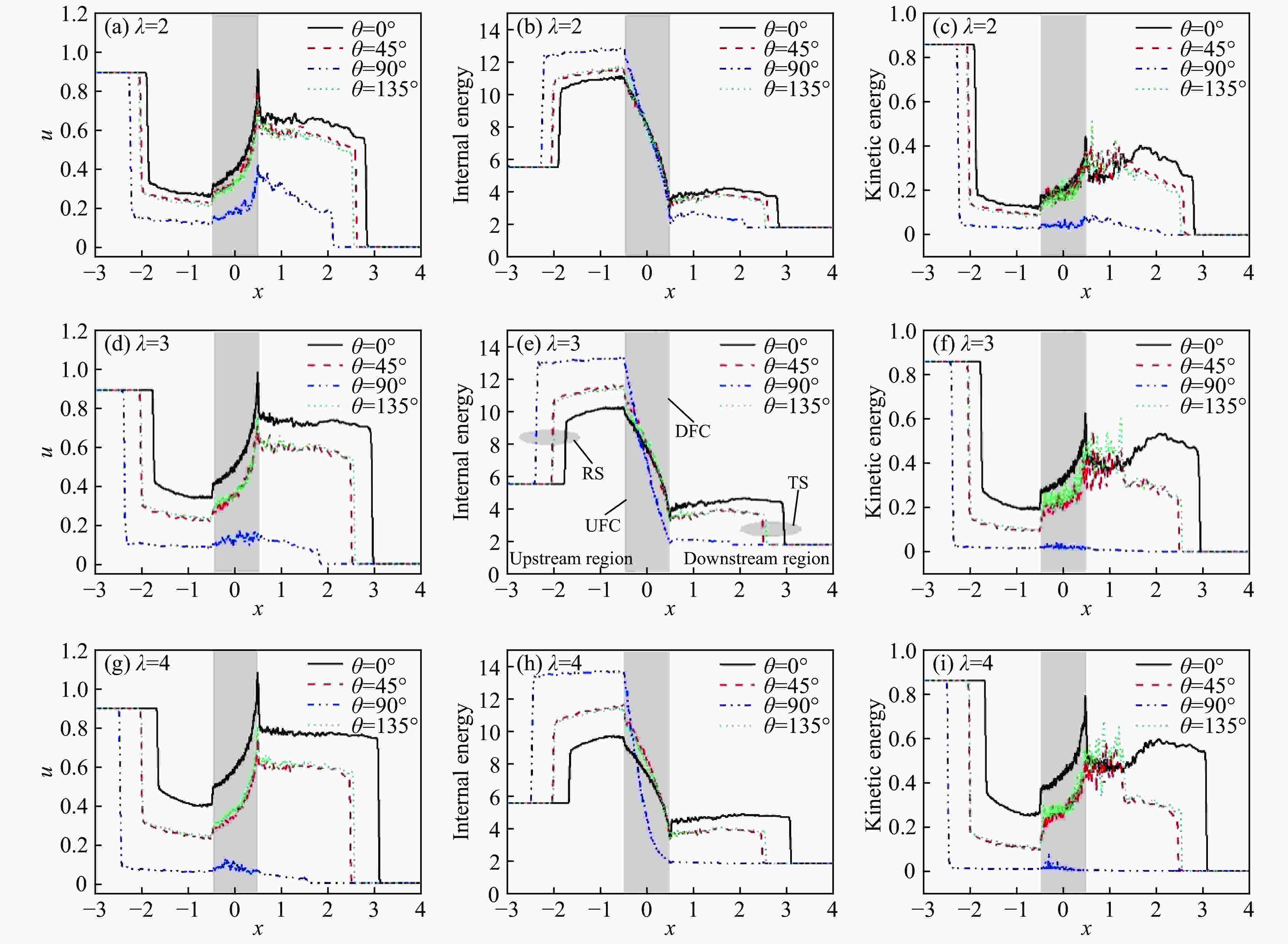
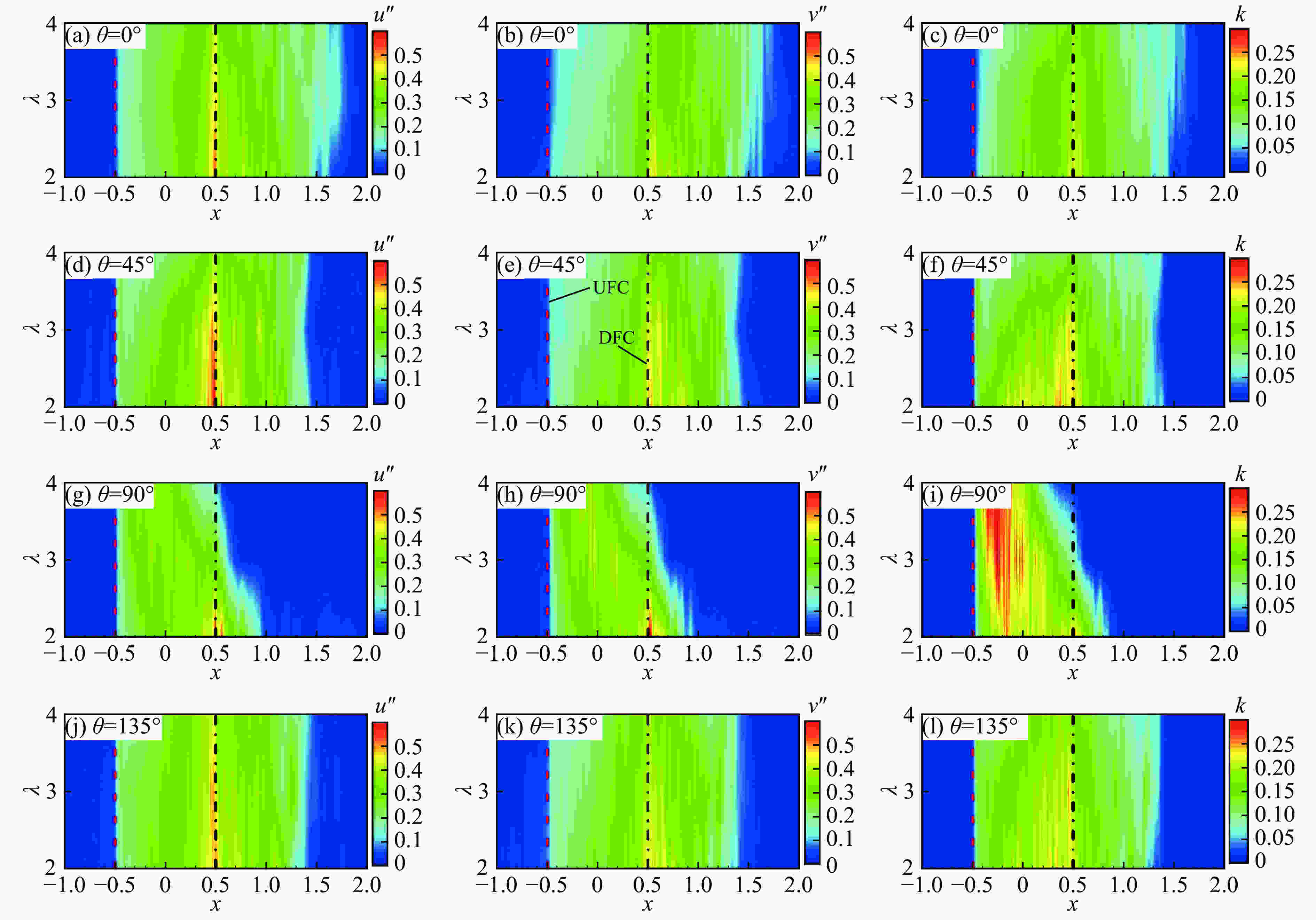
图 6 t = 3.5时不同λ下θ分别为0°、45°、90°、135°时的流场速度、流场内能和流场动能分布(灰色矩形区域表示椭圆柱云,RS、TS、UFC、DFC分别表示反射激波、透射激波、椭圆柱云上游边界、椭圆柱云下游边界)
Figure 6. Distributions of the fluid velocity, fluid internal energy and fluid kinetic energy with different λ when θ equals to 0°, 45°, 90°, 135° at dimensionless time t = 3.5 (The gray rectangular regions stand for the elliptical cylinder cloud. Hereafter, RS, TS,UFC and DFC mean reflected shock, transmitted shock, the upstream front of elliptical column cloud, and the downstream front of elliptical column cloud, respectively.)
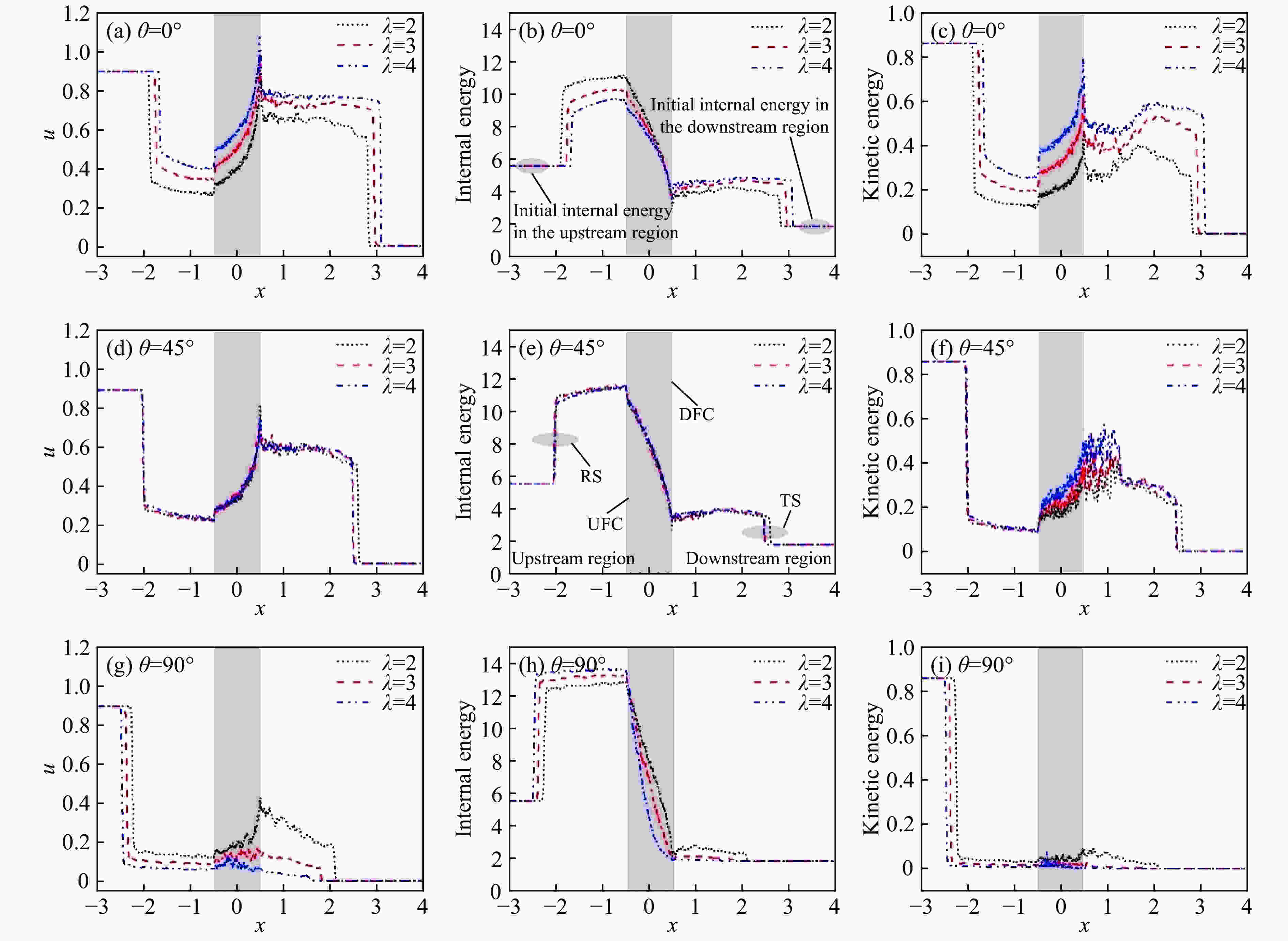
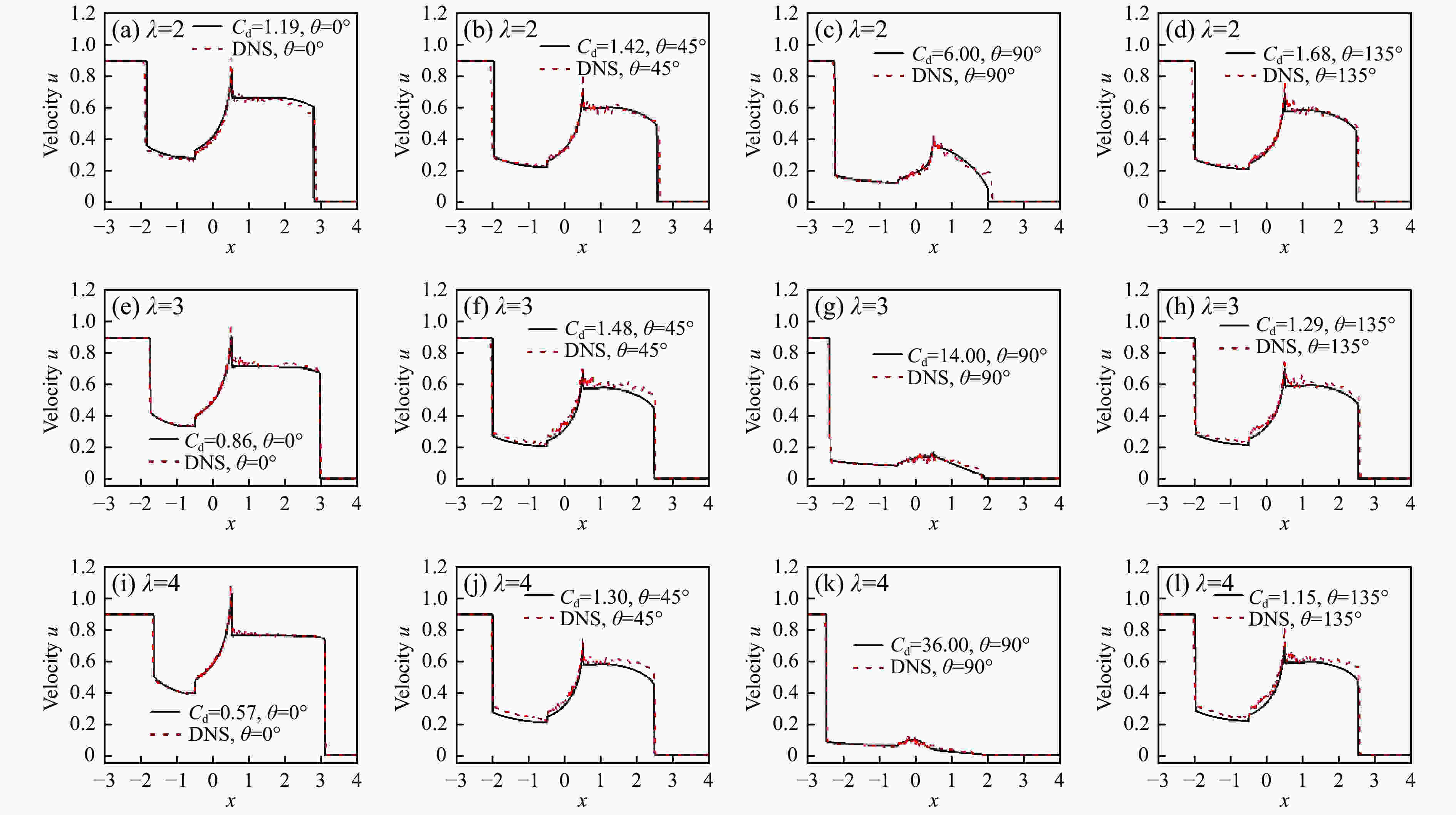
图 7 t = 3.5时不同θ下λ分别为2、3、4时,流场速度、流场内能和流场动能的分布(灰色矩形区域表示椭圆柱云)
Figure 7. Distributions of the fluid velocity, fluid internal energy and fluid kinetic energy with different θ, when λ equals to 2, 3, 4, at dimensionless time t = 3.5, where the gray rectangular regions stand for the elliptical cylinder cloud
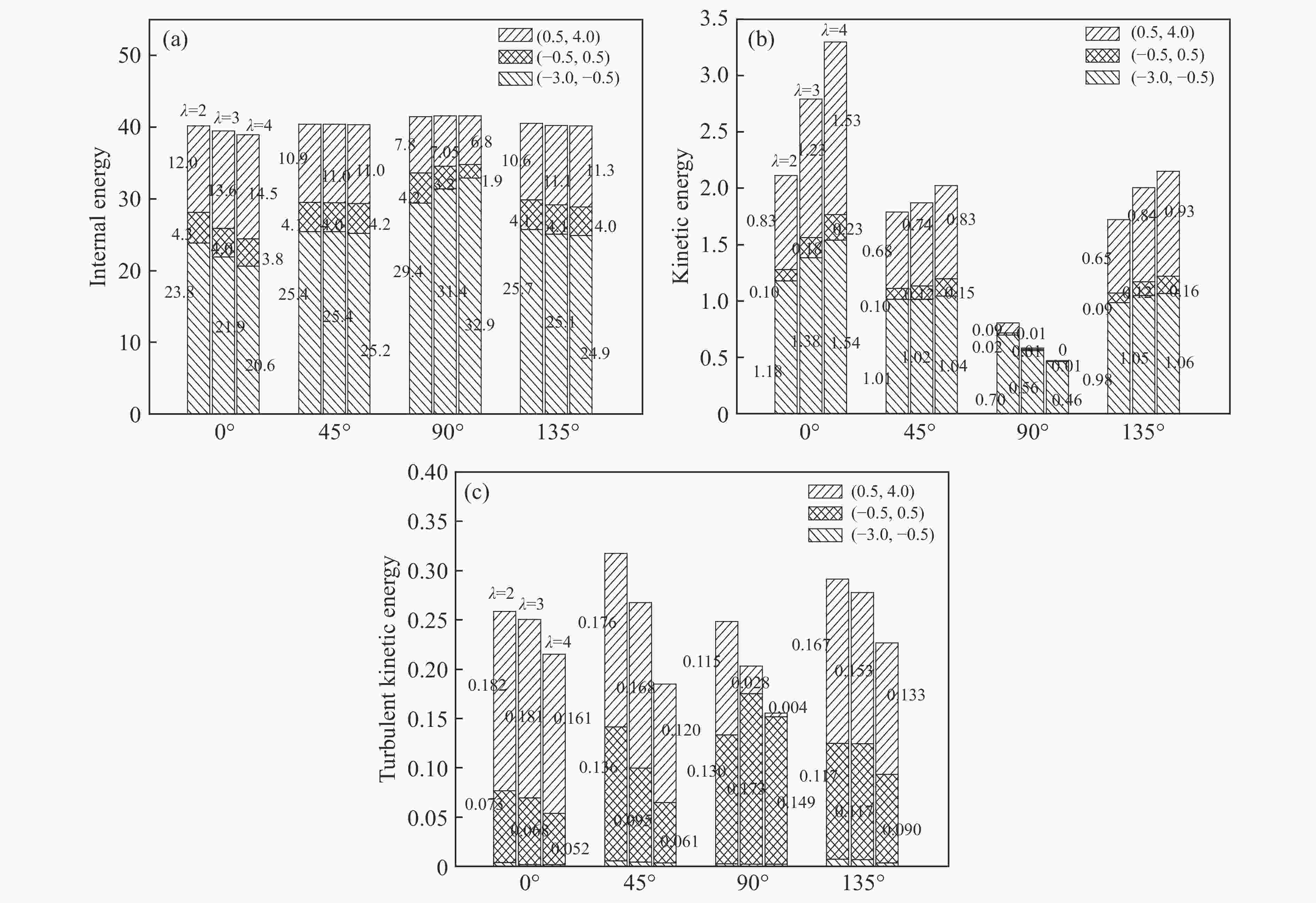
图 9 t = 3.5时不同θ和λ下流场内能、流场动能和流场湍动能在计算域上游区域(
$x \in \left[ { - 3.0, - 0.5} \right]$ )、椭圆柱云区域($x \in \left[ { - 0.5,0.5} \right]$ )和计算域下游区域($x \in \left[ {0.5, 4.0} \right]$ )分布Figure 9. Distributions of the fluid internal energy, fluid kinetic energy and fluid turbulent kinetic energy at different θ and λ in three different regions, that is the upstream area of the domain
$x \in \left[ { - 3.0, - 0.5} \right]$ , elliptical column cloud area$x \in \left[ { - 0.5,0.5} \right]$ , the downstream area of the domain$x \in \left[ {0.5, 4.0} \right]$ at dimensionless time t = 3.5表 1 网格收敛性分析实验中使用的4种网格
Table 1. Four meshes used in the convergence analysis experiment
Mesh nb Nx Ny 1 8 112 64 2 16 224 128 3 32 448 256 4 64 896 512 表 2 平面激波与椭圆柱云相互作用数值模拟使用的网格设置
Table 2. Mesh settings in numerical simulation of the interaction between plane shock and elliptical column cloud
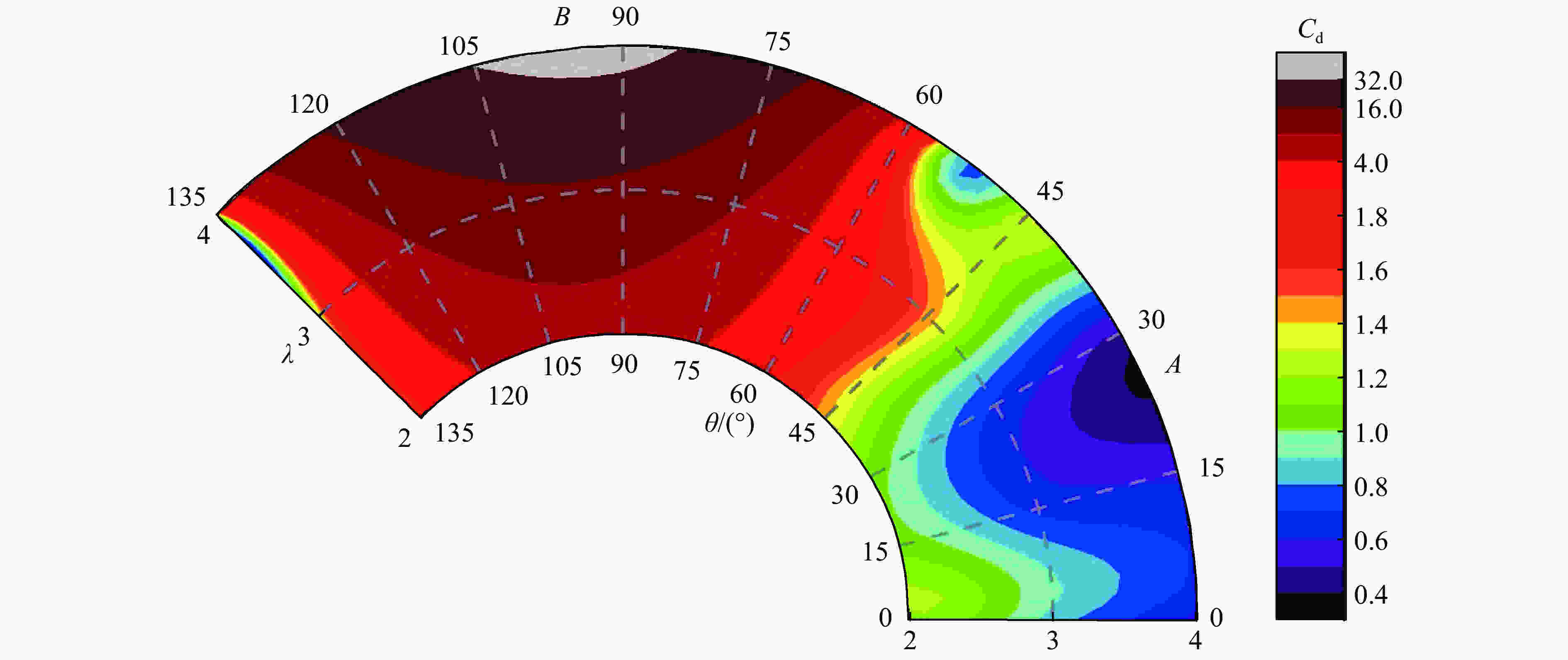
λ Np a b Δx/10–4 Nx Ny N/106 2 440 0.029 44 0.014 72 4.59 3 894 2 176 8.5 3 440 0.036 04 0.012 02 3.75 4 763 2 666 12.7 4 440 0.041 64 0.010 41 3.25 5 500 3 078 16.9 表 3 人工有效阻力系数Cd的最优取值
Table 3. Optimal values of artificial effective drag coefficient Cd
λ Cd θ = 0° θ = 15° θ = 30° θ = 45° θ = 60° θ = 90° θ = 135° 2 1.19 1.06 1.06 1.42 2.22 6.00 1.68 3 0.86 0.67 0.69 1.48 2.80 14.00 1.29 4 0.57 0.58 0.47 1.30 3.00 36.00 1.15 -
[1] 罗志全. 核心坍缩型超新星的相关物理过程及爆发机制的研究 [D]. 成都: 四川大学, 2006.LUO Z Q. Research on the physical process and explosion mechanism of core-collapse supernova [D]. Chengdu: Sichuan University, 2006. [2] CHOJNICKI K, CLARKE A B, PHILLIPS J C. A shock-tube investigation of the dynamics of gas-particle mixtures: implications for explosive volcanic eruptions [J]. Geophysical Research Letters, 2006, 33(15): 292–306. [3] 张莉聪, 徐景德, 吴兵, 等. 甲烷-煤尘爆炸波与障碍物相互作用的数值研究 [J]. 中国安全科学学报, 2004(8): 85–88.ZHANG L C, XU J D, WU B, et al. Study on numerical value of reaction between barrier and explosion wave of methane-coal dust [J]. China Safety Science Journal, 2004(8): 85–88. [4] QUINLAN N J, KENDALL M A F, BELLHOUSE B J, et al. Investigations of gas and particle dynamics in first generation needle-free drug delivery devices [J]. Shock Waves, 2001, 10(6): 395–404. doi: 10.1007/PL00004052 [5] 张晓立, 解立峰, 洪滔, 等. 激波管驱动石英砂颗粒抛洒的数值模拟 [J]. 高压物理学报, 2014, 28(1): 97–102. doi: 10.11858/gywlxb.2014.01.016ZHANG X L, XIE L F, HONG T, et al. Numerical simulation of quartz sand dispersion under shock tube loading [J]. Chinese Journal of High Pressure Physics, 2014, 28(1): 97–102. doi: 10.11858/gywlxb.2014.01.016 [6] ZHANG F, FROST D L, THIBAULT P A, et al. Explosive dispersal of solid particles [J]. Shock Waves, 2001, 10(6): 431–443. doi: 10.1007/PL00004050 [7] RUDINGER G. Fundamentals of gas-particle flow [M]. Elsevier Scientific Publishing Company, 1980. [8] REGELE J D, RABINOVITCH J, COLONIUS T, et al. Unsteady effects in dense, high speed, particle laden flows [J]. International Journal of Multiphase Flow, 2014, 61: 1–13. doi: 10.1016/j.ijmultiphaseflow.2013.12.007 [9] ZAREI Z, FROST D L, TIMOFEEV E V. Numerical modelling of the entrainment of particles in inviscid supersonic flow [J]. Shock Waves, 2011, 21(4): 341–355. doi: 10.1007/s00193-011-0311-5 [10] JACOBS G B, DON W S, DITTMANN T. High-order resolution Eulerian-Lagrangian simulations of particle dispersion in the accelerated flow behind a moving shock [J]. Theoretical and Computational Fluid Dynamics, 2012, 26(1/2/3/4): 37–50. doi: 10.1007/s00162-010-0214-6 [11] ROGUE X, RODRIGUEZ G, HAAS J F, et al. Experimental and numerical investigation of the shock-induced fluidization of a particles bed [J]. Shock Waves, 1998, 8(1): 29–45. doi: 10.1007/s001930050096 [12] WAGNER J L, BERESH S J, KEARNEY S P, et al. A multiphase shock tube for shock wave interactions with dense particle fields [J]. Experiments in Fluids, 2012, 52(6): 1507–1517. doi: 10.1007/s00348-012-1272-x [13] WAGNER J L, KEARNEY S P, BERESH S J, et al. Flash X-ray measurements on the shock-induced dispersal of a dense particle curtain [J]. Experiments in Fluids, 2015, 56(12): 213. doi: 10.1007/s00348-015-2087-3 [14] THEOFANOUS T G, MITKIN V, CHANG C H. The dynamics of dense particle clouds subjected to shock waves. Part 1. experiments and scaling laws [J]. Journal of Fluid Mechanics, 2016, 792: 658–681. doi: 10.1017/jfm.2016.97 [15] THEOFANOUS T G, CHANG C H. The dynamics of dense particle clouds subjected to shock waves. Part 2. modeling/numerical issues and the way forward [J]. International Journal of Multiphase Flow, 2017, 89: 177–206. doi: 10.1016/j.ijmultiphaseflow.2016.10.004 [16] WANG L P, ROSA B, GAO H, et al. Turbulent collision of inertial particles: point-particle based, hybrid simulations and beyond [J]. International Journal of Multiphase Flow, 2009, 35(9): 854–867. doi: 10.1016/j.ijmultiphaseflow.2009.02.012 [17] LING Y, WAGNER J L, BERESH S J, et al. Interaction of a planar shock wave with a dense particle curtain: modeling and experiments [J]. Physics of Fluids, 2012, 24(11): 113301. doi: 10.1063/1.4768815 [18] HU H H. Direct simulation of flows of solid-liquid mixtures [J]. International Journal of Multiphase Flow, 1996, 22(2): 335–352. doi: 10.1016/0301-9322(95)00068-2 [19] XIONG Q, LI B, ZHOU G, et al. Large-scale DNS of gas-solid flows on Mole-8.5 [J]. Chemical Engineering Science, 2012, 71: 422–430. doi: 10.1016/j.ces.2011.10.059 [20] PICANO F, BREUGEM W P, BRANDT L. Turbulent channel flow of dense suspensions of neutrally buoyant spheres [J]. Journal of Fluid Mechanics, 2015, 764: 463–487. doi: 10.1017/jfm.2014.704 [21] WANG S, VANELLA M, BALARAS E. A hydrodynamic stress model for simulating turbulence/particle interactions with immersed boundary methods [J]. Journal of Computational Physics, 2019, 382: 240–263. doi: 10.1016/j.jcp.2019.01.010 [22] ZHU C, YU Z, SHAO X. Interface-resolved direct numerical simulations of the interactions between neutrally buoyant spheroidal particles and turbulent channel flows [J]. Physics of Fluids, 2018, 30(11): 115103. doi: 10.1063/1.5051592 [23] ZASTAWNY M, MALLOUPPAS G, ZHAO F, et al. Derivation of drag and lift force and torque coefficients for non-spherical particles in flows [J]. International Journal of Multiphase Flow, 2012, 39: 227–239. doi: 10.1016/j.ijmultiphaseflow.2011.09.004 [24] 邹立勇, 廖深飞, 刘金宏, 等. 双椭圆界面Richtmyer-Meshkov流动中的相互干扰效应 [J]. 高压物理学报, 2015, 29(3): 191–198. doi: 10.11858/gywlxb.2015.03.005ZOU L Y, LIAO S F, LIU J H, et al. Interaction effect of two ellipse Richtmyer-Meshkov flows [J]. Chinese Journal of High Pressure Physics, 2015, 29(3): 191–198. doi: 10.11858/gywlxb.2015.03.005 [25] JIANG L J, DENG X L, TAO L. DNS study of initial-stage shock-particle curtain interaction [J]. Communications in Computational Physics, 2018, 23(4): 1202–1222. [26] STEWART H B, WENDROFF B. Two-phase flow: models and methods [J]. Journal of Computational Physics, 1984, 56(3): 363–409. doi: 10.1016/0021-9991(84)90103-7 [27] CHANG C H, LIOU M S. A robust and accurate approach to computing compressible multiphase flow: stratified flow model and AUSM(+)-up scheme [J]. Journal of Computational Physics, 2008, 227(10): 5360–5360. doi: 10.1016/j.jcp.2008.01.041 [28] DENG X, JIANG L, DING Y. Direct numerical simulation of long-term shock-particle curtain interaction [C]//2018 AIAA Aerospace Sciences Meeting. Florida: American Institute of Aeronautics and Astronautics, 2018. [29] LIOU M S. Ten years in the making-AUSM-family [C]//15th AIAA Computational Fluid Dynamics Conference, 2001: 2521. [30] LIOU MS. A sequel to AUSM, Part II: AUSM+-up for all speeds [J]. Journal of Computational Physics, 2006, 214(1): 137–170. doi: 10.1016/j.jcp.2005.09.020 -






 下载:
下载: