Energy Dissipation of Tungsten Alloys Cylindrical Rods Hypervelocity Impacting Thin Steel Target
-
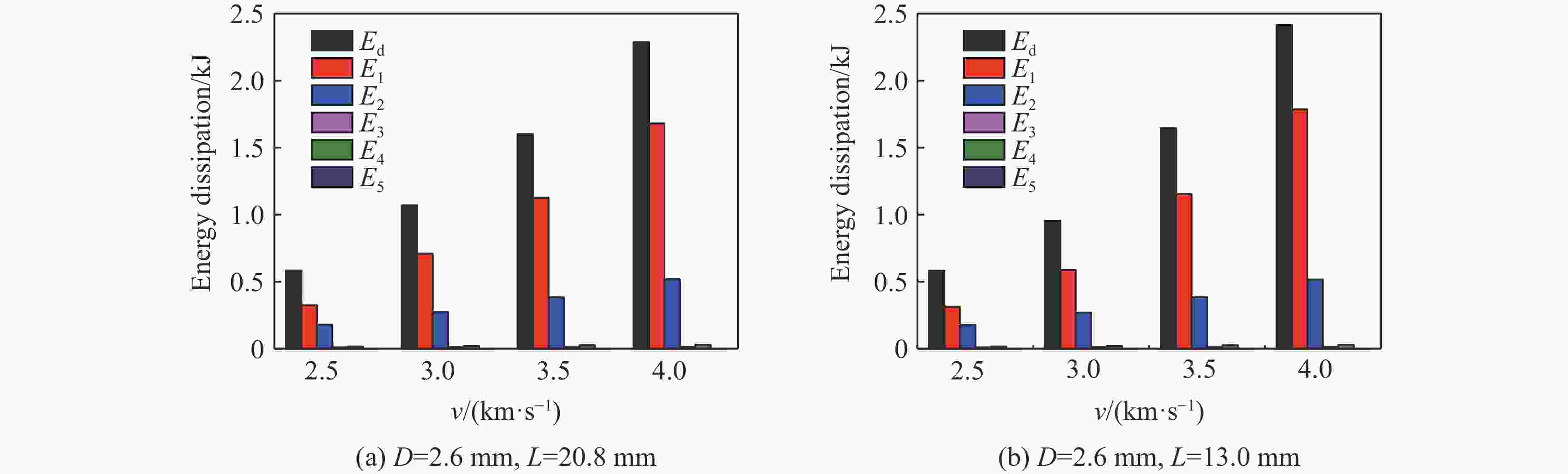
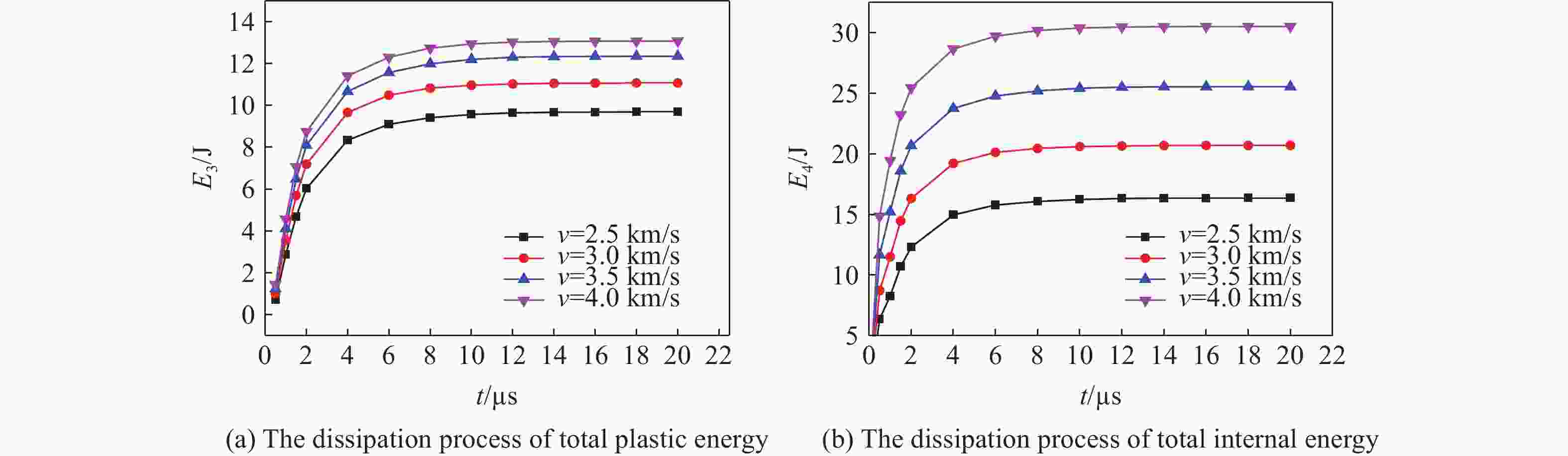
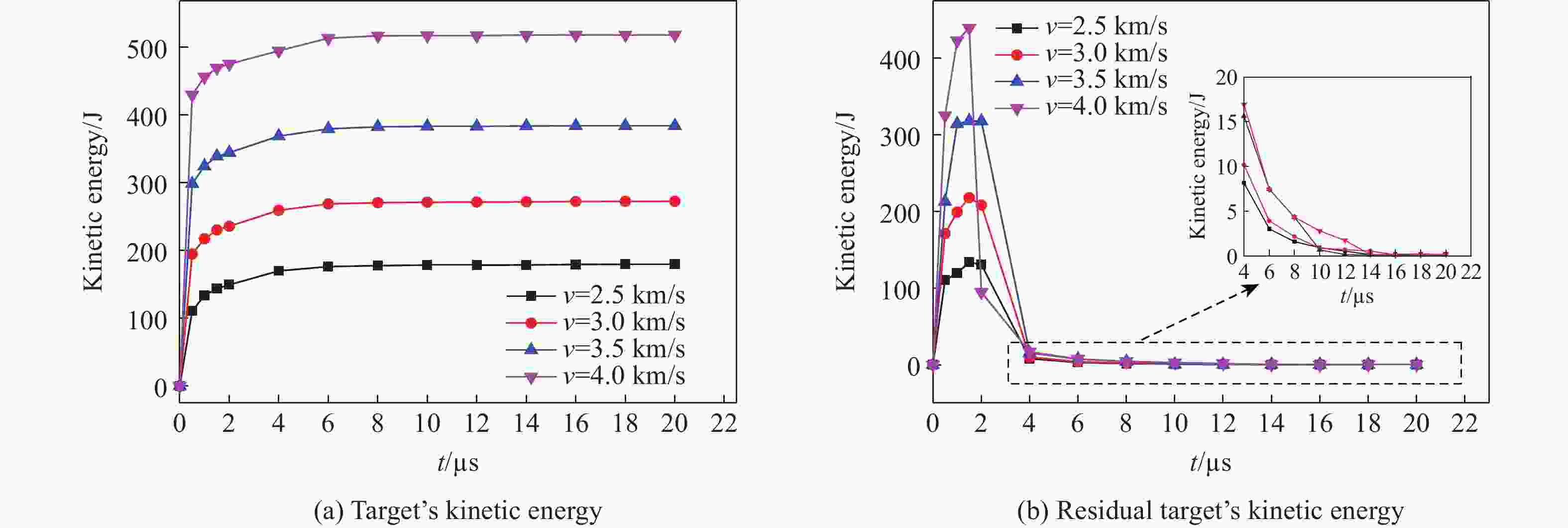
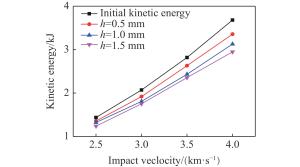
摘要: 超高速撞击过程伴随着复杂的物理过程。为分析杆式圆柱形钨合金弹超高速撞击薄钢靶时的物理过程,采用AUTODYN/SPH数值仿真计算方法获得了撞击过程模型及每个光滑粒子流体动力学信息,并通过广度搜索破片识别程序识别每个破片所含粒子,利用MATLAB编程对破片粒子数据信息进行统计分析,获得弹靶撞击过程的变化特性、弹靶破片数量、相关能量随撞击时间的变化规律。通过分析发现:随着弹体撞击速度的增加,剩余弹体被严重侵蚀,且弹体能量损耗增加,弹体损失的能量主要转变为弹靶破片动能;计算得到了撞击20
${\text{μ}}{\rm{s}}$ 时的能量损耗直方图,同时分析了发生撞击时靶板的能量变化过程,并简要描述了该过程。-
关键词:
- 超高速撞击 /
- 光滑粒子流体动力学方法 /
- 弹靶破片 /
- 能量耗散 /
- 破片识别
Abstract: The complex physical process is always accompanied with hypervelocity impact. In this paper, the physical process of rod-shaped cylindrical tungsten alloy bomb impact thin steel target has been studied. The impact process model and fluid dynamic information of every particle were obtained by means of AUTODYN/SPH method and the fragment particles were identified through range search and fragment identification program. Some information of the elastic target change process, the number of the target fragment, the change of the relative energy with the time during the impact were obtained by MATLAB. It is found that with the increase of impact speed, the residual body is eroded seriously, and the energy loss of missile body is increased, and the energy of the body loss is mainly converted into the kinetic energy of the bomb target. The energy loss histogram of the impact at the time of 20 μs and energy change process for the target plate impacted have been analyzed. -
表 1 状态方程参数
Table 1. Parameters of equation of state
Material S C0/(m·s–1) ${\varGamma}$ ${{\rho _0}/\left( {{\rm kg}\cdot {{\rm m}^{-3}}} \right)}$ Tungsten alloy 1.23 4 040 1.67 17.6 Q345 Steel 1.49 4 569 2.17 7.83 表 2 钨合金的Steinberg-Guinan强度模型参数
Table 2. Steinberg-Guinan strength model parameters of tungsten alloy
${{G_0}/{\rm GPa}}$ ${{Y_0}/{\rm GPa}}$ ${ {T_{\rm m}}/{\rm{K} } }$ ${ {G'_p} }$ ${ {G_T'}/({ {\rm{MPa} }\cdot{\rm K}^{ - 1} } })$ ${\,\beta }$ ${n}$ ${ {Y'_p} }$ 132 1.4 4 520 1.794 –40 1.3 0.1 0.019 027 表 3 Q345钢的Johnson-Cook强度模型参数
Table 3. Johnson-Cook strength model parameters of Q345 steel
${A/{\rm GPa}}$ ${B/{\rm GPa}}$ ${n}$ ${C}$ ${m}$ ${{T_{{\rm{melt}}}}/{\rm K}}$ T0/K G/GPa 0.374 0.795 7 0.454 5 0.015 86 0.885 6 1 759 300 80.47 表 4 实验与数值仿真结果
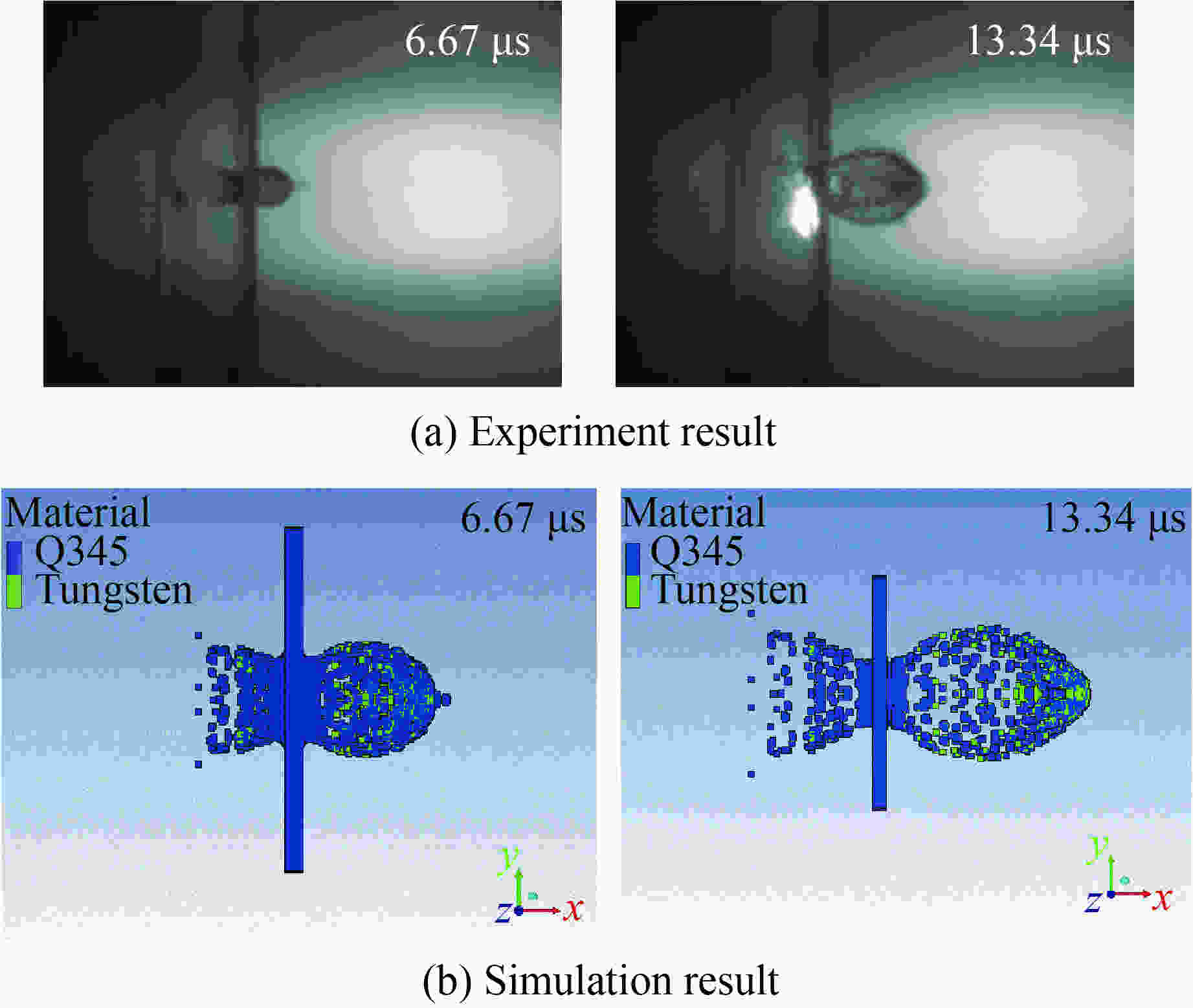
Table 4. Results of simulation and experiment
Method Residual projectile’s
kinetic energy/(km·s–1)Residual projectile’s
length/mmExperiment 2.945 12.510 Simulation 2.952 11.823 -
[1] 武强, 张庆明, 孙浩勇, 等. 超高速撞击下PTFE/Al含能材料薄板的载荷特性分析 [J]. 航天器环境工程, 2017, 34(1): 1–7. doi: 10.3969/j.issn.1673-1379.2017.01.001WU Q, ZHANG Q M, SUN H Y, et al. The loading characteristics of PTFE/Al energetic materialsunder hypervelocity impact [J]. Spacecraft Environment Engineering, 2017, 34(1): 1–7. doi: 10.3969/j.issn.1673-1379.2017.01.001 [2] 迟润强, 庞宝君, 何茂坚. 球形弹丸超高速正撞击薄板破碎状态实验研究 [J]. 爆炸与冲击, 2009, 29(3): 231–236. doi: 10.3321/j.issn:1001-1455.2009.03.002CHI R Q, PANG B J, HE M J. Experimental investigation for deformation and fragmentation of spheres penetrating sheets at hypervelocity [J]. Explosion and Shock Waves, 2009, 29(3): 231–236. doi: 10.3321/j.issn:1001-1455.2009.03.002 [3] 曲广吉, 韩增尧. 空间碎片超高速撞击动力学建模与数值仿真技术 [J]. 中国空间科学技术, 2002(5): 26–30. doi: 10.3321/j.issn:1000-758X.2002.05.005QU G J, HAN Z Y. Dynamical modeling and numerical simulation of hypervelocity space debris impact [J]. Chinese Space Science and Technology, 2002(5): 26–30. doi: 10.3321/j.issn:1000-758X.2002.05.005 [4] 张伟, 庞宝君, 贾斌, 等. 弹丸超高速撞击防护屏碎片云数值模拟 [J]. 高压物理学报, 2004, 18(1): 47–52. doi: 10.3969/j.issn.1000-5773.2004.01.009ZHANG W, PANG B J, JIA B, et al. Numerical simulation of debris cloud produced by hypervelocity impact of projectile on bumper [J]. Chinese Journal of High Pressure Physics, 2004, 18(1): 47–52. doi: 10.3969/j.issn.1000-5773.2004.01.009 [5] 童宗保, 王金相, 彭楚才. 2~3km/s初速下球形破片对金属薄靶的侵彻效应分析 [J]. 科学技术与工程, 2014, 14(33): 215–219. doi: 10.3969/j.issn.1671-1815.2014.33.040TONG Z B, WANG J X, PENG C C. Analysis of the effect of the circle fragment penetration the tine metal target with the initial velocity between 2km/s and 3km/s [J]. Science Technology and Engineering, 2014, 14(33): 215–219. doi: 10.3969/j.issn.1671-1815.2014.33.040 [6] FA W K, JIE H. Test study on the performance of shielding configuration with stuffed layer under hypervelocity impact [J]. Acta Astronautica, 2016(127): 553–560. [7] SHI C L, YI L. Research on the technique of identifying debris and obtaining characteristic parameters of large-scale 3D point set [J]. International Journal of Impact Engineering, 2013(56): 27–31. [8] 唐恩凌, 徐名扬, 张庆明. 超高速撞击厚靶过程的能量分配研究 [J]. 固体力学学报, 2016, 37(2): 152–160.TANG E L, XU M Y, ZHANG Q M. Study on partitioning of energy in hypervelocity impact on thick target [J]. Chinese Journal o f Solid Mechanics, 2016, 37(2): 152–160. [9] Thomson W T. An approximate theory of armor penetration [J]. Journal of Applied Physics, 1955, 26: 80–82. doi: 10.1016/0734-743X(95)00023-4 [10] WOODWARD R L. The penetration of metal targets by conical projectiles [J]. International Journal of Mechanical Sciences, 1978, 20: 349–359. doi: 10.1016/0020-7403(78)90038-3 [11] WIERZBICKI T. Petalling of plates under explosive and impact loading [J]. International Journal of Impact Engineering, 1999, 22: 935–954. doi: 10.1016/S0734-743X(99)00028-7 [12] WANG B, XIONG J. Energy absorption efficiency of carbon fiber reinforced polymer laminates under high velocity impact [J]. Materials and Design, 2013(50): 140–148. [13] 汪庆桃, 吴克刚, 陈志阳. 圆柱形长杆超高速正碰撞薄板结构破碎效应 [J]. 振动与冲击, 2017, 36(5): 53–60.WANG Q T, WU K G, CHEN Z Y. Fragmentation effect of a long cylindrical rod with a hypervelocity normally impacting a thin plate structure [J]. Journal of Vibration and Shock, 2017, 36(5): 53–60. [14] 汪庆桃, 吴克刚, 李必红, 等. 球形弹丸超高速碰撞破碎特性 [J]. 振动与冲击, 2014, 33(22): 46–50.WANG Q T, WU K G, LI B H, et al. Fragmentation properties of spherical projectiles impacting at hypervelocity [J]. Journal of Vibration and Shock, 2014, 33(22): 46–50. [15] 陈鸿, 周智炫, 黄洁. 带迎角钨杆斜侵彻铝板数值仿真研究 [J]. 实验流体力学, 2014, 28(2): 85–89. doi: 10.11729/syltlx2014pz29CHEN H, ZHOU Z X, HUANG J. Numerical simulation study on tungsten rod oblique penetrating aluminum plate with attack angle [J]. Journal of Experiments in Fluid Mechanics, 2014, 28(2): 85–89. doi: 10.11729/syltlx2014pz29 [16] 王芳, 李磊, 金俊. 空间碎片超高速碰撞的数值方法研究 [J]. 中国安全科学学报, 2006, 16(5): 26–30. doi: 10.3969/j.issn.1003-3033.2006.05.005WANG F, LI L, JIN J. Study on numerical simulation of hypervelocity impact of debris in outer space [J]. China Safety Science Journal, 2006, 16(5): 26–30. doi: 10.3969/j.issn.1003-3033.2006.05.005 -







 下载:
下载: